как найти через диаметр, радиус или длину окружности, формула расчета, примеры
Содержание:
-
Основные способы вычисления площади круга, формулы
- Через радиус
- Через диаметр
- Через длину окружности
- Площадь круга описанного вокруг квадрата
- Нахождение через площадь сектора круга
- Примеры задач с решением
-
Основные способы вычисления площади круга, формулы
- Через радиус
- Через диаметр
- Через длину окружности
- Площадь круга описанного вокруг квадрата
- Нахождение через площадь сектора круга
- Примеры задач с решением
Основные способы вычисления площади круга, формулы
Перед тем, как рассмотреть методы нахождения площади круга, введем основные понятия.
Круг — это участок плоскости, который расположен внутри окружности.
Окружность — это замкнутая плоская кривая, включающая множество точек, находящихся на одинаковом расстоянии от центра.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Радиус представляет собой отрезок, ограниченный с одной стороны центром круга, с другой — любой точкой, находящейся на внешней окружности данной фигуры.
Диаметром называется такой отрезок, который проходит через центр окружности и соединяет две точки рассматриваемой кривой.
Теперь разберем основные способы нахождения площади круглой фигуры.
Через радиус
Данный метод предполагает, что нам известен радиус круга, площадь которого нужно найти. Вычисления выполняются по формуле, согласно которой площадь круга равна квадрату радиуса, умноженному на число Пи. В записи указанная формула имеет вид:
\(S=\mathrm{πr}^2\)
Через диаметр
Если мы располагаем информацией о диаметре, то для расчета площади круга можно применить выражение, по которому искомая величина будет равна квадрату диаметра, умноженного на частное числа Пи и 4. 2$.
2$.
Использована формула для площади прямоугольника, однако получившаяся фигура — не совсем прямоугольник, поэтому и был написан знак приближённого равенства. При этом понятно, что если круг делить на большее количество одинаковых частей, то отличие от прямоугольника будет всё меньше и меньше. В пределе, фигура не будет отличаться от прямоугольника, а значит, такая модель не только наглядна, но и вполне законна.
Модель можно изготовить из дерева и полоски кожи. Кожу стоит подбирать отличного от дерева цвета, чтобы явно выделялась окружность в круге и длинные стороны в почти прямоугольнике. В одной из половинок круга один из секторов стоит разбить на две части — так, чтобы внешние детали были половинками стандартных секторов. Тогда получившаяся после сложения фигура будет больше походить на прямоугольник. В противном случае — на параллелограмм.
Чтобы воспользоваться формулой площади треугольника соберём круг из концентрически расположенных полосок, например, кожи. 2$.
2$.
Использована формула для площади треугольника, однако получившаяся фигура — не совсем треугольник, поэтому и был написан знак приближённого равенства. При этом понятно, что если круг делать из всё более тонких полосок, то ступеньки на боковых сторонах будут всё меньше. И в пределе, фигура не будет отличаться от треугольника, а значит, такое рассуждение вполне законно.
Другие модели раздела «Круг, окружность»
Число πВписанные углы: игра с резинкамиМатематические этюды
Площадь сектора круга Формула
Сектор – это сечение круга, ограниченное двумя его радиусами и дугой, которая их соединяет. Полукруг, который представляет собой половину круга, является наиболее часто встречающимся сектором круга. Сектор круга представляет собой сектор круга, образованный дугой и двумя ее радиусами. Сектор получается, когда участок окружности круга (также известный как дуга) и два радиуса встречаются на обоих концах дуги.
На приведенной выше диаграмме меньший сектор представляет собой часть окружности OAXB, а большой сектор — часть окружности OAYB.
Площадь сектора круга — это количество пространства, занимаемого внутри сектора границы круга. Сектор всегда начинается в центре круга. Полукруг также является сектором круга; в этом случае круг имеет два сектора одинакового размера.
Формула
A = (θ/360°) × πr 2
где
, 9 градусов, угол сектора в центре дуги0003
r — радиус окружности.
Если вытянутый угол θ выражен в радианах, площадь определяется как A = 1/2 × r 2 × θ.
Вывод
Примеры задач
Рассмотрим окружность с центром O и радиусом r, предположим, что OAPB — ее сектор, а θ (в градусах) — угол, образуемый дугами в центре.
Мы знаем, что площадь всей круглой области определяется выражением πr².
Если стягиваемый угол равен 360°, площадь сектора равна площади всего круга, то есть πr².
Применить унитарный метод, чтобы найти площадь сектора для любого угла θ.
Если стягиваемый угол равен 1°, площадь сектора определяется как πr²/360°.
Следовательно, когда угол равен θ, площадь сектора OAPB = (θ/360°) × πr 2
Отсюда выводится формула площади сектора круга.
Задача 1. Найти площадь сектора для данного круга радиусом 5 см, если угол его сектора равен 30°.
Решение:
Имеем r = 5 и θ = 30°.
Используйте формулу A = (θ/360°) × πr 2 , чтобы найти площадь.
A = (30/360) × (22/7) × 5 2
= 550/840
= 0,65 кв.см
Задача 2. Найти площадь сектора для заданного круга радиусом 9 см, если угол его сектора равен 45°.
Решение:
Имеем r = 9 и θ = 45°.
Используйте формулу A = (θ/360°) × πr 2 , чтобы найти площадь.
A = (45/360) × (22/7) × 9 2
= 1782/56
= 31,82 кв. см
Задача 3. Найти площадь сектора для заданного круга радиусом 15 см, если угол его сектора равен π/2 радиан.
Решение:
2 90. Найти угол 4. стягиваемый в центре круга, если площадь его сектора 770 кв. см, а радиус 7 см.Имеем r = 15 и θ = π/2.
Используйте формулу A = 1/2 × r 2 × θ, чтобы найти площадь.
A = 1/2 × 15 2 × π/2
= 1/2 × 225 × 11/7
= 2475/14
= 176,78 кв. см
Решение:
Имеем r = 7 и A = 770.
Используйте формулу A = (θ/360°) × πr 2 , чтобы найти значение θ.
=> 770 = (θ/360) × (22/7) × 7 2
=> 770 = (θ/360) × 154
=> θ/360 = 5
=> θ = 1800°
Задача 5. Найти площадь круга его сектор равен 132 кв. см, а угол, опирающийся на центр окружности, равен 60°.
Найти площадь круга его сектор равен 132 кв. см, а угол, опирающийся на центр окружности, равен 60°.
Решение:
Имеем θ = 60° и A = 132.
Используйте формулу A = (θ/360°) × πr 2 , чтобы найти значение θ.
=> 132 = (60/360) × (22/7) × r 92$), полученный до введения исчисления?
Область во многом является концепцией, принадлежащей Исчислению. В этом отношении найти площадь чего-либо без использования исчисления — это почти оксюморон, но мы можем иметь интуитивное (и не слишком общее) понятие площади, основанное на следующих моментах:
- Любой прямоугольник заслуживает площади (т.е. это измеримое множество) и площадь прямоугольника $R$ со сторонами $a,b,a,b$ равна $\mu(R)=ab$;
- Изометрические измеримые множества имеют одинаковую площадь, и если прямая разбивает некоторое измеримое множество $R$ на две компоненты $R_1,R_2$, то $R_1,R_2$ измеримы и $\mu(R_1)+\mu(R_2)=\ мю (R) $.
Это фиксирует площади параллелограммов, треугольников, ограниченных многоугольников; 92$ и $A\subsetneq B$ длина $\partial A$ меньше длины $\partial B$. (см. также этот вопрос)
Архимедово-подобный геометрический подход для численной аппроксимации $\pi$ заключается в следующем: окружность радиуса $1$ можно разложить как объединение восьмиугольника со стороной $\sqrt{2-\sqrt{2} }$ и восемь круговых сегментов. Такие отрезки можно аппроксимировать параболическими отрезками, площадь которых просто равна $\frac{2}{3}\text{base}\cdot\text{height}$. Параболические сегменты немного меньше соответствующих сегментов круга, поэтому следующая конструкция
ведет к нижней границе
$$\pi > \frac{16}{3}\sqrt{2-\sqrt{2}}-\frac{2}{3}\sqrt{2}= 3,13914757\ldots$$
точность которого сравнима с реальной архимедовой аппроксимацией $\pi\leq\frac{22}{7}$. Параболический метод, примененный к правильному двенадцатиугольнику, приводит к хорошей оценке
$$ \pi > 4\sqrt{6}-4\sqrt{2}-1 = 3,1411\ldots $$
что также объясняет близость между $\pi$ и $\sqrt{2}+\sqrt{3}$.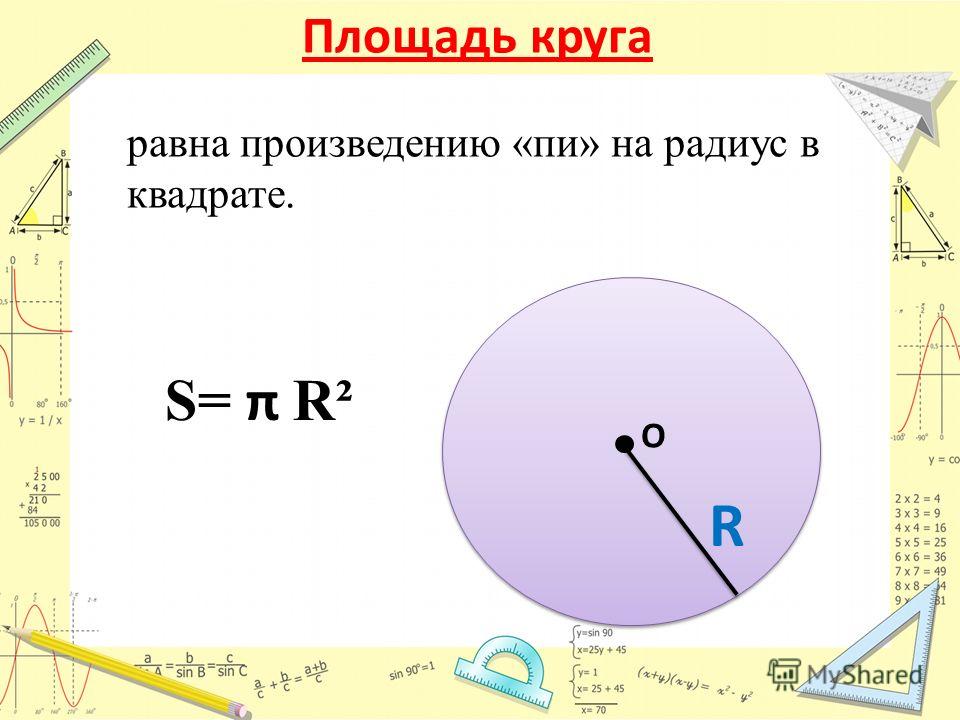



 Это фиксирует площади параллелограммов, треугольников, ограниченных многоугольников; 92$ и $A\subsetneq B$ длина $\partial A$ меньше длины $\partial B$. (см. также этот вопрос)
Это фиксирует площади параллелограммов, треугольников, ограниченных многоугольников; 92$ и $A\subsetneq B$ длина $\partial A$ меньше длины $\partial B$. (см. также этот вопрос)