Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия
Поиск по сайту:
| Справочник по математике | Геометрия (Стереометрия) | Призмы |
Введем следующие обозначения:
| V | объем призмы |
| Sбок | площадь боковой поверхности призмы |
| Sполн | площадь полной поверхности призмы |
| Sосн | площадь основания призмы |
| Pосн | периметр основания призмы |
| Pперп | периметр перпендикулярного сечения призмы |
| Sперп | площадь перпендикулярного сечения призмы |
V объем призмы |
Sбок площадь боковой поверхности призмы |
Sполн площадь полной поверхности призмы |
Sосн площадь основания призмы |
Pосн периметр основания призмы |
Pперп периметр перпендикулярного сечения призмы |
Sперп площадь перпендикулярного сечения призмы |
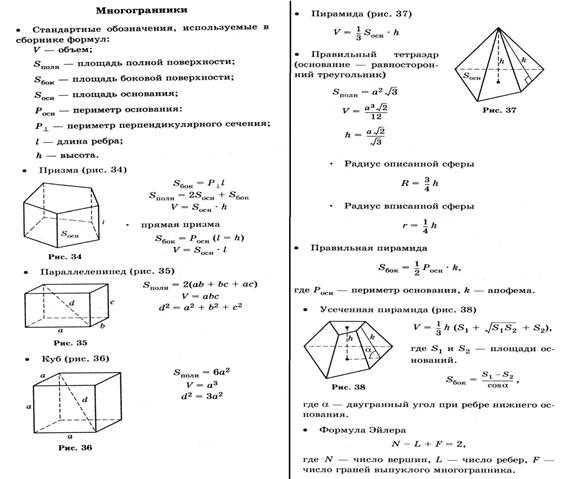
Используя эти обозначения, составим таблицу с формулами для вычисления объемов, площадей боковой поверхности и площадей полной поверхности различных видов призм.
| Призма | Рисунок | Формулы для объема, площади боковой и полной поверхности |
| Куб | V = a3, Sбок = 4a2, Sполн = 6a2, где a – длина ребра куба. | |
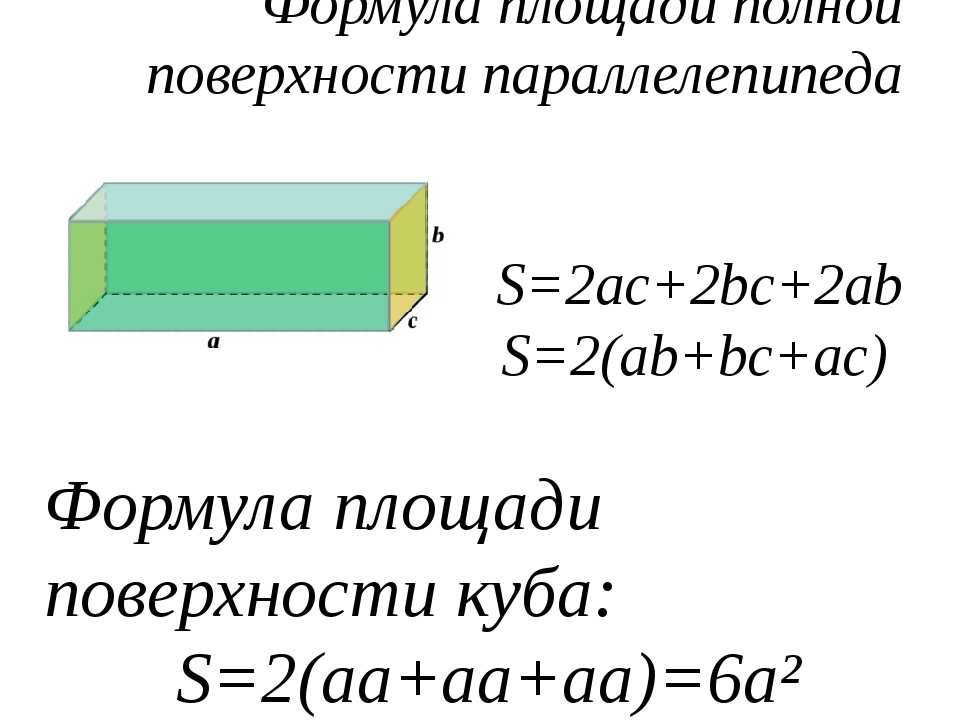
| Прямоугольный параллелепипед | V = abc, Sбок = 2ac + 2bc, Sполн = 2ac + 2bc +2ab, где | |
| Прямой параллелепипед, в основании которого лежит параллелограмм со сторонами a, b и углом φ | Sосн = ab sin φ, V = Sоснh = abh sin φ, Sбок = 2ah + 2bh, Sполн = 2ab sin φ + 2ah +2bh, где | |
| Произвольный параллелепипед | Sосн = ab sin φ, V = Sоснh = abh sin φ, V = Sперпс, Sбок = Pперпс, Sполн = 2ab sin φ + Pперпс, где | |
| Прямая призма | V = Sоснh, Sбок = Pоснh, Sполн = 2Sосн + Sбок, где | |
| Правильная n – угольная призма | (см. раздел «правильные многоугольники»), V = Sоснh, Sбок = Pоснh = anh, Sполн = 2Sосн + Sбок, где | |
| Произвольная призма | V = Sоснh, V = Sперпl, Sбок = Pперпl, Sполн = 2Sосн + Sбок, где |
| Куб |
Формулы для объема, площади боковой и полной поверхности: V = a3, Sбок = 4a2, Sполн = 6a2, где a – длина ребра куба. |
| Прямоугольный параллелепипед |
Формулы для объема, площади боковой и полной поверхности: V = abc, Sбок = 2ac + 2bc, Sполн = 2ac + 2bc +2ab, где |
| Прямой параллелепипед, в основании которого лежит параллелограмм со сторонами a, b и углом φ |
Формулы для объема, площади боковой и полной поверхности: Sосн = ab sin φ, V = Sоснh = abh sin φ, Sбок = 2ah + 2bh, Sполн = где |
| Произвольный параллелепипед |
Формулы для объема, площади боковой и полной поверхности: Sосн = ab sin φ, V = Sоснh = abh sin φ, V = Sперпс, Sбок = Pперпс, Sполн = где |
| Прямая призма |
Формулы для объема, площади боковой и полной поверхности: V = Sоснh, Sбок = Pоснh, Sполн = 2Sосн + Sбок, где |
| Правильная n – угольная призма |
Формулы для объема, площади боковой и полной поверхности: (см. раздел «правильные многоугольники»), V = Sоснh, Sбок = Pоснh = anh, Sполн = 2Sосн + Sбок, где |
| Произвольная призма |
Формулы для объема, площади боковой и полной поверхности: V = Sоснh, V = Sперпl, Sбок = Pперпl, Sполн = 2Sосн + Sбок, где |
Замечание 1. С понятием призмы и различными видами призм можно ознакомиться в разделе «Призмы».
Замечание 2. С определением сечения призмы и способами построения сечений призмы можно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Как найти площадь поверхности вращения с помощью интеграла
- Вычисление площади поверхности вращения, заданной в прямоугольных координатах
- Вычисление площади поверхности вращения, заданной параметрически
- Вычисление площади поверхности вращения, заданной в полярных координатах
Прежде чем перейти к формулам площади поверхности вращения, дадим краткую формулировку самой
поверхности вращения.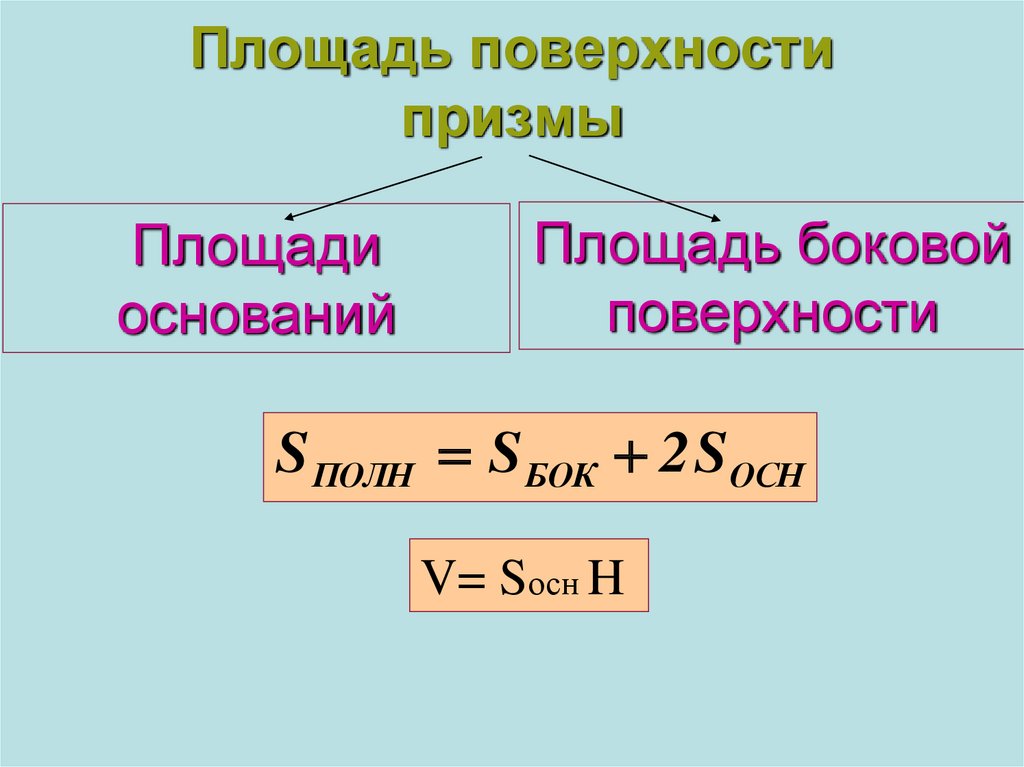 Поверхность вращения, или, что то же самое — поверхность тела вращения — пространственная
фигура, образованная вращением отрезка AB кривой вокруг оси Ox (рисунок ниже).
Поверхность вращения, или, что то же самое — поверхность тела вращения — пространственная
фигура, образованная вращением отрезка AB кривой вокруг оси Ox (рисунок ниже).
Представим себе криволинейную трапецию, ограниченную сверху упомянутым отрезком кривой.
Тело, образованное вращением этой трапеции вокруг то же оси Ox, и есть тело вращения. А площадь
поверхности вращения или поверхности тела вращения — это его внешняя оболочка, не считая кругов,
образованных вращением вокруг оси прямых
Заметим, что тело вращения и соответственно его поверхность могут быть образованы также вращением фигуры не вокруг оси Ox, а вокруг оси Oy.
Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая, вращением которой вокруг координатной оси образовано тело вращения.
Формула для вычисления площади поверхности вращения следующая:
(1).
Пример 1. Найти площадь поверхности параболоида, образованную вращением вокруг оси Ox дуги параболы , соответствующей изменению x от x = 0 до x = a.
Решение. Выразим явно функцию, которая задаёт дугу параболы:
Найдём производную этой функции:
Прежде чем воспользоваться формулу для нахождения площади поверхности вращения, напишем ту часть её подынтегрального выражения, которая представляет собой корень и подставим туда найденную только что производную:
Далее по формуле (1) находим:
Ответ: длина дуги кривой равна
.
Пример 2. Найти площадь поверхности, образуемой вращением вокруг оси Ox астроиды .
Решение. Достаточно вычислить площадь поверхности, получающейся от вращения
одной ветви астроиды, расположенной в первой четверти, и умножить её на 2.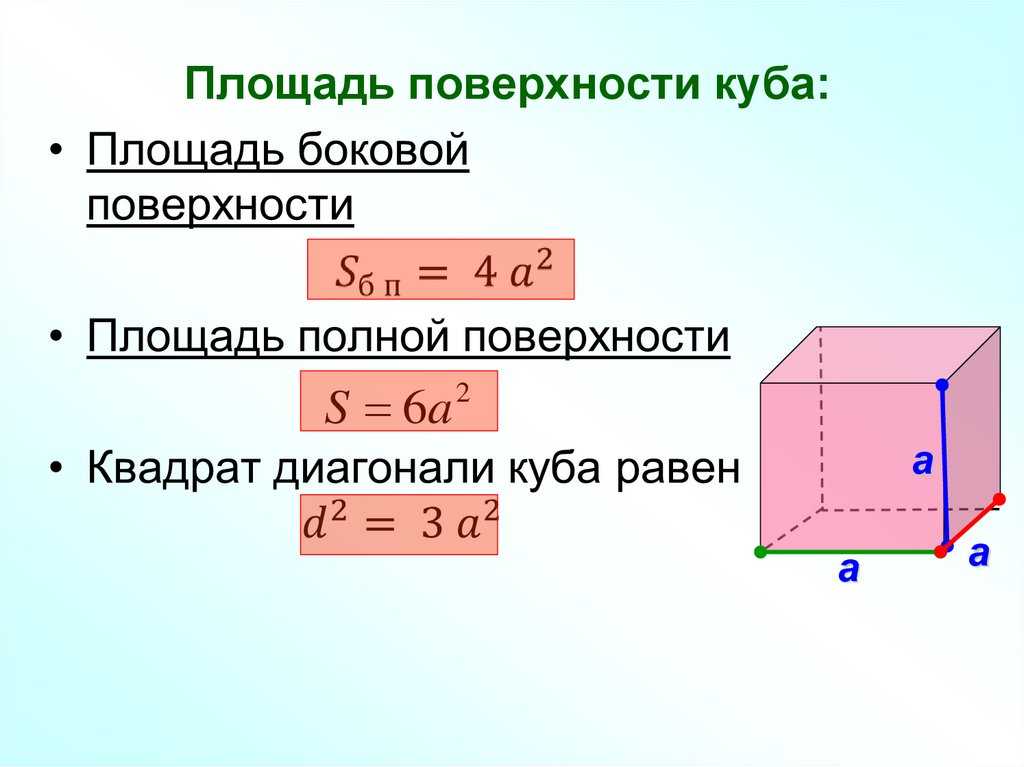 Из уравнения астроиды
выразим явно функцию, которую нам нужно будет подставить в формулу для нахождения площади повержности
вращения:
Из уравнения астроиды
выразим явно функцию, которую нам нужно будет подставить в формулу для нахождения площади повержности
вращения:
.
Производим интегрирование от 0 до a:
Ответ: площадь поверхности вращения равна .
Рассмотрим случай, когда кривая, образующая поверхность вращения, задана параметрическими уравнениями
Тогда площадь поверхности вращения вычисляется по формуле
(2).
Пример 3. Найти площадь поверхности вращения, образованной вращением вокруг оси Oy фигуры, ограниченной циклоидой и прямой y = a. Циклоида задана параметрическими уравнениями
Решение. Найдём точки пересечения циклоиды и прямой. Приравнивая уравнение циклоиды и уравнение прямой y = a, найдём
Из этого следует, что границы интегрирования соответствуютТеперь можем применить формулу (2).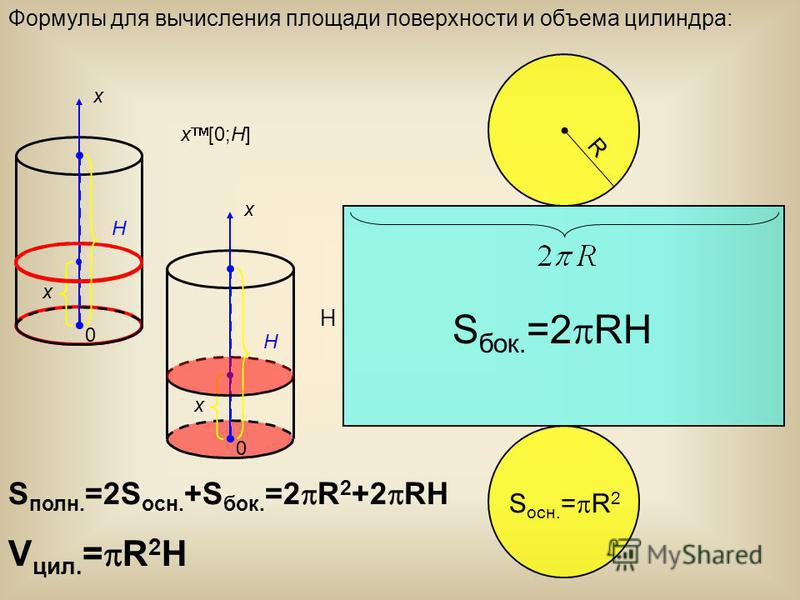 Найдём производные:
Найдём производные:
Запишем подкоренное выражение в формуле, подставляя найденные производные:
Найдём корень из этого выражения:
.
Подставим найденное в формулу (2):
.
Произведём подстановку:
И, наконец, находим
В преобразовании выражений были использованы тригонометрические формулы
Ответ: площадь поверхности вращения равна .
Нет времени вникать в решение? Можно заказать работу!
Пусть кривая, вращением которой образована поверхность, задана в полярных координатах:
Площадь поверхности вращения вычисляется по формуле:
(3).
Пример 4. Найти площадь поверхности, образованной вращением
лемнискаты
вокруг полярной оси.
Решение. Действительные значения для ρ получаются при , то есть при (правая ветвь лемнискаты) или при (левая ветвь лемнискаты).
Решение. Дифференциал корня из формулы площади поверхности вращения равен:
В свою очередь произведение функции, которой задана лемниската, на синус угла равно
.
Поэтому площадь поверхности вращения найдём следующим образом:
.
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Интеграл
Начало темы «Интеграл»
Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов
Найти неопределённый интеграл: начала начал, примеры решений
Метод замены переменной в неопределённом интеграле
Интегрирование подведением под знак дифференциала
Метод интегрирования по частям
Интегрирование дробей
Интегрирование рациональных функций и метод неопределённых коэффициентов
Интегрирование некоторых иррациональных функций
Интегрирование тригонометрических функций
Определённый интеграл
Площадь плоской фигуры с помощью интеграла
Определение работы силы с помощью интеграла
Несобственные интегралы
Вычисление двойных интегралов
Что такое формула площади поверхности? – Обзоры Вики
Площадь поверхности — это сумма площадей всех граней (или поверхностей) 3D-фигуры.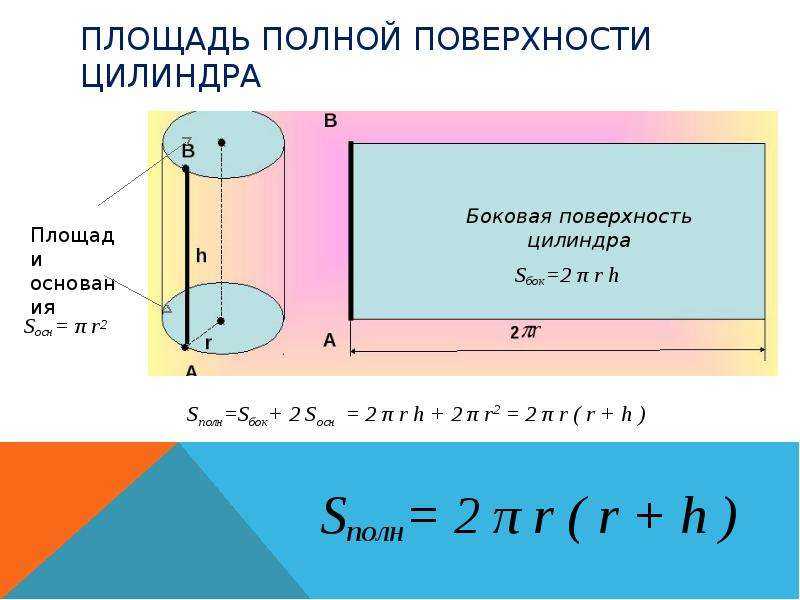 … Мы также можем обозначить длину (l), ширину (w) и высоту (h) призмы и использовать формулу SA = 2lw + 2lh + 2hw, чтобы найти площадь поверхности.
… Мы также можем обозначить длину (l), ширину (w) и высоту (h) призмы и использовать формулу SA = 2lw + 2lh + 2hw, чтобы найти площадь поверхности.
Из этого следует, как рассчитать объем цилиндра? Объем цилиндра
- V = А ч.
- Поскольку площадь круга = π r 2, формула для объема цилиндра имеет следующий вид:
- V = π р 2 ч.
Почему вы считаете площадь поверхности? Площадь поверхности важна в химической кинетике. Увеличение площади поверхности вещества обычно увеличивает скорость химической реакции.. Например, железо в мелком порошке воспламеняется, в то время как в твердых блоках оно достаточно стабильно для использования в конструкциях.
Как найти поверхность? Площадь поверхности – это площадь всех внешних обращенных поверхностей на объекте. Общая площадь поверхности рассчитывается по формуле добавление всех областей на поверхность: площади основания, верхней и боковой поверхностей (боков) объекта. Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Это делается с использованием различных формул площади и измеряется в квадратных единицах.
Как рассчитать объем в литрах?
Первое, что вам нужно сделать, это умножить длину на ширину на высоту. Это дает количество кубических миллиметров. Чтобы рассчитать количество литров, затем делите это число на миллион.
Как вы рассчитываете объем? В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема: длина × ширина × высота.
Как найти площадь поверхности половины цилиндра? Какова формула площади поверхности полуцилиндра? Общая формула общей площади поверхности полуцилиндра имеет вид: Общая площадь поверхности полуцилиндр = πrh + πr2 + 2рх, где «r» — радиус, а «h» — высота цилиндра.
Какая форма цилиндра?
Цилиндр трехмерная форма, состоящая из двух параллельных круглых оснований, соединенных изогнутой поверхностью. Центры круглых оснований накладываются друг на друга, образуя правильный цилиндр. Отрезок, соединяющий два центра, является осью, обозначающей высоту цилиндра.
Отрезок, соединяющий два центра, является осью, обозначающей высоту цилиндра.
Также Как найти боковую поверхность и площадь поверхности цилиндра? Эту площадь боковой поверхности можно рассчитать по формуле умножение периметра основания на высоту призмы. Для прямого кругового цилиндра радиуса r и высоты h боковая площадь равна площади боковой поверхности цилиндра: A = 2πrh.
Какова формула площади поверхности круга?
Площадь круга равна пи, умноженному на квадрат радиуса. (А = πr²).
По какой формуле рассчитать объем? В то время как основная формула площади прямоугольной формы – длина × ширина, основная формула объема – длина × ширина × высота.
Как рассчитать объем воды в баллоне?
Как посчитать галлоны в цилиндре?
Цилиндр имеет объем, который определяется его высотой и радиусом.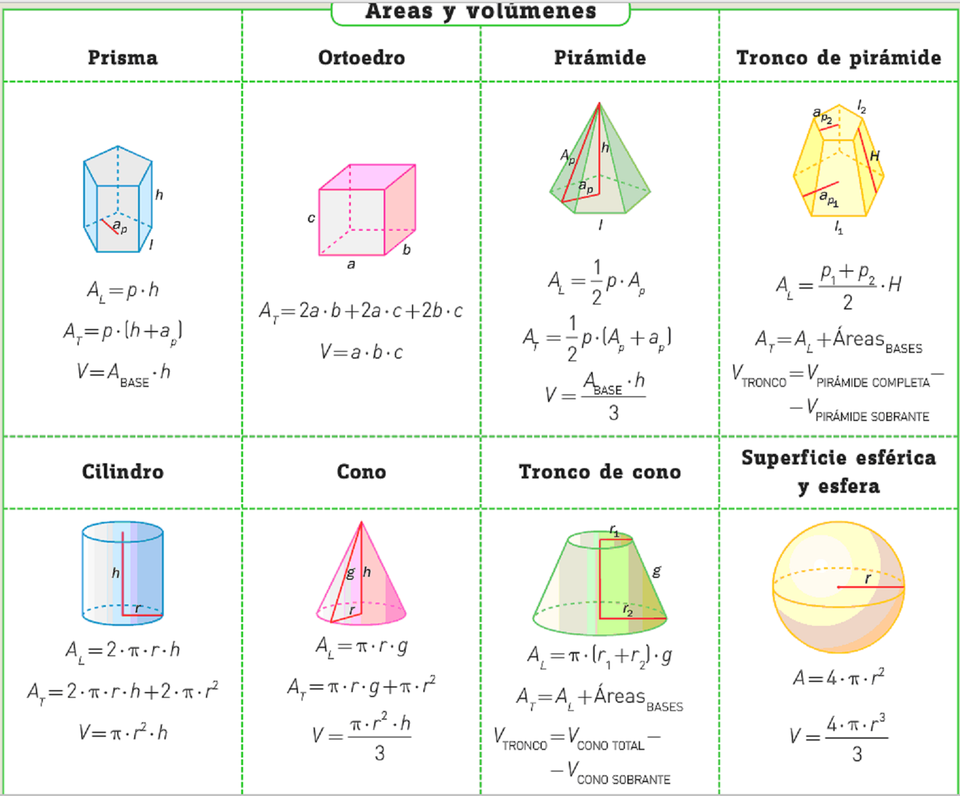 Рассчитать объем цилиндра в галлонах можно по следующей формуле: V = πr2h, где r — радиус, h — высота.
Рассчитать объем цилиндра в галлонах можно по следующей формуле: V = πr2h, где r — радиус, h — высота.
Как рассчитать объем цилиндрического резервуара для воды в литрах? V (резервуар) = πr2l
Вычислите заполненный объем горизонтального цилиндрического резервуара, сначала найдя площадь A круглого сегмента и умножив ее на длину l. Площадь круглого сегмента, заштрихованная серым цветом, равна A = (1/2) r.2(θ — sinθ), где θ = 2 * arccos (m / r) и θ в радианах.
Как найти кубические футы цилиндра? Объем цилиндра в кубических футах равен π умножить на радиус в футах в квадрате на высоту в футах.
Как вы рассчитываете объем и площадь поверхности?
Он дает долю площади поверхности на единицу объема объекта (например, сферы, цилиндра и т. Д.). Следовательно, формула для расчета отношения площади поверхности к объему следующая: SA / VOL = площадь поверхности (x2) / объем (x3) SA / VOL = x–1 , где x — единица измерения.
Почему формула объема цилиндра? Объем цилиндра — это плотность цилиндра, которая означает количество материала, которое он может нести, или количество любого материала, которое может быть погружено в него. Объем цилиндра определяется по формуле, πr2h, где r — радиус круглого основания, h — высота цилиндра.
Как найти площадь поверхности 1/4 цилиндра?
Каковы 3 измерения цилиндра? Цилиндр — это трехмерная фигура, имеющая две круглые грани, одну вверху и одну внизу. одна изогнутая поверхность. Цилиндр имеет высоту и радиус. Высота цилиндра — это перпендикулярное расстояние между верхней и нижней гранями.
Что такое примеры цилиндрической формы?
Цилиндр можно определить как твердую геометрическую фигуру с прямыми параллельными сторонами и круглым или овальным поперечным сечением.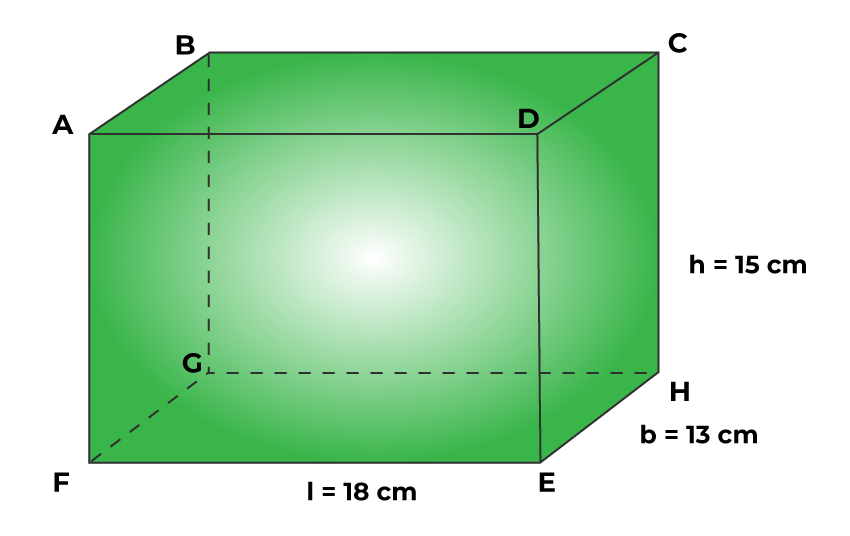 Примеры: Производство труб . Банки для холодных напитков.
Примеры: Производство труб . Банки для холодных напитков.
Пример цилиндра? Цилиндр — это трехмерная твердая фигура, имеющая два одинаковых круглых основания, соединенных криволинейной поверхностью на определенном расстоянии от центра, равном высоте цилиндра. Рулоны туалетной бумаги, банки для прохладительных напитков представляют собой реальные примеры цилиндров.
Площади фигур (плоских и объемных)
Сначала мы рассмотрим площади плоских фигур.
Слышал ты что-нибудь про формулу Пика? Когда ее можно применять, а когда нельзя?
Сколько ты знаешь способов нахождения площади фигур на клетчатой бумаге? А их на самом деле три! И хотя задачу по нахождению площади фигур на клетчатой бумаге убрали из ЕГЭ, сам навык очень полезен для понимания планиметрии!
Во второй части мы рассмотрим как находить площади объемных фигур (призмы и пирамиды)
ПЛОЩАДИ ПЛОСКИХ ФИГУР
Способы нахождения площади фигур на клетчатой бумаге:
Способ 1.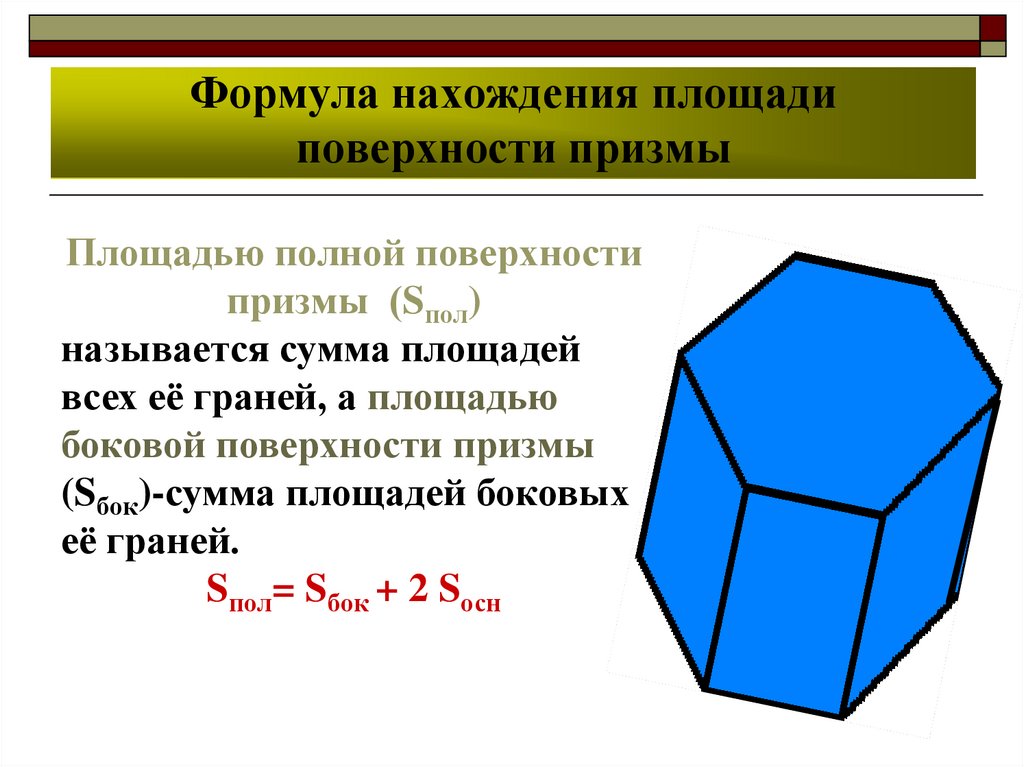
Удобен для стандартных фигур: треугольника, трапеции и т.д.
- Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
- Подставить найденные значения в уравнение площади.
Способ 2. Дострой до прямоугольника и вычти лишнее
Очень удобен для сложных фигур, но и для простых неплох
- Достроить искомую фигуру до прямоугольника;
- Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
- Из площади прямоугольника вычесть сумму площадей всех лишних фигур.
Способ 3. Формула Пика
Работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
- Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.
Подсчитаем, сколько узлов попадает в нашу фигуру.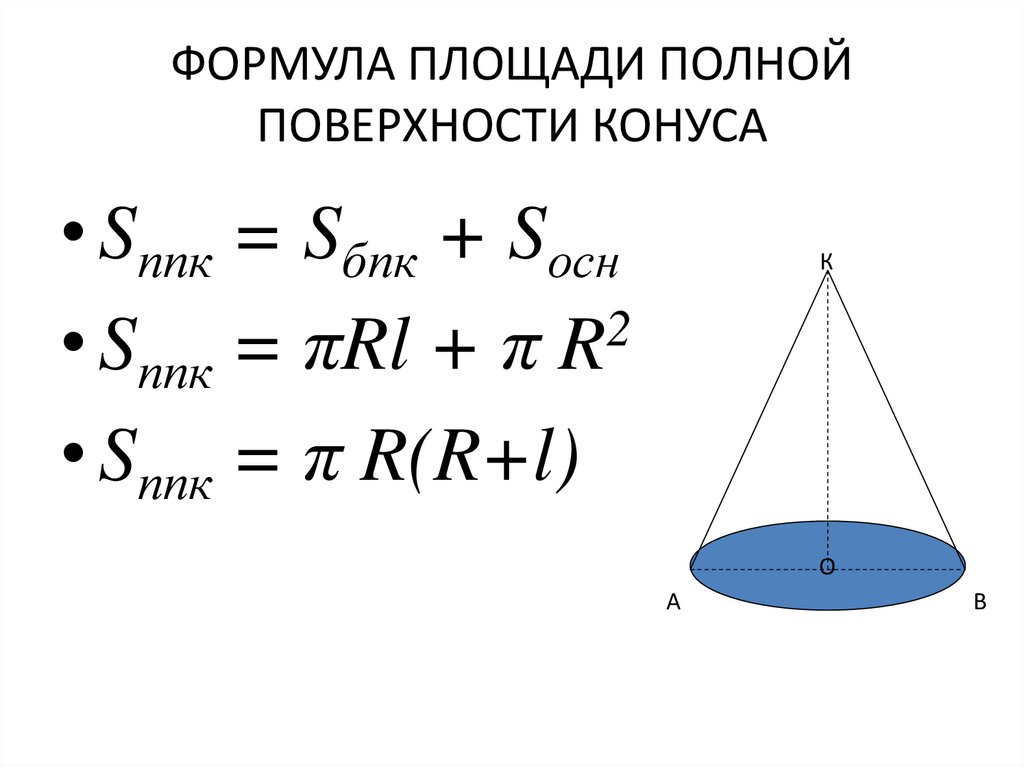 Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
В примере на рисунке получилось \( Г = 22\) на границе и \( В = 32\) внутри.
Формула Пика. Делим границу пополам, прибавляем внутренности и вычитаем 1:\( S = Г/2 + В – 1 \)
В примере на рисунке:
\( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.\)
Способ 1. Считай клетки и применяй формулыУдобен для стандартных фигур: треугольника, трапеции и т.д.
- Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
- Подставить найденные значения в уравнение площади.
Пусть нужно найти площадь трапеции, построенной на листе в клетку.
Просто считаем клеточки и видим, что в нашем случае \( \displaystyle a=17\), \( \displaystyle b=6\) и \( \displaystyle h=6\).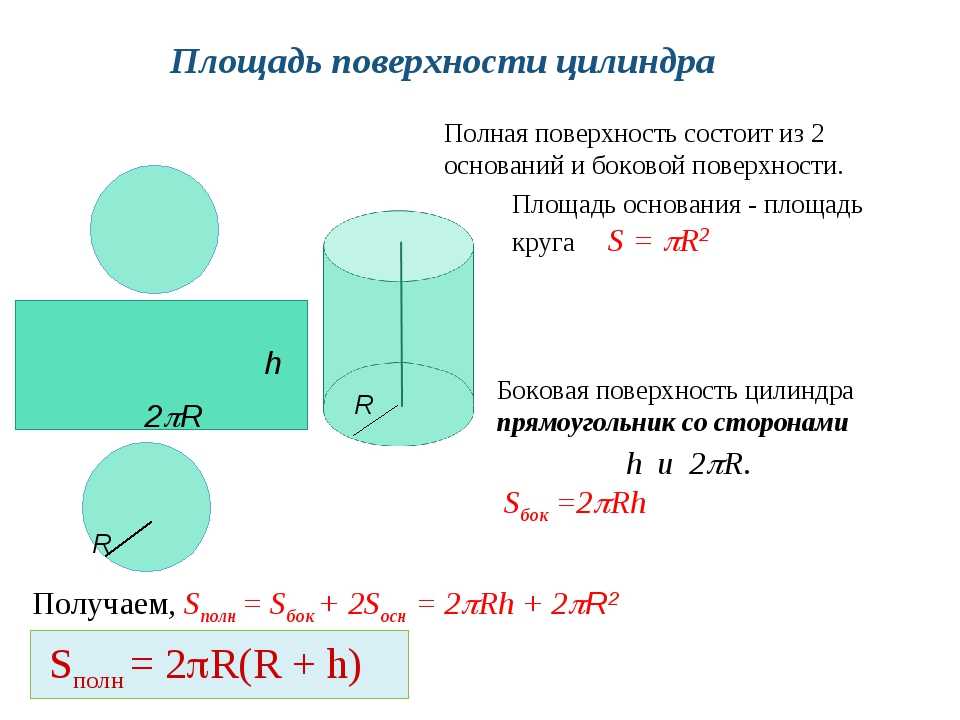 {2}}=13\).
{2}}=13\).
\( \displaystyle b=\sqrt{13}\)
Подставляем в формулу:
\( \displaystyle S=\frac{1}{2}\cdot ab=\frac{1}{2}\cdot 2\sqrt{13}\cdot \sqrt{13}=13\).
Способ 2. Дострой до прямоугольника и вычти лишнееОчень удобен для сложных фигур, но и для простых неплох
- Достроить искомую фигуру до прямоугольника;
- Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
- Из площади прямоугольника вычесть сумму площадей всех лишних фигур.
Давай посчитаем площадь того же треугольника вторым способом.
Нужно окружить нашу фигуру прямоугольником. Вот так:
Получился один (нужный) треугольник внутри и целых три ненужных треугольника снаружи. Но зато площади этих ненужных треугольников легко считаются на листе в клетку!
Вот мы их посчитаем, а потом просто вычтем из целого прямоугольника:
\( \displaystyle {{S}_{прямоугольника}}=6\cdot 7=42\)
\( \displaystyle {{S}_{1}}=\frac{1}{2}\cdot 6\cdot 4=12\)
\( \displaystyle {{S}_{2}}=\frac{1}{2}\cdot 7\cdot 4=14\)
\( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 3\cdot 2=3\)
\( \displaystyle \Rightarrow S=42-12-14-3=13\)
Почему бы просто не считать клеточки?
Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать.
Вот, например, трапеция:
Посчитаем клеточки: их всего 46, верно?
Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе \( 36+\frac{10}{2} = 41\)
Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…
Как всё это учитывать?
Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.
А жёлтые сколько занимают? Постарайтесь ответить сами.
Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.
Итак, 2 жёлтых куска = 1 клетка.
Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.
Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это \( 36+\frac{6}{2}=39\) клетки.
Итого клеток: \( 1 + 2 + 39 = 42\).
Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.
Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).
Способ 3. Формула ПикаСуществует довольно удобная формула, которая использует клеточки для вычисления площади. А то, что мы только что проделали, – очень полезное упражнение, которое поможет эту формулу понять.
Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.
Теперь вместо клеточек или их частей подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
Сколько насчитали?
У меня получилось \( Г = 22\) на границе и \( В = 32\) внутри.
Ну а теперь сама формула:
Делим границу пополам, прибавляем внутренности и вычитаем 1:
\( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.\)
Называется она формулой Пика, поскольку доказал её математик Георг Пик 120 лет назад (да, она не специально для ЕГЭ была придумана, но очень нам помогает) 🙂
Как запомнить формулу Пика
Всё, что внутри, берём целиком (клетки внутри фигуры целые).
Граница режет клетки надвое, поэтому берём половину узлов границы.
Минус 1 – это надо просто запомнить. Очень легко себя проверить на квадрате 1×1. Его площадь равна 1. Сколько там точек на границе? \( Г = 4.\) А сколько внутри? \( В = 0\) (нисколько)
Границу делим пополам, получаем 2. Прибавляем внутренности (+0) – ничего не поменялось.
Прибавляем внутренности (+0) – ничего не поменялось.
Очевидно, что осталось вычесть 1, чтобы получить 1.
Проверьте эту формулу на других простых фигурах, чтобы убедиться и закрепить.
Вычислите площадь простых фигур тремя способами
Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.
Вычислите площадь произвольных фигур по формуле Пика
Вычислите самостоятельно площади фигур с помощью формулы Пика:
Посчитайте площадь корабля и котика по формуле Пика
Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!
Фигуры с отверстиями — посчитайте площади двумя способами
Ну и напоследок фигуры с «дырками». Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?
Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?
Проверим на простом примере: это квадрат \( 4\times 4\), и в нём вырезан прямоугольник \( 1\times 2\), значит, его площадь \( 16-2=14\).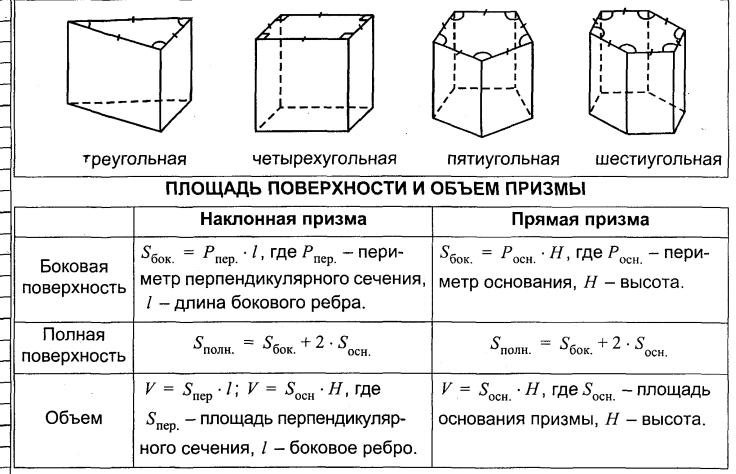
А теперь по точкам. На границах (включая внутренние) \( Г = 22\). Внутри \( В = 3\). Тогда площадь по формуле Пика
\( S = \frac{22}{2} + 3 -1 = 13.\)
Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.
Сосчитай сам и проверь.
Что получилось?
У меня снова на 1 меньше.
Так может быть просто формулу немного «подкрутить»? Нет!
Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.
Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.
Когда формулу Пика применять нельзя?
Естественно, эта формула не работает для окружностей и любых других фигур с «кривыми» границами.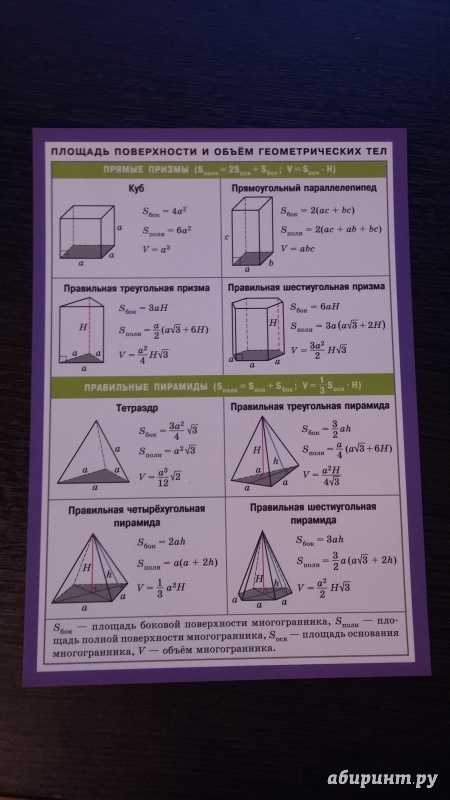
Также она не сработает, если хотя бы одна из вершин не попадает на узел, например, вот для такой, как на рисунке.
Почему я уверен, что не сработает? Ведь можно взять и не учитывать эту вершину, раз она не в узле. То есть
\( Г = 10, В = 2, S = \frac{10}{2} + 2 – 1 = 6.\)
А очень просто: я возьму и «отрежу» эту вершину. Тогда будет не треугольник, а трапеция, и площадь, очевидно, станет меньше на тот отрезанный кусочек.
Но по формуле она останется такой же, ведь количество узлов не изменилось ни на границе, ни внутри. То есть мы получим, что площадь уменьшенного треугольника равна площади целого, чего, конечно же, не может быть.
Итак, формула Пика работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
Какой способ лучше?
Второй и третий способы универсальные. Они помогут посчитать площадь даже самых замысловатых фигур.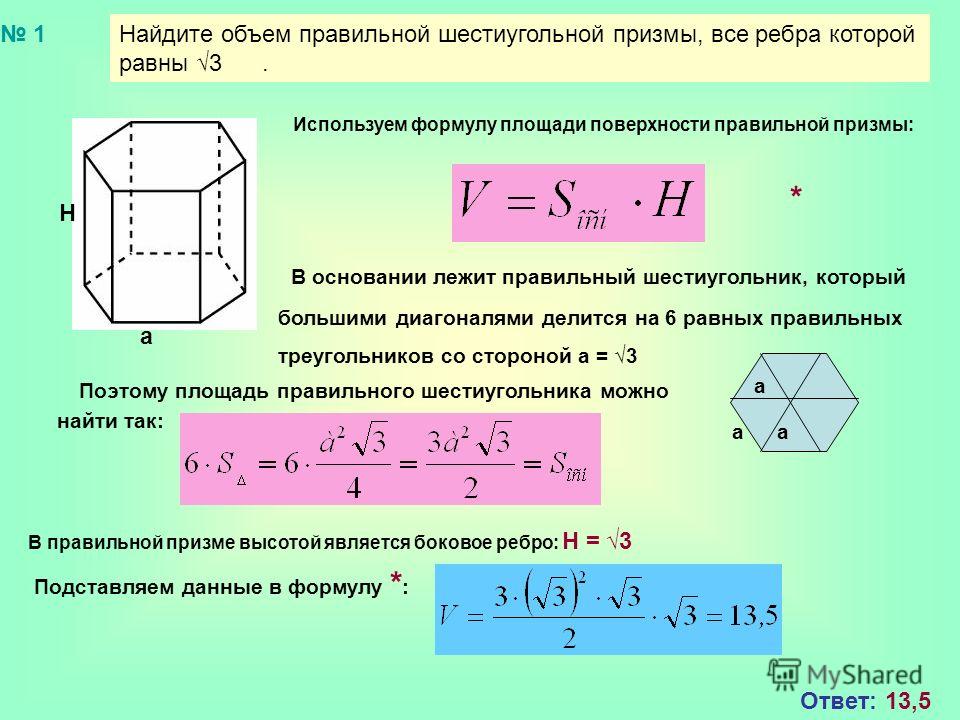 Вернемся еще раз ко второму способу.
Вернемся еще раз ко второму способу.
Вот смотри, нужно посчитать площадь такой фигуры:
Окружаем ее прямоугольником и снова получаем одну нужную, но сложную площадь и много ненужных, но простых.
А теперь чтобы найти площадь \( \displaystyle S\) просто находим площадь прямоугольника и вычитаем из него оставшуюся площадь фигур на клетчатой бумаге \( \displaystyle {{S}_{1}}+{{S}_{2}}+{{S}_{3}}+{{S}_{4}}\).
\( \displaystyle {{S}_{прямоугольника}}=6\cdot 11=66\)
\( \displaystyle {{S}_{1}}=\frac{1}{2}\cdot 6\cdot 4=12\)
\( \displaystyle {{S}_{2}}=\frac{1}{2}\cdot a\cdot h=\frac{1}{2}\cdot 5\cdot 4=10\) (обрати внимание, \( \displaystyle {{S}_{2}}\) площадь НЕ прямоугольного треугольника, но все равно легко считается по основной формуле).
\( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 5\cdot 2=5\)
\( \displaystyle {{S}_{4}}=\frac{1}{2}\cdot 1\cdot 11=5,5\).
Значит, \( \displaystyle S={{S}_{прямоугольника}}-{{S}_{1}}-{{S}_{2}}-{{S}_{3}}-{{S}_{4}}\).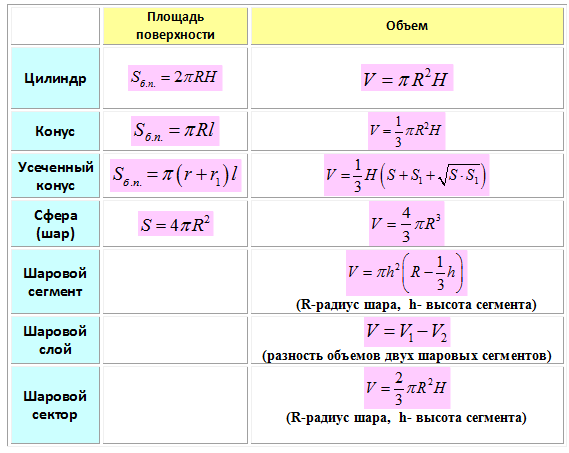
\( \displaystyle S=66-12-10-5-5,5=33,5\)
Вот и ответ: \( \displaystyle S=33,5\).Ну как тебе этот способ?
Вот смотри. С одной стороны, когда фигура занимает много клеточек, их замучаешься считать и можно ошибиться.
С другой стороны, когда мы дорисуем до прямоугольника, нужно считать много площадей.
Поэтому использование того или иного способа зависит лишь от конкретной задачи.
ПЛОЩАДИ ОБЪЕМНЫХ ФИГУР
Площадь поверхности призмы
Есть ли общая формула? Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.
Площадь полной поверхности призмы – это сумма площадей всех граней.
\( \displaystyle {{S}_{полн. пов.\ \ }}={{S}_{боков.пов.\ \ }}+2\cdot {{S}_{основания\ \ }}\)
Формулу можно написать для прямой призмы:
\( \displaystyle {{\text{S}}_{боков.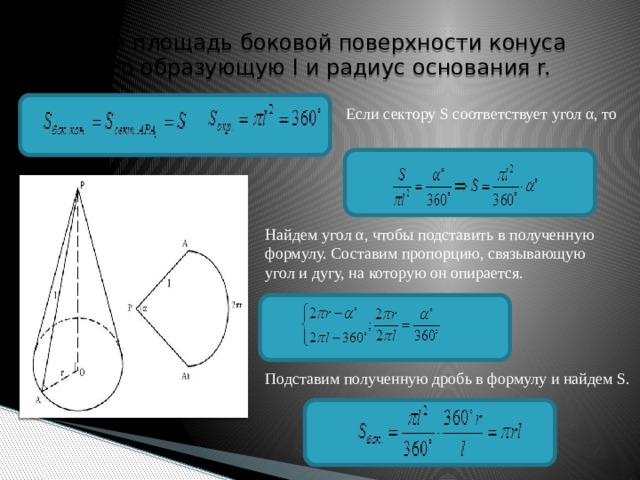 {2}}\).
{2}}\).
Площадь поверхности пирамиды
Для пирамиды тоже действует общее правило:
Площадь полной поверхности пирамиды – это сумма площадей всех граней.\( \displaystyle {{S}_{полн. пов.\ \ }}={{S}_{боков.пов.\ \ }}+{{S}_{основания\ \ }}\)
Теперь давай посчитаем площадь поверхности самых популярных пирамид.
Площадь поверхности правильной треугольной пирамиды
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle {{S}_{осн}}\) и \( \displaystyle {{S}_{ASB}}\).
И тогда
\( \displaystyle {{S}_{полн. пов.\ \ }}=3{{\text{S}}_{ASB}}+{{\text{S}}_{\text{осн}.}}\)
Вспомним теперь, что
\( \displaystyle {{S}_{осн}}\) — это площадь правильного треугольника \( \displaystyle ABC\).
И еще вспомним, как искать эту площадь.
Используем формулу площади:
\( \displaystyle S=\frac{1}{2}ab\cdot \sin \gamma \). 2}{4}}\)
2}{4}}\)
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
Этот вебинар посвящен заданию №3 из ЕГЭ на нахождение площади фигур, длин отрезков и т.д на клетчатой бумаге.
И хотя эту задачу убрали из ЕГЭ в 2021 году, сам навык очень полезен для того, чтобы начать учить геометрию, для понимания планиметрии!
Ну и просто этот вебинар легкий и классный! Послушайте его и получите удовольствие!
ЕГЭ №3. Площадь фигур на клетчатой бумаге
Площадь поверхности конуса равна. Общая площадь поверхности конуса. Площадь конус формула.
- Альфашкола
- Статьи
- Площадь поверхности конуса
Для того чтобы найти площадь всей поверхности конуса применим формулу:
\(S=\pi*r(l+r)\)
где \(r-\)радиус
\(l-\)длина боковой стороны
R конуса :
L конуса :
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Евгений Борисович Царенков
Репетитор по математике
Стаж (лет)
Образование:
Брестский государственный университет им. А.С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 6-9 классов. Буду рад помочь разобраться с предметом, успешно усвоить материал школьной программы по математике. Устраню пробелы в пройденном материале, подниму текущий уровень знаний по математике. Доношу материал понятно и грамотно, акцентирую внимание на важных и значимых вещах. Не оставляю материал непонятым.
В отличии от школы мы никуда не торопимся — будем разбирать тему до тех пор, пока не сформируем компетенцию. Нет ничего сложного ни в каком предмете, если его преподают с любовью.
Буду рад помочь разобраться с предметом, успешно усвоить материал школьной программы по математике. Устраню пробелы в пройденном материале, подниму текущий уровень знаний по математике. Доношу материал понятно и грамотно, акцентирую внимание на важных и значимых вещах. Не оставляю материал непонятым.
В отличии от школы мы никуда не торопимся — будем разбирать тему до тех пор, пока не сформируем компетенцию. Нет ничего сложного ни в каком предмете, если его преподают с любовью.
Владимир Валерьевич Ковалев
Репетитор по математике
Стаж (лет)
Образование:
Пятигорский государственный педагогический институт иностранных языков
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по французскому языку для 7-11 классов. Французский язык для меня — это «любовь с первого взгляда и на всю жизнь». В нём — красота и пластичность, математическая логика и дипломатичность, простота и невероятные связи с русским. Не было ни одного дня, чтобы я не совершенствовался в нём, и всякий раз нахожу что-то новое. За 40 прошлых лет были и более 20 лет преподавания в высшей школе, и более 10 лет переводческой работы, подготовка переводчиков к Всемирной шахматной Олимпиаде, Олимпиаде в Сочи и чемпионату мира по футболу-2018. Примерно 25 лет назад во Франции была разработана методика преподавания французского, как иностранного. С тех пор я применял её, как на группах, так и индивидуально, на разных возрастных группах, и, главное — на своих детях. Во всех случаях методика била по эффективности все ВУЗовские программы. Многократно подтверждено: 350 часов занятий, и ученик понимает и говорит на любые общебытовые темы.»
Французский язык для меня — это «любовь с первого взгляда и на всю жизнь». В нём — красота и пластичность, математическая логика и дипломатичность, простота и невероятные связи с русским. Не было ни одного дня, чтобы я не совершенствовался в нём, и всякий раз нахожу что-то новое. За 40 прошлых лет были и более 20 лет преподавания в высшей школе, и более 10 лет переводческой работы, подготовка переводчиков к Всемирной шахматной Олимпиаде, Олимпиаде в Сочи и чемпионату мира по футболу-2018. Примерно 25 лет назад во Франции была разработана методика преподавания французского, как иностранного. С тех пор я применял её, как на группах, так и индивидуально, на разных возрастных группах, и, главное — на своих детях. Во всех случаях методика била по эффективности все ВУЗовские программы. Многократно подтверждено: 350 часов занятий, и ученик понимает и говорит на любые общебытовые темы.»
Анжела Валентиновна Самсонова
Репетитор по математике
Стаж (лет)
Образование:
Костанайской педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Информатика: 5-11 класс (объяснение материала, корректировка знаний по темам, решение логических задач), подготовка к контрольным работам, ОГЭ, ЕГЭ. Математика: 3-6 класс (объяснение материала, корректировка знаний по темам, решение логических задач), подготовка к контрольным работам, ВПР.
Математика: 3-6 класс (объяснение материала, корректировка знаний по темам, решение логических задач), подготовка к контрольным работам, ВПР.
Похожие статьи
- Тригонометрическая единичная окружность, функция синуса, косинуса, тангенса и котангенса
- Свойства скалярного произведения
- Как разделить число в отношении
- ЕГЭ по математике, базовый уровень. Задачи на координатной решетке
- Работа по математике
- Нахождение числа по его части
- Задачи на исследование функций
- 10 техник самообладания, чтобы не срываться по мелочам
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Площадь и объём поверхность шара: формулы и их применение
Имея при себе всего одну формулу и зная изначально, чему равен диаметр или радиус, можно с лёгкостью вычислить площадь поверхности шара.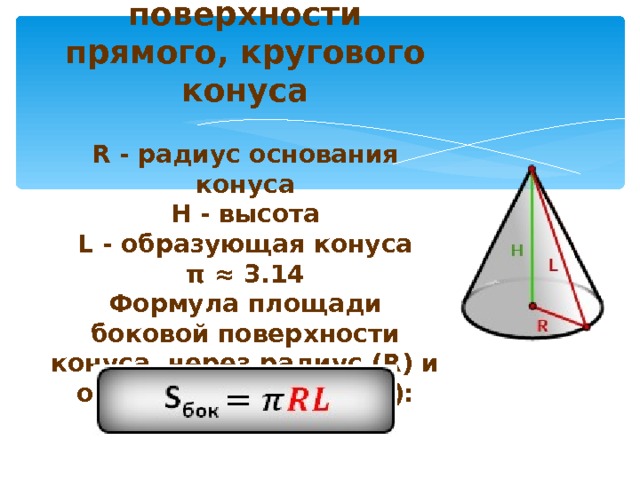 Формула будет иметь вид S =4πR2, где число «пи» умножается на 4, затем на радиус шара в квадратной степени. Но перед непосредственными вычислениями следует сразу разобраться в терминах.
Формула будет иметь вид S =4πR2, где число «пи» умножается на 4, затем на радиус шара в квадратной степени. Но перед непосредственными вычислениями следует сразу разобраться в терминах.
Содержание:
- Трактовка значений
- Занимательные факты
- Применение формулы
- Рождение формулы
- Видео
Трактовка значений
Это следует знать:
- Шар – геометрический объект, получившийся в результате вращательных полукруговых движений вокруг центра. Любая точка поверхности шара находится на одинаковом расстоянии от центра.
- Сфера – не то же самое, что шар. Если тот является объёмным объектом и включает в себя внутреннее пространство, то сфера – это лишь поверхность данного объекта и имеет только свою площадь. Иными словами – нельзя сказать, что сфера имеет такой-то объём, в отличие от шара.
- Число «пи» — это постоянное число, равное отношению длины окружности к её диаметру.
 В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр! - Радиус шара равен ½ его диаметру. Точный диаметр можно вычислить с использованием нескольких плоских и ровных предметов. Нужно лишь зажать шар между этими предметами, которые зажимают шар и расположены перпендикулярно друг к другу, а затем измерить получившийся диаметр.
- Квадратная степень обозначается в виде двойки и означает то, что это число надо умножить на само себя один раз. Если бы степень числа была в виде тройки, то умножать на само себя нужно было бы два раза. Записав выражение на бумаге, можно понять, почему используются именно двойка и тройка, а не единица и двойка.
- Объём – величина, обозначающая размер в пространстве, занимающее объектом. От диаметра зависит объём шара. Формула будет равна четырём трети, умноженным на число «пи» и вновь умноженным на его радиус в кубе.

- Площадь – величина, обозначающая размер поверхности объекта, но не внутреннего пространства.
Занимательные факты
Это интересно:
- У числа «пи» есть собственные фан-клубы по всему миру. Члены общества пытаются запомнить как можно больше знаков из этого числа, а также пытаются разгадать вселенские тайны, сокрытые в числе.
- Площадь суши Земли составляет всего 29,2 % от её общей поверхности. Точное число площади сложно назвать из-за неравномерного рельефа Земли, такие как впадины и горы.
- Знания о формуле площади шара можно применять и в быту. Также этими знаниями можно подавлять соперника в споре.
Продемонстрировав объём своих знаний в области геометрии, можно изначально заставить вас уважать, а ремонтникам и продавцам можно дать понять, что вас просто так не обмануть.
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
Но как быть, если не представляется возможным измерить объект? Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Рождение формулы
Принято считать, что первый, кто нашёл и вывел формулу объёма и площади шара, был Архимед. Это величайший древнегреческий учёный, живший за 300 лет до нашей эры. Он был не только математиком, но и физиком, и инженером. Он один из первых людей, кто попытался «оцифровать» окружающий нас мир. Его теоремы и труды используются по сей день.
Именно Архимед определил границы числа «пи» и обозначил их, не имея никаких современных гаджетов. Сам Архимед очень гордился найденной формулой, с помощью которой вычисляется объём шара. Его потомки в честь этого изобразили на его могильном камне цилиндр и шар.
Если бы каким-то чудом он переродился в наше время, то он сразу же смог бы преобразить этот мир и вывести его на новый уровень.
Видео
На примере этого видео вам будет легко понять, как найти площадь поверхности шара.
Формулы площади поверхности — вывод, примеры
Формула площади поверхности — это математическое решение для нахождения общей площади любого трехмерного объекта, занимаемой всеми его поверхностями. Давайте подробно разберемся с формулами площади поверхности различных трехмерных форм.
Что такое формула площади поверхности?
Формула площади поверхности используется для нахождения суммы всех площадей поверхности любого трехмерного объекта. Формула площади поверхности подразделяется на две категории:
- Формула площади криволинейной поверхности или формула площади боковой поверхности
- Формула общей площади поверхности
Посмотрите на приведенную ниже таблицу формул площади поверхности, на которой показаны формулы площади поверхности соответствующих трехмерных фигур.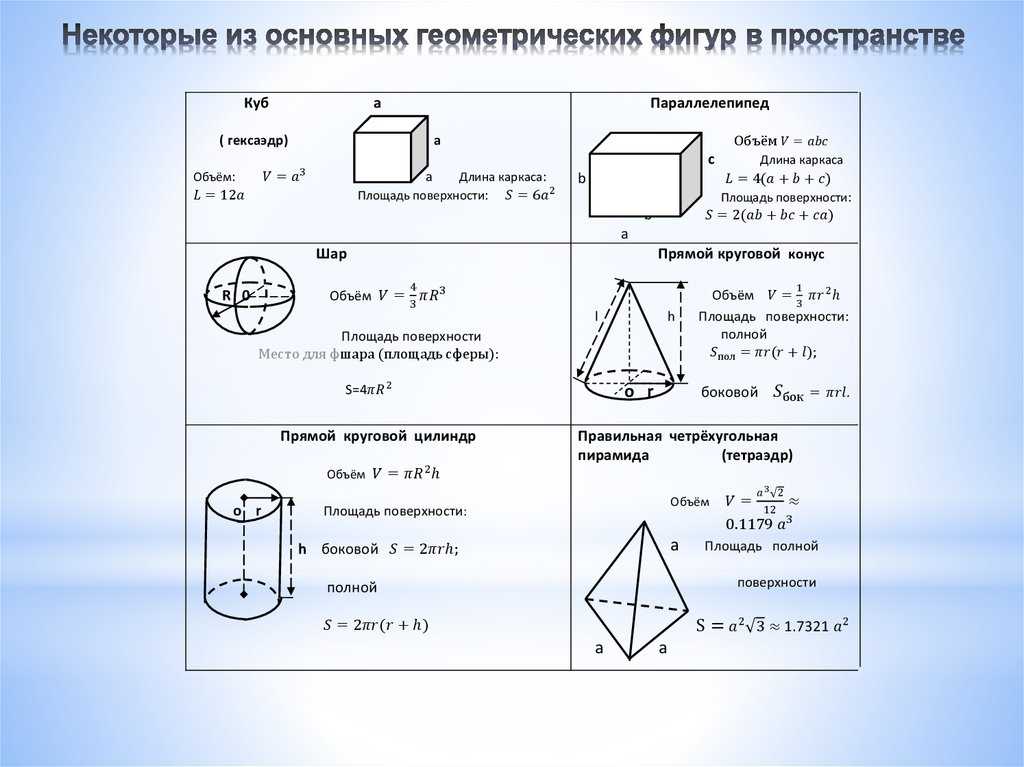
Давайте подробно узнаем об общих формулах площади поверхности различных форм.
Формулы площади поверхности различных форм
Любой трехмерный объект имеет боковые поверхности и базовую поверхность(и). Общая площадь поверхности относится к сумме площади боковой/криволинейной поверхности и площади базовой поверхности. В этом разделе мы узнаем о формулах площади поверхности различных трехмерных форм.
Формула площади поверхности куба
Площадь поверхности куба — это общая площадь, покрываемая всеми шестью гранями куба. Общая формула площади поверхности куба имеет вид:
- Формула общей площади поверхности куба будет равна сумме площадей вертикальных поверхностей куба и площади основания. Формула общей площади поверхности куба = 6a 2 , где «a» — длина стороны.
- Формула площади боковой поверхности куба представляет собой сумму площадей всех боковых граней куба. ЛСА = 4а 2 где «а» — длина стороны.

Формула площади поверхности прямоугольного параллелепипеда
Формула общей площади прямоугольного параллелепипеда получается путем сложения площадей всех шести граней. Общая площадь поверхности и площадь боковой поверхности могут быть выражены через ее размеры: длину (l), ширину (b) и высоту прямоугольного параллелепипеда (h) как:
- Общая площадь прямоугольного параллелепипеда, S = 2 (lb + bh + lh) шт. 2
- Площадь боковой поверхности прямоугольного параллелепипеда, L = 2h (l + b) ед. 2
Формула площади поверхности конуса
Конус представляет собой трехмерную форму с круглым основанием, радиусом «r» и диаметром «d». У него криволинейная поверхность, поэтому у нас может быть формула площади его криволинейной поверхности, а также формула общей площади поверхности. Если радиус основания конуса равен «r», а наклонная высота конуса равна «l», площадь поверхности конуса определяется как:
- Общая площадь поверхности конуса, T = πr(r + л)
- Площадь криволинейной поверхности конуса, S = πrl
Формула площади поверхности цилиндра
Цилиндр имеет криволинейную поверхность с двумя круглыми основаниями, расположенными на обоих концах.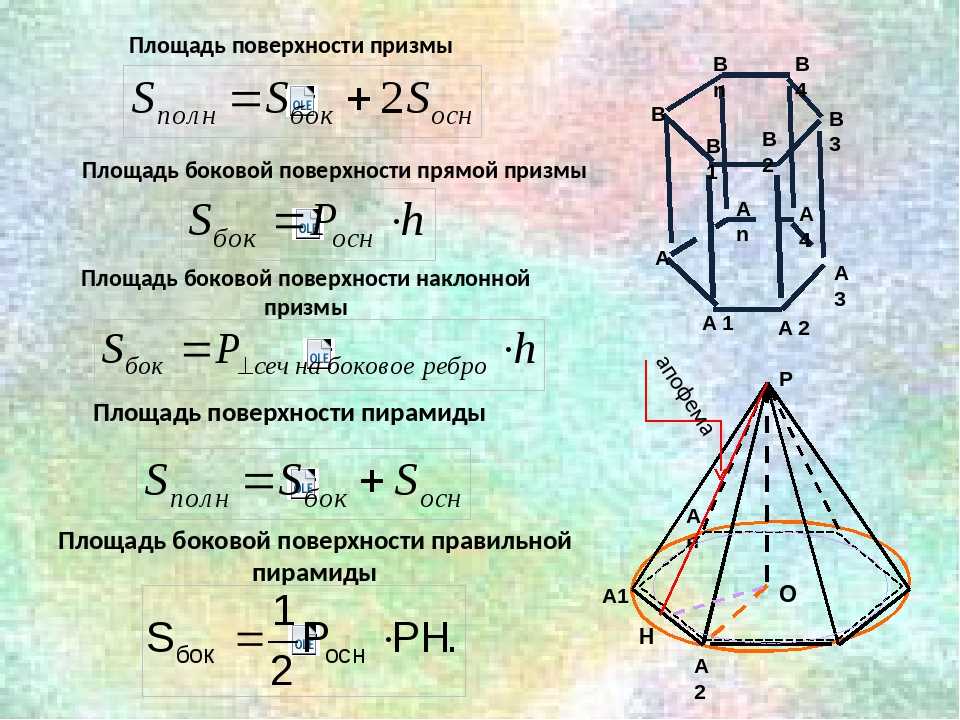 Если радиус основания цилиндра равен «r», а высота цилиндра равна «h», площадь поверхности цилиндра определяется как:
Если радиус основания цилиндра равен «r», а высота цилиндра равна «h», площадь поверхности цилиндра определяется как:
- Общая площадь поверхности цилиндра, T = 2πr(h + r )
- Площадь криволинейной поверхности цилиндра, S = 2πrh
Формула площади поверхности сферы
Сфера — это трехмерный твердый объект с круглой структурой. Площадь поверхности шара – это сумма площадей окружающих его граней. Формула площади поверхности сферы задается как:
⇒ Площадь поверхности Сферы, S = 4πr 2 квадратных единиц.
Формула площади поверхности полушария
Полушарие – это половина сферы. Площадь поверхности полушария – это общая площадь, которую покрывает его поверхность. Формулу площади поверхности полушария можно разделить на две категории:
- Площадь криволинейной поверхности полушария (CSA) = ½ (площадь криволинейной поверхности сферы) = ½ (4 π r 2 ) = 2 π r 2 , где «r» — радиус полушария.

- Общая площадь поверхности полушария (TSA) = площадь криволинейной поверхности + площадь основания = 2 π r 2 + π r 2 = 3 π r 2 , где «r» — радиус полушария.
Формула площади поверхности призмы
Площадь боковой поверхности призмы представляет собой сумму площадей всех ее боковых граней, тогда как общая площадь поверхности призмы представляет собой сумму площади ее боковой поверхности и площади ее оснований. Формулы площади поверхности призмы могут быть приведены
- Площадь боковой поверхности призмы = периметр основания × высота
- Общая площадь поверхности призмы = площадь боковой поверхности призмы + площадь двух оснований = (2 × площадь основания) + площадь боковой поверхности или (2 × площадь основания) + (периметр основания × высота).
Существует семь типов призм в зависимости от формы основания призмы. Основания призм разных типов различаются, как и формулы для определения площади поверхности призмы.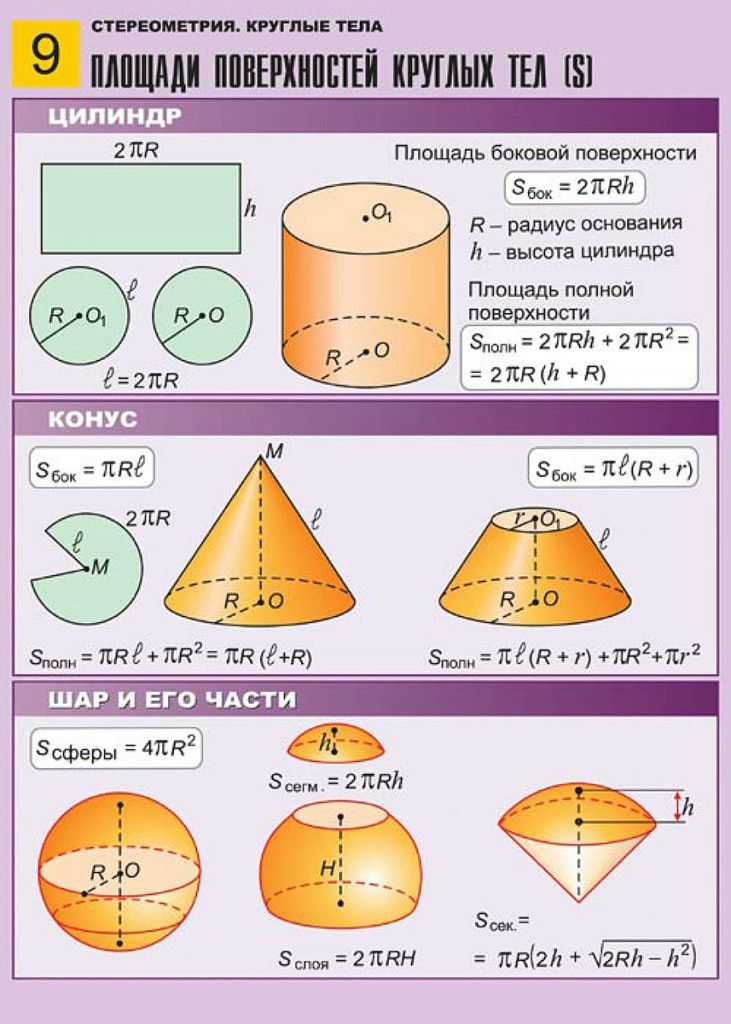 Ознакомьтесь с призмой, чтобы понять концепцию формул площади поверхности различных призм.
Ознакомьтесь с призмой, чтобы понять концепцию формул площади поверхности различных призм.
Формула площади поверхности пирамиды
Если пирамида имеет основание в виде правильного многоугольника с высотой, проходящей через центр основания, то формулы площади боковой поверхности и общей площади поверхности для пирамиды могут быть представлены как:
Рассмотрим правильный пирамида, у которой периметр основания равен «P», площадь основания равна «B», а высота наклона (высота каждого треугольника) равна «s». Тогда
- Площадь боковой поверхности пирамиды (LSA) = (1/2) Ps
- Общая площадь поверхности пирамиды (TSA) = LSA + площадь основания = (1/2) Ps + B
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Заказать бесплатный пробный урок
Примеры с использованием формулы площади поверхности
Пример 1: Цилиндрический резервуар имеет радиус 4 ярда и высоту 8 ярдов, используя формулу площади поверхности цилиндра.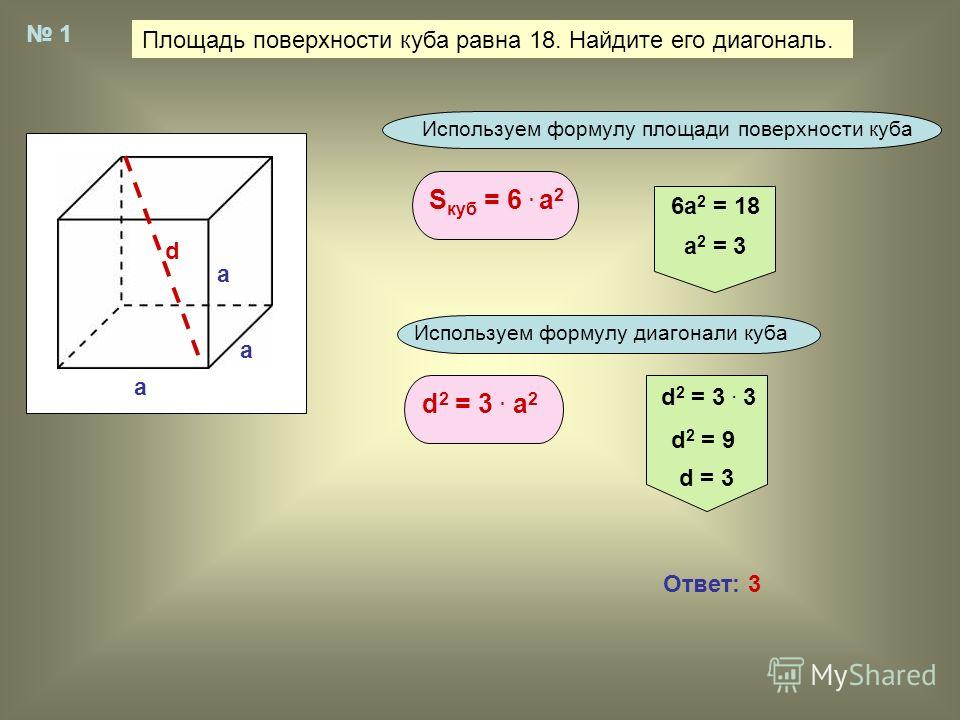 . Если стоимость покраски цилиндрического резервуара составляет 6 долларов за ярд 2 , сколько будет стоить картина?
. Если стоимость покраски цилиндрического резервуара составляет 6 долларов за ярд 2 , сколько будет стоить картина?
Решение:
Мы знаем, что формула общей площади поверхности цилиндра = площадь криволинейной поверхности цилиндра + площадь верхней и нижней граней
=2πrh + 2πr 2
=2πr(r + h)
=2 × 22/7 × 4 × (4 + 8)
=301,68 ярда 2
Стоимость картины 6 долларов США за ярд 2 = 301,68 × 6 = 1810,08
долларов США. Стоимость картины – 1810,08 долларов США.
Пример 2: Учитывая, что радиус конуса равен 6 дюймов, а наклонная высота конуса – 9 дюймов. Используя формулу общей площади поверхности конуса, вычислите площадь поверхности конуса.
Решение:
Дано: радиус = 6 дюймов и наклонная высота = 9 дюймов
Формула общей площади поверхности конуса = T = πr(r + l)
=3,14 × 6 × (6 + 9)
=282,6 дюйма 2
∴Площадь поверхности конуса будет 282,6 дюйма 2
Пример 3: Используя формулу площади поверхности куба, найдите площадь поверхности куба, сторона которого равна 4 дюймам.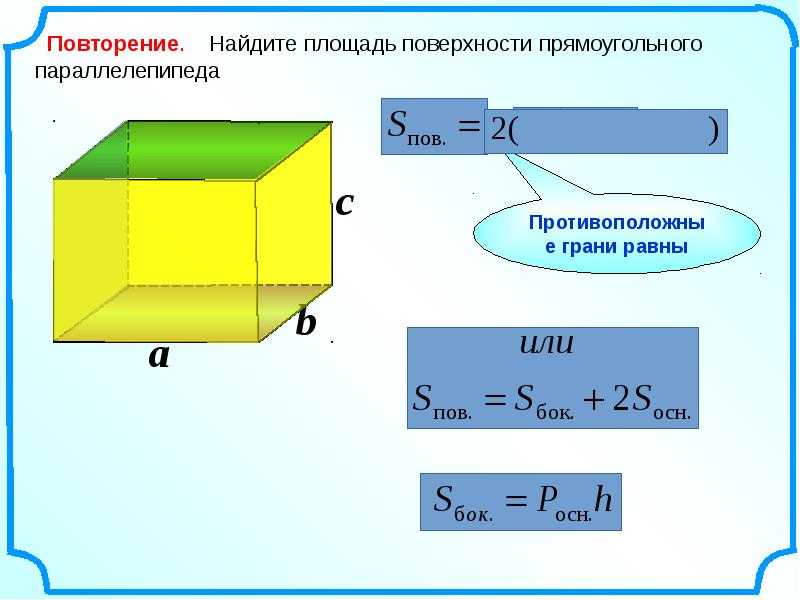
Решение: Дана длина стороны куба = 4 дюйма
Формула площади поверхности куба = 6a 2
а = 4 дюйма
О подстановке значений в формулу площади поверхности куба.
= 6 (4) 2
= 6 (16)
= 96 дюймов 2
∴Площадь поверхности куба будет 96 дюймов 2
Часто задаваемые вопросы о формулах площади поверхности
Что такое формула площади поверхности для прямоугольного параллелепипеда?
Формула площади поверхности прямоугольного параллелепипеда: 2(lb + bh + hl). Здесь «l», «b» и «h» обозначают 3 измерения: длину, ширину и высоту прямоугольного параллелепипеда.
Какая связь между формулой площади криволинейной поверхности для сферы и полусферы?
Формула площади криволинейной поверхности полушария равна половине площади криволинейной поверхности сферы. Это дается как:
CSA полушария = ½ (площадь криволинейной поверхности сферы) = ½ (4 π r 2 ) = 2 π r 2 , где «r» — радиус полушария/сферы.
Какова формула площади поверхности конуса?
Формула общей площади поверхности конуса задается как T = πr(r + l).
Формула площади криволинейной поверхности конуса задается как S = πrl.
Здесь «r» — радиус основания конуса, а «l» — наклонная высота конуса.
Какова формула площади поверхности цилиндра?
Формула площади поверхности цилиндра представляет собой общую площадь, покрытую поверхностью цилиндрической формы. Математически это выражается как 2πr(h+r), где «r» — радиус круглого основания цилиндра, а «h» — высота цилиндра. Площадь поверхности цилиндра указана в квадратных единицах, например, м 2 , дюймы 2 , см 2 , ярды 2 и т. д.
6.5: Формулы площади, площади поверхности и объема
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 51016
- Эми Лагускер
- Колледж Каньонов
Формулы площади
Пусть \(b\) = основание
Пусть \(h\) = высота
Пусть \(s\) = сторона
Пусть \(r\) = радиус
Имя формы | Форма | Формула площади |
|---|---|---|
Прямоугольник | \(А=ч\) 9{2}\конец{массив}\) | |
Параллелограмм | \(А=ч\) | |
Треугольник | \(A=\dfrac{1}{2} б ч\) | |
Круг 9{2}\) | ||
Трапеция | \(A=\dfrac{1}{2} h\left(b_{1}+b_{2}\right)\) |
Формулы площади поверхности
Переменные :
\(SA\) = площадь поверхности
\(B\) = площадь основания фигуры
\(P\) = периметр основания фигуры
\(h\) = высота
\(s\) = наклонная высота
\(r\) = радиус
Формула площади поверхности | Площадь поверхности Значение | |
|---|---|---|
| \(S A=2 B+P h\) | Найдите площадь каждой грани. |
«> | \(S A=B+\dfrac{1}{2} s P\) | Найдите площадь каждой грани. Сложите все области. |
| 9{2}\) | Найдите площадь большого круга и умножьте ее на 4. | |
\(S A=B+\pi r S\) | Найдите площадь основания и прибавьте произведение радиуса, умноженное на наклонную высоту, на число PI. |
Формулы объема
Переменные :
\(SA\) = площадь поверхности
\(B\) = площадь основания фигуры
\(P\) = периметр основания фигуры
\(h\) = высота
\(s\) = наклонная высота
\(r\) = радиус
Геометрическая фигура | Объем Формула | Том Значение | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
\(V=B ч\) | Найдите площадь основания и умножьте ее на высоту | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\(V=\dfrac{1}{3} B h\) | Найдите площадь основания и умножьте ее на 1/3 высоты. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(V=B ч\) | Найдите площадь основания и умножьте ее на высоту. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9{3}\) | Найдите площадь большого круга и умножьте ее на радиус, а затем умножьте на 4/3. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \( V=\dfrac{1}{3} B h\) | Найдите площадь основания и умножьте ее на 1/3 высоты. | 9{2} ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Формулы площади поверхности |
| (Математика | Геометрия | Формулы площади поверхности) |
( пи = = 3,141592. ..)
..)
Поверхность
Формулы площади
Обычно площадь поверхности представляет собой сумму
все площади всех фигур, которые покрывают поверхность объекта.
Куб | Прямоугольный
призма | призма | Сфера
| Цилиндр | Единицы
Примечание: «ab» означает «а» умножить на «б». «а
2 » означает «а в квадрате», что равно «а», умноженному на «а».Будьте осторожны!! Считаются единицы. Используйте одни и те же единицы измерения для всех измерений. Примеры
| Площадь поверхности куба = 6 а 2 |
(а — длина стороны каждое ребро куба)
Другими словами, площадь поверхности куба — это площадь шести квадратов, которые
накрой это. Площадь одного из них равна a*a, или a 2 . Поскольку эти
одинаковы, вы можете умножить одно из них на шесть, так что поверхность
площадь куба в 6 раз больше одной из сторон в квадрате.
Поскольку эти
одинаковы, вы можете умножить одно из них на шесть, так что поверхность
площадь куба в 6 раз больше одной из сторон в квадрате.
| Площадь поверхности прямоугольника Призма = 2ab + 2bc + 2ac |
(a, b и c — длины трех сторон)
Другими словами, площадь поверхности прямоугольной призмы равна площади шести прямоугольники, которые его закрывают. Но нам не нужно вычислять все шесть, потому что мы знаем, что верх и низ одинаковы, перед и зад равны одинаковые, а левая и правая стороны одинаковые.
Площадь верха и низа (длины сторон а и
в) = а*с. Так как их два, то получается 2ac. Спереди и сзади
имеют длины сторон b и c. Площадь одного из них равна b*c, и там
их два, поэтому площадь поверхности этих двух равна 2bc. Левый и
правая сторона имеет длины сторон a и b, поэтому площадь поверхности одной из
они а*б. Опять же, их два, поэтому их общая площадь поверхности
это 2аб.
Левый и
правая сторона имеет длины сторон a и b, поэтому площадь поверхности одной из
они а*б. Опять же, их два, поэтому их общая площадь поверхности
это 2аб.
| Площадь поверхности любой призмы |
(b — форма из концов)
Площадь поверхности = боковая площадь + площадь двух концов
(Боковая площадь) = (периметр формы b ) * L
Площадь поверхности = (периметр формы b ) * L+ 2 * (Площадь формы b )
| Площадь поверхности сферы = 4 пи г 2 |
(r — радиус окружности)
| Площадь поверхности цилиндра = 2 пи r 2 + 2 пи r ч |
(h высота цилиндр, r — радиус вершины)
Площадь поверхности = площади сверху и снизу + площадь сбоку
Площадь поверхности = 2 (площадь верха) + (периметр верха) * высота
Площадь поверхности = 2( pi r 2 ) + (2 pi r)*h
На словах проще всего представить банку. Площадь поверхности – это
площади всех частей, необходимых для покрытия банки. Это верх, низ,
и бумажная этикетка, которая оборачивается вокруг середины.
Площадь поверхности – это
площади всех частей, необходимых для покрытия банки. Это верх, низ,
и бумажная этикетка, которая оборачивается вокруг середины.
Можно найти площадь верха (или низа). Это формула площадь круга ( pi r 2 ). Так как есть и вершина, и дно, которое умножается на два.
Сторона похожа на этикетку банки. Если вы очистите его и положите плоский это будет прямоугольник. Площадь прямоугольника есть произведение две стороны. С одной стороны высота банки, с другой периметру круга, так как этикетка один раз оборачивается вокруг банки. Так площадь прямоугольника равна (2 pi r)*h.
Сложите эти две части вместе, и вы получите формулу поверхности. площадь цилиндра.
Площадь поверхности = 2( pi r 2 ) + (2 pi r)*h
Совет! Не забывайте про единицы. |
Эти уравнения дадут вам правильные ответы, если вы держите единицы измерения прямыми. Например, чтобы найти площадь поверхности куба со стороной 5 дюймов, уравнение:
Площадь поверхности = 6*(5 дюймов) 2
= 6*(25 квадратных дюймов)
= 150 кв. дюймов
Калькулятор площади поверхности
Квадратная пирамида
ч = высота
с = наклонная высота
а = длина стороны
e = длина боковой кромки
р = а/2
В = громкость
S to = общая площадь поверхности
S lat = площадь боковой поверхности
S бот = площадь нижней поверхности
Рассчитайте больше с помощью
Калькулятор пирамид
Калькулятор Используйте
Онлайн-калькулятор для расчета площади поверхности геометрических тел, включая капсулу, конус, усеченный конус, куб, цилиндр, полусферу, пирамиду, прямоугольную призму, сферу, сферическую крышку и треугольную призму
Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты. Единицы используются для обозначения порядка результатов, таких как футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты дадут V в мм 3 и S в мм 2 .
Единицы используются для обозначения порядка результатов, таких как футы, футы 2 или футы 3 . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты дадут V в мм 3 и S в мм 2 .
Ниже приведены стандартные формулы для площади поверхности.
Формулы площади поверхности:
Калькулятор площади поверхностиПлощадь поверхности капсулы
- Объем = πr 2 ((4/3)r + a)
- Площадь поверхности = 2πr(2r + a)
Площадь поверхности круглого конуса
- Объем = (1/3)πr 2 ч
- Площадь боковой поверхности = πrs = πr√(r 2 + ч 2 )
- Площадь базовой поверхности = πr 2
- Общая площадь поверхности
= L + B = πrs + πr 2 = πr(s + r) = πr(r + √(r 2 + h 2 ))Площадь поверхности круглого цилиндра
- Объем = πr 2 ч
- Площадь верхней поверхности = πr 2
- Площадь нижней поверхности = πr 2
- Общая площадь поверхности
= L + T + B = 2πrh + 2(πr 2 ) = 2πr(h+r)Площадь конической усеченной поверхности
- Объем = (1/3)πh (r 1 2 + r 2 2 + (r 1 * r 2 ))
- Площадь боковой поверхности
= π(r 1 + r 2 )s = π(r 1 + r 2 )√((r 1 — r 2 ) 2 + h 2 )- Площадь верхней поверхности = πr 1 2
- Площадь базовой поверхности = πr 2 2
- Общая площадь поверхности
= π(r 1 2 + r 2 2 + (r 1 * r 2 ) * s)
= π[ r 1 2 + r 2 2 + (r 1 * r 2 ) * √((r 1 — r 2 ) 2 + h 2 ) ]Площадь поверхности куба
- Объем = а 3
- Площадь поверхности = 6a 2
Площадь поверхности полушария
- Объем = (2/3)πr 3
- Площадь криволинейной поверхности = 2πr 2
- Площадь базовой поверхности = πr 2
- Общая площадь поверхности = (2πr 2 ) + (πr 2 ) = 3πr 2
Площадь поверхности пирамиды
- Объем = (1/3)а 2 ч
- Площадь боковой поверхности = a√(a 2 + 4h 2 )
- Базовая площадь поверхности = a 2
- Общая площадь поверхности
= L + B = а 2 + а√(а 2 + 4h 2 ))
= а(а + √(а 2 + 4h 2 ))Площадь поверхности прямоугольной призмы
- Объем = лвч
- Площадь поверхности = 2(lw + lh + wh)
Площадь поверхности сферы
- Объем = (4/3)πr 3
- Площадь поверхности = 4πr 2
Площадь поверхности сферической крышки
- Объем = (1/3)πh 2 (3R — h)
- Площадь поверхности = 2πRh
Площадь поверхности треугольной призмы
Площадь верхней поверхности треугольной призмы Формула
\[ A_{top} = \dfrac{1}{4} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]
\[ A_{top} = \dfrac{1}{4} \sqrt{\begin{align}(a+&b+c)(b+c-a)\\&\times(c+a-b)(a+b-c )\конец{выровнено}} \]
Площадь нижней поверхности треугольной призмы Формула
\[ A_{bot} = \dfrac{1}{4} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \]
\[ A_{bot} = \dfrac{1}{4} \sqrt{\begin{выровнено}(a+&b+c)(b+c-a)\\&\times(c+a-b)(a+b-c )\конец{выровнено}} \]
Площадь боковой поверхности треугольной призмы Формула
\[ A_{широта} = h (a+b+c) \]Суммарная площадь поверхности треугольной призмы Формула
\[ A_{tot} = A_{top} + A_{bot} + A_{lat} \]
| Определение
Создано Богной Шик и Ханной Памула, кандидатом наук
Отредактировано Стивеном Вудингом и Джеком Боуотером
Последнее обновление: 06 апреля 2022 г.
- Что такое площадь поверхности? Определение площади поверхности
- Формула площади поверхности…
- Площадь поверхности сферы
- Площадь поверхности цилиндра
- Площадь поверхности конуса
- Площадь поверхности куба
- Площадь поверхности пирамиды
- Площадь поверхности прямоугольной призмы
- Площадь поверхности треугольной призмы
- Площадь поверхности тела
- Как вычислить площадь поверхности сферы?
- Другие соображения
Этот калькулятор площади поверхности поможет вам найти площадь наиболее распространенных трехмерных тел. Если вы когда-нибудь задавались вопросом, как найти площадь поверхности или что такое площадь боковой поверхности, этот калькулятор здесь, чтобы помочь вам. Площадь поверхности имеет гигантский список приложений в каждой области, например, в аэродинамике. В этой статье вы можете найти формулы площади поверхности сферы, куба, цилиндра, конуса, пирамиды и прямоугольной/треугольной призмы. Мы также объясним, как рассчитать площадь поверхности сферы в качестве примера.
Мы также объясним, как рассчитать площадь поверхности сферы в качестве примера.
Что такое площадь поверхности? Определение площади поверхности
Площадь поверхности равна общей площади, которую занимает поверхность объекта . Другими словами, это общая площадь поверхности 3D-объекта.
Иногда площадь поверхности может быть разделена на сумму площади(ей) основания и площади боковой поверхности . Боковая поверхность – это площадь всех сторон объекта, исключая его основание и вершину. Это деление используется для форм, в которых есть очевидное различие между основанием и другой частью, например, для цилиндра, конуса, пирамиды или треугольной призмы. Он редко применяется к твердым телам, для которых мы не уверены, какие грани следует рассматривать как основания (например, в кубе или параллелепипеде), и мы не используем его для гладких поверхностей, таких как сфера.
Формула площади поверхности…
Наш калькулятор площади поверхности может найти площадь поверхности семи различных твердых тел. Формула зависит от типа твердого тела.
Формула зависит от типа твердого тела.
- Площадь поверхности сферы:
A = 4πr², где r — радиус сферы. - Площадь поверхности куба:
A = 6a², где a — длина стороны. - Площадь поверхности цилиндра:
A = 2πr² + 2πrh, где r — радиус, а h — высота цилиндра. - Площадь поверхности конуса:
A = πr² + πr√(r² + h²), где r — радиус, а h — высота конуса. - Площадь поверхности прямоугольной призмы (коробки):
A = 2(ab + bc + ac), где a , b и c — длины трех сторон прямоугольного параллелепипеда. - Площадь поверхности треугольной призмы:
A = 0,5 * √((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)) + h * (a + b + c), где a , b и c — длины трех сторон основания треугольной призмы, а h — высота (длина) призмы.
- Площадь поверхности пирамиды:
A = l * √(l² + 4 * h²) + l², где l — длина стороны квадратного основания и h — это высота пирамиды.
Но откуда берутся эти формулы? Как найти площадь поверхности основных трехмерных фигур? Продолжайте читать, и вы узнаете!
Площадь поверхности сферы
Чтобы вычислить площадь поверхности сферы, все, что вам нужно знать, это радиус сферы или ее диаметр.
-
A = 4 * π * r², гдеr— радиус.
Как мы знаем, диаметр шара равен двум радиусам d = 2r , мы можем преобразовать уравнение в другую форму:
-
A = 4 * π * (d / 2)² = π * d², гдеd— диаметр сферы.
Вывод этой формулы площади поверхности требует интегрирования. Если вам интересно, посмотрите это доказательство.
Площадь поверхности цилиндра
Чтобы узнать площадь поверхности цилиндра, необходимо иметь две величины: радиус (или диаметр) основания и высоту цилиндра. Общее уравнение как обычно — площадь основания раз высота . В нашем случае круг является основой.
Общее уравнение как обычно — площадь основания раз высота . В нашем случае круг является основой.
-
А = 2πr² + 2πrh
Откуда взялась эта формула? Вы можете написать уравнение для площади поверхности цилиндра как:
-
A = A(боковая) + 2 * A(основная)
Площадь основания найти легко — помним известную формулу площади круга: A(основание) = π * r² . Но какова форма площади боковой поверхности? Попробуйте представить, что мы его «разворачиваем». Вы признаете это? это прямоугольник ! Длина одной стороны — это высота цилиндра, а вторая — длина окружности в развернутом виде.
-
А(основание) = π * r² -
A(поперечный) = h * (2 * π * r)
Площадь поверхности конуса
Мы можем разделить площадь поверхности конуса на две части:
-
A = A(боковая) + A(основание), так как у нас есть только одно основание, напротив к цилиндру.
Основание снова равно площади круга A(основание) = π * r² , но происхождение площади боковой поверхности может быть не столь очевидным:
-
A(боковая) = π * r * √(r² + h²)
Давайте посмотрим на этот пошаговый вывод:
- Раскатайте боковую поверхность до плоского состояния. Круговой сектор, являющийся частью окружности радиусом s ( s высота наклона конуса).
- Для круга с радиусом s, длина окружности равна
2 * п * с. Длина дуги сектора равна2 * π * r. - Площадь сектора — боковой поверхности конуса — определяется по формуле:
-
A(поперечный) = (s * (длина дуги)) / 2 = (s * 2 * π * r) / 2 = π * r * s
Формулу можно получить из пропорций, так как отношение площадей фигур такое же, как отношение длины дуги к длине окружности:
(площадь сектора) / (площадь большого круга) = (длина дуги) / (длина окружности большого круга) итак:
(площадь сектора) / (π * s²) = (2 * π * r) / (2 * π * s)
(площадь сектора) = (π * s²) * (2 * π * r) / (2 * π * s)
-
A(боковой) = π * r * с
Чтобы найти недостающий член этого отношения, вы также можете попробовать наш калькулятор отношений!
- Обычно у нас нет
s 9Задано значение 1409, ноh, что равно высоте конуса. Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора:
Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора:
-
r² + h²= s², извлекая квадратный корень, получаемs = √(r² + h²)
Таким образом, формула площади боковой поверхности выглядит следующим образом:
-
A(боковая) = π * r * √(r² + h²)
- Наконец, сложите площади основания и боковой части, чтобы найти окончательная формула площади поверхности конуса :
-
A = A(боковой) + A(основной) = π * r * s + π * r²заданоrиsили -
A = π * r * √(r² + h²) + π * r²учитываяrиh.
Площадь поверхности куба
Площадь поверхности куба проще всего представить: каждая из сторон представляет собой квадрат! Поскольку каждый куб имеет шесть одинаковых квадратных граней, площадь поверхности равна:
-
A = 6 * (боковая часть)
Так как площадь квадрата является произведением длины его сторон, окончательная формула площади поверхности куба будет следующей:
-
A = 6 * l², гдеl— квадрат сторона
Площадь поверхности пирамиды
Пирамида представляет собой трехмерное тело с многоугольным основанием и треугольными боковыми гранями. Когда вы слышите пирамида , обычно подразумевается обычная квадратная пирамида . Но в зависимости от формы основания, это могла быть и шестиугольная пирамида, и прямоугольная пирамида. Обычный означает, что он имеет правильное многоугольное основание и представляет собой правильную пирамиду (вершина прямо над центром тяжести его основания), а квадрат - что он имеет эту форму в качестве основания. Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности.
Когда вы слышите пирамида , обычно подразумевается обычная квадратная пирамида . Но в зависимости от формы основания, это могла быть и шестиугольная пирамида, и прямоугольная пирамида. Обычный означает, что он имеет правильное многоугольное основание и представляет собой правильную пирамиду (вершина прямо над центром тяжести его основания), а квадрат - что он имеет эту форму в качестве основания. Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности.
Формула площади поверхности пирамиды:
-
A = l * √(l² + 4 * h²) + l²гдеlсторона основания иhвысота пирамиды
Опять же, мы можем разделить уравнение на:
-
A = A(основание) + A(бок) = A(основание) + 4 * A(боковая сторона)
Основание имеет форму квадрата, поэтому A(основание) = l² . Для расчета площади боковой поверхности начнем с площади одной треугольной грани:
- Чтобы найти высоту треугольника, нам снова понадобится формула гипотенузы:
-
с = √(а² + b²)
- Вычислить гипотенузу треугольника ABC (которая одновременно является высотой треугольной грани):
-
c = √(h² + (l/2)²) = √(h² + l²/4)
- Площадь треугольника (в нашем случае это равнобедренный треугольник) можно рассчитать как:
-
A = высота * основание / 2поэтому -
A(боковая сторона) = √(h² + l²/4) * l / 2
- Итоговая формула площади поверхности пирамиды:
-
A = l² + 4 * √(h² + l²/4) * l / 2 = l² + 2 * l * √(h² + l²/4) -
A = l² + l * √(4 * h² + l²)
Площадь поверхности прямоугольной призмы
Чтобы вычислить площадь поверхности прямоугольной призмы, достаточно вычислить площади сторон прямоугольника:
-
A = 2 * (A1 + A2 + A3)
где:
-
A1 = l * w -
A2 = Ш * В -
A3 = Д * В
Таким образом, окончательная формула:
-
A = 2 * (l * w + w * h + l * h)
Площадь поверхности треугольной призмы
Чтобы понять, откуда берется формула площади поверхности треугольной призмы, давайте посмотрим на этот вывод:
- Часть площади боковой поверхности в этом случае легко вычислить.
 Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:
Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:
-
A(боковой) = a * h + b * h + c * h = h * (a + b + c)
, что мы также можем записать в виде:
-
A(боковое) = h * P, гдеP— периметр базового треугольника
- Затем найдите площадь треугольного основания. Вы можете сделать это разными способами, в зависимости от того, что вам дано. В нашем калькуляторе мы реализовали расчет на основе формулы Герона — она используется, когда у вас есть три стороны треугольника (SSS).
A(основание) = 0,25 * √((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)))
- Окончательная формула площади поверхности треугольной призмы:
-
A = A(боковой) + 2 * A(базовый) -
A = h * (a + b + c) + 0,5 * √((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c) ))
Площадь поверхности тела
Вы можете вычислить поверхность любого твердого тела, например, вашего тела - это не обязательно должна быть простая фигура из геометрии! Если вам интересно, какова площадь внешней поверхности человеческого тела, посмотрите этот калькулятор площади поверхности тела.
Как рассчитать площадь поверхности шара?
Если вы хотите найти площадь поверхности сферы, вам необходимо выполнить следующие действия:
- Определите радиус сферы. Мы можем принять радиус 10 см.
- Введите это значение в формулу
A = 4πr². - Рассчитайте результат:
А = 4π * 10² = 1256 см². - Вы также можете использовать этот калькулятор площади поверхности, чтобы найти радиус сферы, если вы знаете ее площадь.
Прочие соображения
Единицами площади поверхности всегда являются квадратные единицы длины. Например, вы можете выразить его в см², дюймах², футах², м², а также в акрах и гектарах.
Если вы хотите найти объем любого из этих тел, воспользуйтесь нашим калькулятором объема.
Богна Шик и Ханна Памула, кандидаты наук
Радиус (r)
Площадь поверхности
Площадь поверхности
Посмотрите 20 похожих калькуляторов 3D-геометрии 📦
Площадь полушарияКубКуб Вычислить: найти v, a, d… Еще 17
Калькулятор площади поверхности
Используйте приведенные ниже калькуляторы для расчета площади поверхности нескольких распространенных форм.
Площадь поверхности шара
Площадь поверхности конуса
Площадь поверхности куба
Площадь поверхности цилиндрического резервуара
Площадь поверхности прямоугольного резервуара
| |||||||||
Площадь поверхности капсулы
Площадь поверхности крышки
Для расчета укажите любые два значения ниже.
| |||||||||
Площадь конической усеченной поверхности
| |||||||||
Площадь поверхности эллипсоида
| |||||||||
Площадь поверхности квадратной пирамиды
Калькулятор связанных объемов | Калькулятор площади | Калькулятор площади поверхности тела
Площадь поверхности твердого тела является мерой общей площади, занимаемой поверхностью объекта. Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах Калькулятор объема и Калькулятор площади. Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для более подробной информации о каждом отдельном объекте.
Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах Калькулятор объема и Калькулятор площади. Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для более подробной информации о каждом отдельном объекте.
Сфера
Площадь поверхности (SA) сферы можно рассчитать с помощью уравнения:
SA = 4πr 2
где r — радиус
Ксаэль не любит ни с кем делиться своими шоколадными трюфелями. Когда она получает коробку трюфелей Lindt, она начинает вычислять площадь поверхности каждого трюфеля, чтобы определить общую площадь поверхности, которую ей нужно облизать, чтобы уменьшить вероятность того, что кто-нибудь попытается съесть ее трюфели. Учитывая, что каждый трюфель имеет радиус 0,325 дюйма:
SA = 4 × π × 0,325 2 = 1,327 дюйма 2
Конус
Площадь поверхности круглого конуса можно рассчитать, суммируя площади поверхности каждого из его отдельных компонентов. «Основной SA» относится к кругу, который содержит основание в замкнутом круглом конусе, в то время как боковой SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого, а также общего SA замкнутого круглого конуса показаны ниже:
«Основной SA» относится к кругу, который содержит основание в замкнутом круглом конусе, в то время как боковой SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого, а также общего SA замкнутого круглого конуса показаны ниже:
база SA = πr 2
боковой SA = πr√r 2 + h 2
общая SA = πr(r + √r 2 + h 2 )
где r — радиус, а h — высота
Афина недавно заинтересовалась культурой Юго-Восточной Азии и особенно очарована конической шляпой, обычно называемой «рисовой шляпой», которая обычно используется в ряде стран Юго-Восточной Азии. Она решает сшить свое собственное и, будучи очень практичным человеком, не погрязшим в сентиментальности, достает свадебное платье своей матери из темных ниш шкафа, в котором оно находится. Она определяет площадь поверхности материала, которая ей нужна для создания шляпы радиусом 1 фут и высотой 0,5 фута, следующим образом:
боковая сторона SA = π × 0,4√0,4 2 + 0,5 2 = 0,805 фута 2
куб
СА = 6а 2
где a — длина ребра
Анна хочет подарить своему младшему брату кубик Рубика на день рождения, но знает, что у ее брата короткая продолжительность концентрации внимания и он легко расстраивается. Она заказывает кубик Рубика, в котором все грани черные, и должна заплатить за настройку в зависимости от площади поверхности кубика с длиной ребра 4 дюйма.
Она заказывает кубик Рубика, в котором все грани черные, и должна заплатить за настройку в зависимости от площади поверхности кубика с длиной ребра 4 дюйма.
SA = 6 × 4 2 = 96 дюймов 2
Цилиндрический резервуар
Площадь поверхности закрытого цилиндра можно вычислить, суммируя площади его основания и боковой поверхности:
основание SA = 2πr 2
боковой SA = 2πrh
общая СА = 2πr(r + h)
где r — радиус, а h — высота
У Джереми есть большой цилиндрический аквариум, в котором он купается, потому что он не любит душ или ванну. Ему любопытно, остывает ли его нагретая вода быстрее, чем в ванне, и ему нужно рассчитать площадь поверхности его цилиндрического резервуара высотой 5,5 фута и радиусом 3,5 фута.
общая SA = 2π × 3,5(3,5 + 5,5) = 197,920 футов 2
Прямоугольный резервуар
Площадь поверхности прямоугольного резервуара равна сумме площадей каждой из его сторон:
SA = 2лв + 2лв + 2вч
где l — длина, w — ширина, h — высота
Банана, старшая дочь в длинной череде банановых фермеров, хочет научить свою избалованную гнилую младшую сестру, Банан-Хлеб, урок о надежде и ожиданиях. Banana-Bread всю неделю требовала новый набор ящиков для своих новых фигурок Бэтмена. Таким образом, Банана покупает ей большой кукольный дом Барби с кухонной утварью ограниченного выпуска, духовкой, фартуком и реалистичными гниющими бананами для Бэтмена. Она упаковывает их в прямоугольную коробку тех же размеров, что и ящик, который хочет Banana-Bread, и ей нужно определить количество оберточной бумаги, которое ей нужно, чтобы завершить презентацию подарка в виде сюрприза 3 фута × 4 фута × 5 футов:
Banana-Bread всю неделю требовала новый набор ящиков для своих новых фигурок Бэтмена. Таким образом, Банана покупает ей большой кукольный дом Барби с кухонной утварью ограниченного выпуска, духовкой, фартуком и реалистичными гниющими бананами для Бэтмена. Она упаковывает их в прямоугольную коробку тех же размеров, что и ящик, который хочет Banana-Bread, и ей нужно определить количество оберточной бумаги, которое ей нужно, чтобы завершить презентацию подарка в виде сюрприза 3 фута × 4 фута × 5 футов:
SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 фута 2
Капсула
Площадь поверхности капсулы можно определить путем объединения уравнения площади поверхности шара и площади боковой поверхности цилиндра. Обратите внимание, что площадь поверхности оснований цилиндра не включена, поскольку она не составляет часть площади поверхности капсулы. Общая площадь поверхности рассчитывается следующим образом:
СА = 4πr 2 + 2πrh
где r радиус и h высота
Горацио производит плацебо, предназначенное для оттачивания индивидуальности, критического мышления и способности объективно и логически подходить к различным ситуациям. Он уже протестировал рынок и обнаружил, что подавляющее большинство населения из выборки не обладает ни одним из этих качеств и очень готово покупать его продукт, еще больше укореняясь в чертах, от которых они так отчаянно стремятся избавиться. Горацио нужно определить площадь поверхности каждой капсулы, чтобы он мог покрыть их чрезмерным слоем сахара и обратиться к предрасположенным к сахару языкам населения, готовясь к своему следующему плацебо, которое «излечивает» все формы сахарного диабета. Учитывая, что в каждой капсуле R из 0,05 дюйма и ч 0,5 дюйма:
Он уже протестировал рынок и обнаружил, что подавляющее большинство населения из выборки не обладает ни одним из этих качеств и очень готово покупать его продукт, еще больше укореняясь в чертах, от которых они так отчаянно стремятся избавиться. Горацио нужно определить площадь поверхности каждой капсулы, чтобы он мог покрыть их чрезмерным слоем сахара и обратиться к предрасположенным к сахару языкам населения, готовясь к своему следующему плацебо, которое «излечивает» все формы сахарного диабета. Учитывая, что в каждой капсуле R из 0,05 дюйма и ч 0,5 дюйма:
SA = 4π × 0,05 2 + 2π × 0,05 × 0,5 = 0,188 в 2
Spherical Cap
в зависимости от высоты рассматриваемого сегмента. Предоставленный калькулятор предполагает твердую сферу и включает основание колпачка в расчет площади поверхности, где общая площадь поверхности представляет собой сумму площади основания и площади боковой поверхности сферического колпачка. Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Имея два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, приведенных в калькуляторе объема. Уравнения площади поверхности следующие:
Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Имея два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, приведенных в калькуляторе объема. Уравнения площади поверхности следующие:
сферический колпачок SA = 2πRh
основание SA = πr 2
Общая твердая сфера SA = 2πRh + πr 2
где R — радиус сферической крышки, r — радиус основания, а h — высота
Дженнифер завидует глобусу, который ее старший брат Лоуренс получил на день рождения. Поскольку Дженнифер на две трети младше своего брата, она решает, что заслуживает одну треть земного шара своего брата. Вернув ручную пилу отца в сарай для инструментов, она вычисляет площадь поверхности своей полой части земного шара с помощью 9.0856 R 0,80 фута и h 0,53 фута, как показано ниже:
SA = 2π × 0,80 × 0,53 = 2,664 фута площадей его двух круглых концов и площади его боковой поверхности:
круглый конец SA = π(R 2 + r 2 )
боковой SA = π(R+r)√(R-r) 2 + h 2
общая SA = π(R 2 + r 2 ) + π(R+r)√(R-r) 2 + h 2
где R и r — радиусы концов, h — высота
Пол делает вулкан в форме усеченного конуса для своего проекта научной ярмарки. Пол рассматривает извержения вулканов как насильственное явление и, выступая против всех форм насилия, решает сделать свой вулкан в виде закрытого конического усеченного конуса, который не извергается. Хотя его вулкан вряд ли произведет впечатление на судей научной выставки, Пол все же должен определить площадь поверхности материала, который ему нужен, чтобы покрыть внешнюю стену своего вулкана R 1 фут, r 0,3 фута и h 1,5 фута:
Пол рассматривает извержения вулканов как насильственное явление и, выступая против всех форм насилия, решает сделать свой вулкан в виде закрытого конического усеченного конуса, который не извергается. Хотя его вулкан вряд ли произведет впечатление на судей научной выставки, Пол все же должен определить площадь поверхности материала, который ему нужен, чтобы покрыть внешнюю стену своего вулкана R 1 фут, r 0,3 фута и h 1,5 фута:
всего SA = π(1 2 + 0,3 2 ) + π(1 + 0,3) √ 0,3) 2 + 1,5 2 = 10,185 футов 2
Эллипсоид
Вычисление площади поверхности эллипсоида не имеет простой и точной формулы, такой как куб или другая более простая форма. Калькулятор выше использует приблизительную формулу, которая предполагает почти сферический эллипсоид:
SA ≈ 4π 1,6 √(а 1,6 б 1,6 + а 1,6 в 1,6 + б 1,6 9) 30 9007 9 в 19003 где a , b и c — оси эллипса
Колтейн всегда любила готовить и недавно выиграла на конкурсе керамический нож. К несчастью для его семьи, которая питается почти исключительно мясом, Колтейн практиковал свою технику нарезки на чрезмерном количестве овощей. Вместо того чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических надрезов кабачка с осями 0,1, 0,2 и 0,35 дюйма:
К несчастью для его семьи, которая питается почти исключительно мясом, Колтейн практиковал свою технику нарезки на чрезмерном количестве овощей. Вместо того чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических надрезов кабачка с осями 0,1, 0,2 и 0,35 дюйма:
SA ≈ 4π 1,6 √ (0,1 1,6 0,2 1,6 + 0,1 1,6 0,35 1,6 + 0,2 1,6 0,35 1.6 )/3 = 0,562 в 2 2 3 .. 2 2 2 2 2 2 2 2 2 .. 2 2 . Площадь поверхности квадратной пирамиды состоит из площади ее квадратного основания и площади каждой из четырех треугольных граней. Учитывая высоту h и длину ребра a , площадь поверхности можно рассчитать с помощью следующих уравнений: база SA = a 2 В классе Вонквайлы недавно завершилось строительство модели Великой пирамиды Гизы.
боковой SA = 2a√(a/2) 2 + h 2
всего SA = a 2 + 2a√(a/2) 2 + h 2 



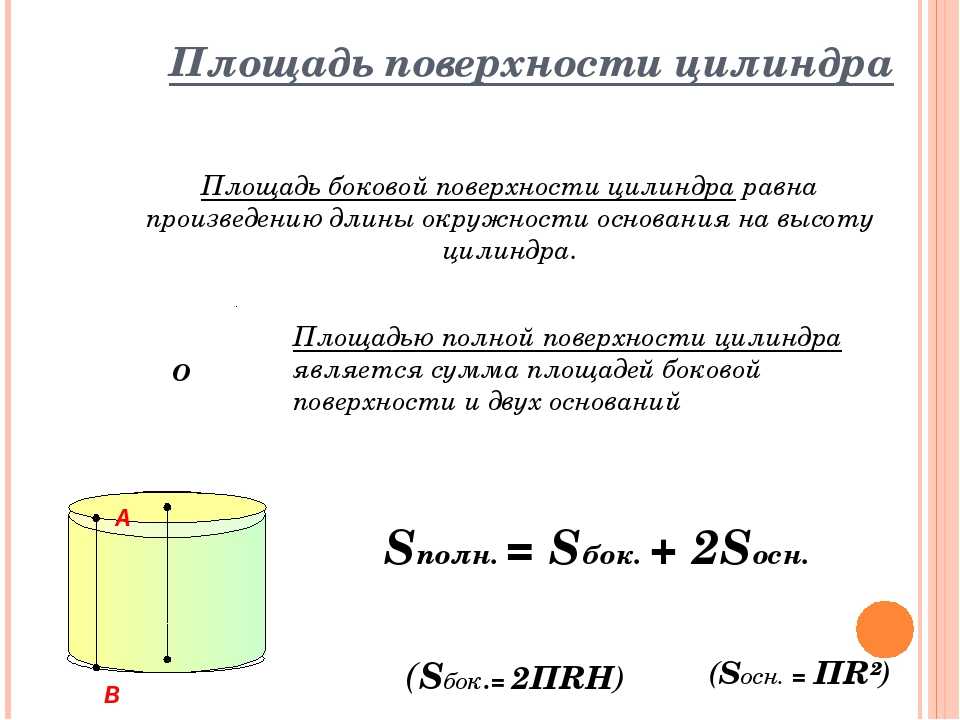
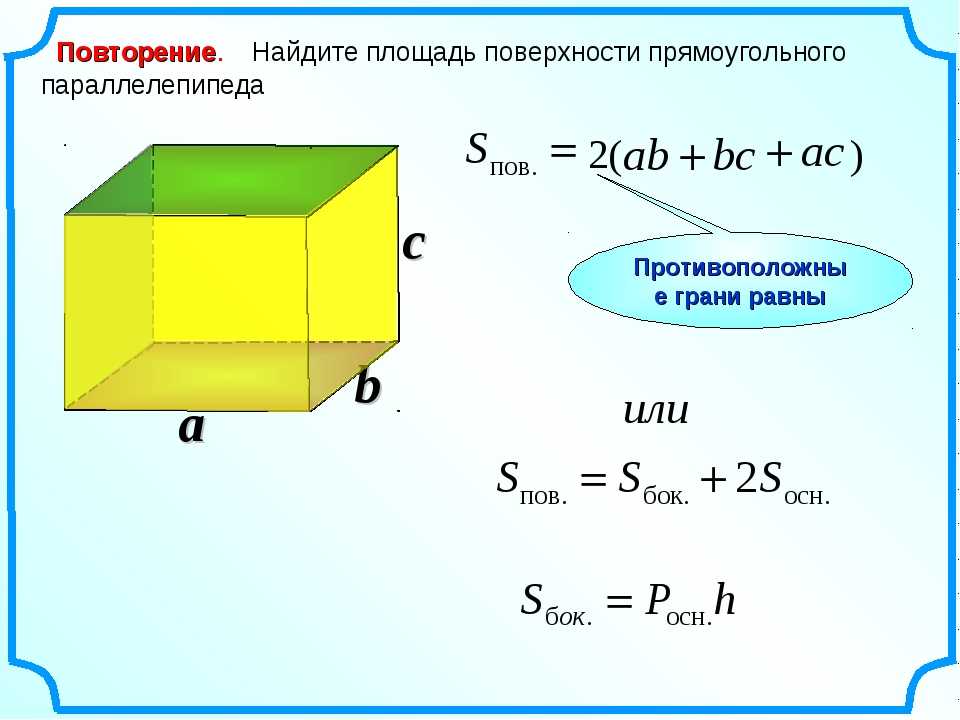

 В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
В сокращённом виде его принято обозначать числом, равным 3,14. Но на самом деле, после тройки идёт больше тысячи цифр!
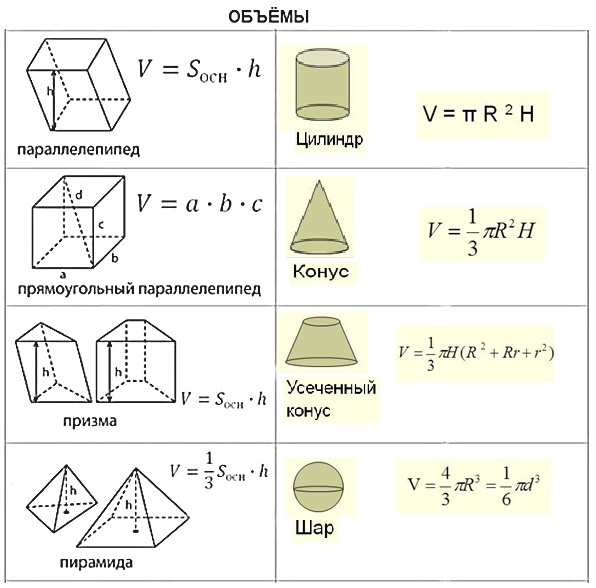
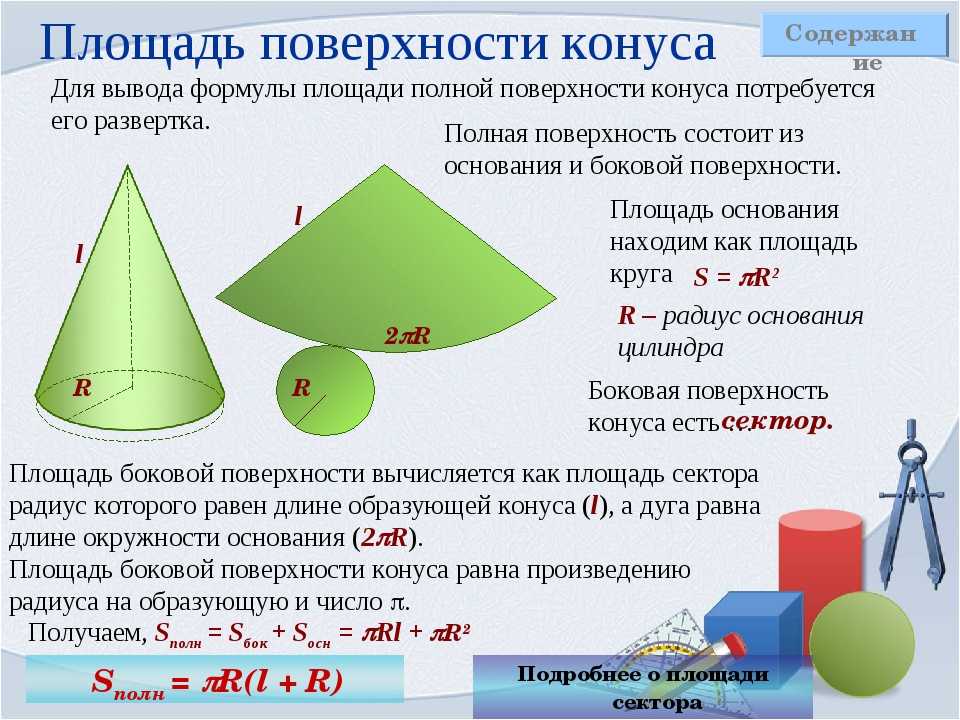
 5.1: Формулы площади
5.1: Формулы площади 5.2: Формулы площади поверхности
5.2: Формулы площади поверхности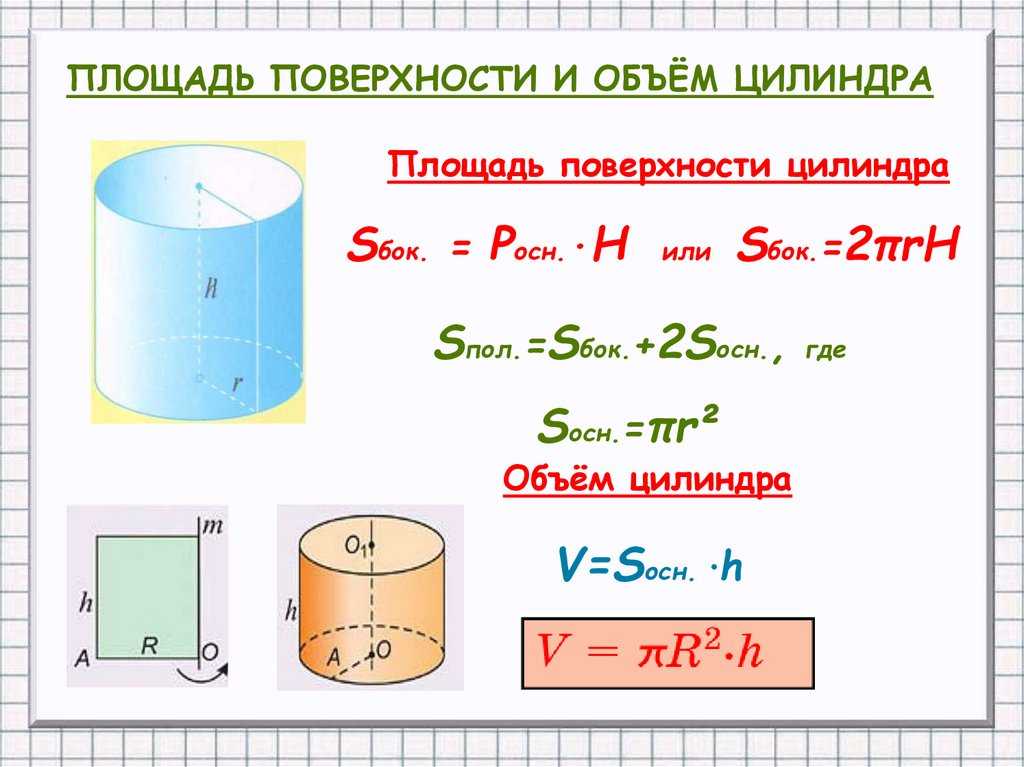 Сложите все области.
Сложите все области.