По заданным графикам найти начальные координаты: №22. По заданным графикам (рис. 9) найти начальные координаты тел и проекции скорости их движения. Написать уравнения движения тел х = x(t). Из графиков и уравнений найти время и место встречи тел, движения которых описываются графиками II и III.

№ 22. ГДЗ Физика 10 класс Рымкевич. Помогите написать уравнения движения тел – Рамблер/класс

№ 22. ГДЗ Физика 10 класс Рымкевич. Помогите написать уравнения движения тел – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

По заданным графикам (рис. 15) найти начальные координаты тел и проекции скорости их движения. Написать уравнения движения тел х = x(t). Из графиков и уравнений найти время и место встречи тел, движения которых описываются графиками II и III.

 

ответы

Закон движения в общем случае имеет вид x(t) = х₀ + vt. Согласно рисунку, для тела I х₀₁ = 5 м, v₁ = 0,    для   тела   II   при   t = 0   х₂ = х₀₂ = 5 м,    х₂(20 с) = -15 м, значит,
 
Для тела III при t = 0
х₃ = х₀₃ = -10 м
х₃(20 с) = -15 м,
тогда

Из уравнений
 
следует, что встреча произойдет через промежуток времени t = 10 с в точке х = -5 м.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.

Я.

Досуг

Химия

похожие вопросы 5

ГДЗ по Физике Громов 10 класс, вопросы. Гл.4§22№4. . На чем основа- на гравиметрическая разведка?

Помогите ответить на вопрос Гл.4§22№4. 
На чем основана гравиметрическая разведка?
 

ГДЗ10 классГромов С.В.Физика

ГДЗ.Физика 11. класс.Рымкевич.Глава 10.Электрический ток в различных средах..Задание 859.Найти приблизительно температуру накала вольфрамовой нити.

Решите пожалуйста:
          На баллоне электрической лампы написано 220 В,
100 Вт. Для измерения сопротивления нити накала (Подробнее…)

ГДЗФизика11 классРымкевич А.П.

ГДЗ по Физике 10 класс Громов, вопросы. Гл.5§31№1. Чему равна полная механическая энергия?

Как ответить на вопрос Гл.5§31№1.
Чему равна полная механическая энергия?

ГДЗФизика10 классГромов С. В.

Выполните деление. ГДЗ Математика 6 класс Чесноков. Дидактические материалы по математике для 6 класса. Вар.1 Вопр.161

Кто сможет? Выполните деление:
  (Подробнее…)

ГДЗМатематика6 классЧесноков А.С.

ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№45. Зад.№1.Под руководством Ященко. Помогите найти значение выражения.

Здравствуйте! Помогите найти значение выражения: (Подробнее…)

ГДЗЭкзаменыМатематикаЯщенко И.В.

Сборник задач — Приступа

ОГБОУ «Колледж индустрии питания, торговли и сферы услуг»

Сборник

вопросов и задач

по физике

для студентов 1 курса обучающимся по специальностям среднего профессионального образования

Томск – 2013

Автор составитель:

Приступа Татьяна Юрьевна,

преподаватель физики КИПТСУ

Приступа Т.Ю.

Физика. Вопросы и задачи по физике для студентов 1 курса

обучающимся по специальностям среднего профессионального

образования / Т. Ю. Приступа. Томск: КИПТСУ, 2013 – 89 с.

2

Предисловие

Овладеть курсом физики – это значит не только понять физические явления и закономерности, но и научится применять их на практике. Всякое примененние общих положений физики для разрешения конкретного, частного вопроса есть решение физической задачи. Умение решать задачи делает знания действенными, практичеки применимыми.

Приступая к решению задачи, нужно прежде всего вникнуть в смысл задачи и установить какие физические явления и закономерности лежат в основе, какие из описанных в ней процессов являются главными и какими можно пренебречь. Надо выяснить, какие упрощающие положения можно ввести для решения задачи. Рассчитывая, например, времяпадения тела с некоторой высоты, исходят из следующих упрощений: тело считают материальной точкой, ускорение свободного падения – постоянным, сопротивление воздуха не учитывают.принятые допущения отмечают при анализе задачи.

В тексте задач сборника не указывается степень точности некоторых числовых данных, устанавливаемая путем прибавления справа значащих нулей (2 м, 0,3 А и т. д.), следует считать либо условно точечными (наперед значммыми), либо приближенными с той степенью точности, с которой заданы другие величины, входящие в задачу. Точность ответа не должна превышать точности исходных данных.

Используя табличные значения величин и физических постоянных, следует округлять их со степенью точности, определяемой условием конкретной задачи.

3

В задачах с конкретным содержанием из области: техники, сельского хозяйства, спорта, быта, а так же в задачах с историческим содержанием приведены реальные паспортные, справочные или исторические данные с точностью, заданной в соответствующих источниках. Вычисления в таких задачах , естественно, становяться более громозкими. Поэтому при их решении целесообразно пользоваться микрокалькулятором. при отсутствии микрокалькулятора данные следует округлить до двух-трех значащих цифр.

Прежде чем приступить к вычислениям, следует все исходные данные выразить в одной системе единиц. В большинстве случаев задачи рекомендуется решать в Международной систме единиц (СИ). При решении задач по квантовой, атомной и ядерной физике рекомендуется пользоваться единицами принятыми в соответствующих отраслях науки, т.е. массу выражать в атомных единицах массы. а энергию – в мегаэлетронвольтах.

Многие задачи целесообразно решать устно. Это относится к большинству качественных задач и вопросам, многим тренеровочным, а также к задачам на исследование функциональной зависимости типа: «Во сколько раз изменится величина y при изменении величины x в n раз?».

4

МЕХАНИКА

Основные понятия классической механики.

1.Что такое кинематика?

2.Что называют перемещением?

3.Как рассчитывать перемещение при равномерном движении?

4.Как рассчитывать перемещение при неравномерном движении?

5.Как вычисляется скорость равномерного прямолинейного движения?

6.Что называют ускорением?

7.Скорость материальной точки изменилась по закону = 4 (м/с). Запишите уравнение движения = ( ), если в начале движения координата точки была 0 = 5 м.

8.При экстренном торможении автомобиль, двигавшийся со скоростью 36 км/ч, останавливается через 3 с после начала торможения. Какой тормозной путь он прошел?

9.Тело переместилось их точки с координатами х1=3; у1=-1 в

точку с координатами х2=5; у2=8. Сделать чертеж, найти перемещение и его проекции на оси координат.

10.	Движение	двух велосипедистов	заданы уравнениями: 1 =
5 ;	2 = 5 − 10 .	Построить графики	зависимости
	. Найти время и место встречи.
11.	По заданным графикам найти начальные
координаты тел. Написать уравнение движения тел
= . Из графика и уравнений			найти место
встречи тел.

12.Через какой промежуток времени с момента

старта мотоциклист, двигаясь с постоянным ускорением а = 5 м с2,

разовьет скорость = 90 км ч? На каком расстоянии от места старта

это произойдет?

5

13.Автомобиль движется в северном направлении со скоростью 90

км/ч. Найдите модуль и направление его постоянного ускорения при

торможении перед светофором за 4 с. Рассчитайте длину тормозного

пути.

14.За какое время, двигаясь равно замедленно с ускорением а, тело уменьшает вдвое начальную скорость 0? Какой путь проходит тело за это время?

15.За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 м/с2, пройдет 30 м?

16.При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найти тормозной путь.

17.Поезд через 10 с после начала движения приобретает скорость

0,6 м/с. Через какое время от начала движения скорость поезда станет

равна 3 м/с?

18. Велосипедист движется под уклон с ускорением 0,3 м/с2. Какую скорость приобретет велосипедист через 20 с, если его начальная скорость равна 4 м/с?

19.За какое время автомобиль, двигаясь с ускорением 0,4 м/с2,

увеличит свою скорость с 12 м/с до 20 м/с?

20. Движение грузового автомобиля описывается уравнением

1 = −270 + 12 , а движение пешехода по обочине того же шоссе – уравнением 2 = −1,5 . Сделать пояснительный рисунок (ось Х направит в право), на котором указать положение автомобиля и пешехода в момент начала наблюдения. С какими скоростями и в каком направлении они двигались? Когда и где они встретились?

21.Движение двух велосипедистов заданы уравнениями: 1 = 5 ,

2 = 150 − 10 . Построить графики зависимости . Найти время и место встречи.

22.По заданным графикам (рис.9) найти начальные координаты

тел. Написать уравнения движения тел = . Из графиков и

6

уравнений найти время и место встречи тел, движение которых описываются графиками II и III.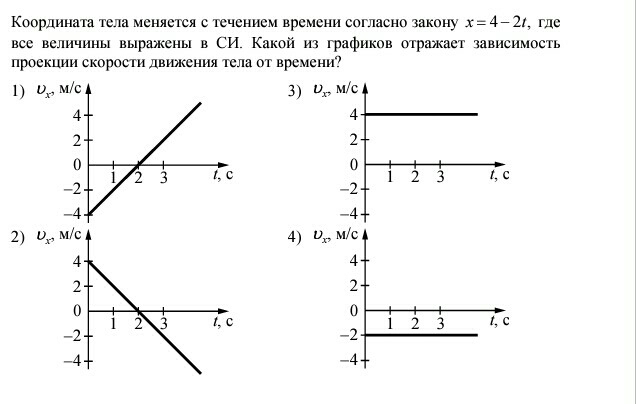

23.Графики движения двух тел представлены на рис.10. Написать уравнение движения = .

24.При экстренном торможении, двигавшийся со скоростью 180 км/ч,

останавливается через 20 с, после начала торможения. Какой тормозной путь он прошел?

25.Через какой промежуток времени с момента старта,

мотоциклист двигаясь с постоянным ускорением 1,5 м/с2, разовьет

скорость 108 км/ч. На каком расстоянии от места старта это

произойдет?

26.Автомобиль двигаясь со скоростью 144 км/ч, тормозит перед светофором за 10 с. Рассчитайте длину тормозного пути.

27.За какое время автомобиль двигаясь из состояния покоя с ускорением 5 м/с2 пройдет 15 м?

28.При аварийном торможении автомобиль двигавшийся со скоростью 162 км/ч, останавливается за 20 с Найдите длину тормозного пути.

29.Велосипедист движется под уклон с ускорением 1,3 м/с2. Какую скорость разовьет велосипедист через 30 с, если его начальная скорость 10 м/с.

30.За какое время автомобиль двигаясь с ускорением 1,4 м/с2

увеличит свою скорость с 2 м/с до 16 м/с

31. При экстренном торможении, двигавшийся со скоростью 360

км/ч, останавливается через 3 минуты, после начала торможения.

Какой тормозной путь он прошел?

7

32.Через какой промежуток времени с момента старта,

мотоциклист двигаясь с постоянным ускорением 2,5 м/с2, разовьет

скорость 126 км/ч. На каком расстоянии от места старта это

произойдет?

33.Автомобиль двигаясь со скоростью 54 км/ч, тормозит перед светофором за 2 с. Рассчитайте длину тормозного пути.

34.За какое время автомобиль двигаясь из состояния покоя с ускорением 8 м/с2 пройдет 24 м?

35.При аварийном торможении автомобиль двигавшийся со скоростью 288 км/ч, останавливается за 4 минуты. Найдите длину тормозного пути.

36.Велосипедист движется под уклон с ускорением 0,5 м/с2. Какую скорость разовьет велосипедист через 1,5 минуты, если его начальная скорость 18 км/ч.

37.За какое время автомобиль двигаясь с ускорением 2,5 м/с2

увеличит свою скорость с 5 м/с до 72 км/ч

38. При экстренном торможении, двигавшийся со скоростью 216

км/ч, останавливается через 45 с, после начала торможения. Какой

тормозной путь он прошел?

39.Через какой промежуток времени с момента старта,

мотоциклист двигаясь с постоянным ускорением 4,5 м/с2, разовьет

скорость 198 км/ч. На каком расстоянии от места старта это

произойдет?

40.Автомобиль двигаясь со скоростью 234 км/ч, тормозит перед светофором за 2,5 минуты. Рассчитайте длину тормозного пути.

41.За какое время автомобиль двигаясь из состояния покоя с ускорением 6 м/с2 пройдет 36 м?

42.При аварийном торможении автомобиль двигавшийся со скоростью 252 км/ч, останавливается за 2 минуты. Найдите длину тормозного пути.

8

43.Велосипедист движется под уклон с ускорением 0,8 м/с2. Какую скорость разовьет велосипедист через 40 с, если его начальная скорость 9 км/ч.

44.За какое время автомобиль двигаясь с ускорением 1,2 м/с2

увеличит свою скорость с 5 м/с до 54 км/ч

Динамические характеристики движения

45Какие свойства тел характеризует масса?

46Что понимают под аддитивностью массы?

47Что характеризует сила?

48Что называют импульсом тела?

49Что называют импульсом силы?

50Чем материальная точка отличается от геометрической?

51В каких случаях можно применять модель материальной точки?

52Что такое абсолютно твердое тело?

53Какую силу в горизонтальном направлении необходимо приложить, чтобы сдвинуть стоящий на горизонтальном полу ящик массой 20 кг, если коэффициент трения между ящиком и полом 0,5?

54На сколько сантиметров растянется пружина жесткостью 100

Н/м, если к ней подвесить гирю массой 200 г?

55С какой скоростью должен ехать мотоциклист, чтобы его импульс был равен импульсу легкового автомобиля, движущегося со скоростью 60 км/ч? масса мотоцикла 350 кг, масса автомобиля 1,05 т.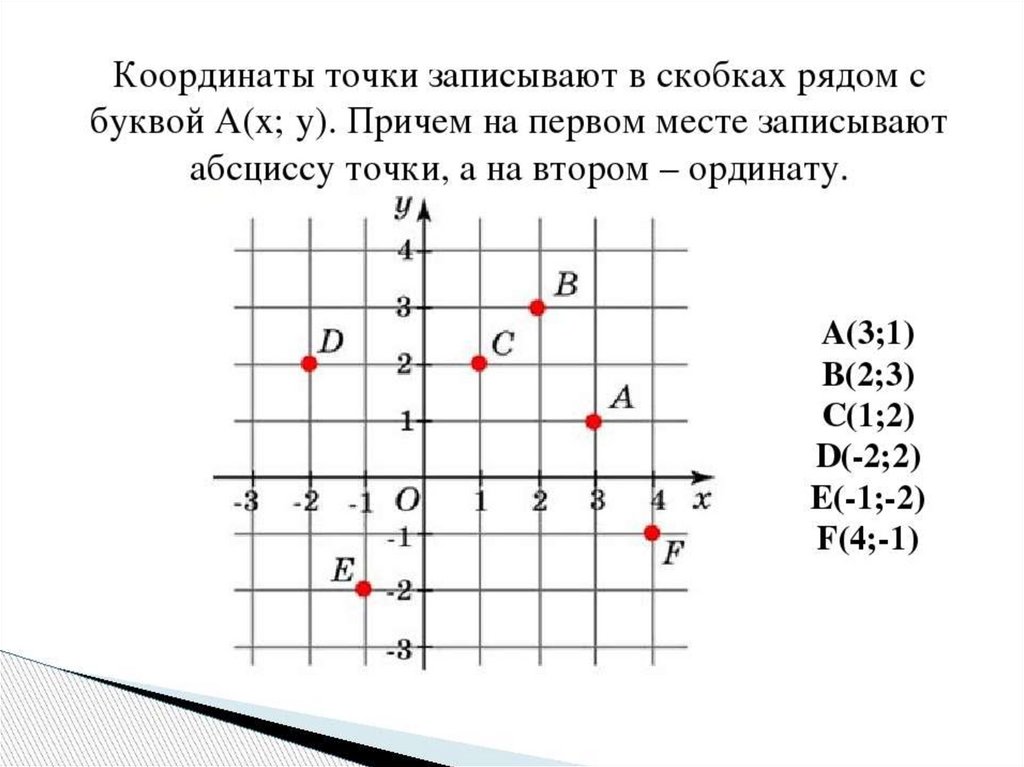

56Когда четыре человека массой по 70 кг садятся в автомобиль,

пружина амортизатора автомобиля сжимается на 2,5 см. Найдите жесткость одной пружины, если всего пружин – четыре.

57 Найти массу стального бруска, равномерно скользящего по горизонтальной стальной поверхности под действием силы 20 Н. Сила

9

направлена вдоль поверхности стола. Коэффициент трения

скольжения равен 0,4.

58С какой силой упряжка собак равномерно перемещает сани с грузом массой 250 кг, если коэффициент трения скольжения 0,1?

59Для сооружения памятника Петру I в XVIII в. гранитную глыбу массой 1600 т перевозили на салазках, катившихся по пушечным ядрам. Зная силу тяги 157 кН при равномерном движении, найдите коэффициент трения качения.

60Деревянный брусок массой 1 кг тянут равномерно по горизонтальной деревянной доске с помощью пружины жесткостью

100 Н/м. Найдите удлинение пружины, если коэффициент трения

скольжения 0,5.

61Какие силы надо приложить к концам проволоки, жесткость которой 100 кН/м, чтобы растянуть ее на 1 мм?

62Две пружины разной длины, скрепленные одними концами,

растягивают за свободные концы руками. Пружина жесткостью 100

Н/м, удлинилась на 5 см. Какова, жесткость второй пружины, если ее

удлинение равно 1 см?

63Упряжка собак при движении саней по снегу может действовать с максимальной силой 0,5 кН. Какой массы сани с грузом может перемещать упряжка, если коэффициент трения равен 0,1?

64На соревнованиях лошадей тяжелоупряжных пород одна из них перевезла груз массой 23 т. Найти коэффициент сопротивления, если сила тяги лошади 2,3 кН.

65Деревянный брусок массой 2 кг тянут по деревянной доске,

расположенной горизонтально, с помощью пружины жесткостью 100

Н/м. Коэффициент трения равен 0,3. Найти удлинение пружины.

66 Найти импульс грузового автомобиля массой 10 т, движущегося со скоростью 36 км/ч, и легкового автомобиля массой 1 т,

движущегося со скоростью 25 м/с.

10

графиков

графиков

Цели
Изучив этот отряд, вы сможете:

• Определите оси x и y .
• Определите источник . на графике.
• Определение координат точки x и y .
• Точки на графике.

Элементы графика

Мы часто используем графики, чтобы получить представление о отношения между переменными. Сначала рассмотрим основные построение графиков.

График — это визуальное представление отношения между двумя переменными, x и y . График состоит из двух осей, называемых x (по горизонтали) и и (вертикальные) оси. Эти оси соответствуют переменным мы относимся. В экономике мы обычно придаем осям разные имена, такие как Цена и Количество. Точка пересечения двух осей называется исходной точкой . Начало координат также определяется как точка (0, 0).

Координаты точек

Точка — это основное отношение, отображаемое на графике. Каждая точка определяется парой чисел, содержащих две координаты. Координата является одним из набора чисел используется для определения местоположения точки на графике. Каждый точка обозначается как x и y координата . В этом модуле вы научитесь находить обе координаты для любого точка. Вы также узнаете правильные обозначения для маркировки координаты точки. Сначала вы начнете с определения x-координата точки.

Идентификация x-координаты

x -координата пункта — это значение, которое сообщает вам, как далеко от начала координат находится точка по горизонтали, или x — ось. Чтобы найти координату x точка на графике:

Проведите прямую линию из точки прямо до оси x . Число, где линия достигает оси x является значением координаты x . Справа график с двумя точками, B и D. В этом цифра: x — координата точки B равна 100. Координата точки D размером x равна 400.

Определение координаты Y

Как мы уже упоминали, каждая точка определяется двумя координатами , координаты x и y . Теперь, когда вы знаете, как чтобы найти x -координату точки, вы должны быть в состоянии найти у -координата. у -координата точки — это значение, которое говорит вам, как далеко от начала координат точка находится на вертикальной оси или y -оси. Найти y -координата точки на графике:

Проведите прямую линию из точки прямо к оси и . Число, где линия касается оси, является значение у -координата. Оглядываясь назад на график с нашими точками B и D, мы теперь определить координату y для каждого. y -координата точки B равна 400. y -координата точки D равна 100.

Обозначение для обозначения точек

Когда у вас есть координаты точки, вы можете использовать упорядоченный парная запись для обозначения точек. Обозначение простое. Точки идентифицируются заданием их координат в виде ( х , и ). Обратите внимание, что x -координата всегда приходит первый. Например, на рисунке, который мы использовали, мы определили обе координаты x и y для каждой из точек Б и Д.

x -координата точки B равна 100. y -координата точки B равна 400. Координаты точки B (100, 400) Координата точки D размером x равна 400. y -координата точки D равна 100. Координаты точки D (400, 100)

Точки на осях

Если точка лежит на оси, линии рисовать не нужно определить координаты точки. На рисунке ниже точка А лежит на y 9Ось 0010, а точка C лежит на оси x . Когда точка лежит на оси, одна из ее координат должна быть равна нулю.

Точка А. Если вы посмотрите, как далеко находится точка от начала координат по оси x , ответ равен нулю. Следовательно, координата x равна нулю. Любая точка, которая лежит на оси y имеет координату нуля x .   Если двигаться по y -ось найти y -координата, точка находится в 400 от начала координат. Координаты точки А (0, 400)

• Точка C. Если вы посмотрите, как далеко находится точка от начала координат по оси y ответ равен нулю. Следовательно, координата y равна нулю. Любая точка, которая лежит на оси x есть y -координата нуля.
   
  Если вы перемещаетесь по оси x , чтобы найти координату x , точка находится в 200 от начала координат. Координаты точки С (200, 0)

Пример

Какая точка находится на оси y ? Какая точка помечена (20, 60)? Какие точки имеют y -координата из 30?

Ответы на пример

1. Какая точка находится на оси y ? Точка А
2. Какая точка помечена (20, 60)? Точка Б
3. Какие точки имеют y -координату из 30? Пункты А и С

 

[решение к примеру]

Нанесение точек на график

Бывают случаи, когда вам дают точку и нужно будет найти его расположение на графике. Этот процесс часто называют построение точки и использует те же навыки, что и определение координат точки на графике. Показан процесс нанесения точки используя пример.

Пример

Нанесите точку (200, 300).

Шаг первый	Шаг второй	Шаг третий
Сначала нарисуйте линию, идущую от оси x в x -координата точки. В нашем примере это на 200.	Затем нарисуйте линию, идущую от оси y в y -координата точки. В нашем примере это на 300.	Точка пересечения этих двух прямых находится в точке, которую мы строят, (200, 300).

Теперь вы готовы решить тренировочную задачу. Если вы уже выполнили первую практическую задачу для этого модуля, который вы можете пожелать попробовать дополнительную практику.

[практика]	[дополнительный практика]	[Таблица содержания]	[раздел одно резюме]

2.3 Графики положения и времени

Цели обученияПозиция на графике как функция времениУчебные задачиПроверьте свое понимание

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Объяснять значение наклона на графиках зависимости положения от времени
• Решение задач с использованием графиков положения и времени

«>

Ключевые термины раздела

зависимая переменная

независимая переменная

тангенс

График позиции как функции времени

График, как и картинка, стоит тысячи слов. Графики не только содержат числовую информацию, они также показывают отношения между физическими величинами. В этом разделе мы исследуем кинематику, анализируя графики положения во времени.

Графики в этом тексте имеют перпендикулярные оси, одна горизонтальная, а другая вертикальная. Когда две физические величины нанесены друг против друга, горизонтальная ось обычно считается независимой переменной, а вертикальная ось — зависимой переменной. В алгебре вы бы назвали горизонтальную ось цифрой 9.0413 x — ось и вертикальная ось как y — ось. Как и на рис. 2.11, линейный график имеет общий вид y=mx+by=mx+b.

Здесь м – уклон, определяемый как подъем, деленный на длину (как видно на рисунке) прямой. Буква b — это точка пересечения y , точка пересечения прямой с вертикальной осью y . С точки зрения физической ситуации в реальном мире эти величины приобретут особое значение, как мы увидим ниже. (Рисунок 2.11.)

Рисунок 2.11 На диаграмме показан линейный график. Уравнение прямой линии y равно m x + b .

В физике время обычно является независимой переменной. Говорят, что другие величины, такие как смещение, зависят от него. Таким образом, график зависимости положения от времени будет иметь положение на вертикальной оси (зависимая переменная) и время на горизонтальной оси (независимая переменная). В этом случае к какому бы наклону и y -ссылка на перехват? Давайте вернемся к нашему исходному примеру при изучении расстояния и смещения.

Дорога в школу находилась в 5 км от дома. Предположим, что поездка заняла 10 минут, и ваш родитель все это время ехал с постоянной скоростью. График зависимости положения от времени для этого участка пути будет выглядеть так, как показано на рисунке 2.12.

Рис. 2.12 Показан график зависимости местоположения от времени для поездки в школу. Как бы выглядел график, если бы мы добавили обратный путь?

Как мы уже говорили, d ₀ = 0, потому что мы называем домом наше O и начинаем вычисления оттуда. На рис. 2.12 линия также начинается с d = 0. Это b в нашем уравнении для прямой линии. Нашей начальной позицией на графике зависимости положения от времени всегда является место, где график пересекает ось x в точке t = 0. Каков наклон? Подъем — это изменение положения (т. е. смещение) и прогон это изменение времени. Это отношение также можно записать

2.4ΔdΔt.ΔdΔt.

Это соотношение было тем, как мы определили среднюю скорость. Следовательно, наклон графика d по сравнению с t представляет собой среднюю скорость.

Советы по достижению успеха

Иногда, как в случае, когда мы отображаем как поездку в школу, так и обратную дорогу, поведение графика выглядит по-разному в разные промежутки времени. Если график выглядит как серия прямых линий, то вы можете рассчитать среднюю скорость для каждого временного интервала, глядя на наклон. Если затем вы хотите рассчитать среднюю скорость за всю поездку, вы можете сделать средневзвешенное значение.

Давайте посмотрим на другой пример. На рис. 2.13 показан график зависимости положения автомобиля с реактивным двигателем от времени на очень плоском высохшем дне озера в Неваде.

Рисунок 2.13 На диаграмме показан график зависимости положения автомобиля с реактивным двигателем от времени на соляных равнинах Бонневилля.

Используя взаимосвязь между зависимыми и независимыми переменными, мы видим, что наклон на графике на рис. 2.13 представляет собой среднюю скорость, v _avg , а точка пересечения представляет собой перемещение в нулевое время, то есть д ₀ . Подстановка этих символов в y = m x + b дает

2.5d=vt+d0d=vt+d0

или

2.6d=d0+vt.d=d0+vt.

Таким образом, график зависимости положения от времени дает общую взаимосвязь между перемещением, скоростью и временем, а также предоставляет подробную числовую информацию о конкретной ситуации. Из рисунка видно, что автомобиль занимает позицию 400 м при т = 0 с, 650 м при t = 1,0 с и так далее. И мы также можем узнать о скорости объекта.

Snap Lab

График движения

В этом упражнении вы отпустите мяч вниз по пандусу и построите график смещения мяча в зависимости от времени.

Меры предосторожности

• Выберите открытое место с достаточным пространством для раскладывания, чтобы было меньше шансов споткнуться или упасть из-за катящихся шаров.

Материалы

• 1 шарик
• 1 доска
• 2 или 3 книги
• 1 секундомер
• 1 рулетка
• 6 шт. малярной ленты
• 1 лист миллиметровой бумаги
• 1 карандаш

Процедура

1. Постройте пандус, поместив один конец доски поверх стопки книг. При необходимости отрегулируйте местоположение до тех пор, пока на пути прямой линии от нижней части пандуса до следующих 3 м не будет препятствий.
2. Отметьте расстояния 0,5 м, 1,0 м, 1,5 м, 2,0 м, 2,5 м и 3,0 м от нижней части пандуса. Запишите расстояния на ленте.
3. Пусть один человек возьмет на себя роль экспериментатора. Этот человек выпустит мяч с вершины рампы. Если мяч не достигает отметки 3,0 м, увеличьте наклон пандуса, добавив еще одну книгу. Повторяйте этот шаг по мере необходимости.
4. Попросите экспериментатора отпустить мяч. Попросите второго человека, таймера, начать отсчет времени, как только мяч достигнет нижней части пандуса, и остановить отсчет времени, когда мяч достигнет 0,5 м. Попросите третьего человека, регистратора, записать время в таблицу данных.
5. Повторите шаг 4, остановив время на расстоянии 1,0 м, 1,5 м, 2,0 м, 2,5 м и 3,0 м от нижней части рампы.
6. Используйте свои измерения времени и смещения, чтобы построить график зависимости положения от времени движения мяча.
7. Повторите шаги с 4 по 6, при этом разные люди берут на себя роли экспериментатора, таймера и записывающего устройства. Получаете ли вы одинаковые значения измерений независимо от того, кто выпускает мяч, измеряет время или записывает результат? Обсудите возможные причины расхождений, если таковые имеются.

Проверка захвата

Верно или неверно: средняя скорость мяча будет меньше средней скорости мяча.

1. Правда
2. Ложь

Решение проблем с использованием графиков зависимости положения от времени

Итак, как мы можем использовать графики для решения вещей, которые мы хотим знать, таких как скорость?

Рабочий пример

Использование графика положение-время для расчета средней скорости: реактивный автомобиль

Найдите среднюю скорость автомобиля, положение которого показано на рис. 1.13.

Стратегия

Наклон графика d по сравнению с t представляет собой среднюю скорость, поскольку наклон равен превышению над пробегом.

2.7slope =ΔdΔt=vslope =ΔdΔt=v

Поскольку здесь наклон является постоянным, для его определения можно использовать любые две точки на графике.

Решение

1. Выберите две точки на прямой. В этом случае выбираем точки, отмеченные на графике: (6,4 с, 2000 м) и (0,50 с, 525 м). (Обратите внимание, однако, что вы можете выбрать любые две точки.)
2. Подставьте значения d и t выбранных точек в уравнение. Помните, что при расчете изменения (Δ) мы всегда используем конечное значение минус начальное значение.

   2,8v=ΔdΔt=2000 м-525 м6,4 с-0,50 с=250 м/с, v=ΔdΔt=2000 м-525 м6,4 с-0,50 с=250 м/с,

Обсуждение

Это впечатляюще высокая наземная скорость (900 км/ч, или около 560 миль/ч): намного больше, чем типичный предел скорости на шоссе в 27 м/с или 96 км/ч, но значительно меньше рекорд 343 м/с или 1234 км/ч, установленный в 1997.

А что, если график позиции сложнее прямой линии? Что, если объект ускорится или развернется и пойдет назад? Можем ли мы узнать что-нибудь о его скорости из графика такого движения? Давайте еще раз посмотрим на автомобиль с реактивным двигателем. График на рис. 2.14 показывает его движение по мере того, как он набирает скорость после старта из состояния покоя. Время для этого движения начинается с нуля (как если бы его измеряли секундомером), а перемещение и скорость изначально равны 200 м и 15 м/с соответственно.

Рис. 2.14 На диаграмме представлен график положения автомобиля с реактивным двигателем в течение промежутка времени, когда он разгоняется. Наклон графика зависимости расстояния от времени — это скорость. Это показано в двух точках. Мгновенная скорость в любой точке равна наклону касательной в этой точке.

Рис. 2.15 Реактивный автомобиль ВВС США мчится по рельсам. (Мэтт Тростл, Flickr)

График зависимости положения от времени на рис. 2.14 представляет собой кривую, а не прямую линию. Наклон кривой становится круче с течением времени, показывая, что скорость увеличивается с течением времени. Наклон в любой точке графика зависимости положения от времени представляет собой мгновенную скорость в этой точке. Его находят, проводя прямую линию, касающуюся кривой в интересующей точке, и измеряя наклон этой прямой. Касательные линии показаны для двух точек на рисунке 2.14. Средняя скорость равна чистому перемещению, деленному на пройденное время.

Рабочий пример

Использование графика положение-время для расчета средней скорости: реактивный автомобиль, второй дубль

Рассчитайте мгновенную скорость реактивного автомобиля за 25 с, найдя наклон касательной в точке Q на этом рисунке. .

Стратегия

Наклон кривой в точке равен наклону прямой, касательной к кривой в этой точке.

Решение

1. Найдите касательную к кривой в момент времени t=25 st=25 с.
2. Определите конечные точки касательной. Они соответствуют положению на 1300 м в момент времени 19 с и положению на 3120 м в момент времени 32 с.
3. Подставьте эти конечные точки в уравнение для определения наклона v .

   2,9уклон=vQ=ΔdQΔtQ=(3120−1300) м(32−19) с=1820 м13 с=140 м/суклон=vQ=ΔdQΔtQ=(3120−1300) м(32−19) с=1820 м13 с =140 м/с

Обсуждение

Полный график v против t может быть получен таким образом.

Практические задачи

Рисунок 2.16

Рассчитайте среднюю скорость объекта, показанного на графике ниже, за весь интервал времени.

1. 0,25 м/с
2. 0,31 м/с
3. 3,2 м/с
4. 4,00 м/с

Верно или неверно: взяв наклон кривой на графике, вы можете убедиться, что скорость реактивного автомобиля составляет 115 м/с при t = 20 с.

1. Правда
2. Ложь

Проверьте свое понимание

Упражнение 9

Какую из следующих сведений о движении можно определить, глядя на график зависимости положения от времени, который представляет собой прямую линию?

1. система отсчета
2. среднее ускорение
3. скорость
4. направление приложенной силы

Упражнение 10

Верно или неверно: график зависимости положения от времени ускоряющегося объекта представляет собой прямую линию.