Полное исследование функции и построение графика функции: Исследование функции и построение графика функции

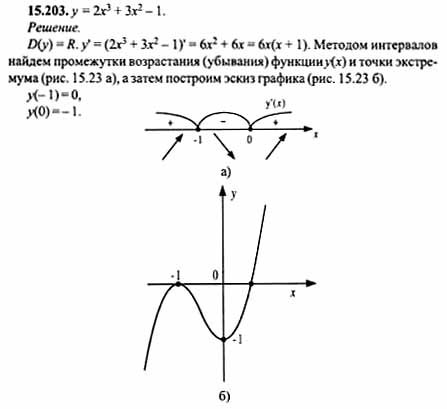
6.4 Полное исследование функции и построение её графика.

Для построения графика функции нужно знать её свойства. Это, прежде всего, область определения функции, непрерывность, поведение функции вблизи границ области определения и точек разрыва, вертикальные асимптоты. Если функция периодична, то исследовать функцию достаточно в пределах одного периода. Графики четных функций симметричны относительно оси у, нечетных – относительно начала координат, это позволяет исследовать поведение функции только при . Если это не вызывает больших вычислительных трудностей, определяются точки пересечения с осями координат и участки знакопостоянства функции. По этим данным рисуется график функции в первом приближении.

Для уточнения графика функции вычисляем первую производную и исследуем функцию на монотонность и экстремумы. Далее, находим вторую производную, участки выпуклости и вогнутости, точки перегиба.

В заключение, ищем наклонные асимптоты и рисуем окончательный график функции.

Отметим, что порядок действий при исследовании функций не догма и может быть изменен исследователем. Более того, при необходимости можно получить дополнительный ряд значений функции при некоторых частных значений аргумента.

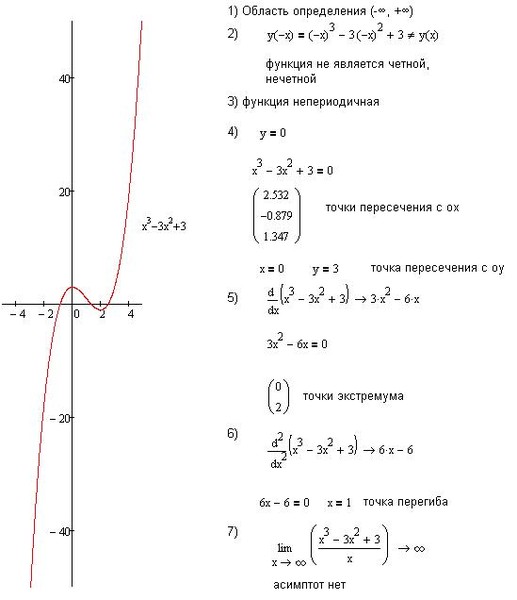
Ниже, на рисунке приведен схематический график функции , исследование которой мы, практически, полностью провели в предыдущих разделах. Отметим только очевидные свойства функции — непериодична, не является ни четной, ни нечетной и при значения функции

6.5. Наименьшее и наибольшее значения функции

Рассматривая непрерывные функции, мы отмечали такой важное свойство: функция непрерывная на замкнутом отрезке [a;b] достигает на этом отрезке своего наибольшего и наименьшего значения, причем эти значения могут приниматься либо в критических точках внутри отрезка, либо на его границе.

Таким образом, задача нахождения этих экстремальных значений достаточно проста и разбивается на несколько этапов.

Этап 1. Находим критические точки первой производной и выбираем из них те, которые лежат в рассматриваемом интервале (a;b).

Этап 2. Вычисляем значения функции в найденных критических точках и на концах интервала в точках a и b.

Этап 3. Выбираем из полученных значений наибольшее и наименьшее.

Пример. Найти наибольшее и наименьшее значения функции на отрезке [-2;1].

Решение. Находим первую производную и приравниваем к нулю, . Решаем полученное уравнение: , получим стационарные (критические) точки , которые обе лежат в заданном промежутке.

Вычисляем значения функции в критических точках и в граничных точках отрезка: . Простой визуальный анализ полученных значений показывает, что .

6.6 Экономическая интерпретация первой производной (предельный анализ)

В экономических приложениях первая производная обычно понимается как предельная или маржинальная функция. Поскольку , то приближенно описывает изменение функции при изменении независимой переменной на одну единицу, т.е. при значение производной равно изменению функции .

В отличие от средних величин, широко используемых в экономике — средняя стоимость продукции, средняя производительность труда, средний доход, средний объем продаж и т.д., дифференциальное исчисление позволяет ответить на вопрос: на какую величину вырастет результат, если будут увеличены затраты, или, наоборот, насколько уменьшится результат, если затраты сократятся, т.е. изучить процесс в динамике. В подобных задачах находят предел отношения приращений рассматриваемых величин или, как говорят, предельный эффект.

Пример 1. Пусть функция выражает зависимость суммарного дохода R от количества товара Q, тогда производная — выражает, по определению, предельный доход. Он приближенно равен изменению суммарного дохода при изменении количества реализованного товара на единицу т.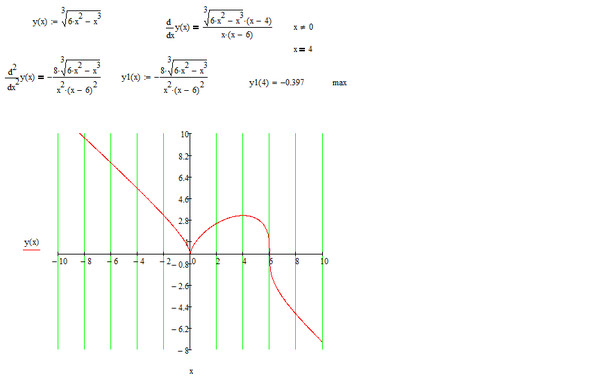 е. показывает насколько вырастет суммарный доход, если количество реализованного товара увеличится на единицу.

Пример 2. Если C= f(Q) – функциональная зависимость издержек (затрат) С от объема продукции Q, то — это предельные издержки, т.е. показывает изменение полных издержек при изменении выпуска продукции на единицу.

Пример 3. Пусть Q=f(L)- производственная. Функция, выражает зависимость количества выпускаемой продукции Q от приложенного труда L ( численности персонала) , тогда — предельная производительность труда, показывает приближенно, насколько изменится (увеличится или уменьшится) объем выпускаемой продукции при изменении численности персонала на единицу.

Рассмотрим производственную функцию , можно считать, что это эмпирическая зависимость. Предельная производительность труда в этом случае дается формулой Проанализируем зависимость предельной производительности труда от численности персонала. Для этого произведем некоторые расчеты, которые сведем в следующую таблицу.

L	1	25	100	2500
	146	26	11	-1

Из таблицы видно, что предельная производительность труда падает с ростом численности персонала, причем, начиная с некоторого значения, она становится отрицательной. Это означает, что при дальнейшем росте численности персонала будет падать не только предельная производительность, но и производство продукции

Отметим, что рассмотренные предельные величины характеризуют абсолютные изменения функции в отличие от эластичности, описывающей относительные изменения функции как реакцию на относительные изменения аргумента.

Полное исследование функции и построение графика — Студопедия

Поделись  

Полное исследование функций и построение их графиков удобно выполнять по следующей схеме:

1) найти область определения функции;

2) выяснить, не является ли функция чётной или нечётной, периодической;

3) исследовать непрерывность, найти точки разрыва и выяснить характер разрывов;

4) найти асимптоты графика функции;

5) исследовать монотонность функции и найти ее экстремумы;

6) найти точки перегиба, установить интервалы выпуклости и вогнутости графика функции;

7) обозначить дополнительные точки графика функции, например, точки его пересечения с осями координат.

Результат каждого пункта должен сразу отражаться на графике и согласовываться с результатами исследования по предыдущим пунктам.

Пример 1.

Провести полное исследование функции и построить график .

Решение.

1. Функция определена в интервалах хÎ (–¥; 1) È (–1; +¥).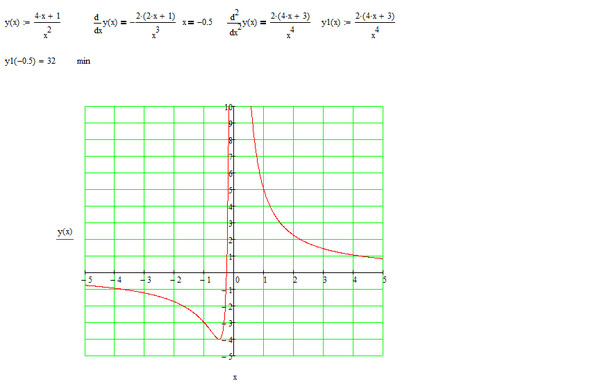

2. Функция не может быть четной или нечетной, т.к. ее область определения не является симметричной относительно 0. Следовательно, данная функция общего вида, т.е. свойством четности не обладает. Также функция не является периодической.

Напомним определения:

Функция называется четной, если выполняются два условия:

a) ее область определения симметрична относительно нуля,

b) для всех значений х из области определения выполняется равенство .

График четной функции имеет осевую симметрию относительно оси OY.

Функция называется нечетной, если

a) ее область определения функции симметрична относительно нуля,

b) при «х из области определения.

График нечетной функции имеет центральную симметрию относительно начала координат.

Функция называется периодической, если существует число Т > 0, такое что выполняется равенство для «х из области определения.

Число Т называется периодом функции, а ее график достаточно построить на любом промежутке длиной Т, а затем периодически продолжить на всю область определения.

3. Функция является непрерывной при всех хÎ (–¥; –1) È (–1; +¥).

Данная функция является элементарной, которая образована делением двух непрерывных основных элементарных функций и . Поэтому, по свойствам непрерывных функций, данная функция непрерывна во всех точках, в которых она определена.

Точка х = –1 является точкой разрыва, т.к. в ней данная функция не определена. Чтобы определить характер (тип) разрыва, вычислим . Следовательно, при х = –1

функция имеет бесконечный разрыв (разрыв II рода).

4. Асимптоты графика функции.

Вертикальной асимптотой является прямая х = –1 (это следует из исследования разрыва функции).

Наклонные асимптоты ищем уравнением , где

= ,

= =–1.

Таким образом, – это уравнение наклонной асимптоты (при х® ±¥).

5. Монотонность и экстремумы функции определим с помощью ее первой производной:

.

Критические точки определяем из условий:

Достаточные условия монотонности и экстремумов:

y_max=y(–3)= .

 

6. Интервалы выпуклости и вогнутости графика функции, ее точки перегиба находим с помощью второй производной:

.

Подозрительные на перегиб точки определяем из условий:

Достаточные условия выпуклости, вогнутости и точек перегиба:

y(0)= .

Точка О(0; 0) является точкой перегиба графика.

Часто результаты исследования функции с помощью первой и второй производной оформляют в виде общей таблицы, отражающей основные свойства графика функции:

x	(–¥;-3)	–3	(–3;–1)	–1	(–1;0)		(0;+¥)
	+		–	не существует	+		+
	–	–	–	не существует	–		+
	возрастает, вогнута	max	Убывает, вогнута	не существует	возрастает, вогнута	= 0 точка перегиба	возрастает, выпукла

Все полученные результаты исследования функции отражаются ее графиком.

Пример 2.

.

Решение.

ООФ: хÎ (–¥; – ) È (– ; ) È ( ;+¥).

Функция является нечетной, так как ее область определения симметрична относительно нуля и для «хÎ ООФ выполняется равенство:

.

Поэтому график функции имеет центральную симметрию относительно начала координат.

Функция является непрерывной при всех хÎ (–¥; – ) È (– ; ) È ( ; +¥), т.к. элементарная функция непрерывна на своей ООФ. Точки х=– и х= являются точками бесконечного разрыва, так как ,

.

Вертикальными асимптотами графика являются прямые х = – и х = .

Наклонные асимптоты: , где

1,

= = 0.

– это уравнение наклонной асимптоты.

Интервалы возрастания и убывания функции, ее экстремумы.

.

Необходимые условия экстремумов:

Þ х₁ = 0, х₂ = 3, х₃ = –3 – критические точки.

Достаточные условия монотонности и экстремумов:

y_max=y(–3)= ;

y_min=y(3)= .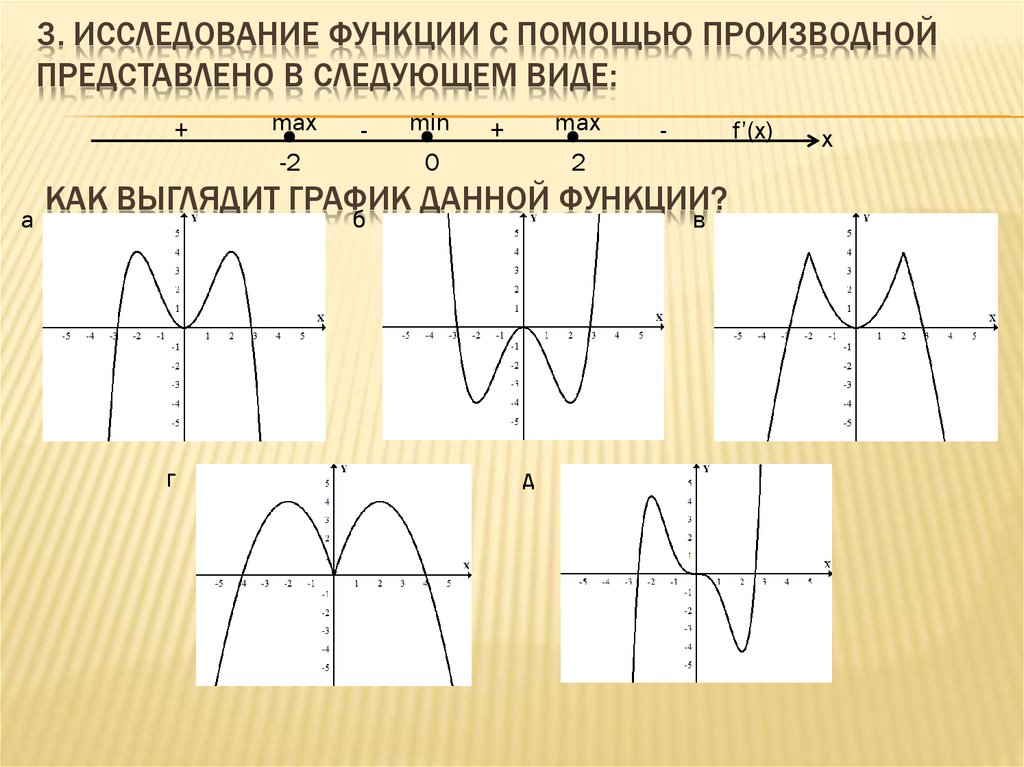

 

Интервалы выпуклости, вогнутости графика функции и точки перегибов:

.

Точка х = 0 подозрительная на перегиб.

Достаточные условия:

Точка О(0; 0) является точкой перегиба.

Общую таблицу основных свойств графика для данной функции можно составить только для хÎ [0; +¥) в следствие центральной симметрии графика относительно точки (0; 0):

x						(3;+¥)
		–	не существует	–		+
		–	не существует	+	+	+
	= 0 точка перегиба	убывает, вогнута	не существует	убывает, выпукла		возрастает, выпукла

График функции:

Пример 3.

.

Решение.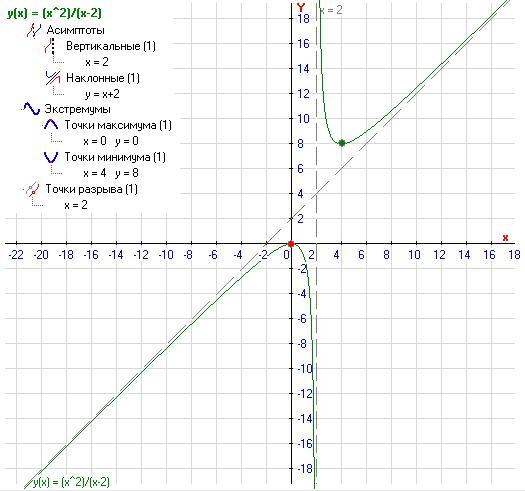

ООФ: хÎ (–¥; +¥).

, . и Þ функция свойством четности не обладает, т.е. не является ни четной, ни нечетной.

Функция непрерывна при «хÎ (–¥; +¥), точек разрыва нет.

Вертикальных асимптот нет, т.к. нет точек разрыва.

Наклонные асимптоты: , где

k= –1,

= 2.

Следовательно, – наклонная асимптота (при х®±¥).

Монотонность и экстремумы.

.

Необходимое условие экстремума:

Получились три критические точки: х₁ = 0, х₂ = 4, х₃ = 6, причем две из них х₁ = 0 и х₃ = 6 являются подозрительными на острый экстремум.

Достаточные условия монотонности и экстремумов:

y_max=y(4)= 3,17 – гладкий максимум;

y_min=y(0)= 0 – острый минимум;.

Выпуклость, вогнутость, точки перегиба:

.

Необходимое условие для точек перегиба:

Достаточные условия:

в точке (6; 0) график функции имеет перегиб.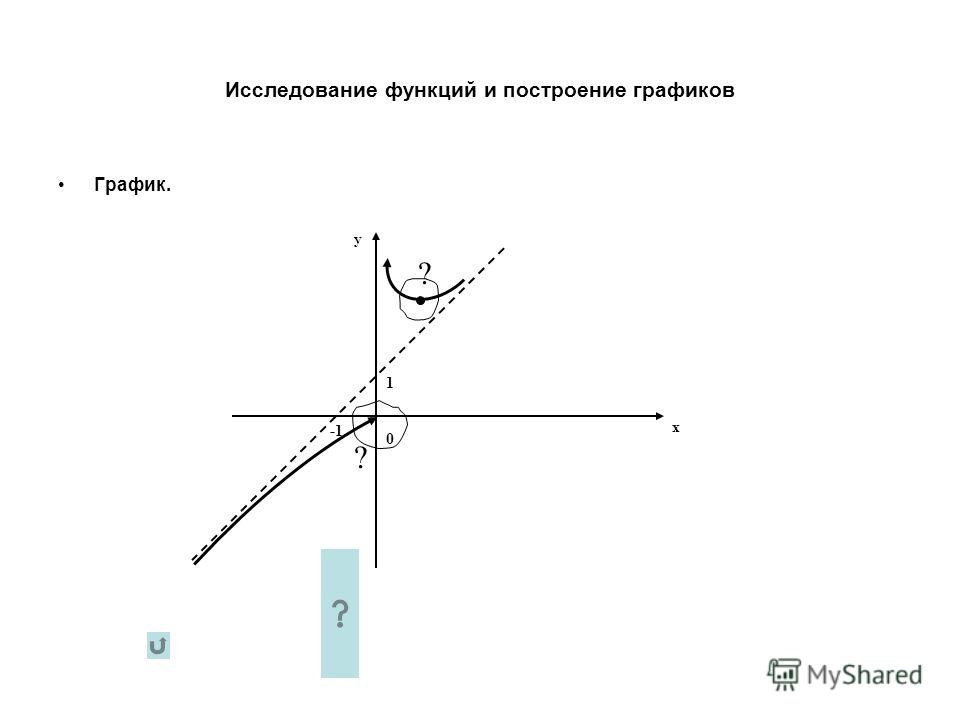

Общая таблица свойств исследуемой функции:

x					(4;6)		(6;+¥)
	–	не существует	+		–		–
	–	не существует	–	–	–	не существует	+
	убывает, вогнута	= 0 – острый min	возрастает, вогнута	вогнута	убывает, вогнута	= 0 – точка перегиба	убывает, выпукла

График функции:

Пример 4.

.

Решение.

1. ООФ: хÎ (0; +¥).

2. Функция свойством четности не обладает, т.к. ее ООФ не является симметричной относительно нуля.

3. Функция непрерывна при «хÎ (0; +¥), точек разрыва нет.

4. Асимптоты графика.

Возможна вертикальная асимптота на границе ООФ. Вычисляем

–¥ Þ

прямая х = 0 является правосторонней вертикальной асимптотой графика.

Наклонная асимптота (при х® +¥): ,

где 0,

= = 0.

Следовательно, – горизонтальная асимптота (при х®+¥).

5. Монотонность и экстремумы.

– существует при «хÎООФ.

Стационарная точка: (т.к. ).

Достаточное условие монотонности и экстремумов:

y_max = y( ) = » 0,37.

6. Выпуклость, вогнутость, точки перегиба:

– существует при «хÎ ООФ.

0, если –3 + 2 Þ Þ – это подозрительная на перегиб точка.

Достаточные условия:

0,33.

График функции :

Дополнительные упражнения.

Провести полное исследование функции и построить график.

1. ;	2. ;
3. ;	4. ;
5. .

Ответы.

1. ООФ: ;

;

точка перегиба (0; 0).

2. ООФ: ;
асимптоты ; ;

точка перегиба (0; 0).

3. ООФ: ;

асимптота ;

;

;

точки перегиба имеют абсциссы:

; .

4. ООФ: ;
асимптоты ; ; ;

.

5. ООФ: ;

асимптота ;

;

точки перегиба:

и .



Математическая сцена — Функции 2 — Урок 4

Математическая сцена — Функции 2 — Урок 4 — Исследование функций с помощью производных

2009  Расмус Эф    и Джанн Сак

Урок 4

Исследование функций с помощью производных

---

Производная функции является мерой градиент графика, поэтому мы можем сделать следующие выводы:

Функция возрастает, если производная положительный (+) и убывает, если производная отрицательна ().

Это означает, что когда производная меняет знак от положительного к отрицательному или от отрицательного к положительному должен быть поворотный момент или вершина на графе. Это так называемые максимальные и минимальные точки. Они есть не обязательно наибольшие или наименьшие общие значения функции.

Глядя на таблицу знаков производной показывает нам, где находятся эти стационарные точки.

Помните, непрерывная функция не может изменяться между отрицательными и положительными значениями, не переходя через ноль, поэтому мы ищите стационарные точки, выясняя, когда производная равна 0,

Пример 1

Найдите производную f(x) = x ² , составьте таблицу знаков и используйте ее, чтобы нарисовать график функции f(x).

   Если f(x) = x ² тогда f(x) = 2x.

Стационарные точки возникают, когда f(x) = 2x = 0 , то есть когда x = 0. Ниже приведена таблица, показывающая знак f (x)

.

 

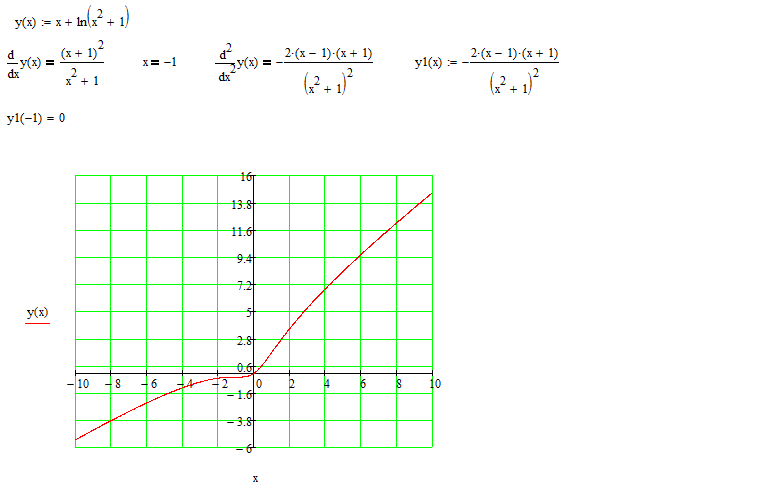
Y = х ²

Производная равна 0 когда х = 0 а градиент меняется с на +, так что это точка минимума.

 

Пример 2

Найдите производную f(x) = x ³ 3x ² + 4, составьте таблицу знаков производной и используйте это для нахождения стационарных точек. Сравните свои результаты с графиком, показанным на ваш графический калькулятор.

   Если f(x) = x ³ 3x ² + 4, затем f(x) = 3x ² 6x.

Найти производную 0.

    3x ² 6х = 0

   3x(x 2) = 0

Это уравнение имеет решения х = 0 и х = 2 и в этих точках производная меняет знак. Находим знак f(x) = 3x ² 6x.

Мы могли бы составить таблицу без факторизации во-первых, просто выбирая значения x между нулями и находя знак производная.

   ж(1) = 3(1) ² 6(1) = 3 + 6 = 9    (+)

   ж(1) = 31 ² 61 = 3 ()

   ж(3) = 33 ² 63 = 9 (+)

Это дает более простую таблицу выше, но показывает ту же информацию.

Из таблицы мы можем сделать вывод, что у нас есть максимум, когда x = 0. Градиент равен 0, поэтому график горизонтальный, а градиент изменяется от + (подъем) до (снижение). Производная также равна нулю, когда x = 2. и градиент меняется с на +, так что здесь у нас есть минимум. Мы можем найти максимальное и минимальное значения функции, помещая эти значения x в Формула исходной функции.

   ж(0) = 0 ³ 30 ² + 4 = 4

Функция имеет максимум стоимость в точке (0, 4) .

   f(2) = 2 ³ 32 ² + 4 = 8 12 + 4 = 0

Функция имеет минимум значение в точке (2, 0).

Графический калькулятор показывает следующий график.

 

Иногда производная от функция равна нулю без изменения знака производной по ходу через нулевую точку. В таких случаях нет никакой стационарной точки, но то, что называется точкой перегиба.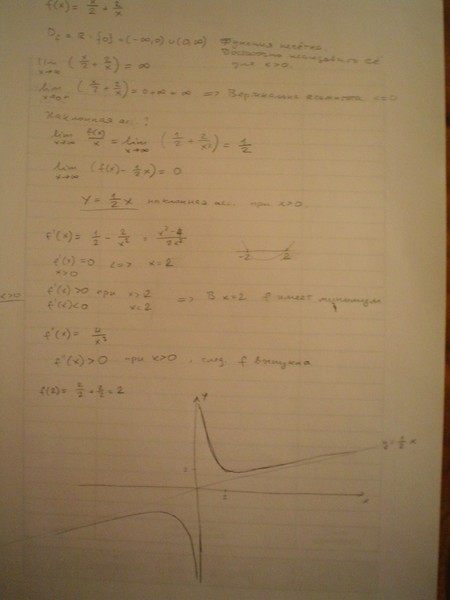

Пример 3

Рассмотрим функцию f(x) = x ³ .

Производная f(x) = 3x ² и равен нулю, когда x = 0,

Ниже приведена таблица знаки производной.

Точка (0, 0) — это точка сгибания. График возрастает до x = 0, горизонтален по x = 0 и затем продолжает увеличиваться после 0,

 

Расчеты с использованием производная имеет множество практических применений, в частности, для нахождения максимальных и минимальные значения. Следующие два примера демонстрируют это.

Пример 4

Мы хотим сделать картон коробку из квадратного картона со стороной 1 м. Для этого сгибаем углы, как показано на схеме. Сколько нам нужно вырезать из углы в порядке чтобы коробка имела вид как можно больший объем?

 

Назовите это x , что означает длину каждой стороны коробки будет в 2 раза короче карты, то есть в 1 2 раза. высота ящика тоже будет х, а объем V можно записать так:

   V = высотадлинаширина

       = х(1 2х)(1 2х)

       = x(1 4x + 4x ² )

       = x 4x ² + 4x ³

Различие этого и нахождение, когда производная равна 0, дает нам:

   V = 1 8x + 12x ² = 0

Это квадратное уравнение можно решить с помощью калькулятора или квадратной формулы.

Очевидно, что мы не может быть х = , как если бы мы отрезали метр не было бы коробка осталась. Таким образом, это должно дать минимальное значение объема. Максимальный объем будет когда х = .

   V() = (1 2)(1 2) = м ³

Максимальный объем коробка будет м ³ когда мы режем м с каждого угла.

 

Пример 5

Прямоугольник рисуется как показано на схеме. Одна сторона образована линией y = 3 и одним углом, P, лежит на графике f(x) = x ² .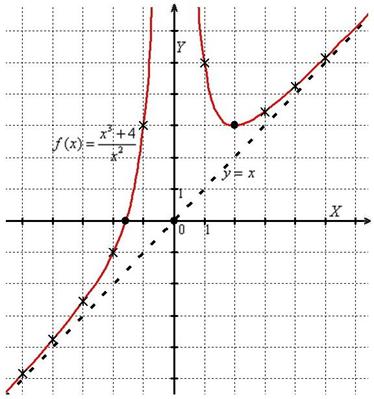 Найдите координаты точки P, чтобы прямоугольник имел максимально возможная площадь.

Стороны прямоугольника х и  3 года или 3 x ² так как точка P лежит на графике f(x) = x ² . Следовательно, площадь равна

   A = длина в ширину

      = x(3 x ² ) = 3x ³

Различие этого и поиск, где производная равна нулю, дает:

   А = 3 3x ² = 0

     3 = 3x ²

     х = 1

Прямоугольник находится в положительный квадрант, поэтому мы не можем иметь x = 1. Максимальная площадь достигается, когда x = 1 поэтому мы можем подставить это значение в формулу площади.

   А = 3x ³ = 3 1 = 2

---

Попрактикуйтесь в этих методах, затем попробуйте Тест 4 по функциям 2.  
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.

 

 

 

 

 

 

 

 

Объяснение урока: Преобразование функций: Расширение

В этом объяснении мы узнаем, как идентифицировать преобразования функций, включающие горизонтальное и вертикальное растяжение или сжатие.

При работе с функциями нас часто интересует получение графика как средства визуализации и понимания общего поведения. В сочетании со знанием конкретной информации, такой как корни, 𝑦-перехват и любые максимумы или минимумы, построение графика График функции может дать полную картину точного известного поведения, а также более общее качественное понимание. Однажды выражение для функции было задано или получено, нас часто будет интересовать, как эта функция может быть записана алгебраически, когда она подвергаются геометрическим преобразованиям, таким как повороты, отражения, переводы и расширения.

В этом объяснении мы исследуем понятие расширения, которое является общим термином для растяжения или сжатия функции (в этом в горизонтальном или вертикальном направлении) с фиксированным масштабным коэффициентом. Геометрически такие преобразования иногда могут быть довольно интуитивно понятны для визуализации, хотя их алгебраическая интерпретация может показаться немного нелогичной, особенно при растяжении по горизонтали направление. Соответственно, мы начнем с изучения расширения в вертикальном направлении, прежде чем переходить к этой несколько более сложной форме расширения.

Определение: расширение в вертикальном направлении

Рассмотрим функцию 𝑦=𝑓(𝑥), построенную в 𝑥𝑦-плоскости. Растягиваем его в вертикальном направлении масштабным коэффициентом 𝑎, вызывая преобразование 𝑓(𝑥)→𝑎𝑓(𝑥). Кроме того, корни функции неизменны, как и 𝑥-координаты любых точек поворота. Значение 𝑦-перехват, как и 𝑦-координата любой точки поворота, будут умножены на масштабный коэффициент.

Мы продемонстрируем это определение, работая с квадратным выражением 𝑓(𝑥)=𝑥−𝑥−2. Мы не будем давать обоснование здесь, но эта функция имеет два корня, один, когда 𝑥=−1, и один, когда 𝑥=2, с 𝑦-перехватом −2, а также минимум в точке 12, −94. График функции 𝑦=𝑓(𝑥) приведен ниже.

Теперь мы растянем функцию по вертикали с коэффициентом масштабирования 3. Согласно нашему определению, это означает, что нам нужно будет применить преобразование 𝑓(𝑥)→3𝑓(𝑥) и, следовательно, нарисовать функцию 𝑦=3𝑓(𝑥)=3𝑥−𝑥−2=3𝑥−3𝑥−6. 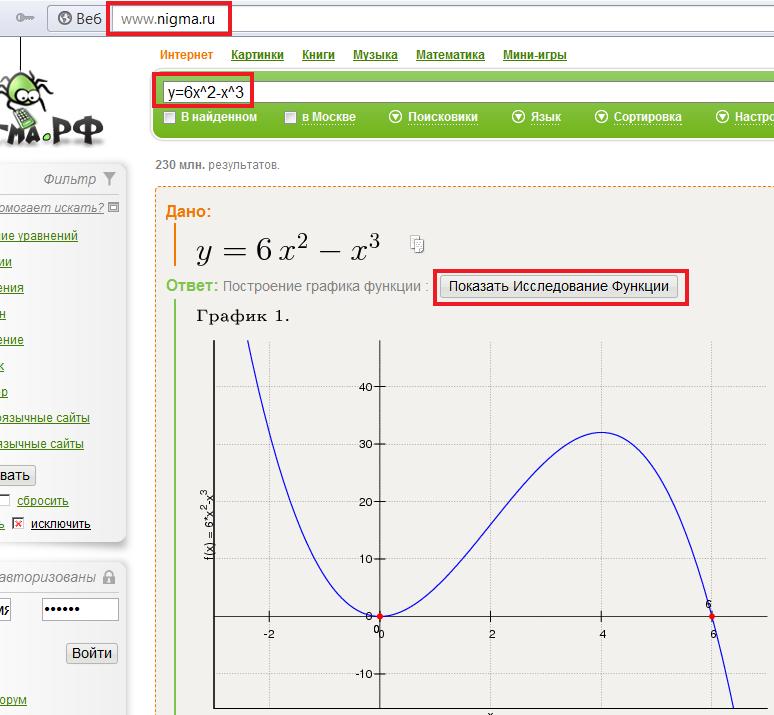

Мы могли бы исследовать эту новую функцию и обнаружить, что расположение корней не изменилось. Тем не менее, оба 𝑦-перехват и точка минимума сместились. Значение 𝑦-перехвата было умножено на масштаб фактор 3 и теперь имеет значение -6. Хотя мы не будем приводить здесь работу, 𝑥-координата точки минимум также не изменился, хотя новая 𝑦-координата в три раза превышает предыдущую, а это означает, что положение новой минимальный балл 12,−274. Эта информация обобщена на графике ниже, с оригинальным функция отображается синим цветом, а новая функция — фиолетовым.

Точно так же мы могли бы сжать функцию 𝑓(𝑥), растянув ее по вертикали по шкале коэффициент числа от 0 до 1. Например, предположим, что мы решили растянуть его в вертикальном направлении с масштабным коэффициентом 13, применив преобразование 𝑓(𝑥)→13𝑓(𝑥). Мы будем затем постройте функцию 𝑦=13𝑓(𝑥)=13𝑥−𝑥−2=13𝑥−13𝑥−23.

Эта новая функция имеет те же корни, что и 𝑓(𝑥), но значение 𝑦-перехвата теперь равно −23. Кроме того, положение точки минимума 12,−34. Эта новая функция показана ниже золотым цветом и наложена на предыдущий график.

Здесь стоит отметить, что мы только расширили функцию в вертикальном направлении на положительный масштабный коэффициент. Если бы мы выбрали отрицательный масштабный коэффициент, мы также должны были бы отражать функцию на горизонтальной оси. Это имеет смысл, так как общеизвестно, что функцию 𝑓(𝑥) можно отразить на горизонтальной оси, применив преобразование 𝑓(𝑥)→−𝑓(𝑥). Например, растягивая функцию по вертикали с масштабным коэффициентом −2 можно рассматривать как сначала растягивающую функцию с преобразованием 𝑓(𝑥)→2𝑓(𝑥), а затем отражая ее, переводя 𝑓(𝑥)→−𝑓(𝑥). Это позволяет нам думать об отражении функции по горизонтальной оси как о растяжении ее по вертикали с масштабным коэффициентом −1.

Предположим, что мы решили растянуть данную функцию 𝑓(𝑥) на масштабный коэффициент −2 в вертикальное направление с помощью преобразования 𝑓(𝑥)→−2𝑓(𝑥). Тогда у нас было бы строил график функции 𝑦=−2𝑓(𝑥)=−2𝑥−𝑥−2=−2𝑥+2𝑥+4.

Опять же, корни этой функции не изменились, но 𝑦-перехват был умножен на масштабный коэффициент −2 и теперь имеет значение 4. 𝑥-координата минимума не изменилась, но 𝑦-координата умножается на масштабный коэффициент. Новая точка поворота 12,92, но теперь это локальный максимум в отличие от локального минимума. Новая функция показана ниже зеленым цветом и наложена поверх предыдущего графика. Мы можем увидеть что новая функция является отражением функции 𝑦=2𝑓(𝑥) по горизонтальной оси.

Пример 1. Выражение вертикальных растяжений с помощью обозначения функций

Функция 𝑦=𝑓(𝑥) растягивается в вертикальном направлении с масштабным коэффициентом, равным 12. Запишите в терминах 𝑓(𝑥) уравнение преобразованной функции .

Ответ

Растяжение функции по вертикали с масштабным коэффициентом 𝑎 даст преобразование 𝑓(𝑥)→𝑎𝑓(𝑥). Поскольку данный коэффициент масштабирования равен 12, новый функция 𝑦=𝑓(𝑥)2.

Поначалу работа с расширениями в горизонтальном направлении может показаться нелогичной. Как бы это ни было, мы подойдем к лечению расширения в горизонтальном направлении через почти ту же структуру, что и для расширения в вертикальном направлении, обсуждая эффекты на ключевых точках, таких как корни, 𝑦-перехваты и точки поворота интересующей нас функции. Мы начнем с соответствующим определением, а затем продемонстрируем эти изменения, ссылаясь на ту же квадратичную функцию, которую мы использовали ранее.

Определение: расширение в горизонтальном направлении

Рассмотрим функцию 𝑦=𝑓(𝑥), построенную в 𝑥𝑦-плоскости. Растягиваем его в горизонтальном направлении масштабным коэффициентом 𝑎, создав новую функцию 𝑓(𝑥)→𝑓1𝑎𝑥. Значение 𝑦-перехвата, как и 𝑦-координата любой точки поворота, останется неизменной. Корни функции умножаются на масштабный коэффициент, как и 𝑥-координаты любых точек поворота.

Мы будем использовать ту же функцию, что и раньше, для понимания расширения в горизонтальном направлении. Напомним, у нас была квадратичная функция 𝑓(𝑥)=𝑥−𝑥−2, график которого приведен ниже. Мы знаем, что эта функция имеет два корня, когда 𝑥=−1 и 𝑥=2, также с точкой пересечения 𝑦, равной −2, и точкой минимума с координатой 12,−94.

Сначала мы продемонстрируем эффекты расширения в горизонтальном направлении. Мы выберем произвольный масштабный коэффициент 2, используя преобразование 𝑓(𝑥)→𝑓12𝑥, и наше определение подразумевает, что мы должны затем построить функция 𝑦=𝑓12𝑥=𝑥2−𝑥2−2=14𝑥−12𝑥−2.

𝑦-координата точки минимума также не изменяется. Корни исходной функции находились в точках 𝑥=−1 и 𝑥=2, и мы видим, что корни новой функции были умножены на масштабный коэффициент и находятся при 𝑥=−2 и 𝑥=4 соответственно. По диаграмме трудно сказать, но 𝑥-координата минимальной точки также умножается на масштабный коэффициент, что означает, что минимальная точка теперь имеет координату 1,−94, тогда как для исходной функции было 12,−94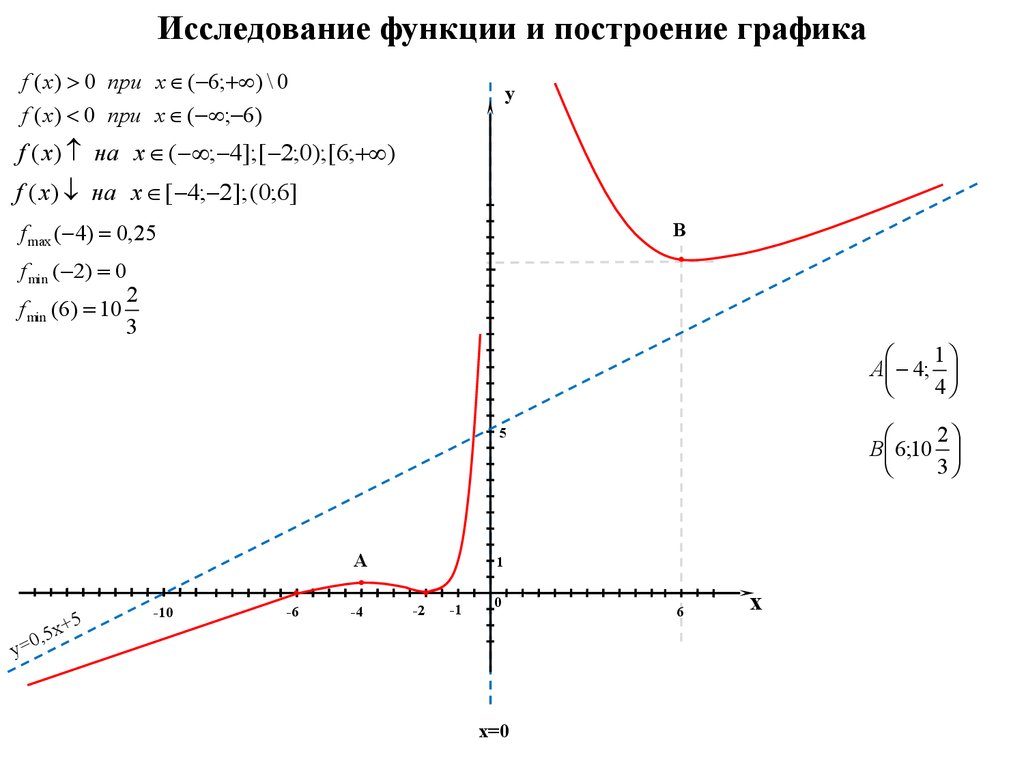. Эта информация представлена ​​на диаграмме ниже, где исходная функция показана синим цветом, а расширенная функция — фиолетовым.

Теперь мы продолжим изучение вышеприведенного определения, растянув функцию на коэффициент масштабирования от 0 до 1, и в этом случае мы выберите масштабный коэффициент 12. Чтобы создать этот эффект расширения исходной функции, мы используем преобразование 𝑓(𝑥)→𝑓1𝑥, что означает, что мы должны построить функцию 𝑦=𝑓1𝑥=𝑓(2𝑥)=(2𝑥)−(2𝑥)−2=4𝑥−2𝑥−2.

В этой новой функции 𝑦-пересечение и 𝑦-координата точки поворота не изменяются. Однако, мы могли бы сделать вывод, что значение корней уменьшилось вдвое, и теперь корни имеют значения 𝑥=−12 и 𝑥=1. Кроме того, 𝑥-координата точки поворота также уменьшена вдвое, что означает, что новое местоположение 14,−94. Это резюмируется на графике ниже, хотя и не с наибольшей ясностью, где новые функция выделена золотом и наложена поверх предыдущего графика.

В нашей последней демонстрации мы продемонстрируем эффекты расширения в горизонтальном направлении с отрицательным коэффициентом масштабирования. Как и при расширении в вертикальном направлении, мы ожидаем, что будет задействовано отражение, хотя на этот раз в вертикальная ось вместо горизонтальной ось. Мы выберем расширение функции в горизонтальном направлении с масштабным коэффициентом -2, что потребует преобразования 𝑓(𝑥)→𝑓1−2𝑥. Затем мы построили бы следующую функцию: 𝑦=𝑓1−2𝑥=𝑓−12𝑥=−12𝑥−−12𝑥−2=14𝑥+12𝑥−2.

Эта новая функция имеет тот же 𝑦-перехват, что и 𝑓(𝑥), и 𝑦-координату точка поворота не изменяется при этом расширении. Однако корни новой функции были умножены на −2 и теперь равны 𝑥=2 и 𝑥=−4, тогда как ранее они были равны 𝑥=−1 и 𝑥=2 соответственно. 𝑥-координата точки поворота также умножается на масштабный коэффициент, и новое местоположение точки поворота равно при −1,−94. Мы построили график расширенной функции ниже, где мы можем видеть влияние отражение по вертикальной оси в сочетании с эффектом растяжения. Для ясности мы построили только исходную функцию 𝑓(𝑥) синим цветом, а новая функция — фиолетовым.

Пример 2. Выражение горизонтального растяжения с использованием обозначения функций

Функция 𝑦=𝑓(𝑥) растягивается в горизонтальном направлении с масштабным коэффициентом, равным 2. Запишите в терминах 𝑓(𝑥), уравнение преобразованной функции.

Ответ

Растяжение функции в горизонтальном направлении с масштабным коэффициентом 𝑎 даст преобразование 𝑓(𝑥)→𝑓1𝑎𝑥. Поскольку данный масштабный коэффициент равен 2, преобразование 𝑓(𝑥)→𝑓12𝑥 и, следовательно, новая функция 𝑦=𝑓𝑥2.

Как мы упоминали ранее, может быть полезно понимать расширения с точки зрения эффектов, которые они оказывают на ключевые точки функции, такие как 𝑦-перехват, корни и расположение любых точек поворота. Если эта информация известна точно, то она обычно бывает достаточно, чтобы сделать вывод о конкретном расширении без дальнейшего исследования. Если мы работаем исключительно с дилатацией в вертикальном направлении, то 𝑥-координаты любых ключевых точек не изменятся. Точно так же, если мы работаем исключительно с расширение в горизонтальном направлении, то 𝑦-координаты не будут затронуты. Мы будем использовать этот подход в оставшихся примерах. в этом объяснителе, где мы будем расширяться только в вертикальном или горизонтальном направлении.

Пример 3. Идентификация графика заданной функции после расширения

На рисунке показан график 𝑦=𝑓(𝑥).

Что из следующего является графиком 𝑦=12𝑓(𝑥)?

Ответ

Функция 𝑦=12𝑓(𝑥) представляет расширение в вертикальном направлении с масштабным коэффициентом 12, это означает, что это компрессия. Учитывая, что мы растягиваем функцию по вертикали, 𝑥-координаты любые ключевые точки не будут затронуты, и вместо этого мы уделим внимание 𝑦-координатам.

Это означает, что мы можем игнорировать корни функции и вместо этого сосредоточимся на 𝑦-перехвате функции 𝑓(𝑥), которая оказывается в точке (0,2). Если бы мы построили график функции 𝑦=12𝑓(𝑥), то мы уменьшим вдвое 𝑦-координату, что даст новую 𝑦-перехват в точке (0,1). Из приведенных графов единственный граф, который соблюдает это свойство является вариантом (e), что означает, что это должен быть правильный выбор. Обратите внимание, что на корни этого графа данное расширение не влияет, что дает свидетельство того, что мы сделали правильный выбор.

В следующем вопросе приводится довольно типичный пример преобразования графа, в котором данное растяжение изображается графически, а затем нас просят определить точное алгебраическое преобразование, которое представляет это. Несмотря на то, что стиль вопроса немного более сложный, чем в предыдущем примере, основной подход практически не изменился. Обращая внимание на поведение ключевых точек, мы увидим, что можем быстро вывести эту информацию. с небольшим другим расследованием.

Пример 4. Выражение растяжения с помощью функционального обозначения, где расширение показано графически

Красный график на рисунке представляет уравнение 𝑦=𝑓(𝑥), а зеленый график представляет уравнение 𝑦=𝑔(𝑥). Выразите 𝑔(𝑥) как преобразование 𝑓(𝑥).

Ответ

Начнем с того, что отметим ключевые точки функции 𝑓(𝑥), отмеченные красным цветом. Во-первых, 𝑦-перехват находится в начале координат, следовательно, точка (0,0), что означает, что он также является корнем 𝑓(𝑥). Расширение ни в вертикальном, ни в горизонтальном направлении не повлияет на эту точку, поэтому мы игнорировать его впредь.

Просто взглянув на график, мы можем увидеть, что функция была растянута в горизонтальном направлении, что указывает на то, что функция расширена в горизонтальном направлении. Чтобы сделать это рассуждение более точным, отметим, что помимо корня в начале координат есть также корни 𝑓(𝑥), когда 𝑥=−2 и 𝑥=1, следовательно, они находятся в точках (−2,0) и (1,0). Однако в новой функции 𝑔(𝑥) изображены зеленым цветом, мы видим, что корни есть, когда 𝑥=−4 и 𝑥=2, следовательно, они находятся в точках (−4,0) и (2,0). Это указывает на то, что мы расширили масштаб в 2 раза.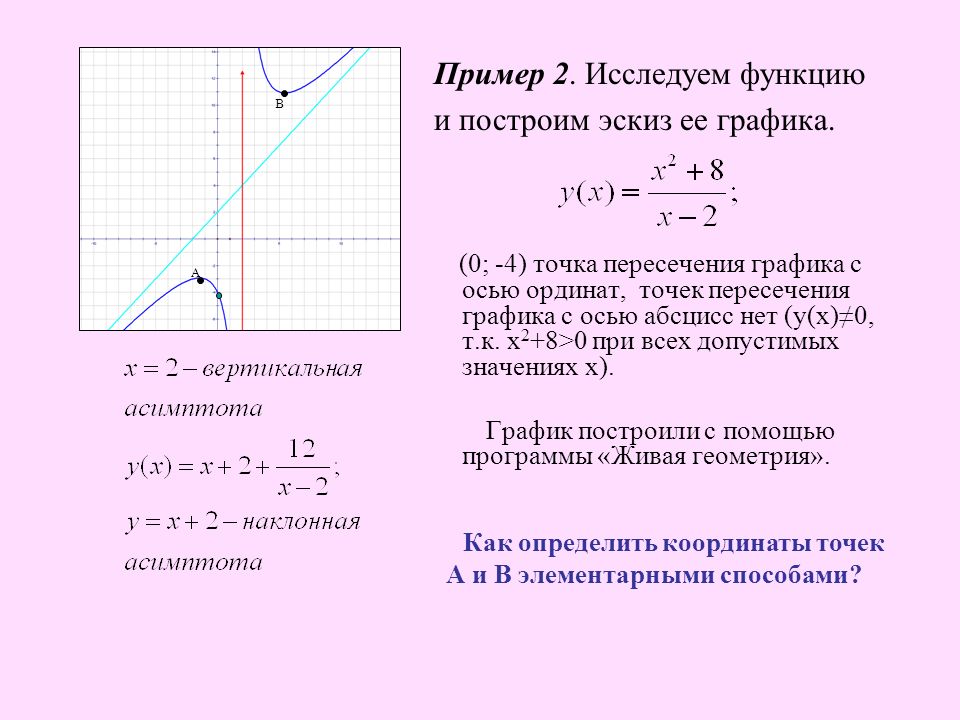 расстояние от корней до начала координат удвоилось, что означает, что мы действительно расширили функцию в горизонтальном направлении на коэффициент 2,

Мы должны перепроверить, чтобы изменения в любых поворотных точках соответствовали этому пониманию. Мы видим, что есть местный максимум 𝑓(𝑥), который находится слева от вертикальной оси, и что есть локальный минимум справа вертикальной оси. Теперь, сравнивая с 𝑔(𝑥), мы видим, что 𝑥-координата этих точки поворота удвоились, тогда как 𝑦-координата не изменилась. Хотя это не совсем подтверждают то, что мы нашли, поскольку мы не можем быть точными с поворотными точками на графике, он, безусловно, выглядит так, как будто он согласуется с нашим решением. Следовательно, имеем отношение 𝑔(𝑥)=𝑓𝑥2.

Пример 5: Нахождение координат точки на кривой после расширения исходной функции

На рисунке показан график 𝑦=𝑓(𝑥) и точки 𝐴. Точка 𝐴 является локальный максимум. Определите соответствующий локальный максимум для преобразования 𝑦=𝑓(2𝑥).

Ответ

Преобразование 𝑦=𝑓(2𝑥) представляет собой расширение в горизонтальном направлении с масштабным коэффициентом 12. Это уменьшит вдвое значение 𝑥-координат ключевых точек, не влияя на 𝑦-координаты. В частности, корни 𝑓(𝑥) при 𝑥=1 и 𝑥=3 соответственно имеют координаты (1,0) и (3,0), что также являются двумя локальными минимумами функции. При рассмотрении функции 𝑦=𝑓(2𝑥) 𝑥-координаты изменятся и, следовательно, дадут новые корни в 𝑥=12 и 𝑥=32, которые будут соответственно иметь координаты 12,0 и 32,0. Относительно локального максимума в точке (2,1) 𝑥-координата будет уменьшена вдвое, а 𝑦-координата не изменится, а это означает, что локальный максимум 𝑦=𝑓(2𝑥) будет в точка (1,1).

Этот объяснитель до сих пор работал с функциями, которые были непрерывными при определении на действительной оси, при этом все поведения были «гладкими», даже если они сложные.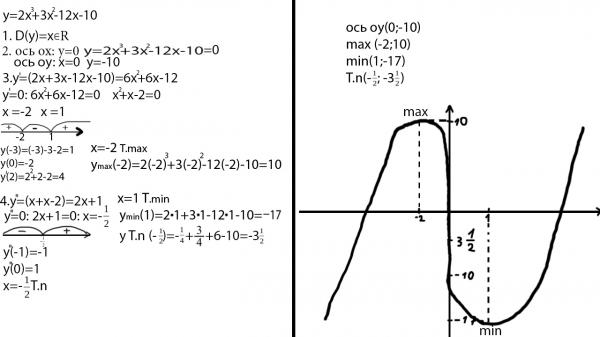 Это не обязательно так, и вместо этого мы можем работать с функцией, которая не непрерывным или иным образом описывается кусочно. В этих ситуациях не совсем уместно использовать такую ​​терминологию, как «перехват» или «корень», поскольку эти термины обычно зарезервированы для использования с непрерывными функциями. Тем не менее принципы по-прежнему применяются, и мы можем перейти к этим проблемам, ссылаясь на определенные ключевые моменты и последствия, которые они будут испытывать. при вертикальном или горизонтальном расширении.

Пример 6. Определение графика заданной функции после растяжения

На диаграмме показан график функции 𝑦=𝑓(𝑥) для −3≤𝑥≤3.

Что из следующего показывает график 𝑦=13𝑓(𝑥)?

Ответ

Заметим, что функция пересекает ось 𝑦 в точке (0,−3) и что функция пересекает ось 𝑥 в точках −32,0 и 52,0. Есть и другие точки, которые легко определить и записать в виде координат. Например, точки (−3,3),(1,−3) и (3,1).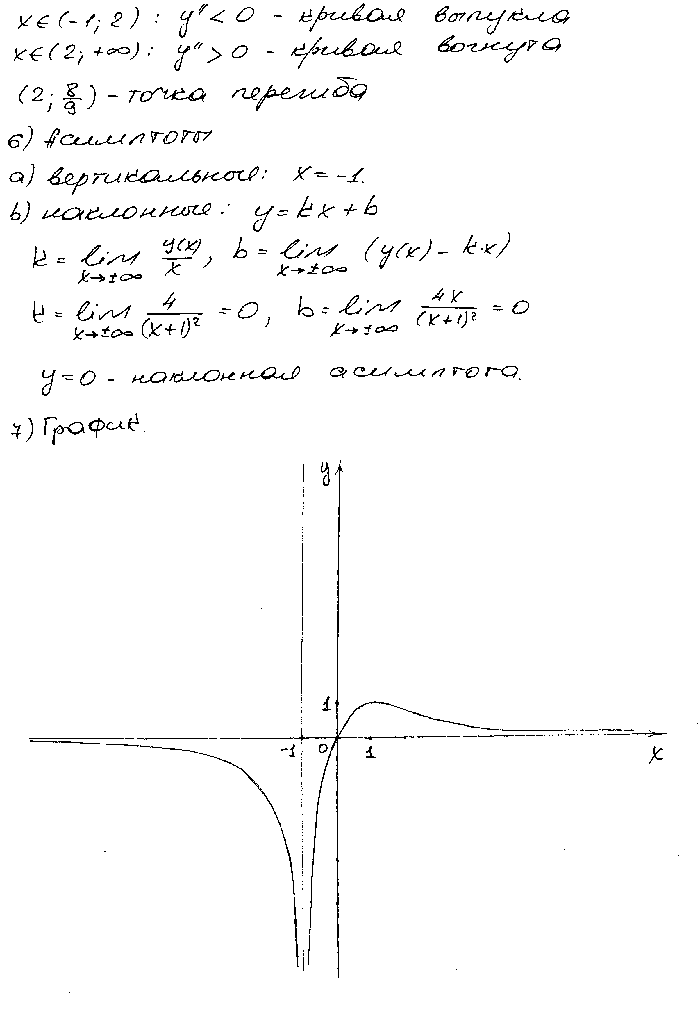

Расширение 𝑦=13𝑓(𝑥) соответствует сжатию в вертикальном направлении в 3 раза. означает, что функция должна быть «сжата» в 3 раза параллельно оси 𝑦. С точки зрения эффектов на известных координатах функции любые отмеченные точки не будут иметь своей 𝑥-координаты и их 𝑦-координата будет разделена на 3. Ссылаясь на ключевые моменты в предыдущем абзаце, они преобразуются в следующие: соответственно: −32,0, 52,0, (−3,1), (1,−1) и 3,13.

Единственным графиком, где функция проходит через эти координаты, является вариант (c). Мы можем визуально подтвердить, что эта функция действительно работает. был сжат в вертикальном направлении в 3 раза.

В этом объяснении мы работали только с дилатациями, которые были строго либо по вертикальной, либо по горизонтальной оси; мы не рассматривали расширение, которое происходит в обоих направлениях одновременно. Такие преобразования бывает трудно изобразить даже с помощью точных графиков. инструменты, особенно если один из коэффициентов масштабирования отрицателен (это означает, что любой из них включает отражение относительно оси). Результат, однако, на самом деле очень просто заявить. Предположим, что существует функция 𝑦=𝑓(𝑥), и мы хотим расширить ее с помощью масштабного коэффициента 𝑎 в вертикальном направлении и масштабный коэффициент 𝑏 в горизонтальном направлении. Тогда мы бы получили новую функцию в силу преобразования 𝑓(𝑥)⟶𝑎𝑓1𝑏𝑥.

Во многом наша работа над этим объяснением может быть резюмирована следующим результатом, описывающим эффект одновременного расширение по обеим осям. Предположим, что мы возьмем любую координату на графике этой новой функции, которую обозначим (𝑥,𝑦). Теперь возьмите исходную функцию и увеличьте ее масштабным коэффициентом 𝑎 по вертикали. направление и масштабный коэффициент 𝑏 в горизонтальном направлении, чтобы дать новую функцию 𝑔(𝑥)=𝑎𝑓1𝑏𝑥. Тогда точка (𝑏𝑥,𝑎𝑦) лежит на график 𝑔(𝑥). Этот результат обобщает более ранние результаты о специальных точках, таких как пересечения, корни и поворотные моменты.

Ключевые точки

• Функция 𝑓(𝑥) может быть расширена по вертикали с масштабным коэффициентом 𝑎 на создание новой функции 𝑓(𝑥)→𝑎𝑓(𝑥).
• При растяжении функции по вертикали корни функции не изменяются, как и 𝑥-координаты каких-либо переломных моментов.
• При расширении в вертикальном направлении значение 𝑦-перехвата, а также 𝑦-координаты любой поворотной точки, также будет умножаться на масштабный коэффициент.
• При расширении в вертикальном направлении с отрицательным коэффициентом масштабирования функция будет отражена по горизонтальной оси, кроме того к эффекту растяжения/сжатия, возникающему, когда коэффициент масштабирования не равен отрицательной единице. Это преобразование станет локальным минимумов в локальные максимумы и наоборот.
• Функция 𝑓(𝑥) может быть расширена в горизонтальном направлении с масштабным коэффициентом 𝑎 на создание новой функции 𝑓(𝑥)→𝑓1𝑎𝑥.

  No related posts.