Проведите по общей схеме исследование функции заданной графиком — Bitbucket
Created by verrotising1972
snippet.markdown
———————————————————
>>> СКАЧАТЬ ФАЙЛ <<<
———————————————————
Проверено, вирусов нет!
———————————————————
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
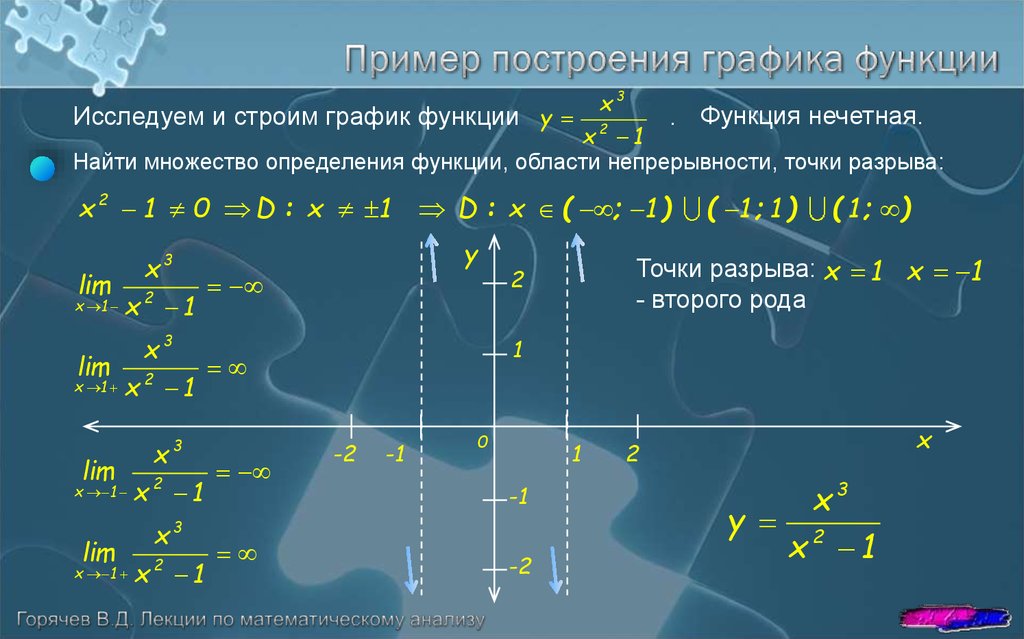
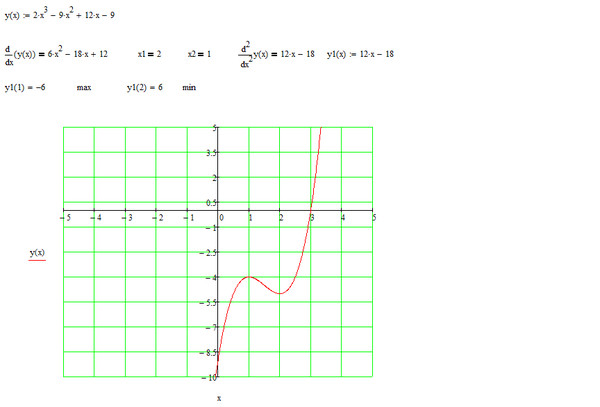
Проведите по общей схеме исследование функции, заданной графиком (рис. Постройте график функции f, если известны ее свойства (см. таблицу). Цель урока: познакомить учащихся со схемой исследования функций;. и проведите по общей схеме исследование функции, заданной графиком.
Проведите по общей схеме исследование функции и постройте её график. 98. в) f(x) = x ³ + x 1. Область определения и область. Полное исследование функции и построение графика функции методом. Исследование проводится по следующей примерной схеме. 2) Функция нечетная, так как f(-x) = -f (x), и, следовательно, ее график симметричен. отправления в соответствующие пункты назначения задана матрицей тарифов. Построение графика функции онлайн, а также исследование функции: нахождение точек пересечения с осями координат; экстремумы функции. Общая схема исследования; Полный пример исследования функции. Провести полное исследование и построить график функции y(x)=x2+81−x. Проведите исследование функции с построением графика. y=x32(x+5)2. Полная схема исследования функции с примерами и подробными объяснениями. Итак, вооружившись общей схемой исследования, где рассмотрена. Примерная схема исследования функции с целью построения ее графика имеет следующую. Задание. Исследовать функцию и построить ее график.
deleted]][[/deleted]]
This comment is currently being rendered in creole. Editing the comment will cause it to be rendered in markdown.
[[/convert_markup]]Cancel
This comment is currently being rendered in creole. Editing the comment will cause it to be rendered in markdown.
Исследование функций и построение графиков. Возрастание и убывание функции одной переменной. Определение. (Семинар 12)
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике.
Базовый уровень Сложные задачи
Семинар 12. Исследование функций и построение графиков
Возрастание и убывание функции одной переменной
Определение
Функция f(x) возрастает на интервале (a,b), если любому большему значению
аргумента х в этом интервале соответствует большее значение функции, то
есть, для x2 x1 f ( x2 ) f ( x1 )
Функция f(x) убывает на интервале (a,b), если любому большему значению
есть, для x x f ( x ) f ( x )
2
1
2
1
Теорема 1 Необходимый признак возрастания (убывания) функции
Если дифференцируемая функция возрастает в некотором интервале, то
производная этой функции неотрицательна в этом интервале
Если дифференцируемая функция убывает в некотором интервале, то производная
этой функции неположительна в этом интервале
Теорема 2 Достаточный признак возрастания (убывания) функции
Если производная дифференцируемой функции положительна внутри некоторого
интервала, то функции возрастает на этом интервале.
Если производная дифференцируемой функции отрицательна внутри некоторого
интервала, то функции убывает на этом интервале.
Экстремум функции одной переменной
Определение
Функция f(x) имеет максимум f ( x1 )при значении x1
аргумента х, если в некоторой
окрестности точки x1 выполняется неравенствоf ( x1 ) f ( x), ( x x1 )
Аналогично
Функция f(x) имеет минимум при значении x 2 аргумента х, если в некоторой
окрестности точки x 2 выполняется неравенство
1.Необходимое условие экстремума функции
Теорема
В точке экстремума функции (двустороннего) дифференцируемой функции ее
производная равна нулю.
2.Достаточное условие экстремума
Теорема 1
Если производная функции f(x) равна нулю при x x0 и меняет знак при переходе
через x 0 то x 0 — точка экстремума, причем
1) x 0- точка максимума, если знак меняется с плюса на минус;
2) x 0 — точка минимума, если знак меняется с минуса на плюс
Направление выпуклости графика функции
Теорема
Если вторая производная функции положительна в некотором интервале, то ее
график является выпуклым вниз, если вторая производная функции
отрицательна, то ее график является выпуклым вверх в соответствующем
интервале.
Точки перегиба графика функции
Точкой перегиба графика функции называется такая точка, при переходе через
которую выпуклость меняется на вогнутость.
Теорема
Если при x x0
вторая производная функции f(x) равна 0 и меняет знак при
переходе через эту точку, то данная точка есть точка перегиба графика функции.
Асимптоты графика функции
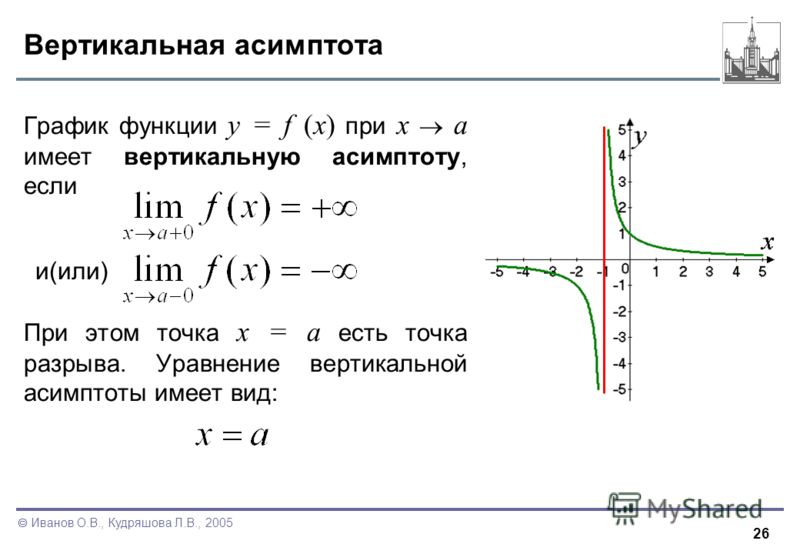
Прямую, определяемую уравнением х=а, называют вертикальной асимптотой
графика функции y=f(x), если хотя бы один из односторонних пределов функции
в точке а является бесконечным. lim x a 0 f ( x) или lim x a 0 f ( x)
Прямую, определяемую уравнением y=kx+b (1) называют невертикальной
в виде
(2) где lim x ( x) 0
(3)
f ( x) kx b ( x)
Если график функции y=f(x) имеет невертикальную асимптоту (1), тогда существуют
f ( x)
два предела
lim
k ; lim
( f ( x) (4)
kx) b
x
Исследование функций и построение их графиков
Под исследованием функций понимают изучение их изменения в зависимости от
изменения аргумента.
x
x
Исследование функций и построение их графиков проводят по схеме, приведенной
ниже.
1.Нахождение области определения функции.
2.Изучение изменения функции при стремлении аргумента к концам промежутков
области определения (находятся соответствующие односторонние пределы).
3.Нахождение промежутков возрастания и убывания функции, исследуя знак ее первой
производной.
4.Нахождение точек экстремумов функции. Стационарные и критические точки.
Исследование первой и второй производной. Вычисление экстремумов функции.
5.Нахождение промежутков выпуклости, вогнутости графика функции, точек перегиба.
6.Нахождение асимптот графика функции
7.Нахождение точек пересечения графика функции с осями координат. Решение систем
уравнений y f ( x ) y f ( x )
x 0
y 0
Кроме того, учитывается четность и нечетность функции, ее периодичность.
Примеры с решениями
f ( x) x 3 3 x 2
1.
Исследовать функцию на возрастание и убывание
Решение
f ‘ ( x) 3x 2 3 3( x 1)( x 1) f ‘ ( x) 0; x1 1; x2 1
Эти значения разбивают ось ОХ на три интервала ( ,1], [ 1;1], [1, )
-функция возрастает
f ‘ ( x) 0 x ( ,1] [1, )
f ‘ ( x) 0 x ( 1;1) -функция убывает
2.
Найти экстремумы функцииf ( x) x 3 3x
Решение f ‘ ( x) 3x 2 3 3( x 1)( x 1) 0 x1 1; x2 1. поскольку f’(x)>0 при x<-1,
f’(x)<0 при -1<x<1, f’(x)>0 при x>1, то — точка максимума, — точка минимума
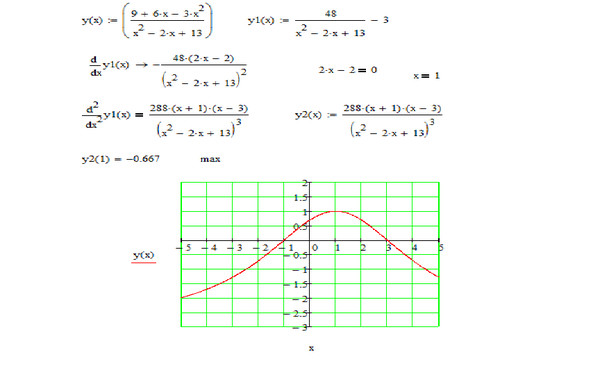
3. Найти экстремумы функции f ( x) x 3 1,5x 2 18 x 8
Решение f ‘ ( x) 3x 2 3x 18 3( x 2 x 6) 3(x+2)(x-3)=0 x1 2; x2 3
f’’(x)=6x-3; f’’(-2)=-15<0, тогда — точка максимума
f’’(x)=15>0, тогда — точка минимума.
4. Найти промежутки выпуклости и вогнутости графика функции f ( x) x 3 3x 2 1
Решение
y’ f ‘ ( x ) 3x 2 6 x f ‘ ‘ ( x ) 6 x 6 6( x 1)
f’’(x)>0, при x>1 – выпуклость вниз, f’’(x)<0, при x<1 – выпуклость вверх
5. Найти точку перегиба графика функции f ( x ) x 3 6 x 2 9 x 4
Решение
f ‘ ( x) 3x 2 12 x 9 f ‘ ‘ ( x ) 6 x 12 0; x 2
При x<2 f’’(x)<0; при x>2 f’’(x)>0. Следовательно, М(2,6) – точка перегиба.
6. Исследовать функции и построить ее график y f ( x) x 3 3x 2 2
Решение
1)
ОДЗ: x R функция общего вида
2) x , f ( x ) ; x , f ( x )
3) f ‘ ( x) 3x 2 6 x 0 x 0; x 2 ( ,0) (2, ) возраст.
;[0;2] — убыв.4) f’(x)=0; — точка максимума; x2 2- точка минимума;
5) Значения экстремумов f(0)=2; f(2)=-2
6) ) f’’(x)=6x-6=6(x-1), x<1, f’’(x)<0; x>1, f’’(x)>0 — x=1 – точка перегиба
7)
Асимптот нет.
8) y f ( x) x 3 3x 2 2 =0 x 1; x 1 3; x 1 3
— нули функции. x=0,y=2
Примеры для самостоятельного решения
Провести полное исследование функции и построить ее график
1) y( x 1) x 2
2)
1
y x2 2
x
3) xy ( x 2 1)( x 2)
x
ex
4)
y
5)
ex
y
x
6) y ln( x 2 1)
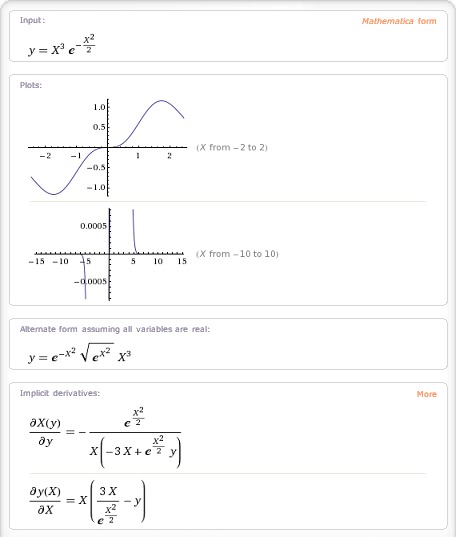
7)
2 x2
y x e
8) y
1
ex 1
9) y x ln x
x
10)
y x sin x
11) y ln cos x
12) y 8 x 8 x
13) y ln( 1 e x )
14)
y x x 3
English Русский Правила
Контрольная карта — статистические контрольные карты процесса
- Дом /
- Качественные ресурсы /
- Контрольная карта
Ищете более качественные инструменты?
Попробуйте Plan-Do-Study-Act (PDSA) Plus QTools™ Training:
- График выполнения
- Блок-схема
- QTools TM Комплект
- Plan-Do-Study-Act плюс QTools TM
Глоссарий качества Определение: контрольная карта
Также называется: диаграмма Шухарта, статистическая контрольная карта процесса
Контрольная карта представляет собой график, используемый для изучения изменений процесса во времени.
Данные нанесены во временной последовательности. Контрольная диаграмма всегда имеет центральную линию для среднего значения, верхнюю линию для верхнего контрольного предела и нижнюю линию для нижнего контрольного предела. Эти линии определяются из исторических данных. Сравнивая текущие данные с этими линиями, можно сделать выводы о том, является ли изменение процесса постоянным (контролируемым) или непредсказуемым (неуправляемым, подверженным особым причинам отклонения). Этот универсальный инструмент сбора и анализа данных может использоваться в различных отраслях и считается одним из семи основных инструментов обеспечения качества.
Контрольные карты для переменных данных используются парами. Верхняя диаграмма отслеживает среднее значение или центрирование распределения данных процесса. Нижняя диаграмма отслеживает диапазон или ширину распределения. Если вашими данными были выстрелы в стрельбе по мишеням, среднее значение показывает, где выстрелы сгруппированы, а диапазон — насколько плотно они сгруппированы.
Контрольные карты для атрибутивных данных используются отдельно.
- Когда использовать контрольную карту
- Основная процедура
- Создать контрольную карту
- Ресурсы контрольной карты
Пример контрольной диаграммы
- При управлении текущими процессами путем обнаружения и устранения проблем по мере их возникновения
- При прогнозировании ожидаемого диапазона результатов процесса
- При определении устойчивости процесса (в статистическом контроле)
- При анализе закономерностей изменения процесса по особым причинам (нештатные события) или общим причинам (встроенным в процесс)
- При определении того, должен ли ваш проект по улучшению качества быть направлен на предотвращение конкретных проблем или на внесение фундаментальных изменений в процесс
- Выберите соответствующую контрольную диаграмму для ваших данных.
- Определите подходящий период времени для сбора и построения графика данных.
- Соберите данные, постройте диаграмму и проанализируйте данные.
- Найдите на контрольной диаграмме «неконтролируемые сигналы». При обнаружении одного из них отметьте его в таблице и исследуйте причину. Документируйте, как вы исследовали, что вы узнали, причину и как она была исправлена.
Неконтролируемые сигналы
- Продолжайте отображать данные по мере их создания. При построении каждой новой точки данных проверяйте наличие новых неконтролируемых сигналов.
- Когда вы начинаете новую контрольную карту, процесс может выйти из-под контроля. Если да, то контрольные пределы, рассчитанные по первым 20 точкам, являются условными пределами. Когда у вас есть не менее 20 последовательных точек из периода, когда процесс работает под контролем, пересчитайте контрольные пределы.
Посмотрите образец контрольной диаграммы и создайте собственную с помощью шаблона контрольной диаграммы (Excel).
Вы также можете выполнять поиск в статьях, тематических исследованиях и публикациях для ресурсов контрольных диаграмм. (PDF) вымышленный. При использовании тематического исследования в классах или организациях читатели должны быть в состоянии создать контрольную карту и интерпретировать ее результаты, а также определить ситуации, подходящие для анализа контрольной карты.
Трудности с качеством: интерпретация сигналов из правил выполнения в контрольных диаграммах Шухарта ( Инженерия качества ) Пример Douwe Egberts, голландского производителя/дистрибьютора чая и кофе, демонстрирует, как можно использовать правила выполнения и контрольную диаграмму Шухарта. как эффективный инструмент статистического управления технологическими процессами.
Статьи
Пространственные контрольные карты для среднего ( Journal of Quality Technology ) Свойства этой контрольной карты для средств пространственного процесса исследуются с помощью смоделированных данных, и метод иллюстрируется примером с использованием ультразвуковой технологии.
для получения неразрушающих измерений толщины бутылки.
Надежная контрольная диаграмма стандартного отклонения ( Technometrics ) Большинство надежных оценок, описанных в литературе, устойчивы либо к диффузным возмущениям, либо к локализованным возмущениям, но не к обоим одновременно. Авторы предлагают интуитивно понятный алгоритм, который устойчив к обоим типам помех и имеет более высокую общую производительность, чем существующие оценщики.
Видео
Контрольная таблица
Выдержки из Инструментарий качества , ASQ Quality Press.
Избранные рекламодатели
Как правильно выбрать диаграмму для ваших данных
Как выбрать правильную диаграмму или график для ваших данных?
Если у вас есть данные, которые вы хотите визуализировать, убедитесь, что вы используете правильные диаграммы. Хотя ваши данные могут работать с несколькими типами диаграмм, вы должны выбрать тот, который обеспечит четкость и точность вашего сообщения.
Помните, что данные ценны только в том случае, если вы знаете, как их визуализировать и дать контекст.
Мы дадим вам обзор различных типов диаграмм и объясним, как выбрать правильный.
О чем рассказывают ваши данные?
Прежде чем создавать диаграмму, важно понять, зачем она вам нужна. Диаграммы, карты и инфографика помогают людям понимать сложные данные, находить закономерности, выявлять тенденции и рассказывать истории. Подумайте о сообщении, которым вы хотите поделиться со своей аудиторией.
Следуйте рекомендациям по составлению графиков. Ваши числа должны складываться, и диаграммы должны быть соответственно масштабированы. Что бы вы хотели показать? Существует четыре основных типа диаграмм:
Источник: The Extreme Presentation Method
Узнайте, как использовать передовой опыт сторителлинга для создания потрясающих изображений и эффектных презентаций, привлекающих аудиторию.
Сравнение Сравнительные диаграммы используются для сравнения одного или нескольких наборов данных.
Они могут сравнивать предметы или показывать различия во времени.
Диаграммы взаимосвязей используются для отображения связи или корреляции между двумя или более переменными.
КомпозицияДиаграммы композиции используются для отображения частей целого и изменения во времени.
РаспределениеДиаграммы распределения используются, чтобы показать, как переменные распределяются во времени, помогая выявить выбросы и тенденции.
Выбор правильного типа диаграммы
Спросите себя, сколько переменных вы хотите отобразить, сколько точек данных вы хотите отобразить и как вы хотите масштабировать свою ось.
Линейные, гистограммы и гистограммы отображают изменения во времени. Пирамиды и круговые диаграммы отображают части целого. В то время как точечные диаграммы и древовидные карты полезны, если у вас есть много данных для визуализации.
youtube.com/embed/3JUa6oFR3Ts?t=22s»> Типы диаграмм
Линейные диаграммы
Линейная диаграмма показывает тенденции или изменения во времени. Линейные диаграммы можно использовать для отображения взаимосвязей в непрерывном наборе данных, и их можно применять к широкому спектру категорий, включая ежедневное количество посетителей сайта или колебания цен на акции.
Рекомендации по созданию линейных диаграмм:
Четко обозначьте свои оси. Убедитесь, что зритель знает, что он оценивает.
Удалите отвлекающие элементы диаграммы. Сетки, различные цвета и громоздкие легенды могут отвлекать зрителя от быстрого просмотра общей тенденции.
Увеличьте масштаб оси Y, если ваш набор данных начинается выше нуля. В некоторых случаях изменение масштаба оси Y упрощает задачу.
- Избегайте сравнения более 5-7 строк. Вы не хотите, чтобы ваша диаграмма была загромождена или ее было трудно читать. Визуализируйте данные, необходимые для рассказа вашей истории, не более того.
Визуализируйте данные, необходимые для рассказа вашей истории, не более того.Круговые диаграммы
Круговая диаграмма является одним из наиболее часто используемых и ненавистных типов диаграмм всех времен. Круговые диаграммы используются для отображения частей целого. Круговая диаграмма представляет числа в процентах, а общая сумма всех разделенных сегментов равна 100 процентам.
Рекомендации по созданию круговых диаграмм:
Убедитесь, что ваши сегменты в сумме составляют 100. Звучит очевидно, но это распространенная ошибка.
Содержите его в чистоте и последовательности. Сравните всего несколько категорий, чтобы донести свою точку зрения. Если секторы круговой диаграммы имеют примерно одинаковый размер, рассмотрите возможность использования гистограммы или гистограммы.
- Не используйте трехмерные изображения и не наклоняйте круговую диаграмму. Это часто делает ваши данные нечитаемыми, потому что ваш зритель пытается быстро сравнить ракурсы.
Гистограммы и гистограммы
Гистограммы и гистограммы используются для сравнения различных элементов. Столбцы на столбчатой диаграмме расположены вертикально, а столбцы на столбчатой диаграмме — горизонтально. Гистограммы обычно используются, чтобы избежать беспорядка, когда одна метка данных длинная или если у вас есть более 10 элементов для сравнения. Их легко понять и создать.
Рекомендации по созданию столбчатых и столбчатых диаграмм:
- Начать ось Y с нуля. Наши глаза чувствительны к области столбцов на диаграмме. Если эти полосы усечены, зритель может сделать неверные выводы.
- Пометить оси. Пометка осей дает контекст для вашего средства просмотра.
- Поместите метки значений на стержни — это помогает сохранить четкие линии длин стержней.
- Избегайте использования слишком большого количества цветов с эффектом радуги. Гораздо лучше использовать один цвет или различные оттенки одного и того же цвета. Вы можете выделить одну полосу, в частности, если это сообщение, которое вы хотите донести.
Вы можете выделить одну полосу, в частности, если это сообщение, которое вы хотите донести.Карта дерева
Карты дерева показывают части целого. Они отображают иерархическую информацию в виде кластера прямоугольников разного размера и цвета в зависимости от значения данных. Размер каждого прямоугольника представляет количество, а цвет может представлять числовое значение или категорию.
Древовидные карты позволяют просматривать тенденции и быстро проводить сравнения, особенно если один цвет особенно выделяется. В то время как электронные таблицы могут отображать несколько строк данных, древовидные карты могут содержать сотни тысяч элементов в одном организованном отображении, что позволяет легко выявлять закономерности за считанные секунды. Кроме того, если они сделаны правильно, они очень эффективно используют пространство.
Рекомендации по созданию древовидной карты
- Начните с чистых данных и четкого сообщения. Древовидные карты часто могут содержать много данных, поэтому важно точно знать, что вы хотите выделить.
- Используйте яркие, контрастные цвета, чтобы легко определить каждую область. Но не забывайте избегать «эффекта радуги». Выбирайте цвета с умом.
- Надлежащим образом пометьте каждый регион текстом или цифрами, чтобы зрителю было проще безошибочно оценить вашу древовидную карту.
- Не загромождайте карту дерева слишком большим количеством блоков. Карты дерева могут содержать любое количество блоков, но пространство ограничено! Вы не хотите, чтобы ваша древовидная карта была трудной для чтения.
Древовидные карты часто могут содержать много данных, поэтому важно точно знать, что вы хотите выделить.Диаграмма с двумя осями
С диаграммой с двумя осями вы, по сути, объединяете несколько диаграмм и добавляете вторую ось Y для сравнения. Некоторые члены сообщества визуализации данных скептически относятся к использованию диаграмм с двумя осями, потому что они часто могут сбивать с толку, иметь плохой дизайн и вводить зрителя в заблуждение.
Давайте рассмотрим различные типы диаграмм с двумя осями и лучшие способы их использования:
Столбчатая и линейная диаграмма — Эта диаграмма с двумя осями сочетает в себе столбчатую диаграмму с линейной диаграммой.
Двухлинейная диаграмма — Эта двухосевая диаграмма сравнивает две линейные диаграммы. При необходимости может быть больше двух строк.
Двухстолбцовая диаграмма — эта двухосевая столбчатая диаграмма показывает два набора данных, отображаемых рядом.
Многоосевая схема — отображает самую сложную версию диаграммы с двумя осями. Здесь вы видите три набора данных — с тремя осями Y.
Диаграмма с областями
Диаграммы с областями очень похожи на линейные диаграммы, но с небольшими отличиями. Они могут отображать изменения с течением времени, общие тенденции и непрерывность в наборе данных. Но хотя диаграммы с областями могут функционировать так же, как линейные диаграммы, пространство между линией и осью заполняется, указывая на объем.
Рекомендации по созданию диаграмм с областями
Сделайте его легко читаемым — избегайте окклюзии. Это происходит, когда один или несколько слоев закрывают важную информацию на диаграмме.
Используйте диаграмму с областями с накоплением — если у вас есть несколько наборов данных и вы хотите подчеркнуть отношения части к целому.
Используйте диаграммы с областями, чтобы увидеть более широкую картину. Возьмем, к примеру, население: линейные диаграммы хороши для отображения чистого изменения численности населения с течением времени, а диаграммы с областями хороши для отображения общей численности населения с течением времени.
Пирамидальная диаграмма
Пирамидальная диаграмма (треугольная диаграмма или треугольная диаграмма) — это увлекательный способ визуализации фундаментальных отношений. Они отображаются в виде треугольника, разделенного на горизонтальные секции с категориями, помеченными в соответствии с их иерархией.
Они могут быть ориентированы вверх или вниз в зависимости от отношений, которые они представляют. Сложенные слои также могут отображать порядок шагов в конкретном процессе.
Рекомендации по созданию пирамидальных диаграмм
Выберите тему и четко обозначьте подкатегории. Решите, какую информацию вы хотите передать с помощью пирамиды, и четко обозначьте слои.
Организуйте свои подкатегории. Определите порядок и значение каждого раздела в вашей пирамиде.
Организуйте подкатегории на основе их иерархии.
Будьте последовательны. Сохраняйте равные интервалы между разделами и выбирайте приятную цветовую палитру.
Сведите количество подкатегорий к минимуму. Добавление большого количества слоев и цветов может затруднить чтение вашей пирамиды.
Облако слов
Облака слов (также известные как облака тегов) представляют собой тип взвешенного списка.
Облака слов отображают текст шрифтом разного размера, веса или цвета, чтобы показать частоты или категории. Они могут быть расположены в алфавитном порядке или в случайном порядке. Они помогают людям выявлять тенденции и закономерности, которые иначе было бы трудно увидеть.
Рекомендации по созданию Word Cloud
Предоставление контекста. Облака слов визуально привлекают внимание и предоставляют информацию о частоте, но часто не дают зрителю никакого контекста.
Используйте облака слов, чтобы показать частоту. Не используйте их для отображения сложных тем, таких как бюджет или кризис здравоохранения.
Следите за длиной слова. Более длинные слова занимают больше места и могут ввести в заблуждение.
Облака Word отлично подходят для фильтрации и анализа данных.
Не делайте слова слишком похожими по размеру или цвету.
Таблицы
В таблицах данные отображаются в строках и столбцах.