Положительно заряженная частица с зарядом q и массой m влетает в однородное: Положительно заряженная частица с зарядом q и массой m влетает в однородное электрическое поле с…

\circ\), \(B_2=2B_1\), \(\frac{\nu_2}{\nu_1}-?\)

Решение задачи:

Под действием силы Лоренца заряженная частица в магнитном поле будет совершать равномерное движение по окружности. Очевидно, что если частица движется по окружности радиуса \(R\) со скоростью \(\upsilon\), то период обращения \(T\), то есть время, за которое частица сделает один оборот (или пройдет одну длину окружности, равную \(2\pi R\)), можно найти так:

\[T = \frac{{2\pi R}}{\upsilon }\]

Частоту вращения частицы \(\nu\) можно найти как величину, обратную периоду обращения \(T\):

\[\nu = \frac{1}{T}\]

\[\nu = \frac{\upsilon }{{2\pi R}}\;\;\;\;(1)\]

Силу Лоренца \(F_Л\) определяют по следующей формуле:

\[{F_Л} = B\upsilon q\sin \alpha \;\;\;\;(2)\]

Здесь \(B\) – индукция магнитного поля, \(\upsilon\) – скорость заряженной частицы, \(q\) – модуль заряда частицы, \(\alpha\) – угол между вектором скорости и вектором магнитной индукции.

Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца. 2}}}{R}\]

Имеем:

\[Bq\sin \alpha = \frac{{m\upsilon }}{R}\]

Откуда отношение \(\frac{\upsilon}{R}\), которое нам будет нужно в ходе дальнейшего решения, равно:

\[\frac{\upsilon }{R} = \frac{{Bq\sin \alpha }}{m}\]

Полученное выражение подставим в (1):

\[\nu = \frac{{Bq\sin \alpha }}{{2\pi m}}\]

Запишем полученную формулу дважды для двух случаев, описанных в условии задачи:

\[\left\{ \begin{gathered}
{\nu _1} = \frac{{{B_1}q\sin \alpha }}{{2\pi m}} \hfill \\
{\nu _2} = \frac{{{B_2}q\sin \alpha }}{{2\pi m}} \hfill \\
\end{gathered} \right.\]

Поделим нижнее равенство на верхнее, тогда искомое отношение \(\frac{\nu_2}{\nu_1}\) равно:

\[\frac{{{\nu _2}}}{{{\nu _1}}} = \frac{{{B_2}}}{{{B_1}}}\]

По условию величину индукции магнитного поля увеличивают в два раза, то есть \(B_2=2B_1\), поэтому:

\[\frac{{{\nu _2}}}{{{\nu _1}}} = \frac{{2{B_1}}}{{{B_1}}} = 2\]

Ответ: увеличится в 2 раза.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.2.23 Электрон движется в магнитном поле с индукцией 2 мТл по винтовой линии радиусом
8.2.25 Протон и альфа-частица (4He2), ускоренные одинаковой разностью потенциалов, влетают
8.2.26 Протон и дейтрон (ядро изотопа водорода 2h2), имеющие одинаковые скорости, влетают

Движение заряженного тела в электрическом поле

1. Движение вдоль линий напряженности

Рассмотрим сначала случай, когда действующей на тело силой тяжести можно пренебречь по сравнению с силой, которая действует на тело со стороны электрического поля. Это всегда имеет место, когда речь идет о движении заряженных микрочастиц, например электронов. Напомним, кстати, что электрон имеет отрицательный заряд, а протон – положительный.

? 1. Объясните, почему при рассмотрении движения частицы в электрическом поле нельзя пренебрегать массой частицы даже в том случае, когда сила тяжести пренебрежимо мала по сравнению с силой, действующей на частицу со стороны электрического поля.

? 2. Заряженная частица движется в однородном электрическом поле. Что можно сказать о начальной скорости этой частицы, если траектория ее движения – прямолинейная?

Рассмотрим, как при таком движении изменяется кинетическая и потенциальная энергия частицы.

? 3. Электрон движется прямолинейно в однородном электрическом поле из точки с потенциалом 700 В в точку с потенциалом 200 В.
а) Совпадает ли направление начальной скорости электрона с направлением линий напряженности поля или эти направления противоположны?
б) Как изменилась полная энергия электрона?
в) Чему равно изменение потенциальной энергии электрона?
г) Чему равно изменение кинетической энергии электрона?
д) Какова минимальная начальная скорость электрона?

При движении в электрическом поле заряженная частица может изменить направление движения на противоположное.

? 4. Электрон влетает в однородное электрическое поле с начальной скоростью 8 * 10⁶ м/с. Потенциал поля в точке, в которую влетает электрон, равен 500 В. Направление начальной скорости электрона совпадает с направлением линий напряженности поля.
а) До точки с каким минимальным значением потенциала поля долетит электрон?
б) С какой по модулю скоростью электрон вернется в начальную точку?
в) Чему равна напряженность поля, если электрон вернулся в начальную точку через 9,1 * 10^-9 с?
г) Чему равен путь, пройденный электроном до его возвращения в начальную точку?

Сравним движение в одном и том же поле двух частиц с одинаковыми по модулю зарядами, но с различными массами.

? 5. Электрон и протон находятся на одной линии напряженности однородного электрического поля на расстоянии 1 см друг от друга. Они начинают двигаться из состояния покоя в противоположные стороны.
а) Чему равна напряженность поля, если через 10^-8 с расстояние между частицами стало равным 9,8 см?
б) На какое расстояние от своей начальной точки удалился к этому моменту протон?
в) Чему равны в этот момент скорости электрона и протона?

2.

Движение заряженной частицы в конденсаторе

Если силой тяжести можно пренебречь по сравнению с силой, действующей на заряженную частицу со стороны электрического поля, то ее движение в поле конденсатора будет аналогично движению тела, брошенного горизонтально или под углом к горизонту, только роль силы тяжести будет играть сила, действующая на заряженную частицу со стороны электрического поля.

? 6. По какой траектории будет двигаться заряженная частица в однородном электрическом поле, если ее начальная скорость направлена под углом к линиям напряженности поля?

При рассмотрении тела, брошенного горизонтально или под углом к горизонту, мы использовали горизонтально направленную ось координат x и вертикально направленную ось y. В данном случае также удобно ввести оси координат x и y, как показано на рисунке 56.1.

Если начальная скорость частицы направлена горизонтально, направление оси y удобно выбрать так, чтобы проекция силы, действующей на эту частицу со стороны электрического поля конденсатора, была положительной. Начало координат совместим с начальным положением частицы.

? 7. Частица с зарядом q и массой m влетает в электрическое поле плоского конденсатора в точке, находящейся посередине между пластинами (рис. 56.1). Пластины конденсатора расположены горизонтально. Расстояние между пластинами равно d, длина пластин l, напряжение между пластинами U. Начальная скорость частицы равна по модулю v0 и направлена горизонтально.
а) Чему равны проекции ускорения частицы на оси координат при ее движении внутри конденсатора?
б) Как зависят от времени проекции скорости частицы?
в) Как зависят от времени координаты частицы?
г) Сколько времени частица будет лететь сквозь весь конденсатор, если не столкнется с его пластиной?
д) При каком соотношении между указанными выше параметрами частица пролетит сквозь весь конденсатор и вылетит из него?
е) Чему равен тангенс угла между скоростью частицы и горизонталью в тот момент, когда частица вылетает из конденсатора?
ж) Чему равен модуль скорости частицы, когда она вылетает из конденсатора?

? 8. Электрон влетает в конденсатор посередине между его пластинами со скоростью, направленной параллельно пластинам. Расстояние между пластинами равно 1 см, длина пластин 10 см. Начальная скорость электрона 5 * 10⁷ м/с.
а) Какова должна быть разность потенциалов между пластинами конденсатора, чтобы электрон не пролетел сквозь весь конденсатор?
б) На какую пластину в таком случае попадет электрон?
в) На каком расстоянии от положительной пластины будет находиться электрон в момент вылета из конденсатора, если напряжение между его пластинами равно 100 В?
г) Чему в этом случае будет равен тангенс угла между скоростью электрона и горизонталью в момент его вылета из конденсатора?
д) Как в этом случае изменится потенциальная энергия электрона за время его движения в конденсаторе?
е) На сколько процентов увеличится кинетическая энергия электрона за время движения в конденсаторе?

Рассмотрим случай, когда начальная скорость частицы направлена под углом к пластинам конденсатора.

Возможные типы траектории движения частицы схематически изображены на рисунке 56.2. Для определенности мы выбрали положительно заряженную частицу.

? 9. Каков знак заряда верхней пластины конденсатора, если положительно заряженная частица движется по одной из траекторий, изображенных красным пунктиром? синим пунктиром?

3. Движение заряженного тела в электрическом поле с учетом силы тяжести

Рассмотрим теперь случай, когда надо учитывать не только силу, действующую на тело со стороны электрического поля, но и силу тяжести.

? 10. Две большие пластины заряженного плоского конденсатора расположены вертикально (рис. 56.3). Разность потенциалов между пластинами равна U, а расстояние между ними равно d. Посередине между пластинами находится шарик с зарядом q и массой m. В начальный момент шарик покоится. Через некоторое время после того, как шарик отпустили, он столкнулся с одной из пластин конденсатора. Направим оси координат, как показано на рисунке.
56.3
а) Чему равна по модулю сила, действующая на шарик со стороны электрического поля?
б) Чему равна проекция ускорения шарика на ось х?
в) Через какой промежуток времени шарик столкнется с пластиной? Каков знак заряда этой пластины?
г) Насколько уменьшится высота шарика над землей к моменту столкновения по сравнению с его начальной высотой?
д) Какова форма траектории шарика?
е) Чему равно ускорение шарика во время движения?
ж) Чему равна скорость шарика в момент столкновения с пластиной?

Дополнительно вопросы и задания

11. Крупинка массой 10^-5 г влетает в электрическое поле горизонтально расположенного плоского конденсатора в точке, находящейся посередине между пластинами. Верхняя пластина конденсатора заряжена положительно. Начальная скорость крупинки направлена горизонтально. Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение между пластинами 1 кВ. Начальная скорость пылинки 6 м/с. Заряд крупинки равен по модулю 3 * 10^-12 Кл.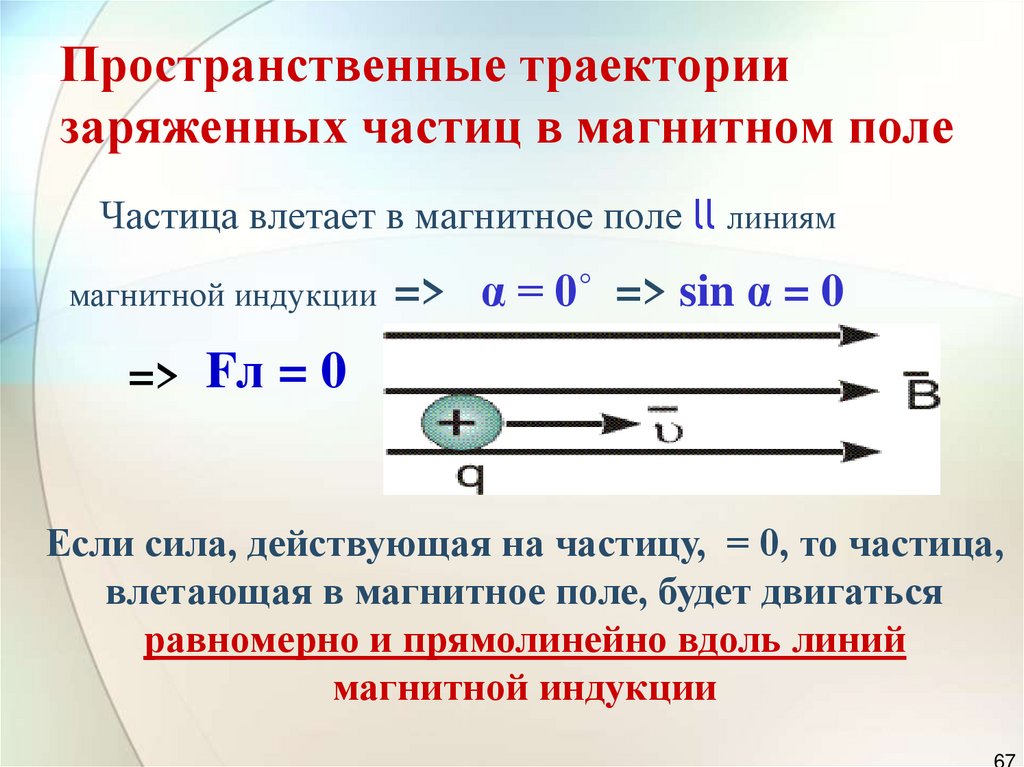
а) Чему равно отношение модулей силы тяжести и силы, действующей на крупинку со стороны электрического поля? При каком знаке заряда крупинки эти силы направлены одинаково?
б) Чему равно и как направлено ускорение крупинки, если у нее избыток электронов? недостаток электронов?
в) При каком знаке заряда крупинки она пролетит конденсатор насквозь?

12. Заряженная частица влетает в однородное электрическое поле с начальной скоростью, перпендикулярной линиям напряженности поля. В момент вылета из поля направление ее скорости составляет угол 60º с направлением начальной скорости. Во сколько раз увеличилась кинетическая энергия частицы при движении в электрическом поле? Считайте, что силой тяжести можно пренебречь.

Электрическая потенциальная энергия (U) и электрический потенциал (В): (Примечания к C

Электрическая потенциальная энергия (U) и электрический потенциал (V): ( Заметки из лекций C. Erkals PHYS 221 )

 

электрическое поле между его большими пластинами. Это достигается подключением каждой пластины к одному из выводов источник питания (например, аккумулятор).

 

 

 

Рисунок 1: Электрическое поле создается заряженными пластинами разделены расстоянием l. обвинения на пластинах +Q и Q.

 

Рис. 2: Электрический заряд q перемещается из точки A в направлении точка B с внешней силой T против электрической силы qE.

 

Рис. 3, 4: При перемещении на расстояние d его потенциальная энергия в точке B равна qEd относительно точки A.

 

Рис. 5. При выходе из положения B (T = 0) оно ускоряется к нижней пластине. Как он движется по направлению к нижней пластине ее потенциальная энергия уменьшается, а ее кинетическая энергия увеличивается. Когда он достигает нижней пластина (где мы можем выбрать Потенциальную энергию равной нулю), ее потенциал энергия в точке A полностью преобразуется в кинетическую энергию в точке B:

 

 

Обратите внимание, что qEd — это работа, совершаемая полем в виде заряда движется под действием силы qE из В в А. Здесь m — масса заряда q, а v — его скорость при достижении точка А. Здесь мы предполагали, что электрические поле однородное! Работа, проделанная полем E:

 

 

 

 

Давайте вспомним теорему о кинетической энергии-работе (рабочая энергия принцип):

 

 

 

где мы ввели понятие потенциальной энергии и консервативная сила (сила, под действием которой можно определить потенциальную энергию так, что совершенная работа зависит только от разницы потенциальной энергии функция оценивается в конечных точках).

 

Эмпирическое правило для принятия решения о том, является ли EPE возрастание:

Если заряд движется в направлении, в котором он нормально двигаться, его электрическая потенциальная энергия уменьшается. Если заряд перемещается в направлении, противоположном чтобы он нормально двигался, его электрическая потенциальная энергия увеличивается.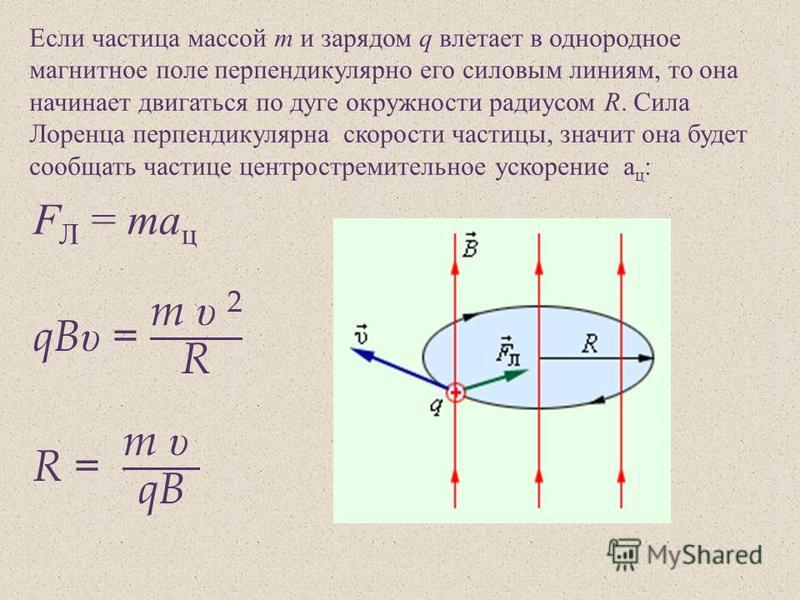 Эта ситуация аналогична ситуации постоянное гравитационное поле (g = 9,8 м/с ² ). Когда вы поднимаете предмет, вы увеличивает свою гравитационную потенциальную энергию. Точно так же, когда вы опускаете объект, его гравитационная энергия уменьшение.

 

Общая формула для разности потенциалов:

 

Работа, совершаемая полем E при воздействии на заряд q для перемещения это из точки А в точку Б определяется как разность электрических потенциалов между точки A и B:

 

 

Ясно, что функция потенциала V может быть поставлена ​​в соответствие каждой точка в пространстве, окружающем распределение заряда (например, параллельная тарелки). Приведенная выше формула обеспечивает простой рецепт для расчета работы, совершаемой при перемещении заряда между двумя точками где мы знаем величину разности потенциалов. Приведенные выше утверждения и формула справедливы независимо от пути, по которому перемещается заряд. Особый интерес представляет потенциал точечного заряда Q. Его можно найти, просто выполнив интегрирование по простому пути (например, по прямой) из точки A чье расстояние от Q равно r до бесконечности. Путь выбирается по радиальной линии так, чтобы

становится просто Edr. Поскольку электрическое поле Q равно кОм/р ² ,

 

Этот процесс определяет электрический потенциал точечной обвинение. Обратите внимание, что потенциальная функция скалярная величина, в отличие от электрического поля, являющегося векторной величиной. Теперь мы можем определить электрический потенциал энергия системы зарядов или зарядовых распределений. Предположим, мы вычисляем работу, совершенную против электрические силы при перемещении заряда q из бесконечности в точку на расстоянии r от заряд Q. Работа определяется:

 

 

Обратите внимание, что если q отрицательно, его знак должен использоваться в уравнение! Таким образом, система состоящий из отрицательного и положительного точечных зарядов, имеет отрицательный потенциальная энергия.

Отрицательная потенциальная энергия означает, что необходимо совершить работу против электрического поля при раздвигании зарядов!

Теперь рассмотрим более общий случай, связанный с потенциал в окрестности ряда зарядов, как показано на рисунке ниже:

 

Пусть r ₁ ,r ₂ ,r ₃ расстояния зарядов до точки поля А, и r ₁₂ , r ₁₃ , r ₂₃ представляют расстояние между зарядами. Электрический потенциал в точке А равен:

 

 

Пример:

Если мы принесем заряд Q из бесконечности и поместим его в точку А проделанная работа будет:

 

 

Полная электрическая потенциальная энергия этой системы зарядов, а именно работа, необходимая для приведения их в текущую позицию, может быть рассчитывается следующим образом: сначала принесите q1 (ноль работы, так как нет заряда вокруг еще), то в поле q1 вносим q2, то в поля q1 и q2 принести Q3.

Добавьте всю работу, необходимую для вычислить общую работу. Результат будет:

 

 

 

Определение электрического поля по электрическому потенциалу:

 

Составляющая E в любом направлении является отрицательной скорость изменения потенциала с расстоянием в этом направлении:

 

Символ называется градиентом. Электрическое поле – это градиент электрического потенциала. Линии электрического поля всегда перпендикулярно эквипотенциальным поверхностям.

 

Эквипотенциальные поверхности:

Это воображаемые поверхности, окружающие заряд. распределение. В частности, если распределение заряда сферическое (точечный заряд или равномерно заряженная сфера), поверхности сферические, концентрические с центром заряда распределение. Линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Уравнение

подразумевает, что из-за отрицательный знак, направление E противоположно направлению, в котором V увеличивается; E направлена ​​от высших к низшим уровням V (от высших потенциал к более низкому потенциалу). Другая Другими словами, градиент скаляра (в данном случае поля E) нормальен к поверхности постоянного значения (эквипотенциальная поверхность) скаляра и в направлении максимальная скорость изменения постоянного скаляра. Помните об этом утверждении, когда будете проводить эксперимент.

электромагнетизм. Есть ли интуитивное объяснение того, почему сила Лоренца перпендикулярна скорости частицы и магнитному полю?

Аргумент псевдовектора

Существует интуитивный аргумент, но первое, что нужно сделать, это взять двойственный Пуанкаре B. В трех измерениях существует эпсилон-тензор $\epsilon_{ijk}$, который является инвариантным — он не меняется при вращениях. Он имеет $\epsilon_{123}=1$ и все перестановки дают знак минус, так что значение $\epsilon$ равно нулю, если два индекса равны, а знак перестановки получить 123, если они все разные. Эпсилон-тензор, сжатый с тремя векторами $v_1,v_2,v_3$, дает площадь со знаком, натянутую на параллелепипед, который они образуют. \mu$, а это $v\times B$

В теории относительности это представляется единственно естественным, так как поля E и B вместе составляют антисимметричный 2-тензор, а четырехкратная сила Лоренца представляет собой этот тензор, сжатый с 4-скоростью. Эта форма настолько естественна и интуитивно понятна, что не требует подробного обоснования.

Более физическое переформулирование аргумента

Вышеизложенное звучит как формальное, но оно просто говорит следующее: магнитное поле не меняет знак при изменении координат пространства на противоположное. Чтобы увидеть это физически, рассмотрим соленоид тока, вытянутый вдоль оси z от -а до а, с током в основном в плоскости х-у вдоль каждой обмотки, и отразим этот соленоид в осях х-у-z. Отражение x меняет направление тока, отражение y возвращает его в исходное положение, а отражение z не меняет соленоид.

Так как ток один и тот же, B тоже самое! Таким образом, B от соленоида не меняется при отражении. Таким образом, сила, действующая на частицу, не может действовать вдоль направления В, потому что сила меняет направление при отражении, а В — нет. Сила может быть направлена ​​только на величину, которая имеет обратное направление, и простейшая такая величина есть $v\times B$. При отражении v меняет направление, а B — нет, поэтому сила Лоренца правильно меняет направление.

Этот аргумент предполагает симметрию отражения, которая является симметрией электромагнетизма, но на самом деле не является фундаментальной симметрией в нашей Вселенной. Тот же аргумент отражения показывает, что магнитный заряд не является должным образом симметричным электрическому заряду, поскольку магнитный заряд меняет знак при отражении (отражая все координаты с зарядом в начале координат — поле перемещается в новое место, но указывает на то же самое). направлении, поэтому смысл магнитного заряда меняется на противоположный). Это свойство означает, что магнитные монополи были ранним признаком того, что природа не является инвариантной по четности, и может объяснить, почему Дирак не был удивлен, когда было показано, что слабые взаимодействия нарушают четность.

Другое предположение состоит в том, что сила является простейшей инвариантной к отражению комбинацией B и v. Если отказаться от идеи, что сила линейно пропорциональна B, существуют более сложные комбинации, которые также работают, чтобы дать инвариантный к отражению закон силы . Эти комбинации обычно не подчиняются закону сохранения энергии.

Для автоматического сохранения энергии (и автоматического фазового пространства с симплектическими свойствами) вы должны вывести уравнения движения из действия. 92\свыше 2м + \фи}$$ $$ \partial_t x = {p — eA \over m}$$

Объединение уравнений в уравнение второго порядка для ускорения x дает закон силы Лоренца. Та же самая замена в гамильтониане, $p$ на $p-eA$, работает в теории относительности, чтобы дать правильный четырехмерный закон силы Лоренца.

Отождествление B с $\nabla \times A$ может быть обосновано инвариантностью уравнений относительно добавления градиента к A. Классически-физической частью A является его ротор, и его целесообразно отождествлять с B в Уравнения Максвелла.