Как рассчитать логарифм в Excel. Функция LOG для расчета логарифма в Эксель
Главная » Уроки MS Excel
Автор Елизавета КМ На чтение 6 мин Опубликовано
В Microsoft Excel есть большое количество функций, позволяющих быстро производить математические расчёты. Одной из самых распространённых и востребованных функций является LOG, с помощью которой можно рассчитывать логарифмы. В данной статье будет рассмотрен принцип её работы и характерные особенности.
Содержание
- Как вычислить логарифм в Excel
- Как в Microsoft Excel вычислить десятичный логарифм
- Как пользоваться логарифмической функцией в Excel
- Использование оператора LOG10 в Excel
- Альтернативный метод расчета логарифмов в Excel
- Заключение
Как вычислить логарифм в Excel
LOG позволяет считать логарифм числа по указанному основанию. В общем виде формула логарифма в Эксель, независимо от версии программы, записывается следующим образом: =LOG(число;[основание]). В представленной формуле присутствует два аргумента:
В общем виде формула логарифма в Эксель, независимо от версии программы, записывается следующим образом: =LOG(число;[основание]). В представленной формуле присутствует два аргумента:
- Число. Это записанное пользователем числовое значение, из которого нужно вычислить логарифм. Число можно записать вручную в поле ввода формулы или указать курсором мыши на нужную ячейку с прописанным значением.
- Основание. Это одна из составляющих логарифма, по которой он вычисляется. Основание также может быть записано в виде числа.
Обратите внимание! Если в Excel у логарифма не заполнить основание, то программа автоматически выставит нулевое значение.
Как в Microsoft Excel вычислить десятичный логарифм
Для простоты расчётов в Эксель есть отдельная функция, вычисляющая только десятичные логарифмы — это LOG10. Данная формула задаёт основание равное 10. После выбора функции LOG10 пользователю потребуется прописать только число, из которого будет высчитываться логарифм, а основание автоматически задаётся 10. Запись формулы выглядит так: =LOG10(число).
Запись формулы выглядит так: =LOG10(число).
Как пользоваться логарифмической функцией в Excel
Независимо от версии программного обеспечения, установленного на компьютере, расчёт логарифмов подразделяется на несколько этапов:
- Запустить Excel и создать небольшую таблицу из двух столбцов.
- В первом столбце прописать семь любых чисел. Их количество выбирается на усмотрение пользователя. Во второй колонке будут выводиться значения логарифмов числовых значений.
- Кликнуть ЛКМ по числу в первом столбце, чтобы выделить его.
- В левой части строки формул найти значок математической функции и нажать по нему. Это действие означает «Вставить функцию».
- После выполнения предыдущей манипуляции отобразится окошко «Вставка функции». Здесь нужно развернуть колонку «Категория», нажав по стрелочке справа, из списка выбрать вариант «Математические» и щёлкнуть по «ОК».

- В открывшемся списке операторов кликнуть по строке «LOG», а затем нажать на «ОК» для подтверждения действия. Теперь должно отобразиться меню настроек логарифмической формулы.
- Указать данные для расчёта. В поле «Число» нужно записать числовое значение, из которого будет рассчитываться логарифм, кликнув мышкой по соответствующей ячейке в созданной таблице, а в строчке «Основание» в данном случае потребуется прописать число 3.
- Нажать на «Enter» либо на «ОК» внизу окна и проверить результат. Если действия выполнены правильно, то в выбранной ранее ячейке таблицы отобразится результат вычисления логарифма. Если нажать на это число, то в строке сверху появится расчётная формула.
- Проделать ту же операцию с оставшимися числами в таблице, чтобы посчитать их логарифм.

Растягивание формулы для автоматического заполнения оставшихся строкДополнительная информация! В Excel не обязательно вручную считать логарифм каждого числа. Для простоты вычислений и экономии времени надо навести указатель мышки на крестик в правом нижнем углу ячейки с рассчитанным значением, зажать ЛКМ и растянуть формулу на оставшиеся строчки таблицы, чтобы они заполнились автоматически. Причём нужная формула пропишется для каждого числа.
Использование оператора LOG10 в Excel
На основании рассмотренного выше примера можно изучить работу функции LOG10. Для упрощения задачи оставим таблицу с теми же числами, предварительно удалив рассчитанные ранее логарифмы во втором столбце. Принцип работы оператора LOG10 можно охарактеризовать следующим образом:
- Выделить первую ячейку во втором столбце таблицы и нажать на кнопку «Вставить функцию» слева строки для ввода формул.
- По рассмотренной выше схеме указать категорию «Математические», выбрать функцию «LOG10» и щелкнуть по «Enter или нажать на «ОК» внизу окошка «Вставка функции».

- В открывшемся меню «Аргументы функции» нужно прописать только числовое значение, по которому будет производиться логарифмирование. В данном поле необходимо указать ссылку на ячейку с числом в исходной таблице.
- Нажать на «ОК» или на «Enter» и проверить результат. Во втором столбце должен посчитаться логарифм указанного числового значения.
- Аналогичным образом растянуть посчитанное значение на оставшиеся в таблице строки.
Важно! При настройке логарифмирования в Excel в поле «Число» можно вручную написать нужные цифры из таблицы.
Альтернативный метод расчета логарифмов в Excel
В Microsoft Office Excel есть более простой способ вычисления логарифмов тех или иных чисел. Он помогает сэкономить время, необходимое на выполнение математической операции. Данный метод вычисления подразделяется на следующие шаги:
- В свободной ячейке программы написать число 100.
 Можно указать любое другое значение, это не принципиально.
Можно указать любое другое значение, это не принципиально. - Выделить курсором мыши другую свободную ячейку.
- Переместиться в строку формул в верхней части главного меню программы.
- Прописать формулу «=LOG(число;[основание])» и нажать «Enter». В данном примере после открытия скобки надо выделить мышкой ячейку, в которой прописано число 100, затем поставить точку с запятой и указать основание, к примеру 10. Далее следует закрыть скобку и кликнуть по «Enter», чтобы завершить формулу. Значение посчитается автоматически.
Обратите внимание! Быстрый расчёт десятичных логарифмов выполняется аналогично с использованием оператора LOG10.
Заключение
Таким образом, в Excel алгоритмы вычисляются с помощью функций «LOG» и «LOG10» в кратчайшие сроки. Подробно методы расчёта были описаны выше, благодаря чему каждый пользователь сможет выбрать для себя наиболее комфортный вариант. c=b \)
c=b \)
Простыми словами:
Логарифм это степень в которую нужно возвести низ чтобы получить верх.
\( \log_7 49=2 \)
\( \log_9 81=2 \)
\( \log_2 8=3 \)
1. Вычислить, руководствуясь определением логарифма:
\( \log_8 64 \)
В какую степень нужно возвести 8 чтобы получить 64 ?
\( \log_8 64=2 \)
Пройти простейший тест на эту тему
2. Вычислить, руководствуясь определением логарифма:
\( \log_{10} 100 \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести 10 чтобы получить 100 ?
\( \log_{10} 100=2 \)
Пройти легкий тест на эту тему
3. Вычислить, руководствуясь определением логарифма:
Вычислить, руководствуясь определением логарифма:
\( \log_{2} 8 \)
В какую степень нужно возвести 2 чтобы получить 8 ?
\( \log_{2} 8=3 \)
4. Вычислить, руководствуясь определением логарифма:
\( \log_{2} 16 \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести 2 чтобы получить 16 ?
\( \log_{2} 16=4 \)
5. Вычислить, руководствуясь определением логарифма:
\( \log_{3} 27 \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести 3 чтобы получить 27 ?
\( \log_{3} 27=3 \)
6. Вычислить, руководствуясь определением логарифма:
Вычислить, руководствуясь определением логарифма:
\( \log_{10} 1000 \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести 10 чтобы получить 1000 ?
\( \log_{10} 1000=3 \)
Пройти простейший тест на эту тему
7. Вычислить, руководствуясь определением логарифма:
\( \log_{2} 32 \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести 2 чтобы получить 32 ?
\( \log_{2} 32=5 \)
Пройти легкий тест на эту тему
8. Вычислить, руководствуясь определением логарифма:
\( \log_{2} 128 \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести 2 чтобы получить 128 ?
\( \log_{2} 128=7 \)
9. Вычислить, руководствуясь определением логарифма:
Вычислить, руководствуясь определением логарифма:
\( \log_{41} 41 \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести 41 чтобы получить 41 ?
\( \log_{41} 41=1 \)
10. Вычислить логарифм
\( \log_{\frac{1}{2}} \frac{1}{4} \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести \(\dfrac{1}{2} \) чтобы получить \(\dfrac{1}{4} \) ?
\( \log_{\frac{1}{2}} \frac{1}{4}=2 \)
11. Вычислить, руководствуясь определением логарифма:
\( \log_{\frac{4}{5}} \frac{16}{25} \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести \(\dfrac{4}{5} \) чтобы получить \(\dfrac{16}{25} \) ?
\( \log_{\frac{4}{5}} \frac{16}{25}=2 \)
12. Вычислить логарифм
Вычислить логарифм
\( \log_{\frac{2}{3}} \frac{16}{81} \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести \(\dfrac{2}{3} \) чтобы получить \(\dfrac{16}{81} \) ?
\( \log_{\frac{2}{3}} \frac{16}{81}=4 \)
13. Вычислить, руководствуясь определением логарифма:
\( \log_{0,5} 0,25 \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести \( 0,5 \) чтобы получить \( 0,25 \) ?
\( \log_{0,5} 0,25 =2 \)
Пройти легкий тест на эту тему
14. Вычислить логарифм
\( \log_{0,5} 0,125 \)
Показать подсказку
Показать решение
Видеорешение
В какую степень нужно возвести \( 0,5 \) чтобы получить \( 0,125 \) ?
\( \log_{0,5} 0,125 =3 \)
15. {0,5} = 0,5 \)
{0,5} = 0,5 \)
33. Вычислить, руководствуясь определением логарифма:
\( \log_{2} 1 \)
Показать подсказку
Показать решение
Видеорешение
любое число в нулевой степени равно единице
В какую степень нужно возвести \( 2 \) чтобы получить \( 1 \) ?
\( \log_{2} 1 = 0 \)
34. Вычислить, руководствуясь определением логарифма:
\( \log_{32} 1 \)
Показать подсказку
Показать решение
Видеорешение
любое число в нулевой степени равно единице
В какую степень нужно возвести \( 32 \) чтобы получить \( 1 \) ?
\( \log_{32} 1 = 0 \)
35. Вычислить, руководствуясь определением логарифма:
\( \log_{x} 1 \)
Показать подсказку
Показать решение
Видеорешение
Любое число в нулевой степени равно единице
В какую степень нужно возвести \( x \) чтобы получить \( 1 \) ?
\( \log_{x} 1 = 0 \)
36. 3}=\dfrac{1}{0,125}=8 \)
3}=\dfrac{1}{0,125}=8 \)
В какую степень нужно возвести \( 0,5 \) чтобы получить \( 8 \) ?
\( \log_{0,5} 8 = -3 \)
как вычислить? Любое число \(a\) может быть представлено как логарифм с основанием \(b\): \(a=\log_{b}{b{a}}\)
Область допустимых значений (ОДЗ) логарифма
Теперь поговорим об ограничениях (ОДЗ — область допустимых значений переменных).
Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:
То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться.
Почему так?
Начнем с простого: допустим, что. Тогда, например, число не существует, так как в какую бы степень мы не возводили, всегда получается. Более того, не существует ни для какого. Но при этом может равняться чему угодно (по той же причине — в любой степени равно). Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.
Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.
Похожая проблема у нас и в случае: в любой положительной степени — это, а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что).
При мы столкнемся с проблемой возведения в дробную степень (которая представляется в виде корня: . Например, (то есть), а вот не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:
Решим уравнение.
Вспомним определение: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. И по условию, эта степень равна: .
И по условию, эта степень равна: .
Получаем обычное квадратное уравнение: . Решим его с помощью теоремы Виета: сумма корней равна, а произведение. Легко подобрать, это числа и.
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
Это явно неверно, так как основание не может быть отрицательным, то есть корень — «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
Тогда, получив корни и, сразу отбросим корень, и напишем правильный ответ.
Пример 1 (попробуй решить самостоятельно):
Найдите корень уравнения. Если корней несколько, в ответе укажите меньший из них.
Решение:
В первую очередь напишем ОДЗ:
Теперь вспоминаем, что такое логарифм: в какую степень нужно возвести основание, чтобы получить аргумент? Во вторую. То есть:
Казалось бы, меньший корень равен. Но это не так: согласно ОДЗ корень — сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: .
Но это не так: согласно ОДЗ корень — сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: .
Ответ: .
Основное логарифмическое тождество
Вспомним определение логарифма в общем виде:
Подставим во второе равенство вместо логарифм:
Это равенство называется основным логарифмическим тождеством . Хотя по сути это равенство — просто по-другому записанное определение логарифма :
Это степень, в которую нужно возвести, чтобы получить.
Например:
Реши еще следующие примеры:
Пример 2.
Найдите значение выражения.
Решение:
Вспомним правило из раздела : , то есть, при возведении степени в степень показатели перемножаются. Применим его:
Пример 3.
Докажите, что.
Решение:
Свойства логарифмов
К сожалению, задачи не всегда такие простые — зачастую сперва нужно упростить выражение, привести его к привычному виду, и только потом будет возможно посчитать значение. Это проще всего сделать, зная свойства логарифмов . Так что давай выучим основные свойства логарифмов. Каждое из них я буду доказывать, ведь любое правило проще запомнить, если знать, откуда оно берется.
Это проще всего сделать, зная свойства логарифмов . Так что давай выучим основные свойства логарифмов. Каждое из них я буду доказывать, ведь любое правило проще запомнить, если знать, откуда оно берется.
Все эти свойства нужно обязательно запомнить, без них большинство задач с логарифмами решить не получится.
А теперь обо всех свойствах логарифмов подробнее.
Свойство 1:
Доказательство:
Пусть, тогда.
Имеем: , ч.т.д.
Свойство 2: Сумма логарифмов
Сумма логарифмов с одинаковыми основаниями равна логарифму произведения: .
Доказательство:
Пусть, тогда. Пусть, тогда.
Пример: Найдите значение выражения: .
Решение: .
Только что выученная формула помогает упростить сумму логарифмов, а не разность, так что сразу эти логарифмы не объединить. Но можно сделать наоборот — «разбить» первый логарифм на два:А вот обещанное упрощение:
.
Зачем это нужно? Ну например: чему равно?
Теперь очевидно, что.
Теперь упрости сам:
Задачи:
Ответы:
Свойство 3: Разность логарифмов:
Доказательство:
Все точно так же, как и в пункте 2:
Пусть, тогда.
Пусть, тогда. Имеем:
Пример из прошлого пункта теперь становится еще проще:
Пример посложнее: . Догадаешься сам, как решить?
Здесь нужно заметить, что у нас нету ни одной формулы про логарифмы в квадрате. Это что-то сродни выражению — такое сразу не упростить.
Поэтому отвлечемся от формул про логарифмы, и подумаем, какие вообще формулы мы используем в математике чаще всего? Еще начиная с 7 класса!
Это — . Нужно привыкнуть к тому, что они везде! И в показательных, и в тригонометрических, и в иррациональных задачах они встречаются. Поэтому их нужно обязательно помнить.
Если присмотреться к первым двум слагаемым, становится ясно, что это разность квадратов :
Ответ для проверки:
Упрости сам.
Примеры
Ответы.
Свойство 4: Вынесение показателя степени из аргумента логарифма:
Доказательство: И здесь тоже используем определение логарифма:пусть, тогда. Имеем: , ч.т.д.
Можно понять это правило так:
То есть степень аргумента выносится вперед логарифма, как коэффициент.
Пример: Найдите значение выражения.
Решение: .
Реши сам:
Примеры:
Ответы:
Свойство 5: Вынесение показателя степени из основания логарифма:
Доказательство: Пусть, тогда.
Имеем: , ч.т.д.
Запоминаем: из основания степень выносится как обратное число, в отличии от предыдущего случая!
Свойство 6: Вынесение показателя степени из основания и аргумента логарифма:
Или если степени одинаковые: .
Свойство 7: Переход к новому основанию:
Доказательство: Пусть, тогда.
Имеем: , ч.т.д.
Свойство 8: Замена местами основания и аргумента логарифма:
Доказательство: Это частный случай формулы 7: если подставить, получим: , ч. т.д.
т.д.
Рассмотрим еще несколько примеров.
Пример 4.
Найдите значение выражения.
Используем свойство логарифмов № 2 — сумма логарифмов с одинаковым основанием равна логарифму произведения:
Пример 5.
Найдите значение выражения.
Решение:
Используем свойство логарифмов № 3 и № 4:
Пример 6.
Найдите значение выражения.
Решение:
Используем свойство № 7 — перейдем к основанию 2:
Пример 7.
Найдите значение выражения.
Решение:
Как тебе статья?
Если ты читаешь эти строки, значит ты прочитал всю статью.
И это круто!
А теперь расскажи нам как тебе статья?
Научился ты решать логарифмы? Если нет, то в чем проблема?
Пиши нам в комментах ниже.
И, да, удачи на экзаменах.
На ЕГЭ и ОГЭ и вообще в жизни
Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Область определения, множество значений, возрастание, убывание
Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.
| Область определения | 0 | 0 |
| Область значений | — ∞ | — ∞ |
| Монотонность | монотонно возрастает | монотонно убывает |
| Нули, y = 0 | x = 1 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет | нет |
| + ∞ | — ∞ | |
| — ∞ | + ∞ |
Частные значения
Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:
Логарифм по основанию e называется натуральным логарифмом :
Основные формулы логарифмов
Свойства логарифма, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Логарифмирование — это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей преобразуются в суммы членов.
При логарифмировании, произведения сомножителей преобразуются в суммы членов.
Потенцирование — это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов преобразуются в произведения сомножителей.
Доказательство основных формул логарифмов
Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.
Рассмотрим свойство показательной функции
.
Тогда
.
Применим свойство показательной функции
:
.
Докажем формулу замены основания.
;
.
Полагая c = b
,
имеем:
Обратная функция
Обратной для логарифма по основанию a является показательная функция с показателем степени a .
Если , то
Если , то
Производная логарифма
Производная логарифма от модуля x
:
.
Производная n-го порядка:
.
Вывод формул > > >
Для нахождения производной логарифма, его нужно привести к основанию e .
;
.
Интеграл
Интеграл от логарифма вычисляется интегрированием по частям : .
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексного числа z :
.
Выразим комплексное число z через модуль r и аргумент φ :
.
Тогда, используя свойства логарифма, имеем:
.
Или
Однако, аргумент φ определен не однозначно. Если положить
, где n
— целое,
то будет одним и тем же числом при различных n .
Поэтому логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
ОПРЕДЕЛЕНИЕ
Десятичным логарифмом называется логарифм по основанию 10:
Title=»Rendered by QuickLaTeX. com»>
com»>
Этот логарифм является решением показательного уравнения . Иногда (особенно в зарубежной литературе) десятичный логарифм обозначается еще как , хотя первые два обозначения присущи и натуральному логарифму.
Первые таблицы десятичных логарифмов были опубликованы английским математиком Генри Бригсом (1561-1630) в 1617 г. (поэтому иностранные ученые часто называют десятичные логарифмы еще бригсовыми), но эти таблицы содержали ошибки. На основе таблиц (1783 г.) словенского и австрийского математики Георга Барталомея Веги (Юрий Веха или Веховец, 1754-1802) в 1857 г. немецкий астроном и геодезист Карл Бремикер (1804-1877) опубликовал первое безошибочное издание. При участии русского математика и педагога Леонтия Филипповича Магницкого (Телятин или Теляшин, 1669-1739) в 1703 г. в России были изданы первые таблицы логарифмов. Десятичные логарифмы широко применялись для вычислений.
Свойства десятичных логарифмов
Этот логарифм обладает всеми свойствами, присущими логарифму по произвольному основанию:
1. {-5}=\)\(\frac{1}{32}\)
{-5}=\)\(\frac{1}{32}\)
Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:
Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».
Как вычислить логарифм?
Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
Например , вычислите логарифм: а) \(\log_{4}{16}\) б) \(\log_{3}\)\(\frac{1}{3}\) в) \(\log_{\sqrt{5}}{1}\) г) \(\log_{\sqrt{7}}{\sqrt{7}}\) д) \(\log_{3}{\sqrt{3}}\)
а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому:
\(\log_{4}{16}=2\)
\(\log_{3}\)\(\frac{1}{3}\) \(=-1\)
в) В какую степень надо возвести \(\sqrt{5}\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!
\(\log_{\sqrt{5}}{1}=0\)
г) В какую степень надо возвести \(\sqrt{7}\), чтобы получить \(\sqrt{7}\)? В первую – любое число в первой степени равно самому себе. {b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
{b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
\(\log_{4}{10}=5x-4\)
Зеркально перевернем уравнение, чтобы икс был слева
\(5x-4=\log_{4}{10}\)
Перед нами . Перенесем \(4\) вправо.
И не пугайтесь логарифма, относитесь к нему как к обычному числу.
\(5x=\log_{4}{10}+4\)
Поделим уравнение на 5
\(x=\)\(\frac{\log_{4}{10}+4}{5}\)
Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.
Ответ : \(\frac{\log_{4}{10}+4}{5}\)
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\).
 {\log_{6}{5}}\)
{\log_{6}{5}}\)Решение :
Ответ : \(25\)
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_{2}{4}\) равен двум. Тогда можно вместо двойки писать \(\log_{2}{4}\).
Но \(\log_{3}{9}\) тоже равен \(2\), значит, также можно записать \(2=\log_{3}{9}\) . Аналогично и с \(\log_{5}{25}\), и с \(\log_{9}{81}\), и т.д. То есть, получается
\(2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…\)
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как \(\log_{2}{8}\), или как \(\log_{3}{27}\), или как \(\log_{4}{64}\)… Здесь мы как аргумент пишем основание в кубе:
\(3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}. {a}}\)
{a}}\)
Пример : Найдите значение выражения \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)
Решение :
Ответ : \(1\)
Нередко берут цифру десять. Логарифмы чисел по основанию десять именуют десятичными . При проведении вычислений с десятичным логарифмом общепринято оперировать знаком lg , а не log ; при этом число десять, определяющие основание, не указывают. Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .
Для десятичных логарифмов типичны те же особенности, которые есть у логарифмов при основании, большем единицы. А именно, десятичные логарифмы характеризуются исключительно для положительных чисел. Десятичные логарифмы чисел, больших единицы, положительны, а чисел, меньших единицы, отрицательны; из двух не отрицательных чисел большему эквивалентен и больший десятичный логарифм и т. д. Дополнительно, десятичные логарифмы имеют отличительные черты и своеобразные признаки, которыми и поясняется, зачем в качестве основания логарифмов комфортно предпочитать именно цифру десять.
Перед тем как разобрать эти свойства, ознакомимся с нижеследующими формулировками.
Целая часть десятичного логарифма числа а именуется характеристикой , а дробная — мантиссой этого логарифма.
Характеристика десятичного логарифма числа а указывается как , а мантисса как {lg а }.
Возьмем, скажем, lg 2 ≈ 0,3010.Соответственно = 0, {lg 2} ≈ 0,3010.
Подобно и для lg 543,1 ≈2,7349. Соответственно, = 2, {lg 543,1}≈ 0,7349.
Достаточно повсеместно употребляется вычисление десятичных логарифмов положительных чисел по таблицам.
Характерные признаки десятичных логарифмов.
Первый признак десятичного логарифма. целого не отрицательного числа, представленного единицей со следующими нулями, есть целое положительное число, равное численности нулей в записи выбранного числа.
Возьмем, lg 100 = 2, lg 1 00000 = 5.
Обобщенно, если
То а = 10 n , из чего получаем
lg a = lg 10 n = n lg 10 = п .
Второй признак. Десятичный логарифм положительной десятичной дроби , показанный единицей с предыдущими нулями, равен — п , где п — численность нулей в представлении этого числа, учитывая и нуль целых.
Рассмотрим, lg 0,001 = — 3, lg 0,000001 =-6.
Обобщенно, если
,
То a = 10 -n и получается
lga= lg 10 n =-n lg 10 =-п
Третий признак. Характеристика десятичного логарифма не отрицательного числа, большего единицы, равна численности цифр в целой части этого числа исключая одну.
Разберем данный признак 1) Характеристика логарифма lg 75,631 приравнена к 1.
И правда, 10
lg 10
1 .
Отсюда следует,
lg 75,631 = 1 +б,
Смещение запятой в десятичной дроби вправо или влево равнозначно операции перемножения этой дроби на степень числа десять с целым показателем п (положительным или отрицательным). И следовательно, при смещении запятой в положительной десятичной дроби влево или вправо мантисса десятичного логарифма этой дроби не меняется.
Так, {lg 0,0053} = {lg 0,53} = {lg 0,0000053}.
Функция логарифма в Excel: формула расчета
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Уроки Excel Как рассчитать логарифм в Excel с помощью функции LOG
Вычисление логарифмов – это одна из самых востребованных математических задач, в том числе, в программе Эксель, в которой специально для этого разработана функция под названием LOG. В этой статье мы рассмотрим, каким образом работает данная функция.
Содержание
- Вычисление логарифма в Эксель
- Использование оператора LOG
- Применение оператора LOG10
- Заключение
Вычисление логарифма в Эксель
Смотрите также: “Расширенный фильтр Excel: как пользоваться”
Функция в Excel, позволяющая считать логарифмы из определенного числа по указанному основанию, называется LOG.
Формула функции LOG выглядит следующим образом:
=LOG(число;[основание])
Как мы видим, формула имеет два аргумента:
- “Число” – конкретное число (или адрес ячейки, которая содержит число), из которого требуется вычислить логарифм.

- “Основание” – также выражается числом (либо содержит координаты ячейки с требуемым числом), которое является основанием, по которому вычисляется логарифм. Наличие этого аргумента не является обязательным, и его можно и не указывать. В этом случае автоматически будет присвоено нулевое значение.
Помимо вышеописанной функции, в Эксель есть еще один оператор – LOG10, который вычисляет логарифмы с основанием, равным цифре 10. Другими словами, он умеет работать исключительно с десятичными логарифмами.
Формула функции LOG10 выглядит следующим образом:
=LOG10(число).
В данном случае оператор имеет только один аргумент – “Число”, который, как и в случае с функцией LOG, прописывается в виде числового выражения (либо ссылкой на ячейку с требуемым числом). Это и есть то значение, логарифм которого нужно рассчитать. Второго аргумента под названием “Основание” в этой формуле нет, так как ему присваивается безусловное значение, равное 10.
Использование оператора LOG
Для лучшего понимания работы функции LOG давайте разберем ее, применив на практике. Для этого возьмем таблицу имеющую колонку с числами. Наша задача – в отдельном столбце вычислить логарифмы из этих числовых значений по основанию, равному 3.
Давайте начнем выполнение нашей задачи:
- Выбираем первую ячейку столбца, в которой хотим произвести вычисления. Затем кликаем по кнопке “Вставить функцию” (с левой стороны от строки формул).
- В результате откроется окно Мастера функций. Здесь мы щелкаем по текущей категории и в открывшемся перечне выбираем строку “Математические”.
- Из предложенного списка операторов кликаем по функции “LOG” и подтверждаем действие нажатием OK.
- В открывшемся окне задаем настройки функции, после чего нажимаем OK. Согласно количеству аргументов оператора, в открывшемся окне имеется два поля:
- в поле “Число” указываем координаты ячейки с числом, из которого требуется рассчитать логарифм.
 Можно прописать информацию вручную, но есть более простой и удобный метод. Кликаем сначала по области поля “Число”, после чего – по требуемой ячейке.
Можно прописать информацию вручную, но есть более простой и удобный метод. Кликаем сначала по области поля “Число”, после чего – по требуемой ячейке. - в поле “Основание” в нашем случае указываем значение “3”.Примечание: В поле “Число” можно сразу напечатать конкретное числовое значение.
- в поле “Число” указываем координаты ячейки с числом, из которого требуется рассчитать логарифм.
- После проделанных действий результат вычислений незамедлительно отобразится в выбранной ячейке с формулой LOG.
- Теперь остается скопировать формула расчета для оставшихся исходных числовых значений, представленных в первом столбце. Прописывать или вставлять формулу для каждой ячейки слишком долго, и к счастью, это вовсе не обязательно, ведь есть куда более быстрый способ это сделать, причем, исключив возможные ошибки и опечатки. Для этого наводим указатель мыши на нижний правый угол ячейки с формулой, и после того, как курсор изменит форму на крестик, зажав левую кнопку мыши растягиваем формулу на оставшиеся строки ниже.
- В результате проделанных действий мы получим результат вычислений по всем строкам.

Применение оператора LOG10
А сейчас предлагаем познакомимся с оператором LOG10. Теперь наша задача – это получении десятичных логарифмов исходных чисел.
- Проделываем те же действия, что и при первом способе, т.е. выбираем верхнюю ячейку столбца, куда будем выводить результаты и жмем кнопку “Вставить функцию”.
- В перечне математических операторов кликаем по строке “LOG10”, после чего подтверждаем выбор нажатием OK.
- Затем выполняем настройку функции. В данном случае она имеет всего лишь один аргумент – “Число”. Указываем адрес нужной ячейки с числом, логарифм из которого нужно рассчитать, и жмем кликаем по кнопке OK, чтобы получить результат.
- В итоге, в выбранной ячейке с формулой будет выведен результат вычислений десятичного логарифма от заданного числового значения. Методом, который был описан в первом способе, растягиваем формулу на все оставшиеся строки результирующего столбца.
Заключение
Итак, в Microsoft Excel вычисление логарифма от заданного числового значения по указанному основанию реализовано через функцию “LOG”, которая также позволяет рассчитать логарифм по основанию, равному 10. Однако, для десятичных логарифмов целесообразнее и проще использовать специально разработанный для этого отдельный оператор под названием “LOG10”.
Однако, для десятичных логарифмов целесообразнее и проще использовать специально разработанный для этого отдельный оператор под названием “LOG10”.
Смотрите также: “Как посчитать количество символов в ячейке таблицы Excel”
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Как рассчитать логарифм в Excel.
 Функция LOG для расчета логарифма в Эксель — Информатика ► Информатика в школе и дома
Функция LOG для расчета логарифма в Эксель — Информатика ► Информатика в школе и домаПрактические работы в MS Excel — задания, советы, решения и ответы
Информатика и ИКТОставить комментарийна Как рассчитать логарифм в Excel. Функция LOG для расчета логарифма в Эксель — Информатика
Оглавление:
- 1 Как рассчитать логарифм в Excel. Функция LOG для расчета логарифма в Эксель — Разбираем подробно
- 2 Как вычислить логарифм в Excel
- 3 Как в Microsoft Excel вычислить десятичный логарифм
- 4 Как пользоваться логарифмической функцией в Excel
- 5 Использование оператора LOG10 в Excel
- 6 Альтернативный метод расчета логарифмов в Excel
- 7 Заключение
Want create site? Find Free WordPress Themes and plugins.
Как рассчитать логарифм в Excel. Функция LOG для расчета логарифма в Эксель — Разбираем подробно
В Microsoft Excel есть большое количество функций, позволяющих быстро производить математические расчёты. Одной из самых распространённых и востребованных функций является LOG, с помощью которой можно рассчитывать логарифмы. В данной статье будет рассмотрен принцип её работы и характерные особенности.
Одной из самых распространённых и востребованных функций является LOG, с помощью которой можно рассчитывать логарифмы. В данной статье будет рассмотрен принцип её работы и характерные особенности.
Как вычислить логарифм в Excel
LOG позволяет считать логарифм числа по указанному основанию. В общем виде формула логарифма в Эксель, независимо от версии программы, записывается следующим образом: =LOG(число;[основание]). В представленной формуле присутствует два аргумента:
Обратите внимание! Если в Excel у логарифма не заполнить основание, то программа автоматически выставит нулевое значение.
Как в Microsoft Excel вычислить десятичный логарифм
Для простоты расчётов в Эксель есть отдельная функция, вычисляющая только десятичные логарифмы — это LOG10. Данная формула задаёт основание равное 10. После выбора функции LOG10 пользователю потребуется прописать только число, из которого будет высчитываться логарифм, а основание автоматически задаётся 10. Запись формулы выглядит так: =LOG10(число).
Как пользоваться логарифмической функцией в Excel
Независимо от версии программного обеспечения, установленного на компьютере, расчёт логарифмов подразделяется на несколько этапов:
Создание таблицы чисел для вычисления логарифмов в Excel

Открытие окна «Вставка функций». Нужно нажать на значок слева от строки формул
Выбор функции LOG для первого значения в таблице
Заполнение аргументов функции. Надо указать число и основание для логарифмирования
 Если действия выполнены правильно, то в выбранной ранее ячейке таблицы отобразится результат вычисления логарифма. Если нажать на это число, то в строке сверху появится расчётная формула.
Если действия выполнены правильно, то в выбранной ранее ячейке таблицы отобразится результат вычисления логарифма. Если нажать на это число, то в строке сверху появится расчётная формула.Проверка результата. Необходимо навести курсор мыши на строку формул сверху окна
Дополнительная информация! В Excel не обязательно вручную считать логарифм каждого числа. Для простоты вычислений и экономии времени надо навести указатель мышки на крестик в правом нижнем углу ячейки с рассчитанным значением, зажать ЛКМ и растянуть формулу на оставшиеся строчки таблицы, чтобы они заполнились автоматически. Причём нужная формула пропишется для каждого числа.
Растягивание формулы для автоматического заполнения оставшихся строк
Использование оператора LOG10 в Excel
На основании рассмотренного выше примера можно изучить работу функции LOG10. Для упрощения задачи оставим таблицу с теми же числами, предварительно удалив рассчитанные ранее логарифмы во втором столбце. Принцип работы оператора LOG10 можно охарактеризовать следующим образом:
Для упрощения задачи оставим таблицу с теми же числами, предварительно удалив рассчитанные ранее логарифмы во втором столбце. Принцип работы оператора LOG10 можно охарактеризовать следующим образом:
Заполнение аргумента для расчета десятичного логарифма в Эксель

Важно! При настройке логарифмирования в Excel в поле «Число» можно вручную написать нужные цифры из таблицы.
Альтернативный метод расчета логарифмов в Excel
В Microsoft Office Excel есть более простой способ вычисления логарифмов тех или иных чисел. Он помогает сэкономить время, необходимое на выполнение математической операции. Данный метод вычисления подразделяется на следующие шаги:
 Значение посчитается автоматически.
Значение посчитается автоматически.Альтернативный метод расчёта логарифмов в Excel
Обратите внимание! Быстрый расчёт десятичных логарифмов выполняется аналогично с использованием оператора LOG10.
Заключение
Таким образом, в Excel алгоритмы вычисляются с помощью функций «LOG» и «LOG10» в кратчайшие сроки. Подробно методы расчёта были описаны выше, благодаря чему каждый пользователь сможет выбрать для себя наиболее комфортный вариант.
Did you find apk for android? You can find new Free Android Games and apps.
Найти:Рубрики
РубрикиВыберите рубрикуIT Новости — технологии, софт, гаджеты со всего мира и России (347)Все статьи (1 778)ЕГЭ учебные пособия – Подготовка по информатике к экзамену скачать читать бесплатно (3)Информатика — учебники 1-11 класс онлайн читать (214) Учебники Информатики 1 класс онлайн, скачать, читать (5) Учебники Информатики 10 класс онлайн, скачать, читать (22) Учебники Информатики 11 класс онлайн, скачать, читать (18) Учебники Информатики 2 класс онлайн, скачать, читать (17) Учебники Информатики 3 класс онлайн, скачать, читать (28) Учебники Информатики 4 класс онлайн, скачать, читать (31) Учебники Информатики 5 класс онлайн, скачать, читать (19) Учебники Информатики 6 класс онлайн, скачать, читать (20) Учебники Информатики 7 класс онлайн, скачать, читать (35) Учебники Информатики 8 класс онлайн, скачать, читать (35) Учебники Информатики 9 класс онлайн, скачать, читать (37)КИМ Информатика 8 класс Масленикова (15)Методическая копилка — Дошкольная Информатика (3)Методическая копилка по информатике: уроки, конспекты, занимательные задачи (47) Методическая копилка по информатике — 5 класс — уроки, конспекты, занимательные задачи (3) Методическая копилка по информатике — 6 класс — уроки, конспекты, занимательные задачи (18)НОВОСТИ об ИГРАХ — новинки, обновления, свежие игровые новости (377)ОГЭ учебные пособия — Подготовка по информатике к экзамену скачать читать бесплатно (6)Решебник ГДЗ Информатика учебник 9 класс Угринович (22)Решебник ГДЗ Семакин Информатика 8 класс Учебник (27)Решебник ГДЗ Учебника Информатика 9 КЛАСС Босова Вопросы и задания (22)Решебник Информатика 2 класс Горячев, Горина, Суворова (128)Решебник Информатика 2 класс Матвеева, Челак (102)Решебник Информатика 3 класс Горячев, Горина, Суворова (72)Решебник Информатика 3 класс Матвеева, Челак (129)Решебник Информатика 4 класс Горячев, Горина, Суворова (105)Решебник Информатика 4 класс Матвеева, Челак (189)Решебник Информатика Рабочая тетрадь 9 класс Семакин (14)Решебник к Рабочей тетраде Информатика 5 класс Босова (131)Решебник к Рабочей тетраде Информатика 6 класс Босова (202)Решебник к Рабочей тетраде Информатика 7 класс Босова (147)Решебник к Рабочей тетраде Информатика 8 класс Босова (202)Решебник к учебнику Информатика 5 класс Босова (36)Решебник к учебнику Информатика 6 класс Босова (18)Решебник к учебнику Информатика 7 класс Босова (27)Решебник к учебнику Информатика 8 класс Босова (11)Решебник к учебнику Информатика 9 класс Семакин (27)Решебник учебника Информатика 8 класс Угринович (5)Решение задач по информатике для школьников (2 174) Задачи и советы по работе в MS Office — практика и теория (1 892) Практические работы в MS Access — задания, советы, решения и ответы (165) Практические работы в MS Excel — задания, советы, решения и ответы (1 285) Практические работы в MS Power Point — задания, советы, решения и ответы (145) Практические работы в MS Word — задания, советы, решения и ответы (297) Задачи по программированию с решением для школьников (267) Занимательные задачи по информатике для школьников (15)Сайтостроение — создать с нуля, уроки, новости, полезное (355)Логарифм (Журналы) — Примеры | Натуральный логарифм и обыкновенный логарифм
Логарифмы — это еще один способ записи показателей степени. Мы знаем, что 2 5 = 32. Но если нас попросят найти, какое число заменяет вопросительный знак в 2 ? = 32, то методом проб и ошибок мы можем просто найти, что ответ равен 5. Но что, если нас попросят найти вопросительный знак в 2 ? = 30? Существует ли такое число, что при возведении к нему 2 будет 30? Нет, тогда как решить? Решение — логарифмы (или журналы).
Мы знаем, что 2 5 = 32. Но если нас попросят найти, какое число заменяет вопросительный знак в 2 ? = 32, то методом проб и ошибок мы можем просто найти, что ответ равен 5. Но что, если нас попросят найти вопросительный знак в 2 ? = 30? Существует ли такое число, что при возведении к нему 2 будет 30? Нет, тогда как решить? Решение — логарифмы (или журналы).
Давайте узнаем больше о логарифмах и их свойствах на примерах.
| 1. | Что такое логарифм? |
| 2. | Определение журналов |
| 3. | Натуральное бревно и бревно обыкновенное |
| 4. | Правила логов |
| 5. | Как сжимать/расширять логарифмы? |
| 6. | Часто задаваемые вопросы о логарифмах |
Что такое логарифм?
Логарифм — это не что иное, как еще один способ выражения показателей степени, и его можно использовать для решения задач, которые нельзя решить, используя только понятие показателей степени. Разобраться в логах не так уж и сложно. Чтобы понимать логарифмы, достаточно знать, что логарифмическое уравнение — это просто еще один способ записи показательного уравнения.
Разобраться в логах не так уж и сложно. Чтобы понимать логарифмы, достаточно знать, что логарифмическое уравнение — это просто еще один способ записи показательного уравнения.
Логарифм и экспонента являются обратными формами друг друга. Это можно понять из раздела ниже. Первоначально математик по имени Джон Нейпир ввел логарифмы для упрощения расчетов, и эта концепция быстро была принята другими учеными, инженерами и т. д.
Вот математическое определение бревен.
Определение журналов
Логарифм определяется с помощью показателя степени.
- б х = а ⇔ log б а = х
Здесь «log» означает логарифм. Правая часть стрелки читается как «Логарифм а по основанию b равен х».
Очень простой способ запомнить это: «база остается базовой в обеих формах» и «база не остается с показателем степени в логарифмической форме». Обратите внимание, что «b» является основанием как в левой, так и в правой частях подразумеваемого символа, а в логарифмической форме видно, что основание b и показатель степени x не остаются на одной стороне уравнения.
Здесь
- a и b — два положительных действительных числа.
- х — действительное число.
- а, который внутри лога называется «аргумент».
- b, который внизу журнала называется «база».
Приведенное выше уравнение имеет две вещи, которые нужно понять (из символа ⇔):
- b x = a ⇒ log b a = x. Это называется «экспоненциальной формой в логарифмическую форму»
- log б а = х ⇒ б х = а . Это называется «переведение в экспоненциальную форму»
Вот таблица для понимания преобразований из одной формы в другую.
| Экспоненциальная форма | Логарифмическая форма |
|---|---|
| 2 5 = 32 | журнал 2 32 = 5 |
| 6 2 = 36 | журнал 6 36 = 2 |
| 3 -2 = 1/9 | log 3 (1/9) = -2 |
| e 2 = 7,389 | log e 7,389 = 2 |
| 10 3 = 1000 | журнал 10 1000 = 3 |
Натуральное бревно и обыкновенное бревно
Обратите внимание на две последние строки приведенной выше таблицы. У них лог e и журнал 10 . Эти два журнала имеют особое значение и определенные имена в логарифмах.
У них лог e и журнал 10 . Эти два журнала имеют особое значение и определенные имена в логарифмах.
- бревно e называется натуральным бревном
- журнал 10 называется общим журналом
Давайте узнаем больше о каждом из них.
Натуральный логарифм
Натуральный логарифм есть не что иное, как логарифм с основанием e. То есть натуральный журнал означает log e . Но обычно он не представляется как log e 9.0078 . Вместо этого он представлен как пер. т. е.
- log e = ln
Примеры:
- e x = 2 ⇒ log e 2 = x (или) ln 2 = x.
- e x = 7 ⇒ log e 7 = x (или) ln 7 = x.
Десятичный логарифм
Десятичный логарифм есть не что иное, как логарифм с основанием 10. То есть десятичный логарифм означает log 10 . Но обычно вместо записи log 9 достаточно написать «log».0077 10 . т. е.
Но обычно вместо записи log 9 достаточно написать «log».0077 10 . т. е.
- логарифм 10 = логарифм
т.е. если нет базы для лога значит его лог 10 . Другими словами, это десятичный логарифм.
Примеры:
- 10 2 = 100 ⇒ log 10 100 = 2 (или) log 100 = 2
- 10 -2 = 0,01 ⇒ log 10 0,01 = -2 (или) log 0,01 = -2
Обратите внимание, что в этих примерах мы не написали 10 в качестве основы, потому что это очевидно.
Правила журналов
Правила журналов используются для упрощения логарифма, расширения логарифма или сжатия группы логарифмов в один логарифм. Вот правила (или) свойства журналов. Если вы хотите увидеть, как выводятся все эти правила, нажмите здесь.
Давайте рассмотрим каждое из этих правил одно за другим.
Log 1
Значение log 1 независимо от основания равно 0. Поскольку из свойств показателей мы знаем, что 0 = 1 для любого «а». Преобразовав это в логарифмическую форму, запишите a 1 = 0 для любого «а». Очевидно, что при a = 10 log 10 1 = 0 (или) просто log 1 = 0.
Поскольку из свойств показателей мы знаем, что 0 = 1 для любого «а». Преобразовав это в логарифмическую форму, запишите a 1 = 0 для любого «а». Очевидно, что при a = 10 log 10 1 = 0 (или) просто log 1 = 0.
Если мы расширим это до натурального логарифма, то получим, поскольку e 0 = 1 ⇒ ln 1 = 0
Log
a aПоскольку a 1 = a, для любого «a», преобразуя это уравнение в логарифмическую форму, log a a = 1. Таким образом, логарифм любого числа к одному и тому же основание всегда равно 1. Например:
- журнал 2 2 = 1
- журнал 3 3 = 1
- логарифм 10 = 1
- лн е = 1
Логарифм произведения
Логарифм произведения двух чисел представляет собой сумму логарифмов отдельных чисел, т. е.
Обратите внимание, что базы всех журналов здесь должны быть одинаковыми. Это напоминает / получено из правила произведения показателей степени: x м ⋅ х n = х м+n .
Примеры:
- log 6 = log (3 x 2) = log 3 + log 2
- лог (5x) = лог 5 + лог х
Правило частного логарифма
Логарифм частного двух чисел представляет собой разность между логарифмами отдельных чисел, т. е. а п
Обратите внимание, что базы всех журналов здесь также должны быть одинаковыми. Это напоминает / получено из частного правила показателей степени: x м / х н = х м-н .
Примеры:
- log 4 = log (8/2) = log 8 — log 2
- лог (х/2) = лог х — лог 2
Степенное правило логарифма
Показатель аргумента логарифма можно поставить перед логарифмом, т. е.
- log a m n = n log 8 a 7
Здесь основания должны быть одинаковыми с обеих сторон. Это напоминает / происходит из правила степени степени показателей: (x м ) н = х мн .
Правило изменения основания
С помощью этого свойства можно изменить основание логарифма. Он говорит:
- log b a = (log꜀ a) / (log꜀ b)
Другой способ записать это правило: log b a · log꜀ b = log꜀ a.
Используя это свойство, мы можем изменить основание на любое другое число. Следовательно, мы также можем изменить основание на 10. Тогда получаем: log b а = (логарифм а) / (логарифм б). Таким образом:
- log 2 3 = (log 3) / (log 2)
- лог. 3 2 = (лог. 2) / (лог. 3)
Правило равенства логарифмов
Это правило используется при решении уравнений, содержащих логарифмы. т. е.
- log b a = log b c ⇒ a = c
Это своего рода журнал отмены с обеих сторон.
Число поднято до свойства журнала
Когда в логарифм возводится число, основание которого совпадает с числом, результатом является просто аргумент логарифма. т. е.
т. е.
- a log a x = x
Вот несколько примеров этого свойства.
- 2 бревно 2 5 = 5
- 10 журнал 6 = 6
- е In 3 = 3
Свойство отрицательного журнала
Негативные журналы имеют форму -log б а. Мы можем вычислить это, используя правило степени логарифмов.
-Log B A = log B A -1 = log B (1/A)
Таким образом,
- −Log B A = log B (1/10077 B A = log B (1//log B A = log B (1/. а)
т. е., чтобы преобразовать отрицательный журнал в положительный, мы можем просто взять обратное значение аргумента. Кроме того, чтобы преобразовать отрицательный логарифм в положительный логарифм, мы можем взять обратное основание, то есть
- −log b a = log 1/b a
Как сжимать/расширять логарифмы?
Мы можем либо сжать группу журналов в один журнал, либо развернуть один журнал в группу журналов, используя приведенные выше правила журналов. Но важные правила, которые мы используем в этом процессе, следующие:
Но важные правила, которые мы используем в этом процессе, следующие:
- log a mn = log a m + log a n (правило произведения логарифмов)
- журнал a m/n = log a m — log a n (частное правило логарифмов)
- log a m n = n log a m (Степенное правило логарифмов)
Расширение логарифмов
Расширим логарифм (3x 2 y 3 ).
журнал (3x 2 и 3 )
= log (3) + log (x 2 ) + log (y 3 ) (по правилу произведения)
= log 3 + 2 log x + 3 log y (по степенному правилу)
Сокращение логарифмов
Давайте просто возьмем указанную выше сумму логарифмов и сократим ее. Мы должны вернуть лог (3x 2 y 3 ).
лог. 3 + 2 лог. x + 3 лог. у
= log (3) + log (x 2 ) + log (y 3 ) (по степенному правилу)
= log (3x 2 y 3 ) (По правилу произведения)
Важные примечания по логарифмам:
- Логарифм 0 НЕ определяется, поскольку одно число, возведенное в другое число, никогда не дает 0 в результате.

- Экспоненциальное уравнение преобразуется в логарифмическое уравнение и наоборот, используя b x = a ⇔ log b a = x.
- Обыкновенный логарифм — это логарифм по основанию 10, т. е. логарифм 10 = логарифм.
- Натуральный логарифм — это логарифм по основанию e, т. е. log e = ln.
- Логарифмы используются для самых сложных вычислений умножения и деления.
☛ Похожие темы:
- Общий калькулятор журнала
- Калькулятор натурального бревна
Часто задаваемые вопросы о логарифмах
Что такое журналы в математике?
Журналы — это другой способ записи показателя степени. Формула преобразования экспоненциальной формы в логарифмическую: b x = a ⇔ log b a = x. Логарифмы очень полезны при решении уравнений с показателями степени.
Каковы значения логарифмов log 0, log 1, log 2, log 3, log 4, log 5, log 10, log 100 и log inf?
Вот значения данных журналов:
- log 0 не определен ни для какой базы, потому что число, увеличенное до любого числа, не дает 0.

- журнал 1 = 0 как 10 0 = 1
- log 2 ≈ 0,3010 (с помощью калькулятора)
- log 3 ≈ 0,4771 (с помощью калькулятора)
- log 4 ≈ 0,6021 (с помощью калькулятора)
- log 5 ≈ 0,6990 (с помощью калькулятора)
- log 10 = 1 как 10 1 = 10
- log 100 = 2 как 10 2 = 100
- логарифм ∞ = ∞
Что такое ln в математике?
Ln в математике используется для представления натуральных логарифмов. т. е. ln = «логарифм с основанием e». Например, e 2 = x ⇔ ln x = 2.
Какие 3 типа логарифмов существуют?
Существует три основных типа логарифмов:
- Десятичный логарифм, который записывается как логарифм без основания. Например: журнал 2
- Натуральный логарифм, который записывается как «ln» (означает log и ). Например: пер 2
- Логарифм по любому другому основанию (без конкретного названия). Например: журнал 3 2.

Каковы значения логарифмов ln e, ln 1 и ln от 0?
Здесь значения заданных натуральных бревен.
- In e = 1 как e 1 = e
- In 1 = 0 как e 0 = 1
- In 0 НЕ определено
Что такое важные логарифмические свойства?
Важными логарифмическими свойствами являются:
- Правило произведения: log a mn = log a m + log a n
- Частное правило: log a m/n = log a m — log a n
- Степенное правило: log a m n = n log a m
Как рассчитать журналы?
Мы можем вычислять логи, используя свойства логарифмов. т. е., используя правила журналов, мы можем либо сжать набор логарифмов в один, либо разложить один логарифм на множество. Мы также используем логарифмическую таблицу и антилогарифмическую таблицу в расчетах.
Какая производная от ln x и log x?
Вот производные:
- Производная от ln x равна d/dx (ln x) = 1/x.

- Производная log x равна d/dx(log a x) (или) (log a x)’ = 1/(x ln a).
Чему равен интеграл от ln x и log x?
Вот данные интегралы:
- Интеграл от ln x равен ∫ln x dx = x ln x — x + C.
- Интеграл от log x равен ∫log x dx = x log x — x/ln 10 + C.
Что такое log ln e?
Мы знаем, что ln e = 1 и log 1 = 0. Используя эти два факта, log ln e = log 1 = 0.
Является ли Log Square x таким же, как 2 Log x?
Нет, логарифм квадратный x НЕ совпадает с 2 log x. Обратите внимание на следующее.
- log x квадрат = log x 2 = 2 log x (с использованием правила мощности)
- log квадрат x = log 2 x = (log x) 2 = (log x) (log x), и это нельзя упростить, используя какое-либо правило.
Функции журнала в Python — GeeksforGeeks
Python предлагает множество встроенных логарифмических функций в модуле « math », что позволяет нам вычислять журналы с помощью одной строки. Существует 4 варианта логарифмических функций, все они обсуждаются в этой статье.
Существует 4 варианта логарифмических функций, все они обсуждаются в этой статье.
1. log(a,(основание)) : Эта функция используется для вычисления натурального логарифма (основание e) числа a. Если передаются 2 аргумента, он вычисляет логарифм желаемого основания аргумента a, численное значение лог(а)/лог(база) .
Синтаксис: math.log (а, база) Параметры : a : Числовое значение Основание : Основание, по которому должен быть вычислен логарифм. Возвращаемое значение: Возвращает естественный журнал, если передан 1 аргумент, и журнал с указанная база, если передаются 2 аргумента. Исключения : Вызывает ValueError, если отрицательное число. передается как аргумент.
Python3
|
Выход:
Натуральный логаритм 14 IS: 2,6396969Natural Logarithm 14 IS: 2,6396968444444444444444444444444444444444444444444444844844448484484848448484848484848484848484848484848484848484848484889. Логарифм по основанию 5 из 14: 1.63973851319556062. log2(a) : Эта функция используется для вычисления основания логарифма 2 числа a. Отображает более точный результат, чем log(a,2).
Синтаксис: math.log2(а) Параметры : a : Числовое значение Возвращаемое значение: Возвращает логарифм по основанию 2 числа Исключения : Вызывает ValueError, если отрицательное число.передается как аргумент.
Python3
|
Выход:
Основание логарифма 2 из 14 IS: 3,8073547604
3. log10 (a): . Эта функция используется для Compute . Отображает более точный результат, чем log(a,10).
Синтаксис: math.log10(а) Параметры : a : Числовое значение Возвращаемое значение: Возвращает логарифм по основанию 10 числа Исключения : Вызывает ValueError, если отрицательное число.передается как аргумент.
Python3
|
Выход:
4.0057 3. log1p(a) : Эта функция используется для вычисления логарифма (1+a) .Синтаксис: math.log1p(а) Параметры : a : Числовое значение Возвращаемое значение: Возвращает журнал (1+а) Исключения : Вызывает ValueError, если отрицательное число.передается как аргумент.
Python3
"Logarithm (1+a) Значение 14 IS:" , конец = "") |
Выход:
Logarithm (1+a) Значение 14 IS: 2,70805020110221
Исключение
1. valueError: Эта функция return.
Python3
|
Output :
log(a) value of -14 is :
Runtime Error :
Трассировка (последний последний вызов):
Файл "/home/8a74e9d7e5adfdb902ab15712cbaafe2.py", строка 9, в
печать (math.log(-14))
ValueError: ошибка математической области Практическое применение
Одним из применений функции log10() является то, что она используется для вычисления номера . цифр числа . Код ниже иллюстрирует то же самое.
Python3
") 9556 ") 9556 ") 73293 ) + 1 )) |
ОБЪЕКТ: 9009
ОБЪЕКТ: 9009
. 0058 . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам.
0058 . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам.
Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.
Быстрое вычисление логарифмов без калькулятора | Советы и рекомендации MCAT
Челси Майерс
Последнее обновление: Лаура Тернер, 24 июня 2022 г.
Логарифмы — одна из самых сложных математических тем на MCAT, потому что многие из нас не изучали их со средней школы и, вероятно, так и не научились вычислять логарифмы без калькулятора.
Это хорошая/плохая новость. Плохая новость заключается в том, что проблемы pH и интенсивности звука из общей химии и физики потребуют от вас работы с логарифмами без калькулятора. Хорошая новость заключается в том, что есть трюк, который упрощает вычисление логарифмов и поразит ваших друзей своими математическими способностями в уме.
Об объявлениях
Сначала краткий обзор того, что такое логарифмы и почему они важны для MCAT: десятичный логарифм или оператор «логарифм» (иногда называемый «логарифм 10 ») наиболее полезен при описании чего-либо, что измеряется в очень больших масштабах.
Владение логарифмами было необходимо ученым и инженерам в 19-м и начале 20-го веков, потому что их можно было использовать для упрощения всех видов сложных вычислений. Современные компьютеры сделали эти навыки устаревшими, но десятичные логарифмы по-прежнему используются в таких задачах, как расчеты pH, где основная шкала изменяется в соответствии со степенью 10.
В химии кислотность может быть измерена по линейной шкале от [H+] = 0,00000000000001M до [H+] = 1M. Однако разница в 1 млн [H+] на самом деле не имеет значения. Мы видим реальные различия в кислотности между веществами, когда [Н+] одного в 100 или 1000 (и более!) раз больше, чем [Н+] другого.
Расчет рН позволяет нам измерять кислотность по логарифмической шкале от рН=14 до рН=0. Точно так же, как более разумно измерять расстояние между Токио и Лондоном в милях, а не в дюймах, более полезно описывать кислотность, используя pH, а не [H+].
Как именно это работает? Логарифмическая функция используется для решения уравнений, где переменная представляет собой показатель степени с основанием 10. Например, 10 X = 100. Логарифмический оператор позволяет найти X и записать эквивалентное выражение в виде log(100) = X. 10 X = 100 — экспоненциальная форма выражения, а log(100) = X — логарифмическая форма.
Легче всего определить логарифм степени 10, потому что решение равно степени степени. Продолжая приведенный выше пример, мы можем решить уравнение, переписав log(100) как log(10 2 ) = 2.
Продолжая приведенный выше пример, мы можем решить уравнение, переписав log(100) как log(10 2 ) = 2.
Конечно, на MCAT вам потребуется аппроксимировать логарифм значений, которые не являются простыми степенями 10. Обратите внимание, что ключевое слово здесь — приблизительно . Один из самых важных принципов овладения математикой MCAT заключается в том, чтобы помнить, что вам не нужно вычислять точный ответ на каждую задачу, вам просто нужно подобраться достаточно близко, чтобы выбрать правильный ответ из списка возможных вариантов.
Вспомним, что pH – это отрицательный логарифм [H+]. Мы можем аппроксимировать отрицательный логарифм количества, используя формулу
–log(m x 10 -n ) ≈ n – 0.m
, где m — число от 1 до 10, а n — целое число (целое число).
Несколько быстрых примеров с использованием аппроксимации:
–log(3 x 10 -5 ) ≈ 5 – 0,3 = 4,7
–log(7,1 x 10 -9 ≥ 94 9 8,29
– log(2,5 x 10 -2 ) ≈ 2 – 0,25 = 1,75
Вот и все!
Давайте закончим парой проблем с pH:
Мы надеемся, что эти инструкции по вычислению логарифмов без калькулятора помогут вам победить MCAT! Обязательно ознакомьтесь с остальными сериями советов и рекомендаций MCAT:
- Часть I.
 Преобразование единиц измерения в метрическую систему
Преобразование единиц измерения в метрическую систему - Часть III. Использование аппроксимации для выполнения сложных вычислений
- Часть IV. шаги
- Часть V – Тригонометрия
Хотите узнать больше о том, как добиться успеха на MCAT? Посмотрите этот вебинар от Student Doctor Network и MedSchoolCoach, на котором разбираются ключевые факторы для отличного результата
Текстовая версия Quiz
В: Что такое pH A 4,2 x 10 -3 M HNO 3 RELIGHT? RELIGHT? RELIGHT? RELIGHT? RELIGHT? RELIGHT? RELIGHT? RELIGHT? RELICE?
a) 1,61
b) 2,38
c) 3,42
d) 4,20
раствор равен отрицательному логарифму концентрации. В этом случае pH = –log(4,2 x 10 -3 ). Используя приближение, мы можем решить –log(4,2 x 10 -3 ) ≈ 3 – 0,42 ≈ 2,5, что ближе всего к ответу b).
В этом случае pH = –log(4,2 x 10 -3 ). Используя приближение, мы можем решить –log(4,2 x 10 -3 ) ≈ 3 – 0,42 ≈ 2,5, что ближе всего к ответу b).
Q: Наиболее близко к: -7
б) 3,62 х 10 -5
в) 2,40 х 10 -4
г) 7,23 х 10 -2
В этой задаче важно отметить, что когда кислота в растворе, содержащем равные количества кислоты и сопряженного основания, рН равен рК и .
Следовательно, мы имеем pH = 3,62 = pK a . Однако мы пытаемся найти K a , а не pK a (напомним также, что pK a = –log(K a ) ), и нам нужно будет использовать приближение, которое мы изучили ранее. но наоборот.
pH = n – 0,m ≈ –log(m x 10 -n )
Мы можем переписать значение pH 3,62 как 4 – 0,38, представив его в виде n – 0,m, показанном выше . Это дает нам
pH = 4 – 0,38 ≈ –log(m x 10 -n )
Теперь мы можем заменить m и n, чтобы аппроксимировать K на в правой части.
pH = 4 – 0,38 ≈ –log(3,8 x 10 -4 )
Таким образом, приблизительное значение K a равно 3,8 x 0054 - 900 ответить в).
Что такое логарифм?
Что такое логарифм?Понимание математики по Питер Альфельд, кафедра математики, Университет Юты
Что такое логарифм?
Интересно, после того, как я это руководство какое-то время, это оказался вопрос, который мне задавали чаще всего, обычно в терминах, содержащих такие фразы, как «Греческий мне», «бьет меня», или, как указано выше, "что за бред"...
Чтобы понять, что такое логарифм, сначала нужно
понять, что
сила
является. Сначала перейдите по этой ссылке, если вы этого не сделаете!
Сначала перейдите по этой ссылке, если вы этого не сделаете!
Хорошо, вы знаете, что такое сила. Так что это имеет смысл для вас написать что-то вроде
б х = у. (*)
В предыдущем уравнении x должно выглядеть как верхний индекс б . Если это не так, у вас есть маломощный браузер.
После этих предварительных действий мы можем перейти к сути дела.
причина. Уравнение (*) является ключом к
все. Число b является базой ,
число x показатель степени и выражение
что равняется y , является степенью . Если мы подумаем о x в качестве независимой переменной и y в качестве
зависимая переменная, затем (*) определяет экспоненциальная функция .
Теперь в уравнении (*) мы можем сделать вид, что два из даны переменные, и решить для третьего. Если основание и показатель степени даны, мы вычисляем степень , если экспонента и мощность заданы, мы вычисляем корень (или радикал ), и, если питание и базы даны, мы вычисляем логарифм .
Другими словами, Логарифм числа y по основанию b — показатель степени, до которого мы должны поднять b , чтобы получить y.
Мы можем записать это определение как
х = логарифм б у б х = у
и мы говорим, что x это логарифм y с основанием b тогда и только тогда, когда b в степени x равно y .
Проиллюстрируем это определение несколькими примерами. Если у вас есть трудности с какой-либо из этих способностей, вернитесь к моему страница на силы.
Специальные базы
Логарифмы по основанию b=10 называются десятичных логарифмов и логарифмов относительно база е=2,71828... называются натуральных логарифмов.Дополнительная информация
Вы можете найти обширную информацию о логарифмах в любом учебник по алгебре колледжа. Чтобы проверить ваше понимание и направлять свое дальнейшее изучение выяснить ответы на следующие вопросы:
- Почему важны логарифмы?
- Почему экспоненциальные функции важны?
- Как преобразовать логарифм относительно единицы основание в логарифм по другому основанию?
- Почему основание должно быть положительным?
- Почему сила всегда положительна?
- Что делает натуральные логарифмы естественными?
Калькулятор логарифма
Нажмите на этот апплетОднако ваш браузер не поддерживает Ява.
 Если бы это было так, вы бы не увидели это сообщение! Получить Java
совместимый браузер, например
Нетскейп,
достаточно продвинутой версии.
Если бы это было так, вы бы не увидели это сообщение! Получить Java
совместимый браузер, например
Нетскейп,
достаточно продвинутой версии.вызвать калькулятор логарифмов , который позволяет выберите два числа из (*) и вычислите в третьих. Это довольно просто в использовании, но вот документация.
Мелкий шрифт, ваши комментарии, больше ссылок, Питер Альфельд, PA1UM
[27 июня 1997]
Машинное обучение с логистической регрессией в Excel, R и Power BI Online Class
- Все темы
- Технологии
- Наука о данных
- Машинное обучение
С Хелен Уолл Понравилось 389 пользователям
Продолжительность: 2 часа 49 минут
Уровень мастерства: средний
Дата выпуска: 05. 11.2021
11.2021
Начать бесплатную пробную версию на 1 месяц
Детали курса
Просмотреть информационный бюллетень Хелен на LinkedIn
Excel, R и Power BI — это приложения, широко используемые в науке о данных, а также в компаниях и организациях по всему миру. Если вы потратили какое-то время, пытаясь понять, как лучше смоделировать ваши данные, чтобы получить из них полезную информацию, на основе которой вы можете действовать, вы, скорее всего, сталкивались с этими приложениями. В этом курсе Хелен Уолл показывает, как использовать Excel, R и Power BI для логистической регрессии, чтобы моделировать данные для прогнозирования меток классификации, таких как обнаружение мошенничества или успешные медицинские испытания. Хелен рассматривает несколько примеров логистической регрессии. Она показывает, как использовать Excel для реального расчета регрессионной модели, а затем использовать R для более интенсивных расчетов и визуализации. Затем она показывает, как использовать Power BI для интеграции возможностей вычислений Excel и R в масштабируемой модели с возможностью совместного использования.
Она показывает, как использовать Excel для реального расчета регрессионной модели, а затем использовать R для более интенсивных расчетов и визуализации. Затем она показывает, как использовать Power BI для интеграции возможностей вычислений Excel и R в масштабируемой модели с возможностью совместного использования.
Навыки, которые вы приобретете
- Логистическая регрессия
- Машинное обучение
Получите общий сертификат
Поделитесь тем, что вы узнали, и станьте выдающимся профессионалом в желаемой отрасли с сертификатом, демонстрирующим ваши знания, полученные на курсе.
Обучение LinkedIn Обучение
Сертификат об окончанииДемонстрация в вашем профиле LinkedIn в разделе «Лицензии и сертификаты»
Загрузите или распечатайте в формате PDF, чтобы поделиться с другими
Поделитесь изображением в Интернете, чтобы продемонстрировать свое мастерство
Познакомьтесь с инструктором
Хелен Уолл
LinkedIn [in]structor для Microsoft Power BI, Excel, Python, R и AWS | Консультант по науке о данных, визуализации и аналитике
Отзывы учащихся
54 оценки
Общий рейтинг рассчитывается на основе среднего значения представленных оценок. Оценки и обзоры могут быть отправлены только тогда, когда неанонимные учащиеся завершат не менее 40% курса. Это помогает нам избежать поддельных отзывов и спама.
Оценки и обзоры могут быть отправлены только тогда, когда неанонимные учащиеся завершат не менее 40% курса. Это помогает нам избежать поддельных отзывов и спама.
- 5 звезд Текущее значение: 40 74%
- 4 звезды Текущее значение: 8 14%
- 3 звезды Текущее значение: 5 9%
- 2 звезды Текущее значение: 1 1%
Колаволе АДЕЕМО
Колаволе АДЕЕМО
Начинающий инженер-программист
5/5
17 июня 2022 г.
Мне нравится слушать этот курс, он очень познавательный. Я рекомендую этот курс всем, кто стремится изучить машинное обучение с помощью логистической регрессии в Excel, R и Power BI.
Полезный · Отчет
Фади Мерей
Фади Мерей
Руководитель мастерской TRS в Al Masaood Oil Industry Supplies & Services
Содержание
Что включено
- Практикуйтесь, пока учитесь 1 файл с упражнениями
- Проверьте свои знания 5 викторин
- Учитесь на ходу Доступ на планшете и телефоне
Похожие курсы
Скачать курсы
Используйте приложение LinkedIn Learning для iOS или Android и смотрите курсы на своем мобильном устройстве без подключения к Интернету.
Как рассчитать журнал в Excel (6 эффективных методов)
Логарифм — это математическая операция, которая определяет, как конкретное число, называемое основанием, увеличивается с помощью умножения самого себя для получения другого числа. В нашей реальной жизни существует множество примеров логарифмирования, таких как звук (измерение в децибелах), землетрясения (шкала Рихтера), яркость звезд и химия (измерение pH). В этой статье мы покажем вам 6 методов расчета журнала в Excel.
Скачать практическую рабочую тетрадь
6 методов расчета журнала в Excel
1. Использование функции LOG для расчета журнала в Excel
2. Применение функции LOG10 в Excel
3. Реализация функции LN в Excel
4. Изучение библиотеки функций
5. Использование функции вставки
6. Использование кода VBA
Пример расчета журнала в Excel
Распространенные ошибки при расчете журнала в Excel
1. #ЦЕННОСТЬ! Ошибка
#ЦЕННОСТЬ! Ошибка
2. #ЧИСЛО! Ошибка
3. #ДЕЛ/0! Ошибка
То, что нужно запомнить
Вывод
Статьи по Теме
Загрузить рабочую тетрадь
6 методов расчета журнала в Excel
Для расчета журнала в Excel в Excel есть предопределенные формулы, которые называются функциями . Мы можем использовать их 6 различными способами.
1. Использование функции
LOG для расчета журнала в ExcelПрежде чем вычислять логарифм, вы должны знать, что такое логарифм. Мы показываем вам очень простую и базовую формулу для лучшего понимания этого.
Если, b a = x, то Log b x = a
Например,
5 2 = 25, поэтому Log 5 25 = 2
Здесь у нас есть набор данных для применения функции LOG к этому и соответствующие значения логарифма.
Шаги:
- Сначала щелкните ячейку D5 и введите следующую формулу.

=LOG(B5,C5)
- Во-вторых, нажмите ENTER и в результате вы получите 2 как логарифмическое значение 100.
- Наконец, используйте инструмент Fill Handle , чтобы скопировать формулу в нижние ячейки, чтобы получить результаты.
Подробнее: Логарифмическая шкала Excel Начало с 0 (подробный анализ)
2. Применение функции
LOG10 в ExcelФункция LOG10 в основном аналогична функции LOG . Просто здесь постоянно установлена база 10. Таким образом, нам не нужно выбирать базу вручную.
Шаги:
- Сначала введите следующую формулу в ячейку C5 .
=LOG10(B5)
- Теперь нажмите ENTER , чтобы получить результат, и используйте инструмент Fill Handle для достижения логарифмических значений других ячеек.

Примечание : Здесь мы видим, что в ячейках B5 и C5 значения такие же, как в методе 1. В методе 1 для первой строки мы использовали база как 10 и получил значение логарифма 2. Здесь мы также получаем такое же значение. Итак, мы могли быть уверены в том, что в функции LOG10 основание уже определено как 10.
Подробнее: Как рассчитать Antilog в Excel (с 3 примерами)
3. Реализация функции LN в Excel
Функция LN определяет натуральный логарифм значение числа. Требуется с основанием как e , что является математической константой, равной примерно 2,71828.
Шаги:
- Сначала , введите следующую формулу в ячейку C5 .

=ЛН(В5)
- Теперь нажмите ENTER для получения результата и используйте инструмент Fill Handle для получения значений логарифма другой ячейки.
4. Изучение библиотеки функций
Кроме того, мы можем использовать вышеупомянутые 3 метода, изучив их в Библиотеке функций . Для этого мы должны выполнить следующие шаги:
- Во-первых, выберите ячейку D5 . Затем на ленте щелкните Formulas > Math & Trig > LN / LOG / LOG10 (выберите любую функцию по вашему требованию).
- Возьмем, к примеру, функцию LOG из раскрывающегося меню. Мы видим всплывающее диалоговое окно с именем Аргументы функции . В опции Number выберите ячейку B5 , а в опции Base выберите ячейку C5 .
 После заполнения параметра аргументов мы можем увидеть наш результат во всплывающем диалоговом окне. Теперь нажмите OK .
После заполнения параметра аргументов мы можем увидеть наш результат во всплывающем диалоговом окне. Теперь нажмите OK .
- Мы можем увидеть желаемое значение логарифма в ячейке D5 . Наконец, используя инструмент Fill Handle , получите значения других ячеек.
5. Наличие опции функции вставки
Альтернативным способом выполнения той же задачи является использование опции Insert Function . Шаги следующие:
- Сначала выберите ячейку D5 и щелкните символ Вставить функцию . Мы видим диалоговое окно с именем Insert Function . Введите LOG в меню Search и выберите Go . Теперь выберите функцию LOG из выпадающего списка и выберите ОК .
- Теперь у нас есть похожее диалоговое окно с именем Аргументы функции , как и в предыдущем методе.
 Здесь введите Number и Base также в пустых опциях и нажмите OK .
Здесь введите Number и Base также в пустых опциях и нажмите OK .
- На мгновение мы можем увидеть значение логарифма в ячейке D5 . Наконец, используйте инструмент Fill Handle и получите и другие значения.
Подробнее: Как сделать обратный журнал в Excel (3 простых метода)
6. Использование кода VBA
Кроме того, мы можем использовать Visual Basic для приложений ( VBA ) для создания коротких кодов для вычисления логарифмов в Excel. Мы вычислим логарифм 125 с базовым значением 5. Выполните следующие шаги:
- Сначала перейдите на лист, содержащий данные для кода VBA , и щелкните правой кнопкой мыши имя листа . Далее нажмите на Просмотр опции Код .
- Во-вторых, щелкните правой кнопкой мыши Sheet7 (код VBA) из Toggle Folders .
 Затем выберите Вставить > Модуль .
Затем выберите Вставить > Модуль .
- Затем мы увидим коробку Code Module . Теперь введите приведенные ниже коды в это поле и выберите Run .
Функция LogAny(базовое число как двойное, число как двойное) как двойное
LogAny = Журнал (число) / Журнал (база)
Конечная функция
Sub Log_Ex()
MsgBox LogAny(10, 100)
Конец сабвуфера
- В конце концов вы увидите, что значение вашего логарифма возвращается как 3 в окне сообщения, которое совпадает с результатом метода 1–метода 5.
Подробнее: Как регистрировать данные преобразования в Excel (4 простых метода)
Пример расчета входа в Excel
Теперь мы покажем вам реальное применение логарифмирования с использованием функции LOG в Excel.
У нас есть набор данных из 6 растворов с их концентрацией в единицах (мкмоль/литр). Отсюда мы узнаем рН растворов и являются ли они кислыми или щелочными, или нейтральными.
Отсюда мы узнаем рН растворов и являются ли они кислыми или щелочными, или нейтральными.
Итак, шаги следующие:
- Сначала выберите ячейку D5 и запишите формулу, как показано ниже, и нажмите ENTER .
=-(LOG(C5*POWER(10,-6),10))
Здесь мы умножаем значение концентрации в ячейке C5 на 10 -6 , чтобы получить единицу измерения в моль/литр из мкмоль/литр.
- Нажав ENTER , вы можете получить значение рН раствора А в ячейке Д5. Используйте параметр Обработчик заполнения и перетащите вниз, чтобы скопировать формулу в другие ячейки и получить желаемый результат.
- После этого щелкните ячейку E5 и введите следующую формулу, а затем нажмите ENTER .
=ЕСЛИ(D5<7,"Кислотный раствор",IF(D5>7,"Щелочный раствор","Нейтральный раствор"))
Расшифровка формулы:
Здесь мы вставили логику через Функция ЕСЛИ .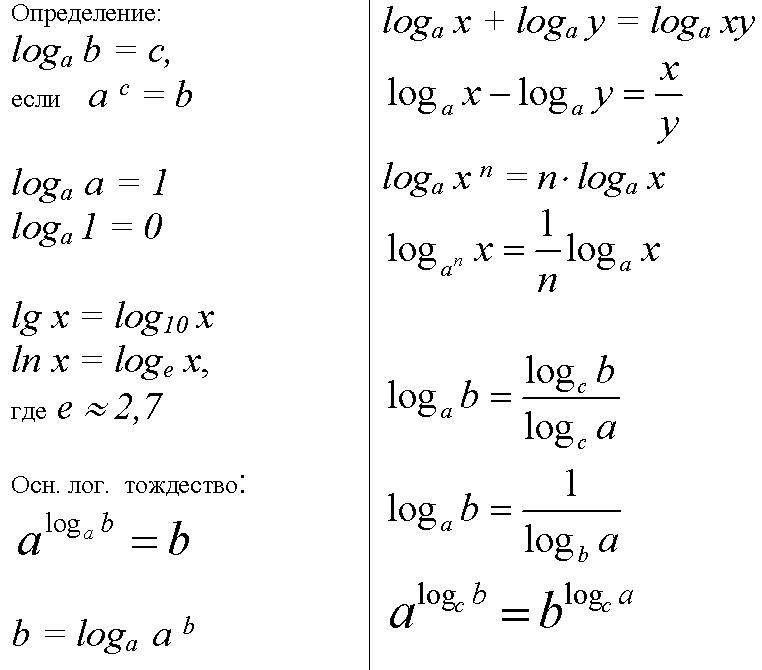 Это так: если наше значение pH меньше 7, то будет отображаться «Раствор кислый»; если наше значение pH больше 7, то будет отображаться «Раствор щелочной», а если вышеуказанная 2 логика не выполняется, в ячейке E5 будет отображаться «Раствор нейтральный».
Это так: если наше значение pH меньше 7, то будет отображаться «Раствор кислый»; если наше значение pH больше 7, то будет отображаться «Раствор щелочной», а если вышеуказанная 2 логика не выполняется, в ячейке E5 будет отображаться «Раствор нейтральный».
- Это покажет заявление «Раствор является кислым», потому что значение pH меньше 7. Теперь используйте инструмент Ручка заполнения и перетащите его вниз, чтобы скопировать формулы в другие ячейки, чтобы получить результаты.
Распространенные ошибки при расчете журнала в Excel
Иногда функция LOG возвращает значение как ошибку. Существует несколько распространенных типов ошибок, и их причины приведены ниже, чтобы защитить вас от возникновения ошибок.
1. #ЦЕННОСТЬ! Ошибка
Это происходит, если аргумент число или основание не является числовым.
2.





 Можно указать любое другое значение, это не принципиально.
Можно указать любое другое значение, это не принципиально.
 Можно прописать информацию вручную, но есть более простой и удобный метод. Кликаем сначала по области поля “Число”, после чего – по требуемой ячейке.
Можно прописать информацию вручную, но есть более простой и удобный метод. Кликаем сначала по области поля “Число”, после чего – по требуемой ячейке.



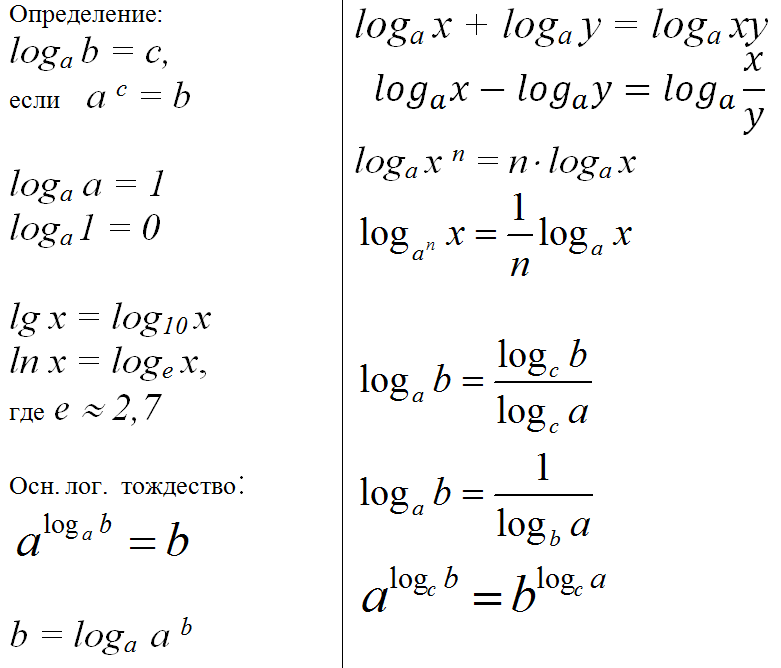
 log (
log ( 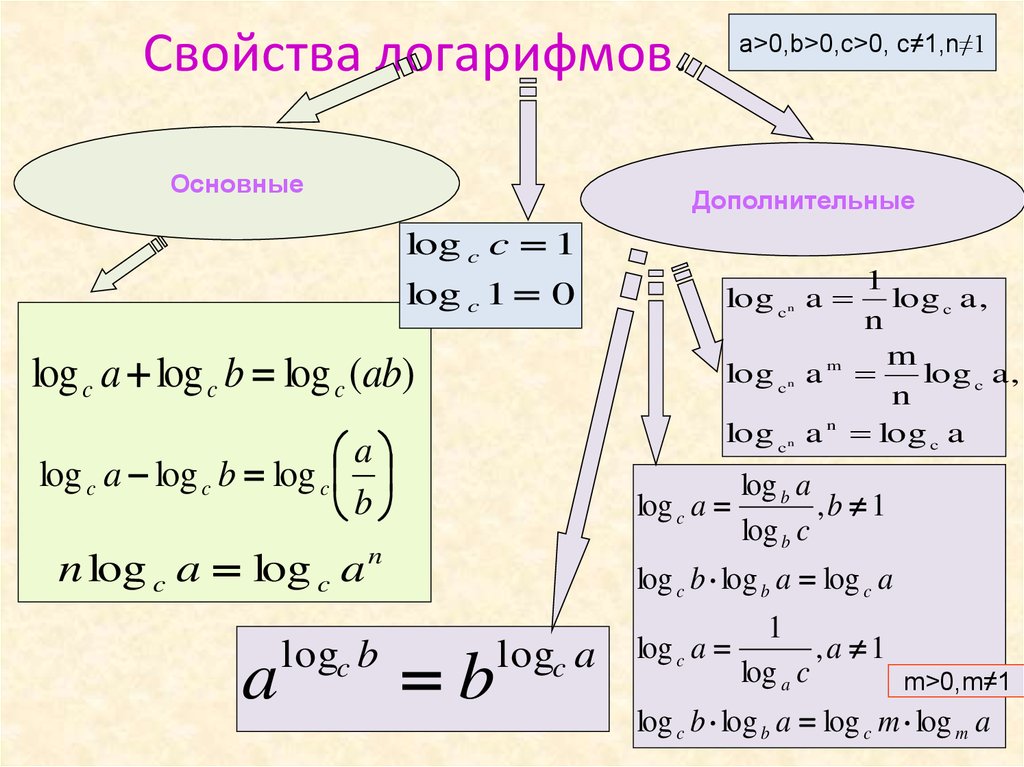 передается как аргумент.
передается как аргумент.  передается как аргумент.
передается как аргумент.  передается как аргумент.
передается как аргумент. 
 Преобразование единиц измерения в метрическую систему
Преобразование единиц измерения в метрическую систему


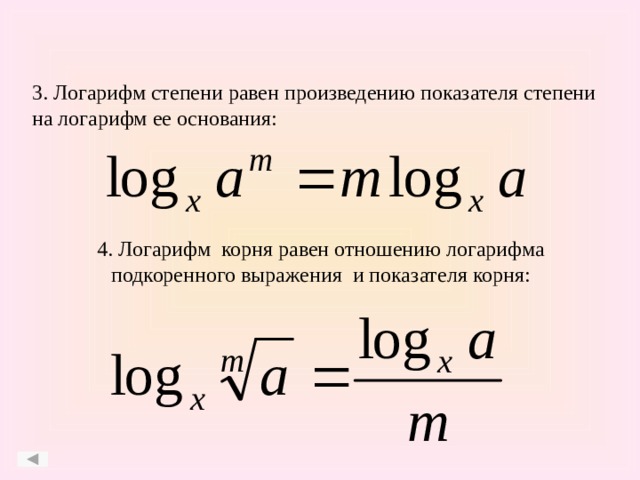 После заполнения параметра аргументов мы можем увидеть наш результат во всплывающем диалоговом окне. Теперь нажмите OK .
После заполнения параметра аргументов мы можем увидеть наш результат во всплывающем диалоговом окне. Теперь нажмите OK . Здесь введите Number и Base также в пустых опциях и нажмите OK .
Здесь введите Number и Base также в пустых опциях и нажмите OK . Затем выберите Вставить > Модуль .
Затем выберите Вставить > Модуль .