Построение фигур по координатам онлайн: Построение геометрических фигур по точкам на координатной плоскости, построение геометрических фигур, программа для построения геометрических фигур

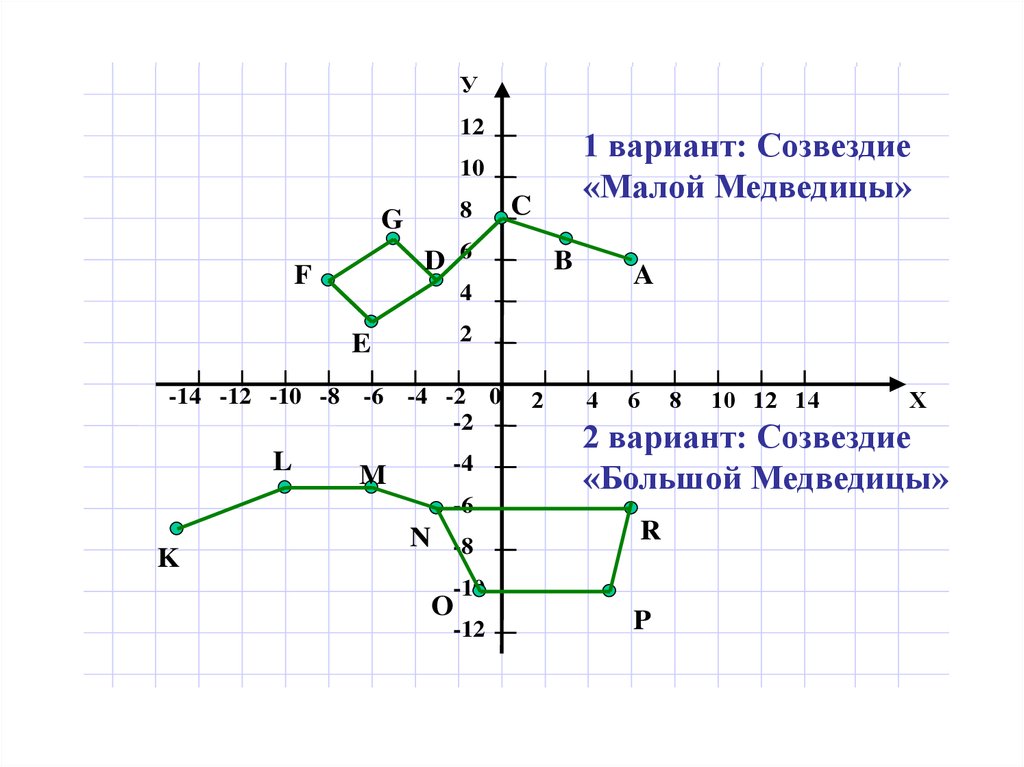
Координатная плоскость. Построение фигур по координатам точек

1. Домашняя работа «Координатная плоскость. Построение фигур по координатам точек.»

2. Вертолет 1) (- 5; 3), (- 3; 5), (6; 5), (10; 3),(10; 1),(9; 0), (- 2; 0),(- 5; 3). 2)(- 5; 3),(- 10; 7), (- 3; 5). 3) (5; 0),

(5; — 1), (6; — 2), (8; — 2), (9; — 2,5), (8; — 3), (- 3; — 3), (- 4; — 2,5), (- 3; — 2),(- 1; 2), (- 2; — 1), (- 2; 0). 4) (- 12; 5), (- 8; 9). 5) (- 6; 7), (10; 7).
6) (2; 5), (2; 7). 7) (- 1; 1), (- 1; 4), (2; 4), (2; 1),(- 1; 1). 8) (5; 5), (5; 2), (10; 2).
.

3. Петушок (-5,7), (-7,9), (-5,10), (-4,9), (-3,10), (-3,8), (-2,8), (-4,7), (-3,3), (-1,2),(1,5), (4,5), (6,1), (4,2),(2,0),

Петушок
(-5,7), (-7,9), (-5,10), (-4,9), (-3,10), (-3,8), (-2,8), (-4,7), (-3,3), (-1,2),(1,5), (4,5), (6,1),
(4,2),(2,0), (4,1),(6,-2), (3,-1),(5,-4),(1,-2),(-1,-3),(-1,-6), (0,-7),(-4,-7), (-2,-6), (-3,-3), (6,-1), (-7,5), (-8,4), (-7,6), (-9,7), (-7,7),(-6,8). Глаз (-6,7).

4.

Лисица 1) (- 3; 0), (- 2; 1), (3; 1), (3; 2),(5; 5), (5; 3), (6; 2), (7; 2), (7; 1,5), (5; 0), (4; 0),(4; — 1,5), (3; — 1), (3;1,5),(4; — 2,5),(4,5; — 2,5), (- 4,5; — 3), (3,5; — 3), (2; — 1,5),(2; — 1), (- 2; — 2),
(- 2; — 2,5), (- 1; — 2,5), (- 1; — 3), (- 3; — 3), (- 3; — 2), (- 2; -1),(- 3; — 1), (- 4; — 2), (- 7; — 2), (- 8; — 1), (7; 0), (- 3; 0). 2)Глаз: (5; 2).

5. Цыплёнок  (1,-6), (-1,-6), (-3,-5), (-4,-3), (-4,1), (-3,3), (-1,5), (-2,7), (-2,9), (-1,10), (1,10), (2,9), (2,8), (3,8),

Цыплёнок
(1,-6), (-1,-6), (-3,-5), (-4,-3), (-4,1), (-3,3), (-1,5), (-2,7), (-2,9), (-1,10),
(1,10), (2,9), (2,8), (3,8), (2,7), (1,5), (3,3), (4,1), (4,-3), (3,-5),(1,-6), (-4,1), (-3,0), (2,1), (-1,0), (0,1), (1,0), (2,1), (3,0), (4,1). Глаз (1,8).

6. Сорока  1) (- 1; 2), (5; 6), (7; 13), (10; 11), (7; 5), (1; — 4), (- 2; — 4), (- 5; 0), (- 3; 0), (- 1; 2), (- 2; 4), (- 5; 5),

Сорока
1) (- 1; 2), (5; 6), (7; 13), (10; 11), (7; 5), (1; — 4), (- 2; — 4), (- 5; 0), (- 3; 0), (- 1; 2),
(- 2; 4), (- 5; 5), (- 7; 3), (- 11; 1), (- 6; 1), (- 7; 3), (- 5; 0), (- 6; 0), (- 10; — 1), (- 7; 1),
(- 6; 0). 2) Крыло: (0; 0), (7; 3), (6; 1), (1; — 3), (0; 0). 3) (1; — 4), (1; — 7).
4) (- 1; — 4), (- 1; — 7). 5) Глаз: (- 5; 3).

7. ВОРОБЕЙ  (- 10;7), (-8;8), (-7;10), (-4;10), (-1;7), (0;6), (8;0), (15;-2), (13;-4), (5;0),(3;-1), (2;-7 ), (-2;-7), (0;-6),

ВОРОБЕЙ
(- 10;7), (-8;8), (-7;10), (-4;10), (-1;7), (0;6), (8;0), (15;-2), (13;-4), (5;0),(3;-1),
(2;-7 ), (-2;-7), (0;-6), (2;-1), (-1;0), (-3;-7), (-7;-7), (-5;-6), (-1;-1),(-2; 0), (-7;2), (8;-5), (-8;7), Глаз: (-6;8).

8. Слон  1) (2;- 3),(2;- 2),(4;- 2),(4;- 1),(3; 1),(2; 1),(1; 2),(0; 0),(- 3; 2),(- 4; 5),(0; 8),(2; 7),(6; 7), (8; 8), (10; 6),

Слон
1) (2;- 3),(2;- 2),(4;- 2),(4;- 1),(3; 1),(2; 1),(1; 2),(0; 0),(- 3; 2),(- 4; 5),(0; 8),(2; 7),(6; 7), (8; 8), (10;
6), (10; 2), (7; 0), (6; 2), (6;- 2), (5;- 3), (2;- 3). 2) (4;- 3),(4;- 5),(3;-9),(0;
— 8),(1;- 5),(1;- 4),(0;- 4),(0;- 9),(- 3;- 9),(- 3;- 3),(- 7;- 3),(- 7;- 7),(- 8;- 7),(- 8;- 8),(- 11; — 8),(- 10;4),(- 11;- 1),(- 14;- 3),(- 12;- 1),(- 11;2),(- 8;4),(- 4;5). 3) Глаза: (2; 4),(6; 4).

9. Самолёт  1) (- 7; 0), (- 5; 2), (7; 2), (9; 5), (10; 5), (10; 1), (9; 0), (- 7; 0). 2) (0; 2), (5; 6), (7; 6), (4; 2). 3) (0;

Самолёт
1) (- 7; 0), (- 5; 2), (7; 2), (9; 5), (10; 5), (10; 1), (9; 0), (- 7; 0). 2) (0; 2), (5; 6), (7; 6), (4;
2). 3) (0; 1), (6; — 3), (8; — 3), (4; 1), (0; 1).

10. Цапля  1) (0; 0), (- 1; 1), (- 3; 1), (- 2; 3), (- 3; 3), (- 4; 6), (0; 8), (2; 5), (2; 11), (6; 10), (3; 9), (4; 5), (3; 0),

Цапля
1) (0; 0), (- 1; 1), (- 3; 1), (- 2; 3), (- 3; 3), (- 4; 6), (0; 8), (2; 5), (2; 11), (6; 10), (3; 9), (4;
5), (3; 0), (2; 0), (1; — 7), (3; — 8), (0; — 8), (0; 0). 2) Глаз: (3; 10).

11. Белый гриб   (6;0),(6;2),(5;1),(4; 3),(2;1),(0;3),(- 2;2),(- 3;5),(- 3;1),(- 4; 2),(- 4;0), (6;0), (3; 2),(3;

Белый гриб
(6;0),(6;2),(5;1),(4; 3),(2;1),(0;3),(- 2;2),(- 3;5),(- 3;1),(- 4; 2),(- 4;0), (6;0),
(3; 2),(3; 8),(2;10),(6;10),(5;12),(4;13),(1;14),(0;14),(-4;12), (-5;10),(-1;10),
(-2;8),(-2;2).
вертолет
6А
петушок
лисица
слон
ципленок
самол
сорока
цапля
воробей
Белый
гриб
вертол
петуш
вертолет
6Б
петушок
лисица
слон
ципленок
самол
сорока
цапля
воробей
Белый
гриб
вертол
петушо

Определение координат центра тяжести фигур и сечений

Определение координат центра тяжести x_C и y_C плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.

Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.

Способы определения координат центра тяжести

Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.

Существует 5 способов расчета координат положения центра тяжести:

1. Аналитический (путем интегрирования).
2. Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3. Экспериментальный. (метод подвешивания тела).
   Этот способ подходит в основном для плоских и линейных тел.
4. Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.

   Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A₁ и A₂ (A = A₁+ A₂).
   

   Рисунок 1.8

   Центры тяжести этих фигур находятся в точках C₁(x₁, y₁) и C₂(x₂, y₂). Тогда координаты центра тяжести тела равны:
   

5. Дополнение (Метод отрицательных площадей или объемов).
   Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.
   Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
   

   Рисунок 1.9

   Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
   

При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).

Пример определения координат центра тяжести плоской фигуры

Задача
Определить координаты центра тяжести плоской фигуры с круглым отверстием

Решение
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.

Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести C_i отдельных фигур:

Прямоугольник (фигура 1)
Площадь
A₁=400×500=200000 мм

2
Положение центра тяжести
x₁=200мм
y₁=250мм

Круг (2) (вычитаемая фигура)
Площадь
A₂=π×200²/4=31416 мм²
Центр тяжести
x₂=200мм
y₂=300мм

Прямоугольный треугольник (3)
Площадь
A₃=400*100/2=20000 мм²
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x₃=400×2/3=266,7мм
y₃=500+100×1/3=533,3мм

Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:

Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами x_C=207,1мм, y_C=271,7мм.

Другие примеры решения задач >
Центры тяжести простейших фигур >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ

• Техническая механика (техмех)
• Теоретическая механика (теормех)
• Сопротивление материалов (сопромат)
• Строительная механика (строймех)
• Теория механизмов и машин (ТММ)
• Детали машин и ОК (ДМ)
• Инженерная механика (инжмех)

---

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

---

Помощь с решением

---

Поиск формул и решений задач

2.

2 Потребность в системах координат

Рисунок 2.2. Декартова система координат.

Авторы и права: © Penn State University, лицензия CC BY-NC-SA 4.0

Места на поверхности Земли измеряются и представляются в виде координат; координата — это набор из двух или более чисел, указывающий положение точки, линии или другой геометрической фигуры по отношению к некоторой системе отсчета. Простейшей системой такого рода является декартова система координат , названный в честь математика и философа XVII века Рене Декарта. Декартова система координат, подобная приведенной выше на рис. 2.2, представляет собой просто сетку, образованную совмещением двух измерительных шкал: горизонтальной (x) и вертикальной (y). Точка, в которой и x, и y равны нулю, называется началом системы координат. На приведенном выше рисунке начало координат (0,0) расположено в центре сетки (на пересечении двух жирных линий). Все остальные позиции указываются относительно начала координат. Координата верхнего правого угла сетки (6,3). Нижний левый угол (-6,-3).

Рисунок 2.3. Географическая (или «геодезическая») система координат.

Авторы и права: © Penn State University, лицензия CC BY-NC-SA 4.0

Декартова и другие двумерные (плоские) системы координат удобны благодаря своей простоте. Они не совсем подходят для указания географического положения. Однако географическая система координат, как показано на рис. 2.3, предназначена специально для определения положения на приблизительно сферической поверхности Земли. Вместо двух линейных шкал измерения x и y 9Географические системы координат 0007 объединяют две изогнутые шкалы измерения.

Вероятно, вы уже встречались с терминами широта и долгота в своих исследованиях. Сравнение этих двух шкал приведено ниже на рис. 2.4. Шкала север-юг, называемая широты (обозначается греческим символом фи ), колеблется от +90° (или 90° северной широты) на северном полюсе до -90° (или 90° южной широты) на южном полюсе. в то время как экватор  составляет 0 °. Линия широты также известна как параллельно .

Шкала восток-запад, называемая долготы (условно обозначаемая греческим символом лямбда ), колеблется от +180° до -180°. Поскольку Земля круглая, +180° (или 180° в.д.) и -180° (или 180° з.д.) являются одной и той же линией сетки. Линия долготы называется меридианом . Эта линия сетки +/- 180 примерно соответствует Международной линии перемены дат , у которой есть отклонения, которые проходят вокруг некоторых территорий и групп островов, так что им не нужно справляться с путаницей близлежащих мест, находящихся в два разных дня. Напротив международной линии перемены дат на другом конце земного шара находится 9-е число.0007 начальный меридиан , линия долготы, определенная международным договором как 0°. В более высоких широтах длина параллелей уменьшается до нуля на 90° северной и южной широты. Линии долготы не параллельны, а сходятся к полюсам. Таким образом, если градус долготы на экваторе равен расстоянию около 111 километров, то на полюсах это расстояние уменьшается до нуля.

Рис. 2.4. Географическая система координат.

Авторы и права: Raechel Bianchetti © Penn State University, лицензия CC BY-NC-SA 4.0

Попробуйте это: Практическое применение географической системы координат

Вы когда-нибудь сталкивались с терминами «широта» или «долгота»? Насколько хорошо вы разбираетесь в географической системе координат? Наш опыт показывает, что, хотя все, кто поступает в этот класс, слышали о широте и долготе, только около половины из них могут указать место на карте, указанное парой географических координат. Веб-сайты, указанные ниже, позволяют вам проверить свои знания. Вы будете практиковаться, нажимая места на земном шаре в соответствии со случайно сгенерированными географическими координатами.

Игра «Викторина по карте»

Практика определения долготы и широты

2.

2.1 Географические координаты

Мы обсудили тот факт, что широта и долгота измеряются в градусах, но что делать, когда нам нужно более точное измерение? Чтобы записать географические координаты, мы можем разделить градусы на минуты и секунды. Градус равен шестидесяти минутам, а каждая минута равна шестидесяти секундам. Географические координаты часто необходимо преобразовывать, чтобы привязать один слой данных к другому. Географические координаты могут быть выражены в десятичных градусов или градусов, минут и секунд . Иногда вам нужно преобразовать одну форму в другую.

Вот как это работает:

Чтобы преобразовать широту -89,40062 из десятичных градусов в градусы, минуты, секунды:

Вычтите число целых градусов (89°) из общего числа (89,40062°). (Знак минус используется в формате десятичных градусов только для обозначения того, что значение представляет собой западную долготу или южную широту.) В этом примере знак минус указывает на юг, поэтому следите за этим.

Умножьте остаток на 60 минут (0,40062 x 60 = 24,0372).

Вычтите из произведения количество целых минут (24 минуты).

Умножьте остаток на 60 секунд (0,0372 x 60 = 2,232). Округлить (в данном случае до ближайшей секунды).

Соберите детали; результат равен 89° 24′ 2″ ю.ш. Если бы отправной точкой была долгота -89,400062, единственная разница состояла бы в том, что указанная выше ю.ш. была бы заменена на западную.

Чтобы преобразовать 43° 4′ 31″ из градусы, минуты, секунды в десятичные градусы, используйте простую формулу ниже:
DD = градусы + (минуты/60) + (секунды/3600)

Разделите количество секунд на 60 (31 ÷ 60 = 0,5166).

Добавьте частное шага (1) к общему количеству минут (4 + 0,5166).

Разделите результат шага (2) на 60 (4,5166 ÷ 60 = 0,0753).

Прибавьте частное шага (3) к числу целых чисел в градусах (43 + 0,0753).

Результат: 43,0753°

Практический тест

Зарегистрированные учащиеся штата Пенсильвания должны вернуться сейчас пройти тест для самооценки около Географические координаты .

Вы можете проходить пробные тесты столько раз, сколько пожелаете. Они не оцениваются и никак не влияют на вашу оценку.

2.2.2 Плоские координаты

До сих пор вы читали о декартовых системах координат, но это не единственный вид двумерных систем координат. Плоскую систему координат можно рассматривать как сопоставление любых двух шкал измерения. Другими словами, если бы вы разместили две линейки под прямым углом так, чтобы отметки «0» на линейках совпали, вы бы определили плоскую систему координат. Линейки называются «топоры». Как и в декартовых координатах, абсолютное положение любой точки в пространстве в плоской системе координат определяется с точки зрения измерения расстояния по осям x (восток-запад) и y (север-юг). Позиция, определяемая координатами (1,1), расположена на одну единицу вправо и на одну единицу вверх от начала координат (0,0). Универсальная поперечная меркаторская сетка (UTM) — это широко используемый тип системы координат на географической плоскости, в которой положения задаются в виде восточного направления (расстояния в метрах к востоку от начала координат) и северного направления (расстояния к северу от начала координат).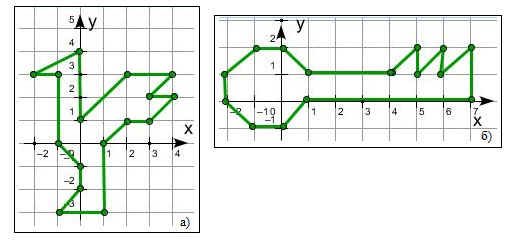

Некоторые преобразования координат просты. Преобразование плоских координат без географической привязки в полярные координаты без географической привязки, более подробно описанное далее в главе, показанной ниже, включает не что иное, как замену одного вида координат другим.

Рисунок 2.5. Одно и то же положение, указанное в двух плоскостных системах координат без географической привязки: декартовой (слева) и полярной (справа).

Авторы и права: из Scales and Transformations Дэвида ДиБиасе, под лицензией CC BY-NC-SA 4.0

2.2.3 UTM: универсальная поперечная Меркатора

Рисунок 2.6. Десять зон UTM, которые охватывают совпадающие территории США.

Авторы и права: Геологическая служба США, общественное достояние, 2004 г. . Как обсуждалось выше, географические координаты могут быть указаны в градусах, минутах и ​​угловых секундах. Изогнутые сетки неудобно использовать для нанесения позиций на плоские карты. Кроме того, вычисление расстояний, направлений и площадей со сферическими координатами громоздко по сравнению с плоскими координатами. По этим причинам картографы и военные чиновники в Европе и США разработали систему координат UTM. Сетки UTM теперь являются стандартом не только для печатных топографических карт, но и для географической привязки цифровых данных, которые составляют появляющуюся «Национальную карту» США (NationalMap.gov).

«Поперечный Меркатор» относится к способу преобразования географических координат из сферической модели Земли в плоские координаты. Действие математического преобразования географических сферических координат в плоские координаты неизбежно приводит к некоторому смещению большей части (но не всех) преобразованных координат. Из-за этого масштаб карты варьируется в проецируемых (плоских) сетках системы координат UTM. Таким образом, координаты UTM обеспечивают точную спецификацию местоположения, но имеют известную величину позиционной ошибки в зависимости от того, где находится место.

Ниже показан юго-западный угол топографической карты Государственного колледжа в масштабе 1:24 000 (где 1 дюйм на карте представляет 2000 футов в мире) в округе Сентер, штат Пенсильвания, опубликованной Геологической службой США (USGS).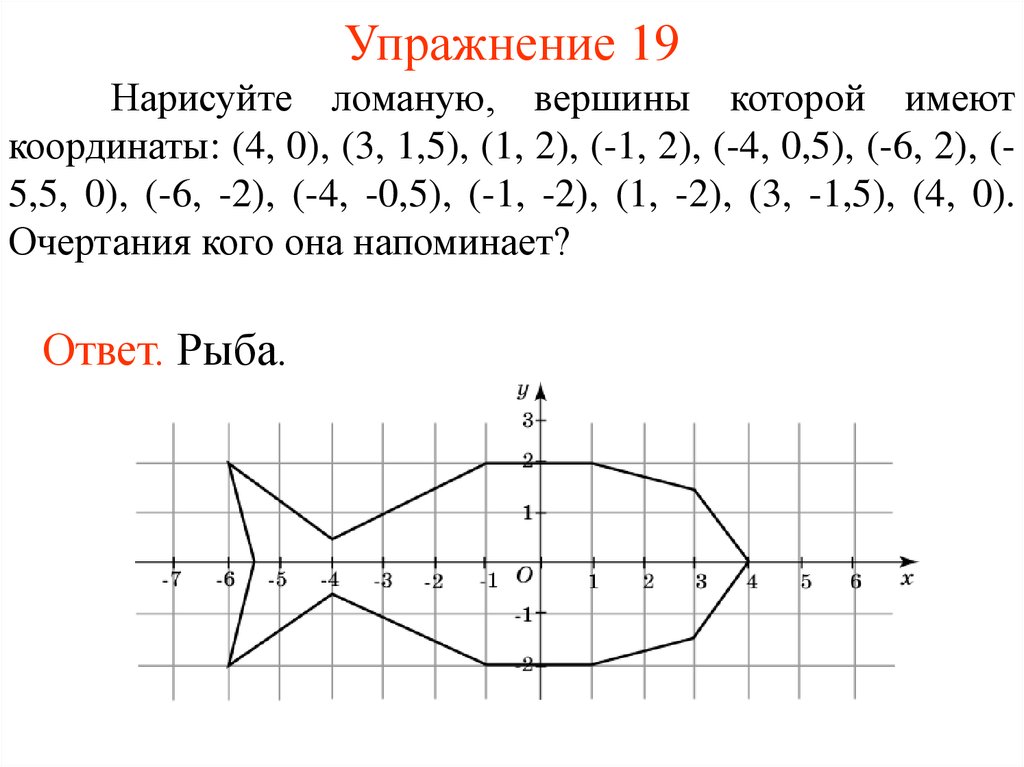 ). Обратите внимание, что географические координаты (40 ° 45 ‘северной широты, 77 ° 52’ 30 «западной долготы) угла указаны. Однако также показаны галочки и метки, представляющие две плоские системы координат, универсальную поперечную меркаторскую (UTM) система координат штата (SPC). Отметка на западном краю карты с пометкой «4515» представляет собой линию сетки UTM (называемую «север»), которая проходит параллельно и на 4 515 000 метров к северу от экватора. Галочки с надписью «258» и «259»» представляют собой линии сетки, которые проходят перпендикулярно экватору и на 258 000 метров и 259 000 метров к востоку, соответственно, от начала сетки UTM Zone 18 North (см. ее расположение на рис. 6 выше). В отличие от линий долготы, «восток» UTM является прямым и не сходятся на полюсах Земли.0003

Универсальная поперечная система Меркатора на самом деле не универсальна, но она покрывает почти всю поверхность Земли. Исключаются только полярные области — широты выше 84° северной широты и 80° южной широты. (Полярные системы координат используются для указания положений за пределами этих широт.) Система UTM делит остальную часть поверхности Земли на 60 зон, каждая из которых охватывает 6 ° долготы. Они пронумерованы с запада на восток от 1 до 60, начиная с 180° западной долготы (примерно совпадает с международной линией перемены дат).

Рисунок 2.8. Меркаторская проекция мира, показывающая 60 зон системы координат UTM, каждая из которых разделена на северную и южную половины на экваторе. Также показаны две полярные системы координат, используемые для указания положений за пределами северной и южной границ системы UTM.

Предоставлено: © Университет штата Пенсильвания, лицензия CC BY-NC-SA 4.0

На приведенном выше рисунке зоны UTM изображены так, как если бы они были одинаково «широки» от экватора до северной и южной границ. Фактически, поскольку меридианы сходятся к полюсам на земном шаре, каждая зона UTM сужается от 666 000 метров в «ширине» на экваторе (где 1 градус долготы составляет около 111 километров в длину) до всего лишь около 70 000 метров на 84 градусе северной широты и около 116 000 метров на 80 ° южной широты.

Чтобы пояснить это, на приведенном ниже рисунке показана область, охватываемая одной зоной сетки системы координат UTM. Каждая зона UTM охватывает 6° долготы, от 84° северной широты до 80° южной широты. Каждая зона UTM подразделяется вдоль экватора на две половины, северную и южную.

Рисунок 2.9. Характеристики зоны системы координат UTM. Желтым цветом обозначены области, в которых координаты UTM действительны для данной зоны. Красные линии, параллельные центральному меридиану, представляют собой две стандартные линии, используемые в каждой поперечной проекции Меркатора. Эти две стандартные линии параллельны каждому центральному меридиану и находятся на расстоянии 180 000 метров к востоку и западу от него. Каждая квадратная ячейка сетки на иллюстрации охватывает 500 000 метров с каждой стороны.

Предоставлено: © Penn State University, лицензия CC BY-NC-SA 4.0

На приведенном выше рисунке показано, как координатные сетки UTM соотносятся с показанной выше зоной покрытия. Северная и южная половины показаны рядом для сравнения. Каждой половине присваивается собственное происхождение . Истоки северно-южной зоны расположены к югу и западу от зоны. Истоки северной зоны расположены на экваторе, в 500 000 метрах к западу от центрального меридиана этой зоны. Исходные точки расположены так, что каждое значение координаты в каждой зоне является положительным числом. Это сводит к минимуму вероятность ошибок в расчетах расстояния и площади. По определению оба начала координат расположены в 500 000 м к западу от центрального меридиана зоны (другими словами, центральный меридиан всегда находится на 500 000 м к востоку). Они считаются «ложными» источниками, поскольку расположены за пределами зон, к которым относятся. Восточные значения UTM, определяющие места в пределах зоны, варьируются от 167 000 метров до 833 000 метров на экваторе. Эти диапазоны сужаются к полюсам. Нортинги варьируются от 0 метров до почти 9400 000 в северных зонах и от чуть более 1 000 000 метров до 10 000 000 метров в южных зонах. Обратите внимание, что положения на широтах выше 84 ° северной широты и 80 ° южной широты определяются в полярных стереографических системах координат, которые дополняют систему UTM.

График искаженного эллипса ниже показывает величину искажения на карте UTM. Этот вид сюжета будет объяснен более подробно ниже; ключевой момент, на который следует обратить внимание, это то, что размер и форма объектов, выделенных красным цветом, указывают на степень искажения размера и формы на карте (широкий диапазон размеров указывает на существенное искажение площади, диапазон от кругов до плоских эллипсов указывает на существенное искажение формы). ). Все эллипсы с центром в выделенной зоне UTM имеют одинаковый размер и форму. Вдали от выделенной зоны эллипсы неуклонно увеличиваются в размерах, хотя их форма остается равномерно круглой. Эта закономерность указывает на то, что искажение масштаба минимально в Зоне 30, а масштаб карты увеличивается по мере удаления от этой зоны. Кроме того, эллипсы показывают, что характер искажения, связанного с этой проекцией, заключается в том, что формы элементов, как они появляются на земном шаре, сохраняются, в то время как их относительные размеры искажаются. Картографические проекции, которые сохраняют форму, жертвуя точностью размеров, называются конформные проекции . Плоские системы координат, наиболее широко используемые в США, UTM и SPC (система координат штата), основаны на конформных проекциях.

Рисунок 2.10. Результат поперечной проекции Меркатора мира с центром в зоне 30 UTM. Красные кружки показывают искажение масштаба, появившееся во время преобразования географических координат в проекционные плоские. На земном шаре все круги были бы одинакового размера.

Предоставлено: © Penn State University, лицензия CC BY-NC-SA 4.0

Поперечная проекция Меркатора, показанная выше, сводит к минимуму искажения в зоне 30 UTM, помещая эту зону в центр проекции. Пятьдесят девять вариаций этой проекции используются для минимизации искажений в других 59 зонах UTM. В любом случае искажение не превышает 1 части на 1000. Это означает, что расстояние в 1000 метров, измеренное в любом месте зоны UTM, будет не хуже, чем + или — 1 метр.

Одним из недостатков системы UTM является необходимость использования нескольких систем координат для учета крупных объектов. Например, нижние 48 Соединенных Штатов распространяются на десять зон UTM. Тот факт, что существует множество узких зон UTM, может привести к путанице. Например, город Филадельфия, штат Пенсильвания, находится к востоку от города Питтсбург. Однако, если вы сравните восток центроидов, представляющих два города, восток Филадельфии (около 486 000 метров) меньше, чем восток Питтсбурга (около 586 000 метров). Почему? Потому что, хотя оба города расположены в американском штате Пенсильвания, они расположены в двух разных зонах UTM. Как оказалось, Филадельфия ближе к началу своей Зоны 18, чем Питтсбург к началу своей Зоны 17. Если бы вы нанесли на карту точки, представляющие два города, игнорируя тот факт, что две зоны представляют собой системы координат, Филадельфия появится к западу от Питтсбурга. Эту ошибку постоянно допускают неопытные пользователи ГИС. К счастью, программное обеспечение ГИС становится достаточно совершенным, чтобы автоматически распознавать и объединять различные системы координат.

Практический тест

Зарегистрированные учащиеся штата Пенсильвания должны вернуться сейчас – пройти тест для самооценки по координатам UTM .

Вы можете проходить пробные тесты столько раз, сколько пожелаете. Они не оцениваются и никак не влияют на вашу оценку.

2.2.4 Координаты состояния на плоскости

Система UTM была разработана для удовлетворения потребности в координатах на плоскости для указания географических местоположений в глобальном масштабе. Сосредоточив внимание только на США, в консультации с различными государственными агентствами Национальная геодезическая служба США (NGS) разработала систему координат штата с учетом нескольких целей проектирования. Главными из них были:

1. координаты плоскости для удобства использования при расчетах расстояний и площадей;
2. все положительные значения для минимизации ошибок вычислений; и
3. максимальная частота ошибок 1 часть на 10 000.

Как обсуждалось выше, плоские координаты определяют позиции в плоских сетках. Картографические проекции необходимы для преобразования координат широты и долготы в координаты на плоскости. Разработчики SPCS сделали две вещи, чтобы свести к минимуму неизбежные искажения, связанные с проецированием Земли на плоскую поверхность. Во-первых, они разделили США на 124 относительно небольшие зоны, охватывающие 50 штатов США. Во-вторых, они использовали несколько разные формулы картографической проекции для каждой зоны, которые минимизируют искажения вдоль линии восток-запад или север-юг в зависимости от ориентации зоны. Изогнутые пунктирные красные линии на приведенном ниже рисунке представляют две

стандартных линий , проходящих через каждую зону. Стандартные линии указывают, где проекция карты имеет нулевую площадь или искажение формы (некоторые проекции имеют только одну стандартную линию).

Как показано ниже, некоторые штаты покрываются одной зоной, а другие разделены на несколько зон.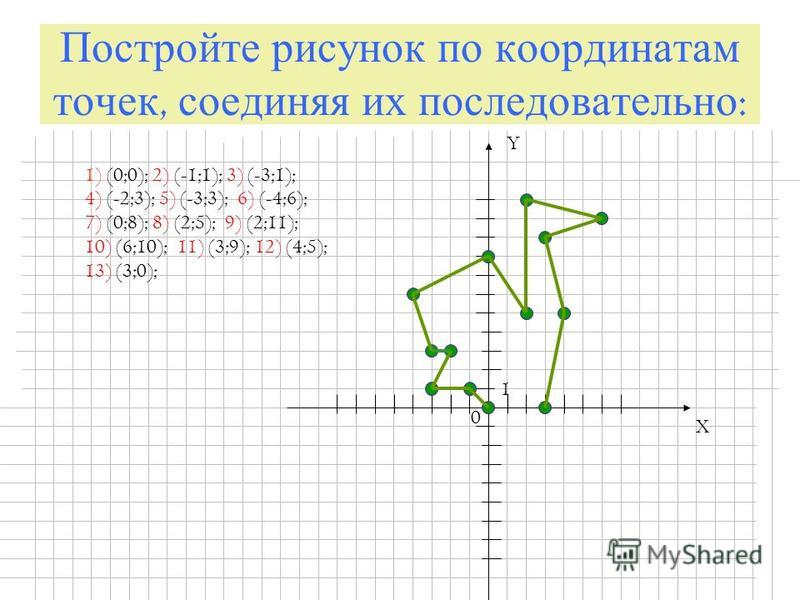 Каждая зона основана на уникальной картографической проекции, которая минимизирует искажения в этой зоне до 1 части из 10 000 или выше. Другими словами, измерение расстояния в 10 000 метров будет в худшем случае ошибкой на один метр (не включая ошибку прибора, человеческую ошибку и т. д.). Частота ошибок варьируется в каждой зоне, от нуля вдоль стандартных линий проекции до максимума в точках, наиболее удаленных от стандартных линий. Ошибки будут намного ниже максимального значения в большинстве местоположений в данной зоне SPC. Зоны SPC обеспечивают лучшую точность, чем зоны UTM, потому что они охватывают меньшие площади и поэтому менее подвержены искажениям, связанным с проекцией.

Рисунок 2.11. Система координат штата США 1983 года состоит из 124 зон. Каждая зона представляет собой отдельную плоскую систему координат. (Аляска и Гавайи не показаны).

Авторы и права: из Scales and Transformations Дэвида ДиБиасе, под лицензией CC BY-NC-SA 4.0

Как мы видели выше, положения в любой системе координат указываются относительно начала координат.

Как и зоны UTM, исходные точки зон SPC определяются таким образом, чтобы каждое направление на восток и север в каждой зоне было положительным числом. Как показано на рисунке ниже, места происхождения SPC расположены к югу от округов, включенных в каждую зону. Исходные точки совпадают с центральным меридианом картографической проекции, на которой основана каждая зона. Ложное происхождение Северной зоны Пенсильвании определяется как 600 000 метров на восток, 0 метров на север. Восток происхождения варьируется от зоны к зоне от 200 000 до 8 000 000 метров на восток.

Рисунок 2.12. Схематическое изображение двух зон системы координат штата, показывающее округа, составляющие каждую зону (желтым цветом), происхождение каждой зоны и стандартные линии картографических проекций, на которых основаны зоны, вдоль которых искажение масштаба равно нулю. .

Предоставлено: © Университет штата Пенсильвания, лицензия CC BY-NC-SA 4.0

Зоны SPCS обозначаются 4-значным кодом FIPS, первые две цифры представляют штат, а вторые — зону (например, PA имеет код FIPS 37 с 2 зонами, 1 и 2, таким образом, 3701 для северной зоны и 3702 для южной). Начальный «0» для состояний в 1-9диапазон обычно снижается; таким образом, для CA, например, самой северной зоной SPCS является 401.

Одно место, где вы можете найти все номера зон, находится здесь: USA State Plane Zones NAD83

Ниже показан юго-западный угол того же масштаба 1:24 000- топографическая карта в масштабе, использованная в качестве примера выше. Наряду с географическими координатами (40 45′ северной широты, 77° 52′ 30″ западной долготы) угла и отметками UTM, о которых говорилось выше, также включены восточное и северное направления SPCS.70 000 FEET» представляет собой линию сетки SPC, которая проходит перпендикулярно экватору и на 1 970 000 футов к востоку от начала северной зоны Пенсильвании. Обратите внимание, что в этом примере системные координаты SPC указаны в футах, а не в метрах. Система SPC переключилась использовать метры в 1983 году, но большинство существующих топографических карт старше этого и до сих пор дают спецификации в футах (как в приведенном ниже примере).

Начало лежит далеко к западу от этого листа карты. Другие линии сетки SPC, называемые » северные направления» (показан один для 220 000 футов), проходят параллельно экватору и перпендикулярно восточным направлениям SPC с шагом 10 000 футов. В отличие от линий долготы, восточное и северное направления SPC прямые и не сходятся на полюсах Земли.

Рисунок 2.13. Юго-западный угол топографической карты Геологической службы США с делениями сетки и метками для трех различных систем координат, включая систему координат SPC.

Авторы и права: Геологическая служба США, общественное достояние.

SPC, как и все плоские системы координат, делают вид, что мир плоский. Основная проблема проектирования, с которой столкнулись геодезисты, разрабатывавшие Государственную плоскую систему координат, заключалась в том, чтобы установить зоны системы координат, которые были бы достаточно малы, чтобы минимизировать искажения до приемлемого уровня, но достаточно велики, чтобы быть полезными.

Большинство зон SPC основаны на картографической проекции Transverse Mercator или Lambert Conic Conformal , параметры которой (такие как стандартные линии и центральные меридианы) оптимизированы для каждой конкретной зоны. «Высокие» зоны, подобные зонам в штатах Нью-Йорк, Иллинойс и Айдахо, основаны на уникальных поперечных проекциях Меркатора, которые сводят к минимуму искажения, проводя две стандартные линии с севера на юг по обе стороны от центрального меридиана каждой зоны, подобно той же проекции. используется для зон UTM. «Широкие» зоны, подобные зонам в Пенсильвании, Канзасе и Калифорнии, основаны на уникальных конформных конических проекциях Ламберта (подробнее об этой и других проекциях см. зона. (Одна из зон Аляски основана на «косом» варианте проекции Меркатора. Это означает, что вместо стандартных линий, параллельных центральному меридиану, как в поперечном случае, косая проекция Меркатора проводит две стандартные линии, наклоненные так, чтобы свести к минимуму искажения вдоль ручек Аляски. )

Эти два типа картографических проекций имеют общее свойство конформности , что означает, что углы, нанесенные на карту в системе координат, равны углам, измеренным на поверхности Земли. Как вы понимаете, конформность — полезное свойство для землеустроителей, зарабатывающих на жизнь измерением углов.

В этом разделе описаны некоторые характеристики картографических проекций и то, как они используются для связи плоскостных координат с земным шаром. Далее мы углубимся в тему картографических проекций, тему, которая веками интересовала многих математиков и других специалистов.

Практический тест

Зарегистрированные учащиеся штата Пенсильвания должны вернуться сейчас – пройти тест для самооценки о координатах самолета штата .

Вы можете проходить пробные тесты столько раз, сколько пожелаете. Они не оцениваются и никак не влияют на вашу оценку.

Отражение точек на координатной плоскости (Видео)

Отражение — это когда графическая линия или фигура зеркально отражается на другой стороне определенной линии или оси. При отражении точек простой способ запомнить, как это сделать успешно, — изменить знак значений неотражающей оси. Например, если вопрос состоит в том, чтобы попросить учащегося отразить точку (-2,3) по оси x, все, что вам нужно сделать, это изменить знак значения противоположной оси, которым в данном случае будет y. -ценить. Таким образом, значение y этой точки равно 3. Это положительное значение. Если вы измените знак на отрицательный, вы получите -3. Таким образом, новая точка (-2,-3) является отражением исходной точки по оси x.

TranscriptPractice

Привет, добро пожаловать в это видео о рефлексии! В этом видео мы рассмотрим отражение фигуры над линией и отражение фигуры в точке. Давайте начнем!

Когда мы думаем о термине отражение , мы, скорее всего, думаем о взгляде в зеркало или неподвижный водоем. Эта идея связана с тем, что происходит, когда мы отражаем фигуры на координатной плоскости . Как я уже упоминал, есть два основных типа отражений: отражения от линии и отражения от точки. Давайте начнем с рассмотрения отражений над линией.

Мы можем отразить фигуру в координатной плоскости над любой линией в координатной плоскости . Вот треугольник, отраженный над линией x=7.

Треугольник слева — это наша исходная фигура, или прообраз , называемый треугольником ABC. Треугольник справа — это наша отраженная фигура, или изображение , называемое треугольником A’B’C’. Штриховое обозначение обозначает цифру, которая является изображением. Точка А на прообразе соответствует точке А’ на изображении и так далее.

Здесь следует отметить несколько моментов:

Во-первых, прообраз и изображение конгруэнтны, но «перевернуты».

Вы также заметите, что все соответствующие точки на прообразе и изображении находятся на одинаковом расстоянии от линии отражения, но в противоположном направлении.

И, наконец, линия отражения делит пополам все отрезки, соединяющие соответствующие точки прообраза и изображения.

Теперь вот трапеция , отраженная тремя разными линиями. Обратите внимание, что три свойства, которые мы только что обсуждали, остаются верными, но также обратите внимание, что для фактического создания отражения часто требуется просто подсчитать расстояния между линией отражения и точками или добавить и вычесть координаты.

В некоторых случаях линия отражения может быть на краю или даже внутри фигуры.

Три распространенных способа отображения фигур — по оси x, оси y и по линии y=x. Когда мы смотрим на них, следует заметить, что знаки координат меняются.

Например, когда фигура отражается по оси x, обратите внимание на изменение знака координаты y.

Когда фигура отражается по оси Y, обратите внимание, что координаты X меняют знак.

Когда фигура отражается над линией y=x, обратите внимание, что порядок координат меняется.

Мы также можем отразить фигуру на координатной плоскости в любой точке на координатной плоскости. Вот дротик, отраженный в точке (12,10).

Точка, над которой отражается дротик, называется, как вы уже догадались, точкой отражения .

Свойства отражений в точках очень похожи на свойства отражений над линиями:

Прообраз и изображение конгруэнтны, но изображение представляет собой поворот прообраза на 180 градусов.

Все соответствующие точки на прообразе и изображении находятся на одном и том же, но противоположном расстоянии от точки отражения.

А, точка отражения является серединой всех отрезков, соединяющих соответствующие точки прообраза и изображения.

Звучит как отражение над линией, верно?

Вот воздушный змей, отражающийся в нескольких разных точках. Точка отражения может быть на краю или даже внутри фигуры. Обратите внимание, как наши свойства остаются в силе.

И, наконец, давайте посмотрим на последнее отражение. Одно часто используемое отражение — это отражение относительно начала координат (0,0). При отражении фигуры относительно начала координат меняются знаки всех координат.

Это все для этого видео. Спасибо за просмотр и удачной учебы!

Вопрос №1:

 
Треугольник ABC, где A\((0,7)\), B\((3,-5)\) и C\((-3,5)\) , отражается поперек оси \(x\), образуя треугольник A’B’C’. Каковы координаты треугольника A’B’C?

А’\((0,-7)\), В’\((-3,5)\), С’\((3,-5)\)

А’\((0,- 7)\), В’\((3,5)\), С’\((-3,-5)\)

А’\((0,7)\), В’\((- 3,-5)\), С’\((3,5)\)

А’\((7,0)\), В’\((-5,3)\), С’\( (5,-3)\)

Показать Ответ

Ответ:

Правило отражения по оси \(x\) — \((x,y)\стрелка вправо (x,-y)\). Применив это правило к точкам вершин треугольника ABC, мы получим A’\((0,-7)\), B’\((3,5)\), C’\((-3, -5)\).

Скрыть ответ

Вопрос №2:

 
Трапецеидальные PQRS, где P\((2,3)\), Q\((6,3)\), R\((8,1)\ ) и S\((0,1)\), отражается через линию \(y=x\) для создания трапеции P’Q’R’S’. Каковы координаты трапеции P’Q’R’S’?

P’\((3,2)\), Q’\((3,6)\), R’\((1,8)\), S’\((1,0)\)

P’\((-3,-2)\), Q’\((-3,-6)\), R’\((-1,-8)\), S’\((-1 ,-0)\)

P’\((2,-3)\), Q’\((6,-3)\), R’\((8,-1)\), S’\ ((0,-1)\)

P’\((-2,3)\), Q’\((-6,3)\), R’\((-8,1)\), S’\((-0,1)\)

Показать ответ

Ответ:

Правило отражения через прямую \(y=x\) таково: \((x,y)\rightarrow(y ,Икс)\). Применяя правило к точкам вершин трапеции PQRS, получаем P’\((3,2)\), Q’\((3,6)\), R’\((1,8) \), S’\((1,0)\)

Скрыть ответ

Вопрос №3:

 
Прямоугольник LMNO был отражен через определенную линию, чтобы создать прямоугольник L’M’N’O’.

Через какую линию отразился прямоугольник LMNO?

\(y\)-ось

\(x\)-ось

\(y=x\)

\(y=-x\)

Показать ответ

Ответ: Мы

2

3

3 начнем с просмотра координат вершин прямоугольников LMNO и L’M’N’O’, расположенных рядом друг с другом.

L\((-6,8)\стрелка вправо\)L’\((-8,6)\), M\((4,8)\стрелка вправо\)M’\((-8,-4)\ ), N\((4,4)\стрелка вправо\)N’\((-4,-4)\) и O\((-6,4)\стрелка вправо\)O’\((-4, 6)\). При внимательном рассмотрении мы видим, что здесь применено правило \((x,y)\стрелка вправо(-y,-x)\), то есть правило отражения через линию \(y=-x\) . Его также можно рассматривать как отражение через линию \(y=x\), а также отражение относительно начала координат, поэтому правило имеет вид \((x,y)\стрелка вправо (-y,-x)\).

Скрыть ответ

Вопрос №4:

 
Четырехугольник ABCD изображен на координатной сетке. Когда четырехугольник ABCD отражается через начало координат, получается четырехугольник A’B’C’D’.

Каковы координаты вершин четырехугольника A’B’C’D’?

A’\((-7,4)\), B’\((-5,2)\), C’\((-3,4)\), D’\((-5,7 )\)

А’\((7,-4)\), В’\((5,-2)\), С’\((3,-4)\), D’\((5 ,-7)\)

А’\((-4,-7)\), В’\((-2,-5)\), С’\((-4,-3)\), Д’\((-7,-5)\)

A’\((7,4)\), B’\((5,2)\), C’\((3,4)\), D’\((5,7)\)

Показать Ответ

Ответ:

Правило отражения через начало координат: \((x,y)\стрелка вправо (-x,-y)\). Мы начнем с нахождения вершин четырехугольника ABCD из координатной плоскости, которые равны A\((-7,-4)\), B\((-5,-2)\), C\((-3, -4)\), Д\((-5,-7)\). Применяя правило, получаем A’\((7,4)\), B’\((5,2)\), C’\((3,4)\), D’\((5 ,7)\).

Скрыть ответ

Вопрос №5:

 
Треугольник DEF, где D\((-6,2)\), E\((4,6)\) и F\((1,-2)\), отражается через некоторую прямую для создания треугольника D’E’F’ с координатами D’\((6,2)\), E’\((-4,6)\) и F’\((-1,-2)\) . Через какую прямую отразился треугольник?

\(y\)-ось

\(x\)-ось

\(y=x\)

\(y=x\)

Показать ответ

Ответ:

2 Мы будем начнем со сравнения исходной точки с ее отраженной точкой, и мы увидим, что значение координаты \(y\) осталось одинаковым во всех трех вершинах, но значение координаты \(x\) имеет противоположный знак от оригинал.

No related posts.