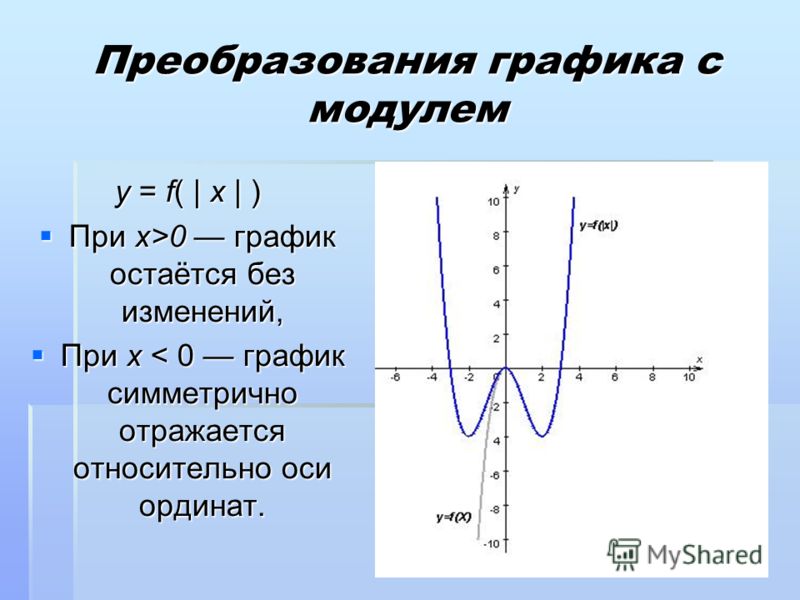
Построение графиков с модулями методом интервалов — ЗФТШ, МФТИ
Если нужно построить график функции вида y=f(|x−a1|,y = f(|x − a_1|,|x−a2|,…,|x−an|)|x − a_2|,…,|x − a_n|), где a1,a_1,a2,…,ana_2,…,a_n – некоторые фиксированные числа, то в общем случае нет иного подхода, помимо раскрытия всех модулей. Ясно, что для всякого k=1,2,3,…,nk = 1, 2, 3,…, n
|x-ak|=|x — a_k| =x-ak=x-ak, если x ≥ak;ak-x, если x<ak.\left|x-a_k\right|=\left\{\begin{array}{l}x-a_k,\;\mathrm{если}\;x\;\geq a_k;\\a_k-x,\;\mathrm{если}\;x<a_k.\end{array}\right.
Однако, например, в случае a1<a2a_1 < a_2 невозможно выполнение одновременно двух условий: x<a1x < a_1 и x>a2x > a_2. Поэтому простое раскрытие модулей приведет к лишним действиям. Чтобы этого избежать, применяют так называемый метод интервалов. Суть его состоит в следующем. Числа a1a_1, a2,…,ana_2,…, a_n упорядочивают по неубыванию и наносят на числовую ось (рис. 35). Если для определённости положить a1<a2<⋯<ana_1 < a_2 < ⋯ < a_n, то это будет выглядеть так:
Получаем, что числовая ось разбивается на n+1n + 1 интервалов. Если xx лежит в любом из них, то мы однозначно можем определить знаки всех выражений под модулями и раскрыть модули. В каждом из получившихся интервалов график функции выстраивается отдельно. Граничную точку (a1,a2,…,an)(a_1, a_2,…, a_n) можно включать в любой из промежутков, концом которого она является. Проиллюстрируем этот алгоритм на примере.
Если xx лежит в любом из них, то мы однозначно можем определить знаки всех выражений под модулями и раскрыть модули. В каждом из получившихся интервалов график функции выстраивается отдельно. Граничную точку (a1,a2,…,an)(a_1, a_2,…, a_n) можно включать в любой из промежутков, концом которого она является. Проиллюстрируем этот алгоритм на примере.
Перед тем как перейти к нахождению наименьшего значения, сделаем небольшое теоретическое отступление.
С помощью графиков удобно исследовать функции на возрастание и убывание. Функцию y=f(x)y = f(x) называют строго возрастающей, если f(x1)<f(x2)f(x_1) < f(x_2) при x1<x2x_1 < x_2. Строго убывающие функции определяются неравенством f(x1)>f(x2)f(x_1) > f(x_2) при x1<x2x_1 < x_2. Если при x1<x2x_1 < x_2 верно f(x1)≤f(x2)f(x_1) ≤ f(x_2), то функцию y=f(x)y = f(x) называют возрастающей, а если f(x2)≤f(x1)f(x_2) ≤ f(x_1), то – убывающей. Для линейных функций признаком возрастания и убывания является знак коэффициента при хх. Если этот коэффициент отрицателен, то такая функция строго убывает на данном интервале. В случае положительности коэффициента функция строго возрастает. Таким образом, можно сделать такой вывод.
Если этот коэффициент отрицателен, то такая функция строго убывает на данном интервале. В случае положительности коэффициента функция строго возрастает. Таким образом, можно сделать такой вывод.
Характер возрастания (возрастание или убывание) функции вида
f(x)=c1|x−a1|+c2|x−a2|+ …+cn|x−an|f(x) = c_1|x − a_1| + c_2|x − a_2| + … + c_n|x − a_n|,
может меняться только в точках x=a1,a2,…,anx = a_1, a_2,…, a_n (здесь a1≤a2≤…≤ana_1 ≤ a_2 ≤ … ≤ a_n, а c1c_1, c2,…,cnc_2,…, c_n – некоторые числа). Поэтому для нахождения наибольшего или наименьшего значения функции такого вида стoит обратить внимание на то, возрастает или убывает такая функция при x<a1x < a_1 и x>anx > a_n, а также сравнить значения функции ff в точках x=a1,a2,…,anx = a_1, a_2,…, a_n.
Возвращаемся к нашей задаче.
Похожую схему рассуждений можно применить и в задачах следующего типа.
Исследовательский проект по математике на тему: «Графики функций, аналитическое задание которых содержит знаки модуля»
Слайд 1
Исследовательский проект по математике на тему: « Графики функций, аналитическое задание которых содержит знаки модуля» Журавлёва Алеся Евгеньевна 10 класс Товменко Светлана Петровна Учитель математики МКОУ Бондаревская СОШ
Слайд 2
Цель моей исследовательской работы: 1.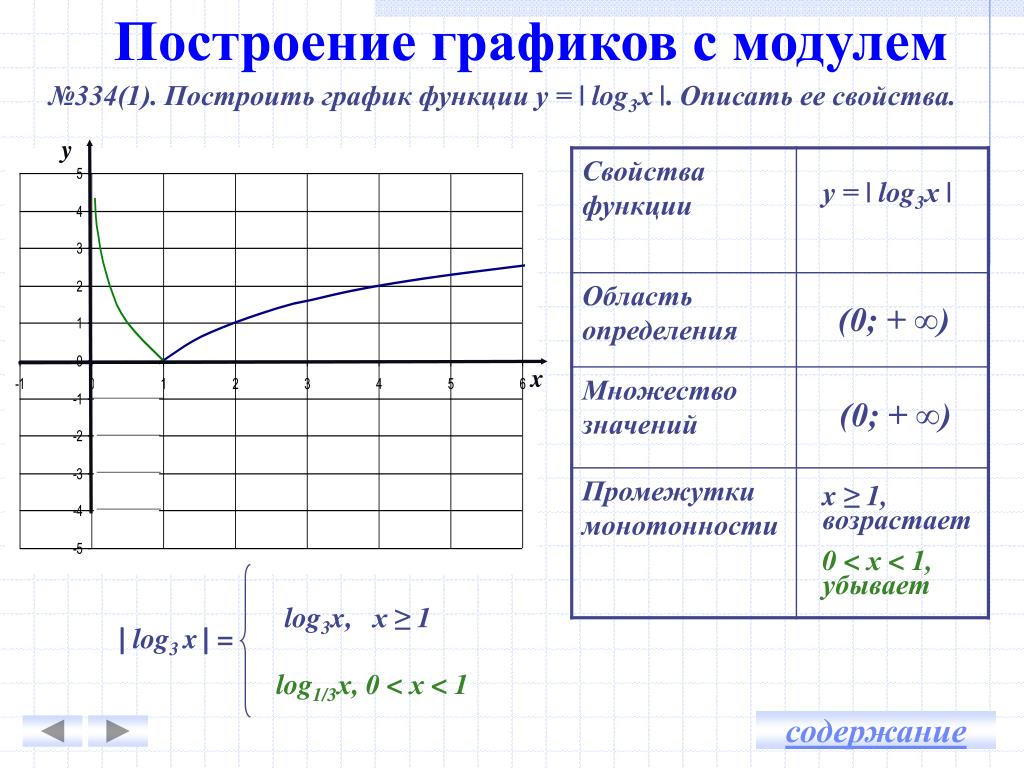 Провести исследование и анализ имеющихся способов построения графиков функций, содержащих переменную под знаком модуля . 2. Выбрать из найденных способов решения наиболее оптимальные. 3. Провести обобщение и систематизацию имеющего материала: а) научиться строить графики функций, содержащих переменную под знаком модуля; б) составить подборку задач по теме «Графики функций, содержащих переменную под знаком модуля «. Объект исследования : функции, содержащие переменную под знаком модуля. Предмет исследования : механизм построения графиков .
Провести исследование и анализ имеющихся способов построения графиков функций, содержащих переменную под знаком модуля . 2. Выбрать из найденных способов решения наиболее оптимальные. 3. Провести обобщение и систематизацию имеющего материала: а) научиться строить графики функций, содержащих переменную под знаком модуля; б) составить подборку задач по теме «Графики функций, содержащих переменную под знаком модуля «. Объект исследования : функции, содержащие переменную под знаком модуля. Предмет исследования : механизм построения графиков .
Слайд 3
Содержание Введение Историческая справка. Определение модуля ………………… 1 §1 . Построение графиков функций, содержащих модуль …..7 1.1 . Построение графика функции у=f(∣x∣ )………………….8 1.2 . Построение графика функции у=∣f(x) ∣ ………………….10 1.3. Построение графиков функций вида ∣у∣=f(x )……………12 1.4. Построение графиков функции вида ∣у∣=∣f(x) ∣ ……………13 1.5. Построение графиков функции вида у=∣f(x)∣ + ∣f1(x)∣ + ∣f2(x)∣+ …+ ∣ fn (x) ∣ ……………………………………………….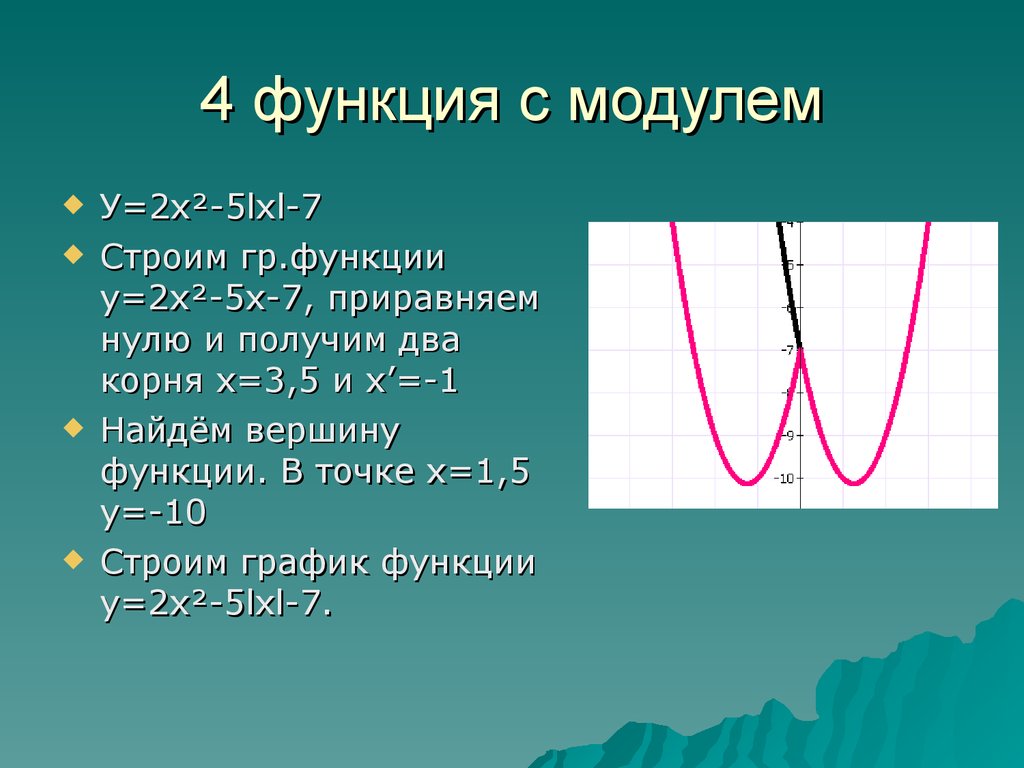 .14 § 2.Решение задач из КИМ ОГЭ по теме «Построение графиков функций, содержащих переменную под знаком модуля »……..16
.14 § 2.Решение задач из КИМ ОГЭ по теме «Построение графиков функций, содержащих переменную под знаком модуля »……..16
Слайд 4
Историческая справка К началу ХVII века алгебра была уже достаточно развитой наукой. Трудами многих поколений учёных были подготовлены условия для нового большого открытия в науке, которое послужило бы толчком к её дальнейшему развитию. Таким открытием явилось введение в математику понятия переменной величины и прямоугольной системы координат. Честь введения в математику функциональной зависимости принадлежит французскому учёному Ренэ Декарту. Ренэ Декарт придумал систему прямоугольных координат, которой пользуемся мы другое. Трудами Декарта алгебра была значительно усовершенствована. Термин «функция» впервые встречается в письме немецкого математика Лейбница В обычное употребление термина введено в начале ХVIII в. Иоганном Бернулли
Слайд 5
Историческая справка Понятие «модуль» является одним из основных понятий элементарной математики. Слово «модуль» произошло от лат.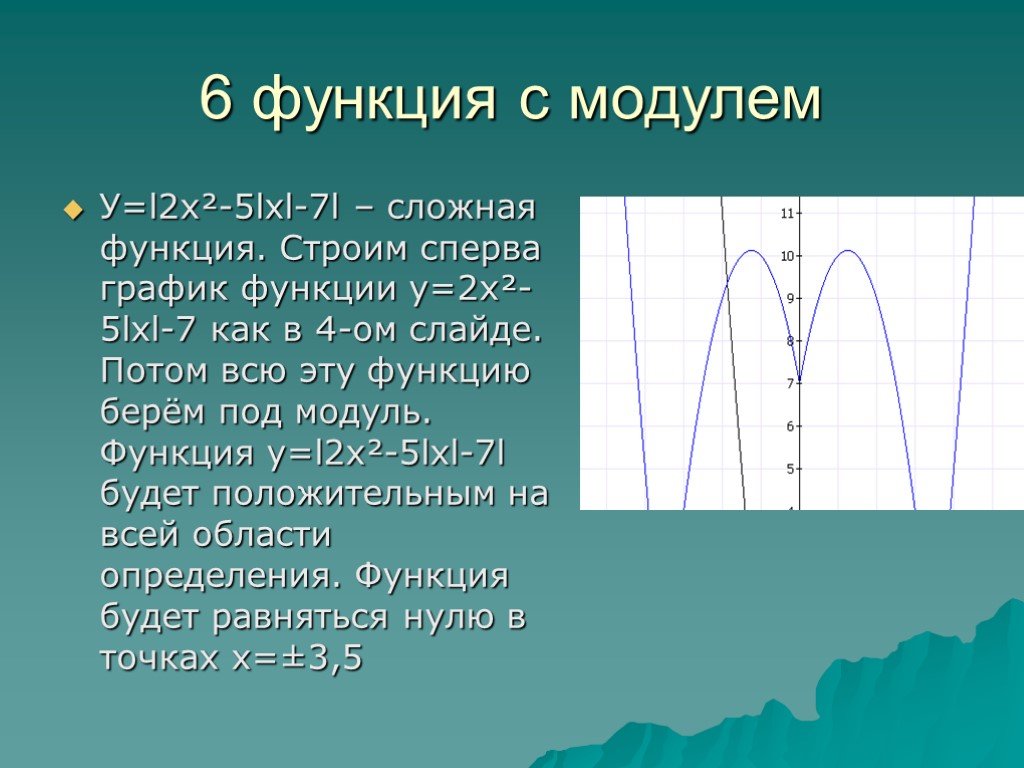 modulus — «маленькая мера»..Знак модуля, пожалуй, одно из самых интересных явлений в математике. Слово «модуль» многозначное слово, которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках. В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов. В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п. Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению.
modulus — «маленькая мера»..Знак модуля, пожалуй, одно из самых интересных явлений в математике. Слово «модуль» многозначное слово, которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках. В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов. В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п. Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению.
Слайд 6
О пределение модуля Определение модуля в математике: Модуль неотрицательного числа a равен самому числу a, модуль отрицательного числа a равен противоположному ему положительному числу –a.
Слайд 7
Построение графиков функций, содержащих модуль Построение графиков следует осуществлять двумя способами: 1) на основании определения модуля; 2) на основании правил (алгоритмов) геометрического преобразования графиков функций.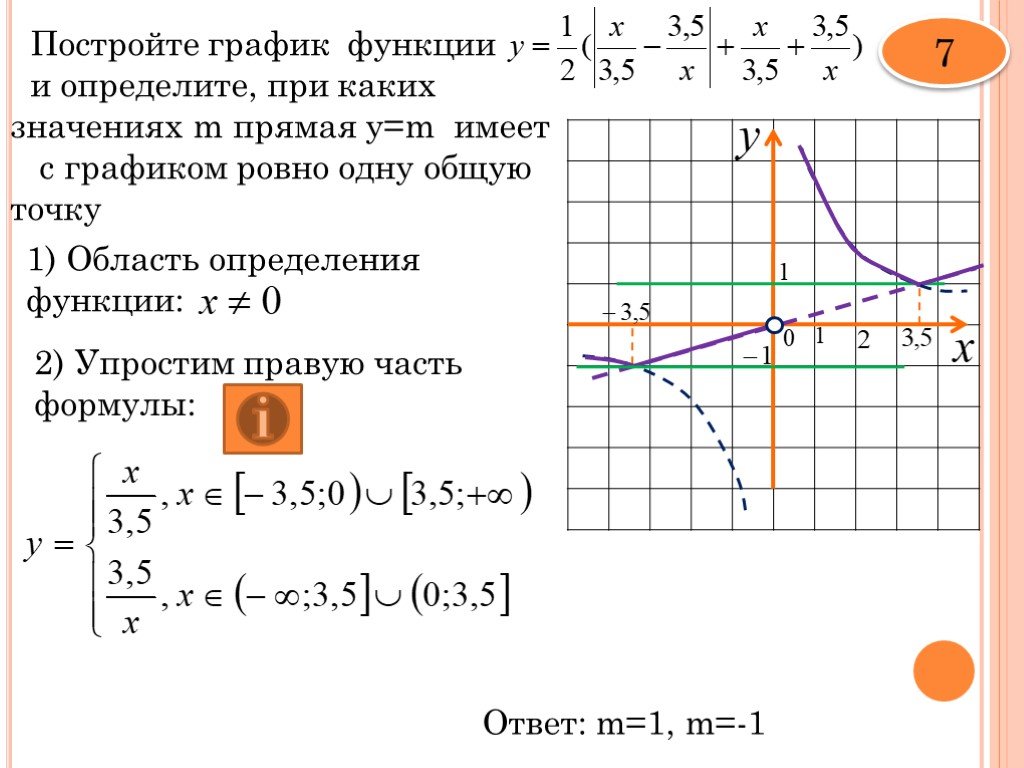
Слайд 8
Построить график функции у=2∣х∣-2. Построение: 1-й способ. 2-й способ. 1) Строим график функции у=2х-2 для х>0. 2) Достраиваем его левую часть для х
Слайд 9
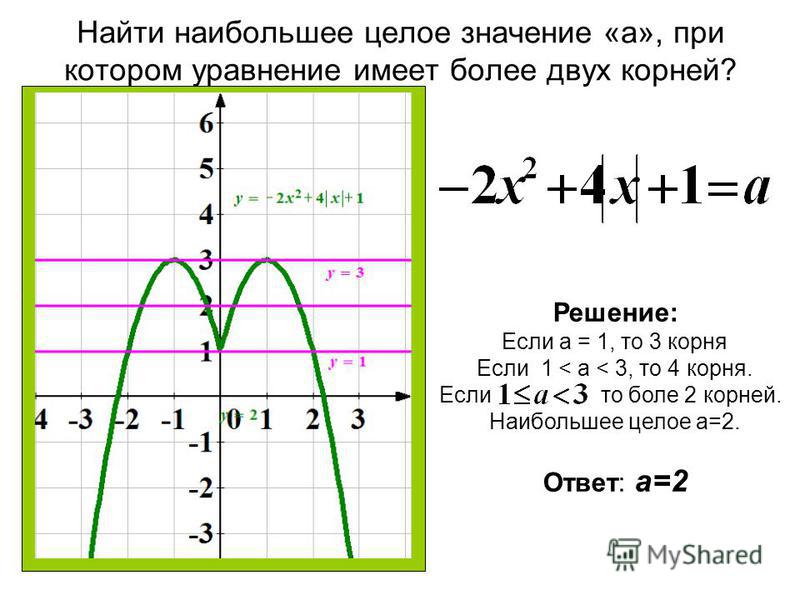
ё Построить график функцииу =х2-2|х|-3. Решение. По свойству модуля, х2=|х|2, значит у=х2-2|х|-3 можно представить в виде у=|х|2-2|х|-3. Тогда для того чтобы построить график у=х2-2|х|-3 нужно построить график функции у=х2-2х-3. Для этого найдём х0=-b/2a=-(-2)/2=1, y0=y(1)=1-2-3=-4, ось параболы х=1, её вершина имеет координаты (1;-4), при у=0 х=3 или х=-1, при х=0 у=-3 Теперь оставим без изменений часть графика, расположенную в правой полуплоскости, и отобразим её симметрично относительно оси У(другую часть графика отбросим).
Слайд 10
1.2. Построение графика функции у=∣f(x)∣ Отсюда вытекает алгоритм построения графиков функции у=∣f(x)∣. а) Строим график функции f(x). б) Часть графика у=f(x), лежащая над осью Ох, сохраняется, часть его, лежащая под осью Ох, отображается симметрично относительно оси Ох.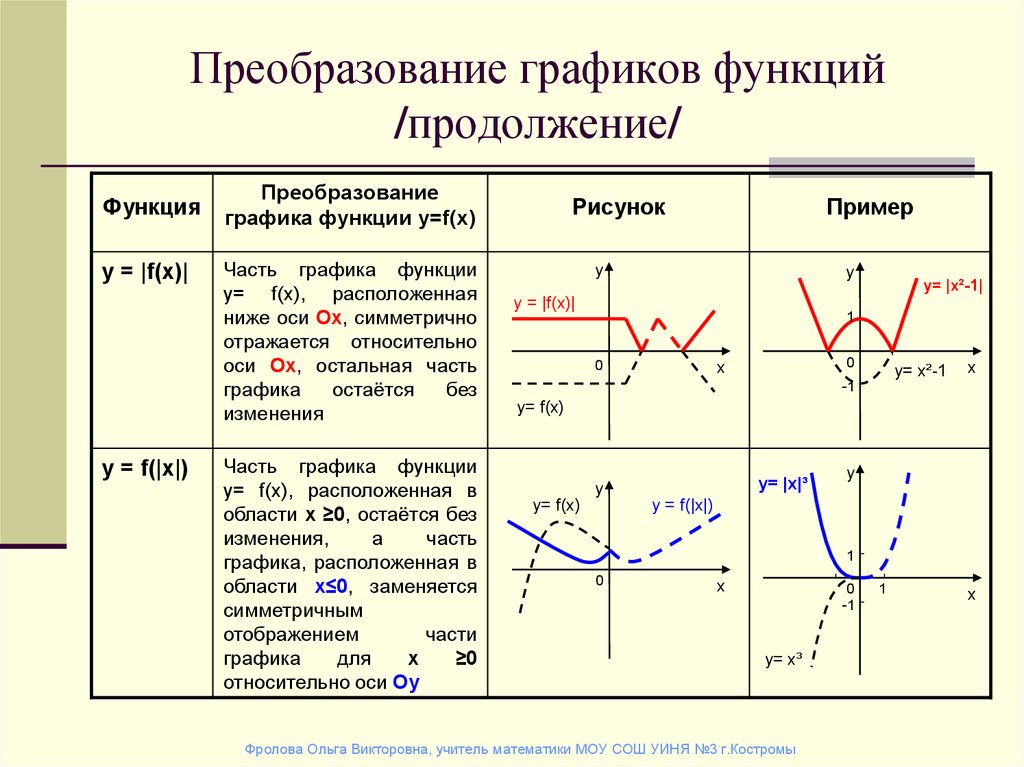
Слайд 11
Построить график функции у=∣х2-2х-3∣. 1) Строим график функции у=х2-2х-3. 2) График нижней полуплоскости отображаем вверх симметрично относительно оси Ох
Слайд 12
Построить график функции ∣у∣= х2-2х-3 1 способ: 2 способ: 1) Строим график функции у=х2-2х-3; 2) Отображаем ту часть графика, которая находится выше оси абсцисс симметрично относительно оси абсцисс.
Слайд 13
Построить график функции ∣у∣=∣1-х∣ Решение: 1 способ. 2 способ. 1. Строим график функции у=1-x. 2. График у=∣1-х∣ получаем из графика у=1-x, симметрично отобразив ту часть, лежащую под осью относительно оси Ох. 3. График ∣у∣=∣1-х∣ получаем из графика у=∣1-х∣, отобразив последний симметрично относительно оси Ох.
Слайд 14
1. Построить график функции у=∣х-1∣+∣х-3∣. Решение: Точки х=1 и х=3 разбивают числовую ось на три промежутка, для каждого запишем функцию: 1) при х≤1 имеем у=4-2х; 2) при 13 имеем у=2х-4
Слайд 15
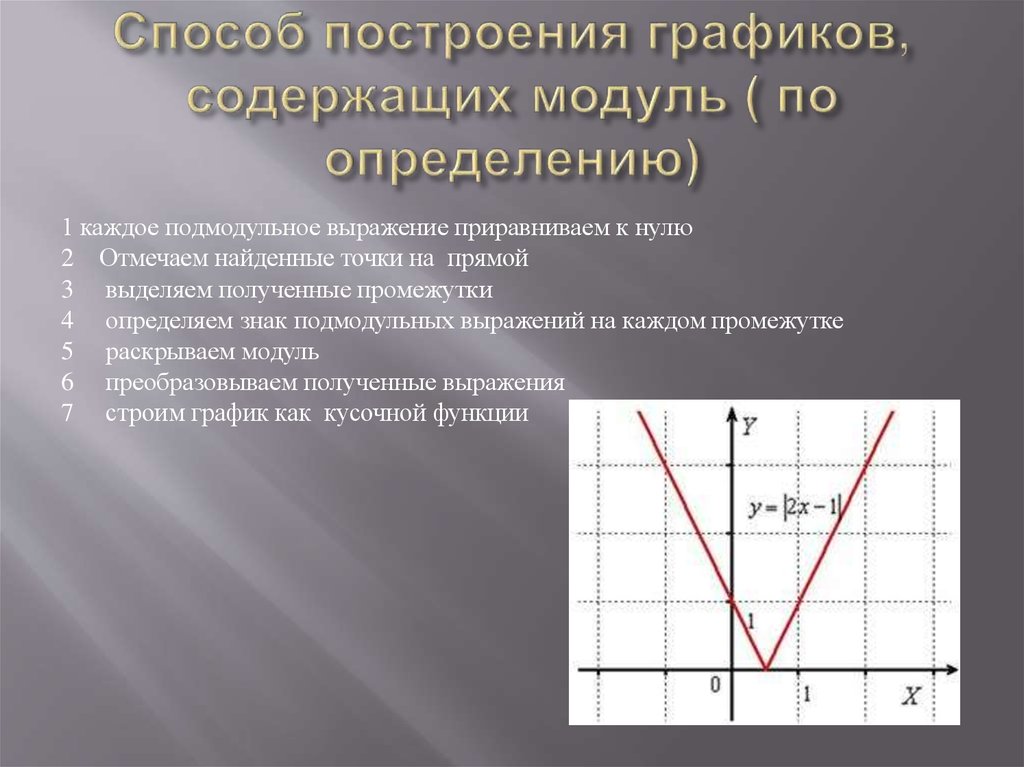
Метод вершин Графиком непрерывной кусочно-линейной функции является ломаная с двумя бесконечными крайними звеньями. Пример: Построить график функции у=∣х∣-∣х-1 ∣ Алгоритм построения: 1) Найдём нули каждого подмодульного выражения х=0 и х=1. 2) Составим таблицу, в которой кроме 0 и 1 записываем по одному целому справа и слева от этих значений. 3 ) Наносим эти точки на координатную плоскость и соединяем последовательно . Точки перелома и есть вершины ломаной х -1 0 1 2 у -1 -1 1 1
Пример: Построить график функции у=∣х∣-∣х-1 ∣ Алгоритм построения: 1) Найдём нули каждого подмодульного выражения х=0 и х=1. 2) Составим таблицу, в которой кроме 0 и 1 записываем по одному целому справа и слева от этих значений. 3 ) Наносим эти точки на координатную плоскость и соединяем последовательно . Точки перелома и есть вершины ломаной х -1 0 1 2 у -1 -1 1 1
Слайд 16
§ 2.Решение задач из ЕГЭ по теме «Построение графиков функций, содержащих переменную под знаком модуля » Постройте график функции — х2-2х+2, если х ≥ — 3 у= -x-4, если x
Слайд 17
Спасибо за внимание
Анализ точки зрения и развитие сюжета: две дороги, главы 10 и 11
ЭЛА 2019 G6:M3:U1:L9
ELA 2019 G6:M3:U1:L8 Анализ точки зрения: две дороги, глава 9 Анализ точки зрения и развитие сюжета: две дороги, глава 12 ELA 2019 G6:M3:U1:L10
В этом уроке
- Ежедневные цели обучения
- Текущая оценка
- Повестка дня
- заранее
- Технологии и мультимедиа
- Поддержка изучающих английский язык
- Словарь
- Материалы предыдущих уроков
- Новые материалы
- Оценка
- Открытие
- Рабочее время
- Закрытие и оценка
- Домашнее задание
Вы здесь:
- ELA 2019 6 класс
- Эла 2019 G6:M3
- Эла 2019 G6:M3:U1
- Эла 2019 G6:M3:U1:L9
Нравится то, что вы видите?
Закажите печатные материалы, руководства для учителей и многое другое.
Как заказать
Помогите нам стать лучше!
Расскажите нам, как учебная программа работает в вашем классе, и пришлите нам исправления или предложения по ее улучшению.
Оставить отзыв
Стандарты Focus: Это стандарты, к которым относится инструкция.
- RL.6.1, RL.6.3, RL.6.4, RL.6.6, L.6.5a, L.6.5c
Вспомогательные стандарты: Это стандарты, которые являются второстепенными — в этом уроке нет прямых указаний, но применение этих стандартов происходит в результате обращения к основным стандартам.
- РЛ.6.10, СЛ.6.1
Скачать материалы
Ежедневные учебные цели
- Я могу анализировать, как Кэл реагирует и меняется в связи с событиями, описанными в главах 10 и 11. (RL.6.3)
- Я могу продемонстрировать понимание глав 10 и 11 из Две дороги . (RL.
 6.1)
6.1) - Я могу проанализировать точку зрения Кэла в главах 10 и 11 и то, как она развивается автором. (РЛ.6.6)
Текущая оценка
- Открытие A: анализ персонажа: Two Roads блокнот (RL.6.1, RL.6.3)
- рабочее время A: суть на стикерах
- рабочее время B: языковое погружение: анализ языка и Точка зрения ( Two Roads , стр. 123) блокнот для заметок (РЛ.6.1, РЛ.6.4, РЛ.6.6, СЛ.6.1, Л.6.5а, Л.6.5с)
Повестка дня
1. Открытие A. Вовлеките ученика — RL.6.3 (5 минут) 2. Время работы A. Читайте Два дороги , главы 10 и 11 — B. Language Dive: Анализ языка и точки зрения — RL.6.6 (15 минут) 3. A. Подведение итогов: Наводящие вопросы к модулю (5 минут) 4. Домашнее задание A. Предварительно прочитанный основной текст: учащиеся предварительно прочитывают главу 12 в Две дороги. эту главу на следующем уроке. | Приведение в соответствие со стандартами оценивания и целью урока
Возможности для расширения обучения
Как это основывается на предыдущей работе
Поддержка всех учащихся
Руководство по оцениванию
Впереди
|
Предварительно
- Предварительно прочитайте главы 10 и 11 из Two Roads , чтобы определить потенциально сложные слова или сюжетные моменты.
- Просмотрите новые материалы, использованные в этом уроке, чтобы убедиться в том, что учащиеся должны знать и уметь.
- Просмотрите упражнение «Передвижные репортеры» из раздела «Закрытие и оценка». A. Заранее определите, какие учащиеся лучше всего подготовлены для выбора наиболее содержательных ответов на направляющие вопросы модуля, и назначьте их в качестве передвижных репортеров.
- Разместите цели обучения и применимые опорные диаграммы (см. список материалов).
Техника и мультимедиа
- Закрытие и оценка A: Создайте якорную диаграмму «Наводящие вопросы модуля» в онлайн-формате, таком как http://eled.
 org/0158, чтобы поделиться с семьями. Призовите родителей присоединиться к обсуждению и размышлению над этими вопросами, добавив свои ответы на цифровую якорную диаграмму.
org/0158, чтобы поделиться с семьями. Призовите родителей присоединиться к обсуждению и размышлению над этими вопросами, добавив свои ответы на цифровую якорную диаграмму.
Поддержка изучающих английский язык
Поддержка частично руководствуется стандартами CA ELD 6.I.A.1, 6.I.A.2, 6.I.B.6 и 6.II.B.1.
Важные моменты самого урока
- Для поддержки ELL на этом уроке проводится первое языковое погружение Модуля 3. передать точку зрения Кэла на критически важную новую информацию, которую он получает от своего отца. Предлагаемые вопросы, встроенные в языковое погружение, структурно идентичны вопросам, с которыми учащиеся столкнутся в конце оценки по Разделу 1 урока 15, предоставляя возможности для практики, которые так важны для ELL.
- ELL может столкнуться с трудностями при освоении нового процесса, представленного во время языкового погружения, поскольку он требует большой самостоятельности. Поощряйте студентов быть избирательными в том, как они проводят свое время во время языкового погружения в малых группах, и напоминайте им, что у них может не быть возможности обсудить все возможные вопросы.

Словарь
Материалы предыдущих уроков
- Палочки акций (из Модуля 1, Раздела 1, Урока 1, Рабочего времени C)
- Анализ характера: Урок 2, рабочее время B)
- Текстовое руководство: Two Roads (для справки учителю) (из модуля 3, раздела 1, урока 2, рабочее время A)
- Основная якорная таблица: Two Roads (пример для учителя) ссылка) (из модуля 3, раздела 1, урока 1, рабочего времени C)
- Якорная диаграмма Gist: Two Roads (одна для отображения; из Модуля 3, Раздела 1, Урока 1, Рабочего времени C)
- Анкерная диаграмма «Наводящие вопросы модуля» (одна для отображения; из Модуля 3, Раздела 1, Урока 1) , Рабочее время B)
- Анализ характера: Two Roads блокнот (по одному на учащегося; из модуля 3, раздела 1, урока 2, рабочее время B)
- Two Roads (текст; по одному на учащегося ; из модуля 3, раздела 1, урока 1, открытия A)
Новые материалы
- Вопросы, которые мы можем задать во время языкового погружения Базовая таблица (пример для справки учителю)
- Вопросы, которые мы можем задать во время языкового погружения Базовая таблица (одна для демонстрации)
- Языковое погружение: Анализ языка и точки зрения ( Two Roads , стр.
 123) (для справки учителю)
123) (для справки учителю) - Language Dive: Two Roads , Page 123 Таблица фрагментов предложений (для справки учителю)
- Language Dive: Two Roads , стр. 123 блокнот для заметок (пример для справочника учителя)
- Language Dive: Two Roads , стр. 123 полоски фрагментов предложений (по одной на пару или группу учащихся)
- стикеры (по две на учащегося)
- Краткое содержание: Two Roads , главы 10 и 11 (по одной на учащегося)
- Language Dive: Analyze Language and Point of View (Two Roads, page 123) (по одной на учащегося)
Оценка
Каждый раздел в учебной программе 6-8 Language Arts имеет два встроенных оценивания на основе стандартов, одно оценивание в середине и одно оценивание в конце. Модуль завершается заданием в конце модуля 3, чтобы обобщить понимание учащимися того, чего они добились с помощью поддерживаемого письменного письма, основанного на стандартах.
Отверстие
A. Вовлечение учащегося – RL.6.3 (5 минут)
|
Рабочее время
A. Прочитайте Две дороги , главы 10 и 11 – RL.6.1 (20 минут) ссылка) для вопросов понимания и словарного запаса по мере необходимости. Студенты, которые готовы читать самостоятельно или в малых группах, должны быть освобождены от этой самостоятельности. Студенты продолжают записывать суть на стикеры , распаковывайте и записывайте незнакомую лексику и размышляйте о прочитанном по своему усмотрению. Учащиеся продолжают определять, как персонажи в тексте демонстрируют привычки характера. См. якорную таблицу Gist: Две дороги (пример для справки учителю) и Краткий обзор: Две дороги , главы 10 и 11 по мере необходимости, а также любые другие соответствующие ресурсы. |
|
B. Language Dive: Анализ языка и точки зрения — RL.6.6 (15 минут)
«Что вы помните о ролях учителя и ученика в последнем языковом погружении из Модуля 2?» (Это было под руководством учителя, когда учитель задавал вопросы о фрагментах предложений, а ученики отвечали.)
«Подумайте о нашей работе с Language Dives. Какие вопросы мы задаем о предложениях? Какие вопросы мы задаем о фрагментах? Какие вопросы мы задаем о словах?» Скажите учащимся, что им будет предоставлено время подумать и обсудить это со своим партнером. (Ответы будут разными.)
«Как наши собственные вопросы для языкового погружения помогут нам во время языкового погружения?» Скажите учащимся, что им будет предоставлено время подумать и обсудить с партнером. (Вопросы помогут нам понять важные особенности языка в предложении.)
«Теперь, когда мы завершили наше первое новое языковое погружение, какие дополнительные вопросы мы должны добавить в нашу якорную таблицу вопросов, которые мы задаем во время языкового погружения?» (Ответы будут разными.)
| Для более легкой поддержки
Для Тяжелой Поддержки
|
Закрытие и оценка
A. Подведение итогов: вопросы к модулю (5 минут)
|
Домашнее задание
A. Предварительно прочитанный анкорный текст
|
Copyright © 2013-2022 EL Education, Нью-Йорк, штат Нью-Йорк.
Урок 12 | Статистика | Математика 6-го класса
Цель
Анализ блочных диаграмм и других представлений, а также обобщение числовых данных в контексте.
Общие базовые стандарты
Основные стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89506.СП.Б.4 — Отображение числовых данных в виде графиков на числовой прямой, включая точечные графики, гистограммы и ящичные диаграммы.

6.СП.Б.5 — Суммировать наборы числовых данных по отношению к их контексту, например:
Критерии успеха
Основные концепции, которые учащиеся должны продемонстрировать или понять для достижения цели урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Сделать выводы о наборе данных, анализируя коробчатую диаграмму.
- Сравните диаграммы различных наборов данных.
Советы учителям
Рекомендации для учителей по проведению этого урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Этот Boxplot Grapher от IMathAS — хороший инструмент для создания коробчатых диаграмм.
Fishtank Plus
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Проблемы с якорем
Задачи, предназначенные для изучения ключевых моментов урока, и наводящие вопросы, помогающие ученикам понять
А628D5C3-5B97-4E03-B1EC-5AD5C66D8950Проблема 1
Лорна интересуется типичной продолжительностью фильма. Она случайным образом выбирает несколько фильмов и записывает их продолжительность в минутах. Она определяет следующую сводку из пяти чисел для набора данных:
Она случайным образом выбирает несколько фильмов и записывает их продолжительность в минутах. Она определяет следующую сводку из пяти чисел для набора данных:
Минимум: 75
Нижний квартиль: 90
Медиана: 110
Верхний квартиль: 120
Максимум: 135
9001 График данные.Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Проблема 2
94 человека попросили взять столько конфет Tootsie Pops, сколько они смогут удержать. Вот диаграмма для этих данных. Используйте его, чтобы ответить на следующие вопросы.
- Чем можно объяснить изменчивость количества Tootsie Pops, схваченного 94 людьми?
- Определите пятизначную сводку набора данных.

- Каков диапазон количества Tootsie Pops, которые схватили средние 50% людей?
- Ответьте Верно или Неверно на следующие утверждения:
- В период между 22–42 Тутси Попсами хватало больше людей, чем между 20–22 Тутси Попс.
- Столько же людей схватили от 7 до 18 Тутси Попс, сколько и людей, которые схватили от 18 до 20 Тутси Попс.
- Около 50% людей захватили от 22 до 42 Тутси Попс.
- Среднее количество схваченных Тутси Попс составляло от 18 до 22.
- Это должно быть правдой, что по крайней мере один человек схватил 42 Тутси Попса.
- Это должно быть правдой, что по крайней мере один человек схватил 20 Тутси Попс.
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Каталожные номера
EngageNY Mathematics Grade 6 Mathematics > Модуль 6 > Тема C > Урок 15 — Пример 1
Математика для 6 класса > Модуль 6 > Тема C > Урок 15 Общей основной учебной программы штата Нью-Йорк по математике от EngageNY и Great Minds. © 2015 Великие умы. Лицензировано EngageNY Департамента образования штата Нью-Йорк в соответствии с лицензией США CC BY-NC-SA 3.0. По состоянию на 2 декабря 2016 г., 17:15.
© 2015 Великие умы. Лицензировано EngageNY Департамента образования штата Нью-Йорк в соответствии с лицензией США CC BY-NC-SA 3.0. По состоянию на 2 декабря 2016 г., 17:15.
Изменено Fishtank Learning, Inc.
Проблема 3
На трех диаграммах ниже показано количество правильно отвеченных вопросов викторины из 20 вопросов для учащихся трех разных классов.
- Назовите хоть одно наблюдение того, почему данные всех трех классов совпадают.
- Назовите хотя бы одно наблюдение о том, чем отличаются классы 1 и 2.
- Назовите хотя бы одно наблюдение о том, чем отличаются классы 1 и 3.
- Если бы вы были студентом, какую блочную диаграмму вы бы хотели представлять для данных вашего класса? Подтвердите свой ответ информацией из диаграмм.
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Каталожные номера
EngageNY Mathematics Grade 6 Mathematics > Модуль 6 > Тема C > Урок 15 — Упражнения 11-15
Математика для 6 класса > Модуль 6 > Тема C > Урок 15 Общей основной учебной программы штата Нью-Йорк по математике от EngageNY и Great Minds. © 2015 Великие умы. Лицензировано EngageNY Департамента образования штата Нью-Йорк в соответствии с лицензией США CC BY-NC-SA 3.0. По состоянию на 2 декабря 2016 г., 17:15.
Изменено Fishtank Learning, Inc.
Набор проблем
Набор предлагаемых ресурсов или типов задач, которые учителя могут превратить в набор задач
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Следующие ресурсы включают проблемы и действия, связанные с целью урок, который можно использовать для создания собственного набора задач.
- Open Up Resources Практические задачи для 6 класса 8 раздела — Урок 17
- Smarter Balanced Assessment Consortium: Спецификации элементов и задач MAT.
 06.ER.3.000SP.F.195 —
(Задайте другие вопросы в дополнение к включенному.)
06.ER.3.000SP.F.195 —
(Задайте другие вопросы в дополнение к включенному.) - Иллюстративная математика Описание распределений — Наборы данных 5 и 6
- EngageNY Mathematics Grade 6 Mathematics > Модуль 6 > Тема C > Урок 16 — Упражнения и набор задач
- Задачи итоговой оценки MARS для средней школы Представление данных с помощью сгруппированных частотных диаграмм и диаграмм — Существует большая активность по сопоставлению коробчатых диаграмм с соответствующими частотными графиками. Дополнительные вопросы анализа также могут быть заданы о ящичковых диаграммах.
Целевая задача
Задание, которое представляет собой пик мышления урока — мастерство покажет, была ли достигнута цель офис. На блочной диаграмме ниже показаны эти данные.
Какие из следующих утверждений верны? Если утверждение неверно, измените его, чтобы оно стало истинным.
а. По крайней мере, одна кошка весит 11 фунтов.

 6.1)
6.1)  Завершение и оценка
Завершение и оценка 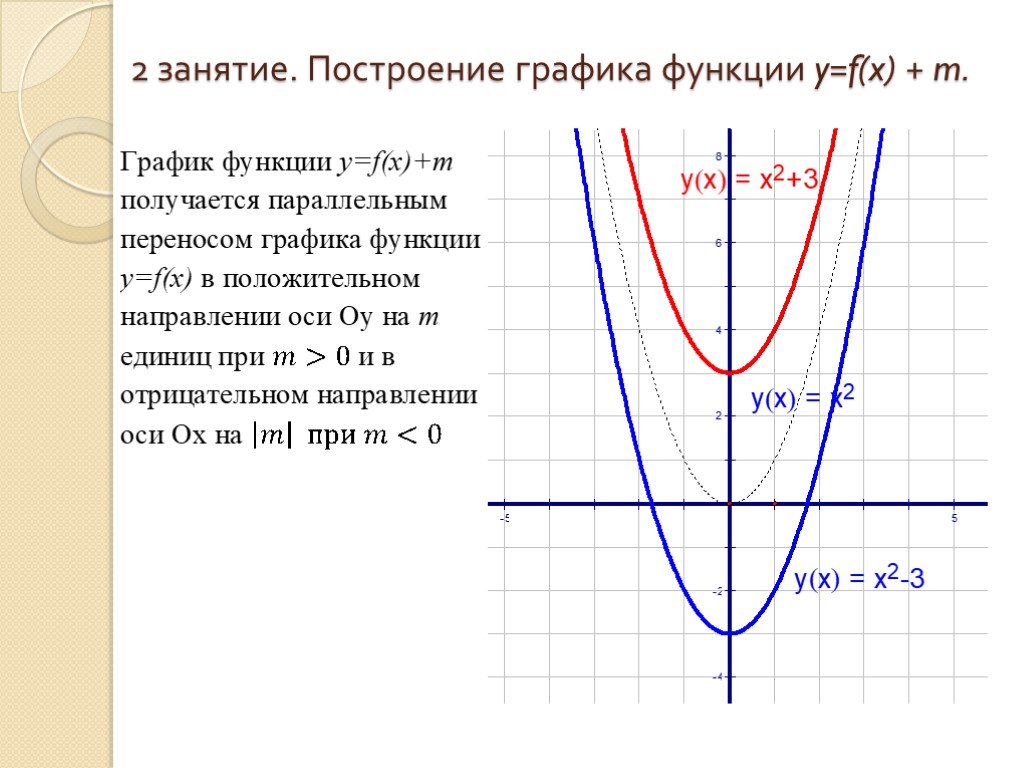 6.6 – Рабочее время B: Во время языкового погружения учащиеся анализируют, как ключевое предложение из текста помогает развить сюжет Две дороги .
6.6 – Рабочее время B: Во время языкового погружения учащиеся анализируют, как ключевое предложение из текста помогает развить сюжет Две дороги .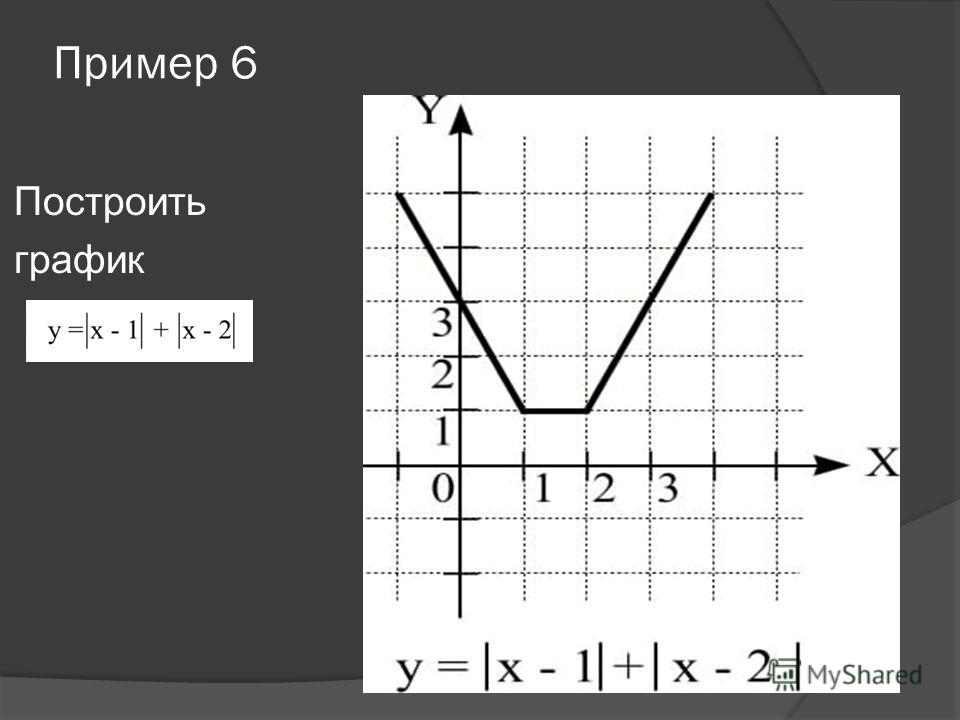 Они узнали, что точка зрения — это один из способов, которым автор развивает характер. Учащиеся продолжают анализировать развитие характера Кэла в главах, которые они читают к этому уроку.
Они узнали, что точка зрения — это один из способов, которым автор развивает характер. Учащиеся продолжают анализировать развитие характера Кэла в главах, которые они читают к этому уроку.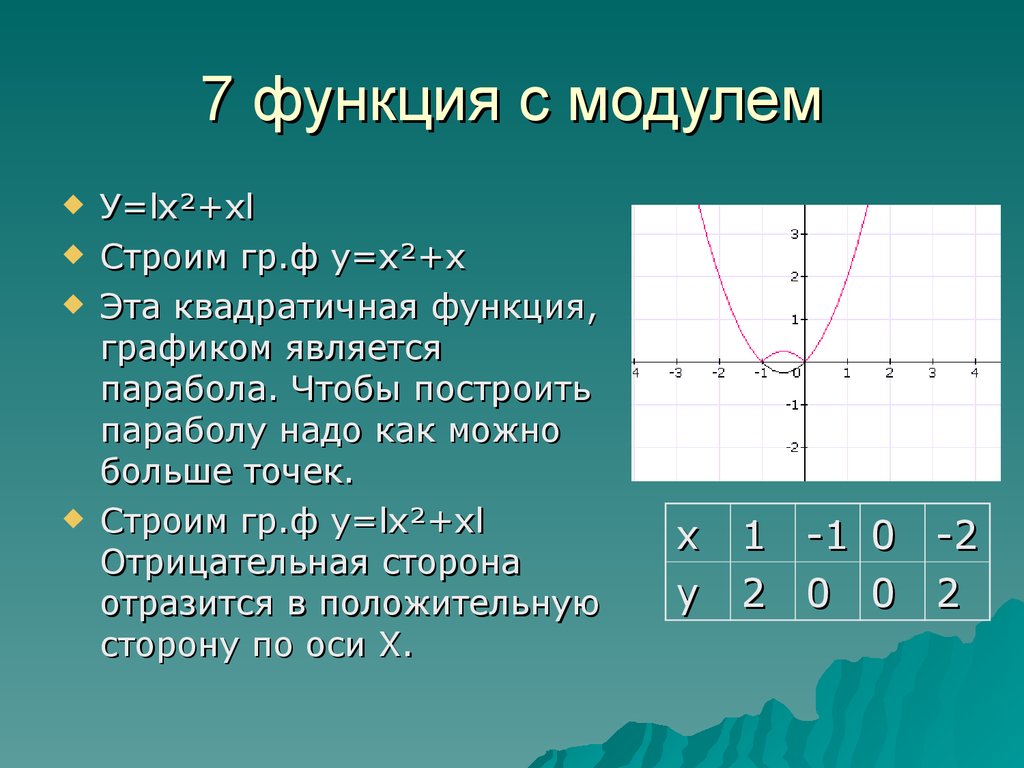 Он говорит: «Папа говорит, что я индиец. Но я никогда не чувствовал себя индийцем, никогда не думал о себе таким образом. Я просто хочу быть самим собой» (124). Идея о том, что идентичность может быть многогранной, противоречивой и сложной, может показаться верной для некоторых учащихся. Подведение итогов во время закрытия и оценки А предлагает учащимся возможность безопасно изучить некоторые из этих идей. Дайте учащимся возможность поделиться своими мыслями с небольшими группами, но не требуйте от них этого.
Он говорит: «Папа говорит, что я индиец. Но я никогда не чувствовал себя индийцем, никогда не думал о себе таким образом. Я просто хочу быть самим собой» (124). Идея о том, что идентичность может быть многогранной, противоречивой и сложной, может показаться верной для некоторых учащихся. Подведение итогов во время закрытия и оценки А предлагает учащимся возможность безопасно изучить некоторые из этих идей. Дайте учащимся возможность поделиться своими мыслями с небольшими группами, но не требуйте от них этого.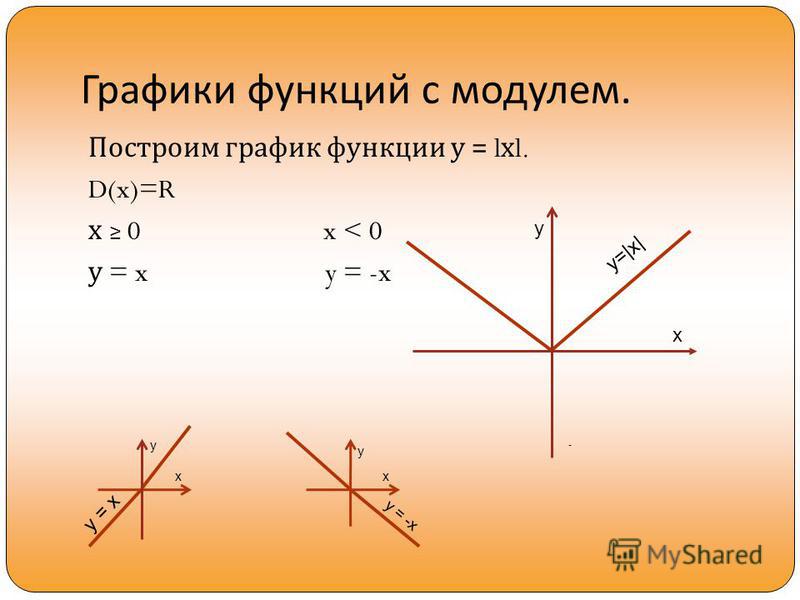 Некоторые студенты могут обидеться на этот язык. Объясните, что автор выбирает диалог, который представляет персонажа; в этом случае, как Поп говорит Кэлу, это не должно быть оскорбительным. Если учащиеся читают вслух, позвольте им пропустить или заменить это слово, если они предпочитают.
Некоторые студенты могут обидеться на этот язык. Объясните, что автор выбирает диалог, который представляет персонажа; в этом случае, как Поп говорит Кэлу, это не должно быть оскорбительным. Если учащиеся читают вслух, позвольте им пропустить или заменить это слово, если они предпочитают.
 org/0158, чтобы поделиться с семьями. Призовите родителей присоединиться к обсуждению и размышлению над этими вопросами, добавив свои ответы на цифровую якорную диаграмму.
org/0158, чтобы поделиться с семьями. Призовите родителей присоединиться к обсуждению и размышлению над этими вопросами, добавив свои ответы на цифровую якорную диаграмму.
 123) (для справки учителю)
123) (для справки учителю)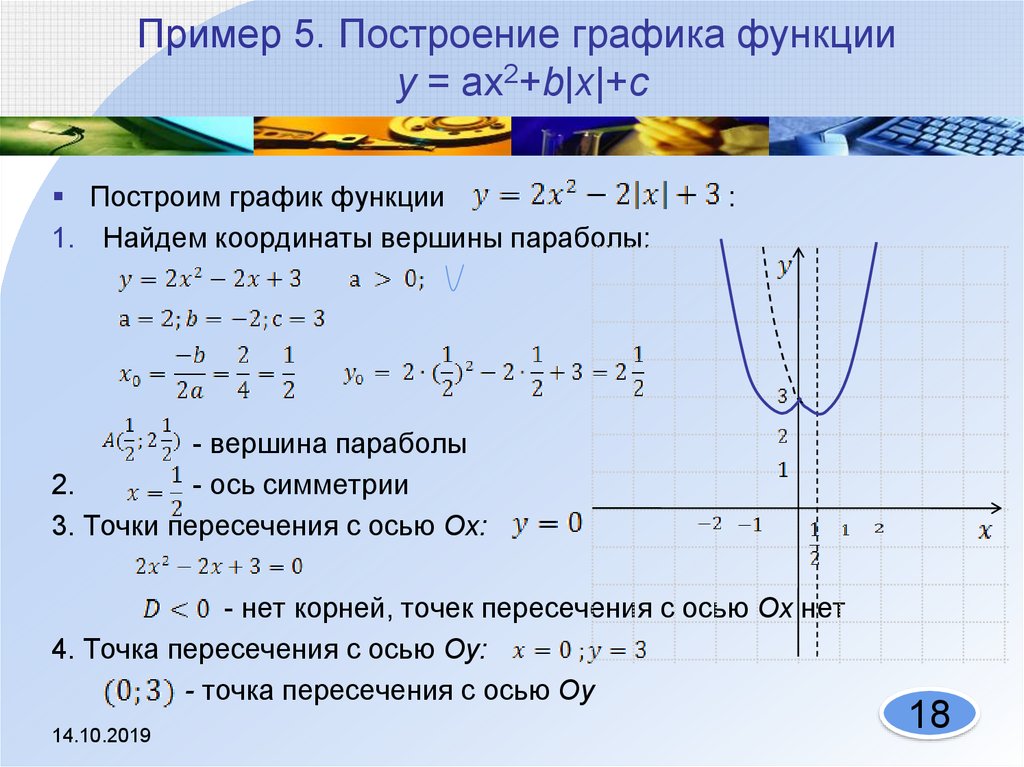 Предложите студентам выбрать для этого урока привычку сосредотачиваться на характере.
Предложите студентам выбрать для этого урока привычку сосредотачиваться на характере.

 При необходимости обратитесь к якорной таблице вопросов, которые мы можем задать во время языкового погружения (пример для справки для учителя) . Убедитесь, что учащиеся понимают, как использовать эти вопросы, отметив, что вопросы, подчеркнутые в опорной таблице, — это вопросы, которые учащиеся всегда должны задавать, когда они углубляются в предложение.
При необходимости обратитесь к якорной таблице вопросов, которые мы можем задать во время языкового погружения (пример для справки для учителя) . Убедитесь, что учащиеся понимают, как использовать эти вопросы, отметив, что вопросы, подчеркнутые в опорной таблице, — это вопросы, которые учащиеся всегда должны задавать, когда они углубляются в предложение.
 Извлеките другие примеры из Две дороги , написанные в прогрессивном аспекте, и поработайте со студентами, чтобы вывести общие «правила» для построения предложений в прогрессивном аспекте. Эти предложения могут включать:
Извлеките другие примеры из Две дороги , написанные в прогрессивном аспекте, и поработайте со студентами, чтобы вывести общие «правила» для построения предложений в прогрессивном аспекте. Эти предложения могут включать: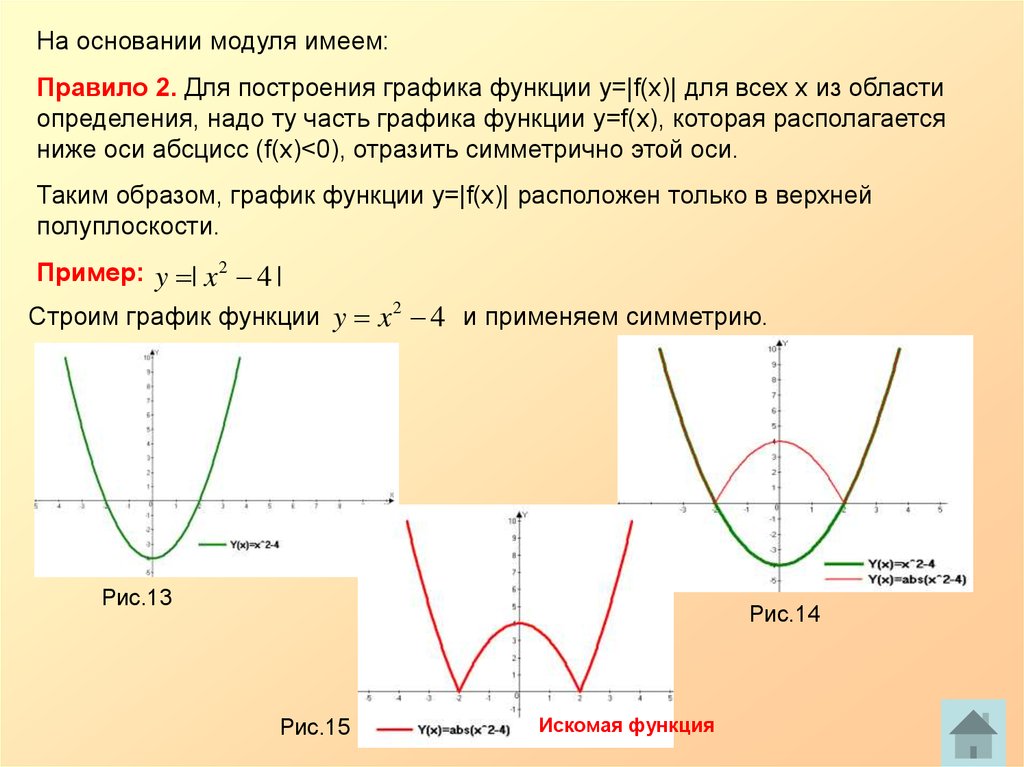

 06.ER.3.000SP.F.195 —
(Задайте другие вопросы в дополнение к включенному.)
06.ER.3.000SP.F.195 —
(Задайте другие вопросы в дополнение к включенному.)