Построить график функции системы онлайн: Построение графика функции онлайн

(1/n) () скобки | | скобки модуля: |x|

Содержание

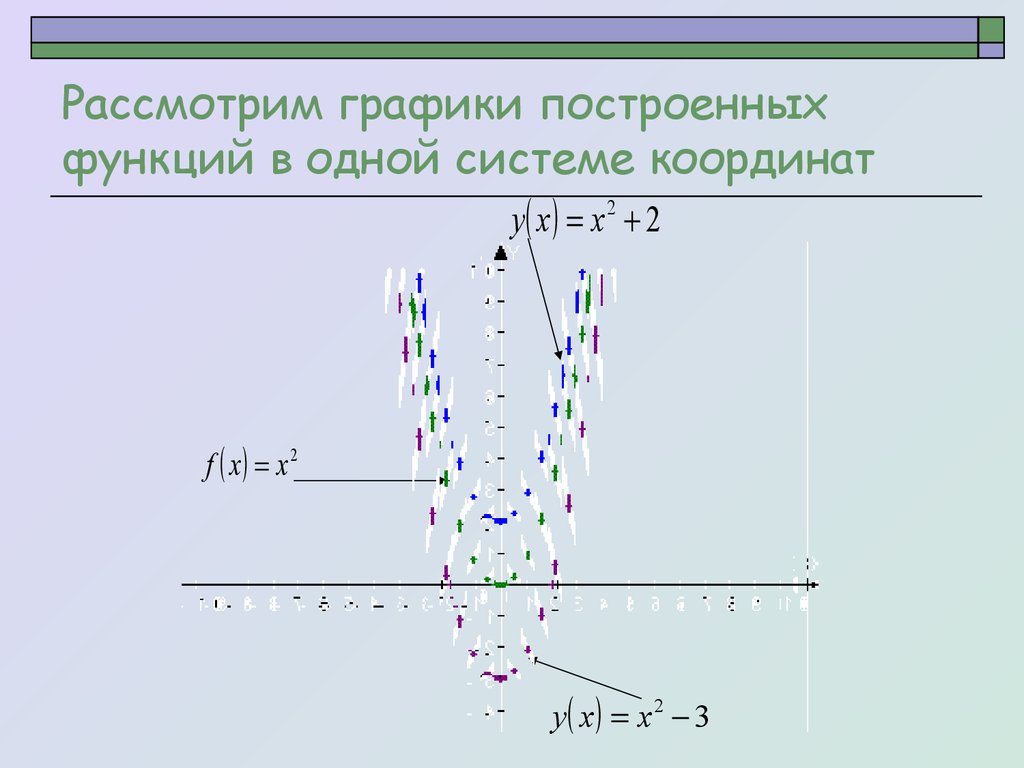
Список функций

Имя	Описание
`log2(x)`	логарифм по основанию 2 от x
`lg(x) или log10(x)`	логарифм по основанию 10 от x
`log(x;b)`	логарифм x по основанию b log(x;3)
`ln(x)`	натуральный логарифм (логарифм по основанию e (2. x	экспонента от х (e в степени x)
`sqrt(x)`	квадратный корень из x
`sign(x)`	функция знака: -1 если x<0, 1 если x>0 и 0 если x=0
Тригонометрические функции
`sin(x)`	синус х
`cos(x)`	косинус х
`tg(x)` или `tan(x)`	тангенс х
`ctg(x)` или `cot(x)`	котангенс х
`arcsin(x)` или `asin(x)`	арксинус х
`arccos(x)` или `acos(x)`	арккосинус х
`arctg(x)` или `atan(x)`	арктангенс х
`arcctg(x)` или `acot(x)`	арккотангенс х
`sinh(x)` или `sh(x)`	гиперболический синус х
`cosh(x)` или `ch(x)`	гиперболический косинус х
`tanh(x)` `th(x)`	гиперболический тангенс х
`coth(x)` или `cth(x)`	гиперболический котангенс х
`asinh(x)`	гиперболический арксинус х
`acosh(x)`	гиперболический арккосинус х
`atanh(x)`	гиперболический арктангенс х
`acoth(x)`	гиперболический арккотангенс х

Встроенные константы

Имя	Описание
`pi`	Пи = 3,14. ..
`e`	e = 2,71828… число Эйлера

График линейных уравнений — MathCracker.com

Инструкции: Используйте этот Linear Equation Grapher для создания графика любого предоставленного вами линейного уравнения, показывающего все шаги. Вам нужно указать линейное уравнение, которое вы хотите построить в форме ниже.

Подробнее об этом графическом редакторе линейных уравнений

Рисование линий — фундаментальная способность, и этот калькулятор поможет вам в этом. Вам необходимо начать с предоставления линейное уравнение, которое вы хотите построить.

Вы можете указать любое линейное уравнение явно, например, x + 3y = 2 или что-то, что не полностью упрощено, как x + 3y = 2/3 x.

Линии графика имеют так много применений, что приобретать их становится очень практичным навыком. Геометрически линии имеют очень простую интуицию, которая позволяет легко график, так как нам не нужно много информации, чтобы указать их.

Как построить график линейных уравнений?

Вы можете использовать этот графический калькулятор для построения линий. Если вы решите сделать это вручную, вы должны знать, что этот подход требует преамбулы, которая будет зависеть от тип предоставляемой информации.

Каковы шаги для построения графика?

Шаг 1: Определите тип предоставленной информации. У вас есть фактическое уравнение, у вас есть две точки, точка и наклон, наклон и y-пересечение? Четко оценить, что
Шаг 2: Независимо от предоставленной информации, используйте ее, чтобы найти две точки, через которые проходит линия. Для заданного уравнения найдите y, например, для x = 0 и x = 1. Для наклона и y-перехвата вы составить уравнение y = a + bx и найти две точки. Если у вас есть одна точка и наклон, определите y = y1 + b(x-x1) и подставьте его на x = 0
Шаг 3. Получив две точки, через которые проходит линия, используйте линейку, чтобы проследить линию, проходящую через них

Линии очень легко рисовать, просто вам нужно быть методичным и знать, какой тип информации у вас есть.

Даже если вы делаете это вручную, всегда приятно иметь удобный онлайн-калькулятор линейных графиков для проверки результатов.

Линии графика

Линии графика имеют множество применений. Например, вы можете решить систему уравнений, построив график соответствующие линии и увидеть, где они пересекаются.

Используя этот метод, когда прямые параллельны и не пересекаются, решений не будет.

Подобно тому, что произошло со сложением и вычитанием, деление дробей просто происходит от умножения дробей: Чтобы разделить две дроби, вы просто умножаете первого на обратную дробь второго (обратная дробь получается заменой числителя на знаменатель в дроби).

Другие применения линейных графиков

Линии или линейные графики действительно присутствуют повсюду. Линейные функции постоянно появляются в приложениях. в исчислении и оптимизации, поэтому они действительно полезно.

Пример: Linear Equation Grapher пример

Нарисуйте следующие уравнения: \(\frac{1}{2}x + \frac{7}{4}y = 0\)

Решение: Нам нужно работать со следующим уравнением:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Сначала работаем с константами:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Результат получается путем размещения (y) слева и (x) и константы справа:

\[\displaystyle \frac{7}{4}y = -\frac{1}{2}x \]

Затем процесс продолжается путем решения для \(y\), а затем путем деления обеих частей уравнения на \(\frac{7}{4}\). Получаем:

\[\ displaystyle y = — \ frac {\ frac {1} {2}} {\ frac {7} {4}} x \]

и после упрощения получается следующее.

\[\displaystyle y=-\frac{2}{7}x\]

Заключение : Мы делаем вывод, что уравнение линии в форме пересечения наклона, основанное на имеющихся данных, имеет вид \(\displaystyle y=-\frac{2}{7}x\) с наклон \(\displaystyle b = -\frac{2}{7}\) и y-пересечение \(\displaystyle n = 0\).

Таким образом, график представленной линии равен

Пример: пример графа линейных уравнений

Получите линию, которая представляет: \(\frac{2}{3}x + \frac{5}{4}y = — \frac{5}{6}x + 2\)

Решение: Мы получили следующее уравнение:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Работа с константами:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Теперь, подставив \(y\) в левую часть, а \(x\) и константу в правую, мы получим

\[\displaystyle \frac{5}{4}y = \left(\frac{-5}{6}-\frac{2}{3}\right)x +2\]

Теперь член, умножающий \(y\), равен \( \frac{5}{4} — 0 = \frac{5}{4}\), а также поскольку \( -\frac{5}{6 } — \frac{2}{3} = -\frac{3}{2}\), получается следующее

\[\displaystyle \frac{5}{4}y=-\frac{3}{2}x+2\]

Теперь, находя \(y\), разделив обе части уравнения на \(\frac{5}{4}\), получаем следующее

\[\ displaystyle y = — \ frac {\ frac {3} {2}} {\ frac {5} {4}} x + \ frac {2} {\ frac {5} {4}} \]

и упрощая окончательно получаем следующее

\[\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\]

Заключение : На основании предоставленных данных мы заключаем, что уравнение линии в форме наклона-пересечения имеет вид \(\displaystyle y=-\frac{6}{5}x+\frac{8}{5} \), с наклоном \(\displaystyle b = -\frac{6}{5}\) и пересечением по оси Y \(\displaystyle n = \frac{8}{5}\).

Линейный график

Другие линейные калькуляторы

Линии настолько важны, что заслуживают отдельного раздела в учебнике по математике. Вы можете вычислять линейные уравнения в различных формах, в зависимости от конкретные потребности.

Для определения линий в конечном итоге потребуются две точки, через которые проходит линия, которые можно указать прямо или косвенно.

Учебное пособие. Первый этап создания графической машины

Это упражнение и последующее домашнее задание предназначены для того, чтобы помочь учащимся на начальных этапах разработки графической утилиты с помощью App Inventor. Целью этого будет дать учащимся другой способ смотреть и понимать уравнения, функции и их графики, а также дать представление о программировании других графических утилит, таких как графический калькулятор. Студенты могут использовать его в течение года, добавляя функции по мере необходимости.

Разминка : Построение графика зависимости расстояния от времени. Это задание предназначено для того, чтобы напомнить учащимся о некоторых проблемах, связанных с графическим представлением данных. Студенты должны будут подумать о единицах измерения, о том, как измерять, как фиксировать данные относительно начала координат и набора осей. Это поднимет вопросы масштаба и, возможно, другие идеи.

Материалы : Секундомер (не обязательно, так как учащиеся могут быть неточным или игнорировать фактическое время здесь), наклейки, скотч, мешки с фасолью, бумага и карандаш для записи данных и нанесения точек через каждые две секунды. Можно также использовать систему CBL/CBR.

Процедура : Это может быть как научный эксперимент, так и хочет учитель. Можно либо генерировать данные, буквально идя/двигаясь по путь в течение заданного периода времени или просто выбор каждой парой некоторых значений y, которые соответствуют некоторым заданным значениям x. С минимальными начальными инструкциями учащиеся будут работать в парах над построением графика зависимости расстояния от времени. Для сбора данных они должны идти с места и они должны вычислить расстояние. Учащиеся будут вычислять расстояния в дискретные моменты времени, бросая боб. пакет/наклейка маленькой наклейки на пол и т. д. каждые две секунды в течение 20 секунд.

Возможные проблемы: контрольная точка (начало), набор осей для расстояние (пифагорейское), Как заставить калькулятор просто построить ряд точек по формуле или уравнению. Студенты должны думать не только о том, как заставить компьютер делать это должным образом, но они должны думать о что указывает на график, как создать или смоделировать непрерывность, проблемы масштабирования в соответствии с требованиями к экрану конкретного устройства.

Основной вопрос: Как калькулятор строит график?

Классная и последующая деятельность ведут к построению плоттера для построения линейного графика. Через год, когда учащиеся будут использовать этот шаблон для построения функций, позволяющих их для построения различных функций в течение года. Конструкция каждого функциональный плоттер дал бы им представление о том, как должен работать калькулятор, чтобы быть умеет составлять уравнения. Это также дает им практический опыт использования функции и процедуры в программировании. В этом есть потенциальная выгода учащиеся получают дополнительное понимание того, как функция принимает ввод значение и должна возвращать значение, в то время как процедура принимает запрос и выполняет какая-то операция, которая может возвращать или не возвращать значение. Предполагается, что учащийся имеет начальный уровень опыта работы с App Inventor и знаком с процедурами, функциями и базовой настройкой.

Создание нашего приложения:

Давайте начнем новый проект под названием functionGrapher. Ваш пользователь интерфейс позволит вам добавить горизонтальное расположение с четырьмя текстовыми полями и три метки, холст и кнопка ниже, как показано здесь.

Текстовые поля и метки должны быть расположены, как указано выше, с текстовые поля имеют ширину 30 пикселей, а метки — 20 пикселей. Также, установите флажки только для чисел во всех четырех текстовых полях.

Как вы могли видеть или не видеть в своей первоначальной деятельности, нам нужна система отсчета, чтобы нарисовать наш график, т.е. набор осей. Я собираюсь используйте процедуру, и я использовал высоту и ширину холста для управления высота и ширина осей, но они, безусловно, могут быть жестко запрограммированы.

Начнем с простой линейной функции. Мы можем либо установить все текстовые поля на 1, или инициализируйте их на единицу, или установите их на единицу в пользовательский интерфейс.

Опять же, я собираюсь использовать процедуру, которая будет называться при нажатии кнопки functionGraphButton. Предоставление учащимся вышеуказанного надеюсь, некоторые из них возразят, что вы все, возможно, думаю прямо сейчас, но пока подыграйте мне, и мы посмотрим, как это выглядит. Итак, теперь пришло время настроить нашу functionGraphButton.

Когда кнопка functionGraphButton нажата, нам нужно несколько вещи, чтобы случиться. Нам нужно, чтобы холст был четким, нам нужно вызвать оси, чтобы тогда нарисуйся.

Мы создали переменные для коэффициента x, yкоэффициент, xpower и ypower так, чтобы было куда добавить добавленные значения в эти ящики для хранения. По мере того, как программа расширяется и становится более сложной, нам потребуются разные значения для этих переменных. Первый раз по программе со студентами эти значения могут быть предварительно заданы либо в пользовательском интерфейсе, либо в приведенном выше вкладки. Мы также можем игнорировать if-else для прямо сейчас и просто используйте диапазон for с линейным вызовом draw. Можете ли вы предсказать, как это будет выглядеть?

Это то, что вы предсказывали?

Здесь представлена первоначальная проблема, с которой вы, вероятно, столкнулись. уже задумался. Наше первое преобразование должно быть сосредоточено на нашем графике. и использовать значения координат, которые будут отображаться на наших осях. Это может быть трудно изначально закодировано, но в конечном итоге мы можем использовать функцию, которая вводит значения x и позволяет корректно выводить значения y на холст, чтобы функция выглядит так, как если бы она была на оси x-y. Наш графограф также ограничен линейными графиками.

Задание в классе будет состоять в том, чтобы создать функцию или функции преобразования, чтобы наш линейный график выглядел так, как должен. Мы хотим, чтобы он включал полный домен отрицательных и положительных значений, чтобы линия шла с одной стороны холста на другую. Результат должен выглядеть примерно так:

В классе учащиеся должны представить график, который выглядит следующим образом:

Домашнее задание:

график квадратичной функции, а также линейной функции. 2.

Вы должны использовать существующий код для линейной функции и добавить квадратичную функцию. Если вам не удалось правильно преобразовать сегодня в классе, посмотрите на код выше. Если возможно, используйте этот же коэффициент преобразования при написании кода для этого задания. Вам не разрешено использовать функцию экспоненты, содержащуюся в математических командах, но вы должны использовать фундаментальную идею того, как работают степени, чтобы написать свой код. Вам не нужно добавлять ни отдельную кнопку, ни какие-либо другие переменные. Убедитесь, что ваш графограф может отображать как линейные, так и квадратичные уравнения, а не только одно или другое.

Ваша первоначальная попытка может выглядеть примерно так.

После преобразования квадратичного уравнения в график, пожалуйста, оцените свои результаты.

Чем вы довольны?

Что бы вы хотели улучшить?

Приходите на занятия, готовые представить идеи по улучшению ваших графиков. 2. Приложение должно соответствующим образом реагировать на значения, указанные в текстовых полях коэффициента и мощности. 10% присуждается за вдумчивый и интересный анализ программы (это значит хорошие вопросы и наблюдения!). Последние 10% будут присуждены за продуманные, творческие идеи, которые помогут улучшить программу. Дополнительные баллы будут начисляться за программу, которая может:

1) реагировать на нажатие кнопки «Нажмите здесь» без значений в текстовых полях «степень x» или «коэффициент x».

2) Создайте отвлечение, чтобы занять пользователя, или сообщение, которое информирует пользователя, пока приложение выполняет данную команду.

Упражнения на расширение: это базовое упражнение может быть расширено настолько, насколько вам этого захочется. Учащиеся могут комбинировать функцию определения местоположения с построением графиков, чтобы учащиеся могли создавать графики своих позиций за заданный период времени. Они могли бы определить это для отношений времени/расстояния или посмотреть на разницу между общим пройденным расстоянием и расстоянием от начала. Первый пример потенциально создает функцию «один к одному», а другой (потенциально) создает функцию «многие к одному». Класс может смотреть на обратные функции. Они могли бы проанализировать эту идею в своем программировании, когда они строят свои функции, либо переключая координаты, либо отменяя исходную функцию с помощью операций. Возможно, было бы проще всего даже создать какое-то отражение над линией y = x. Учащиеся могут посмотреть на отношения, которые не являются функциями, установив для степени y значение >1. Можно добавить тест вертикальной линии, чтобы дать визуальную проверку того, является ли данное уравнение функцией. Студенты также должны подумать, что может означать отрицательное значение x в контексте графика и их проблемы. Что произойдет, если мы также изменим высоту, например, что, если кто-то заберется на стол? Что происходит с расстоянием в самолете? Что происходит с общим расстоянием? Есть много потенциальных вопросов, которые могут возникнуть в связи с обдумыванием и реализацией этого проекта.