Постройте поле корреляции и сформулируйте гипотезу о форме связи
Задание
- Постройте поле корреляции и сформулируйте гипотезу о форме связи.
- Рассчитайте параметры уравнений линейной, степенной и гиперболической парной регрессии.
- Оцените тесноту связи с помощью показателей корреляции и детерминации.
- Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оцените с помощью средней ошибки аппроксимации качество уравнений.
- Оцените с помощью F— критерии Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.
- Рассчитайте
прогнозное значение результата, если
прогнозное значение фактора увеличится
на 10% от его среднего уровня.
- Оцените полученные результаты, выводы оформите в аналитической записке.
- Построим поле корреляции по исходным данным
| № | X | Y |
| 1 | 7,5 | 286 |
| 2 | 8,4 | 300 |
| 3 | 6,2 | 258 |
| 4 | 6,4 | 262 |
| 5 | 5,1 | 237 |
| 6 | 8,4 | 300 |
| 7 | 9,0 | 311 |
| 8 | 5,4 | 243 |
| 9 | 7,3 | 279 |
| 10 | 8,2 | 296 |
| 11 | 8,6 | 303 |
Построив
поле корреляции, можно выдвинуть
гипотезу о том, что связь между
фактором и результатом описывается линейной функцией.
2. Рассчитаем параметры уравнений:
а)
линейной регрессии (y=a+bx)
- 18,97 140,66 0,99
0,9984 0,4968 0,19314
- 75,111 0,252 1,16337
- 75,299 1,87
Все расчеты были произведены с помощью Excel:
| X | Y | XY | X2 | Y2 | (x-xср)2 | yрас | (yрас-yср)2 | (у-уср)2 | (y-рас)2 | |y-рас|/y | |
| 1 | 7,5 | 286 | 2145 | 56,25 | 81796 | 0,181818 | 283 | 3,45038 | 6,454545 | 3,00417 | 0,010504 |
| 2 | 8,4 | 300 | 2520 | 70,56 | 90000 | 1,081818 | 300,1 | 20,5297 | 20,45455 | -0,0752 | 0,000251 |
| 3 | 6,2 | 258 | 1599,6 | 38,44 | 66564 | -1,118182 | 258,3 | -21,2198 | -21,5455 | -0,3256 | 0,001262 |
| 4 | 6,4 | 262 | 1676,8 | 40,96 | 68644 | -0,918182 | 262,1 | -17,4244 | -17,5455 | -0,1211 | 0,000462 |
| 5 | 5,1 | 237 | 1208,7 | 26,01 | 56169 | -2,218182 | 237,5 | -42,0946 | -42,5455 | -0,4509 | 0,001902 |
| 6 | 8,4 | 300 | 2520 | 70,56 | 90000 | 1,081818 | 300,1 | 20,5297 | 20,45455 | -0,0752 | 0,000251 |
| 7 | 9 | 311 | 2799 | 81 | 96721 | 1,681818 | 311,5 | 31,916 | 31,45455 | -0,4614 | 0,001484 |
| 8 | 5,4 | 243 | 1312,2 | 29,16 | 59049 | -1,918182 | 243,1 | -36,4015 | -36,5455 | -0,144 | 0,000593 |
| 9 | 7,3 | 279 | 2036,7 | 53,29 | 77841 | -0,018182 | 279,2 | -0,34504 | -0,54545 | -0,2004 | 0,000718 |
| 10 | 8,2 | 296 | 2427,2 | 67,24 | 87616 | 0,881818 | 296,3 | 16,7343 | 16,45455 | -0,2798 | 0,000945 |
| 11 | 8,6 | 303 | 2605,8 | 73,96 | 91809 | 1,281818 | 303,9 | 24,3252 | 23,45455 | -0,8706 | 0,002873 |
| Сумма Сумкв | 80,5 | 3075 | 22851 | 607,43 | 9E+05 | 18,31636 | 9E+05 | 6596,26 | 6606,727 | 10,4704 | 0,021245 |
Ср. знач. | 7,32 | 280 | 2077,4 | 55,221 | 78746 | 0,001931 |
| b | R2 | rxy | S2 | S2b | S2a | Sa | Sb | ta | tb | fнабл | Э | |
| 18,98 | 140,7 | 0,9984 | 0,9992 | 1,163 | 0,064 | 3,507 | 1,873 | 0,252 | 75,11 | 75,3 | 5669,9 | 0,497 |
| tкр(0,05;9) | Fкрит | t*Sa | t*Sb | дов. интервал(а) | дов.интервал(b) | A | ||||
| 2,262 | 5,12 | 4,24 | 4,7827 | 136,43 | <140,67< | 144,9041 | 18,41 | <19,97< | 19,54715 | 0,19314 |
Данные параметры можно было определить по функциям («Регрессия»):
| Регрессионная статистика | ||||||
| Множественный R | 0,999207284 | |||||
| R-квадрат | 0,998415196 | |||||
| Нормированный R-квадрат | 0,998239106 | |||||
| Стандартная ошибка | 1,078598333 | |||||
| Наблюдения | 11 | |||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1 | 6596,256903 | 6596,256903 | 5669,9349 | 6,50057E-14 | |
| Остаток | 9 | 10,47036927 | 1,163374363 | |||
| Итого | 10 | 6606,727273 | ||||
| Коэффициенты | Станд. ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 140,6678082 | 1,872802119 | 75,11087626 | 6,6483E-14 | 136,4312355 | 144,9043809 |
| X | 18,97706968 | 0,252022965 | 75,29897012 | 6,5006E-14 | 18,40695413 | 19,54718524 |
Уравнение
линейной регрессии:
Выводы:
Линейный коэффициент парной корреляции 0,9992
означает, что связь между фактором и результатом
прямая, очень тесная. Средняя ошибка аппроксимации
показывает, что расчетные значения отклоняются
от фактических на 0,193%. Так как полученное
фактическое значение (F=5669,9) больше, чем Fтабл = 5,12,
то уравнение статистически значимо.
Также
статистически значимы и коэффициенты
регрессии, так как по абсолютному значению
(ta=75,11 и tb=75,29) они превышают
табличное значение Стюдента t=2,262.
б) степенной регрессии
Логарифмируем уравнение и получим уравнение линейной регрессии: . Заменяя значения фактора и результата на логарифмированные, рассчитаем параметры: b=0,479 c=4,68 отсюда Уравнение регрессии примет вид:
Рассчитаем параметры качества уравнения регрессии:
| № п/п | X | Y | lnY | lnX | lnY*lnX | (lnX)2 | Yрас | A |
| 1 | 7,5 | 286 | 5,65599 | 2,014903 | 11,3963 | 4,0598342 | 284,021 | 0,00692083 |
| 2 | 8,4 | 300 | 5,70378 | 2,128232 | 12,139 | 4,5293702 | 299,898 | 0,000338706 |
| 3 | 6,2 | 258 | 5,55296 | 1,824549 | 10,1316 | 3,3289801 | 259,22 | 0,004730343 |
| 4 | 6,4 | 262 | 5,56834 | 1,856298 | 10,3365 | 3,4458422 | 263,201 | 0,004583846 |
| 5 | 5,1 | 237 | 5,46806 | 1,629241 | 8,90879 | 2,6544247 | 236,024 | 0,004119373 |
| 6 | 8,4 | 300 | 5,70378 | 2,128232 | 12,139 | 4,5293702 | 299,898 | 0,000338706 |
| 7 | 9 | 311 | 5,73979 | 2,197225 | 12,6116 | 4,8277958 | 309,996 | 0,003227997 |
| 8 | 5,4 | 243 | 5,49306 | 1,686399 | 9,26349 | 2,8439414 | 242,589 | 0,001692205 |
| 9 | 7,3 | 279 | 5,63121 | 1,987874 | 11,1941 | 3,9516444 | 280,36 | 0,004873447 |
| 10 | 8,2 | 296 | 5,69036 | 2,104134 | 11,9733 | 4,4273805 | 296,45 | 0,001518793 |
| 11 | 8,6 | 303 | 5,71373 | 2,151762 | 12,2946 | 4,6300806 | 303,305 | 0,001005847 |
| Сумма | 80,5 | 3075 | 0,033350091 | |||||
Ср. знач. | 7,32 | 280 | 0,303 |
| b | c | a | Э |
| 0,479 | 4,68 | 107,97 | 0,479 |
Параметры, определенные по функциям («Регрессия»):
| ВЫВОД ИТОГОВ | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,99916262 | |||||
| R-квадрат | 0,99832593 | |||||
Норм. R-квадрат | 0,99813992 | |||||
| Станд. ошибка | 0,00406828 | |||||
| Наблюдения | 11 | |||||
| Дисперс. анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1 | 0,08883079 | 0,08883 | 5367,124 | 8,3E-14 | |
| Остаток | 9 | 0,00014895 | 1,7E-05 | |||
| Итого | 10 | 0,08897975 | ||||
Коэфф. | Станд. ошибка | t-стат-ка | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 4,68191087 | 0,01298829 | 360,472 | 4,95E-20 | 4,65253 | 4,711292 |
| lnX | 0,47999137 | 0,00655183 | 73,2607 | 8,32E-14 | 0,46517 | 0,494812 |
| exp | 107,976204 | |||||
Задача 1. Построить поле корреляции и сформулировать гипотезу о форме связи.
- Главная страница 🏠
- 👉 Эконометрика 👈
- Решение практических задач по курсу: «Эконометрика»
- Задача 1. Построить поле корреляции и сформулировать гипотезу о форме связи.
org/ListItem»>
📚 БиблиотекаНужна помощь в написании работы?
Узнать стоимость
Гипотеза о форме связи: Визуальный анализ полученного графика показывает, что точки поля корреляции располагаются вдоль некоторой воображаемой прямой линии, но не очень плотно, рассеиваясь около неё. Можно предположить, что связь прожиточного минимума и среднего размера назначенных ежемесячных пенсий обратная, не очень тесная.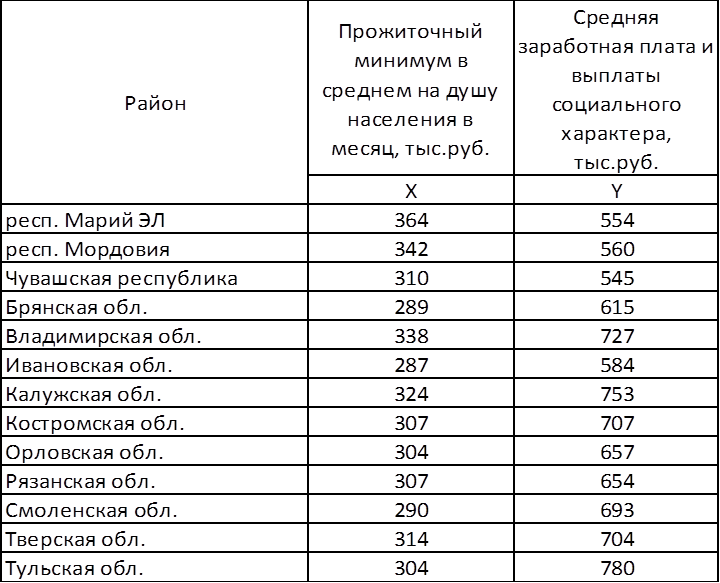
Анализируя расположение точек поля корреляции, предполагаем, что связь между признаками х и у может быть нелинейной вида:.
Поможем написать любую работу на аналогичную тему
Реферат
Задача 1. Построить поле корреляции и сформулировать гипотезу о форме связи.
От 250 руб
Контрольная работа
Задача 1. Построить поле корреляции и сформулировать гипотезу о форме связи.
От 250 руб
Курсовая работа
Задача 1. Построить поле корреляции и сформулировать гипотезу о форме связи.
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Поделись с друзьями
- Содержание
- Меню
Задача 1.
Исходные данныеЗадача 1. Построить поле корреляции и сформулировать гипотезу о форме связи.
Задача 1. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
Задача 1. Оценка тесноты связи с помощью показателей корреляции и детерминации
Задача 1. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
Задача 1.
Оценка качества уравнений с помощью средней ошибки аппроксимации.Задача 1. Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования.
Задача 1. Рассчитаем прогнозное значение результата по линейному уравнению регрессии
Задача 2. Исходные данные
Добавить в избранное (необходима авторизация)
Как написать гипотезу для корреляции
••• Thinkstock/Comstock/Getty Images
Обновлено 25 апреля 2017 г. В то время как некоторые гипотезы предсказывают причинно-следственную связь между двумя переменными, другие гипотезы предсказывают корреляцию между ними.
Согласно базе знаний по методам исследования, корреляция — это одно число, описывающее взаимосвязь между двумя переменными. Если вы не предсказываете причинно-следственную связь или не можете ее объективно измерить, четко укажите в своей гипотезе, что вы просто прогнозируете корреляцию.
Тщательно изучите тему, прежде чем выдвигать гипотезу. Без адекватных знаний о предмете вы не сможете решить, писать ли гипотезу о корреляции или причинно-следственной связи. Прочтите результаты подобных экспериментов, прежде чем выдвигать собственную гипотезу.
Определите независимую переменную и зависимую переменную. Ваша гипотеза будет касаться того, что происходит с зависимой переменной при изменении независимой переменной. При корреляции две переменные изменяются одновременно в значительном числе случаев. Однако это не означает, что изменение независимой переменной вызывает изменение зависимой переменной.
Проведите эксперимент, чтобы проверить свою гипотезу. В корреляционном эксперименте вы должны быть в состоянии измерить точное соотношение между двумя переменными.
Это означает, что вам нужно будет выяснить, как часто происходит изменение обеих переменных с точки зрения определенного процента.
Установить требования эксперимента в отношении статистической значимости. Проинструктируйте читателей, как часто переменные должны коррелировать, чтобы достичь достаточно высокого уровня статистической значимости. Это число будет значительно варьироваться в зависимости от области. Например, в высокотехнологичном научном исследовании переменные могут нуждаться в корреляции 98 процентов времени; но в социологическом исследовании может быть достаточно 90-процентной корреляции. Посмотрите другие исследования в вашей конкретной области, чтобы определить требования к статистической значимости.
Сформулируйте нулевую гипотезу. Нулевая гипотеза дает точное значение, которое подразумевает отсутствие корреляции между двумя переменными. Если результаты показывают процент, равный или меньший, чем значение нулевой гипотезы, то корреляция переменных не доказана.
Запишите и подведите итоги вашего эксперимента. Укажите, соответствовал ли эксперимент минимальным требованиям вашей гипотезы как в процентном отношении, так и в отношении значимости.
Связанные статьи
Ссылки
- Университет Новой Англии; Этапы проверки гипотез на корреляцию; 2000
- База знаний по методам исследования; корреляция; Уильям М.К. Трохим; 2006
- Друзья по науке; Гипотеза
Об авторе
Брайан Гэбриел с 2009 года пишет и ведет блог, сотрудничает с различными интернет-публикациями. Он получил степень бакалавра искусств по истории в Университете Уитворта.
Photo Credits
Thinkstock/Comstock/Getty Images
Тест гипотез на корреляцию: объяснение и пример гипотеза для корреляционного теста.
Что такое проверка гипотезы для коэффициента корреляции?
При наличии выборки двумерных данных (данных, включающих две переменные) можно рассчитать, насколько линейно коррелированы данные, используя коэффициент корреляции.
Коэффициент корреляции момента продукта (PMCC) описывает степень, в которой одна переменная коррелирует с другой. Другими словами, сила корреляции между двумя переменными. PMCC для выборки данных обозначается как r , тогда как PMCC для совокупности обозначается как ρ.
PMCC ограничен значениями от -1 до 1 (включительно).
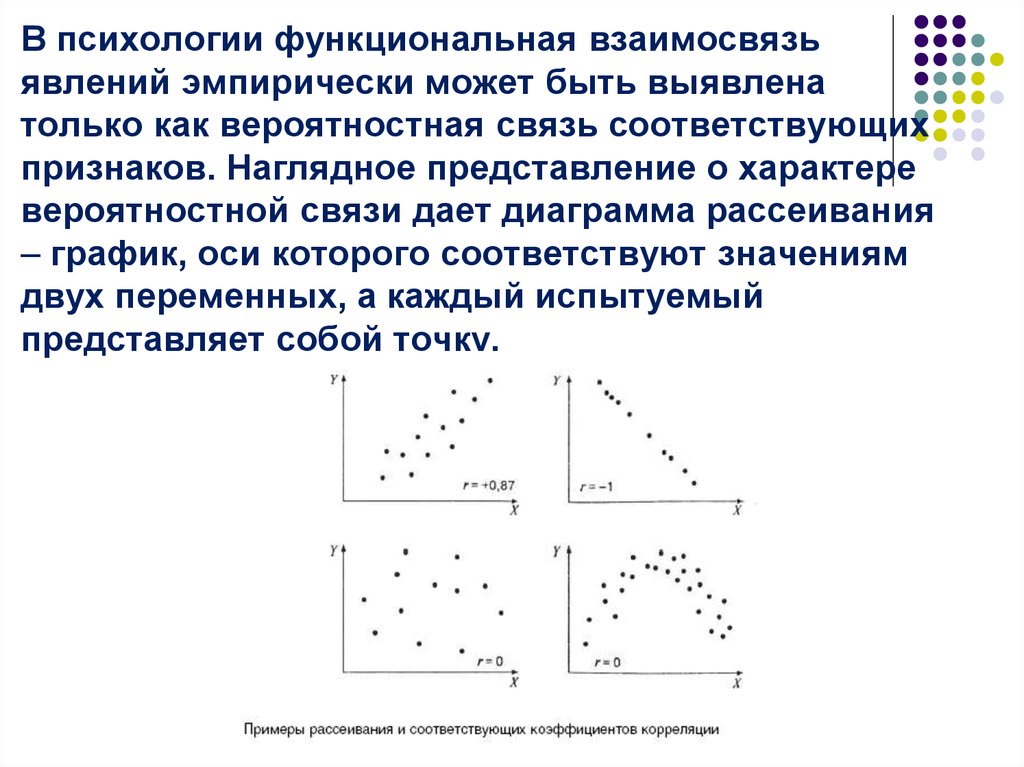
Если существует совершенная положительная линейная корреляция. Все точки лежат на прямой с положительным градиентом, и чем выше одна из переменных, тем выше другая.
Если нет линейной корреляции между переменными.
При наличии идеальной отрицательной линейной корреляции. Все точки лежат на прямой с отрицательным градиентом, и чем выше одна из переменных, тем ниже другая.
Корреляция не эквивалентна причинно-следственной связи, но PMCC, близкий к 1 или -1, может указывать на более высокую вероятность того, что две переменные связаны.
Двумерные данные без корреляции, положительной корреляции и отрицательной корреляции
PMCC должна быть рассчитана с помощью графического калькулятора путем нахождения линии регрессии y на x и, следовательно, нахождения r (это значение автоматически рассчитывается калькулятором) или с помощью формулы, которая находится в формуле буклет.
Чем ближе r к 1 или -1, тем сильнее корреляция между переменными и, следовательно, тем теснее связаны переменные. Вы должны иметь возможность проводить проверку гипотез на выборке двумерных данных, чтобы определить, можем ли мы установить линейную зависимость для всей совокупности. Вычисляя PMCC и сравнивая его с критическим значением, можно определить вероятность существования линейной зависимости.
Что такое проверка гипотезы об отрицательной корреляции?
Чтобы провести проверку гипотезы, необходимо понять ряд ключевых слов:
Нулевая гипотеза ( ) : гипотеза считается правильной, пока не доказано обратное
Альтернативная гипотеза ( ) : сделанный вывод если отвергнут.
Проверка гипотезы: математическая процедура проверки значения параметра совокупности, предложенного нулевой гипотезой, по сравнению с альтернативной гипотезой.
Статистика теста: рассчитывается по выборке и проверяется в таблицах кумулятивных вероятностей или с использованием нормального распределения в качестве последней части теста значимости.
Критическая область: диапазон значений, который приводит к отклонению нулевой гипотезы.
Уровень значимости: фактический уровень значимости — это вероятность отклонения, когда это действительно так.
Нулевая гипотеза также известна как «рабочая гипотеза». Это то, что мы считаем верным для целей теста или до тех пор, пока не будет доказано обратное.
Альтернативная гипотеза — это вывод, сделанный в случае отклонения нулевой гипотезы. Он также определяет, является ли тест односторонним или двусторонним.
Односторонний тест допускает возможность воздействия в одном направлении, а двусторонний тест допускает возможность воздействия в двух направлениях, другими словами, как в положительном, так и в отрицательном направлениях. Метод: Необходимо выполнить ряд шагов, чтобы определить наличие линейной зависимости между двумя переменными. 1 . Запишите нулевую и альтернативную гипотезы ().
Нулевая гипотеза всегда, в то время как альтернативная гипотеза зависит от того, что задано в вопросе. Обе гипотезы должны быть выражены только символами (не словами).
2 . С помощью калькулятора вычислите значение PMCC выборочных данных, r .
3 . Используйте уровень значимости и размер выборки, чтобы определить критическое значение. Это можно найти в таблице PMCC в буклете с формулами.
4 . Возьмите абсолютное значение PMCC и r и сравните их с критическим значением. Если абсолютное значение больше критического значения, нулевая гипотеза должна быть отвергнута. В противном случае следует принять нулевую гипотезу.
5 . Напишите полный вывод в контексте вопроса. Вывод должен быть изложен полностью: как статистическим языком, так и словами, отражающими контекст вопроса. Отрицательная корреляция означает, что альтернативная гипотеза отвергнута: отсутствие одной переменной коррелирует с более сильным присутствием другой переменной, тогда как при положительной корреляции присутствие одной переменной коррелирует с присутствием другой.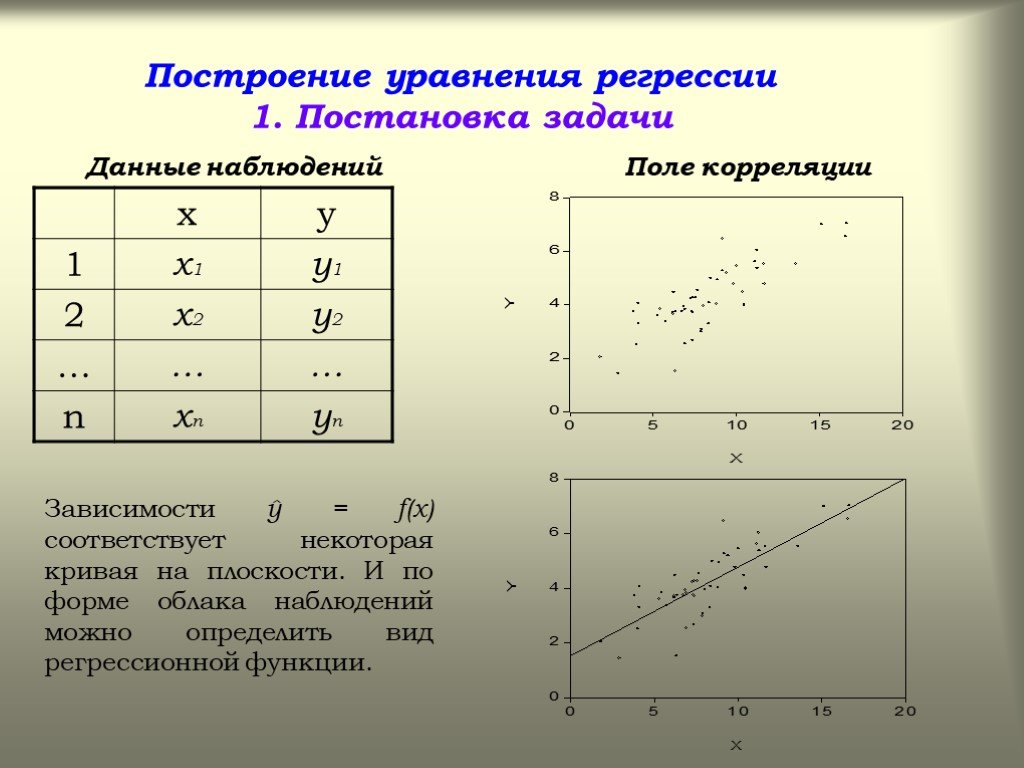
Как интерпретировать результаты, основанные на нулевой гипотезе
На основании наблюдаемых результатов (тестовой статистики) необходимо принять решение, определяющее, отклонять нулевую гипотезу или нет.
Изображение: Repapetilto CC BY-SA 3.0,
Двусторонний тест применяется к нормальному распределению. Изображение: общественное достояние
И односторонний, и двусторонний тест показаны на уровне значимости 5%. Однако 5% распределяются как в положительную, так и в отрицательную сторону в двустороннем тесте и только в положительную сторону в одностороннем тесте.
Из нулевой гипотезы результат может лежать где угодно на графике. Если наблюдаемый результат лежит в заштрихованной области, статистика теста значима на уровне 5%, другими словами, мы отвергаем. Следовательно, на самом деле может быть правдой, но все равно отвергается. Следовательно, уровень значимости 5% — это вероятность, которая отвергается, даже если она верна, другими словами, вероятность, которая отвергается неправильно.
Когда отвергается, (альтернативная гипотеза) используется для написания заключения.
Мы можем определить нулевую и альтернативную гипотезы для односторонних и двусторонних тестов:
Для одностороннего теста:
Для двустороннего теста:
289 Давайте рассмотрим пример проверки корреляции.
12 студентов сдали два экзамена по биологии: теоретический и практический. Результаты приведены в таблице.
Score in theoretical test, t | 5 | 9 | 7 | 11 | 20 | 4 | 6 | 17 | 12 | 10 | 15 | 16 | |||||||||
. Стоимость практического теста, . 6 8 9 13 20 9 8 17 14 8 0190 18 |
0053 p а) Найдите коэффициент корреляции момента продукта для этих данных с точностью до 3 значащих цифр.
b) Учитель утверждает, что учащиеся, которые хорошо справляются с теоретическим тестом, как правило, хорошо справляются с практическим тестом.
Проверьте это утверждение на уровне значимости 0,05, четко изложив свои гипотезы.
а) С помощью калькулятора находим ПМКЦ (вносим данные в два списка и вычисляем линию регрессии. появится ПМКК). r = от 0,935 до 3 знаков. цифры
б) Мы проверяем наличие положительной корреляции, поскольку утверждается, что более высокий балл в теоретическом тесте связан с более высоким баллом в практическом тесте. Теперь мы будем использовать пять шагов, которые мы рассмотрели ранее.
1. Сформулируйте нулевую и альтернативную гипотезы. : ρ = 0 и : ρ > 0
2. Рассчитайте PMCC. Из части а) р = 0,935
3. Определите критическое значение исходя из размера выборки и уровня значимости. Размер выборки n равен 12. Уровень значимости 5%. Гипотеза односторонняя, поскольку мы проверяем только положительную корреляцию. Используя таблицу из брошюры с формулами, показано, что критическое значение равно cv = 0,4973
4.
Абсолютное значение PMCC равно 0,935, что больше, чем 0,4973. Поскольку PMCC больше критического значения на уровне значимости 5%, мы можем сделать вывод.
5. Поскольку PMCC больше критического значения, мы отклоняем нулевую гипотезу. Мы можем заключить, что имеются существенные доказательства в поддержку утверждения о том, что учащиеся, которые хорошо справляются с тестом по теоретической биологии, также, как правило, хорошо справляются с тестом по практической биологии.
Давайте посмотрим на второй пример.
Четырехгранный кубик (четыре грани) бросают 40 раз и наблюдают 6 «единиц». Есть ли какие-либо доказательства на уровне 10%, что вероятность получения 1 балла меньше четверти?
Ожидаемое среднее значение равно 10 . Вопрос спрашивает, является ли наблюдаемый результат (критерий статистики 6 необычно низким.
Теперь мы повторяем ту же серию шагов.
1. Сформулируем нулевую и альтернативную гипотезы. : ρ = 0 и : ρ <0,25
2.
Мы не можем рассчитать PMCC, так как нам даны данные только о частоте «единиц»
3. Требуется односторонний тест ( ρ < 0,25) при 10% уровне значимости. Мы можем преобразовать это в биномиальное распределение, в котором X — это количество «единиц», поэтому мы затем используем кумулятивные биномиальные таблицы. Наблюдаемое значение X = 6. К .
4. Поскольку 0,0962, или 9,62% <10%, наблюдаемый результат лежит в критической области.
5. Отклоняем и принимаем альтернативную гипотезу. Мы заключаем, что есть доказательства того, что вероятность выпадения единицы меньше 9.0003
Проверка гипотезы на корреляцию – основные выводы
- Коэффициент корреляции момента продукта (PMCC), или r , является мерой того, насколько сильно связаны две переменные. Он находится в диапазоне от -1 до 1, что указывает на силу корреляции.
- Чем ближе r к 1 или -1, тем сильнее корреляция (положительная или отрицательная) между двумя переменными.
