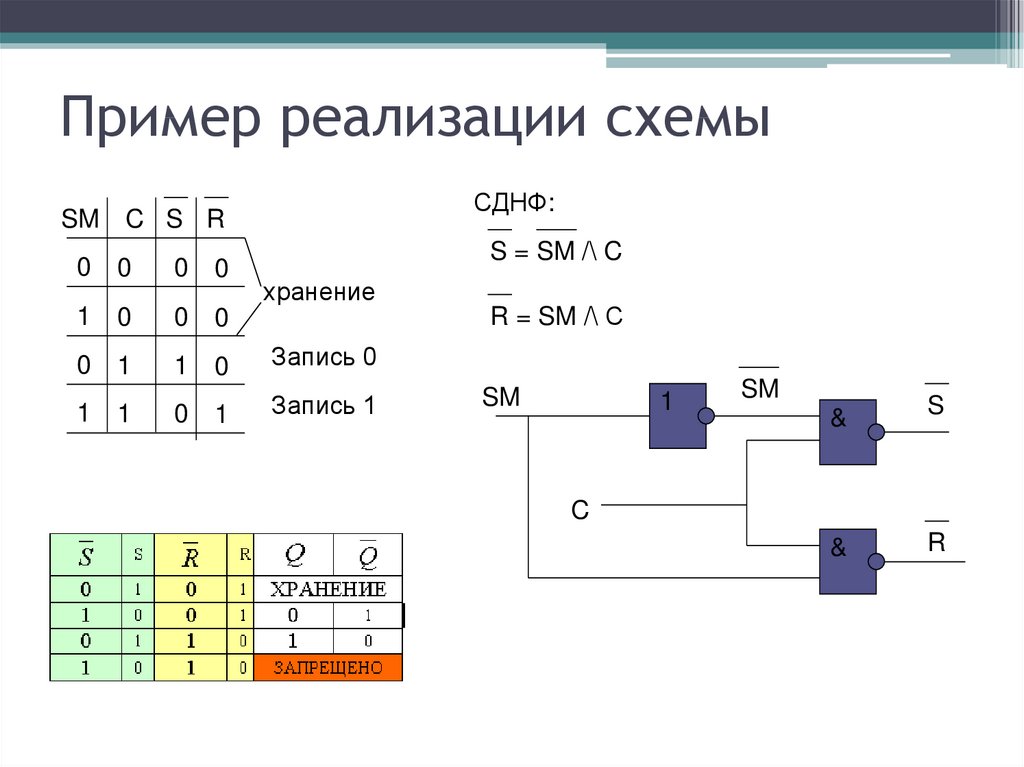
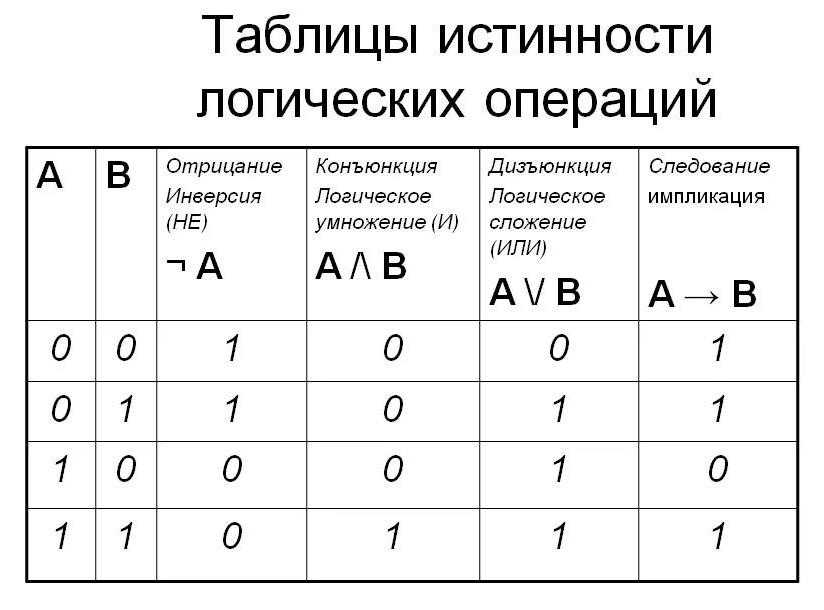
что это, построение по таблице истинности
Что такое СДНФ
Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).
Определение
СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».
ДНФ выглядит следующим образом:
\((A\;\wedge\;\overline B\;\wedge\;C)\;\vee\;(B\;\wedge\;C)\)
СДНФ обладает некоторыми определенными свойствами:
- включает различные элементарные конъюнкции;
- все логические слагаемые формулы содержат все переменные, которые входят в функцию F;
- ни в одном логическом слагаемом не содержится переменная и её отрицание.

К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.
Примечание
При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.
Что такое СКНФ
Определение
СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.
КНФ имеет вид:
\((A\;\vee\;\overline B\;\vee\;C)\;\wedge\;(A\;\vee\;C)\)
Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:
- в ней отсутствуют одинаковые элементарные дизъюнкции;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную нормальную функцию такого типа.

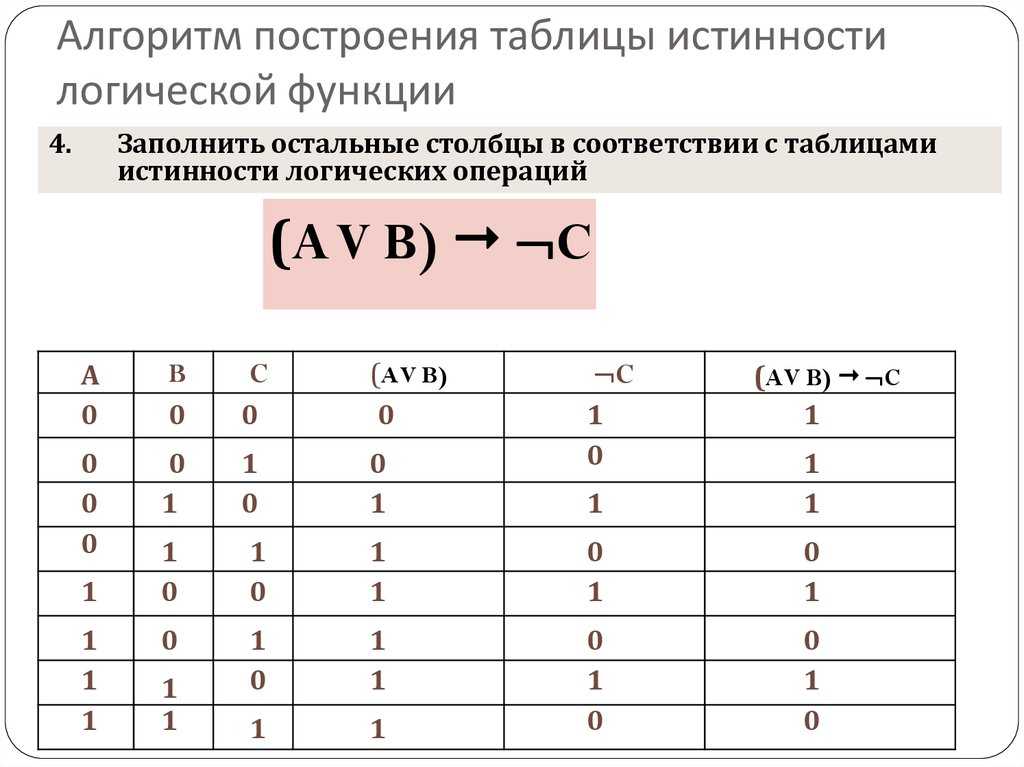
Правила построения по таблице истинности
Дизъюнктивная форма
Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.
Конъюнктивная форма
Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.
Алгоритм приведения к СДНФ и СКНФ
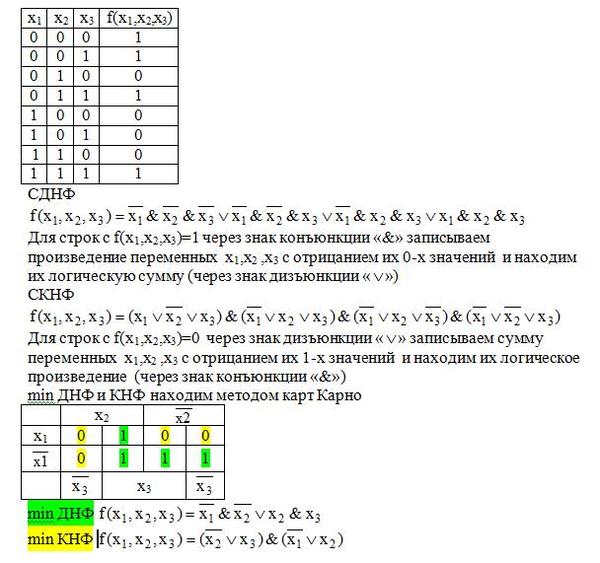
Рассмотрим логическую функцию в виде таблицы истинности.
Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:
- Отметить наборы переменных, значение функции F на которых равно 1.
- Записать для всех отмеченных наборов конъюнкцию всех переменных так: если значение некоторой переменной в этом наборе равняется 1, в конъюнкцию включается сама переменная.
 В случае противного результата, в конъюнкцию включается ее отрицание.
В случае противного результата, в конъюнкцию включается ее отрицание. - Связать полученные конъюнкции операциями дизъюнкции.
Построим совершенную ДНФ:
И как результат получим следующую СДНФ:
\(F(x_1,\;x_2,\;x_3)\;=\;(\overline{x_1}\wedge\overline{x_2}\wedge\overline{x_3})\;\vee(\overline{x_1}\;\wedge\;\overline{x_2}\;\wedge\;x_3)\;\vee(x_1\;\wedge\;\overline{x_2}\;\wedge\;\overline{x_3})\;\vee\;(x_1\;\wedge\;\overline{x_2}\;\wedge\;x_3)\;\vee\;(x_1\;\wedge\;x_2\;\wedge\;x_3)\)
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:
- Отметить в таблице истинности наборы переменных, значение функции F на которых равно 0.
- Записать для всех отмеченных наборов дизъюнкцию всех переменных — в том случае, когда значение некоторой переменной в этом наборе равняется 0, в дизъюнкцию включается сама переменная, если происходит наоборот, то в дизъюнкцию включается ее отрицание.

- Связать полученные дизъюнкции операциями конъюнкции.
Построим совершенную КНФ:
И как результат получим следующую СКНФ:
\(F(x_1,\;x_2,\;x_3)\;=\;(x_1\;\vee\;\overline{x_2}\;\vee\;x_3)\;\wedge\;(x_1\;\vee\;\overline{x_2}\;\vee\;\overline{x_3})\;\wedge\;(\overline{x_1}\;\vee\;\overline{x_2}\;\vee\;x_3)\)
Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.
Доказательство эквивалентности
Эквивалентность — понятие, означающее, что две и более формул представляют одну и ту же функцию. Для обозначения эквивалентности могут использоваться следующие знаки: \( \equiv , = , \Leftrightarrow .\)
Доказать эквивалентность формул можно двумя способами.
- Первый заключается в построении и сравнении таблиц истинности обеих функций.
 В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны. - Второй вариант — метод эквивалентных преобразований. Суть этого метода — построение цепи эквивалентных формул на основе ранее доказанных эквивалентностей.
Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.
Поглощение
\(x\;\vee\;xy\;=\;x\)
\(x(x\;\vee\;y)\;=\;x\;\)
Доказательство эквивалентности:
\(x\;\vee\;xy\;=\;x\;\cdot\;l\;\vee\;xy\;=\;x(l\;\vee\;y)\;=\;x\)
\(x(x\;\vee\;y)\;=\;xx\;\vee\;xy\;=\;x\;\vee\;xy\;=\;x\)
Склеивание
\(xy\;\vee\;x\overline y\;=\;x\)
Доказательство эквивалентности:
\(xy\;\vee\;x\overline y\;=\;x(y\;\vee\;\overline y)\;=\;x\;\cdot\;l\;=\;x\)
Обобщенное склеивание
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)
Доказательство эквивалентности
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)
Расщепление
\(x\;\vee\;\overline xy\;=\;x\;\vee\;y\)
Доказательство эквивалентности
\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)
Примеры с решением
Задача №1
Приведите к СКНФ \(((((A\rightarrow B)\rightarrow\overline A)\rightarrow\overline B)\rightarrow\overline C)\).
Через применение закона де Моргана и правила\( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:
\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\)
\(=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline{((\overline A\;\vee\;B)}\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=\)
\(=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline{(\overline{(\overline A\vee B)}\;\vee\;\overline A\;)}\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)
\(=\;(\overline{(\overline{(\overline{(\overline A\;\vee\;B)}\;\vee\;\overline A)}\;\vee\;\overline B)}\;\vee\;\overline C)\;=\;(((A\;\vee\;B)\;\vee\;\overline A)\;\vee\;\overline B)\;\vee\;\overline C\;=\)
\(=\;((\overline{(\overline A\;\vee\;B)}\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=\)
\(=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)
\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)
Далее приведем выражение к КНФ:
\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)
Далее приведем выражение к СКНФ:
\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\)
\(=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)
Задача №2
Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)
\(f(\widetilde x^3) = (\overline{x_1}x_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2)\)
Преобразуем функцию:
\(f(\widetilde x^3) = (\overline{x_1}x_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2) = ((\overline{x_1}x_2\;\cdot\;\overline{x_3}\;)\;\vee\;(\overline{\overline{x_1}x_2}\;\cdot\;x_3))\;\cdot\;(\overline{x_1x_3}\;\vee\;x_2)\;=\)
\(=\;((\overline{x_1}x_2\overline{x_3})\;\vee\;((\overline{\overline{x_1}}\;\vee\;\overline{x_2})\;x_3)\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;=\;((\overline{x_1}x_{2\;}\overline{x_3})\;\vee\;((x_1\;\vee\;\overline{x_2})\;x_3)\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;=\)
\(=\;(\overline{x_1}x_2\overline{x_3}\;\vee\;x_1x_3\;\vee\;\overline{x_2}x_3)\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;=\)
\(=(\overline{x_1}x_2\overline{x_3}\;\cdot(x_1\vee x_3\vee x_2)\;\vee\;x_1x_3\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;\vee\;\overline{x_2}x_3\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2))\;=\)
\(=\;(\overline{x_1}x_2\overline{x_3}\;\vee\;(x_1\;x_3\overline{x_1}\;\vee\;x_1x_3\overline{x_3}\;\vee\;x_1x_3x_2)\;\vee\;(\overline{x_2}x_3\overline{x_1}\;\vee\;\overline{x_2}x_3\overline{x_3}\;\vee\;\overline{x_2}x_3x_2)\;=\)
\(=\;(\overline{x_1}x_2\overline{x_3}\;\vee\;0\;\vee\;0\;\vee\;x_1x_2x_3\;\vee\;\overline{x_1}\overline{x_2}x_3\;\vee\;0\;\vee\;0)\;=\)
\(=\;\overline{x_1}x_2\overline{x_3}\;\vee\;x_1x_2x_3\;\vee\;\overline{x_1}\overline{x_2}x_3\)
Нормальные формы для формул алгебры высказываний
1.
 Понятие элементарного произведения; понятие дизъюнктивной нормальной формы (ДНФ). Методика построения таблицы истинности дляДНФ упрощенным методом. Понятие
Понятие элементарного произведения; понятие дизъюнктивной нормальной формы (ДНФ). Методика построения таблицы истинности дляДНФ упрощенным методом. Понятиеэлементарной дизъюнкции, понятие
конъюнктивной нормальной формы (КНФ).
ЛЕКЦИЯ 23-24
2. Нормальные формы для формул алгебры высказываний
3. 2.1. Нормальные формы для формул алгебры высказываний
2.1. Нормальные формы для формул алгебрывысказываний
Одна и та же логическая формула может быть записана
различным образом. Например, функция F(A,B) может быть
записана следующими эквивалентными выражениями:
F ( A, B) A B A B A B
F ( A, B) A A B
F ( A, B) A ( A B )
Эквивалентность этих формул легко проверить по таблицам
истинности или выполнив необходимые преобразования.
Если логическое выражение содержит большое число
операций, то составлять для него таблицу истинности
достаточно сложно, так как приходится перебирать большое
количество вариантов. В таких случаях формулы удобно
привести к нормальной форме.

Формула имеет нормальную форму, если в ней отсутствуют
знаки эквивалентности, импликации, двойного отрицания,
при этом знаки отрицания находятся только при логических
переменных.
В алгебре высказываний используют две нормальные
формы: дизъюнктивную (ДНФ) и конъюнктивную
нормальные формы (КНФ).
ДНФ
Определение. Высказывательная форма, состоящая из
переменных или отрицательных переменных, применением
только
одной
операции
конъюнкции,
называется
элементарной конъюнкцией (или конъюнктом).
Например, A B C
В
элементарной
конъюнкции
нет
двух
пропозициональных переменных, так как A A ≡ A.
одинаковых
Определение. Высказывательная форма, состоящая из
элементарных конъюнкций, применением только одной
операции дизъюнкции называется дизъюнктивной
нормальной формой (ДНФ).
Например, A B C A B A C
КНФ
Определение.
Высказывательная форма, состоящая из
переменных или отрицания переменных применением
только
одной
операции
дизъюнкции,
называется
элементарной дизъюнкцией (или дизъюнктом).
Например, A B C
В элементарной дизъюнкции
нет
пропозициональных переменных, так как А∨А ≡ А
двух
одинаковых
Определение.
Высказывательная форма, состоящая из
элементарных дизъюнкций, применением только одной
операции
конъюнкции
называется
конъюнктивной
нормальной формой (КНФ).
Например, ( A B C) ( A B) ( A C)
Алгоритм приведения к НФ
Для приведения формулы к нормальной форме
используют законы логики и правила логических
преобразований по следующему алгоритму:
1. Устранить «↔» и «→».
2. Продвинуть отрицание до пропозициональной
переменной.
3. Применить закон дистрибутивности.
4. Постоянно избавляться от двойных отрицаний.
Примеры:
1. Преобразовать формулу к виду ДНФ
F=F1˄(F2∨¬F2)∨F2˄(F1∨¬F1)
Примеры:
2. Преобразовать формулу к виду КНФ
F=F1˄(F1∨F2)∨¬F2˄(F1∨F2)
Примеры:
3. Преобразовать формулу к виду КНФ
F=((F1→(F2∨¬F3))→F4)
Примеры:
4. Преобразовать формулу к виду ДНФ
F=¬(F1˄F2)˄(F1∨F2)
Совершенные НФ
Использование нормальных форм не устраняет полностью
неоднозначности записи логических функций, например
F ( A, B, C ) A B A C A B C
F ( A, B, C ) A B A C B C
F(A,B,C)=A B A C
Поэтому среди нормальных форм выделяют такие, в
которых функции записываются единственным образом.
 Их
Ихназывают совершенными. Применяются совершенная
дизъюнктивная и совершенная конъюнктивная формы
(СДНФ и СКНФ).
СДНФ
Совершенная дизъюнктивная нормальная форма
(СДНФ) — ДНФ, удовлетворяющая условиям:
1. Все элементарные конъюнкции различны.
2. Нет нулевых конъюнкций.
3. Ни одна из элементарных конъюнкций не
повторяется.
4. Каждая элементарная конъюнкция содержит
все переменные или их отрицания.
Примеры СДНФ:
(X Y) ( X Y) (X Y)
(X Y Z) ( X Y Z) (X Y Z) (X Y Z) (X Y Z)
(X1 X2 X3 X4) ( X1 X2 X3 X4) (X1 X2 X3 X4)
СКНФ
Совершенная конъюнктивная нормальная форма
(СДНФ): КНФ — удовлетворяющая условиям:
1. Все элементарные дизъюнкции различны.
2. Нет нулевых дизъюнкций.
3. Ни одна из элементарных дизъюнкций не
повторяется.
4. Каждая элементарная дизъюнкция содержит
все переменные или их отрицания.
Теорема 2.4.1 (о представлении формулы алгебры
высказываний
совершенными
дизъюнктивными
нормальными формами).
 Каждая не тождественно ложная
Каждая не тождественно ложнаяформула алгебры высказываний от n аргументов имеет
единственную (с точностью до перестановки дизъюнктивных
членов) СДНФ.
Теорема 2.4.2 (о представлении формулы алгебры
высказываний
совершенными
конъюнктивными
нормальными формами). Каждая не являющаяся тавтологией
формула алгебры высказываний от n аргументов имеет
единственную (с точностью до перестановки конъюнктивных
членов) СКНФ.
Единственность совершенных нормальных форм у выполнимой ПФ обуславливает их
использование для доказательства равносильностей, идея которого состоит в
следующем: если у двух ПФ их СДНФ (СКНФ) совпадают, то они равносильны.
16. 2.5. Приведение формулы алгебры высказываний к совершенной нормальной форме
2.5. Приведение формулы алгебры высказываний ксовершенной нормальной форме
Способы приведения формул к совершенным
формам следуют из способов задания формул
алгебры высказываний – либо с помощью таблицы,
либо аналитически.
Аналитический способ приведения к совершенным
формам
Для приведения ПФ к СДНФ выполняются равносильные
преобразования, описанные следующей последовательностью
шагов:
1. С помощью равносильных преобразований привести ПФ к
ДНФ.
2. Те элементарные конъюнкции, в которые сомножителями
входят не все переменные, умножить на единицы,
представленные в виде дизъюнкций каждой недостающей
переменной с ее отрицанием.
3. Раскрыть скобки по соответствующему дистрибутивному
закону.
4. Для получения искомой СДНФ исключить повторения.
Аналитический способ приведения к совершенным
формам
Приведение к
элементарным
переменные,
конъюнкций
отрицанием.
СКНФ осуществляется аналогично, но только к
дизъюнкциям, содержащим слагаемыми не все
прибавляют нули, представленные в виде
каждой недостающей переменной с ее
Пример
Пусть ПФ, содержащая переменные X, Y, Z, имеет ДНФ вида X Z Y Z
Используя аналитический способ привести к СДНФ.
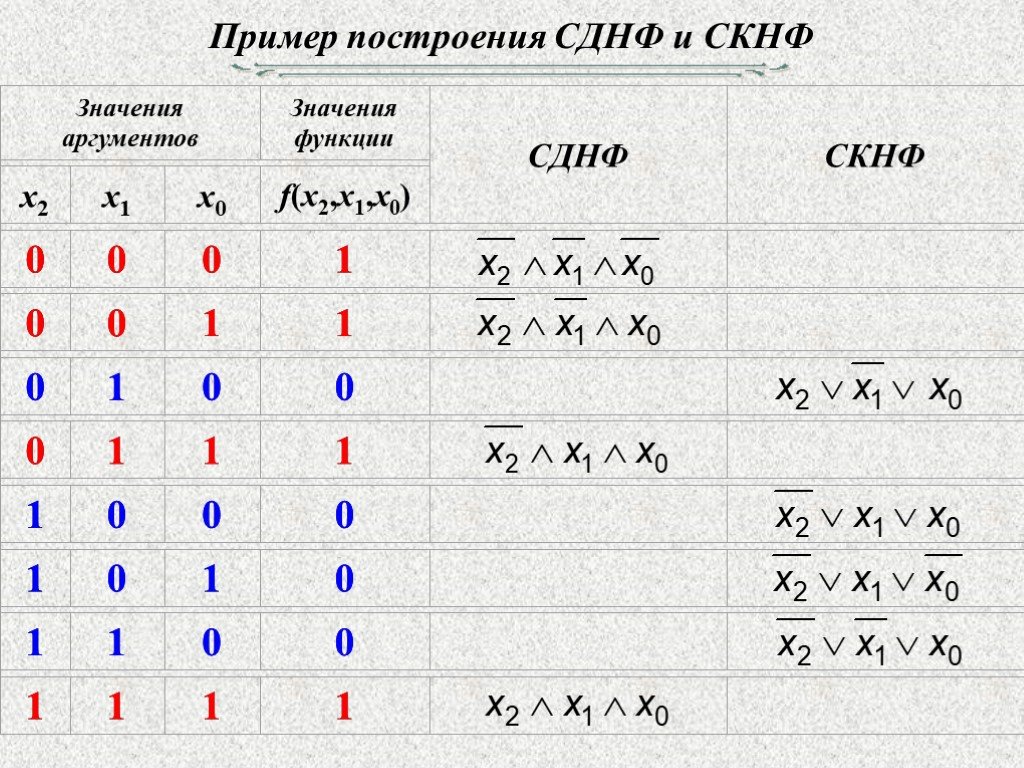
Решение:
В соответствии с процедурой приведения к СДНФ умножим
первую и вторую конъюнкции на 1
1 Y Y
1 X X
X Z Y Z X Z (Y Y ) Y Z ( X X )
X Z Y X Z Y Y Z X Y Z X
X Z Y X Z Y Y Z X СДНФ
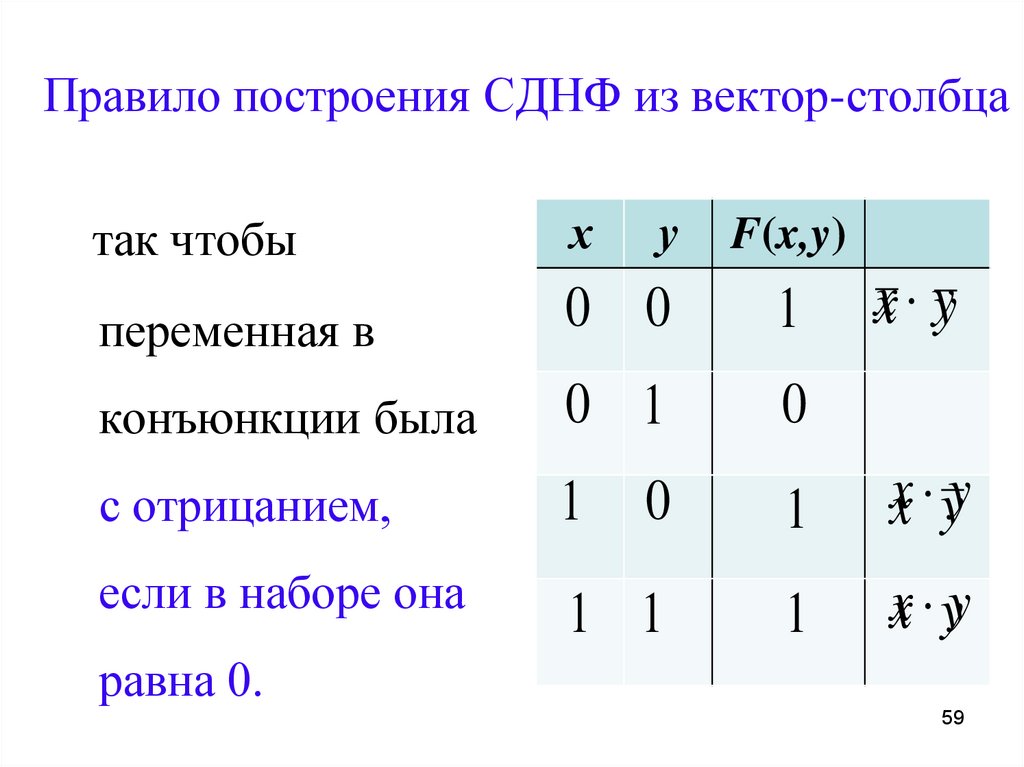
Табличный способ приведения к совершенным
формам
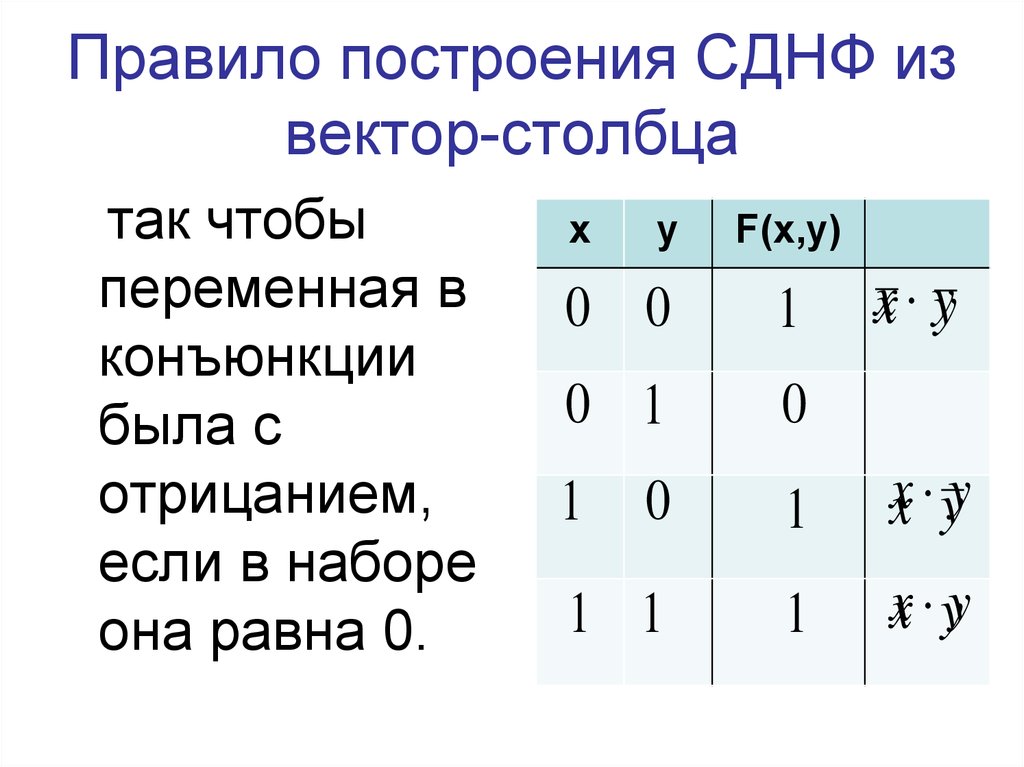
Табличный способ приведения к СДНФ
1. Составить таблицу истинности данной формулы.
2. Рассмотреть те строки, в которых формула принимает истинностное
значение 1. Каждой такой строке поставить в соответствие
элементарную конъюнкцию, причем переменная, принимающая
значение 1, входит в нее без отрицания, а 0 – с отрицанием.
3. Образовать дизъюнкцию всех полученных элементарных конъюнкций,
которая и составит СДНФ.
Табличный способ приведения к СКНФ
1. Составить таблицу истинности данной булевой функции.
2. Рассмотреть те строки, в которых формула принимает истинностное
значение 0. Каждой такой строке поставить в соответствие
элементарную дизъюнкцию, причем переменная, принимающая
значение 1, входит в нее с отрицанием, а 0 – без отрицания.
3. Образовать конъюнкцию всех полученных элементарных дизъюнкций,
которая и составит СКНФ.
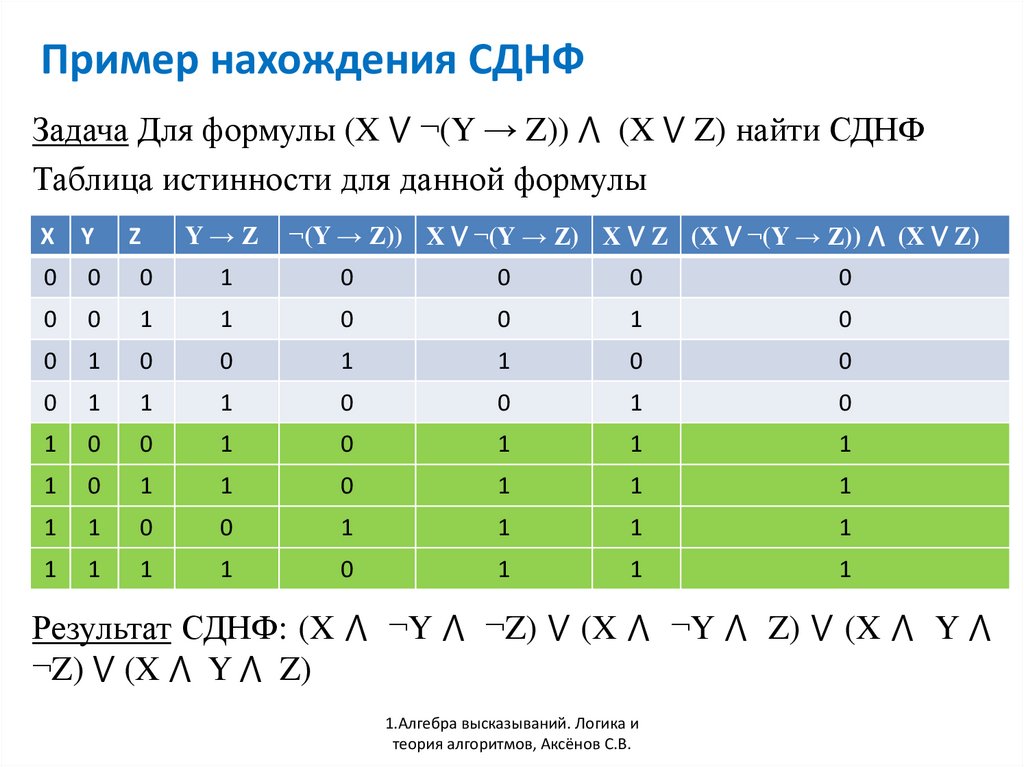
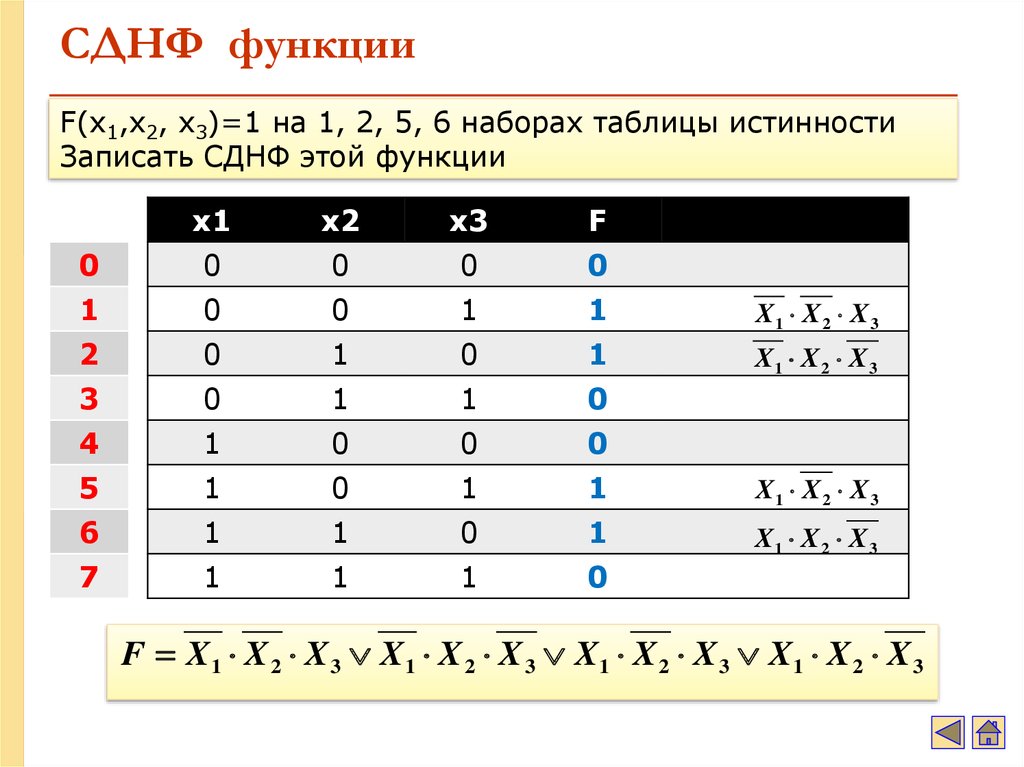
Пример
Найти СКНФ и СДНФ для формулы
X Y Z
Решение:
Построим таблицу истинности и на ее основе составим СДНФ и СКНФ
X
Y
Z
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
X Y Z
СДНФ : X Y Z
Элементарные
конъюнкции
Элементарные
дизъюнкции
0
1
1
0
0
1
0
1
X Y Z X Y Z X Y Z
СКНФ : ( X Y Z ) ( X Y Z ) ( X Y Z ) ( X Y Z )
Критерии тождественной истинности и тождественной
ложности формул алгебры высказываний
Теорема 2.6.1 (признак тождественной истинности формулы).
Формула алгебры высказываний тождественно истинна тогда и
только тогда, когда в каждой элементарной дизъюнкции её КНФ
имеется, по меньшей мере, одна пропозициональная
переменная, входящая в этот одночлен вместе со своим
отрицанием.
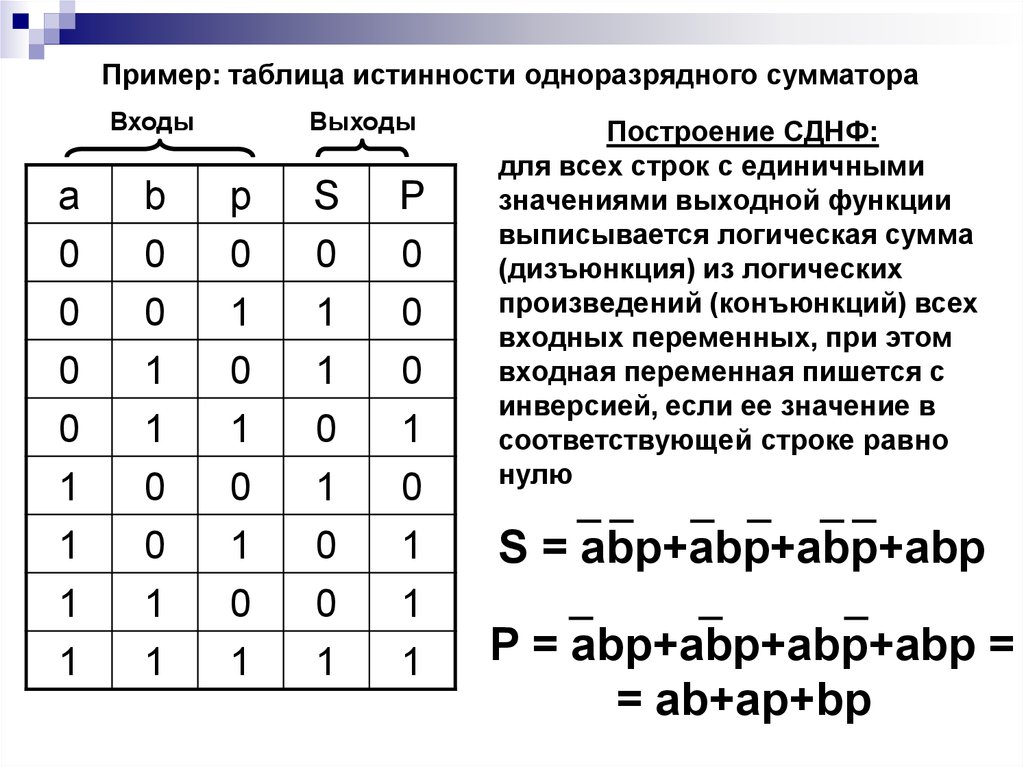
Теорема 2.6.2 (признак тождественной ложности формулы).
Формула алгебры высказываний тождественно ложна тогда и
только тогда, когда в каждой элементарной конъюнкции её ДНФ
имеется, по меньшей мере, одна пропозициональная
переменная, входящая в этот одночлен вместе со своим
отрицанием.
Примеры:
1. Показать, что формула (P (P Q)) Q — тавтология
(P (P Q)) Q ( P ( P Q)) Q P ( P Q) Q
P (P Q) Q ( P P Q) ( P Q Q).
По теорем 2.6.1 формула тождественно истинна.
Примеры:
2. Показать, что формула P ( Q ( P Q)) – тождественно
ложна
P ( Q ( P Q)) (P Q P) ( (P Q Q).
По теорем 2.6.2 формула тождественно ложна.
Задания для закрепления
2. Привести следующие формулы к СДНФ с помощью равносильных преобразований:
a) x y x y ;
b) x y z ;
c)
x y следующие
x y.
3. Привести
формулы к СКНФ с помощью равносильных преобразований:
a) x y z ;
b)
x y xСДНФ
y . и СКНФ для данных формул логики высказываний с помощью таблиц
4.
 Построить
Построитьистинности.
5. Построить простейшую логическую формулу по заданной таблице истинности,
которая имеет нулевые значения при следующих наборах переменных A, B, C:
(001), (010), (011), (110).
Домашнее задание
2. Привести следующие формулы к СДНФ с помощью равносильных преобразований:
a) x y x y ;
b) x y z ;
c) x y x y .
3. Привести следующие формулы к СКНФ с помощью равносильных преобразований:
a) x y z ;
b) x y x y .
4. Построить СДНФ и СКНФ для данных формул логики высказываний с помощью таблиц
истинности.
5. Построить простейшую логическую формулу по заданной таблице истинности,
которая принимает значение 1 при следующих наборах переменных A, B, C: (010),
(101), (111).
Контрольные вопросы
1.
Какая
высказывательная
форма
называется
элементарной
дизъюнкцией?
2. Какая
высказывательная
форма
называется
элементарной
конъюнкцией?
3. Какая
высказывательная форма называется дизъюнктивной
нормальной формой (ДНФ)?
4.
 Какая
Какаявысказывательная форма называется конъюнктивной
нормальной формой (КНФ)?
5. Совершенная
дизъюнктивная
нормальная
форма
(СДНФ),
отличительные особенности?
6. Совершенная конъюктивная нормальная форма (СКНФ), отличительные
особенности?
7. Теоремы о единственности совершенных НФ.
8. Аналитический способ приведения к СДНФ (СКНФ).
9. Табличный способ приведения к СДНФ (СКНФ).
10. Критерии тождественной истинности и тождественной ложности
формул алгебры высказываний.
[Беседка за 5 минут] 004 – Как создать модель беседки в формате SDF
- Узнайте, как создать модель беседки в формате SDF
- Robot Ignite Academy, место, где можно научиться программировать роботов, используя только веб-браузер
- ROS Development Studio (среда, используемая в видео), еще один мощный онлайн-инструмент для практического обучения ROS
- Веб-сайт SDFormat: http://sdformat.org/
- Веб-сайт URDF: http://wiki.
 ros.org/urdf
ros.org/urdf
Чтобы загрузить беседку с помощью ROS, у вас должны быть установлены Gazebo и ROS. Если вы не хотите устанавливать все, мы настоятельно рекомендуем использовать ROSDS (ROS Development Studio), которая дает вам доступ к онлайн-среде с уже установленной ROS. Действительно, мы собираемся использовать этот инструмент для простоты. Вы можете выполнить те же действия и на своем компьютере, если не хотите использовать ROSDS.
Чтобы использовать ROSDS, вы можете просто создать учетную запись и начать ее использовать.
После создания учетной записи вам необходимо создать ROSject, нажав кнопку 9.0021 Новая кнопка ROSject :
Создание нового ROSject в ROSDS
Если у вас есть ROSject, вы можете открыть его, нажав Открыть :
Открытие ROSject в ROSDS
Чтобы запустить что-либо с помощью ROS , мы нужен пакет ROS, поэтому давайте создадим его. Для этого вам понадобится терминал/оболочка. В ROSDS вы можете иметь терминал, нажав Tools -> Shell .
Давайте сначала создадим рабочее пространство. В этом случае давайте назовем его ~/simulation_ws
mkdir ~/simulation_ws/src -p
Теперь давайте скомпилируем нашу пустую рабочую область
исходный код /opt/ros/kinetic/setup.bash источник /usr/доля/gazebo/setup.sh компакт-диск ~/simulation_ws/ catkin_make
Теперь давайте создадим наш пакет ROS. Назовем его my_simulations :
источник ~/simulation_ws/devel/setup.bash cd ~/simulation_ws/src catkin_create_pkg my_simulations
Теперь давайте создадим запустить и папку world внутри пакета my_simulations.
компакт-диск my_simulations mkdir launch world
Теперь в папке launch создадим файл с именем my_world.launch
touch launch/my_world.launch
В этот файл поместим следующее содержимое:
0" кодировка = "UTF-8" ?>
<запуск>
Чтобы поместить содержимое в этот файл, вы можете сделать это с помощью редактора кода. Для этого нажмите Инструменты -> IDE. В этот файл добавим следующее содержимое:
5"> <мировое имя="по умолчанию"> <включить> модель://солнце <включить>модель://ground_plane
Если вы правильно следовали инструкциям, у вас должна быть следующая структура:
user:~/simulation_ws/src$ tree .
.
|-- CMakeLists.txt -> /opt/ros/kinetic/share/catkin/cmake/toplevel.cmake
`--мои_симуляции
|-- CMakeLists.txt
|-- запустить
| `-- my_world.launch
|-- пакет.xml
`-- мир
`-- empty_world.world
3 каталога, 5 файлов Давайте создадим модель с именем
~/simulation_ws/src/my_simulations/ mkdir -p models/my1stmodel
В папке my1stmodel создадим два файла: один с именем model.config , а другой с именем model.sdf .
модели компакт-дисков/my1stmodel/ touch model.config model.sdf
Эти два файла, model.config и model.sdf , необходимы для каждой модели беседки. Вы можете найти эти файлы, например, в модели наземной плоскости, предоставленной Gazebo.
Давайте вставим следующее содержимое в наш my1stmodel/model.config
<модель>Моя первая модель <версия>1.0model.sdf <автор>Ваше имя [email protected] <описание> Моя первая модель беседки
И в наш models/my1stmodel/model.sdf добавим следующее:
<имя модели="my1stmodel"> ложь <имя ссылки="ссылка"> <имя столкновения="столкновение"> <геометрия> <коробка> <размер>3 2 5 <поверхность> <трение> <ода> <му>10050 <визуальное имя="визуальное"> <геометрия> <коробка> <размер>3 2 5 <материал> <скрипт>file://media/materials/scripts/gazebo. material
Беседка/Серый
Давайте изменим наш файл world/empty_world.world , созданный ранее, добавив следующее:
<включить>модель://my1stmodel
В итоге окончательное содержимое файла будет таким:
<мировое имя="по умолчанию"> <включить> модель://солнце <включить>модель://ground_plane <включить>модель://my1stmodel
Теперь, когда у нас все на месте, мы можем запустить наш пакет двумя способами:
Первый вариант : Нажмите Simulation -> Выберите файл , затем выберите my_world. launch. Это должно автоматически загрузить веб-версию беседки под названием gzweb.
launch. Это должно автоматически загрузить веб-версию беседки под названием gzweb.
Пользовательская модель робота-беседки, работающая в ROSDS
Второй вариант : Если вы выполняете тесты на своем компьютере или хотите запустить симуляцию вручную, вы можете просто:
источник ~/simulation_ws/devel/setup.bash roslaunch my_simulations my_world.launch --screen
Если вы находитесь в ROSDS и решили запустить симуляцию вручную, вам нужно вручную открыть Gazebo Web ( gzweb ), нажав Tools -> Gazebo .
Поздравляю. Вы успешно запустили свой первый собственный Gazebo World с помощью ROS.
Если вы плохо поняли все шаги, описанные здесь, или вам нужно больше понять файлы, которые мы создали, помните, что у нас есть живая версия этого поста на YouTube. Кроме того, если вам понравился контент, рассмотрите возможность подписки на наш канал YouTube. Мы публикуем новый контент ~ каждый день.
SDF, часть вторая — Joyrok
Поля расстояний
В SDF нет S без полей расстояний!В ЧАСТИ 1 руководства по SDF я рассмотрел поля расстояния текстуры и то, как они в большинстве случаев не «подписываются», поскольку они не являются отрицательными значениями без повторного сопоставления некоторых диапазонов. В этом есть смысл, а эффекты все же позволяют делать удивительные вещи с такими текстурами:
Это круто, но как мне получить поля расстояний со знаком, сгенерированные сумасшедшей математикой, и вообще не использовать текстуры для создания наших полей расстояний? Без текстур математические SDF могут создавать удивительные градиенты/безумные анимации/дополнения/маски:
Приведенные ниже примеры будут работать в Unreal и Unity, и я постараюсь продемонстрировать оба движка. Я также буду ссылаться на продукты Adobe, но ни один из них не является необходимым для понимания представленных ниже концепций.
Математические поля расстояний со знаком
Начнем с основного круга
Поля расстояний со знаком в качестве текстур очень полезны и делают классные вещи, но, возможно, более интересная концепция SDF заключается в замене текстур чистой математикой! Скажем, например, вы хотели иметь красивый фон в виде круга для какой-либо иконки. Классический подход может состоять в том, чтобы создать круг в графическом редакторе, таком как Photoshop, сохранить его как текстуру, импортировать эту текстуру в движок и поместить ее под иконку. Однако вместо этого можно использовать MATH для создания круга. Преимущества создания визуальных элементов SDF в движке включают гибкость изменения размера/градиента/анимации/штрихов и многое другое. Итак, давайте начнем с примера с кругом.
Классический подход может состоять в том, чтобы создать круг в графическом редакторе, таком как Photoshop, сохранить его как текстуру, импортировать эту текстуру в движок и поместить ее под иконку. Однако вместо этого можно использовать MATH для создания круга. Преимущества создания визуальных элементов SDF в движке включают гибкость изменения размера/градиента/анимации/штрихов и многое другое. Итак, давайте начнем с примера с кругом.
Говоря обо всем, что касается SDF, я захожу на веб-сайт IQ, так как это удивительный ресурс для SDF, который включает уравнения для создания всевозможных форм. Но для примера скажем, что я хотел сгенерировать круг, это довольно просто, если вы посмотрите на 2D-примитивы IQ и первая фигура – это круг:
Теперь, чтобы перевести это уравнение в Unreal или Unity, вам даже не нужно чтобы создать собственный узел HLSL, хотя я расскажу об этом позже. С таким простым уравнением мне просто нужно взять длину UV в уравнении IQ, UV всегда называются vec2 р и отнимем на размер нашего круга р .

Я взял это уравнение из IQ и разбил его на узлы в Unreal. P — это TexCoord[0], затем возьмите длину и вычтите параметр, который я называю Размер круга , и получится круг.
НО что-то не так, кружок на самом деле в верхнем левом углу, а не в центре материала. Это потому, что система координат находится в неправильном диапазоне. Я нарисую очень грубую диаграмму, чтобы продемонстрировать это:
Ось X на этой диаграмме представляет собой КРАСНЫЙ канал, а ось Y — ЗЕЛЕНЫЙ канал. Итак, основываясь на этом графике, SDF рисует свой центр в точке [0,0] и рисует свой радиус в 0,5 (наш размер круга) от центра. ТЕПЕРЬ для удовольствия мы можем посмотреть на Unity здесь, и вы можете увидеть, что у Unity перевернута координата Y, поэтому он всегда рисует [0,0] в левом нижнем углу:
Итак, Unity рисует круг SDF немного по-другому, на самом деле он показывает его внизу слева, а не вверху слева, как Unreal. Потому что, если вы посмотрите на UV-координаты, у них ось Y начинается внизу как 0, а не в Unreal, у которого 0 начинается вверху координат.

Независимо от движка мне нужно установить систему координат в центр [0,0], чтобы оказаться в середине материала. Чтобы это произошло, мне нужно уменьшить координаты и сдвинуть их. Вот gif того, что он будет делать в шейдере с помощью преобразований Photoshop:
Что я, по сути, сделал с точки зрения математики, так это переназначил диапазон от 0-1 до -1-1. Для этого я использую концепцию, называемую шкалой постоянного смещения, и чтобы увидеть этот график, вот что это такое:
Используя этот график, вы можете увидеть, хочу ли я, чтобы диапазон изменялся от 0-1 до -1-1. Мне просто нужно вычесть 0,5 и умножить на 2. Но почему эти случайные числа?
Чтобы переназначить диапазон, если я просто умножу на 2, он будет меняться от 0 до 2, поэтому для масштабирования смещения сначала мне нужно вычесть 0,5, так как это сначала сдвинет диапазон в минус -0,5-0,5, а затем при умножении .5 на 2 вы получите 1. Надеемся, что визуальное представление дает хорошее представление о математике в действии.

Поскольку диапазоны находятся в диапазоне от -1 до 1, SDF теперь должен иметь истинные отрицательные значения для получения внутреннего и внешнего расстояния. [Подробнее об этой концепции см. Предыдущее руководство]
Граф Unreal теперь включает новый диапазон координат UV, который имеет узел вычитания и узел умножения , которые идут ДО расчета длины:
Unreal также имеет 902 00 постоянное смещение узла , что может буквально выполнять вычитание/сложение и умножение за вас в одном узле, поэтому я использую его большую часть времени:
А это тот же диапазон координат UV, переназначенный на графике Unity:
Unity немного более разборчива, так как она хочет, чтобы UV был вектором2 для этого расчета. Я решил это, разделив вектор4 на вектор2. К сожалению, мне нужно было сделать это для этой части руководства, но этот шаг не понадобится позже с пользовательскими формами HLSL. Так что просто обратите внимание, что я сделал это для демонстрации круга, но в этом нет необходимости при использовании узлов пользовательского кода.

ОТЛИЧНО, теперь у меня есть математический кружок SDF… что мне с ним делать? Как и поле расстояния текстуры, я могу сделать его размытым или менее размытым, и это довольно просто, но давайте добавим это, чтобы я мог затвердеть круг, чтобы он был менее размытым, добавив узел smoothstep и инвертирование цветов с один минус узел .
Для движка Unreal используется та же концепция: узел Smoothstep , затем инвертируйте цвета с помощью узла один минус . Мои значения SmoothStep: Min: 0 и Max: 0.01
Теперь как насчет анимации размера круга? Это легко. Я сделал размер этого маленького круга равным 0,5, чтобы заменить его временной анимацией:
Отправка узла времени через узел разлома сбросит время, чтобы всегда анимировать между 0-1, и это идеально подходит для масштабирования круга от 0-1! Вуаля! Легкая анимация? Да, пожалуйста!
Точно такой же график в Unreal.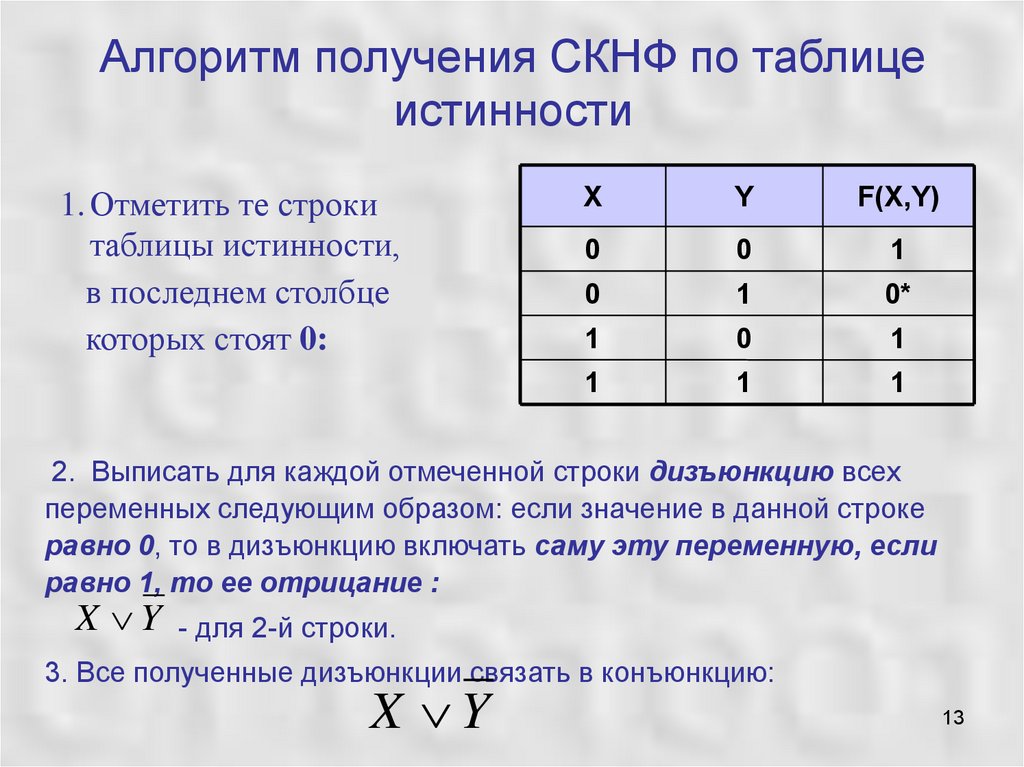
Но я могу сделать больше… Я могу легко преобразовать круг в обведенный круг с помощью SDF… и почему бы не анимировать толщину обводки?
Как напоминание из моего предыдущего урока SDF, вы можете погладить любой SDF с помощью абсолютный узел , затем перейдите в узел вычитания , и число в вычитании — это толщина штриха:
Теперь, если я продолжу анимировать размер круга, а затем назначу толщину обводки и умножу ее на меньший диапазон, я получу потрясающий результат:Я запутался и чуть не вставил в сглаживание вместо толщины обводки на гифке выше. Но по мере того, как круг становится больше, с толщиной штриха происходит обратное.
Вот та же анимация, но в Unreal:
В этом материале не используются текстуры, дополнительная анимация или слои, все делается с помощью элементарной математики… Но тут начинается самое интересное… комбинирование НЕСКОЛЬКО математических фигур SDF!
Математические поля расстояний со знаком — ОБЪЕДИНЕНИЕ, СМЕШИВАНИЕ И МАСКА ФОРМ
Так же, как векторная графика (типа.
 ..) редактор по умолчанию анимирует каждый узел, в отличие от Unreal. Мы надеемся, что эти анимации помогут более четко показать, что происходит с SDF. Однако все эти узлы в следующем разделе существуют и возможны в Unreal, так что не волнуйтесь, это все равно, пока вы не перейдете к пользовательскому HLSL, но я расскажу об этом.
..) редактор по умолчанию анимирует каждый узел, в отличие от Unreal. Мы надеемся, что эти анимации помогут более четко показать, что происходит с SDF. Однако все эти узлы в следующем разделе существуют и возможны в Unreal, так что не волнуйтесь, это все равно, пока вы не перейдете к пользовательскому HLSL, но я расскажу об этом.ОБЪЕДИНЕНИЕ SDFS:
Чтобы объединить фигуры SDF, мне нужно сделать себе другую форму. Итак, я собираюсь добавить еще один круг к моему маленькому материалу, и этот круг должен анимироваться по всему материалу сверху вниз. График Unity ниже показывает, как я анимирую круг, начиная с верхней части материала и анимируя вниз.
Маленькая деталь этого графика заключается в том, что я изменил умножение на 3 . Это было сделано для того, чтобы убедиться, что круг выглядит так, как будто он анимируется из-за пределов материала -> в материальную рамку ->, а затем за пределы рамки. Это звучит немного сложно, однако на практике это довольно легко визуально понять, поскольку это бесшовный круг прокрутки сверху вниз:
Теперь я могу продемонстрировать, как объединить статический круг и круг прокрутки сверху вниз.
 Для этого я использую минимальный узел :
Для этого я использую минимальный узел : По сути, это как если бы вы накладывали статический круг с анимированным кругом друг на друга. Представьте круги как слои Photoshop или слои After Effects, расположенные друг над другом, вот что будет делать минимальный узел . Из того, что я понимаю с моей ограниченной математикой, он сделает быструю ветвь, чтобы найти минимальные значения этих комбинированных SDF, используя эту логику для их объединения.
МАСКИРОВКА SDFS:
Если бы я использовал минимальный узел для объединения SDF, надеюсь, имеет смысл использовать максимальный узел для маскирования SDF. .
Берется страница из другой статьи IQ о 3D SDF. В этой статье есть раздел объединения/вычитания/пересечения. Хотя в этой статье показаны примеры для 3D SDF, она также применима к 2D SDF. Поэтому я буду использовать эти концепции для маскирования и пересечения фигур SDF.
Вычитание берет отрицательное значение вашего SDF и пропускает его через максимальный узел со вторым SDF.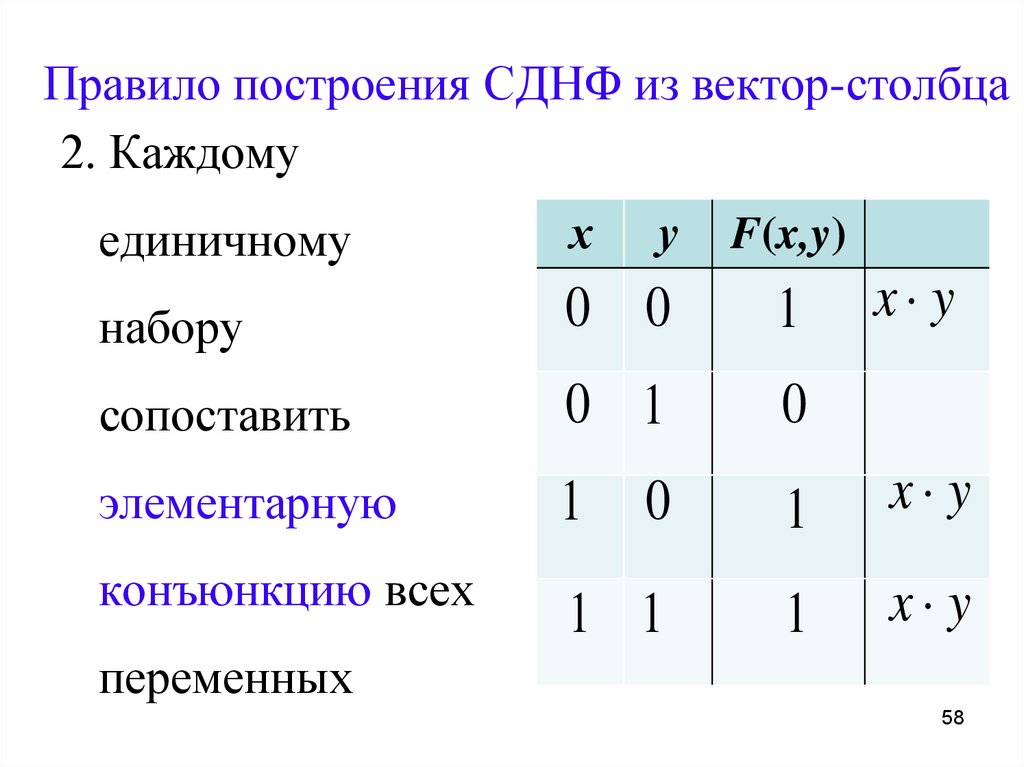 Пересечение — это просто максимальный узел между двумя SDF. Я покажу это, чтобы вы могли увидеть различия, но любой, кто использует Illustrator/Photoshop и инструменты поиска пути, должен быть интуитивно знаком с этими понятиями:
Пересечение — это просто максимальный узел между двумя SDF. Я покажу это, чтобы вы могли увидеть различия, но любой, кто использует Illustrator/Photoshop и инструменты поиска пути, должен быть интуитивно знаком с этими понятиями:Это снимки экрана из Illustrator, инструменты поиска пути, Unite, Minus Front (вычитание) и Intersect. Эти удивительные значки помогают показать, что фигуры визуально делают с нашими комбинациями SDF!
Сначала давайте перейдем к Минус Фронту или вычитанию! Для этого мне просто нужно max(-d1,d2). Я проведу SDF через отрицательный узел (сделаю его отрицательным), который будет SDF, который будет вычитаться из второго SDF в максимальном узле :
В зависимости от того, какую фигуру вы хотите расположить впереди, вычтя из фигуры под ней фигуру, которую вы хотите сделать отрицательной с помощью узла отрицания . Если я хочу, чтобы статический круг вычитал анимационный круг, тогда вы хотите, чтобы статический круг был отрицательным SDF.
 Чтобы заставить анимированный круг вычитаться из статического круга, вы должны превратить анимированный круг в отрицательный (с отрицательным узлом) и запустить его через максимальный узел . Что интересно, так это то, что два круга с другим методом вычитания сверху создают забавную анимацию луны/затмения. Статический круг сверху, вычитаемый из анимационного круга, как бы создает затмение — тень луны загораживает солнце — а другое вычитание выглядит как фаза луны, когда луна проходит через свои полные лунные циклы:
Чтобы заставить анимированный круг вычитаться из статического круга, вы должны превратить анимированный круг в отрицательный (с отрицательным узлом) и запустить его через максимальный узел . Что интересно, так это то, что два круга с другим методом вычитания сверху создают забавную анимацию луны/затмения. Статический круг сверху, вычитаемый из анимационного круга, как бы создает затмение — тень луны загораживает солнце — а другое вычитание выглядит как фаза луны, когда луна проходит через свои полные лунные циклы: Интересно посмотреть, какой SDF отрицательно, прежде чем поместить их обоих в максимальный узел меняет эффект маскировки!
После этой полусложной настройки для вычитания пересечение становится намного проще. Пересечение — это всего лишь максимальный узел между двумя SDF, и вы можете видеть, что он показывает только то место, где они пересекаются:
В IQ есть также гладкие уравнения объединения/вычитания/пересечения, но я не буду подробно останавливаться на них в этой статье.
 Вместо этого я хочу повторить итерацию, как инструмент поиска пути в Illustrator, вы можете объединять/вычитать/пересекать ваши фигуры SDF:
Вместо этого я хочу повторить итерацию, как инструмент поиска пути в Illustrator, вы можете объединять/вычитать/пересекать ваши фигуры SDF: Единица: мин(SDF1, SDF2)
Вычитание: max(-SDF1, SDF2)
Пересечение: max(SDF1, SDF2)
Краткое примечание Unreal не имеет узла отрицания 902 01 , о которых я знаю, так что просто умножьте ваш SDF по телефону -1 :
СМЕШИВАНИЕ SDFS:
Еще одна забавная вещь, которую можно сделать, это смешать два SDF с помощью узла Linear Interpolate , или сокращенно Lerp, что позволит вам определить вес того, сколько каждого SDF будет пытаться смешаться вместе. Это приводит к следующим результатам, когда анимация падения круга теперь влияет на статический круг в различной степени, изменяя lerp между 0 (статический круг) и 1 (падающий круг) где-то посередине, вы можете получить эту прекрасную анимацию слезы.
 Lerping — не единственный способ смешивания SDF и, вероятно, не самый полезный с математической точки зрения. IQ использует настраиваемый сглаженный минимум для смешивания SDF. К
осуществлять
эта техника смешивания я сделал пользовательский узел HLSL , но я расскажу, как это сделать позже. Это показывает уравнение, которое я использовал от IQ, который вдохновил Dreams (видеоигру) на улучшение его исходного кода, и это был один из способов, которым они смешивали формы вместе в своей игре:
Lerping — не единственный способ смешивания SDF и, вероятно, не самый полезный с математической точки зрения. IQ использует настраиваемый сглаженный минимум для смешивания SDF. К
осуществлять
эта техника смешивания я сделал пользовательский узел HLSL , но я расскажу, как это сделать позже. Это показывает уравнение, которое я использовал от IQ, который вдохновил Dreams (видеоигру) на улучшение его исходного кода, и это был один из способов, которым они смешивали формы вместе в своей игре: Я немного перейду к пользовательским узлам. позже в этой записи, так что не беспокойтесь об этой части здесь. Результаты пользовательского SmoothMinimum сильно отличаются от лерповского смешивания, но смешивания потрясающие:
Смесь
IQ демонстрирует силу математических форм SDF по сравнению с текстурами. Визуальные эффекты объединения этих двух полей расстояний могут получить ту липкую восхитительную среднюю область, которую было бы очень сложно сделать с помощью одних только текстур.
 Смесь работает, когда круги расположены близко друг к другу, они почти сливаются в один круг, а по мере того, как они удаляются друг от друга, они превращаются в отдельные круги. В отличие от лерпа, который представляет собой вес между двумя формами, форма которых является более доминирующей для визуального отображения, эта смесь фактически будет работать, чтобы объединить две формы, когда они находятся близко, и разделить их, когда они разделены. Я также могу выбрать, сколько смешивания использовать, поэтому на этом gif-анимации выше небольшое смешивание сохраняет каждый круг своей собственной отчетливой формой, а большее смешивание объединяет круги в одну большую каплю.
Смесь работает, когда круги расположены близко друг к другу, они почти сливаются в один круг, а по мере того, как они удаляются друг от друга, они превращаются в отдельные круги. В отличие от лерпа, который представляет собой вес между двумя формами, форма которых является более доминирующей для визуального отображения, эта смесь фактически будет работать, чтобы объединить две формы, когда они находятся близко, и разделить их, когда они разделены. Я также могу выбрать, сколько смешивания использовать, поэтому на этом gif-анимации выше небольшое смешивание сохраняет каждый круг своей собственной отчетливой формой, а большее смешивание объединяет круги в одну большую каплю.Существуют также различные уравнения для кубических и квадратичных смесей. Я считаю, что эта смесь самая простая и дает общие результаты по довольно низкой цене, поэтому я решил, что именно ее я продемонстрирую здесь. Но если вы чувствуете желание, посмотрите другие способы смешивания и попробуйте их.
ТЕПЕРЬ, если бы я добавил назад нашу обводку и увеличивал обводку с течением времени с помощью некоторых из этих сочетаний/комбинаций/вычитаний/пересечений, я уже мог бы получить потрясающую сумасшедшую анимацию, просто возясь с несколькими из этих узлов в комбинации:
Опять же, они просто сделаны из 2 кругов с различными способами смешивания/объединения/маскирования их вместе для создания этих различных анимаций. Комбинации форм и анимаций кажутся бесконечными, а это всего лишь два круга… что, если я сделаю БОЛЬШЕ фигур? Хорошо давайте сделаем это!
Комбинации форм и анимаций кажутся бесконечными, а это всего лишь два круга… что, если я сделаю БОЛЬШЕ фигур? Хорошо давайте сделаем это!
Создание фигур SDF
Преобразование GLSL в HLSL с помощью пользовательских узлов
Здесь мы начинаем использовать Пользовательский узел HLSL намного больше, и я покажу вам, что я имею в виду. Так что для круга математика была довольно простой:
Но при переходе к большему количеству 2D-форм SDF это превращает это простое длина (p) — r в немного более сложное программирование. Скажем, например, вы хотите сделать форму треугольника:
Вы могли бы сделать с узлами и воссоздать все это… что я сделал… но я не рекомендую этого! Вместо этого вы часто можете скопировать и вставить этот код с небольшим преобразованием в пользовательский узел HLSL в единстве и нереальности, чтобы убрать всю эту математику. Я покажу шаги, которые я предпринимаю для импорта пользовательских SDF в свои графики:
Первый шаг, который я делаю, это копирую текст в какой-нибудь блокнот:
Затем мне нужно преобразовать все, что есть в GLSL, в HLSL.
 И GLSL, и HLSL являются языками кодирования шейдеров и очень похожи. Игровые движки, как правило, используют HLSL и Shadertoy, а некоторые веб-приложения используют GLSL. Формы IQ написаны на GLSL, поэтому мне нужно преобразовать их в HLSL для Unity или Unreal. Есть удобный сайт, который я открываю, если нахожу что-то, что я не знаю, как конвертировать из GLSL в HLSL через Microsoft. Здесь вы можете видеть, что мне нужно заменить vec2 на float2:
Я иду и преобразовываю эти GLSL в HLSL в своем блокноте, чтобы я мог легко скопировать и вставить это в движок:
И GLSL, и HLSL являются языками кодирования шейдеров и очень похожи. Игровые движки, как правило, используют HLSL и Shadertoy, а некоторые веб-приложения используют GLSL. Формы IQ написаны на GLSL, поэтому мне нужно преобразовать их в HLSL для Unity или Unreal. Есть удобный сайт, который я открываю, если нахожу что-то, что я не знаю, как конвертировать из GLSL в HLSL через Microsoft. Здесь вы можете видеть, что мне нужно заменить vec2 на float2:
Я иду и преобразовываю эти GLSL в HLSL в своем блокноте, чтобы я мог легко скопировать и вставить это в движок: И если я использую Unity, я делаю здесь немного больше работы, просто изменяя Возврат на Out =
Отлично, теперь я могу создать пользовательский функциональный узел в Unity или пользовательский узел в Unreal:
И скопировать соответствующий код в нужные разделы:
Для Unreal:
Затем мне нужно сопоставить входы и выходы функции SDF с входами и выходами узла.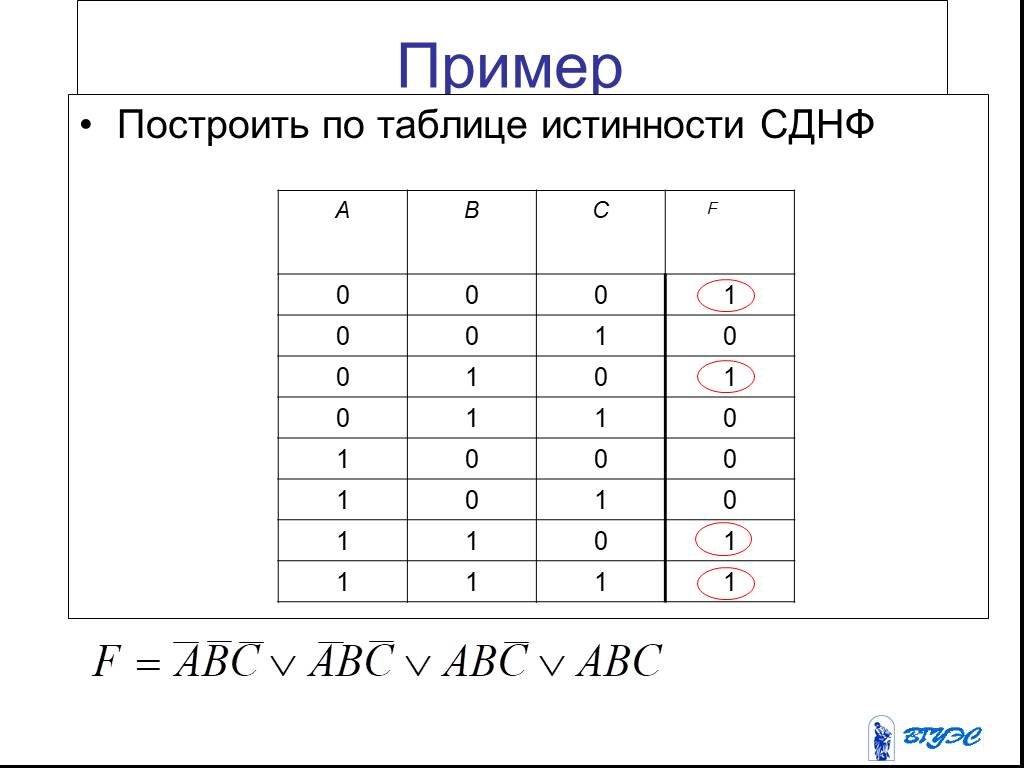 Это всегда должен быть выход с плавающей запятой, а входы могут варьироваться от SDF до SDF.
Это всегда должен быть выход с плавающей запятой, а входы могут варьироваться от SDF до SDF. Затем вы сможете вставить UV-координату для p , поэтому убедитесь, что это UV в правильном координатном пространстве с постоянной шкалой смещения, которую я продемонстрировал ранее. Затем, после того, как ваш SDF пропустите его через узел smoothstep в конце, чтобы сделать его более резким, один минус узел , чтобы инвертировать цвета, и вуаля, у меня есть треугольник SDF: Теперь помните, что координата Y в Unity перевернута из Unreal, поэтому треугольники находятся в разных направлениях, но довольно легко отразить/отразить ваши UV, чтобы получить треугольники в правильной ориентации. Кроме того, треугольник немного БОЛЬШОЙ, поэтому вы также можете манипулировать UV, чтобы изменить масштаб SDF, поскольку этот код треугольника SDF не имеет параметра размера:
Multiply/Divide будет масштабировать UV-координаты, которые, в свою очередь, уменьшат или увеличат SDF в зависимости от значений.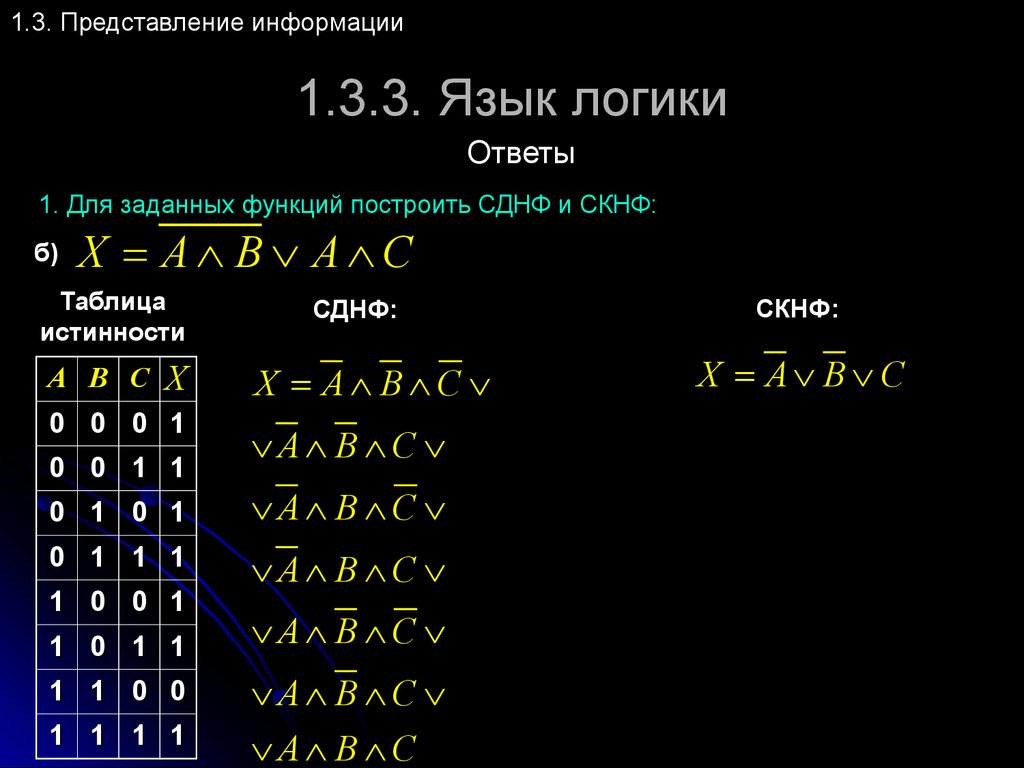 Например, если я умножу на .5 , треугольник будет больше, но если я умножу на 2 , как в примере gif, треугольник уменьшится вдвое. Я предпочитаю умножение вместо деления только потому, что вы можете случайно получить деление на 0, что компьютеры ДЕЙСТВИТЕЛЬНО не любят, поэтому я склонен использовать умножение в большинстве моих приключений масштабирования UV.
Например, если я умножу на .5 , треугольник будет больше, но если я умножу на 2 , как в примере gif, треугольник уменьшится вдвое. Я предпочитаю умножение вместо деления только потому, что вы можете случайно получить деление на 0, что компьютеры ДЕЙСТВИТЕЛЬНО не любят, поэтому я склонен использовать умножение в большинстве моих приключений масштабирования UV.
Чтобы сделать это в Unity и перевернуть треугольник, вы можете проще указать в Unity, какие части вектора умножать:
переверните/зеркально отобразите треугольник, чтобы он указывал вниз, и X на 2 , чтобы уменьшить треугольник вдвое.
Наконец, вот несколько других пользовательских узлов HLSL , создающих несколько других форм, чтобы вы могли увидеть примеры преобразования нескольких других SDF:
Теперь вы можете объединять кучу SDF вместе, обводить их, скруглять края и анимировать их, чтобы делать сумасшедшие вещи. Когда я начал изучать SDF, я был поражен всеми действительно великолепными результатами, полученными от простого экспериментирования с различными методами анимации и их объединения.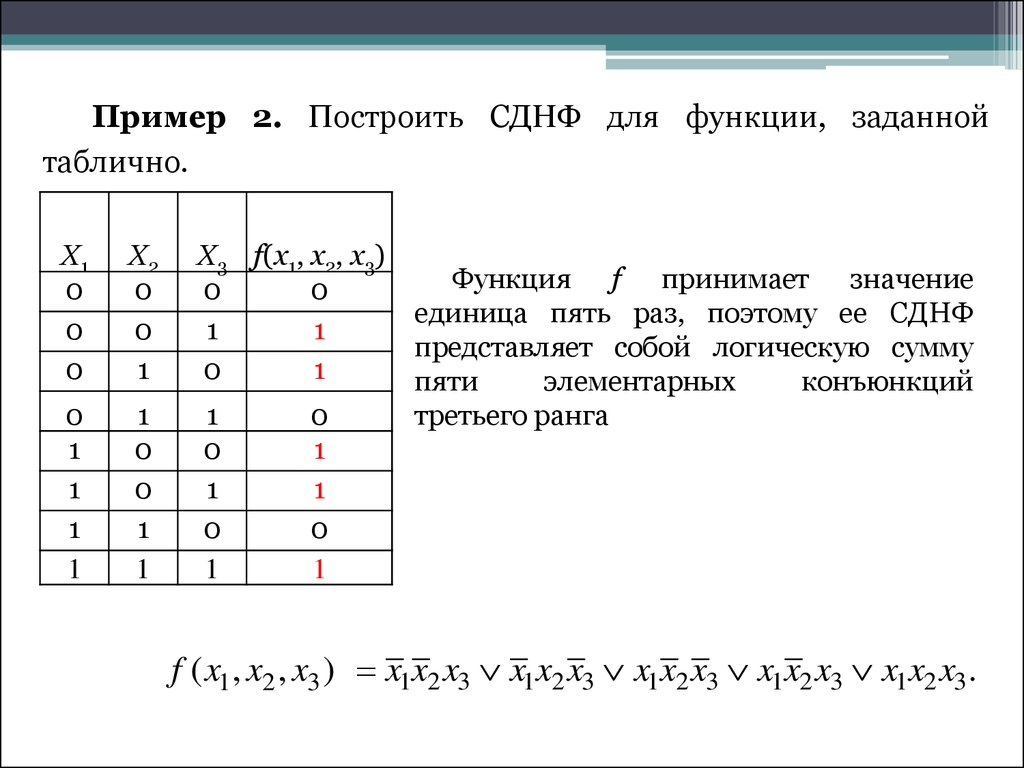



 В случае противного результата, в конъюнкцию включается ее отрицание.
В случае противного результата, в конъюнкцию включается ее отрицание.
 В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.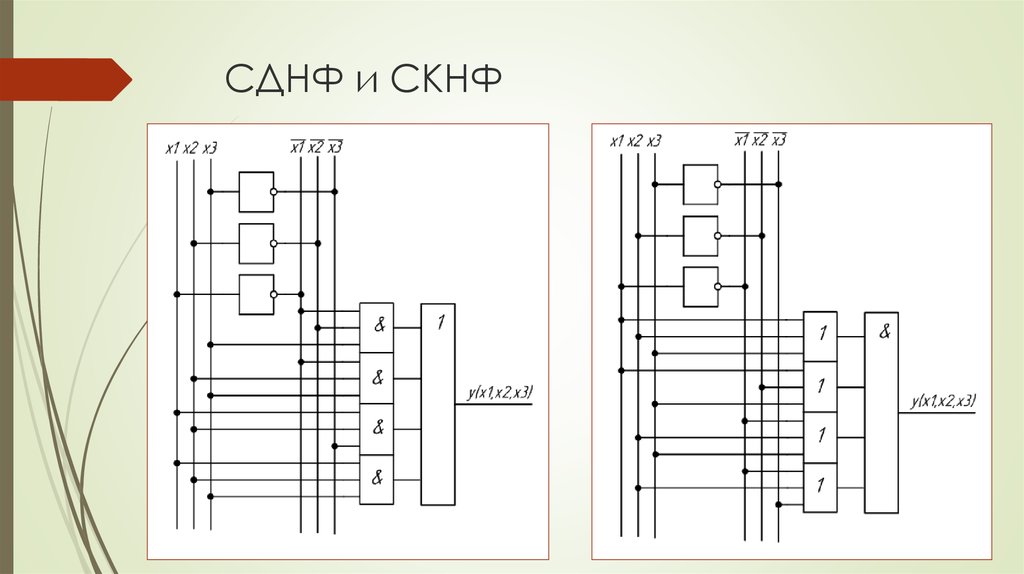
 config model.sdf
config model.sdf 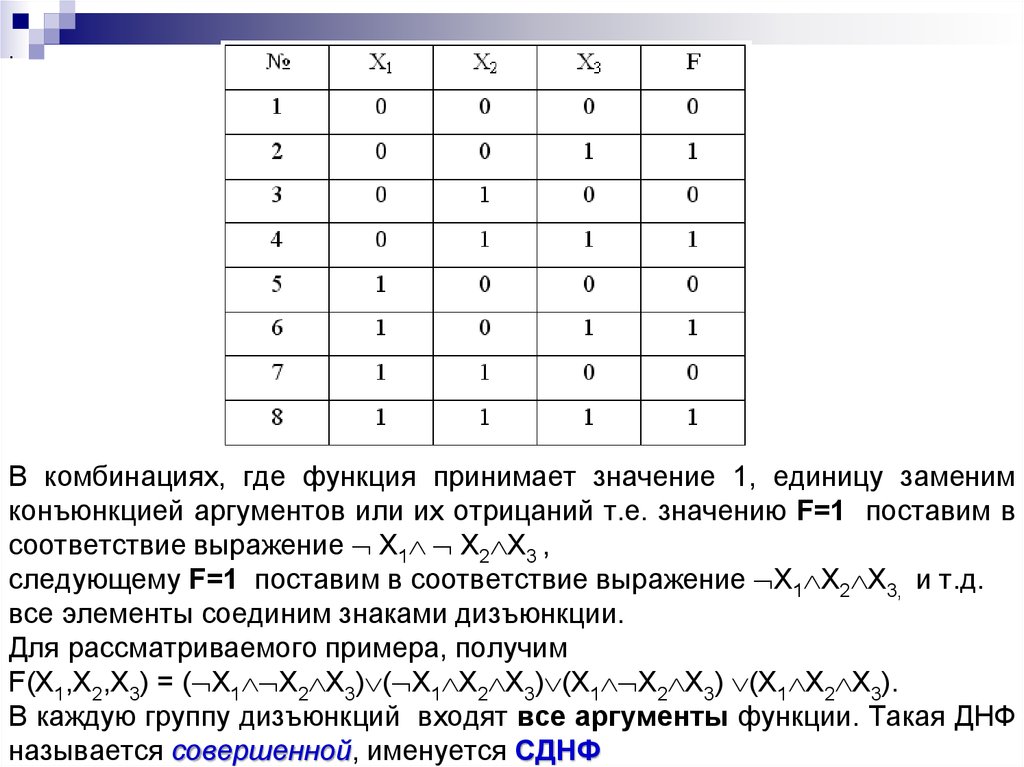 material
material