Функция у = tg х и построение ее графика
Похожие презентации:
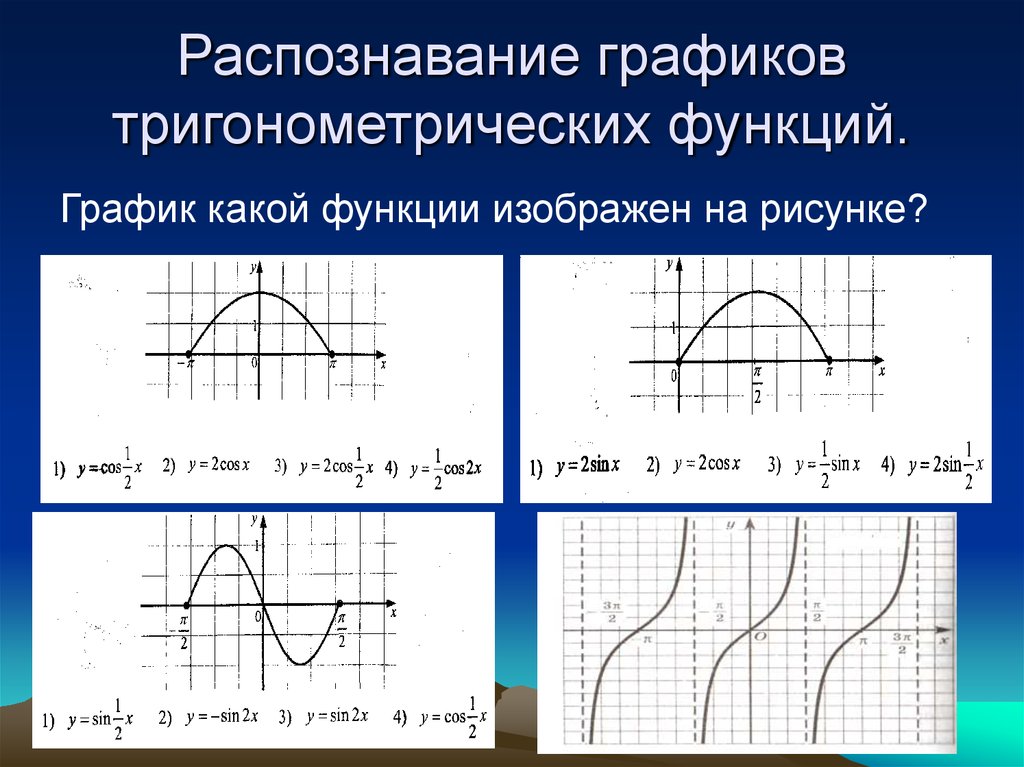
Функции y = tgx и y = ctgx, их свойства и графики
Тигонометрические функции и их графики
Построение графика квадратичной функции
Тригонометрические функции, их свойства и графики
Тригонометрические функции числового аргумента
Функции тангенса и котангенса
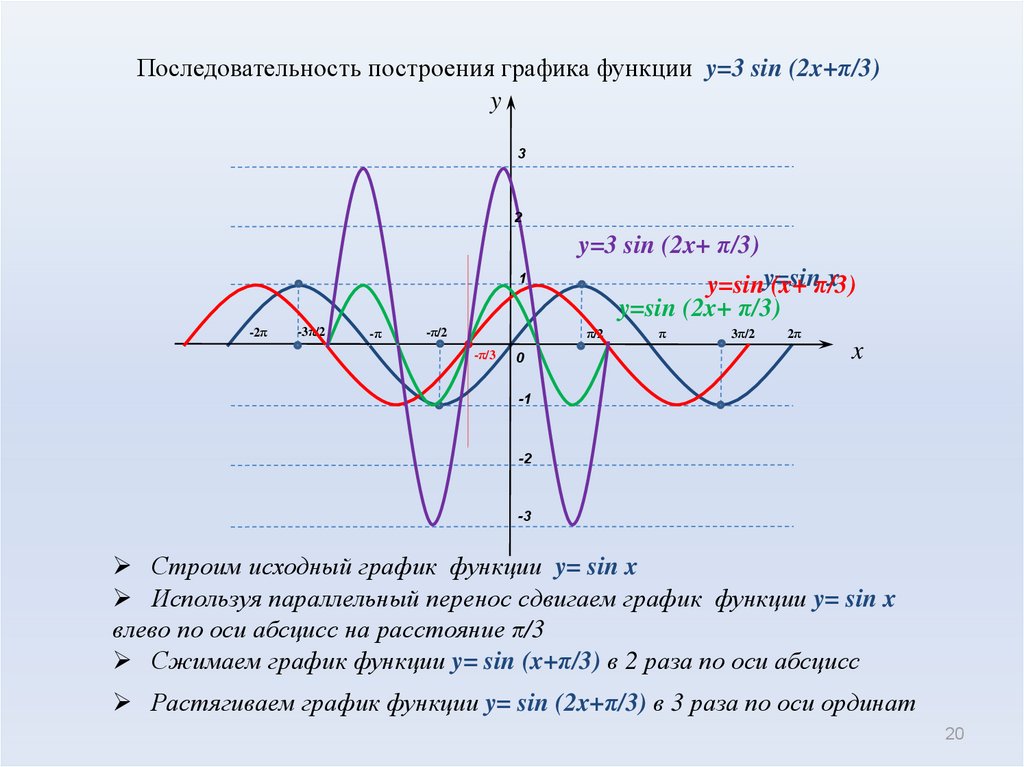
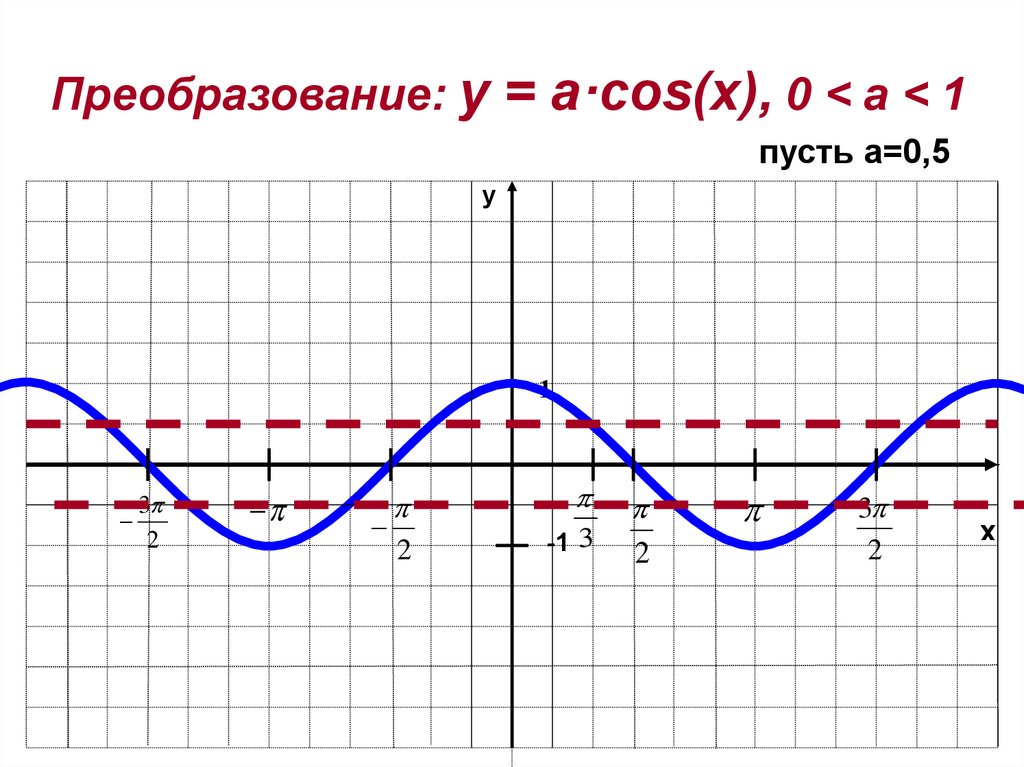
Преобразование графиков тригонометрических функций и их свойства
Построение и преобразование графиков тригонометрических функций
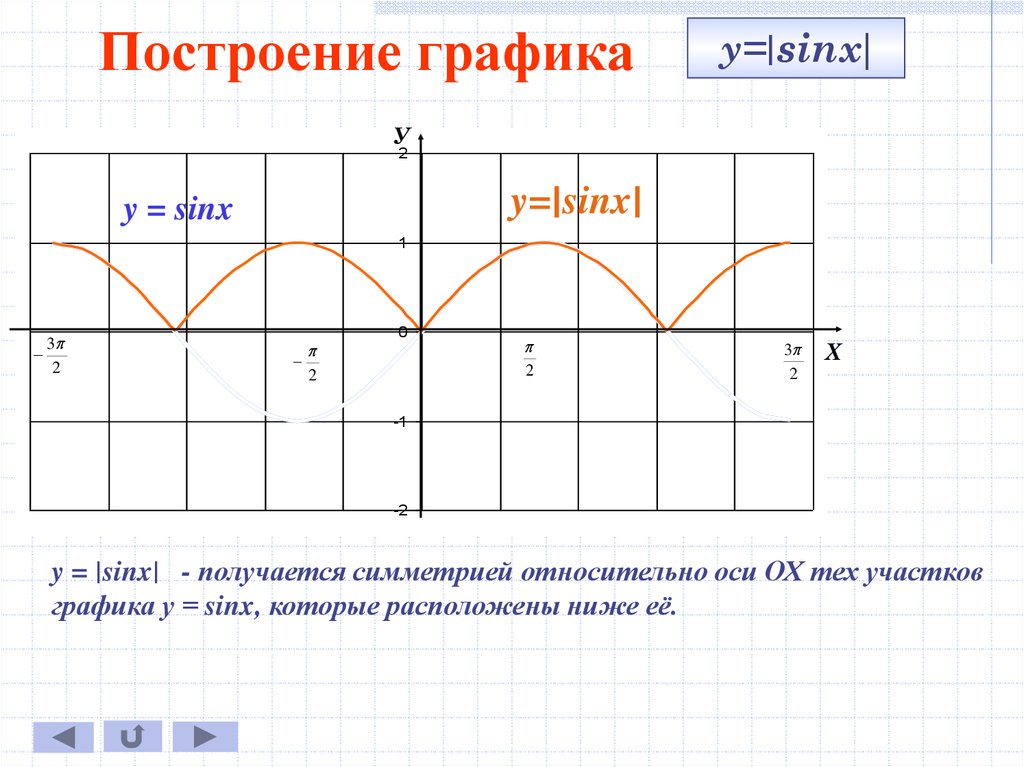
Построение графиков функций со знаком модуля
Функции и их графики
1. Функция у = tg х и построение ее графика.
.3. Определяем цели учебной деятельности
• 1.Выделите слова и словосочетания,встречаемые впервые.
• 2.Определите, знаете ли Вы точное
значение этих слов, а также тех слов и
словосочетаний, которые уже встречались
Вам, но точные их значения и определения
остаются Вам пока неизвестными.
4.
 Определяем цели учебной деятельности3. Какие новые определения и значения каких
Определяем цели учебной деятельности3. Какие новые определения и значения какихпонятий необходимо будет усвоить в рамках
изучения данной темы?
4. Какие умения нужно будет выработать?
5. Какие правила, алгоритмы, способы действий
Вам неизвестны , и для решения каких задач они
Вам будут нужны?
5. Тангенс.
Название «тангенс», происходящее от латинскогоtanger (касаться), появилось в 1583 г. Tangens
переводится как «касающийся»
Тангенсы возникли в связи с решением задачи об
определении длины тени.
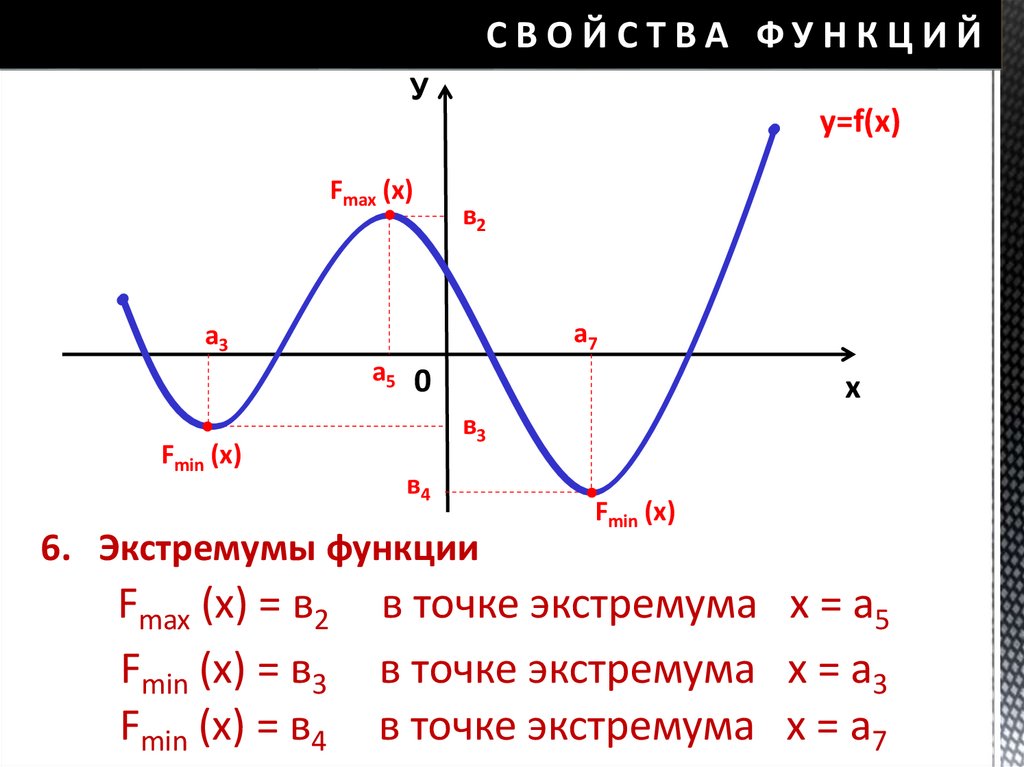
6. Предполагаемые цели учебной деятельности учеников
• 1. Определение функции тангенса, свойств этой функции• 2.Построение графика функции тангенс по таблице
значений и тем свойствам, которые известны для тангенса
(алгоритм построения). Узнать, на какой линии находятся
тангенсы углов.
7. Находим ответы на вопросы в учебнике.
Стр.17 -стр.18:
определение ,
линия тангенсов углов,
область определения,
область значений,
свойства тангенса, известные вам на
сегодняшний день.
8. Рисунок 10 из учебника
9. Функция у = tg х.
• Определение. Числовая функция, заданнаяформулой у = tgх, называется функцией
тангенса.
• Тангенс угла – отношение ординаты точки
на единичной окружности,
соответствующей данному углу, к абсциссе
этой точки.
• А где находятся тангенсы углов?
10. Тригонометрический круг
11. диктант
1Углом какой четверти является угол a, если:a = 185 градусов
a = –185 градусов
a = 102
a = –102
a = 250
a = –250
a = 375
a = 145
a = –145
a = 225
a = –315
a = 210
a = 590
a = –15
12. диктант
• 2. Вычислите:• 1 вариант.
• cos 180 + 5sin 90
sin 180 – 3 cos 0
5ctg 90 – 7tg 180
sin 60 + cos 30
• 2 вариант.
• cos 0 + 3sin 90
sin 270 – 2cos 180
6tg 180 + 2ctg 90
1 + ctg 270 – 5 tg 360
13. Нормы оценок
1.Все задания верны – оценка «5»
2. 1-2 ошибки – оценка «4»
3. 3- 5 ошибок – оценка «3»
4.
 более 5 ошибок – беру дополнительное
более 5 ошибок – беру дополнительноедомашнее задание.
• Успехов в учебе!
14. Ответы к диктанту.
• 1вариант. 1. III,II,II,III,III,II,I.2. 4,-3,0.
• 2вариант. 1.II,III,III,I,III,III,IV.
2. 0,2,4.
• Задание . Заполнить в тетради таблицу
значений для построения графика у = tg х.
Работа в парах.
15. Построение графика.
• Составляем план построения графика,пользуясь учебником.
16. План построения графика.
• 1 . Правильно выбери единичный отрезок.• 2. Найди область определения.
• 3 Проведи прямые у = π/2 + πn, где n
принадлежит целым числам.
• 4. Построй график.
• Работаем в парах.
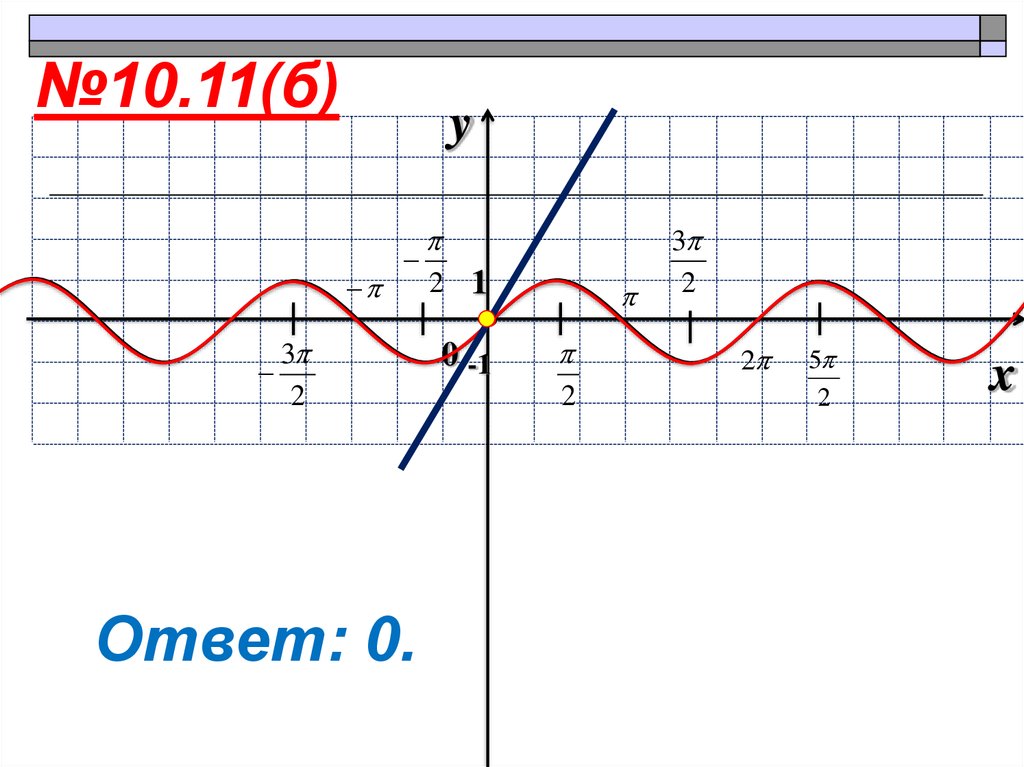
17. Линия тангенса
18. График функции в 1 четверти
• у = tg xy
1
0
6 3 2
x
19. у = tg x
y = tg xу
3
2
2
2
3
2х
20. Выполнение заданий.
• №37(В),33(г). Устно составить планвыполнения задания, обговорить в парах.
• Рефлексия.
 Ответьте на вопросы:
Ответьте на вопросы:• Какие новые знания вы приобрели на этом
уроке?
• Какие новые умения? Все ли цели урока
были достигнуты? .
21. Домашняя работа.
• 1. Построить по аналогичному график функциикотангенс.
• 2.Уметь доказывать по рис 10 из учебника, что
касательная к числовой окр., проведенная в точке
(1,0), является линией тангенсов.
• 36(а,б,в),38(а), 39(а,в,г)
• Творческое задание. По рис.11учебника, доказать,
что касательная прямая, проведенная в точке (0,1)
к числовой окружности, является линией
котангесов. Спасибо за урок.
22. Спасибо за урок.
English Русский Правила
Построение в Excel графиков математических и тригонометрических функций — Трюки и приемы в Microsoft Excel
Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.
Построение графиков математических функций с одной переменной
Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у
Рис. 140.1. Диаграмма представляет собой график функции SIN(x)
Функция выражается в таком виде: у = SIN(x).
Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2).
Чтобы создать эту диаграмму, выполните следующие действия.
- Выделите диапазон
А1:В22. - Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
 2)
2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.
Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂
Построение графиков математических функций с двумя переменными
Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у):
=SIN($A2)*COS($B1)На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.

Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными
Значения х находятся в диапазоне
А2:А22B1:V1.Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид:
=SIN($A2)*C0S(B$1).Чтобы создать диаграмму, выполните приведенные ниже действия.
- Выделите диапазон
A1:V22. - Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)Устройство для построения тригонометрических функций — MathCracker.
 com
comАлгебра Решатели
Инструкции: Используйте этот граф тригонометрических функций, чтобы получить график любой тригонометрической функции и различных параметров такие как период, частота, амплитуда, фазовый сдвиг и вертикальный сдвиг, если применимо:
Введите тригонометрическую функцию, которую вы хотите проанализировать (например, ‘3sin(pi*x+3)-2’ или ‘4cot(2(x-1))’ и т. д.)
Нижний предел домена (необязательно.
 Число, например 1 или 2/3 и т. д.) =
Число, например 1 или 2/3 и т. д.) =Верхний предел домена (Необязательно. Число, например 1 или 2/3 и т. д.) =
Тригонометрические функции имеют свойство повторять свое поведение. То есть они периодические. Математически это означает, что существует число \(P\) со свойством, что
\[е(х+Р) = е(х)\]
для всех значений \(х\). Это число \(P\) называется период . Все это говорит о том, что поведение функции повторяется в триггерных графиках каждые \(P\) единиц по оси X.

Обратите внимание, что во всех тригонометрических функциях, которые вы предоставляете для этого калькулятора, предполагается, что аргумент \(x\) равен измеряется в радианах.
Пример периодических функций
Например, для случая синусоидальной функции \(f(x) = \sin x\) график показан ниже:
Вы можете видеть, что поведение функции повторяется. Действительно, вы можете взять любой интервал длины \(2\pi\), и следующий интервал длины \(2\pi\) будет идентичен предыдущему с точки зрения формы функции.
Почему это происходит? Поскольку \(\sin(x + 2\pi) = \sin(x)\) для всех \(x\), то функция периодическая. Для упрощение с шагами, вы можете использовать этот калькулятор греха.

Что я могу построить с помощью этого плоттера тригонометрических функций?
Вы можете построить любую тригонометрическую функцию. Чаще всего используется для построения графиков синуса и косинуса, но вы можете использовать его для любого триггерная функция.
Вы увидите, что периодические функции можно сделать более сложными, смешивая их с другими алгебраическими выражениями.
Например, как ведет себя функция \(f(x) = 3\sin(2x+1)-4\) Ну, она даже периодическая? Да, вы держите пари. Поведение функции \(f(x) = 3\sin(2x+1)-4\) во всех отношениях аналогично поведению функции \(f(x) = \sin x\).
Этот графограф тригонометрических функций поможет вам найти график и специфические характеристики (период, частоту, амплитуду, фазовый сдвиг и сдвиг по вертикали) более сложных тригонометрических функций, таких как \(f(x) = 3\cos(\pi(x) -2)+3)-\frac{\pi}{4}\)
Скобки имеют значение?
Короткий ответ: ЭТО ЗАВИСИТ.

Графические калькуляторы
Этот граф имеет дело только с тригонометрическими функциями. Для того, чтобы график других функций , вы можете использовать наш плоттер общего назначения , который будет принимать любые функции, не только тригонометрические.
Пример триггерного графика
Вопрос : Рассмотрим функцию \(f(x) = \sin(3x-2)\).
 Найдите период, частоту, амплитуду и фазовый сдвиг. Также,
представить график функции.
Найдите период, частоту, амплитуду и фазовый сдвиг. Также,
представить график функции.Решение:
Предусмотрена следующая функция:
\[f(x) = \sin\left(3x-2\right)\]
На основе переданного аргумента тригонометрической функции частота и период вычисляются следующим образом:
\[ \begin{array}{ccl} \text{Точка} & = & \displaystyle\frac{2\pi}{3} \\\\ \\\\ & \ приблизительно & 2.0944 \end{массив}\]
, а также
\[ \begin{array}{ccl} \text{Частота} & = & \displaystyle\frac{3}{2\pi} \\\\ \\\\ & \ приблизительно & 0,4775 \end{массив}\]На основе предоставленной тригонометрической функции \(f(x) = \sin\left(3x-2\right)\) мы получаем, что:
• Амплитуда в этом случае равна \(A = 1\).

• Фазовый сдвиг равен \(\displaystyle\frac{2}{3} = 0,6667\).
• Вертикальный сдвиг равен \( 0\).
Подводя итог, для данного тригонометрическая функция
- Период = \(2,0944\)
- Частота = \(0,4775\)
- Амплитуда = \(1\)
- Фазовый сдвиг = \(0,6667\)
- Вертикальный сдвиг = \(\displaystyle 0\)
На основе приведенной выше информации получается следующий график:
Алгебра Калькулятор Алгебра Решатель График функций онлайн Геометрический калькулятор График функций синуса и косинуса Графический инструмент Графические инструменты Граф тригонометрических функций
Графики тригонометрических функций — изучите и поймите онлайн
Безусловно, лучший способ понять поведение тригонометрических функций — создать визуальное представление их графиков на координатной плоскости.
 Это помогает нам определить их ключевые особенности и проанализировать влияние этих функций на внешний вид каждого графика. Однако знаете ли вы, какие шаги нужно выполнить, чтобы построить график тригонометрических функций и их обратных функций? Если ваш ответ отрицательный, не беспокойтесь, мы проведем вас через весь процесс.
Это помогает нам определить их ключевые особенности и проанализировать влияние этих функций на внешний вид каждого графика. Однако знаете ли вы, какие шаги нужно выполнить, чтобы построить график тригонометрических функций и их обратных функций? Если ваш ответ отрицательный, не беспокойтесь, мы проведем вас через весь процесс.В этой статье мы определим, что такое графики тригонометрических функций, обсудим их ключевые особенности и покажем вам, как строить графики тригонометрических функций и их обратных функций на практических примерах.
Графики тригонометрических функций представляют собой графическое представление функций или отношений, определенных на основе сторон и углов прямоугольного треугольника. К ним относятся функции синуса (sin), косинуса (cos), тангенса (tan) и соответствующих им обратных функций косеканса (csc), секанса (sec) и котангенса (cot).
Каковы основные особенности графиков тригонометрических функций?
Перед тем, как перейти к построению графика тригонометрических функций, нам необходимо определить некоторые ключевые особенности о них:
Амплитуда
Амплитуда тригонометрических функций относится к коэффициенту вертикального растяжения , который вы можете рассчитать как абсолютное значение половины разницы между его максимальным значением и его минимальным значением.

Амплитуда функций y=sinθ и y=cosθ равна 1-(-1)2=1.
Для функций вида y=asinbθ или y=acosbθ амплитуда равна абсолютному значению a.
Амплитуда=a
Если у вас есть тригонометрическая функция y=2sinθ, то амплитуда функции равна 2. или максимальное значение.
Период
Период тригонометрических функций представляет собой расстояние по оси X от начала узора до точки, где он начинается снова.
Период синуса и косинуса равен 2π или 360º.
Для функций вида y=asinbθ или y=acosbθ, b известен как коэффициент горизонтального растяжения , и вы можете рассчитать период следующим образом:
Period=2πbor360°b
Для функций в
Период=πbor180°b
Найдите период следующих тригонометрических функций: =4ππ= 4
- y=tan13θ
Период=πb=π13=π13=3π
Область и диапазон
Область и область значений основных тригонометрических функций следующие:
901 86Тригонометрическая функция Домен Диапазон Синус Все действительные числа -1≤y≤1 Косинус Все действительные числа 9 0189 -1≤y≤1Тангенс Все действительные числа, кроме nπ2, где n=±1,±3,±5,.  ..
..Все действительные числа Косеканс Все действительные числа, кроме nπ, где n=0,±1,± 2,±3,… (-∞,-1]∪[1,∞) Секанс Все действительные числа, кроме nπ2, где n=±1,±3,±5,. .. (-∞,-1]∪[1,∞) Котангенс Все действительные числа, кроме nπ, где n=0,±1,±2,±3,… Все действительные числа Помните, что все тригонометрические функции являются периодическими , потому что их значения повторяются снова и снова после определенного периода.
Как построить график тригонометрических функций?
Чтобы построить график тригонометрических функций, выполните следующие действия:
Если тригонометрическая функция представлена в виде y=asinbθ, y=acosbθ или y=atanbθ, то определите значения a и b , и определите значения амплитуды и периода, как описано выше.
Создайте таблицу упорядоченных пар для точек, которые вы будете включать в график.
 Первое значение в упорядоченных парах будет соответствовать значению угла θ, а значения y будут соответствовать значению тригонометрической функции для угла θ, например, sin θ, поэтому упорядоченная пара будет (θ , sin θ). Значения θ могут быть либо в градусах, либо в радианах.
Первое значение в упорядоченных парах будет соответствовать значению угла θ, а значения y будут соответствовать значению тригонометрической функции для угла θ, например, sin θ, поэтому упорядоченная пара будет (θ , sin θ). Значения θ могут быть либо в градусах, либо в радианах.
Единичную окружность можно использовать для вычисления значений синуса и косинуса для наиболее часто используемых углов. Пожалуйста, прочитайте о тригонометрических функциях, если вам нужно вспомнить, как это сделать.
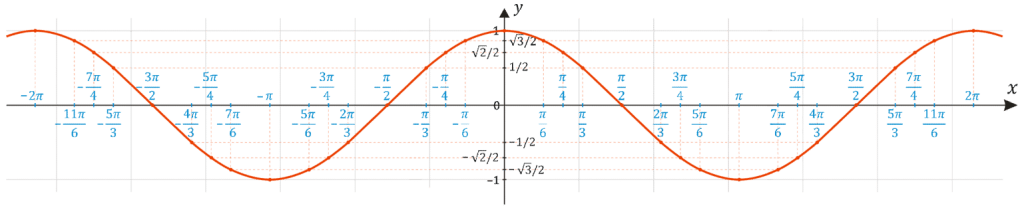
График синусов
Синус — это отношение длины противоположной стороны прямоугольного треугольника к длине гипотенузы.
График синусоидальной функции y=sinθ выглядит следующим образом:
Синусоидальный график, Марилу Гарсия Де Тейлор — StudySmarter Originals 5
график повторяется каждые 2π радиан или 360°.
- Выделите диапазон
Минимальное значение для синуса равно -1.
Максимальное значение для синуса равно 1.

Это означает, что амплитуда графика равна 1, а его период равен 2π (или 360°).
График пересекает ось x в точке 0 и через каждые π радиан до и после этого.
Функция синуса достигает своего максимального значения при π/2 и каждые 2π до и после этого.
Функция синуса достигает минимального значения при 3π/2 и каждые 2π до и после этого.
- Определите значения a и b
- Расчет амплитуды и периода:
- Таблица упорядоченных пар:
- Нанесите точки и соедините их плавной и непрерывной кривой:
График повторяется каждые 2π радиан или 360°.
Минимальное значение косинуса равно -1.
Максимальное значение косинуса 1.
Это означает, что амплитуда графика равна 1, а его период равен 2π (или 360°).
График пересекает ось x в точке π/2 и через каждые π радиан до и после этого.
Функция косинуса достигает своего максимального значения в 0 и каждые 2π до и после этого.
Функция косинуса достигает минимального значения в точке π и каждые 2π до и после этого.

- Определите значения a и b:
- Рассчитайте амплитуду и период: 90 096
- Таблица упорядоченных пар:
- Нанесите точки и соедините их плавной и непрерывной кривой:
График повторяется через каждые π радиан или 180°.
Нет минимального значения.
Нет максимального значения.
Это означает, что функция тангенса не имеет амплитуды и ее период равен π (или 180°).
График пересекает ось x в точке 0 и через каждые π радиан до и после этого.
График касательной имеет асимптот , которые являются значениями, где функция не определена .

Эти асимптоты находятся на π/2 и каждом π до и после этого.
- Определите значения a 9 0156 и б :
- Вычислить амплитуду и период:
- Нанесите точки и соедините их:
- Косеканс является обратной величиной по синусу .
- Секанс является обратной величиной косинуса .

- Котангенс является обратной величиной тангенса .
- График соответствующей функции синуса во-первых, использовать это как ориентир.
- Нарисуйте вертикальные асимптоты во всех точках, где функция синуса пересекает ось x.
- График косеканса коснется функции синуса в ее максимальном и минимальном значениях. Из этих точек нарисуйте отражение функции синуса, которое приближается к вертикальным асимптотам, но никогда не касается их, и простирается до положительной и отрицательной бесконечности.
- a=2,b=1
- Нет амплитуды
- Период=2πb=2π1=2π1=2π Илу Гарсия Де Тейлор — StudySmarter Originals
График секущей
Чтобы построить график функции секанса y=secθ, вы можете выполнить те же шаги, что и раньше, но используя соответствующую функцию косинуса в качестве ориентира.
 График секущих выглядит следующим образом:
График секущих выглядит следующим образом:График секущих, Марилу Гарсия Де Тейлор — StudySmarter Originals
График функции секущей имеет тот же период, что и график косинуса, который равен 2π или 360°, и также не имеет амплитуды.
График обратной тригонометрической функции y=12sec2θ
- a=12,b=2
- Нет амплитуды
- Период=2πb=2π2=2π2=π
Пример графика секущей , Марилу Гарсия Де Тейлор — StudySmarter Originals
График котангенса
График котангенса очень похож на график тангенса, но вместо того, чтобы быть возрастающей функцией, котангенс является убывающей функцией. График котангенса будет иметь асимптоты во всех точках, где функция тангенса пересекает ось x.
График котангенса, Марилу Гарсия Де Тейлор — StudySmarter Originals
Период графика котангенса такой же, как и период графика касательной, π радиан или 180°, и он также не имеет амплитуды.
График обратной тригонометрической функции y=3cotθ
- a=3,b=1
- Без амплитуды
- Период=πb=π1=π1=π
Пример графика котангенса, Марилу Гар Сиа Де Тейлор — StudySmarter Originals
Какие бывают графики обратных тригонометрических функций?
Обратные тригонометрические функции относятся к функциям арксинуса, арккосинуса и арктангенса, которые также могут быть записаны как Sin-1, Cos-1 и Tan-1.
 Эти функции противоположны функциям синуса, косинуса и тангенса, что означает, что они возвращают угол, когда мы подставляем в них значение sin, cos или tan.
Эти функции противоположны функциям синуса, косинуса и тангенса, что означает, что они возвращают угол, когда мы подставляем в них значение sin, cos или tan.Помните, что обратная функция получается путем замены x и y , то есть x становится y и y становится x .
Инверсия y=sinx равна x=siny, и вы можете увидеть ее график ниже:
График инверсии синуса, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Однако для того, чтобы обратные тригонометрические функции стали функциями , нам нужно ограничить свой домен . В противном случае обратные функции не являются функциями, поскольку они не проходят тест вертикальной линии. Значения в ограниченных областях тригонометрических функций известны как основные значения , и чтобы указать, что эти функции имеют ограниченную область применения, мы используем заглавные буквы:
Тригонометрическая функция Обозначение ограниченной области Основные значения Синус y=Sinx -π2≤x≤π2 Косинус y=Cosx 0≤x≤π Тангенс y=Tanx -π2 График арксинуса
Арксинус является обратной функцией синуса.
 Инверсия y=Sinx определяется как x=Sin-1y или x=Arcsiny. Область функции арксинуса будет представлять собой все действительные числа от -1 до 1, а ее диапазон представляет собой набор мер угла от -π2≤y≤π2. График функции арксинуса выглядит следующим образом:
Инверсия y=Sinx определяется как x=Sin-1y или x=Arcsiny. Область функции арксинуса будет представлять собой все действительные числа от -1 до 1, а ее диапазон представляет собой набор мер угла от -π2≤y≤π2. График функции арксинуса выглядит следующим образом:График арксинуса, Марилу Гарсиа Де Тейлор — StudySmarter Originals
График арккосинуса
Арккосинус является обратной функцией косинуса. Инверсия y=Cosx определяется как x=Cos-1y или x=Arccosy. Область функции арккосинуса также будет состоять из всех действительных чисел от -1 до 1, а ее диапазон представляет собой набор мер угла от 0≤y≤π. График функции арккосинуса показан ниже:
График арккосинуса, Марилу Гарсия Де Тейлор — StudySmarter Originals
График арктангенса
Арктангенс является обратной функцией тангенса. Инверсия y=Tanx определяется как x=Tan-1y или x=Arctany.
 домен функции арктангенса будет состоять из действительных чисел, а его диапазон представляет собой набор мер угла между -π2
домен функции арктангенса будет состоять из действительных чисел, а его диапазон представляет собой набор мер угла между -π2График арктангенса, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Если мы начертим все обратные функции вместе, они будут выглядеть так:
Графики арксинуса, арккосинуса и арктангенса вместе, Марилу Гарсия Де Тейлор — StudySmarter Originals
Дополнительные сведения по этой теме см. в статье «Обратные тригонометрические функции».
Графики тригонометрических функций. Ключевые выводы
- Графики тригонометрических функций представляют собой графическое представление функций или отношений, определенных на основе сторон и углов прямоугольного треугольника.
- Ключевые характеристики тригонометрических функций: амплитуда, период, домен и диапазон.
- Амплитуда тригонометрических функций относится к коэффициенту вертикального растяжения, который можно рассчитать как абсолютное значение половины разницы между его максимальным значением и минимальным значением.

График тригонометрической функции y=4sin2θ
a=4,b=2
90 084Амплитуда=а =4=4Period=2πb=2π2=2π2=π
| θ | y=4sin2θ | 0 | 0 |
| π4 | 4 |
| π2 | 0 |
| 3π4 | -4 |
| π | 0 |
Пример синусоидального графика , Марилу Гарсиа Де Тейлор — StudySmarter Originals
График косинуса
Косинус представляет собой отношение длины прилежащей стороны прямоугольного треугольника к длине гипотенузы.
График функции косинуса y=cosθ выглядит точно так же, как график синуса, за исключением того, что он сдвинут влево на π/2 радиана, как показано ниже.
График косинуса, Марилу Гарсия Де Тейлор — StudySmarter Originals
Наблюдая за этим графиком, мы можем определить ключевых характеристик функции косинуса :
График тригонометрической функции y=2cos12θ
a=2,b=12
Амплитуда=a=2=2Период=2πb=2π12 =2π12=4π
θ | y=2cos12θ | 0 | 2 |
| π | 0 |
| 2π | — 2 |
| 3π | 0 |
| 4π | 2 |
Пример графика косинуса, Марилу Гарсия Де Тейлор — StudySmarter Originals
График касательной
Тангенс представляет собой отношение длины противоположной стороны прямоугольного треугольника к длине прилежащей стороны.
График функции тангенса y=tanθ, однако, выглядит несколько иначе, чем функции косинуса и синуса. Это не волна, а прерывистая функция с асимптотами:
Диаграмма тангенса, Марилу Гарсия Де Тейлор — StudySmarter Originals
Наблюдая за этим графиком, мы можем определить ключевых характеристик функции тангенса :
Тангенс угла также можно найти по этой формуле:
tanθ=sinθcosθ
График тригонометрической функции y=34tanθ
a=34,b=1
Касательные функции имеют нет амплитуды . Period=πb=π1=π1=π
Пример касательного графика, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Каковы графики обратных тригонометрических функций?
Каждой тригонометрической функции соответствует обратная функция:
Для построения графика обратной тригонометрической функции можно действовать следующим образом:
График косеканса
График функции косеканса y=cscθ можно получить следующим образом:
График косеканса, Марилу Гарсиа Де Тейлор — StudySmarter Originals
График косеканса имеет тот же период, что и график синуса, т.е. 2π или 360°, и не имеет амплитуды.
График обратной тригонометрической функции y=2cscθ

 2)
2)
 com
com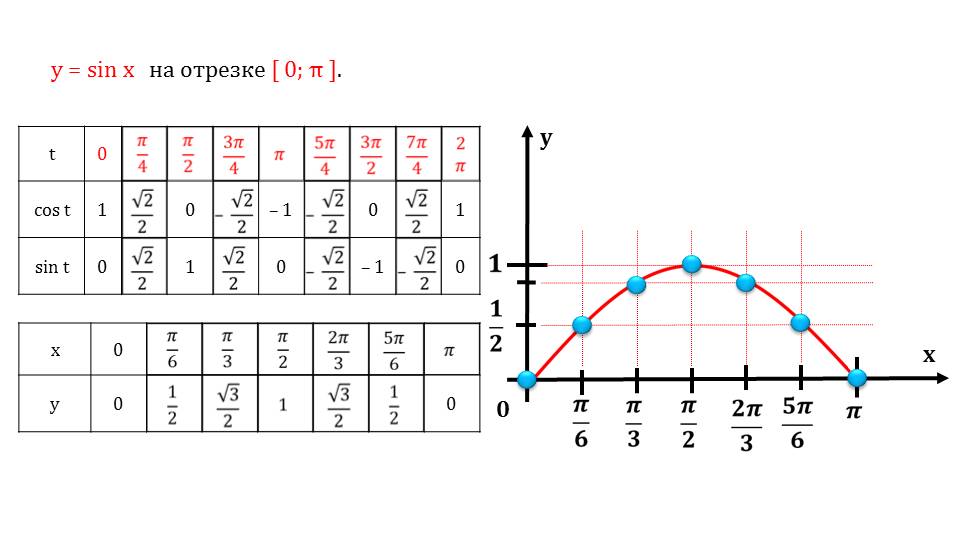 Число, например 1 или 2/3 и т. д.) =
Число, например 1 или 2/3 и т. д.) =

 Найдите период, частоту, амплитуду и фазовый сдвиг. Также,
представить график функции.
Найдите период, частоту, амплитуду и фазовый сдвиг. Также,
представить график функции.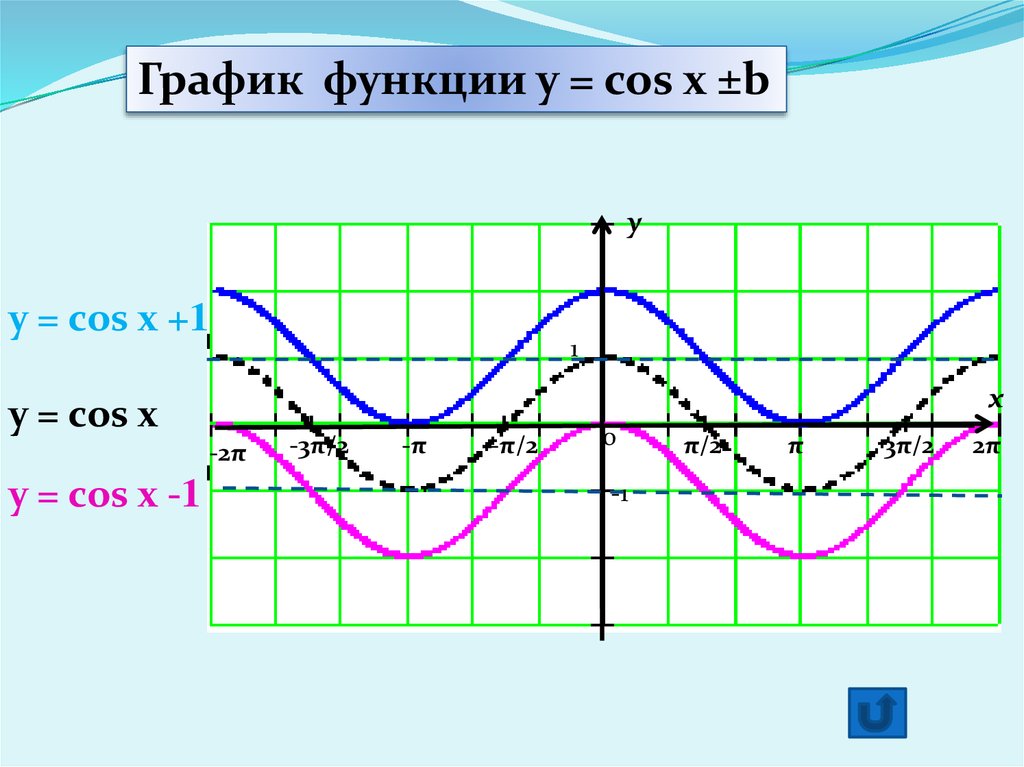
 Это помогает нам определить их ключевые особенности и проанализировать влияние этих функций на внешний вид каждого графика. Однако знаете ли вы, какие шаги нужно выполнить, чтобы построить график тригонометрических функций и их обратных функций? Если ваш ответ отрицательный, не беспокойтесь, мы проведем вас через весь процесс.
Это помогает нам определить их ключевые особенности и проанализировать влияние этих функций на внешний вид каждого графика. Однако знаете ли вы, какие шаги нужно выполнить, чтобы построить график тригонометрических функций и их обратных функций? Если ваш ответ отрицательный, не беспокойтесь, мы проведем вас через весь процесс.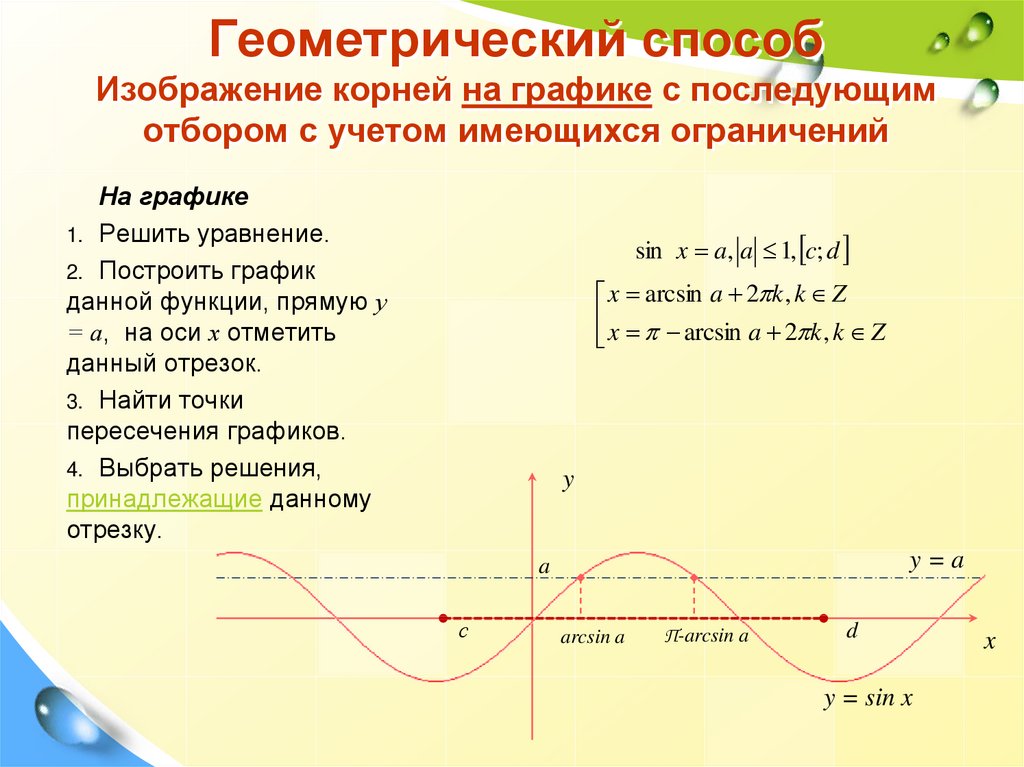
 ..
.. Первое значение в упорядоченных парах будет соответствовать значению угла θ, а значения y будут соответствовать значению тригонометрической функции для угла θ, например, sin θ, поэтому упорядоченная пара будет (θ , sin θ). Значения θ могут быть либо в градусах, либо в радианах.
Первое значение в упорядоченных парах будет соответствовать значению угла θ, а значения y будут соответствовать значению тригонометрической функции для угла θ, например, sin θ, поэтому упорядоченная пара будет (θ , sin θ). Значения θ могут быть либо в градусах, либо в радианах.
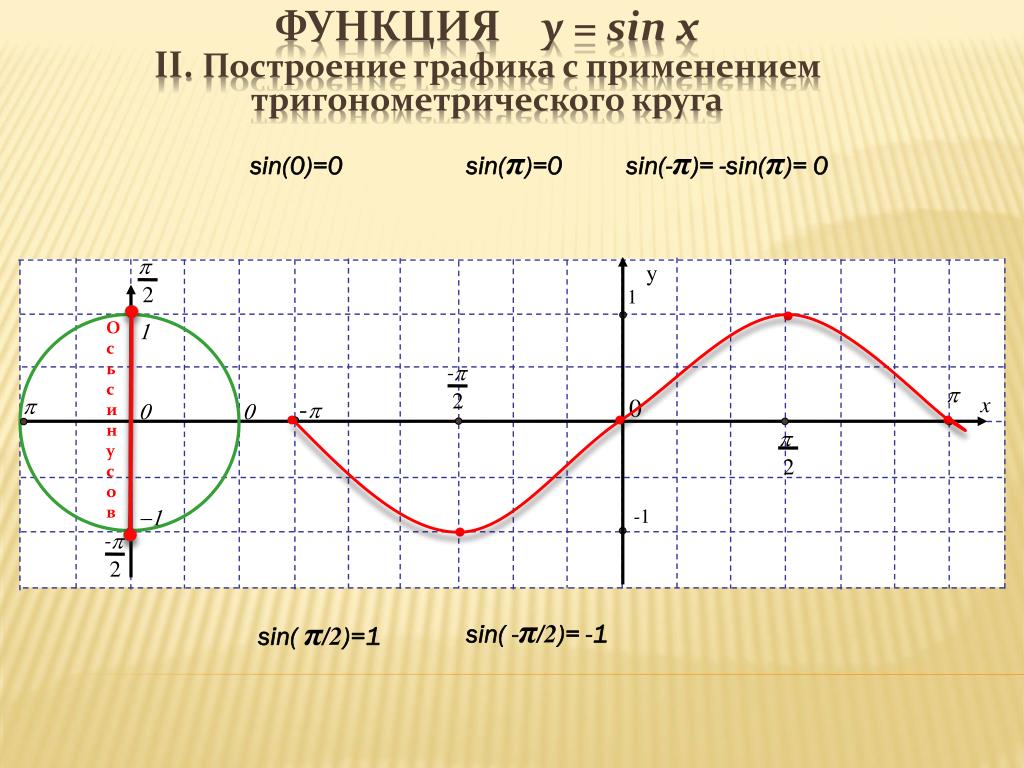
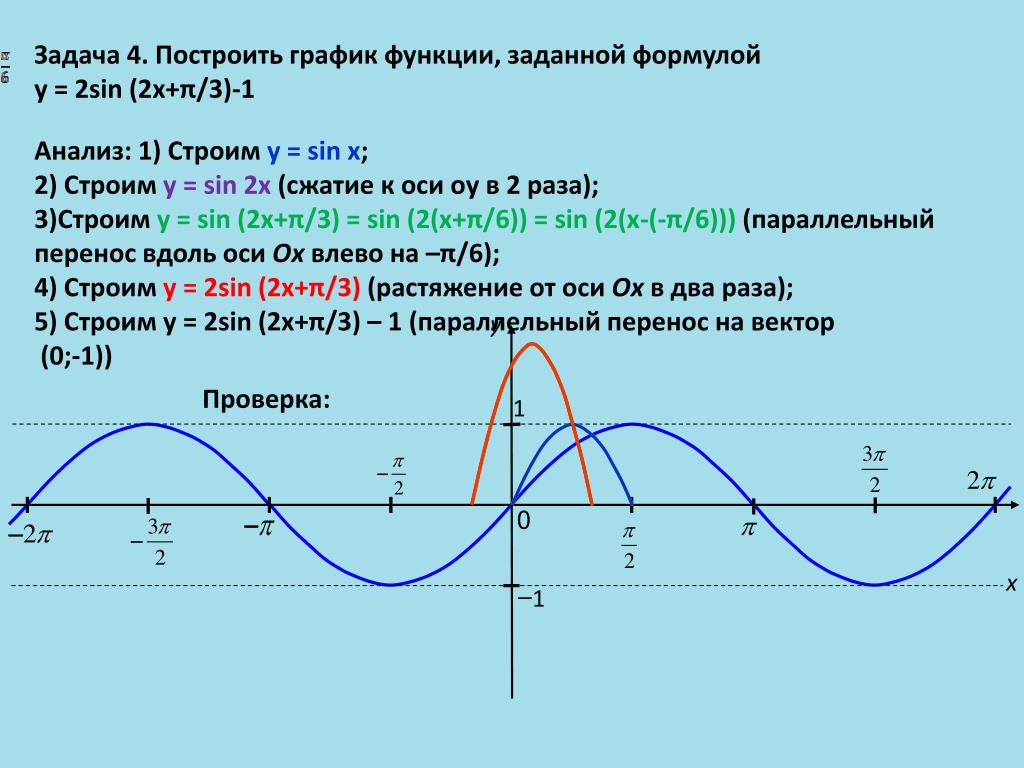
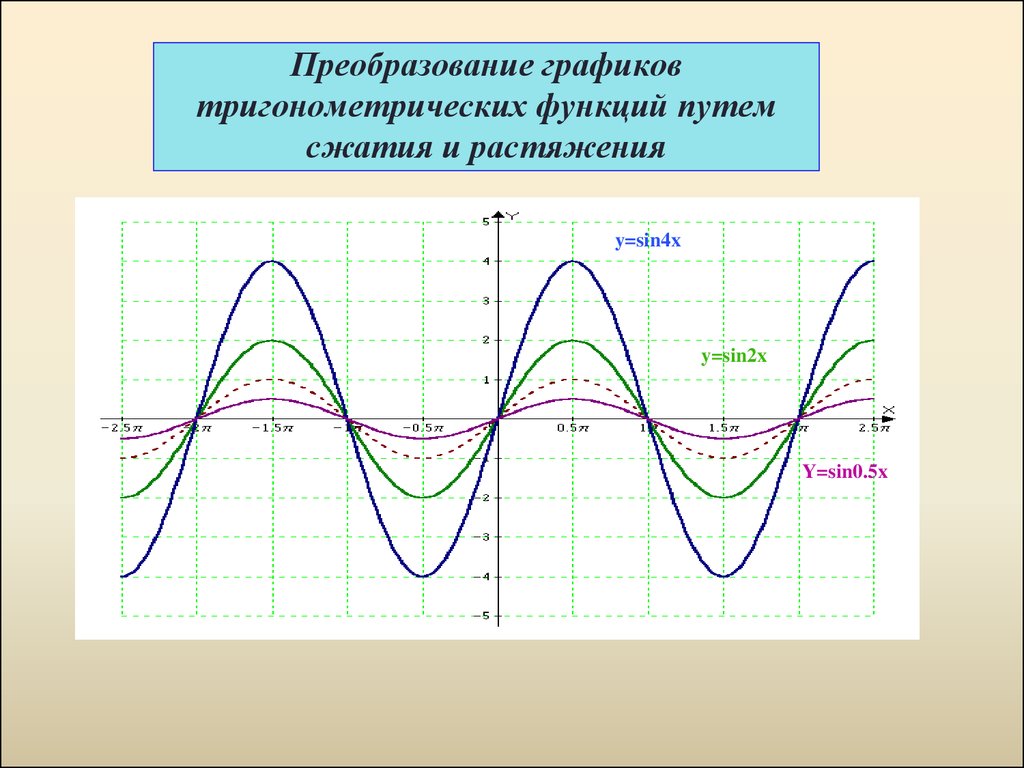 График секущих выглядит следующим образом:
График секущих выглядит следующим образом: Эти функции противоположны функциям синуса, косинуса и тангенса, что означает, что они возвращают угол, когда мы подставляем в них значение sin, cos или tan.
Эти функции противоположны функциям синуса, косинуса и тангенса, что означает, что они возвращают угол, когда мы подставляем в них значение sin, cos или tan.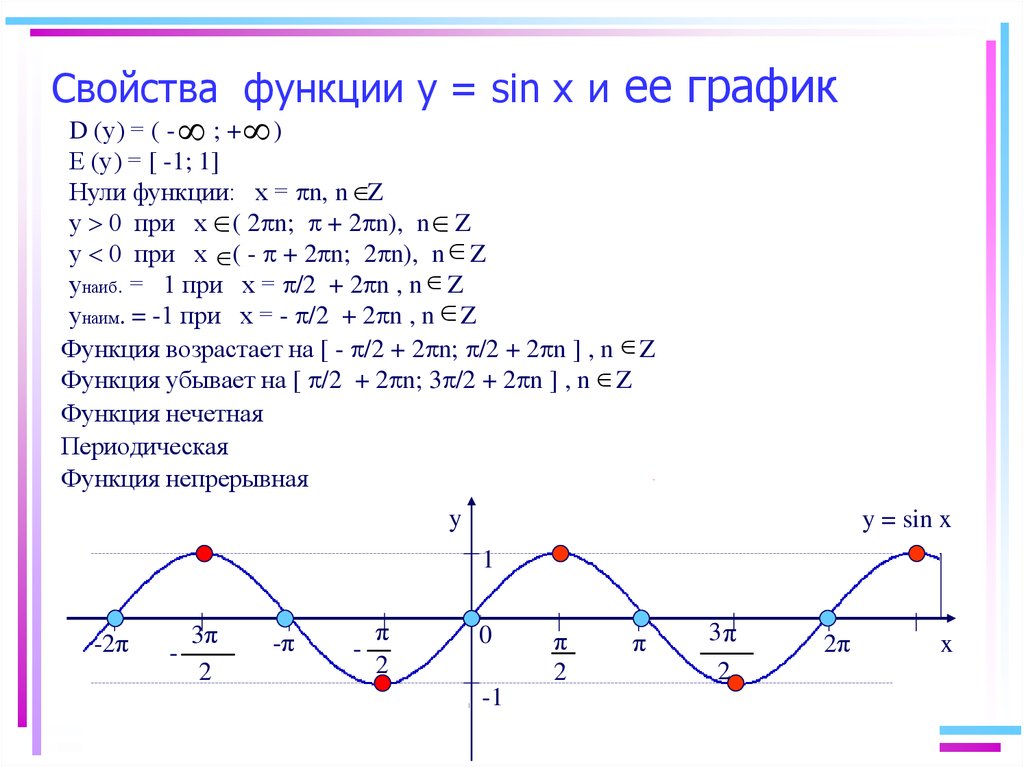 Инверсия y=Sinx определяется как x=Sin-1y или x=Arcsiny. Область функции арксинуса будет представлять собой все действительные числа от -1 до 1, а ее диапазон представляет собой набор мер угла от -π2≤y≤π2. График функции арксинуса выглядит следующим образом:
Инверсия y=Sinx определяется как x=Sin-1y или x=Arcsiny. Область функции арксинуса будет представлять собой все действительные числа от -1 до 1, а ее диапазон представляет собой набор мер угла от -π2≤y≤π2. График функции арксинуса выглядит следующим образом: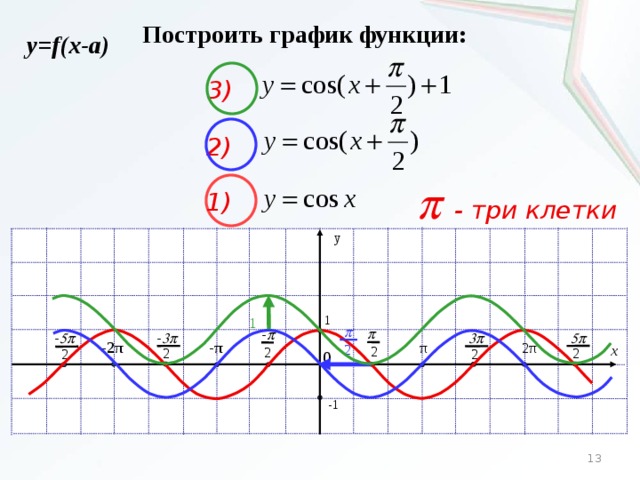 домен функции арктангенса будет состоять из действительных чисел, а его диапазон представляет собой набор мер угла между -π2
домен функции арктангенса будет состоять из действительных чисел, а его диапазон представляет собой набор мер угла между -π2