Постройте график функции с модулем: Графики функций с модулем

График функции с модулем и дробью

График функции с модулем и дробью — ещё одна группа заданий номера 23 ОГЭ по математике.

Подобно функциям с переменной в знаменателе, графики таких функций могут содержать выколотую точку. Как и при построении графиков функций с модулем, рассматриваем два варианта раскрытия модуля.

1) Построить график функции

   

и определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Решение:

Так как x²=|х|², формулу, задающую функцию, перепишем в виде

   

В знаменателе общий множитель |х| вынесем за скобки

   

Найдём область определения функции.

|х|(|х|-1)≠0

|х|≠0; |х|-1≠0

x≠0; |х|≠1

x≠0, x≠±1.

D(y):x∈(-∞;-1)∪(-1;0)∪(0;1)∪(1;∞).

Сократив дробь на (|х|-1), получаем

   

При x>0 |х|=x,

   

— функция обратной пропорциональности. График — гипербола. Для построения гиперболы возьмём несколько точек (включая выколотую x=1):

   

При x<0 |х|=-x,

   

— функция обратной пропорциональности.

   

Прямая y=kx не имеет с графиком общих точек, если она проходит через выколотые точки либо совпадает с осью Ox, то есть при k=±1 и k=0:

Ответ: -1; 0; 1.

2)Постройте график функции

   

и определите, при каких значениях m прямая y=m не имеет с графиком ни одной общей точки.

Решение:

В числителе вынесем за скобки общий множитель 0,25x:

   

Ищем область определения функции.

x+2≠0

x≠-2.

D(y):x∈(-∞;-2)∪(-2;∞).

Сокращаем дробь на (x+2):

   

Получили функцию, содержащую переменную под знаком модуля (при условии x≠-2).
При x=0, y=0,25·0·|0|=0.

При x>0 |х|=x, y=0,25·x·|x|= y=0,25·x·x=0,25x².

y=0,25x² или

   

— квадратичная функция. График — парабола, полученная из параболы y=x² сжатием к оси Ox в 4 раза.

При x<0 |х|=-x, y=0,25·x·|x|= y=0,25·x·(-x)=-0,25x².

   

— квадратичная функция. График — парабола, полученная из параболы y=-x² сжатием к оси абсцисс в 4 раза.

Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку, то есть при m=-1:

Ответ: -1.

3) Построить график функции

   

и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.

Решение:

Найдём область определения функции: x≠0.

D(y):x∈(-∞;0)∪(0;∞).

Если

   

   

   

то есть при x∈[-4;0)∪[4;∞), то

   

   

   

y=x/4 -функция прямой пропорциональности. График — прямая, проходящая через начало координат.

Для построения прямой достаточно взять одну точку, например, при x=4 y=4/4=1. Вторая точка — точка O — на графике выколотая, так как x≠0. Для более точного построения прямой лучше взять ещё одну точку: при x=-4 y=-4/4=-1.

Если

   

то есть при x∈(-∞;-4)∪(0;4), то

   

   

   

y=4/x — функция обратной пропорциональности. График — гипербола.

Для построения гиперболы возьмём несколько точек из промежутков (-∞;-4)∪(0;4) (-4 и 4 также лучше взять для уточнения построения графика).

Прямая y=m имеет с графиком ровно одну общую точку при m=1 и m=-1:

Ответ: -1; 1.

Рубрика: ОГЭ задание 22 | Комментарии

Как построить график модуля функции и график корня

График и свойства функции у = │ах│ (модуль)

Рассмотрим функцию у = │ах│, где а — определенное число.

Областью определения функции у = │ах│, является множество всех действительных чисел. На рисунке изображены соответственно графики функций у = │х│, у = │ 2х │, у = │х/2│.

Можно заметить, что график функции у = | ах | получается из графика функции у = ах, если отрицательную часть графика функции у = ах (она находится ниже оси Ох), отразить симметрично этой оси.

По графику легко усмотреть свойства функции у = │ ах │.

При х = 0, получаем у = 0, то есть графику функции принадлежит начало координат; при х = 0, получаем у > 0, то есть все  другие точки графика лежат выше оси Ох.

Для противоположных значений х, значения у будут одинаковыми; ось Оу это ось симметрии графика.

К примеру, можно построить график функции у = │х³│. Чтобы сравнить функции у = │х³│и у = х³, составим таблицу их значений при одинаковых значениях аргументов.

Из таблицы видим, что для того, чтобы построить график функции у = │х³│, можно начать с построения графика функции у = х³. После этого стоит симметрично оси Ох отобразить ту его часть, которая находится ниже этой оси. В результате получим график, изображенный на рисунке.

График и свойства функции у = x^1/2 (корень)

Рассмотрим функцию у = x^1/2.

Областью определения этой функции является множество неотрицательных действительных чисел, так как выражение x^1/2 имеет значение только при х > 0.

Построим график. Для составления таблицы ее значений используем микрокалькулятор, округляя значения функции до десятых.

После нанесения на координатную плоскость точек, и плавного их соединения, получаем график функции у = x^1/2.

Построенный график позволяет сформулировать некоторые свойства функции у = x^1/2.

При х = 0, получаем у = 0; при х > 0, получаем у > 0; график проходит через начало координат; остальные точки графика расположены в первой координатной четверти.

Теорема. График функции у = x^1/2 симметричен графику функции у = х², где х > 0, относительно прямой у = х.

Доказательство. Графиком функции у = х², где х > 0, является ветвь параболы, расположенная в первой координатной четверти. Пусть точка Р (а; b) — произвольная точка этого графика. Тогда истинно равенство b = а². Поскольку по условию число а неотрицательное, то истинно также и равенство а = b^1/2. А это означает, что координаты точки Q (b; а) превращают формулу у = x^1/2 в истинное равенство, или иначе, точка Q (b; а) принадлежит графику функции у = x^1/2.

Так же доказывается, что если точка М (с; d) принадлежит графику функции у = x^1/2, то точка N (d; с) принадлежит графику у = х², где х > 0.

Получается, что каждой точке Р (а; b) графика функции у = х², где х > 0, соответствует единственная точка Q (b; а) графика функции у = x^1/2  и наоборот.

Остается доказать, что точки Р (а; b) и Q (b; а) симметричны относительно прямой у = х. Опустив перпендикуляры на координатные оси из точек Р и Q, получаем на этих осях точки Е (а; 0), D (0; b), F (b; 0), С (0; а). Точка R пересечения перпендикуляров РЕ и QC имеет координаты (а; а) и поэтому принадлежит прямой у = х. Треугольник PRQ является равнобедренным, так как его стороны RP и RQ равны │ b – а│ каждая. Прямая у = х делит пополам как угол DOF, так и угол PRQ и пересекает отрезок PQ в определенной точке S. Поэтому отрезок RS является биссектрисой треугольника PRQ. Поскольку биссектриса равнобедренного треугольника является его высотой и медианой, то PQ ┴RS и PS = QS. А это означает, что точки Р (а; b) и Q (b; а) симметричные относительно прямой у = х.

Поскольку график функции у = x^1/2 симметричен графику функции у = х², где х > 0, относительно прямой у = х, то графиком функции у = x^1/2 является ветвь параболы.

Модульные функции: определение, уравнения и правила

Модульные функции (также известные как функции абсолютного значения) обычно представляются как f(x)=|x|. Модуль числа x будет числом той же величины, но положительным.

Но что стоит за этим? Это происходит потому, что он представляет собой расстояние от нуля до числа x на числовой прямой.

Расстояние от нуля до 2 равно 2, и расстояние от нуля до -2 также равно 2, поэтому f(2)=|2|=2 и f(-2)=|-2|=2

Функция модуля на числовой прямой, Марилу Гарсиа Де Тейлор — StudySmarter Originals

Вот почему |x| представляет собой значение числа x независимо от его знака.

Если у вас есть выражение внутри функции модуля, вычислите значение внутри, а затем найдите положительную версию результата.

Если у вас есть функция f(x)=|x-3|+1 findf(-2)

f(-2)=|-2-3|+1

f(-2)=|- 5|+1=5+1=6

Уравнение модульных функций

Уравнение модульной функции обозначается следующим образом:

f(x)=|x|=xifx≥0-xifx<0

а диапазон — это набор всех действительных чисел, больших или равных нулю. Из уравнения мы можем сказать, что если число внутри функции модуля уже положительное, вы оставляете его таким, но если число отрицательное, то результатом будет положительная версия этого числа (как если бы вы умножали отрицательное число на -1).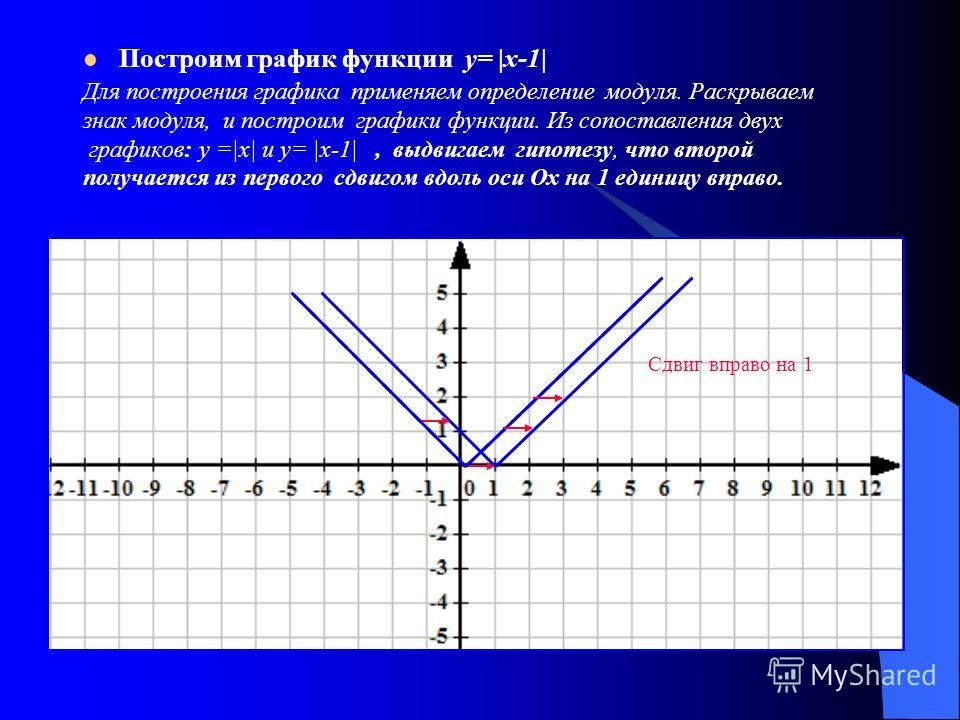

Свойства модульных функций

Свойства модульных функций:

|4|=4,|-5|=5

|x|=|-x|=x

|4|=|-4 |=4

|axb|=|a|x|b|

|2(-3)|=|2|×|-3||-6|=2×36=6

|ab|=|a||b|

|-93|=|-9||3||-3|=933=3

|a±b|≠|a|±|b|

Сумма:

|1+(-2)|≠|1|+|-2||-1|≠1+21≠3

Вычитание:

|1-(-2) |≠|1|-|-2||3|≠1-23≠-1

Имея в виду, что значение x внутри функции модуля может быть как положительным, так и отрицательным, вам необходимо решить уравнение с учетом обоих случаев, поэтому вы получите два решения.

Для уравнения |3x-2|=4 можно получить 2 возможных решения следующим образом:

1) Решение 1:

3x-2=43x=4+23x=6x=63x=2

2) Решение 2:

-(3x-2)=4-3x+2=4-3x=4-2-3x=2x=-23

Как построить график функций модуля?

Чтобы нарисовать график функции модуля, вам нужно подставить значения x в f(x)=|x|, чтобы получить соответствующие значения y, поскольку y=f(x). Вы получите таблицу значений x и y, которые вам нужно будет нанести на координатную плоскость. Подставим значения x от -2 до 2.

9009 1 -1

x	y
-2	2
1
0	0
1	1
2	2

График функции модуля, Марилу Гарсия Де Тейлор — StudySmarter Originals

9000 2 Чтобы нарисовать график функции модуля y=|ax+b|, вам нужно нарисуйте y=ax+b и отразите часть линии, которая идет ниже оси x, в ось x.

Нарисуйте график для y=|x-1| показывая точки, где они пересекают оси координат.

Не обращая внимания на модуль, нужно нарисовать график y=x-1

• Когда y=0, x=1

Линия пересекает ось x в точке (1, 0)

• Когда x=0, ⁣y=-1

Линия пересекает у -ось в точке (0, -1)

Пример графика функции модуля, Марилу Гарсиа Де Тейлор — StudySmarter Originals

• Для отрицательных значений y отразите по оси x. В этом случае (0, -1) становится (0, 1)

Пример графика модульной функции, Марилу Гарсия Де Тейлор — StudySmarter Originals

Решение уравнений с использованием модульных функций

Если у вас есть уравнение типа |3x-1|=5, вы можете использовать его график, чтобы найти его решение, выполнив следующие шаги:

Решение уравнений с использованием модульных функций, Марилу Гарсия Де Taylor — StudySmarter Originals

• Определите точки пересечения двух графиков. В этом случае A соответствует точке пересечения между y = 5 и исходным участком графика |3x-1|=3x-1, а B представляет пересечение между y=5 и отраженным участком графика |3x-1|=-(3x-1).

• Найдите оба решения:

А: 3x-1=5

3x=5+1

3x=6 =63

х=2

В: — (3x-1)=5

-3x+1=5

-3x=5-1

-3x=4

x=-43

Решение неравенств с использованием модульных функций

Основываясь на предыдущем примере, теперь мы собираемся решить неравенство |3x-1|>5. Вам нужно действовать так же, как и раньше, чтобы найти значения x в точках пересечения A и B, которые равны x=2 и x=-43.

После того, как у вас есть точки пересечения, вы можете посмотреть на график, чтобы определить значения x, которые удовлетворяют неравенству |3x-1|>5.

Решение неравенств с использованием модульных функций, Марилу Гарсиа Де Тейлор — StudySmarter Originals

Неравенство верно, когда график y=|3x-1| находится выше графика y=5, это происходит при x<-43 или x>2. В записи множества: {x:x<-43}∪{x:x>2}

Обратная функция модуля

обратная функция модуля не является функцией , если вы не ограничите ее область определения так, чтобы она могла быть взаимно однозначной функцией. Чтобы добиться этого, нам нужно ограничить область его применения только половиной графа. Вы можете выбрать любую половину, если она не указана в вопросе.

Найдите обратную функцию f(x)=|x+1|

Обратные функции модуля, Марилу Гарсия Де Тейлор — StudySmarter Originals

Мы ограничим область определения функции только отраженным участком графика (слева от x = -1), который можно обозначить как f(x)=-(x+1) для x≤-1. Теперь мы можем найти обратную, потому что этот участок графика является взаимно однозначной функцией.

Выполните шаги, чтобы найти обратную функцию:

• Замените f (x) на y

f(x)=-(x+1)

y=-(x+1)

• Поменяйте местами x и y и найдите y

x=-(y+1)

x=-y-1

y=-x-1

f-1(x)=-x-1 Это функция, обратная f(x)=|x+1|

Область определения обратной функции — это диапазон исходной функции, который равен y≥0. Следовательно, область определения обратной функции f-1(x)=-x-1 равна x≥0.

Как отличить функцию модуля?

Чтобы найти производную функции модуля, нам нужно еще раз взглянуть на уравнение функции модуля:

f(x)=|x|=xifx≥0-xifx<0

Мы знаем, что ddxx=1, поэтому можем сказать следующее:

ddx(|x|)=1ifx>0-1ifx<0Notdefinedifx=0

В общем случае ddx(|x|)=x|x| для всех значений x, кроме x=0

Если мы подставим некоторые значения x в предыдущее уравнение, то увидим, что утверждения в приведенной выше кусочной функции верны:

ddx(|-1|)=-1 |-1|=-11=-1

ddx(|0|)=0|0|=00=undefined

ddx(|1|)=1|1|=11=1

Как интегрировать модульная функция?

Чтобы найти интеграл модульной функции, мы можем действовать следующим образом:

Мы знаем, что модульная функция определяется следующим образом:

f(x)=|x|=xifx≥0-xifx<0

Следовательно, нам нужно вычислить интеграл для x и -x.

Помните, что x имеет показатель степени 1 (x=x1)

∫|x|dx=∫x1dxifx≥0∫-x1dxifx<0

Используя формулу интегрирования: ∫xndx=xn+1n+1+c

∫|x|dx=12×2+cifx≥0-(12×2)+cifx<0

Функции модуля — основные выводы

• Модуль числа x будет тем же числом, но положительным.
• Модуль числа x представляет собой расстояние от нуля до этого числа x на числовой прямой.
• Чтобы начертить график функции модуля y=|ax+b|, вам нужно начертить y=ax+b и отразить часть линии, которая идет ниже оси x, в ось x.
• Рисование графиков уравнений или неравенств, включающих модульные функции, может помочь решить их путем нахождения координат x точек пересечения двух графиков.
• Функция, обратная модульной функции, не является функцией, если вы не ограничите ее область определения только половиной графика, чтобы она могла быть взаимно однозначной функцией.
• При нахождении производной и интеграла модульной функции будет два возможных решения, учитывая, что когда f(x)=|x|=x (для x≥0) и когда f(x)=|x|=- х (при х<0).

Как построить график функции абсолютного значения

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительное исчисление
  • Статистика
  • Тригонометрия

  репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский диалект
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочее

  • Бухгалтерский учет
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все ресурсы по алгебре 1

10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Learn by Concept

Алгебра 1 Помощь » Функции и линии » График » Как построить график функции абсолютного значения

Какое из этих уравнений, скорее всего, будет уравнением, соответствующим приведенному выше графику?

Возможные ответы:

Правильный ответ:

Объяснение:

Это график абсолютного значения. Его уравнение принимает вид , в котором  представлено количество единиц, на которые базовый граф переводится вправо и вверх соответственно.

 

Поскольку график  переведен на две единицы вправо и на одну единицу вниз,  и , уравнение будет таким:

или

Сообщить об ошибке -перехват(ы) графика функции

Возможные ответы:

В графе нет -перехватов.

Правильный ответ:

Объяснение:

Чтобы найти -перехват(ы) графика, установите  и решите для .

 

Перепишите это как составное уравнение:

или

 

900 02 Решите каждое отдельно:

 

 

Есть два -перехвата: 

Сообщить об ошибке

 

Какой из них наиболее вероятно будет уравнение, соответствующее приведенному выше графику?

Возможные ответы:

Правильный ответ:

Объяснение:

Это график абсолютного значения. Его уравнение принимает вид , в котором  представлено количество единиц, на которые базовый граф переводится вправо и вверх соответственно.

 

Поскольку график переводится на три единицы влево и на шесть единиц вниз, и .

Подставьте эти значения в общую форму уравнения:

Упростите:

Сообщите об ошибке

Возможные ответы: 90 005

Правильный ответ:

Объяснение:

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

9002 8 Объяснение:

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

9002 8 Объяснение:

Сообщить об ошибке

Уведомление об авторских правах

Посмотреть репетиторов по алгебре

Джордж
Сертифицированный репетитор

Государственный колледж Пенсаколы, бакалавр искусств, математика.