Правила логики: Законы логики – Гуманитарный портал

Законы логики – Гуманитарный портал

Законы логики (или логические законы) — это общее название множества законов, образующих основу логической дедукции (см. Дедукция). Понятие о логическом законе восходит к античному понятию о логосе (см. Логос) как о предпосылке объективной («природной») правильности рассуждений. Поскольку логика (см. Логика) изучает характер связи мыслей в процессе рассуждения, существуют определённые формальные и содержательные правила, следование которым обязательно. Различные по своей структуре и степени сложности рассуждения подчиняются разным правилам. Среди них можно выделить основные и производные: основные правила имеют более общий характер, производные — выводятся из основных. Наряду с этим существует такой тип правил логики, которые можно назвать всеобщими. Обычно такие правила называют законами мышления. Под законом вообще имеют в виду внутреннюю, необходимую и существенную связь явлений. Законы мышления представляют собой операциональные директивы мышления. Их происхождение обусловлено рациональной активностью субъекта. Выраженная в правилах, нормах, рекомендациях, целесообразная активность находит своё воплощение в принципах, имеющих всеобщий характер. В отличие от законов естествознания, которые описывают связь явлений природы, многократно повторяемую в идентичных условиях, законы мышления предписывают определённые способы интеллектуальной деятельности. Цель законов логики — сформулировать основания правил и рекомендаций, следуя которым можно достичь истины. Поэтому законы мышления не являются законами в том смысле, в котором указанный термин используется для описаний явлений природы. Таким образом, законы логики представляют собой законы правильного мышления человека о мире, а не законы самого мира. Правила мышления впервые получают логическое содержание у Аристотеля, положившего начало систематическому описанию и каталогизации таких схем логических связей элементарных высказываний в сложные, истинность которых вытекает из одной только их формы, а точнее — из одного только понимания смысла логических связей, безотносительно к истинностному значению элементарных высказываний. Большинство логических законов, открытых Аристотелем, представляют собой законы силлогизма. Позже были открыты и другие законы, и даже было установлено, что совокупность законов логики бесконечна. В некотором смысле рассмотреть эту совокупность удаётся с помощью различных формальных теорий логического рассуждения — так называемых логических исчислений, в которых интуитивное понятие «логический закон» реализуется в точном понятии «общезначимой формулы» данного исчисления, что, в свою очередь, делает понятие «логический закон» относительным. Однако типом логического исчисления полагаются одновременно и границы этой относительности. При этом тип исчисления, как правило, не является делом произвольного выбора, а диктуется (или подсказывается) «логикой вещей», о которых хотят рассуждать, а также нашей субъективной уверенностью в том или ином характере этой логики. Исчисления, основанные на одной и той же гипотезе о характере «логики вещей», являются эквивалентными в том смысле, что в них каталогизируются одни и те же логические законы. Например, исчисления, основанные на гипотезе двузначности, несмотря на всё их внешнее разнообразие, описывают одну и ту же область классических законов логики — мир тождественных истин (или тавтологий), издавна получивших философскую характеристику «вечных истин» или «истин во всех возможных мирах» (см. Возможные миры). Логикой вещей, отражением которой исторически явились логические законы так называемой интуиционистской логики, является логика умственных математических построений — «логика знания», а не «логика бытия». Логические законы отличаются от логических правил вывода. Первые представляют класс общезначимых выражений и формулируются в объектном языке исчисления. Вторые служат для описания фактов логического следования (см. Логическое следование) одних выражений из других, не обязательно общезначимых, и формулируются в метаязыке исчисления. В отличие от законов логики, правила вывода имеют вид предписаний и носят, по существу, нормативный характер. При построении исчислений без правил вывода обойтись нельзя, а без законов логики, в принципе, можно (именно так и поступают в исчислениях естественного вывода). Тем не менее, изучение логических законов образует естественный исходный пункт логического анализа приемлемых (логически правильных) способов рассуждений (умозаключений), поскольку понятие «приемлемое» или «логически правильное» рассуждение уточняется через понятие «логический закон». В традиционной формальной логике термин «закон логики» имел узкий смысл и применялся только к четырём так называемым основополагающим законам правильного мышления — к закону тождества, закону непротиворечия, к закону исключённого третьего и к закону достаточного основания: Закон тождества. В процессе умозаключения всякое высказывание и суждение должны оставаться тождественными самим себе (см. Закон тождества). Закон непротиворечия. Два противоположных суждения не могут быть истинными в одно и то же время и в одном и том же отношении (см. Закон непротиворечия). Закон исключённого третьего. Из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано (см.  Закон исключённого третьего). Закон достаточного основания. Никакое суждение не может утверждаться без достаточного основания (см. Закон достаточного основания). Указанная «канонизация» термина «закон логики» в настоящее время является данью традиции и не отвечает действительному положению вещей. Тем не менее, эти законы можно принять в методологическом смысле как определённые принципы (или постулаты) теоретического мышления, так как они являются наиболее общими и используются при оперировании понятиями и суждениями, в умозаключениях, доказательствах и опровержениях, и поэтому присутствуют практически во всех логических системах. В этом смысле закон тождества (lex identitatis) истолковывается как принцип постоянства или принцип сохранности предметного и смыслового значений суждений (высказываний) в некотором заведомо известном или подразумеваемом контексте (в выводе, доказательстве, теории). В языке логических исчислений указанная сохранность обычно выражается формулой A ⊃ A. Принятие закона тождества для суждения A не означает, вообще говоря, принятия самого A. Но если A принято, то закон тождества принимается с необходимостью для исчислений с общезначимой формулой A ⊃ (A ⊃ A). Для исчислений, включающих отрицание, это сведение абстракции постоянства суждения к принятию самого суждения имеет форму закона: (A ⊃ ¬ (A ⊃ A) ⊃ ¬ A), то есть если при допущении суждения для него отрицается закон тождества, то тем самым отрицается и само это суждение. Закон непротиворечия (lex contradictionis) указывает на недопустимость одновременного утверждения (в рассуждении, в тексте или теории) двух суждений, из которых одно является логическим отрицанием другого, то есть суждений вида A и ¬ A или их конъюнкции, или эквиваленции, или — в более широком смысле — утверждений о тождестве заведомо различных объектов, поскольку обычно правила логики таковы, что позволяют из противоречия выводить произвольные суждения, что обесценивает содержательный смысл умозаключений или теорий. Наличие противоречия в рассуждении (теории) создаёт парадоксальную ситуацию и нередко указывает на несовместимость посылок, положенных в основу рассуждения (теории). Этим обстоятельством часто пользуются в косвенных доказательствах. Закон исключённого третьего (lex exclusii tertii) на логическом языке записывается формулой A ⌵ ¬ A и утверждает, что нет ничего среднего (промежуточной оценки) между членами противоречивой пары (отсюда другое латинское название этого закона — tertium non datur). В методологическом плане этот закон выражает конструктивно неоправданную идею о разрешимости (потенциально осуществимом указании на истинность или ложность) произвольного суждения. В отличие от формулы, соответствующей закону противоречия, формула, соответствующая закону исключённого третьего, не выводима в интуиционистских и конструктивных исчислениях, хотя и неопровержима в них. Дихотомия установленных истины и лжи неоспорима, но дихотомия утверждения и отрицания оспаривалась неоднократно. Наиболее последовательную критику закона исключённого третьего дал Л. Э. Я. Брауэр. В свете его критики этот закон следует рассматривать только как принцип (или постулат) классической логики. Закон достаточного основания (lex rationis determinatis seu sufficientis) выражает методологическое требование обоснованности всякого знания, всякого суждения, которое мы хотели бы принять за отображение истинного (действительного) положения вещей. В этом смысле он применим не только к выводному знанию (в частности, к аксиомам и постулатам научных теорий), но и ко всей области фактических истин, не имеющих отношения к формальной логике. Не случайно Г. В. Лейбниц, который ввёл этот принцип в научный обиход, относил его в первую очередь не к логике, а ко всем событиям, которые случаются в мире. В приложениях логических законов к конкретным ситуациям с особой наглядностью обнаруживается их общая черта: все они представляют собой тавтологии и не несут содержательной, «предметной» информации. Это — общие схемы, отличительная особенность которых в том, что, подставляя в них любые конкретные высказывания (как истинные, так и ложные), мы обязательно получим истинное выражение. Указанные законы мышления имеют в логике такое же значение, какое в математике имеют аксиомы (см. Аксиома) или постулаты и обладают таким же формальным характером, как и формулы алгебры: в последних не говорится о том, по отношению к каким числовым значениям они выполняются, а законы мышления не содержат в себе содержательных характеристик, то есть не квалифицируют то, что именно должно или не должно отождествляться, что именно и чему должно или не должно противоречить, и так далее. Именно в этом и заключается их обобщающий характер как операциональных директив правильного мышления и рассуждения.

Объясняем 4 главных закона логики на простых примерах

21 декабря 2019 Жизнь Колонка

Это знание необходимо, чтобы не допускать ошибок в рассуждениях и замечать, когда их совершают другие.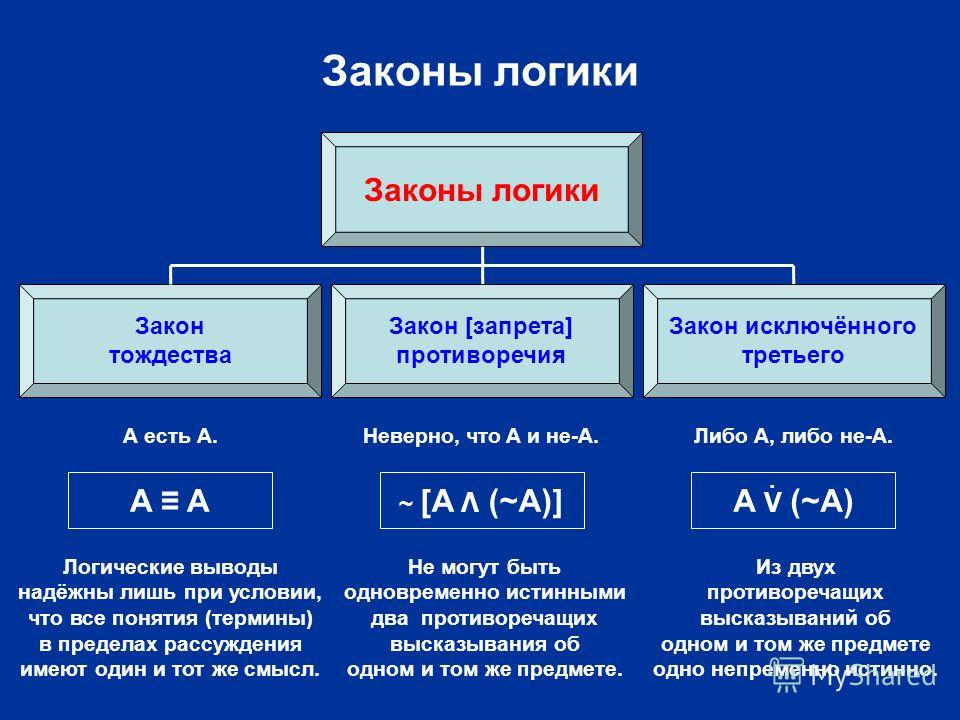

Катя Анисимова

Студент-химик, выпускница мастерской прикладной рациональности «Летней школы» и автор «Общества скептиков».

Мы часто слышим фразы вроде «это нелогично» и «где тут логика». Интуитивно понятно, что логика — это что-то про наши рассуждения, выводы, структуру мыслей. В целом так и есть. Логика — это наука, которая появилась в V веке до нашей эры и изучает законы и форму мышления.

Под формой мышления понимают структуру мысли, а не её содержание. Например, с точки зрения логики выражение «Все шмумрики хжуют тофц с штецеллой на фафлак. Финкус — шмумрик. Финкус хжует тофц с штецеллой на фафлак» абсолютно верно, а «Все планеты Солнечной системы вращаются вокруг Солнца. Земля вращается вокруг Солнца. Следовательно, Земля — планета Солнечной системы» — нет.

Вся логика «живёт» на четырёх законах. Разберёмся, какие это законы и как они работают.

1. Закон тождества

Каждая мысль должна быть равна самой себе, не должна иметь больше одного значения.

В чём суть

Еще до нашей эры Аристотель говорил: «…Иметь не одно значение — значит не иметь ни одного значения; если же у слов нет (определённых) значений, тогда утрачена всякая возможность рассуждать друг с другом, а в действительности и с самим собой, ибо невозможно ничего мыслить, если не мыслить каждый раз что-нибудь одно».

Примеры нарушения

Самый популярный пример нарушения закона тождества — фраза «студенты прослушали лекцию». Слово «прослушали» можно понять в двух значениях: то ли студенты внимательно слушали преподавателя, то ли всё пропустили.

Примером нарушения закона тождества будет и эта шутка:

— Я сломал руку в двух местах.

— Больше не ходи в эти места.

В результате немного более сложных нарушений закона тождества получаются софизмы. Софизм — это внешне правильное доказательство ложной мысли с помощью преднамеренного нарушения логических законов.

Что лучше: вечное блаженство или бутерброд? Конечно же, вечное блаженство. А что может быть лучше вечного блаженства? Конечно же, ничто! Но бутерброд ведь лучше, чем ничто, поэтому бутерброд лучше вечного блаженства.

Подвох здесь в том, что слово «ничто» употребилось сначала в значении «ни один предмет или явление», а потом в значении «отсутствие чего-либо»

Как применять в жизни

Первый закон логики поможет распознать софизмы. Первое, на что стоит обращать внимание, — неоднозначные слова.

2. Закон противоречия

Высказывание и его отрицание не могут быть одновременно истинными.

В чём суть

Если одно суждение что-то утверждает, а другое то же самое отрицает об одном и том же объекте в одно и то же время и в одном и том же отношении, то они не могут одновременно быть истинными.

Например, два суждения — «котик чёрный» и «котик белый» — не могут одновременно быть истинными, если речь идёт об одном и том же котике, в одно и то же время и в одном и том же отношении. То есть цвет котика сравнивается с одной и той же палитрой.

Примеры нарушения

«Этот рыжий кот оставил по всему ковру чёрные шерстинки». И из детства — «Закрой рот и ешь».

Как применять в жизни

Самое сложное — выявить противоречие. Фраза «в детстве у меня не было детства» не нарушает закон противоречия, а «сделал устный доклад в письменной форме» нарушает. Так что, главное — понять, имеет место противоречие или игра слов.

3. Закон исключённого третьего

Два противоречащих суждения об одном и том же предмете в одно и то же время и в одном и том же отношении не могут быть одновременно истинными и не могут быть одновременно ложными

В чём суть

Суждения бывают противоположными и противоречащими.

Противоположные суждения всегда предполагают некий третий, промежуточный вариант. Например, для суждений «дом большой» и «дом маленький» промежуточным будет «дом среднего размера». Для противоречащих суждений нет никакого третьего варианта. Например, для суждений «дом большой» и «дом небольшой» третьего верного варианта не предполагается.

Итак, два противоречащих суждения об одном и том же предмете, в одно и то же время и в одном и том же отношении не могут быть одновременно истинными и не могут быть одновременно ложными.

Пример нарушения

Суждения «кот старый» и «кот нестарый» об одном и том же котике в одно и то же время не могут быть одновременно верными.

Как применять в жизни

Примеры простые до безобразия, но в жизни закон противоречия нарушается скорее так: между противоречащими суждениями есть ещё часть монолога, да и сами суждения могут быть высказаны не очень явно. Как с этим быть? Внимательно вслушиваться в то, что говорит собеседник, и следить за мыслью. Если все остальные законы не нарушаются, присмотритесь ещё раз к формулировкам. Возможно, тут замаскированные противоречащие суждения.

4. Закон достаточного основания

Любая мысль (тезис) для того, чтобы иметь силу, обязательно должна быть доказана какими-либо аргументами, причём эти аргументы должны быть достаточными для основания исходной мысли, то есть она должна вытекать из них.

В чём суть

Помните, что такое презумпция невиновности? Она основана на законе достаточного основания. Принцип презумпции невиновности предписывает считать человека невиновным, даже если он даёт показания против себя, до тех пор, пока его вина не будет достоверно доказана какими-либо фактами. Другими словами, признание вины не гарантирует, что человек действительно совершил преступление, а вот улики и доказательства — вполне могут. То есть признание вины — недостаточное основание, а факты и улики, указывающие на преступника, — достаточное.

Пример нарушения

«Не ставьте мне двойку. Я прочитал весь учебник и, возможно, что-то отвечу». Вывод не вытекает из основания: студент мог прочитать весь учебник, но из этого не следует, что он сможет что-то ответить.

Как применять в жизни

Закон достаточного основания предостерегает от поспешных выводов. Если мы помним о том, что любое утверждение должно быть подкреплено фактами, это поможет распознавать дешёвые сенсации и небылицы.

Читайте также 🧐

• 10 задач на логику и сообразительность
• 26 ошибок мышления, из-за которых мы ничего не понимаем
• Как философия помогает в повседневной жизни

Законы мышления | Определение, теории и факты

Связанные темы:

логика принцип тождества закон исключенного третьего закон противоречия

Просмотреть весь связанный контент →

законы мысли , традиционно три основных закона логики: (1) закон противоречия, (2) закон исключенного третьего (или третьего) и (3) принцип личность. Символически три закона можно сформулировать следующим образом. (1) Для всех предложений p , невозможно, чтобы одновременно p и не p были истинными, или: ∼( p · ∼ p ), где ∼ означает «не», а · означает «и». (2) Либо p , либо ∼ p должны быть истинными, так как между ними нет третьего или среднего истинного предложения, или: p ∨ ∼ p , в котором ∨ означает «или». (3) Если пропозициональная функция F истинна для индивидуальной переменной x , то F истинна для x 9.0014 или: F ( x ) ⊃ F ( x ), где ⊃ означает «формально подразумевает». Другая формулировка принципа тождества утверждает, что вещь тождественна самой себе, или (∀ х ) ( х = х ), где ∀ означает «для каждого»; или просто x равно x .

В качестве примеров аксиом Аристотель приводил законы противоречия и исключенного третьего. Он частично освободил будущие контингенты или заявления о неуверенности в будущих событиях от закона исключенного третьего, утверждая, что не является (сейчас) ни истинным, ни ложным то, что завтра будет морское сражение, но что сложное суждение о том, что либо будет морское сражение завтра или что там не будет (сейчас) правда. В эпоху Principia Mathematica (1910–1913) Альфреда Норта Уайтхеда и Бертрана Рассела, этот закон выступает скорее как теорема, чем как аксиома.

То, что законы мышления являются достаточным основанием для всей логики или что все другие принципы логики являются просто их разработками, было учением, распространенным среди традиционных логиков. Закон исключенного третьего и некоторые родственные ему законы были отвергнуты голландским математиком Л.Э.Дж. Брауэра, основоположника математического интуиционизма, и его школы, которые не допускали их использования в математических доказательствах, в которых задействованы все члены бесконечного класса. Брауэр не принял бы, например, дизъюнкции, состоящей в том, что где-то в десятичном разложении числа π встречаются 10 последовательных семерок, либо нет, так как доказательство любой альтернативы неизвестно, но он принял бы ее, если бы она была применена, например, к первые 10 ¹⁰⁰ десятичных разряда, поскольку в принципе их можно вычислить.

В 1920 году Ян Лукасевич, ведущий представитель польской школы логики, сформулировал исчисление высказываний, которое имело третье значение истинности, ни истинности, ни ложности, для будущих контингентов Аристотеля, исчисление, в котором исключались законы противоречия и средние оба провалились. Другие системы перешли от трехзначной к многозначной логике, например, некоторые вероятностные логики, имеющие различные степени истинности-значения между истиной и ложностью.

Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена ​​Брайаном Дуиньяном.

3.4: Законы логики

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

80507

• Эл Дорр и Кен Левассер
• Массачусетский университет Лоуэлл

В этом разделе мы перечислим самые основные эквивалентности и следствия логики. Большинство эквивалентностей, перечисленных в таблице \(\PageIndex{2}\), должны быть очевидны для читателя. Помните, 0 означает противоречие, 1 — тавтологию. Многие логические законы аналогичны алгебраическим законам. Например, существует логический закон, соответствующий ассоциативному закону сложения, \(a + (b + c) = (a + b) + c\text{.}\) На самом деле ассоциативность как конъюнкции, так и дизъюнкции среди законов логики. Обратите внимание, что, за одним исключением, законы спарены таким образом, что замена символов \(\land\text{,}\) \(\lor\text{,}\) 1 и 0 на \(\lor\text {,}\) \(\land\text{,}\) 0 и 1 соответственно в любом законе дает вам второй закон. Например, \(p \lor 0\Leftrightarrow p\) приводит к \(p \land 1 \Leftrightarrow p\text{.}\) Это называется принцип двойственности . А пока подумайте об этом как о способе запомнить два закона по цене одного. Мы предоставим читателю проверить некоторые из этих законов с помощью таблиц истинности. Однако читатель должен быть осторожен в применении двойственности к условному оператору и импликации, поскольку двойственность предполагает обратное. Например, двойственное слово \(p \land q\Rightarrow p\) равно \(p \lor q \Leftarrow p\text{,}\), что обычно пишется как \(p\Rightarrow p \lor q\text{ .}\)

Пример \(\PageIndex{1}\): проверка закона идентификации

С помощью этой таблицы истинности можно проверить Закон Тождества. Тот факт, что \((p \land 1)\leftrightarrow p\) является тавтологией, служит достоверным доказательством.

Таблица \(\PageIndex{1}\): таблица истинности для демонстрации закона тождества для соединения.

\(р\)	\(1\)	\(р\земля 1\)	\((p\land 1)\leftrightarrow p\)
\(0\)	\(1\)	\(0\)	\(1\)
\(1\)	\(1\)	\(1\)	\(1\)

Некоторые логические законы в таблице \(\PageIndex{3}\) могут быть для вас менее очевидными. Для тех, которые вас не устраивают, замените логические переменные фактическими предложениями. Например, если \(p\) — это «Джон владеет зоомагазином», а \(q\) — «Джон любит домашних животных», закон об отчуждении должен иметь смысл.

Таблица \(\PageIndex{2}\): основные логические законы — эквивалентности

Коммутативные законы
\(p \lor q\Стрелка влево q\lor p\)	\(p \land q\Leftrightarrow q \land p\)
Ассоциативные законы
\((p\lor q)\lor r\Стрелка влево p\lor (q\lor r)\)	\((p\land q)\land r\Стрелка влево p\land (q\land r)\)
Распределительные законы
\(p\land (q\lor r)\Leftrightarrow (p\land q)\lor (p\land r)\)	\(p\lor (q\land r)\Стрелка влево (p\lor q)\land (p\lor r)\)
Законы об идентичности
\(p\lor 0\Стрелка влево p\)	\(p\land 1\Стрелка влево p\)
Законы отрицания
\(p\land\neg p\Стрелка влево 0\)	\(p\lor\neg p\Стрелка влево 1\)
Законы идемпотентов
\(p\lor p\Стрелка влево\)	\(p\land p\Leftrightarrow p\)
Нулевые законы
\(p\land 0\Стрелка влево 0\)	\(p\lor 1\Стрелка влево 1\)
Законы о поглощении
\(p\land (p\lor q)\Leftrightarrow p\)	\(p\lor (p\land q)\Стрелка влево p\)
Законы Де Моргана
\(\neg(p\lor q)\Стрелка влево (\neg p)\земля (\neg q)\)	\(\neg(p\land q)\Leftrightarrow (\neg p)\lor (\neg q)\)
Законы об инволюции
\(\neg(\neg p)\Leftrightarrow p\)

Таблица \(\PageIndex{3}\): основные логические законы – общие импликации и эквивалентности \((p \стрелка вправо q) \land p\стрелка вправо q\) Косвенное рассуждение (AKA Modus Tollens) \((p \to q) \land \neg q \Rightarrow \neg p\) Разделительное дополнение \(p\стрелка вправо (p\lor q)\) Конъюнктивное упрощение \((p \land q) \Rightarrow p\) и \((p \land q) \Rightarrow q\) Дизъюнктивное упрощение \((p \lor q) \land \neg p \Rightarrow q\) и \((p \lor q) \land \neg q\Rightarrow p\) Цепное правило \((p \to q) \land ( q \стрелка вправо r) \Стрелка вправо (p\to r)\) Условная эквивалентность \(p \rightarrow q \Leftrightarrow \neg p \lor q\) Биусловные эквивалентности \((p \leftrightarrow q) \Leftrightarrow (p\rightarrow q) \land (q \rightarrow p)\Leftrightarrow (p \land q) \lor (\neg p \land \neg q)\) Контрапозитив \((p\to q) \Leftrightarrow (\neg q \to \neg p)\)

Упражнения

Упражнение \(\PageIndex{1}\)

Запишите следующее в символической записи и определите, является ли оно тавтологией: «Если я буду учиться, то я буду учиться. Я не буду учиться. Поэтому я не учусь».

Ответить

Пусть \(s=\textrm{Я буду учиться}\text{,}\)\(t=\textrm{Я буду учиться.}\) Аргумент: \(((s\to t)\land ( \neg t))\to (\neg s) ,\) вызвать аргумент \(a\text{.}\)

\begin{equation*} \begin{array}{ccccc} s\text{ } & t\text{ } & s\to t\text{ } & (s\to t)\land (\neg t)\ text{ } & a \\ \hline 0\text{ } & 0\text{ } & 1\text{ } & 1\text{ } & 1 \\ 0\text{ } & 1\text{ } & 1\ text{ } & 0\text{ } & 1 \\ 1\text{ } & 0\text{ } & 0\text{ } & 0\text{ } & 1 \\ 1\text{ } & 1\text{ } & 1\text{ } & 0\text{ } & 1 \\ \end{массив}\text{.} \end{уравнение*}

Так как \(a\) является тавтологией, аргумент верен.

Упражнение \(\PageIndex{2}\)

Покажите, что распространенная ошибка \((p\to q) \land \neg p \Rightarrow \neg q\) не является законом логики.

Упражнение \(\PageIndex{3}\)

Опишите, в общем, как двойственность может быть применена к импликациям, если мы введем отношение \(\Leftarrow\text{,}\), читаемое как «подразумевается». Мы определяем это отношение как

\begin{equation*} (p \Leftarrow q) \Leftrightarrow (q \Rightarrow p)\text{.} \end{equation*}

Ответить

В любом верном утверждении \(S\text{,}\) replace; \(\land\) с \(\lor\text{,}\) \(\lor\) с \(\land\text{,}\) 0 с 1, 1 с 0, \(\Leftarrow\) с \(\Rightarrow \text{,}\) и \(\Rightarrow \) с \(\Leftarrow \text{.}\) Оставьте все остальные связки без изменений.

Упражнение \(\PageIndex{4}\)

Напишите двойное число следующих операторов:

1. \(\displaystyle (p \land q)\Rightarrow p\)
2. \(\displaystyle (p\lor q)\land \neg q\Rightarrow p\)

---

Эта страница под названием 3.4: Законы логики распространяется в соответствии с лицензией CC BY-NC-SA, автором, ремиксом и/или куратором этой страницы являются Эл Доерр и Кен Левассер.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Эл Дорр и Кен Левассер

   Лицензия

   СС BY-NC-SA

   Показать страницу TOC

   нет

2. Теги

   На этой странице нет тегов.

   No related posts.