Правило признаки делимости: Признаки делимости натуральных чисел на 2, 3, 4, 5, 6, 9, 10, 11, 25 и разрядную единицу

Исследовательский реферат по теме «Признаки делимости чисел»

Муниципальный тур краевого форума «Молодежь и наука»
Полное название темы работы	«Признаки делимости»
Название секции форума	Естественные науки и инженерные технологии
Тип работы	Исследовательский реферат
Возрастная номинация	5-6 класс
Фамилия имя отчество (полностью) автора	Мустафин Рустам Равилевич
Домашний адрес автора	г. Боготол, ул. Кирова, д.76, кв.40
Место учебы:	МБОУ «СОШ №3» г. Боготола
Класс	6
Место выполнения работы	МБОУ «СОШ №3» г. Боготола
Руководитель	Меньщикова Галина Викторовна, МБОУ «СОШ №3», учитель математики
Научный руководитель
Ответственный за корректуру текста работы	Меньщикова Галина Викторовна, МБОУ «СОШ №3», учитель математики
e-mail (обязательно) Контактный телефон	[email protected] 8 (39157) 2-49-96

АННОТАЦИЯ

Мустафин Рустам Равильевич

МБОУ «СОШ№3», 6 класс

«Признаки делимости»

руководитель: Меньщикова Галина Викторовна, МБОУ «СОШ№3», учитель математики.

Цель работы: создание таблицы делимости чисел. Методы проведенных исследований: анализ литературных источников, эмпирический метод: анализ систем знаний о признаках делимости, обобщение.

Основные результаты исследования: изучены признаки делимости на простые числа, выведены признаки делимости на составные числа и создана таблица делимости на числа от 2 до 20, на 25 и 125.

СОДЕРЖАНИЕ

1. Введение_______________________________________________________2

2. Признак Паскаля и его частные случаи_____________________________ 3

3. Признаки делимости на составные числа____________________________5

4. Таблица признаков делимости_____________________________________6

5. Заключение_____________________________________________________7

6. Список литературы_______________________________________________8

ВВЕДЕНИЕ

Актуальность:

Математика – одна из великих наук, изучением которой занимались многие великие ученые, такие как Декарт, Паскаль и другие. Одним из важнейших понятий арифметики целых неотрицательных чисел является понятие делимости.

На уроках математики мы изучали признаки делимости на 2, 5, 3, 9, 10. И стало интересно, существуют ли другие признаки делимости, откуда они возникли? Наверняка, существуют более интересные и сложные признаки.

Гипотеза: я предполагаю, что существуют другие признаки делимости.

Цель работы: создание таблицы делимости чисел.

В данной работе проведено исследование признаков делимости на натуральные числа от 2 до 20, на 25 и на 125, кроме тех, что мы изучаем в школьном курсе математики. Я хочу научиться их применять и познакомить с ними других учащихся.

Для достижения данной цели в исследовательском реферате были поставлены следующие задачи:

1. Познакомиться по различным источникам с признаками делимости чисел;

2. Систематизировать полученную информацию;

3. Обобщить результаты исследования и представить их в виде таблицы.

Степень разработанности проблемы:

Изучением признаков делимости занимались с древних времен. Великий французский ученый Блэз Паскаль нашёл общий алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, решение вопроса о делимости чисел признаки делимости сводят к действиям над небольшими числами в уме. Практически все известные ныне признаки делимости являются частным случаем признака Паскаля. Достаточно много различной информации можно найти в книгах, энциклопедиях, Интернете [1].

Новизна результатов исследования заключается в том, что данная работа систематизирует знания о признаках делимости и, думаю, что многие ровесники и старшеклассники не знают, что существуют другие признаки делимости, кто их открыл. А, ведь знание их значительно упрощает процесс вычисления.

В ходе написания исследовательского реферата использованы следующие методы научного исследования: анализ литературных источников, эмпирический метод: анализ систем знаний о признаках делимости, обобщение.

ПРИЗНАК ПАСКАЛЯ И ЕГО ЧАСТНЫЕ СЛУЧАИ

Блэз Паскаль (19.6.1623— 19.8.1662) – один из самых знаменитых людей в истории человечества. Паскаль умер, когда ему было 39 лет, но, несмотря на столь короткую жизнь, вошел в историю как выдающийся математик, физик, философ и писатель. Его именем названы единица давления (паскаль) и весьма популярный сегодня язык программирования [2].

  Круг математических интересов Паскаля был весьма разнообразен. Паскаль нашёл общий алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число (трактат «О характере делимости чисел»)[3].

Общий вид признака Паскаля

Чтобы узнать, делится ли число А на число В, не всегда нужно выполнять письменно деление. В некоторых случаях это можно узнать по десятичной записи чисел. Пусть есть натуральное число записываемое в десятичной системе как ,  где — единицы, — десятки и т.  д.

Пусть — произвольное натуральное число, на которое мы хотим делить и выводить признак делимости на него.

Находим ряд остатков по следующей схеме:

— остаток от деления на

— остаток от деления на

— остаток от деления на

…

— остаток от деления на .

Формально:

Так как остатков конечное число (а именно ), то этот процесс зациклится (не позже, чем через шагов) и дальше можно его не продолжать: начиная с некоторого , где — получившийся период последовательности . Для единообразия можно принять, что .

Тогда имеет тот же остаток от деления на , что и число

[1].

В энциклопедиях признак Паскаля описывают следующим образом:

• Признак делимости — правило, позволяющее сравнительно быстро определить, является ли число кратным заранее заданному без необходимости выполнять фактическое деление. Как правило, основано на действиях с частью цифр из записи числа в позиционной системы счисления (обычно десятичной)[3].

• Признак Паскаля — универсальный признак делимости, позволяющий для любых целых a и b определить, делится ли a на b [1].

Основные частные случаи

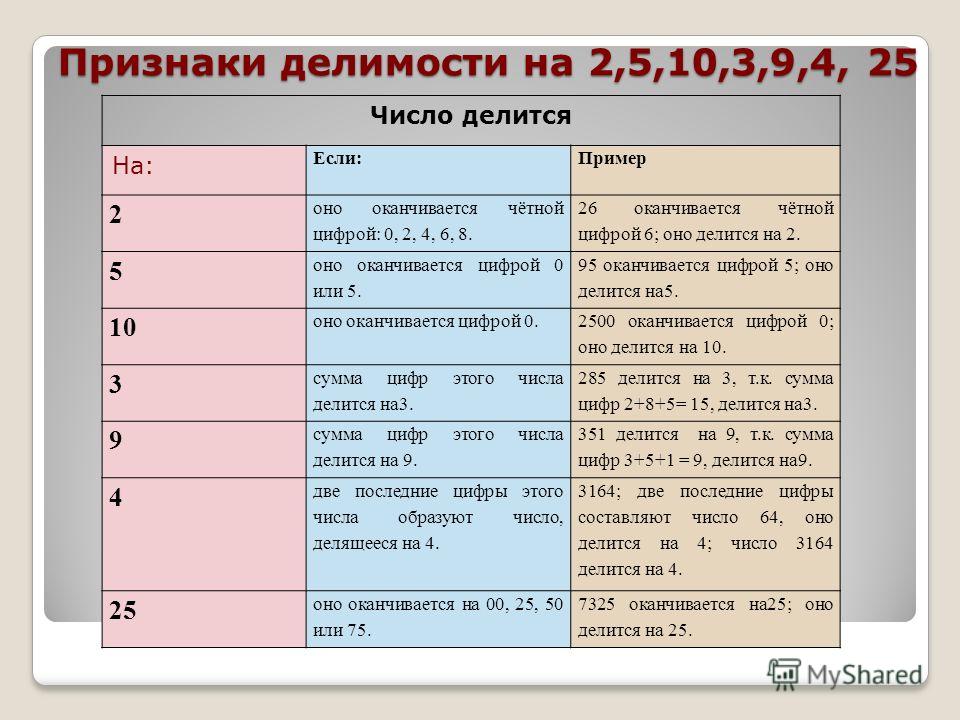
Признак делимости на 2: число делится на 2 без остатка тогда и только тогда, когда оно заканчивается на чётную цифру.

Признаки делимости на 3 и 9: число делится на 3 (9) без остатка тогда и только тогда, когда сумма цифр делится на 3 (9).

Признак делимости на 4: число делится на 4 без остатка тогда и только тогда, когда если число, состоящее из двух его последних цифр, делится на 4.

Признак делимости на 5: число делится на 5 без остатка тогда и только тогда, когда оно заканчивается на цифру 5 или 0.

Признак делимости на 7 и на 13.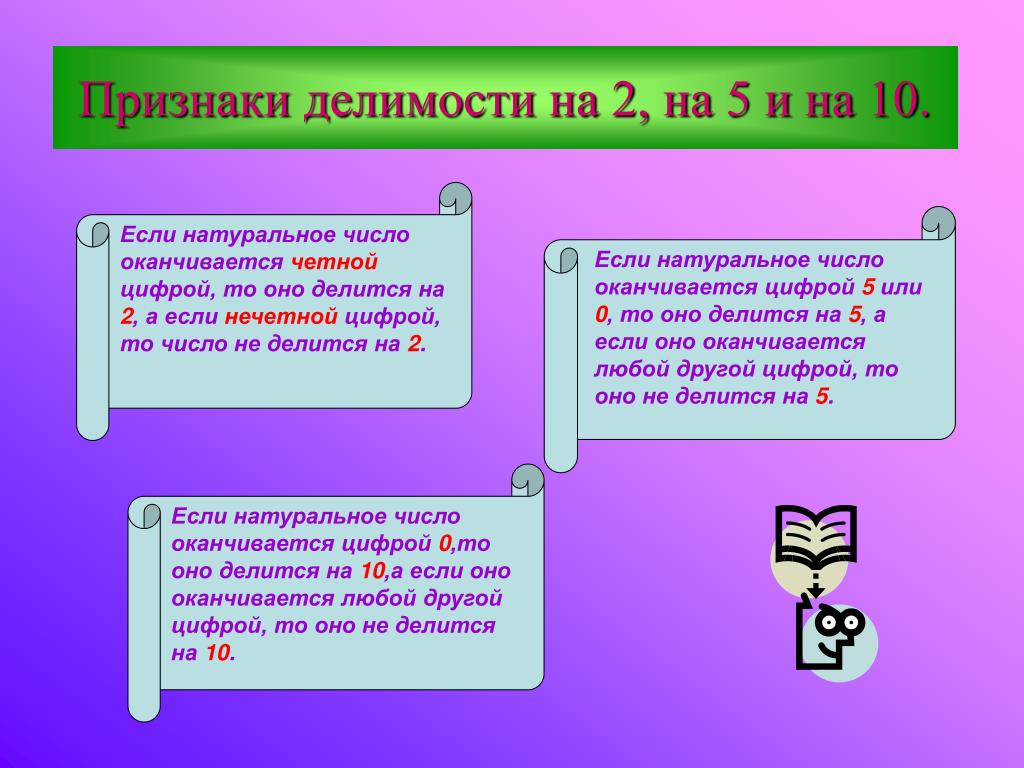 Чтобы узнать, делится ли натуральное число на 7 или на 13, надо разбить его десятичную запись справа налево на группы по три цифры в каждой (самая левая группа может содержать две или одну цифру) и взять группы с нечетными номерами со знаком минус, а с четными номерами со знаком плюс. Если значение получившегося выражения делится на 7 (соответственно на 13), то и заданное число делится на 7 (соответственно на 13) [5].

Признак делимости на 11: Число делится на 11 без остатка тогда и только тогда, когда сумма цифр с чередующимися знаками делится на 11 [5].

Признак делимости на 17: число делится на 17 тогда и только тогда, когда число его десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17 [4].

Признак делимости на 19: число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19 [4].

ПРИЗНАКИ ДЕЛИМОСТИ НА СОСТАВНЫЕ ЧИСЛА

Зная основные признаки делимости на простые числа, можно вывести признаки делимости на составные числа:

Признак делимости на 6: число делится на 6 тогда и только тогда, когда оно заканчивается на чётную цифру и сумма цифр делится на 3.

т.к. 6 = 2 ∙ 3, т.е. число должно делиться на 2 и на 3.

Признак делимости на 12: число делится на 12 тогда и только тогда, когда две последние цифры делятся на 4 и сумма цифр делится на 3.

т.к. 12= 4 ∙ 3, т.е. число должно делиться на 4 и на 3.

Признак делимости на 14: число делится на 14 тогда и только тогда, когда оно заканчивается на чётную цифру и когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.

т.к. 14= 2 ∙ 7, т.е. число должно делиться на 2 и на 7.

Признак делимости на 15: число делится на 15 тогда и только тогда, когда оно заканчивается на 5 и на 0 и сумма цифр делится на 3.

т.к. 15= 3 ∙ 5, т.е. число должно делиться на 3 и на 5.

Признак делимости на 18: число делится на 18 тогда и только тогда, когда оно заканчивается на чётную цифру и сумма его цифр делится на 9.

т.к18= 2 ∙ 9, т.е. число должно делиться на 2 и на 9.

Признак делимости на 20: число делится на 20 тогда и только тогда, когда число заканчивается на 0 и предпоследняя цифра четная.

т.к. 20 = 10 ∙ 2 т.е. число должно делиться на 2 и на 10.

Признак делимости на 25: число, содержащее не менее трех цифр, делится на 25 тогда и только тогда, когда делится на 25 число, образованное двумя последними цифрами.

Признак делимости на 125: число, содержащее не менее четырех цифр, делится на 125 тогда и только тогда, когда делится на 125 число, образованное тремя последними цифрами.

Все выше перечисленные признаки обобщены в виде таблицы.

ТАБЛИЦА ПРИЗНАКОВ ДЕЛИМОСТИ

	Признак	Пример
на 2	Число заканчивается на чётную цифру.	………………2(4,6,8,0)
на 3	Сумма цифр делится на 3.	378015:  3+7+8+0+1+5 = 24. 24:3
на 4	Число из двух последних его цифр нули или делится на 4.	………………12
на 5	Число заканчивается на цифру 5 или 0.	………………0(5)
на 6	Число заканчивается на чётную цифру и сумма цифр делится на 3.	375018:  8-четное число 3+7+5+0+1+8 = 24. 24:3
на 7	Результат вычитания удвоенного последней цифры из этого числа без последней цифры делится на 7.	364: 36 — (2 × 4) = 28, 28:7
на 8	Три его последние цифры числа — нули или образуют число, которое делится на 8.	……………..064
на 9	Сумма его цифр числа делится на 9.	3780153:  3+7+8+0+1+5+3=27. 27:9
на 10	Число оканчивается на ноль	………………..0
на 11	Сумма цифр числа с чередующимися знаками делится на 11.	182 919: 1 — 8 + 2 — 9 + 1 — 9 = −22 -22:11
на 12	Две последние цифры числа делятся на 4 и сумма цифр делится на 3.	216: 2+1+6=9, 9:3 и 16:4
на 13	Число десятков данного числа, сложенное с учетверённым числом единиц, кратно 13.	845: 84 + (4 × 5) = 104, 104:13
на 14	Число заканчивается на чётную цифру и когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.	364: 4 – четное число 36 — (2 × 4) = 28, 28:7
на 15	Число 5 и на 0 и сумма цифр делится на 3.	65480: 6+3+4+8+0=21, 21:3
на 16	Четыре его последние цифры числа — нули или образуют число, которое делится на 16.	…………..0032
на 17	Число десятков данного числа, сложенное с увеличенным в 12 раз числом единиц, кратно 17.	29053→2905+36=2941→294+12= =306→30+72=102→10+24=34. Поскольку 34 делится на 17, то и 29053 делится на 17
на 18	Число заканчивается на чётную цифру и сумма его цифр делится на 9.	2034: 4 — четное число 2+0+3+4=9, 9:9
на 19	Число десятков данного числа, сложенное с удвоенным числом единиц, кратно 19	646: 64 + (6 × 2) = 76, 76:19
на 20	Число заканчивается на 0 и предпоследняя цифра четная	…………………40
на25	Число, состоящее из двух последних цифр делится на 25	……………. 75
на 125	Число, состоящее из трех последних цифр делится на 125	……………375

ЗАКЛЮЧЕНИЕ

В результате изучения различной литературы, гипотеза была подтверждена. Действительно, существуют другие признаки делимости, кроме тех которые мы изучаем в школьном курсе математики. Вывел общий признак делимости великий французский ученый Паскаль. Практически все известные ныне признаки делимости являются частным случаем признака Паскаля.

Систематизировав полученную информацию, зная основные признаки делимости на простые числа, я вывел признаки делимости на составные числа. Полученные результаты были сведены в одну таблицу. С данными этой таблицы я планирую ознакомить учащихся своего класса. Применение этих признаков позволит им значительно упростить процесс вычисления.

Цель достигнута, были изучены признаки делимости от 2 до 20, на 25 и на 125.

Надеюсь, эта работа привлечет интерес к математике.

ЛИТЕРАТУРА

1. Воробьев Н.Н. Признаки делимости—4-е изд.—М.:Наука, 1988.— С. 96.

2. Яковлин М.В. Свойства чисел, аналогичных теореме Безу, «математика в школе», 1991, №6.

3. http://dic.academic.ru/ (Википедии — свободной энциклопедии).

4. http://www.bymath.net (энциклопедия).

5. Виленкин Н.Я. Алгебра 8 кл. Учебное пособие для учащихся школ и классов с углубленным изучением математики.-М. Просвещение, 1995.

8

Признак делимости на 37: green_fr — LiveJournal

?

Category:

• Литература
• reacceptAll()»> Cancel

Когда я был маленьким, я вычитал в какой-то книжке признак делимости на 37. Все знают признак делимости на 3 или на 9, некоторые особо продвинутые товарищи — на 11. А я знал признак делимости на 37 и очень этим гордился.

В двух словах, если заметить, что 111 делится на 37, то и 999 делится, а значит шестизначное число abcdef делится на 37 тогда и только тогда, когда сумма двух трёхзначных чисел abc+def делится на 37.

Совершенно бесполезное знание, но на нём можно построить парочку забавных фокусов для младшеклассников — напиши мне сколь угодно большое число, я припишу к нему две цифры так, чтобы получившееся число делилось без остатка на, скажем… (театральная пауза) 37. В моём детстве всё ограничивалось 8-ю разрядами калькулятора, потому как никто, естественно, не собирался проверять делением в столбик.

---

Сегодня мне как раз 37 лет. В той же книжке был ещё признак делимости на 73, но я его уже не помню. Ничего, время ещё есть 🙂

Tags: ja

Subscribe

• Наталья Конрадова, «Археология русского интернета»

  Вторая книга книжного клуба: Наталья Конрадова, «Археология русского интернета. Телепатия, телемосты и другие техноутопии холодной войны». Здесь моё…

• Ольга Филатова, «Облачно, возможно косатки»

  С лёгкой руки agavr записался в  книжный клуб Просветитель. Там задают одну общую на всех книгу в месяц, мы её читаем, в ходе чтения…

• Акунин, «История», том 5, Пётр I

  Моё главное впечатление от этой книги — пересмотр моего собственного отношения к Петру I. Потому что со школы, с советских фильмов про Петра у меня…

Photo

Hint http://pics.livejournal.com/igrick/pic/000r1edq

Previous
← Ctrl ← Alt

• 1
• 2

Next
Ctrl → Alt →

• Наталья Конрадова, «Археология русского интернета»

  Вторая книга книжного клуба: Наталья Конрадова, «Археология русского интернета. Телепатия, телемосты и другие техноутопии холодной войны». Здесь моё…

• Ольга Филатова, «Облачно, возможно косатки»

  С лёгкой руки agavr записался в  книжный клуб Просветитель. Там задают одну общую на всех книгу в месяц, мы её читаем, в ходе чтения…

• Акунин, «История», том 5, Пётр I

  Моё главное впечатление от этой книги — пересмотр моего собственного отношения к Петру I. Потому что со школы, с советских фильмов про Петра у меня…

Правила делимости | Правила делимости чисел на 2, 3, 4, 5, 6, 7, 8, 9, 10 и 11

Деление используется гораздо чаще, чем вы думаете. При делении еды или денег с друзьями или даже при разрезании пиццы используется разделение. Правила делимости в математике представляют собой набор определенных критериев, которые применяются к числу, чтобы определить, делится ли оно на указанное число. Некоторые хорошо известные правила делимости относятся к числам в диапазоне от 2 до 10.

Эти правила позволяют нам находить делители и кратные числа без необходимости проводить длительные деления. Следуя формуле правила делимости, человек может определить, делится ли число на другое целое число. В этой статье мы узнаем о правилах делимости на примерах.

Правило деления целых чисел

В математике правила деления помогают определить, делится ли одно число на другое число, вместо использования фактического метода деления. Если одно число полностью делится на другое, то частное является целым числом, а остаток всегда равен нулю. Если число не делится полностью на какое-либо другое число, такие числа имеют остаток, отличный от нуля или отличного от нуля. Теперь давайте рассмотрим правила делимости с примерами один за другим.

Правило деления на 2

Если у вас есть число с последней цифрой 0 или четное число, оно делится на 2. Например, число 20 заканчивается нулем. Когда половина числа разделена, результат равен 10, что является четным числом.

Пример: Проверить, делится ли число 257746 на 2.

Ответ: Так как число оканчивается на 6, то оно четное. Следовательно, число 257746 делится на 2.

Правило деления на 3

Если сумма цифр числа делится на три, то число делится на три. Студенты должны уметь делить, чтобы применить эту стратегию, но проверить меньшие числа легче, чем большие. Чтобы получить больше ясности относительно правила делимости на 3, см. таблицу правил деления, приведенную ниже.

Таблица правил деления на 3

Пример: Проверить, делится ли число 168 на 3.

Ответ:

$1+6+8=15$

$\Rightarrow \dfrac{15}{3}=5 $

В результате 168 делится на 3.

Правило деления на 4

Если последние две цифры числа делятся на четыре, то все число делится на 4.

Пример: Проверить, является ли число 7516 делится на 4.

Ответ: Поскольку число 7516 имеет две последние цифры 16, оно делится на 4. Следовательно, число 7516 делится на 4.

Правило деления на 5

Когда последняя цифра числа 0 или 5, значение можно разделить на 5 без остатка. В результате можно разделить 5, 10, 15, 20, 25 и т. д. на 5.

Пример: Проверить, делится ли число 160 на 5.

Ответ: Так как последняя цифра числа 160 равна 0. Значит, 160 делится на 5.

Правило деления на 6

Числа делятся на 6 также можно разделить на 3 и 2. Учащиеся должны проверить число, используя оба правила для 3 и 2. Если число соответствует обоим критериям, оно может быть разделено на 6. Если оно не проходит хотя бы один тест, оно не может пройти.

Пример: Проверить, делится ли число 306 на 6.

Ответ: Поскольку 308 оканчивается на четную цифру, оно делится на два. Однако 3 + 0 + 6 равно 9, которое можно разделить на 3 без остатка. В результате 306 делится на 6.

Правило деления на 8

Большое число делится на 8, если последние три цифры либо делится на 8 или на 000.

Пример: Проверить, делится ли число 9864 на 8.

Ответ: Поскольку последние три цифры делятся на 8 (т. е. $864 \div 8=108$ ). Следовательно, число 864 делится на 8,9.0003

Правило деления для 9

Поскольку 9 можно разделить на 3. Следовательно, правило делимости для 9 такое же, как и для 3. Если сумма цифр числа делится на 9, то и все число делится на 9.

Пример: проверить, делится ли следующее число на 9 или нет.

$549=5+4+9=18$

$\Rightarrow \dfrac{18}{2}=9$

Ответ: В результате 549 делится на 9.

Правило деления на 10

Если последняя цифра 0, то число можно разделить на десять без остатка.

Пример: проверьте, нет ли 1650 делится на 10 или нет?

Ответ: Однако 1650 оканчивается на 0, который делится на 10 без остатка. В результате 1650 делится на 10. с использованием правила делимости на 7.

Ответ: Применение правила 7 деления к числу 2415 покажет, делится оно на 7 или нет.

1. Умножьте цифру единицы (5) на 2. Ответ: 10.

2. Возьмите остаток от числа 241 и вычтите из него произведение (10). (241 — 10 = 231)

3. Мы не уверены, кратно ли 231 7. Следовательно, вернемся к шагу 1 и введем там 231.

4. Умножьте цифру единицы (1) на 2. Ответ: 2.

5. Вычтите это число из общего числа, которое равно 23. (23 — 2 = 21)

6. Так как 21 полностью делится на 7, мы можем сказать, что 2415 делится на 7.

Практические задачи

В 1. Проверьте, делится ли число 198 на 8.

Ответ: Не делится.

В 2. Проверить, делится ли число 6273 на 3.

Ответ: Да.

Резюме

Правило делимости позволяет определить, делится ли число на другое число. Когда два числа можно разделить без остатка, частное всегда равно целому числу, а остаток всегда равен нулю. Если число не полностью делится на другое число, остаток не равен нулю или не равен нулю. Это самый простой и быстрый способ решения деления.

Существуют различные правила проверки делимости. Некоторые хорошо известные правила делимости относятся к числам от 2 до 10. Надеюсь, эта статья поможет вам быстро решить вопросы деления, используя изученное нами правило.

Правила делимости: Полное руководство по тестам на деление

В этом посте мы рассмотрим правила делимости для чисел от 2 до 13 с помощью конкретных примеров, которые помогут нам в тестах на деление. Мы начнем с понимания правила делимости, а затем рассмотрим соответствующие правила деления чисел от 2 до 13.

Что такое правило делимости?

Для заданного числа $x$ правила делимости помогают нам проверить, делится ли это число на число, скажем, $y$, даже не выполняя фактическое деление. Правила делимости очень удобны, когда вы хотите проверить делимость чисел еще до того, как вы сможете разделить число. В этом посте мы рассмотрим правило делимости для соответствующих чисел от 2 до 13.

Правило делимости 2

Чтобы проверить, делится ли число на 2, все, что вам нужно сделать, это проверить, является ли цифра в единицах место числа равно 0 или кратно 2. Другими словами, если цифра единиц числа четная, то число делится на 2.

Числа 64, 762, 540, 634, 758, 976 делятся на 2, так как цифра их единиц четная.

А числа 121, 463, 575, 647, 789 не кратны 2, так как разряд их единиц нечетный.

Теперь что насчет 135648327896. Посмотрите на разряд единиц числа, он заканчивается на 6, что является четным числом и, следовательно, удовлетворяет нашему правилу.

Правило делимости 3

Чтобы число N делилось на 3, нужно найти сумму цифр этого числа. Если сумма цифр этого числа делится на 3, то число определенно делится на 3.

Пример: 1461

Рассмотрим 1461. Сумма его цифр равна 1+4+6+1 = 12. 12 кратно 3. Следовательно, 1461 также кратно 3.

Пример: 12332

Рассмотрим число 12332. Сумма его цифр равна 1+2+3+3+2 = 11. 11 не кратно и, следовательно, не делится на 3

Пример: 267345

Сумма его 2+6+7+3+4+5 = 27. 27 кратно 3. Следовательно, 123321 делится на 3

Пример: 9745321

Сумма цифр этого числа равна 9+7+4+5+3+2+1 = 31. 31 не кратно и, следовательно, не делится на 3

Правило делимости на 4

Правило 2 требует, чтобы мы проверяли последнюю цифру числа. Для правила 4 нам нужно будет проверить, являются ли последние две цифры чисел кратными 4.

Пример: 412

Здесь последние две цифры 12 кратны 4. Следовательно, оно делится на 4.

Пример: 53217

Последние две цифры числа 53217 равны 17, что не кратно 4, и, следовательно, 53217 не кратно 4.

Пример: 67549

Последние две цифры кратно 4 и, следовательно, не делится на 4.

Пример: 123496

Последние две цифры 96 делятся на 4, следовательно, 123496 кратно 4.

Правило деления 5

Это довольно просто вперед. Все, что вам нужно проверить, это является ли последняя цифра числа 0 или 5. Если да, число кратно 5

Числа 45, 50, 735, 8730, 97695 делятся на 2, так как их единица измерения равна 0 или 5 не равно 0 или 5.

Правило деления 6

Чтобы проверить, является ли число кратным 6, мы должны проверить, удовлетворяет ли число следующим двум условиям:

• Оно должно быть кратно 2: Число должно быть четным
• Должно быть кратно 3: Сумма цифр числа должна быть кратна 3.

Пример: 126

Число оканчивается на 6, что является четным и, следовательно, делится на 2, а сумма его цифр равна 9, что кратно 3. Поскольку число удовлетворяет обоим случаям, число делится на 6.

Пример: 3412

Число оканчивается на 2, что является четным, и, следовательно, оно делится на 2, а сумма его цифр равна 10, что не кратно 3. Так как число не делится на 3, число не делится на 6, даже если оно кратно 2.

Пример: 46239

Число не делится на 2, так как оно четное. Следовательно, оно не кратно 6.

Пример: 96312

Число оканчивается на 2, что является четным, а сумма его цифр равна 21, что кратно 3. Поскольку число удовлетворяет обоим случаям, оно делится на 6.

Правило делимости 7

Чтобы проверить, делится ли число на 7, используется общее правило делимости 7 на 9.0003

1. Удвойте цифру единиц числа и вычтите ее из остального числа.
2. Если полученный ответ делится на 7, то и фактическое число делится на 7.
3. Если вы не уверены в делимости полученного ответа, снова примените правило к ответу.

Пример: 126

• Удвоить цифру единиц 6, что дает 12
• Вычесть 12 из остального числа, т.е.0098

Пример: 672

• Умножьте последнюю цифру 2 на 2, что даст 4.
• Вычтите 4 из остатка числа, т.е. 67 – 4 = 63.
  Поскольку 63 делится на 7. 672 на 7

Пример: 1436

• Умножьте последнюю цифру 6 на 6, что даст 36.
• Вычтите 36 из остатка числа, т.е. Давайте повторим процесс: удвоим цифру единиц 7: 2×7 = 14
• Вычесть 14 из остатка числа 10 – 14 = -4
  Так как -4 не делится на 7. 1436 тоже не делится.

Пример: 5201

• Удвоить единицы цифры: 2 × 1 = 2
• Вычтите 2 из 520 => 518
• Double The Units Digit 8 => 16
• . Поскольку 35 кратно 7, 5201 делится на 7.

Пример: 156735

• Удвоить число единиц 5×2 => 10
• Вычесть 10 из 15673 => 15663
• Удвоить цифру единиц 3 => 6
• Вычесть 6 из 1567 => 1561
• Удвоить цифру единиц 1 => 2
• Вычесть 2 из 154 число единиц 4 => 8
• Вычесть 8 из 15 => 7
  Так как 7 кратно 7. Следовательно, 156735 делится на 7

Правило делимости 8

Правило 2 требует, чтобы мы проверили последним цифра номера. Правило 4 требует, чтобы мы проверили 9n$ нам нужно проверить последние n цифр этого числа. Давайте рассмотрим некоторые примеры правил деления на 8.

Пример: 1824

Последние три цифры 824 при делении на 8 дают 103. Поскольку 824 делится, 1824 также делится на 8. На самом деле числа 2824, 9824, 10824 и т. д. также кратны 8, так как их последние цифры 824 кратны 8.

Пример: 45673

Здесь число, кратное 8, никогда не будет нечетным числом. . Следовательно, мы можем легко определить, что 45673 не делится на 8.

Пример: 12474

Здесь последние три цифры 474 при делении на 8 дают в остатке 2. Следовательно, 12474 не делится на 8. на 8. Число 26032 делится на 8

Правило деления для 9

Это правило точно такое же, как делимость на 3, где мы проверяем делимость, находя сумму цифр числа. Если сумма цифр кратна 9, число делится на 9.

Пример: 126

Сумма цифр 1+2+6 = 9, что кратно 9. Следовательно, 126 делится на 9.

Пример: 4329

Сумма цифр 4+3+2+9 = 18, кратна 9 и, следовательно, 4329 делится на 9.

Пример: 14574

Сумма цифр 1+4 +5+7+4 = 19, не делится на 9. Следовательно, 14574 не делится на 9.

Пример: 11106

Сумма цифр 1+1+1+0+6 = 9, что кратно 9. Следовательно, 11106 делится на 9. в 0. Если да, то число кратно 0.

Числа 30, 550, 7360, 8730, 92950 делятся на 10, так как число оканчивается на 0.

В то время как числа 45, 123, 3647, 23429 не оканчиваются на 0 и, следовательно, не делятся на 10.

Правило делимости числа 11

Чтобы проверить, делится ли число на 11, мы вычитаем сумму цифр, стоящих на четных местах, из суммы цифр, стоящих на нечетных местах, и проверяем, делится ли полученное число на 11. Другими словами, если разность из альтернативных цифр номера кратно 11, то число должно делиться на 11

Пример: 451

Сумма цифр в четных местах равна 5
Сумма цифр в нечетных местах равна 4+1 = 5
Разница в сумме четных и нечетных мест 5 – 5 = 0, что делится на 11.
Следовательно, 451 делится на 11

Пример: 4372

Сумма цифр, стоящих на четных местах, равна 4 + 7 = 11
Сумма цифр, стоящих на нечетных местах, равна 3 + 2 = 5
Разница четных и нечетных сумма разрядов 11 – 5 = 6, что не кратно 11.
Следовательно, 4372 не делится на 11

Пример: 92653

Сумма цифр, стоящих на четных местах, равна 2+5 = 7
Сумма цифры в нечетных местах 9+6+3=18
Разница в сумме четных и нечетных мест 18-7 = 11, что кратно 11 и, следовательно, 92563 делится на 11.

Пример: 107415

Сумма цифр в четных местах 1+7+1=9
Сумма цифр в нечетных местах 0+4+5 = 9
Разница в сумма четных и нечетных мест 9-9=0, что делится на 11.
Следовательно, 107415 делится на 11

Правило делимости 12

Подобно правилу 6, чтобы число было кратным 12, оно должно два случая:

• Должно быть кратно 3
• Должно быть кратно 4

Пример: 132

Сумма цифр 1+3+2 = 6, что кратно 3. Следовательно, число делится на 3.
Последние две цифры числа 32 кратны 4. Следовательно число делится на 4.
Так как число делится на 3 и 4. Число делится на 12.

Пример: 1462

Сумма цифр 1+4+6+2 = 13, равна не кратно 3. Следовательно, число не делится на 12.

Пример: 1203

Сумма цифр 1+2+0+3 = 6, что кратно 3. Следовательно, число делится на 3.
Последние две цифры 03 не кратны 4. Следовательно, число не кратно 3. делится на 12

Правило делимости 13

Чтобы проверить, делится ли число на 13, мы умножаем последнюю цифру на 9, а затем вычитаем ее из остальной части числа. Если полученный результат делится на 13, то число делится на 13

Пример: 247

• Умножьте 7 на 9, чтобы получить 63.
• Вычтите 63 из 24, чтобы получить -39.
  -39 делится на 13. Следовательно, 247 делится на 13.

Пример: 2365

• Умножение 5 на 9, что дает 45.
• Подряд 45 из 236, который дает 191998 9098
• .

  No related posts.