Правило прямоугольника онлайн
Правило прямоугольника применяется в методе Жордана-Гаусса.Алгоритм пересчета таблиц по правилу прямоугольника.
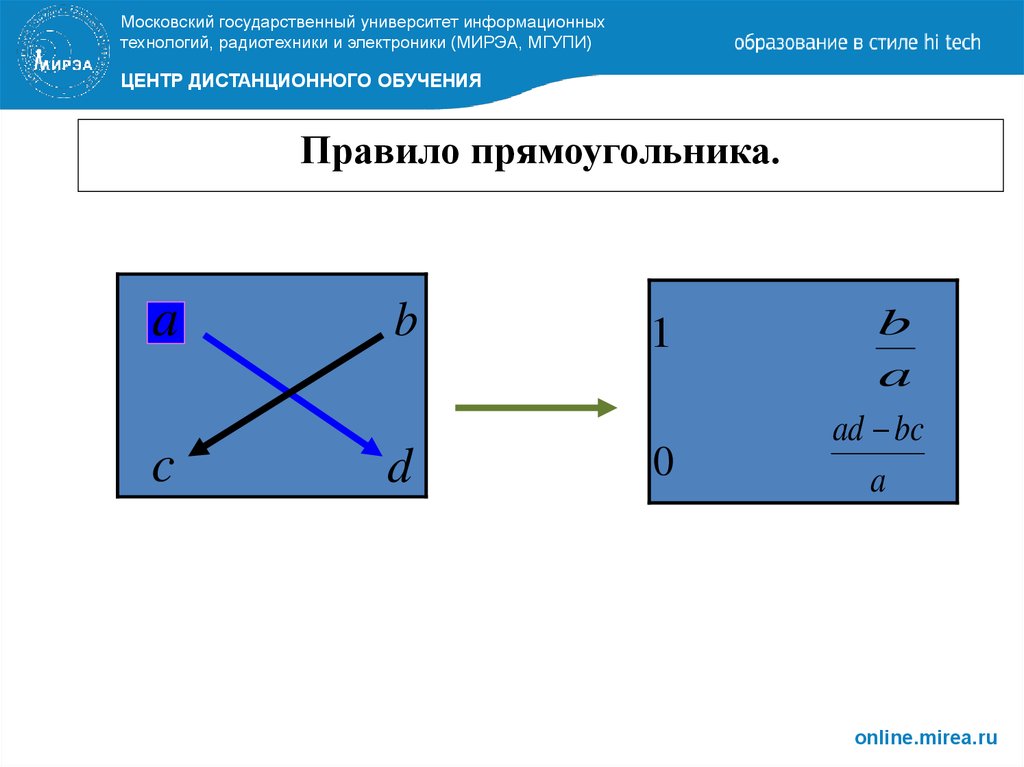
Выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ — (А*В)/РЭ
СТЭ — элемент старого плана, РЭ — разрешающий элемент, А и В — элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.Назначение сервиса. Онлайн-калькулятор Правило прямоугольника предназначен для пересчета таблиц методом жордановских преобразований.
- Шаг №1
- Шаг №2
Выберите размерность таблицы.
2345678910
x
2345678910
Примечание. Данный метод не стоит путать с формулой прямоугольников.
Пример №1. Производится пересчет элементов новой симплекс-таблицы. Каким будет значение элемента x25 в новой симплекс-таблице, если до пересчета x25 = -3 , x27 =5 , х45 = -8 , х47 =2
Решение.
x25 =x25 — x45*x27/x47 = -3 — (-8)*5/2 = -3+20 = 17
Пример №2. По приведенной ниже симплекс-таблице определите, является ли соответствующее ей базисное решение оптимальным. Если решение не является оптимальным, осуществите пересчет таблицы.
| ПЧ | X3 | X4 | |
| F | -5 | 2 | -1 |
| X1 | 4 | 2 | 1 |
| X2 | 3 | 1 | 2 |
Решение.
Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных xj≥0, что эквивалентно условию неотрицательности bj≥0.
Поскольку X1 = 4 > 0, X2 = 3 > 0, то это допустимое базисное решение. Определим, является ли оно оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить. В индексной строке X4 = -1 < 0, поэтому план не является оптимальным. Осуществим пересчет таблицы.
Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: min (4:1 , 3:2 ) = 1
Следовательно, 2-ая строка является ведущей. Вместо переменной x4 в план войдет переменная x2.
Таблица 1
| ПЧ | X3 | X4 | |
| F | -5 | 2 | -1 |
| X1 | 4 | 2 | 1 |
| X2 | 3 | 1 | 2 |
Разрешающий элемент РЭ=2.
Строка, соответствующая переменной x2 , получена в результате деления всех элементов строки x на разрешающий элемент РЭ=2 (см. табл.2) . На месте разрешающего элемента получаем 1. В остальных клетках столбца x 2 записываем нули. Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ — (А*В)/РЭ
СТЭ — элемент старого плана, РЭ — разрешающий элемент (2), А и В — элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ (см. табл.2).
Формируем таблицу.
Таблица 2
| 4-(3 • 1):2 | 2-(1 • 1):2 | 1-(2 • 1):2 |
| 3 : 2 | 1 : 2 | 2 : 2 |
| -5-(3 • -1):2 | 2-(1 • -1):2 | -1-(2 • -1):2 |
Получаем новую таблицу:
Таблица 3
| ПЧ | X2 | ||
| F | -31/2 | 21/2 | 0 |
| X1 | 21/2 | 11/2 | 0 |
| X4 | 11/2 | 1/2 | 1 |
Поскольку X3≥0, X2≥0, то получили оптимальный план.
Пример №3. Решить задачу линейного программирования симплекс-методом, используя в качестве начальной угловой точки:
f(x) = -2x1 + x2 + 4x3 – x4 – x5 → min
x2 + 2x4 – x5 = 1
2x2 + x3 + 2x5 = 4
xj ≥ 0, j=1,..,5, x0 = (1;1;2;0;0)
Решение.
Сведем задачу F(X) → min к задаче F(X) → max. Для этого умножаем F(X) на (-1).
0x1-1x2 + 0x3-2x4 + 1x5 = -1
-1x1 + 0x2 + 0x3 + 1x4 + 1x5 = -1
0x1-2x2-1x3 + 0x4-2x5 = -4
F(x) = 2x1 — x2 — 4x3 + x4 + x5
Затем систему ограничений преобразуем методом Гаусса-Жордана к такой форме, чтобы базисными стали переменные x1, x2, x3, а вектор b = (1, 1, 2)T
|
-1 |
0 | -1 | 0 | -2 | 1 |
| -1 | -1 | 0 | 0 | 1 | 1 |
| -4 | 0 | -2 | -1 | 0 | -2 |
| 0 | -2 | 1 | 4 | -1 | -1 |
Итерация №1.
Разрешающий элемент РЭ=-1.
Формируем таблицу.
Строка, соответствующая переменной x2 , получена в результате деления всех элементов строки x2 на разрешающий элемент РЭ=-1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую таблицу:
| -1 | 0 | -1 | 0 | -2 | 1 |
| 1 | 1 | 0 | 0 | -1 | -1 |
| -4 | 0 | -2 | -1 | 0 | -2 |
| 2 | 0 | 1 | 4 | -3 | -3 |
Итерация №2. Разрешающий элемент РЭ=-1.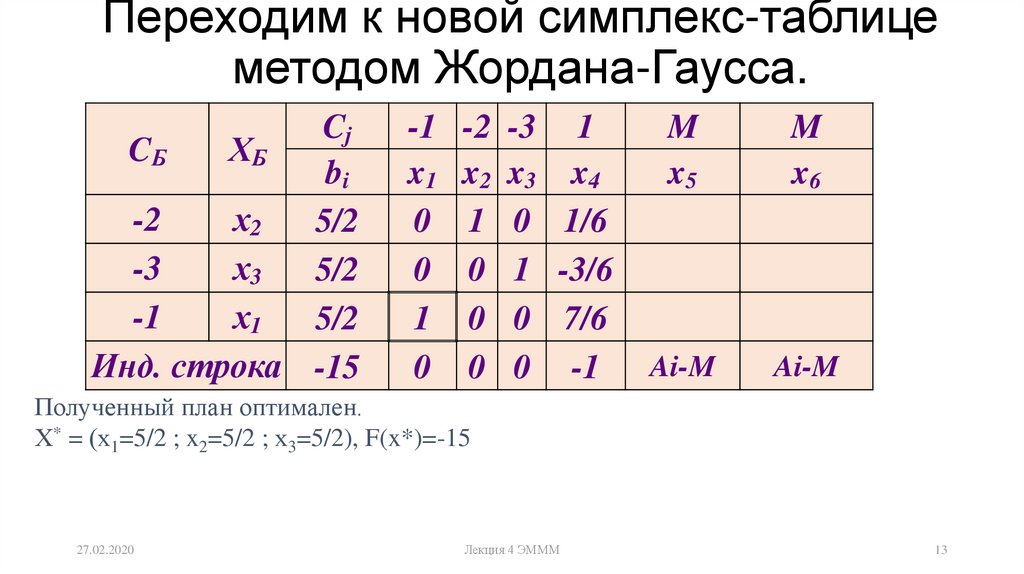
Строка, соответствующая переменной x4, получена в результате деления всех элементов строки x3 на разрешающий элемент РЭ=-1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x4 записываем нули.
Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника.
| -1 | 0 | -1 | 0 | -2 | 1 |
| 1 | 1 | 0 | 0 | -1 | -1 |
| 4 | 0 | 2 | 1 | 0 | 2 |
| -14 | 0 | -7 | 0 | -3 | -11 |
Итерация №3. Разрешающий элемент РЭ=-1. Строка, соответствующая переменной x3 , получена в результате деления всех элементов строки x1 на разрешающий элемент РЭ=-1.
На месте разрешающего элемента получаем 1. В остальных клетках столбца x 3 записываем нули. Все остальные элементы, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую таблицу:
| 1 | 0 | 1 | 0 | 2 | -1 |
| 1 | 1 | 0 | 0 | -1 | -1 |
| 2 | 0 | 0 | 1 | -4 | 4 |
| -7 | 0 | 0 | 0 | 11 | -18 |
Далее необходимо переназначить переменные и решать симплекс-методом.
Табличный симплекс-метод
Для упрощения процесса решения исходные данные задачи линейного программирования при решении ее симплекс методом записываются в специальные симплекс-таблицы.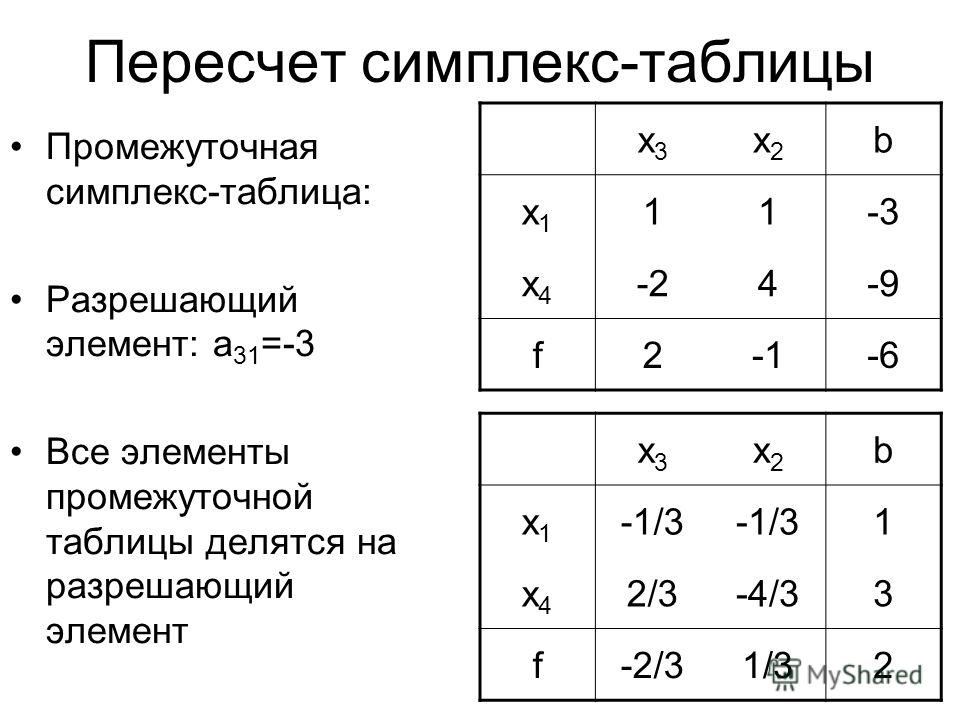
F=a0,1x1+a0,2x2+…a0,nxn +b0 → max
a1,1x1+a1,2x2+…a1,nxn + xn+1=b1
a2,1x1+a2,2x2+…a2,nxn +xn+2 =b2
…………………………………
am,1x1+am,2x2+…am,nxn+xn+m=bm
Исходная таблица для задачи имеет следующий вид:
| x1 | x2 | … | xn-1 | xn | b | |
| F | -a0,1 | -a0,2 | … | -a0,n-1 | -a0,n | -b0 |
| xn+1 | a1,1 | a1,2 | … | a1,n-1 | a1,n | b1 |
| xn+2 | a2,1 | a2,2 | … | a2,n-1 | a2,n | b2 |
| … | … | … | … | … | … | … |
| xn+m | am,1 | am,2 | … | am,n-1 | am,n | bm |
x1, x2, xn – исходные переменные, xn+1, xn+2, xn+m – дополнительные переменные.
Все дополнительные переменные мы приняли как базисные, а исходные переменные как небазисные (дополнительные записаны в первый столбец симплекс-таблицы а исходные в первую строку). При каждой итерации элементы симплекс-таблицы пересчитывают по определенным правилам.
Алгоритм симплекс-метода.
Подготовительный этап
Приводим задачу ЛП к каноническому виду
F=a0,1x1+a0,2x2+…a0,nxn +b0 → max
a1,1x1+a1,2x2+…a1,nxn+xn+1=b1
a2,1x1+a2,2x2+…a2,nxn+xn+2=b2
…………………………………
am,1x1+am,2x2+…am,nxn+xn+m=bm
В случае если в исходной задаче необходимо найти минимум – знаки коэффициентов целевой функции F меняются на противоположные a0,n=-a0,n.
Знаки коэффициентов ограничивающих условий со знаком “≥” так же меняются на противоположные. В случае если условие содержит знак “≤” – коэффициенты запишутся без изменений.
Шаг 0. Составляем симплексную таблицу, соответствующую исходной задаче
| x1 | x2 | … | xn-1 | xn | b | |
| F | -a0,1 | -a0,2 | … | -a0,n-1 | -a0,n | -b0 |
| xn+1 | a1,1 | a1,2 | … | a1,n-1 | a1,n | b1 |
| xn+2 | a2,1 | a2,2 | … | a2,n-1 | a2,n | b2 |
| … | … | … | … | … | … | … |
| xn+m | am,1 | am,2 | … | am,n-1 | am,n | bm |
Шаг 1.
Проверка на допустимость.
Проверяем на положительность элементы столбца b (свободные члены), если среди них нет отрицательных то найдено допустимое решение (решение соответствующее одной из вершин многогранника условий) и мы переходим к шагу 2. Если в столбце свободных членов имеются отрицательные элементы то выбираем среди них максимальный по модулю – он задает ведущую строку k. В этой строке так же находим максимальный по модулю отрицательный элемент ak,l – он задает ведущий столбец – l и является ведущим элементом. Переменная, соответствующая ведущей строке исключается из базиса, переменная соответствующая ведущему столбцу включается в базис. Пересчитываем симплекс-таблицу согласно правилам.
Если же среди свободных членов есть отрицательные элементы – а в соответствующей строке – нет то условия задачи несовместны и решений у нее нет.
Если после перерасчета в столбце свободных членов остались отрицаетельные элементы, то переходим к первому шагу, если таких нет, то ко второму.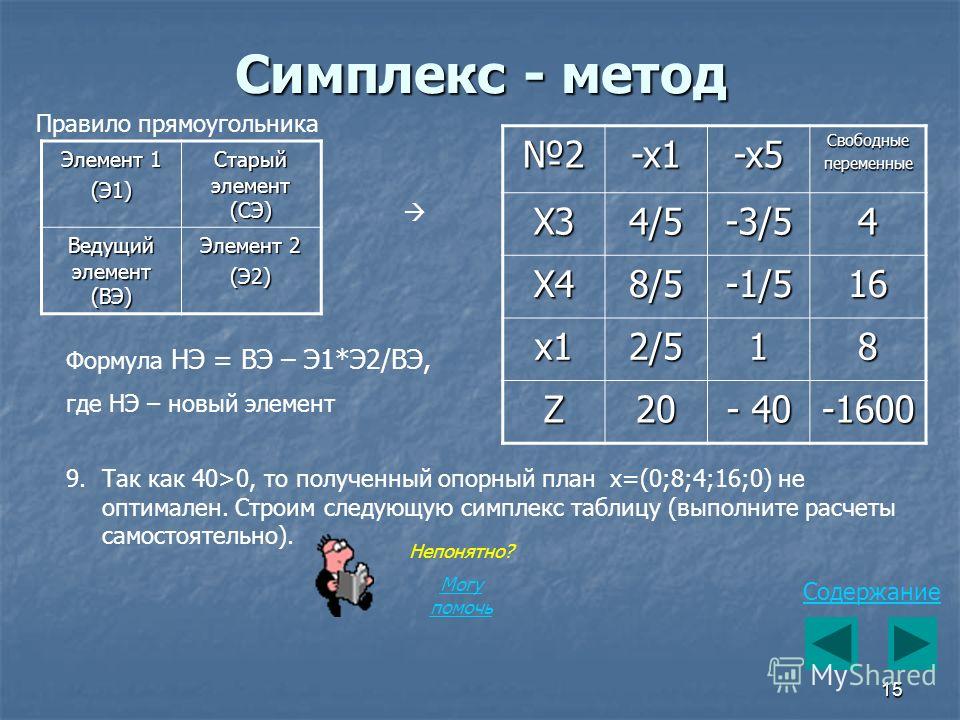
Шаг 2. Проверка на оптимальность.
На предыдущем этапе найдено допустимое решение. Проверим его на оптимальность Если среди элементов симплексной таблицы, находщихся в строке F (не беря в расчет элемент b0 – текущее значение целевой функции) нет отрицательных, то найдено оптимальное решение.
Если в строке F есть отрицательные элементы то решение требует улучшения. Выбираем среди отрицательных элементов строки F максимальный по модулю (исключая значение функции b0)
a0,l=min{a0,i }
l – столбец в котором он находится будет ведущим. Для того, что бы найти ведущую строку, находим отношение соответсвующего свободного члена и элемента из ведущего столбца, при условии, что они неотрицательны.
bk/ak,l =min {bi/ai,l } при ai,l>0, bi>0
k – cтрока, для которой это отношение минимально – ведущая.
Элемент ak,l – ведущий (разрешающий). Переменная, соответствующая ведущей строке (xk) исключается из базиса, переменная соответствующая ведущему столбцу (xl) включается в базис.
Пересчитываем симплекс-таблицу по формулам. Если в новой таблице после перерасчета в строке F остались отрицательные элементы переходим к шагу 2
Если невозможно найти ведущую строку, так как нет положительных элементов в ведущем столбце, то функция в области допустимых решений задачи не ограничена – алгоритм завершает работу.
Если в строке F и в столбце свободных членов все элементы положительные, то найдено оптимальное решение.
Правила преобразований симплексной таблицы.
При составлении новой симплекс-таблицы в ней происходят следующие изменения:
- Вместо базисной переменной xk записываем xl; вместо небазисной переменной xl записываем xk.
- ведущий элемент заменяется на обратную величину ak,l‘= 1/ak,l
- все элементы ведущего столбца (кроме ak,l) умножаются на -1/ak,l
- все элементы ведущей строки (кроме ak,l) умножаются на 1/ak,l
- оставшиеся элементы симплекс-таблицы преобразуются по формуле ai,j‘= ai,j– ai,lx ak,j/ ak,l
- Вместо базисной переменной xk записываем xl; вместо небазисной переменной xl записываем xk.
Схему преобразования элементов симплекс-таблицы (кроме ведущей строки и ведущего столбца) называют схемой ”прямоугольника”.
Преобразуемый элемент ai,j и соответствующие ему три сомножителя как раз и являются вершинами ”прямоугольника”.
Пример
Подробнее
Табличные процессоры
Реферат, Информатика
Выполнил: EkaterinaKonstantinovna
Решение ЗЛП симплекс-методом
Решение задач, Информационные технологии
Выполнил: user2202984
Так же вы можете купить уже выполненные похожие работы.
Для удобства покупки
работы размещены на независимой бирже. Подробнее об условиях покупки тут.
Ответ в исследовании операций для Vaishu #185201
Решение.
Определим максимальное значение целевой функции F(X) = 4×1 + 3×2 при следующих условиях ограничений.
2×1 + x2≤1000
x1 + 2×2≤800
x1≤400
x2≤700
Для построения первого эталонного плана система неравенств сводится к системе уравнений путем введения дополнительных переменных.
2х1 + х2 + х3 = 1000
x1 + 2×2 + x4 = 800
x1 + x5 = 400
x2 + x6 = 700
Матрица коэффициентов A = a (ij) этой системы уравнений имеет вид:
A =
2 1 1 0 0 0
1 2 0 1 0 0
1 0 0 0 1 0
0 1 0 0 0 1
Решим систему уравнений относительно основных переменных: x3, x4, x5, x6
Предполагая, что свободные переменные равны 0, мы получаем первую базовую линию:
X0 = (0,0,1000,800,400,700)
Базовое решение называется допустимым, если оно неотрицательно.
один.
Текущий базовый план не оптимален, так как в индексной строке имеются отрицательные шансы.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю.
Подсчитаем значения Di построчно как частное от деления: bi/ai1
и выберем из них наименьшее:
min (1000:2, 800:1, 400:1, -) = 400
Следовательно, 3-я линия является ведущей.
Преобразователь (1) находится на пересечении ведущего столбца и начального ряда.
Основа B x1 x2 x3 x4 x5 x6 мин.
x3 1000 2 1 1 0 0 0 500
x4 800 1 2 0 1 0 0 800
x5 400 1 0 0 0 400
x6 700 0 10002 0 0 0 1 —
F (X1) 0 -4 -3 0 0 0 0
Вместо переменной x5 в план 1 будет включена переменная x1.
Строка, соответствующая переменной x1 в плане 1, получается делением всех элементов строки x5 в плане 0 на разрешающий элемент RE = 1. Вместо разрешающего элемента получаем 1. В оставшиеся ячейки запишем нули столбец х1.
Таким образом, в новом плане 1 заполнены строка x1 и столбец x1. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают в себя разрешающий элемент РЭ.
NE = SE — (A*B)/RE
STE — элемент старого плана, RE — разрешающий элемент (1), A и B — элементы старого плана, образующие прямоугольник с элементами STE и ЧП.
Получаем новую симплексную таблицу:
Базис Б x1 x2 x3 x4 x5 x6
x3 200 0 1 1 0 -2 0
x4 400 0 2 0 1 -1 0
x1 0 400 0 1 0
x6 700 0 1 0 0 0 1
F (X1) 1600 0 -3 0 0 4 0
2.
Текущий базовый план не является оптимальным, поскольку в индексной строке имеются отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю.
Вычисляем значения Di построчно как частное от деления: bi/ai2
и выбираем наименьшее из них:
min (200:1, 400:2, -, 700:1) = 200
Следовательно, 1-я линия является ведущей.
Преобразователь (1) находится на пересечении ведущего столбца и начального ряда.
Основание B x1 x2 x3 x4 x5 x6 мин.0003
x6 700 0 1 0 0 0 1 700
F (X2) 1600 0 -3 0 0 4 0
Поскольку в последнем столбце есть несколько минимальных элементов из 200, номер строки выбираем по правилу Крако. Элементы строки, имеющие одинаковое наименьшее значение min = 200, делятся на элементы предполагаемого разрешения, а результаты записываются в дополнительные строки. Для ведущей строки выбирается та, в которой наименьшее частное встречается ранее при чтении таблицы слева направо по столбцам.
Формируем следующую часть симплексной таблицы. Вместо переменной x3 в план 2 будет включена переменная x2.
Строка, соответствующая переменной x2 в плане 2, получается делением всех элементов строки x3 в плане 1 на разрешающий элемент RE = 1. Вместо разрешающего элемента получаем 1. В оставшиеся ячейки запишем нули столбец х2.
Таким образом, в новом плане 2 заполнены строка x2 и столбец x2.
Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
• -3): 1 0- (0 • -3): 1 4 — (- 2 • -3): 1 0- (0 • -3): 1
Получаем новую симплексную таблицу:
Основание B x1 x2 x3 x4 x5 x6
x2 200 0 1 1 0 -2 0
x4 0 0 0 -2 1 3 0
x1 400 1 0 0 0 1 0
x6 500 0 20 -1 1
F (X2) 2200 0 0 3 0 -2 0
Номер итерации 2.
1. Проверка критерия оптимальности.
Текущий базовый план не оптимален, так как в индексной строке имеются отрицательные шансы.
2. Определение новой базовой переменной.
В качестве ведущего выберем столбец, соответствующий переменной x5, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Подсчитаем значения Di построчно как частное от деления: bi/ai5
и выберем из них наименьшее:
min(-, 0:3, 400:1, 500:2) = 0
Следовательно, 2-я строка является ведущей.
Разрешающий элемент (3) находится на пересечении ведущего столбца и начального ряда.
Основание B x1 x2 x3 x4 x5 x6 мин
x2 200 0 1 1 0 -2 0 —
x4 0 0 0 -2 1 3 0 0 0 0 -1 0 2 1 250
F (X3) 2200 0 0 3 0 -2 0
4. Пересчет симплексной таблицы. Вместо переменной x4 план 3 будет включать переменную x5.
Строка, соответствующая переменной x5 в плане 3, получается делением всех элементов строки x4 в плане 2 на разрешающий элемент RE = 3. Вместо разрешающего элемента получаем 1. В оставшиеся ячейки запишем нули столбец х5.
Итак, в новом плане 3 заполнены строка x5 и столбец x5. Все остальные элементы нового плана 3, включая элементы индексной строки, определяются по правилу прямоугольника.
B x1 x2 x3 x4 x5 x6
200- (0 • -2): 3 0- (0 • -2): 3 1- (0 • -2): 3 1 — (- 2 • -2) : 3 0- (1 • -2): 3 -2- (3 • -2): 3 0- (0 • -2): 3
0: 3 0: 3 0: 3 -2: 3 1: 3 3: 3 0: 3
400- (0 • 1): 3 1- (0 • 1): 3 0- (0 • 1): 3 0 — (- 2 • 1): 3 0- (1 • 1): 3 1- (3 • 1): 3 0- (0 • 1): 3
500- (0 • 2): 3 0- (0 • 2): 3 0- (0 • 2): 3 -1 — (- 2 • 2): 3 0- (1 • 2): 3 2 — ( 3 • 2): 3 1- (0 • 2): 3
2200- (0 • -2): 3 0- (0 • -2): 3 0- (0 • -2): 3 3 — (- 2 • -2): 3 0- (1 • -2): 3 -2- (3 • -2): 3 0- (0 • -2): 3
Получаем новую симплексную таблицу:
Основание B x1 x2 x3 x4 x5 x6
x2 200 0 1 -1/3 2/3 0 0
x5 0 0 0 -2/3 1/3 1 0
x1 400 1 0 2/3 — 1/3 0 0
x6 500 0 0 1/3 -2/3 0 1
F (X3) 2200 0 0 5/3 2/3 0 0
1.
Проверка критерия оптимальности.
В строке индекса нет отрицательных значений. Поэтому эта таблица определяет оптимальный план задач.
Окончательный вариант симплекс-таблицы:
Базис Б x1 x2 x3 x4 x5 x6
x2 200 0 1 -1/3 2/3 0 0
x5 0 0 0 -2/3 1/3 1 0
x1 400 1 0 2/3 -1/3 0 0
x6 500 0 0 1/3 -2/3 0 1
F (X4) 2200 0 0 5/3 2/3 0 0
оптимальный план можно записать так:
x1 = 400, x2 = 200
F (X) = 4 * 400 + 3 * 200 = 2200.
Ответ. 2200.
линейное программирование — Как симплекс-метод обрабатывает тестовые коэффициенты с нулями?
Я столкнулся с проблемой выбора опорной точки при наличии ограничений с нулевой правой стороной. Похоже, что иногда при поиске минимального коэффициента проверки следует включать нулевые тестовые коэффициенты, а иногда нет. Каково жесткое и быстрое правило для обработки нулевых тестовых коэффициентов?
Для простой демонстрации предположим, что вы хотите максимизировать $y$ при $x + y \le 1$ и $y \le x$.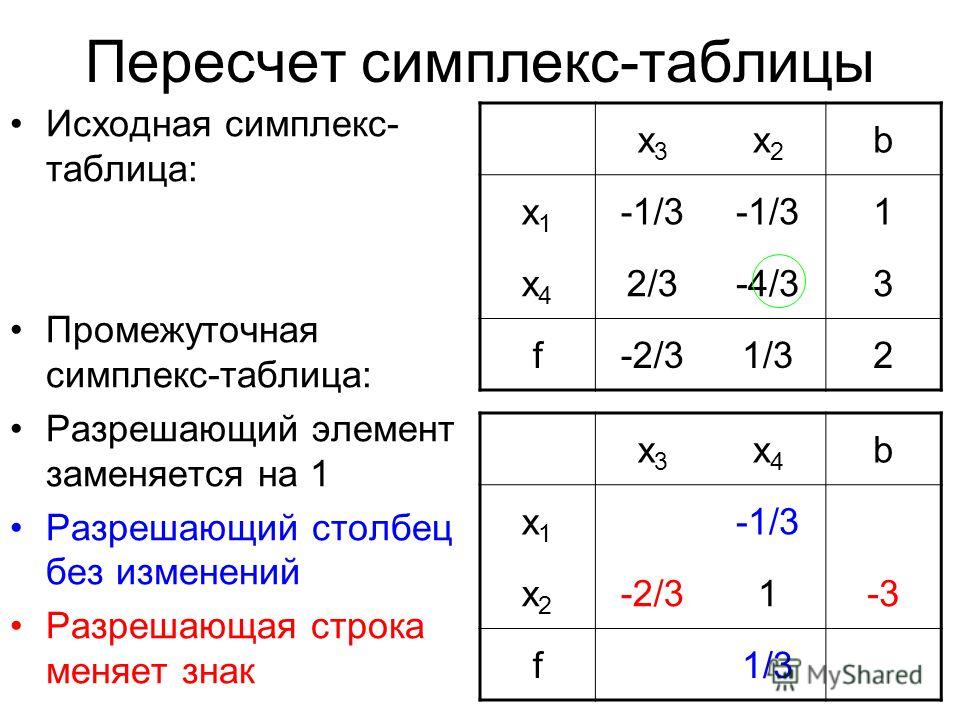
График x/y пространства решений показывает треугольник с вершиной в точке $x = \frac{1}{2}, y = \frac{1}{2}$. Чтобы максимизировать $y$, мы должны оказаться в этой точке.
Первая таблица: $$0: \begin{bматрица} & х & у & s_1 & s_2 & = \\ s_1 & 1 & 1 & 1 & 0 & 1 \\ s_2 & -1 & 1 & 0 & 1 & 0 \\ & 0 & -1 & 0 & 0 & 0 \end{bmatrix} $$
Единственная возможная переменная — $y$ с отрицательной стоимостью -1. Затем, чтобы выбрать опорную строку, мы находим два отношения. Строка 1 $1/1 = 1$, строка 2 $0/1 = 0$. Вот в чем проблема. Как я понял, чтобы выбрать сводную строку, тест отношения должен быть положительным . Если мы будем следовать этому правилу, останется только одна возможность оставить переменную, $s_1$. Итак, попробуем следовать правилу: $$1: \begin{bматрица} & х & у & s_1 & s_2 & = \\ у и 1 и 1 и 1 и 0 и 1 \\ s_2&-2&0&-1&1&-1\ & 1 & 0 & 1 & 0 & 1 \end{bmatrix} $$
Это нарушает еще одно правило: $s_2$ не должно быть отрицательным, верно? Во-вторых, в целевом ряду нет отрицательных значений, так что мы закончили.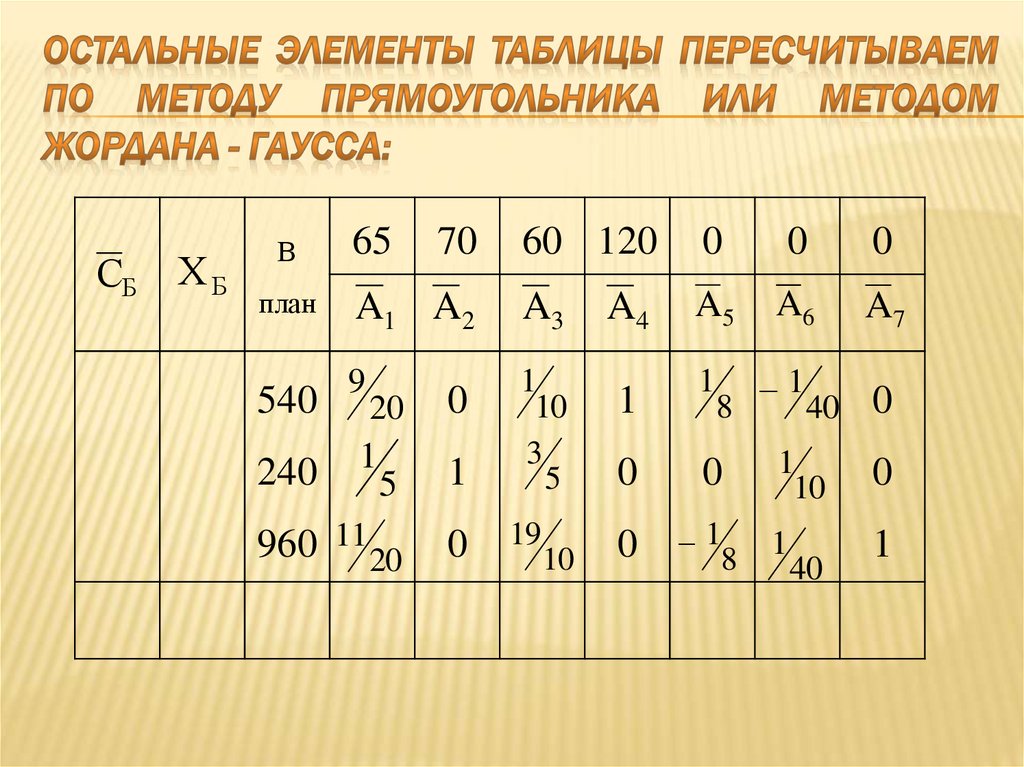
Но мы находимся в $x = 0, y = 1$, что даже не является решением, потому что $s_2$ является недопустимым значением. Давайте попробуем вместо этого выбрать строку 2, ту, у которой тестовый коэффициент равен 0:
$$1′:
\begin{bматрица}
& х & у & s_1 & s_2 & = \\
s_1 & 2 & 0 & 1 & -1 & 1 \\
у и -1 и 1 и 0 и 1 и 0 \\
&-1 & 0 & 0 & 1 & 0
\end{bmatrix}
$$
Теперь нужно ввести $x$. Мы должны ориентироваться только на положительные тестовые коэффициенты. В прошлый раз мы не следовали этому правилу, но теперь будем произвольно следовать ему, и $s_1$ уйдет: $$2: \begin{bматрица} & х & у & s_1 & s_2 & = \\ x & 1 & 0 & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ y & 0 & 1 & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ & 0 & 0 & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{bmatrix} $$
И это ответ. Из любопытства, поскольку мы произвольно нарушили «положительное» правило для опорной точки $1’$ и произвольно следовали ему для опорной точки $2$, давайте попробуем быть последовательными и всегда включать ноль при поиске минимального тестового отношения.