Сумма двух векторов. Законы сложения векторов. Сумма нескольких векторов. Правило параллелограмма. Вычитание векторов 9
Тема 24.
Сумма векторов. Разность векторов.
Рассмотрим пример. Пусть материальная точка переместилась из точки A в точку B, а затем из точки B в точку C. В результате этих перемещений, которые можно представить векторами AB⃗ и BC⃗, материальная точка переместилась из точки A в точку C. Поэтому результирующее перемещение можно представить вектором AC⃗. Поскольку перемещение из точки A в точку C складывается из перемещения из A в B и перемещения из B в C, то вектор AC⃗ естественно назвать суммой векторов AB⃗ и BC⃗:AC⃗=AB⃗+BC⃗.
Рассмотренный пример приводит нас к понятию суммы двух векторов.
Пусть a⃗ и b⃗ – два вектора. Отметим произвольную точку A и отложим от этой точки вектор AB⃗ равный a⃗.
Затем от точки
Сумма векторовa⃗ и b⃗ обозначается так: a⃗+b⃗.
Складывая по правилу треугольника произвольный вектор a⃗ с нулевым вектором, получаем, что для любого вектора a⃗ справедливо равенство
a⃗+0⃗=a⃗
Правило треугольника можно сформулировать также следующим образом: если A, B и C – произвольные точки, то AB⃗+BC⃗=AC⃗.
Это равенство справедливо для произвольных точек A, B и C, в частности, в том случае, когда две из них или даже все три совпадают.
Теорема
Для любых векторов a⃗,b⃗ и c⃗ справедливы равенства:
1. a⃗+b⃗=b⃗+a⃗ (переместительный закон).
2. a⃗+b⃗+c⃗=a⃗+b⃗+c⃗ (сочетательный закон).
Докажем первое равенство. Рассмотрим случай, когда векторы a⃗ и b⃗ не коллинеарны. От произвольной точки A отложим векторы ABAD и на этих векторах построим параллелограмм ABCD. По правилу треугольника AC⃗=AB⃗+BC⃗=a⃗+b⃗. Аналогично AC⃗=AD⃗+DC⃗=b⃗+a⃗. Отсюда следует, что a⃗+b⃗=b⃗+a⃗.
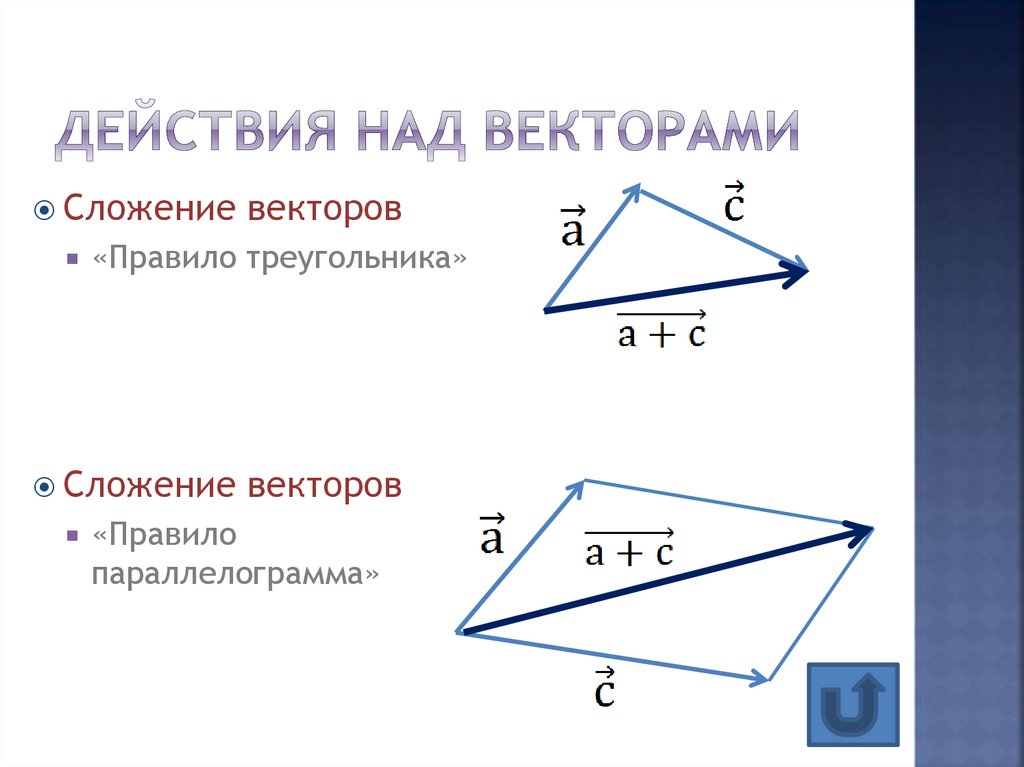
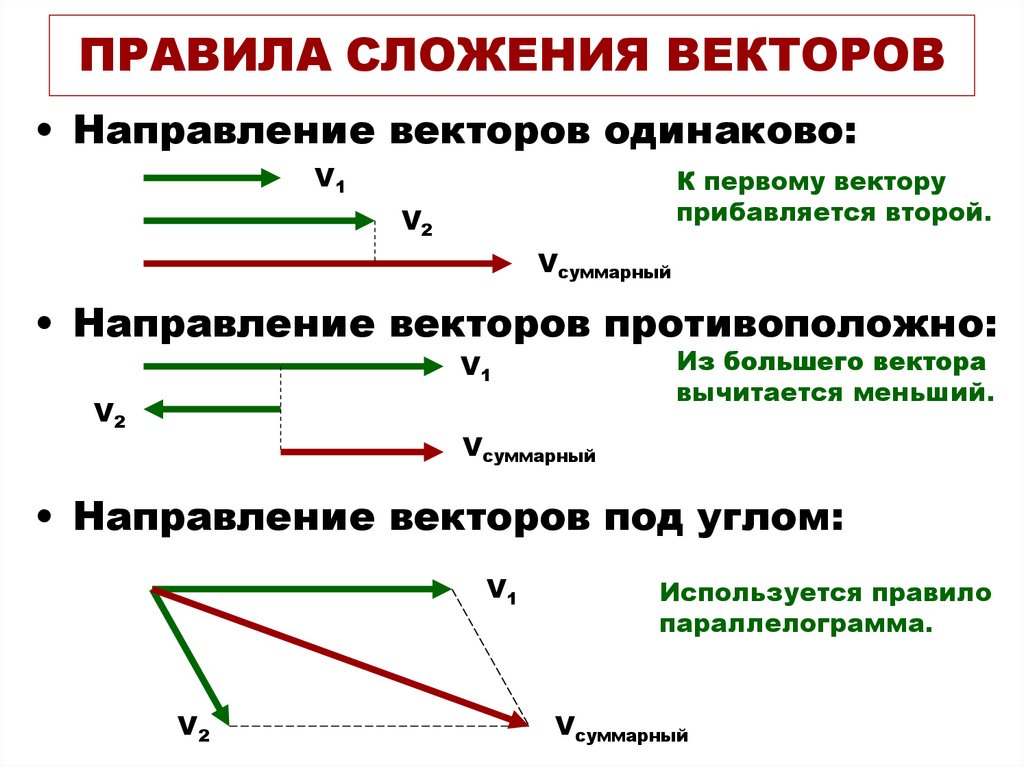
При доказательстве первого свойства мы обосновали так называемое правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы a⃗ и b⃗, нужно отложить от какой-нибудь точки A векторы AB⃗=a⃗ и AD⃗=b⃗ и построить параллелограмм ABCD. Тогда вектор AC⃗ равен a⃗+b⃗. Правило параллелограмма часто используется в физике, например при сложении двух сил.
Сложение нескольких векторов производится следующим образом: первый вектор складывается со вторым, затем их сумма складывается с третьим вектором и т.д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.
Аналогично можно построить сумму четырех, пяти и вообще любого числа векторов. Это правило построения суммы нескольких векторов называется правилом многоугольника.
Разностью векторов a⃗ и b⃗ называется такой вектор, сумма которого с вектором b⃗ равна вектору a⃗.
Разность векторов a⃗ и b⃗ обозначается так:a⃗-b⃗.
Рассмотрим задачу о построении двух векторов.
Даны векторы a⃗ и b⃗. Построить вектор a⃗-b⃗.
Отметим на плоскости произвольную точку O и отложим от этой точки векторы OA⃗=a⃗ и OB⃗=b⃗.
По правилу треугольника OB⃗+BA⃗=OA⃗ или b⃗+BA⃗=a⃗. Таким образом, сумма векторов BA⃗ и b⃗ равна a⃗.
По определению разности векторов это означает, что BA⃗=a⃗-b⃗, то есть вектор BA⃗ искомый.
Пусть a⃗ – произвольный ненулевой вектор. Вектор a1⃗ называется противоположным вектору a⃗, если векторы a⃗ и a1⃗ имеют равные длины и противоположно направлены.
Вектор, противоположный вектору a⃗, обозначается так: -a⃗. Очевидно, что a⃗+-a⃗=0⃗.
Теорема
Для любых векторов a⃗ и b⃗ справедливо равенство a⃗-b⃗=a⃗+-b⃗.
Сегодня мы научились складывать и вычитать векторы. Узнали правило треугольника, правило параллелограмма и правило многоугольника.
Сложение и вычитание векторов – правила
4.6
Средняя оценка: 4.6
Всего получено оценок: 766.
4.6
Средняя оценка: 4.6
Всего получено оценок: 766.
Сложение и вычитание векторов – это одно из немногих действий на стыке математики и геометрии. Дело в том, что выражения из векторов можно складывать и вычитать арифметически, ориентируясь только на буквенные обозначения векторов, но для того, чтобы получить числовой результат или его геометрическое отображение придется выполнить ряд построений.
Разберемся подробнее в правилах сложения и вычитания векторов.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Что такое вектор?
Вектор – это отрезок с направлением.
Вектор и луч часто путают и допускают грубую ошибку. Вектор – это направленный отрезок, а любой отрезок имеет величину, то есть его можно измерить линейкой. Луч имеет начало и направление, но он бесконечен, то есть измерить его невозможно. Так же, как нельзя и складывать лучи между собой или луч с вектором.
Вектор иногда помещают в декартову систему координат. Тогда, проведя перпендикуляры к каждой из осей, можно получить проекции вектора на оси Ох и Оу. Каждая из этих проекций будет отрезком. При этом, если из проекций составить прямоугольник, то его гипотенуза и будет начальным вектором. Это иногда используется при сложении векторов.
Рис. 1. Вектор в системе координат.Сложение и вычитание векторов
Способов и методов сложения векторов всего два.
Существует и третий, но его не считают отдельным методом, так как он вытекает из первых двух. Но мы его рассмотрим отдельно, чтобы не возникало вопросов при дальнейшем изучении темы.
Правило многоугольника
Для того, чтобы сложить векторы правилом многоугольника, необходимо параллельным переносом совместить конец первого вектора с началом второго, конец второго с началом третьего и так далее, пока не кончатся векторы, которые необходимо сложить.
После этого нужно начало первого вектора соединить с концом последнего последнего вектора и указать направление. Получившийся вектор будет направлен в сторону последнего из участвовавших в сложении.
Складывать таким способом можно любое количество векторов. Если так складывается только два вектора, то способ называют правилом треугольника
Нужно понять и запомнить, что у отрезка одна определяющая величина: размер. У вектора определяющих величин две: размер и направление. Поэтому нельзя менять направление вектора и его размер.
Любые действия нужно осуществлять с помощью параллельного переноса, то есть без изменения направления.
Правило параллелограмма
Правило параллелограмма сложнее, его можно применять только для 2 векторов. Если вам нужно этим способом сложить большее количество векторов, например, три, то действие выполняют в следующем порядке:
- Складывают два любых вектора правилом параллелограмма. Результатом будет некий вектор и у нас остается еще один, который в сложении не участвовал.
- Получившийся и оставшийся векторы складывают по тому же правилу.
- Этот процесс можно повторять столько раз, сколько требуется по условию задачи.
Само правило параллелограмма заключается в том, что начала двух векторов совмещаются. После этого получившуюся фигуру достраивают до параллелограмма. Диагональ, которая выходит из начала двух векторов и есть результат сложения. Вектор должен быть направлен в противоположную сторону от совмещенного начала двух векторов.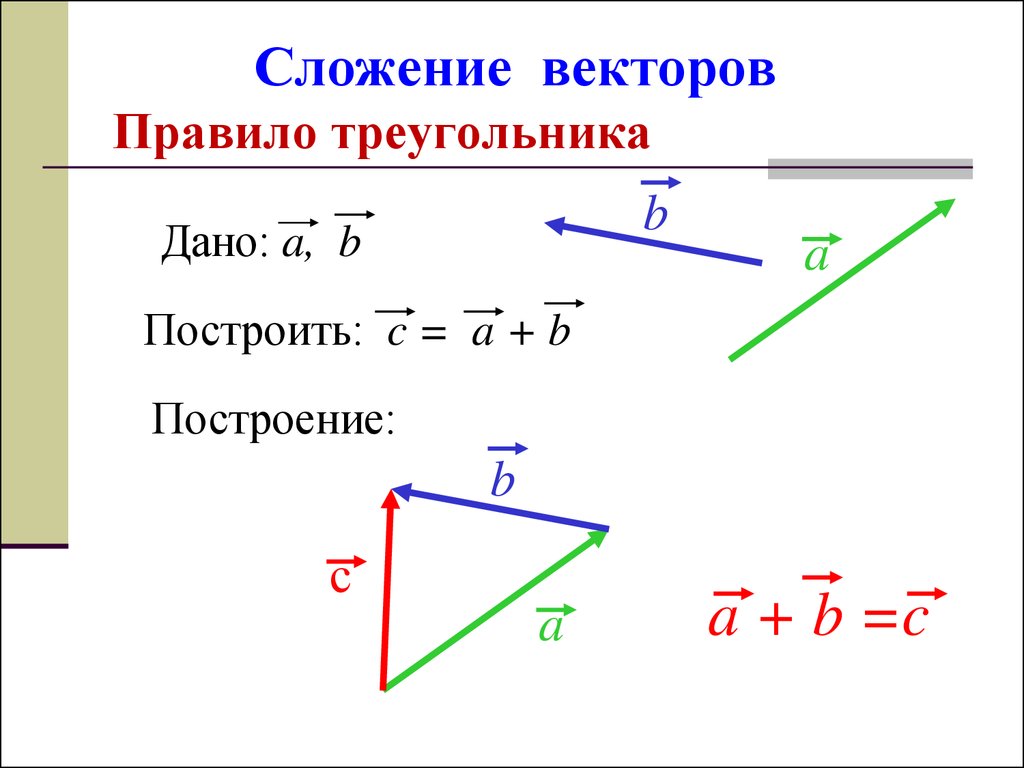
Для того чтобы вычесть векторы любым способом, направление вектора, который является вычитаемым, меняют на противоположное. Получившиеся векторы складывают любым из методов.
Рис. 3. Правило многоугольника.Сложение в декартовой системе
В декартовой системе все векторы раскладывают на проекции, после чего отрезки проекций складывают: проекции на ось Ох отдельно, на ось Оу отдельно. После из получившихся двух проекций снова собирают вектор.
Что мы узнали?
Мы узнали, что такое вектор. Поговорили о правилах сложения и вычитания векторов. Обсудили, чем отличается вектор от луча и обсудили метод действий с векторами в декартовой системе координат.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Нина Трофимова
8/10
Vlad Turlov
10/10
-
Никита Негин
10/10
Evgeniy Salakov
10/10
Артем Карнаух
8/10
Оценка статьи
4.
6
Средняя оценка: 4.6
Всего получено оценок: 766.
А какая ваша оценка?
Сложение векторов — Формула, Законы, Сумма
Сложение векторов означает объединение двух или более векторов. При добавлении векторов мы добавляем два или более векторов, используя операцию сложения, чтобы получить новый вектор, равный сумме векторов. Сложение векторов находит свое применение в физических величинах, где векторы используются для представления скорости, смещения и ускорения.
В этой статье давайте узнаем о сложении векторов, их свойствах и различных законах с решенными примерами.
| 1. | Что такое векторное сложение |
| 2. | Свойства векторного сложения |
| 3. | Добавление векторов графически |
| 4. | Законы сложения векторов |
| 5. | Треугольный закон сложения векторов |
6. | Параллелограммный закон сложения векторов |
| 7. | Формулы сложения векторов |
| 8. | Часто задаваемые вопросы о добавлении векторов |
Что такое сложение векторов?
Векторы представляются комбинацией направления и величины и записываются с помощью алфавита и стрелки над ними (или) с помощью алфавита, выделенного жирным шрифтом. Два вектора, a и b можно сложить вместе, используя векторное сложение , и результирующий вектор можно записать как: a + b . Прежде чем узнать о свойствах добавления векторов, нам нужно знать об условиях, которые необходимо соблюдать при добавлении векторов. Условия следующие:
- Векторы можно добавлять, только если они имеют одинаковую природу. Например, к ускорению нужно добавить только ускорение, а не массу 9.0076
- Мы не можем складывать векторы и скаляры вместе
Рассмотрим два вектора C и D .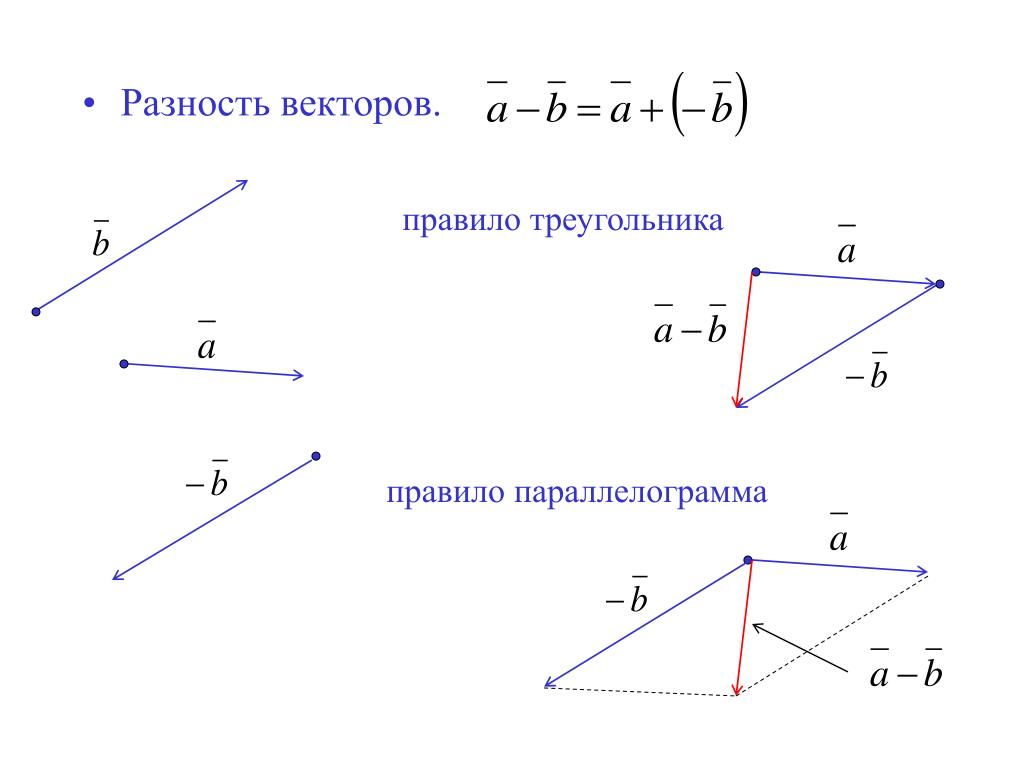
Где, C = C x i + C y j + C z k и D = D x i + D y j + Dzk. Тогда результирующий вектор (или векторная сумма) R = C + D = (C x + D x )i + (C y + D y )j + (C z + C z ) к
Свойства векторного сложения
Векторное сложение отличается от алгебраического сложения. Вот некоторые из важных свойств, которые следует учитывать при сложении векторов:
| Свойство сложения векторов | Пояснение |
|---|---|
| Наличие личности | Для любого вектора v , v + 0 = v Здесь вектор 0 является аддитивной идентичностью. |
| Наличие обратного | Для любого вектора v , v + — v = 0 , и, таким образом, для каждого вектора существует аддитивный обратный. |
| Коммутативность | Сложение коммутативно; для любых двух произвольных векторов c и d , в + д = д + в |
| Ассоциативность | Сложение ассоциативно; для любых трех произвольных векторов i , j и k , i + j + k = i + j + k , т. е. порядок добавления не имеет значения. |
Добавление векторов графически
Добавление векторов возможно графическими и математическими методами. Эти методы следующие:
- Сложение векторов с использованием компонентов
- Треугольный закон сложения векторов
- Закон параллелограмма сложения векторов
Сложение векторов с использованием компонентов
Векторы, представленные в декартовых координатах, могут быть разложены на вертикальные и горизонтальные компоненты.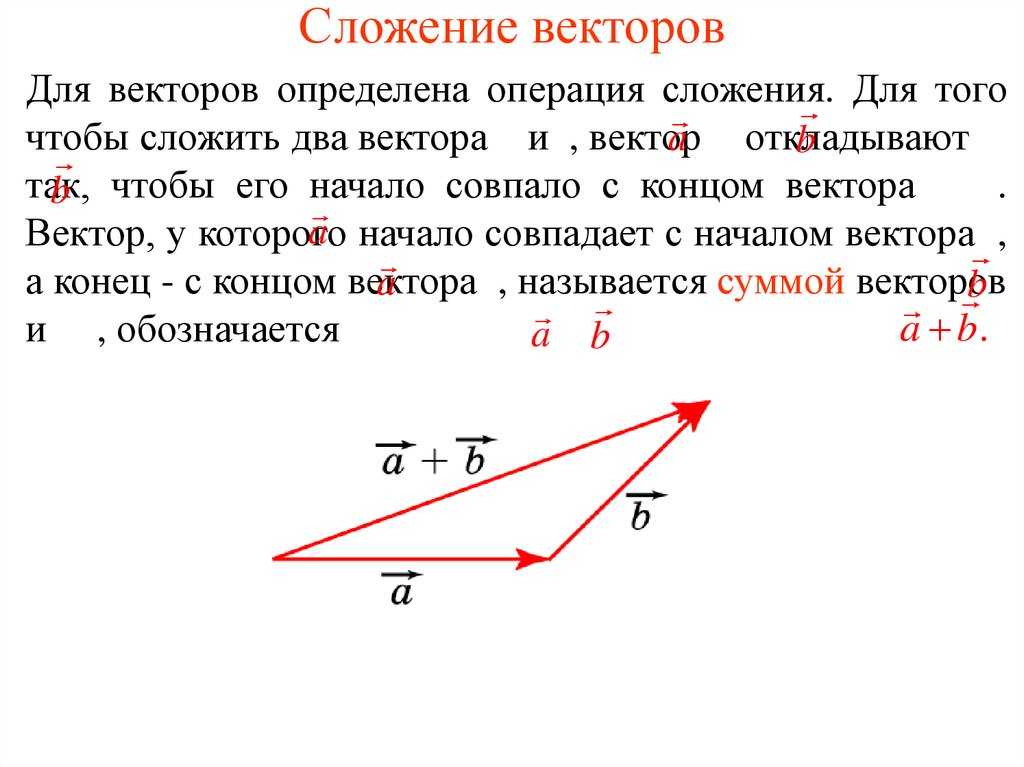
Например, вектор A под углом Φ, как показано на изображении ниже, может быть разложен на его вертикальную и горизонтальную составляющие следующим образом:
, представляет компонент вектора A по горизонтальной оси (ось x) и
Мы можем заметить, что три вектора образуют прямоугольный треугольник и что вектор A может быть выражен как: величина и угол данного вектора, мы можем определить компоненты вектора.
A x = A cos Φ
A y = A sin Φ
Для двух векторов, если известны их горизонтальная и вертикальная составляющие, можно вычислить результирующий вектор. Например, если заданы значения A x и A y , то мы сможем вычислить угол и модуль вектора A следующим образом:
| А | = √ (( A x ) 2 +( A Y ) 2 )
, а угол можно найти в виде:
φ = TAN-1 ( A Y / A a Y / A 7 Следовательно, мы можем сделать вывод, что: Точно так же мы можем выполнять сложение векторов, используя их компоненты, если эти векторы выражены упорядоченными парами, т.е. векторами-столбцами. Например, рассмотрим два вектора P и Q . P = (P 1 , P 2 ) Q = (Q 1 , Q 2 ) . два вектора P и Q , путем сложения соответствующих компонентов x и y этих двух векторов. M = P + Q M = (p 1 +q 1 , p 90 7 8 q 8098). Это можно явно выразить как: M x = p 1 + q 1 M y = p 2 0 2 90 88 + q 9. Формула величины для нахождения величины результирующего вектора М это: | М | = √ ((M x ) 2 + (M y ) 2 ) Существует два закона сложения векторов (как упоминалось в предыдущем разделе). Используя эти два закона, мы собираемся доказать, что сумма двух векторов получается путем присоединения их головы к хвосту, а сумма векторов определяется вектором, соединяющим свободный хвост и свободную голову. Давайте подробно изучим каждый из этих законов в следующих разделах. Знаменитый закон треугольника можно использовать для сложения векторов, и этот метод также называется методом головы к хвосту. По этому закону два вектора можно сложить, поместив их вместе таким образом, чтобы голова первого вектора соединилась с хвостом второго вектора. Таким образом, когда два вектора M и N складываются по закону треугольника, мы можем видеть, что треугольник образован двумя исходными векторами M и N и вектором суммы С . Другим законом, который можно использовать для сложения векторов, является закон параллелограмма сложения векторов. Возьмем два вектора p и q , как показано ниже. Они образуют две смежные стороны параллелограмма по своей величине и направлению. Сумма p + q представлена по величине и направлению диагональю параллелограмма, проходящей через их общую точку. Это закон параллелограмма сложения векторов. На приведенном выше рисунке, используя закон Треугольника, мы можем заключить следующее: OP + PR = ИЛИ OP + OQ = ИЛИ , так как PR = OQ Следовательно, мы можем заключить, что треугольные законы сложения векторов и параллелограммный закон сложения векторов эквивалентны друг другу. Мы используем одну из следующих формул для сложения двух векторов a = 1 Важные примечания по сложению векторов Вот несколько моментов, которые следует помнить при изучении сложения векторов: ☛ Статьи по теме: Ознакомьтесь со следующими страницами, посвященными добавлению векторов: Добавление векторов означает объединение двух или более векторов. При добавлении векторов мы добавляем два или более векторов, используя операцию сложения, чтобы получить новый вектор, который равен сумме двух или более векторов. Два вектора, a и b , можно сложить вместе, используя сложение векторов, и результирующий вектор можно записать как: a + b . Пример: Даны два вектора, a = (2, 5) и b = (4, -2), сумма этих двух векторов равна (6,3) Это формула сложения векторов: Даны два вектора a = (a 1 , a 2 ) и b = (b 1 , b 2 ), тогда вектор сумма, M = (a 1 + b 1 , a 2 + b 2 ) = (M x , M y ). В этом случае Это правила, которым необходимо следовать при добавлении векторов. Условия правил следующие: Согласно закону параллелограмма сложения векторов, для двух заданных векторов u и v , заключающих в себе угол θ, модуль суммы, | и + v |, определяется как √( u 2 + v 2 +2 uv cos(θ)). Да, сложение векторов коммутативно; для любых двух произвольных векторов c и d , c + d = d + c . Для любых двух заданных векторов, согласно закону сложения векторов треугольника, третья сторона треугольника станет результирующим вектором суммы. Сложение ассоциативное; для любых трех произвольных векторов a , b и c , a + b + c = a + b + c. , т. е. порядок добавления не имеет значения. Закон треугольника сложения векторов гласит, что два вектора можно сложить, поместив их вместе таким образом, чтобы голова первого вектора соединилась с хвостом второго вектора. Таким образом, соединяя хвост первого вектора с головой второго вектора, мы можем получить результирующий вектор суммы. С векторами и над ними можно выполнять различные математические операции. Одной из таких операций является сложение векторов. Эти правила суммирования векторов были применены к диаграммам свободного тела, чтобы определить результирующую силу (т. е. векторную сумму всех отдельных сил). Примеры приложений показаны на диаграмме ниже. В этом разделе задача суммирования векторов будет распространена на более сложные случаи, когда векторы направлены в направлениях, отличных от чисто вертикального и горизонтального направлений. Существует множество методов определения величины и направления результата сложения двух или более векторов. Два метода, которые будут обсуждаться в этом уроке и использоваться на протяжении всего раздела: Теорема Пифагора — полезный метод для определения результата сложения двух (и только двух) векторов , образующих прямой угол друг с другом. Этот метод неприменим для добавления более двух векторов или для добавления векторов, которые равны , а не под углом 90 градусов друг к другу. Чтобы увидеть, как работает метод, рассмотрим следующую задачу: В этой задаче требуется определить результат сложения двух векторов смещения, расположенных под прямым углом друг к другу. Результатом (или равнодействующей) прохождения 11 км на север и 11 км на восток является вектор, направленный на северо-восток, как показано на диаграмме справа. Поскольку смещение на север и смещение на восток находятся под прямым углом друг к другу, теорему Пифагора можно использовать для определения равнодействующей (то есть гипотенузы прямоугольного треугольника). Результат сложения 11 км, север плюс 11 км, восток — вектор с величиной 15,6 км. Давайте проверим ваше понимание с помощью следующих двух практических задач. В каждом случае используйте теорему Пифагора, чтобы определить величину векторной суммы . Когда закончите, нажмите кнопку, чтобы просмотреть ответ. Большинство студентов помнят значение полезной мнемоники SOH CAH TOA из курса тригонометрии. SOH CAH TOA — это мнемоника, которая помогает запомнить значение трех общих тригонометрических функций — функций синуса, косинуса и тангенса. Эти три функции связывают острый угол прямоугольного треугольника с отношением длин двух сторон прямоугольного треугольника. функция синуса связывает меру острого угла с отношением длины стороны, противоположной углу, к длине гипотенузы. Эти три тригонометрические функции можно применить к задаче путешественника, чтобы определить направление общего перемещения путешественника. Процесс начинается с выбора одного из двух углов (кроме прямого угла) треугольника. После того, как угол выбран, можно использовать любую из трех функций для определения меры угла. Напишите функцию и выполните соответствующие алгебраические шаги, чтобы найти меру угла. Работа представлена ниже. Как только мера угла определена, можно найти направление вектора. В этом случае вектор образует угол 45 градусов с востоком. Таким образом, направление этого вектора записывается как 45 градусов. Мерой угла, определенной с помощью SOH CAH TOA, является , а не всегда направление вектора. Следующая диаграмма сложения векторов является примером такой ситуации. Обратите внимание, что угол внутри треугольника определяется как 26,6 градусов с помощью SOH CAH TOA. Этот угол представляет собой южный угол поворота, который вектор R делает по отношению к западу. Тем не менее, направление вектора, выраженное с помощью соглашения CCW (против часовой стрелки с востока), составляет 206,6 градуса. Проверьте свое понимание двух векторов практического использования SOH CAH, пытаясь определить направление использования SOH CAH. В приведенных выше задачах величина и направление суммы двух векторов определяется с помощью теоремы Пифагора и тригонометрических методов (SOH CAH TOA). Процедура ограничена добавлением двух векторов, образующих прямые углы друг к другу . Когда два вектора, которые должны быть сложены, не образуют прямых углов друг к другу или когда нужно сложить более двух векторов, мы будем использовать метод, известный как метод сложения векторов «голова к хвосту». Этот метод описан ниже. Величина и направление суммы двух или более векторов также могут быть определены с помощью точно нарисованной векторной диаграммы в масштабе. Используя масштабированную диаграмму, метод головы к хвосту используется для определения векторной суммы или результирующей. Метод «голова к хвосту» включает в себя рисование вектора в масштабе на листе бумаги, начиная с заданной начальной позиции. Ниже приведен пошаговый метод применения прямого метода для определения суммы двух или более векторов. Пример использования прямого метода показан ниже. Задача состоит в сложении трех векторов: Метод «голова к хвосту» используется, как описано выше, и определяется результат (обозначен красным). Его величина и направление обозначены на диаграмме. Интересно, что порядок, в котором складываются три вектора, не влияет ни на величину, ни на направление равнодействующей. Результирующая по-прежнему будет иметь ту же величину и направление. Например, рассмотрим сложение тех же трех векторов в другом порядке. При суммировании в другом порядке эти три вектора по-прежнему дают результирующую с той же величиной и направлением, что и раньше (20 м, 312 градусов). ). Порядок, в котором векторы добавляются методом «голова к хвосту», не имеет значения. . 
)
Законы сложения векторов
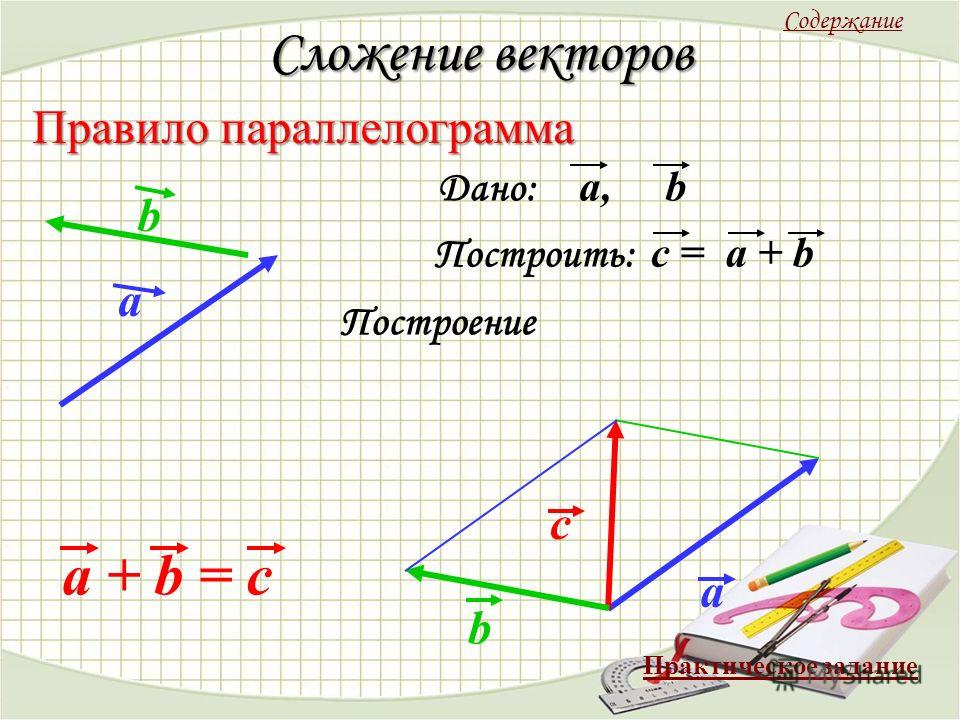
Треугольный закон сложения векторов
Таким образом, соединяя хвост первого вектора с головой второго вектора, мы можем получить результирующую векторную сумму. Сложение векторов по закону треугольника может быть выполнено со следующими шагами:
Закон параллелограмма сложения векторов
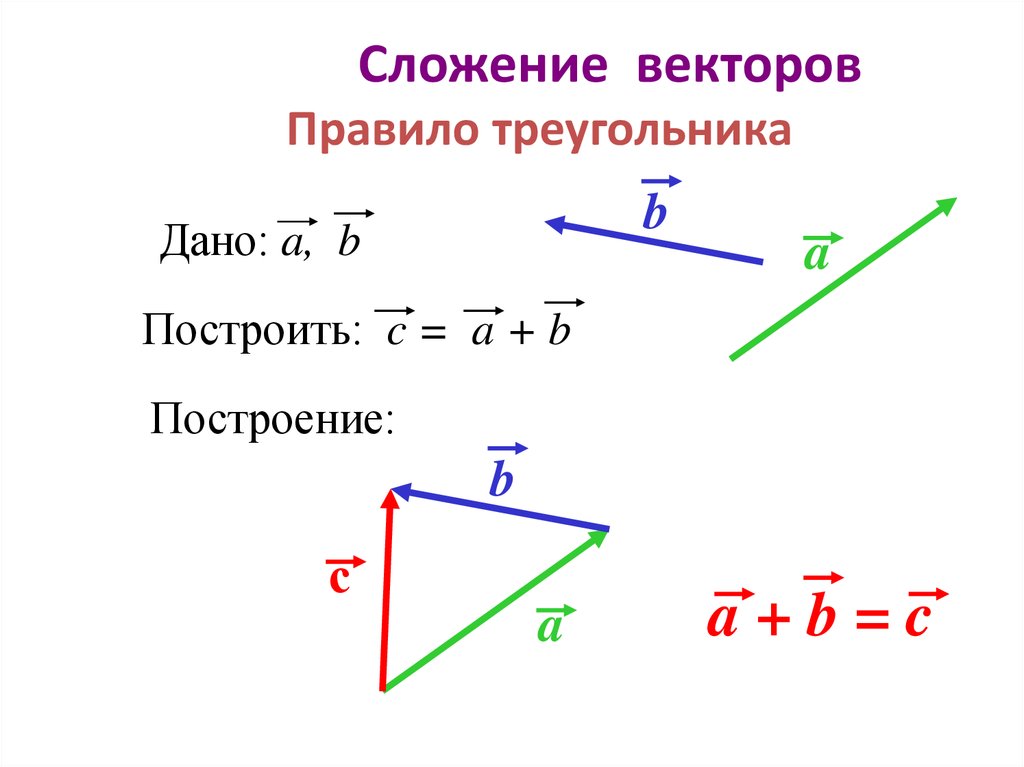
Формулы сложения векторов
+ b 1 , a 2 + b 2 8 , a 2 + b 2 8 , a 3 >.
представление. Часто задаваемые вопросы о добавлении векторов
Что такое сложение векторов?
Какова формула сложения векторов?
Что такое правило сложения векторов?
Что такое формула параллелограмма закона сложения векторов?
Является ли сложение векторов коммутативным?
В чем разница между законом сложения векторов треугольника и законом сложения векторов параллелограмма?
Принимая во внимание, что согласно закону сложения векторов параллелограмма диагональ становится результирующим вектором суммы. Что такое ассоциативное свойство сложения векторов?
Что такое треугольный закон сложения векторов?
Сложение векторов
Два вектора могут быть сложены вместе, чтобы определить результат (или результирующую). Этот процесс добавления двух или более векторов уже обсуждался в предыдущем разделе. Вспомним в нашем обсуждении законов движения Ньютона, что результирующая сила , воздействующая на объект, была определена путем вычисления векторной суммы всех отдельных сил, действующих на этот объект. То есть результирующая сила была результатом (или равнодействующей) сложения всех векторов сил. В течение этого модуля правила суммирования векторов (например, векторов силы) оставались относительно простыми. Обратите внимание на следующие суммы двух векторов силы:
Например, вектор, направленный вверх и вправо, будет добавлен к вектору, направленному вверх и влево. векторная сумма будет определена для более сложных случаев, показанных на диаграммах ниже.
Теорема Пифагора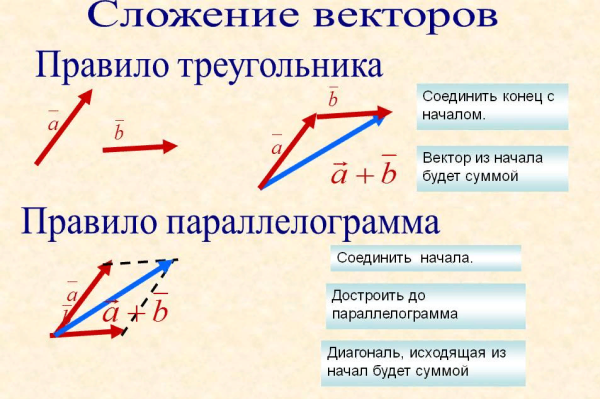 
Теорема Пифагора — это математическое уравнение, связывающее длину сторон прямоугольного треугольника с длиной гипотенузы прямоугольного треугольника. Эрик покидает базовый лагерь и проходит 11 км на север, а затем 11 км на восток. Определите результирующее перемещение Эрика.
Позже будет рассмотрен метод определения направления вектора.
Функция косинуса связывает меру острого угла с отношением длины стороны, прилегающей к углу, к длине гипотенузы. Касательная функция связывает меру угла с отношением длины стороны, противоположной углу, к длине стороны, прилегающей к углу. Три приведенных ниже уравнения суммируют эти три функции в форме уравнения.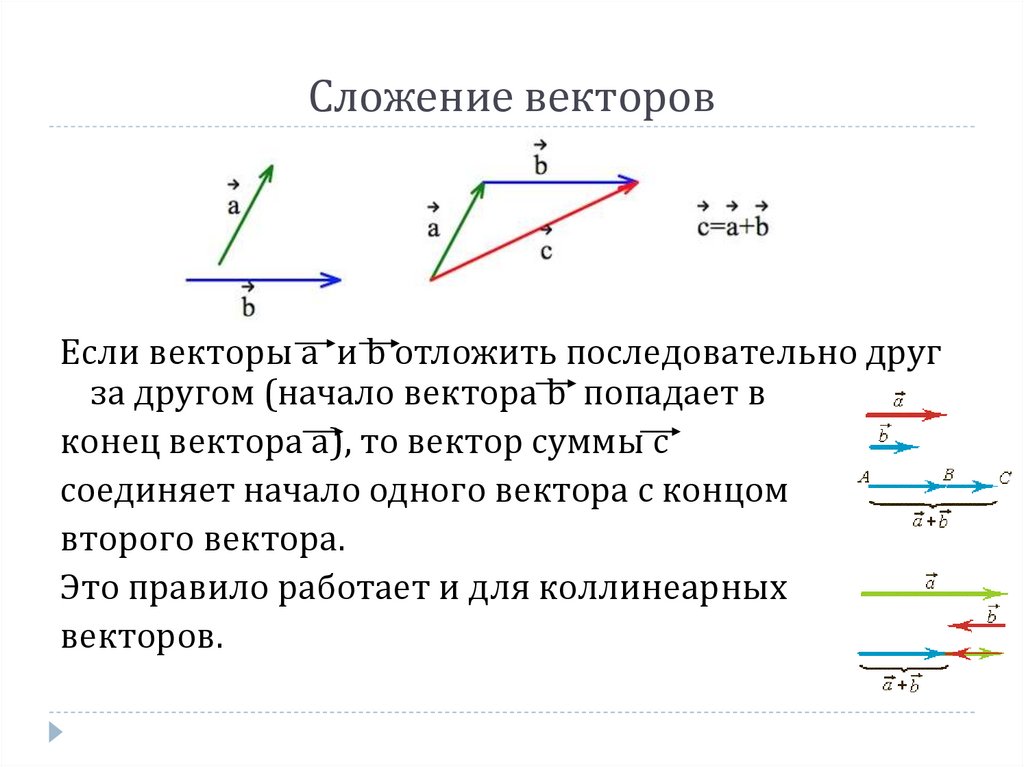
(Напомним, что ранее в этом уроке направление вектора — это угол поворота против часовой стрелки, на который вектор поворачивается строго на восток.)
В каждом случае используйте SOH CAH TOA, чтобы определить направление равнодействующей. Когда закончите, нажмите кнопку, чтобы просмотреть ответ.
Обычная лаборатория по физике включает обходов векторов . Либо используя сантиметровые смещения на карте, либо метровые смещения на большой открытой местности, учащийся делает несколько последовательных перемещений, начиная с обозначенной начальной позиции. Предположим, вам дали карту вашего района и набор из 18 направлений, которым нужно следовать. Начиная с исходная база , эти 18 векторов смещения могут быть последовательно сложены вместе для определения результата сложения набора из 18 направлений. Возможно, первый вектор измеряется в 5 см на восток. Там, где заканчивалось это измерение, начиналось следующее измерение. Процесс будет повторяться для всех 18 направлений. Каждый раз, когда заканчивалось одно измерение, начиналось следующее измерение. По сути, вы будете использовать метод сложения векторов «голова к хвосту».
Там, где заканчивается голова этого первого вектора, начинается хвост второго вектора (таким образом, метод «голова к хвосту» ). Процесс повторяется для всех добавляемых векторов. После того, как все векторы были сложены «голова к хвосту», результирующий результат рисуется от хвоста первого вектора к началу последнего вектора; то есть от начала до конца. После того, как результирующая нарисована, ее длину можно измерить и преобразовать в реальных единиц при использовании данного масштаба. Направление равнодействующей можно определить с помощью транспортира и измерения его угла поворота против часовой стрелки с востока.
Обозначьте величину и направление масштаба на диаграмме (например, МАСШТАБ: 1 см = 20 м).
+ 15 м, 210 град.
