Сложение и вычитание векторов — презентация онлайн
Похожие презентации:
Сложение и вычитание векторов. Законы сложения
Сложение и вычитание векторов
Сложение и вычитание векторов
Сложение и вычитание векторов
Сложение и вычитание векторов
Сложение и вычитание векторов
Сложение векторов. Правило треугольника
Векторы в пространстве. (10-11 класс)
Векторы в пространстве
Векторы на плоскости и в пространстве. Основные понятия
Какая запись является верной?
В
450
С
А
AВ > BC;
AВ > BC
AC = BC ;
AC = BC
Сложение векторов. Правило треугольника.
АВ + ВС = АС
С
!
a+b
b
А
a
b
a
В
Для любого нулевого вектора
справедливо равенство
a+0=a
!
Докажем, что если при сложении векторов точку А
заменить другой точкой А1, то полученный вектор А1С1
будет равен АС. Рассмотрим случай.
a
b
В
b
a
С
А
В1
a
А1
параллелограмм
ВСС1В1 –
параллелограмм
АСС1А1 –
параллелограмм
b
С1
Правило треугольника.

АВ + ВС = АС
АS + SС =
АО + ОР = АР
NM + ML = NL
MN + NR = MR
RP + PR = RR = 0
MK + KM = MM = 0
ZK + KZ =
MK + OM = OM + MK
DE + KD = KD + DE =
= OK
АС
ZZ = 0
= KE
Правило треугольника.
АС = АВ + ВС
из ОВN
ON = OB + ВN
OB = ON + NВ
из ASR
AS = AR + RS
RA = RS + SA
из XKH
XH = XK + KH
KX = KH + HX
из АMD
MD = MA + AD
AD = AM + MD
из FPO
OP = OF + FP
FO = FP + PO
По правилу треугольника складываются и
коллинеарные векторы, хотя при их сложении
треугольника и не получается
b
a+b
a
b
a
b
a+b
a
f
c
c+ f
Законы сложения векторов
Теорема
Для любых векторов
1
2
a, b, c
a+b=b+a
справедливы равенства:
!
переместительный закон
(a + b) + c = a + (b + c)
сочетательный закон
!
11
12
Чтобы применить
правило
параллелограмма,
надо отложить
векторы от одной
точки, как стрелки
часов.

1
10
2
3
9
4
8
7
6
5
Сложение векторов. Правило параллелограмма.
11
10
12
a
8
a
b
2
a+b
b
9
1
3
4
7
6
5
Сложение векторов.
Правило многоугольника.
АВ + ВС + СD + DO = АO
n
m
a
m
c
c
a
n
Правило многоугольника можно сформулировать также
следующим образом: если А1, А2, …, Аn – произвольные
точки плоскости, то А1А2 + А2А3 + … + Аn-1An = А1An
А6
А7
А1
А4
А5
А3
А2
!
Если начало первого вектора совпадает с концом
последнего вектора, то сумма данных векторов равна
2
3
4
5
нулевому вектору.
a +a +a +a +a
=0
a3
a3
a5
a2
a4
a4
a1
a2
a1
a5
a1 называется противоположным
вектору a, если векторы a и a1 имеют равные
Вектор
длины и противоположно направлены.
a1
a
А
-b
a1
-b, противоположный вектору b
Вектор
b
a = a1 ; a
А
Вектор ВА, противоположный
вектору АВ
ВА = – АВ
В
В
a + (-a) = 0
№ 766 На рисунке изображены векторы
a, b, c, d
ХУ.
 Представьте вектор ХУ в виде суммы остальных или им
Представьте вектор ХУ в виде суммы остальных или импротивоположных векторов.
–b
–a
c
Х
d
–a–b+c+d=
ХУ
У
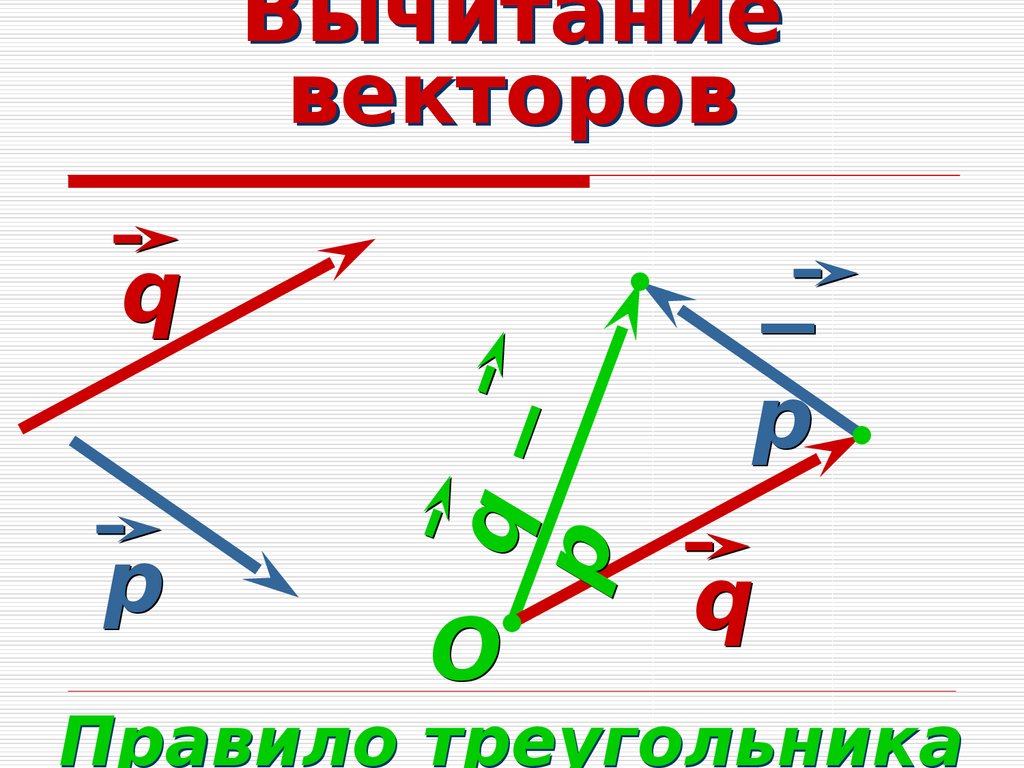
Вычитание векторов.
a – b = a +(–b)
-b
b
-b
a
a
a- b
Вычитание векторов.
MF — SF =
MF + FS = MS
RO — RM = RO + MR = MR + RO = MO
MD — SD =
MD + DS = MS
RO — AO = RO + OA = RA
RO — RO = RO + OR = RR = 0
— OS — ST =
SO + TS = TS + SO = TO
1.Упростите выражение
MN+XY=MX
а) MX
в) NY
б) MY
г) YM
19
2.Найдите вектор х :
АВ + х = АК
а) ВК
в) КК
б) КВ
г) СК
20
3.Найдите вектор a+b,
используя правило треугольника :
b
а)
в)
a
a
a+b
a+b
b
б)
г)
a
a+b
b
a
a+b
b
21
4.Найдите вектор a+b,
используя правило параллелограмма:
а)
в)
a
a
a+b
a+b
b
b
б)
г)
a
a+b
b
a
a+b
b
22
23. Ответы:
12
3
4
Б
А
Г
Б
За верно выполненные 2 задания – оценка «3»
3 задания – оценка «4»
4 задания – оценка «5»
23
№ 768 Точки М и N – середины сторон АВ и АС
треугольника АВС.
 Выразите векторы ВМ, NC, MN, BN
Выразите векторы ВМ, NC, MN, BNa = АМ
и
b = АN
В
М
a
ВМ =
-a
NC =
b
из AMN
MN = MA + AN =
А
b
N
С
-a + b
из ABN
BN = BA + AN =
-a-a + b
Найдите
АВ + AD – DC – OD
ABCD — прямоугольник
B
C
5
О
А
(
4
)
3
D
= АС – DC – OD = АС + CD + DO = АО
1
АО 5 2,5
2
АВ + ВС =
АS + SС =
АО + ОР =
NM + ML =
MN + NR =
RP + PR =
MK + KM =
ZK + KZ =
MK + OM =
DE + KD =
из ОВN
из ASR
из XKH
из АMD
из FPO
AS =
из ОВN
из ASR
RA =
XH =
из XKH
KX =
ON =
MD =
OP =
из АMD
из FPO
OB =
AD =
FO =
English Русский Правила
Сумма нескольких векторов
Урок 6. Геометрия 9 класс ФГОС
В этом уроке излагается правило сложения нескольких векторов — правило многоугольника.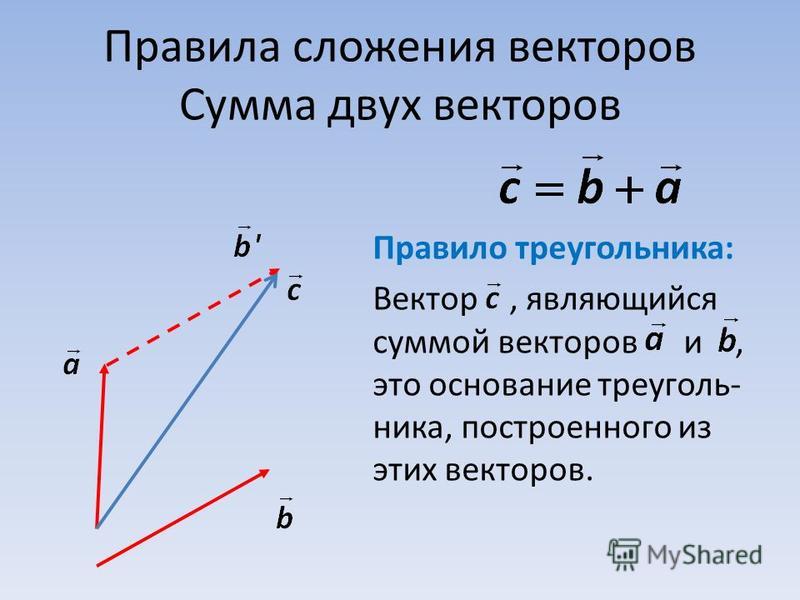 Так же на конкретных примерах рассматриваются его частные случаи.
Так же на конкретных примерах рассматриваются его частные случаи.
Конспект урока «Сумма нескольких векторов»
Вам уже известны правила сложения двух векторов.
Cегодня мы будем учиться складывать несколько векторов.
Построим
вектор суммы векторов , , .
От некоторой точки А отложим вектор
. Далее от точки B
отложим вектор .
А от точки C отложим вектор
.
Будем последовательно складывать наши векторы, пользуясь правилом треугольника.
Сумма векторов , равна вектору .
Теперь к вектору добавим вектор . В результате мы получаем вектор .
Тогда можем сказать, что сумма .
Так, последовательно складывая первый вектор со вторым, затем их сумму с третьим и так далее, можно найти суммы четырёх, пяти и большего числа векторов.
Такое
правило построения суммы векторов называют правилом многоугольника.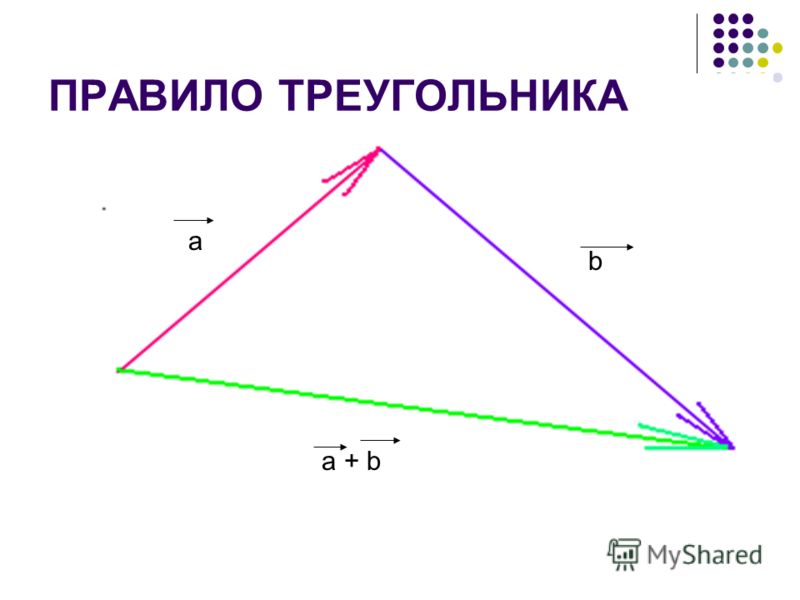
Сформулируем его в общем виде.
Если А1, А2, …, An — произвольные точки плоскости, то сумма векторов
.
Это равенство справедливо для любых точек А1, А2, …, An. И, в частности, для случая, когда некоторые из них совпадают.
Например, если начало первого вектора совпадает с концом последнего, то сумма данных векторов равна нулевому вектору.
Задача. Построить вектор суммы попарно неколлинеарных векторов , , , и .
Построение
.
Задача. В соответствии с правилом многоугольника составить равенство,выражающее сумму нескольких векторов.
Посмотрим на первый рисунок. Мы
видим, что последовательно складывают векторы . Но, так как
начало вектора совпадает
с концом вектора ,
то сумма данных векторов равна нулевому вектору .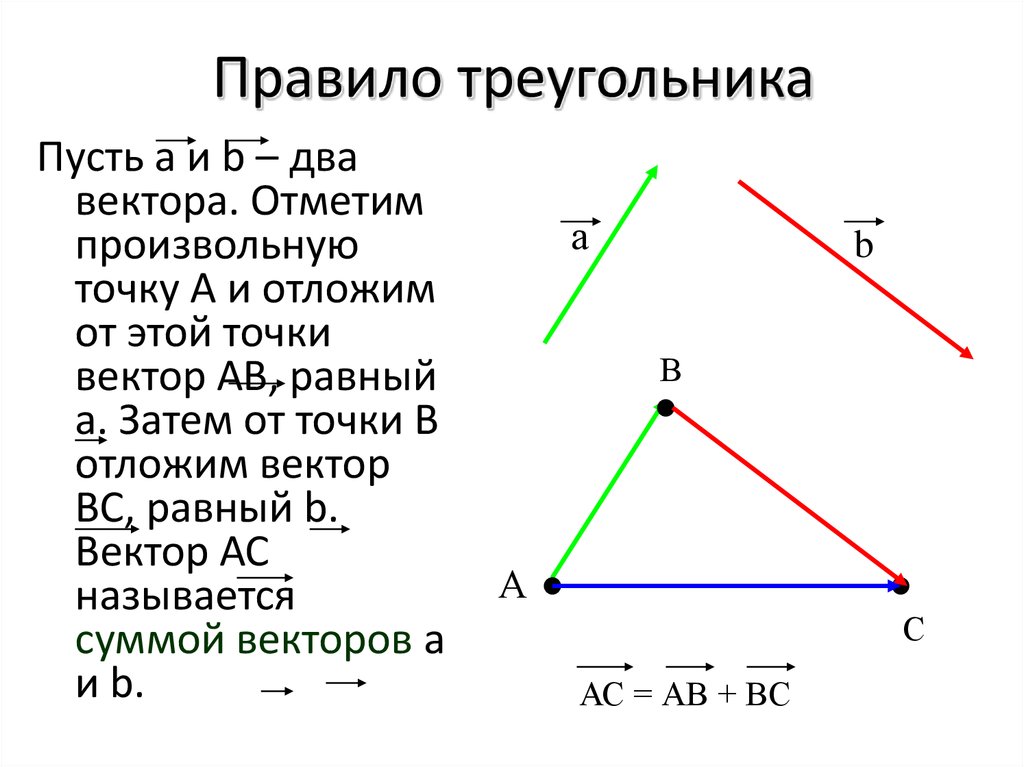
Перейдём к следующему случаю.
Видим, что сумма состоит из векторов . А вот вектор , как раз таки, и равен ей.
На рисунке в последовательно, друг за другом, отложены векторы Ну, а вектор равен их сумме.
На последнем рисунке последовательно, друг за другом, отложены векторы . При этом Начало вектора К совпадает с концом вектора С. Поэтому сумма данных векторов равна нулевому вектору .
Задача. равнобокая трапеция. и — её основания, боковая сторона равна . Построить вектор и найти его длину.
Построение
Решение.
Ответ:
А теперь подведём итоги нашего урока.
Сегодня мы познакомились с правилом многоугольника, которое позволяет строить вектор суммы нескольких векторов.
Его
суть заключается в том, что векторы-слагаемые последовательно откладывают друг от
друга, суммой является вектор, начало которого совпадает с началом первого
вектора-слагаемого, а конец совпадает с концом последнего вектора-слагаемого.
Если эти точки совпадают, то сумма данных векторов равна нулевому вектору.
Предыдущий урок 5 Законы сложения векторов. Правило параллелограмма
Следующий урок 7 Вычитание векторов
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 9 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Треугольный закон сложения векторов
Состояние Треугольный закон сложения векторов или Укажите и объясните треугольный закон сложения векторов:
Треугольный закон сложения векторов гласит, что когда два вектора представляются как две стороны треугольника с величина и направление, то величина и направление результирующего вектора представлены третьей стороной треугольника, взятого в обратном порядке.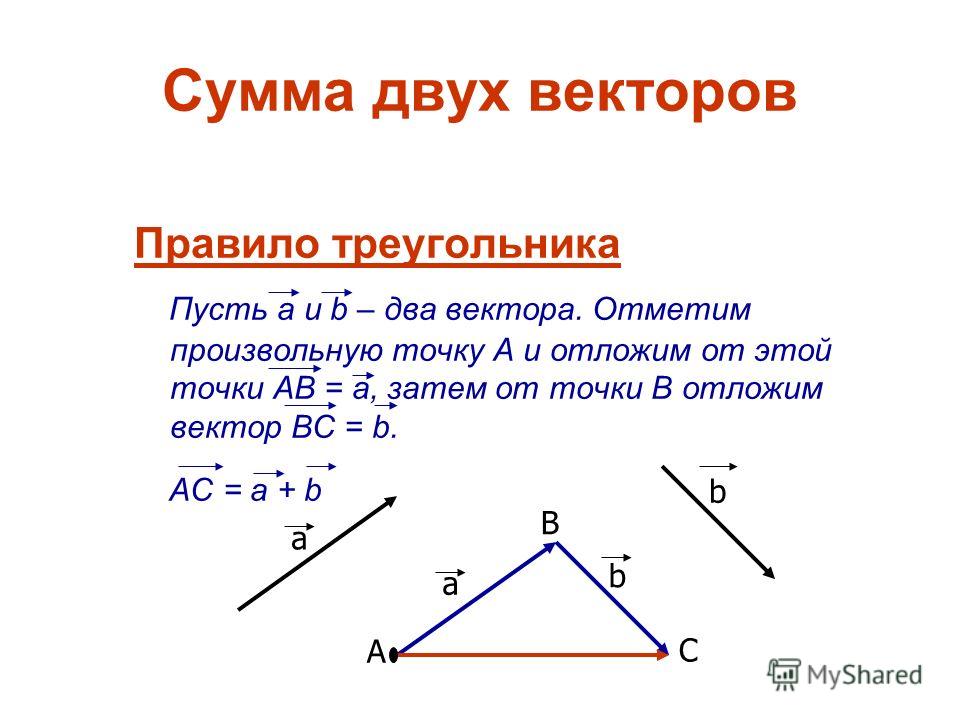
Полигональный закон сложения векторов
Государственный закон сложения векторов многоугольников
Закон сложения векторов многоугольников гласит, что если стороны многоугольника взяты в одном порядке для представления множества векторов по величине и направлению, то результирующий вектор может быть представлен по величине и направление по замыкающей стороне многоугольника в обратном порядке.
(Источник: Использование Paint)
Законы сложения векторов
Векторы записываются/представляются с помощью алфавита и стрелки над ними и представляются как комбинация направления и величины. Добавление двух или более векторов называется добавлением векторов. Когда мы добавляем векторы, мы используем операцию сложения, чтобы сложить два или более векторов, чтобы получить новый вектор, равный сумме двух или более векторов. Сложение векторов можно использовать для объединения двух векторов, a и b , и, таким образом, результирующий вектор может быть выражен как:
R = a + b здесь жирным шрифтом показано, что R, a и b являются векторами
Существуют разные законы сложения векторов:
Закон сил треугольника
Закон сил треугольника применим, когда на тело, находящееся в равновесии, действуют три силы. Затем две силы представляются как две стороны треугольника в том же порядке, с масштабированием их величины до подходящего масштаба, а результирующая в противоположном порядке является третьей стороной или замыкающей стороной треугольника.
Затем две силы представляются как две стороны треугольника в том же порядке, с масштабированием их величины до подходящего масштаба, а результирующая в противоположном порядке является третьей стороной или замыкающей стороной треугольника.
Закон Треугольника Сил также можно использовать для вычисления равнодействующей двух сил, действующих в точке.
также прочитайте —
- NCERT Solutions для физики класса 11
- NCERT Solutions для физики класса 12
- NCERT Solutions для всех субъектов
Закон о векторе VecT силы сложения векторов треугольника?
Треугольный закон сложения векторов гласит, что если два вектора представлены сторонами треугольника, взятыми в порядке величины и направления, то результирующая сумма векторов определяется третьей стороной треугольника в обратном порядке величины и направление.
(Источник: использование Paint)
Сформулируйте и докажите закон сложения векторов треугольника или вывод из закона сложения векторов треугольника
Рассмотрим два вектора P и Q , представленные по величине и направлению сторонами OA и AB треугольника ОАВ соответственно. Пусть R будет произведением/результатом треугольного закона сложения векторов. Следовательно, результирующая P и Q представлена стороной OB в соответствии с треугольным законом сложения или треугольным законом сложения векторов.
Пусть R будет произведением/результатом треугольного закона сложения векторов. Следовательно, результирующая P и Q представлена стороной OB в соответствии с треугольным законом сложения или треугольным законом сложения векторов.
(Источник: использование инструментов ms)
У нас есть,
R=P+Q
Расширьте A до C и проведите перпендикуляр BC.
Из Triangle OCB у нас есть,
OB 2 = OC 2 +BC 2
OB 2 = (OA +OC) 2 +BC 2 …
В треугольнике ACB,
cosθ=AC/AB
AC=ABcosθ=Qcosθ
Также
Sinθ=BC/AB
BC=ABsinθ=Qsinθ
900 Абсолютная величина:0005
Замените значения для AC и BC в (I),
R 2 = (P +QCOSθ) 2 +(QSINθ) 2
R 2 = P 2 +2PQCOS + + + + + + +2PQCOS.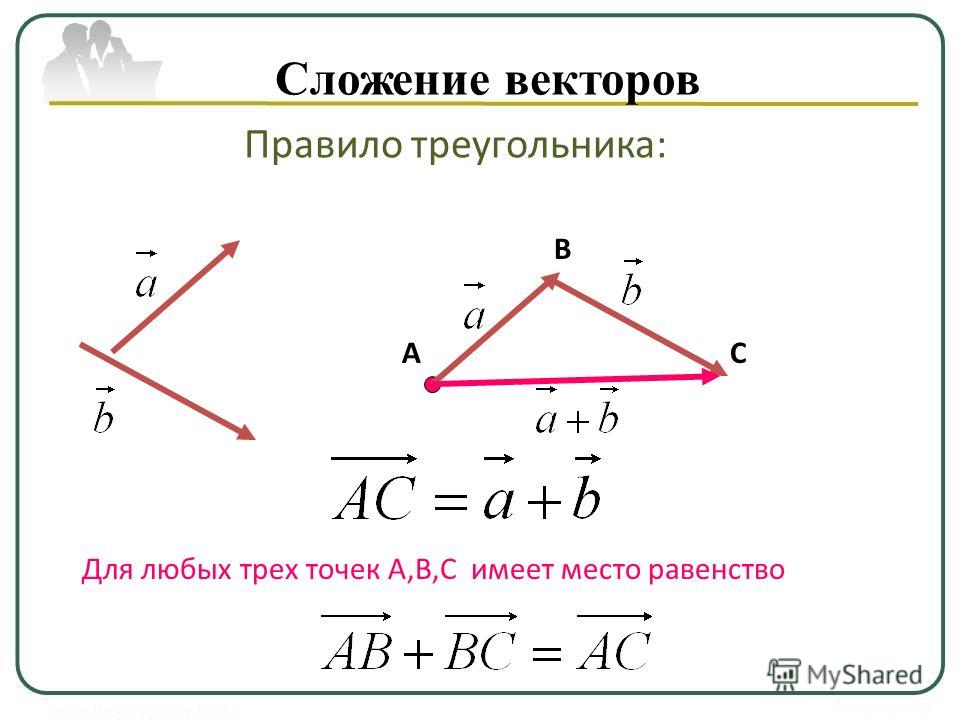 Q 2
Q 2
R2=√(P 2 +2PQcosθ+Q 2 )
Приведенное выше уравнение дает нам величину равнодействующей.
Найти модуль и направление результирующего вектора
Направление модуля результирующего вектора определяется выражением;
Из треугольника OBC,
tan∅=BC/OC
Так как, OC=OA+AC.
tan∅=BC/(OA+AC)
tan∅=Qsinθ/(P+Qcosθ)
Приведенное выше уравнение дает нам направление результирующего вектора.
Читайте также:
- Решения NCERT для класса 11 Физика Глава 3 Движение по прямой линии
- Пример NCERT Пример 11 Решения по физике Глава 3 Движение по прямой прямая
Примеры треугольного закона сложения векторов
Пример: Два вектора A и B величиной 5 единиц и 7 единиц соответственно составляют угол 60 o . Определите величину результирующего вектора.
Определите величину результирующего вектора.
Решение: Следуя треугольному закону сложения векторов, результирующий вектор определяется как:
R=A+B
Величина R равна:
R=|R|=√7 2 +5 2 +2*5*7cos60 o
R=√25+49+70/2
R=√109 единиц
Важные примечания о сложении векторов
Вот некоторые моменты, которые следует учитывать при изучении сложения векторов:
направление и величина.
Если мы знаем компоненты вектора, мы можем вычислить направление результирующего вектора.
Для сложения векторов можно использовать хорошо известный закон сил треугольника, и этот метод также известен как метод «голова к хвосту».
Также проверка-
- NCERT Пример класса 11th Physics Solutions
- NCERT Пример класса.
 Физика
Физика - NCERT Notes 12 класс Физика
- NCERT Notes для всех предметов
Треугольник Закон сложения векторов
Треугольник Закон сложения векторов — это математическое понятие, которое используется для нахождения суммы двух векторов. Этот закон используется для сложения двух векторов, когда голова первого вектора соединяется с хвостом второго вектора, а затем присоединяется хвост первого вектора к началу второго вектора, чтобы сформировать треугольник, и, следовательно, получить результирующий вектор суммы . Вот почему треугольный закон сложения векторов также называют прямым методом сложения векторов.
Изучим треугольный закон сложения векторов, его формулировку, формулу и доказательство. Этот закон используется для определения чистого смещения, скорости, ускорения и т. д. Мы также будем решать вопросы и примеры, основанные на законе сложения векторов треугольника, чтобы понять его применение и концепцию.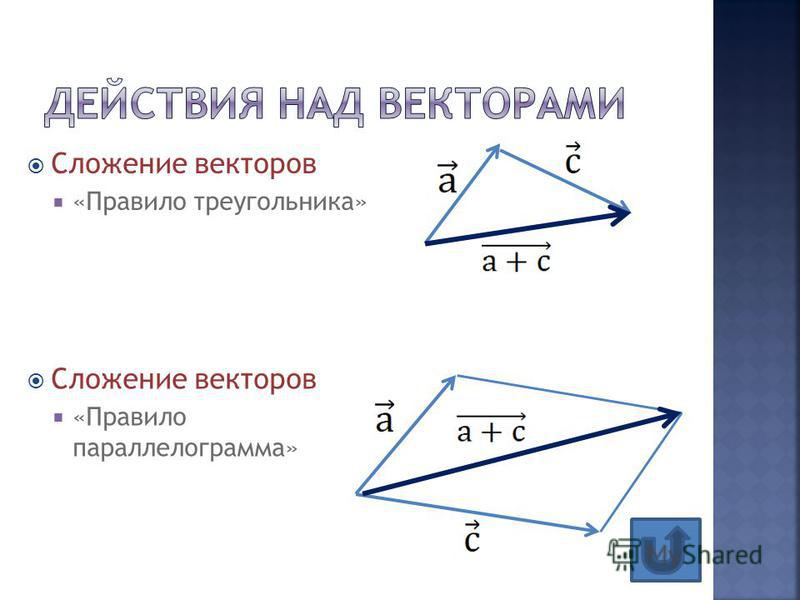
| 1. | Что такое треугольный закон сложения векторов? |
| 2. | Формула сложения векторов по закону треугольника |
| 3. | Закон треугольника векторного сложения Доказательство |
| 4. | Часто задаваемые вопросы о законе сложения векторов треугольника |
Что такое треугольный закон сложения векторов?
Закон треугольника сложения векторов — это закон, который используется в векторной алгебре для определения результирующего вектора суммы при сложении двух или более векторов. Предположим, у нас есть автомобиль, который движется из точки А в точку Б, как показано на рисунке ниже. Как только он достигает точки B, он снова начинает двигаться до точки C. Теперь, чтобы определить чистое перемещение автомобиля, мы используем концепцию сложения векторов. Чистое перемещение автомобиля задается вектором AC, который можно рассчитать, используя треугольный закон сложения векторов, как:
\(\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC}\)
Аналогично, если у нас есть два вектора P и Q, как указано ниже, и нам нужно найти их сумму, то мы можем двигаться вектор Q таким образом, не меняя своей величины и направления, что его хвост соединяется с головой вектора P.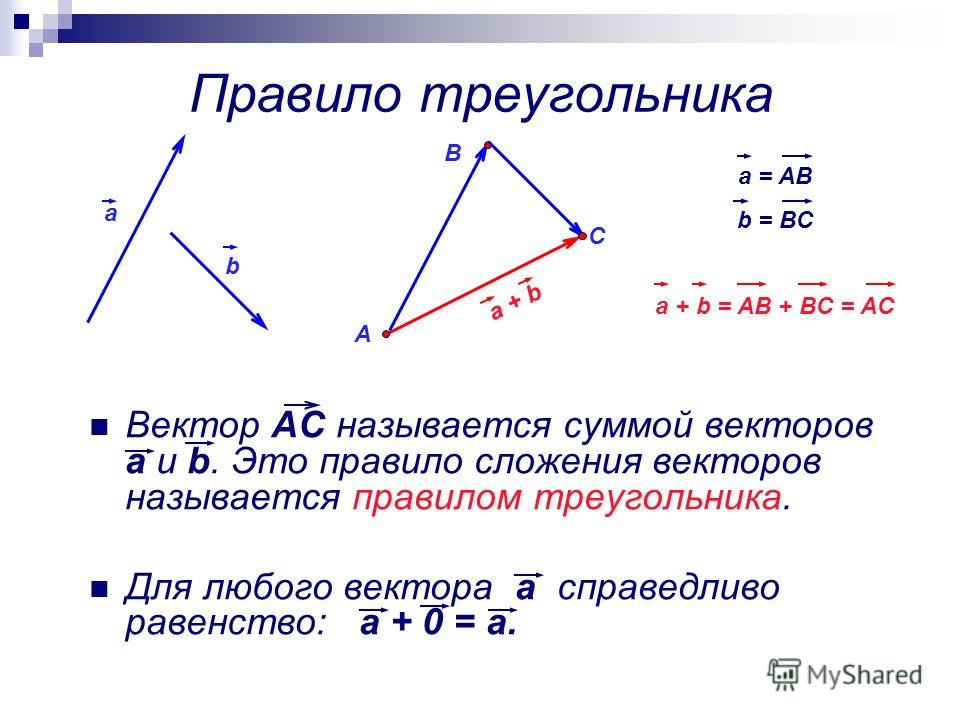 Тогда сумма векторов P и Q с использованием треугольного закона сложения векторов определяется выражением
Тогда сумма векторов P и Q с использованием треугольного закона сложения векторов определяется выражением
\( \overrightarrow{R} = \overrightarrow{P} + \overrightarrow{Q}\)
Треугольный закон векторной формулы сложения
Рассмотрим два вектора P и Q, угол между которыми равен θ, а их результирующий вектор суммы с использованием треугольного закона сложения векторов определяется вектором R. Формула для величины |R| и направление ϕ результирующего вектора R с использованием закона треугольника для сложения векторов определяется как
|R| = √(P 2 + Q 2 + 2PQ cos θ)
ϕ = тангенс -1 [(Q sin θ)/(P + Q cos θ)]
Треугольный закон векторного сложения Доказательство
Прежде чем перейти к доказательству закона треугольника, давайте сначала посмотрим на формулировку закона треугольника сложения векторов:
Утверждение: Если два вектора, действующие одновременно на тело, представлены как по величине, так и по направлению двумя стороны треугольника, взятые в порядке, то результирующий вектор суммы (как величина, так и направление) этих двух векторов определяется третьей стороной этого треугольника, взятой в обратном порядке.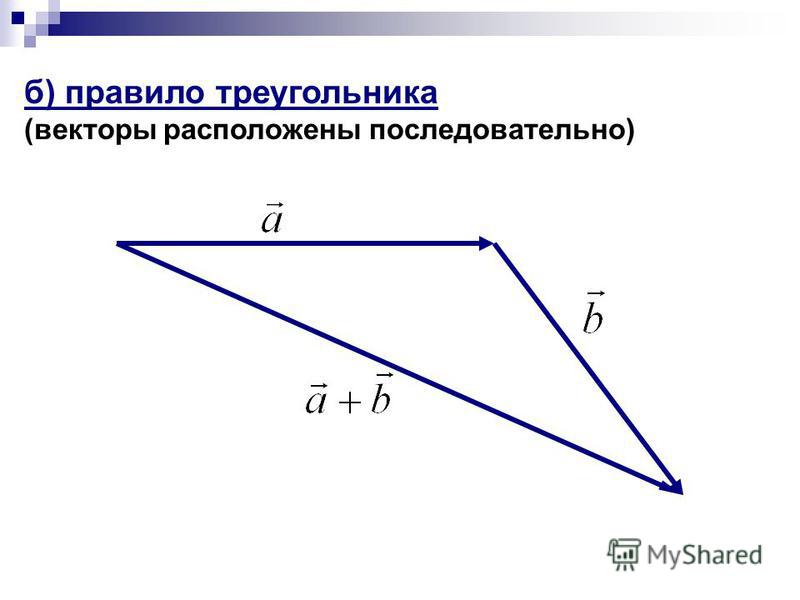
На приведенном ниже рисунке рассмотрим два вектора P и Q, величины которых заданы сторонами OA и AB соответственно. Теперь сумма этих векторов с использованием треугольного закона сложения векторов определяется результирующим вектором R (сторона OB треугольника), величина и направление которого равны
- |R| = √(P 2 + Q 2 + 2PQ cos θ)
- ϕ = тангенс -1 [(Q sin θ)/(P + Q cos θ)]
Теперь продолжим сторону OA до точки C так, чтобы BC была перпендикулярна к OC, а угол между векторами P и Q был равен θ. Кроме того, направление результирующего вектора R задается углом ϕ. В прямоугольном треугольнике OBC имеем
OB 2 = OC 2 + BC 2
⇒ OB 2 = (OA + AC) 2 + BC 2 — (1)
в правой Triangle ABC ABC ABC ABC ABC ABC. , имеем
cos θ = AC/AB и sin θ = BC/AB
⇒ AC = AB cos θ и BC = AB sin θ
⇒ AC = Q cos θ и BC = Q sin θ — ( 2)
Подставляя значения из (2) в (1), имеем
R 2 = (P + Q cos θ) 2 + (Q sin θ) 2
⇒ R 2 = P 2 + Q 2 COS 2 θ + 2PQ COS θ + Q 2 SIN 2 θ
⇒ R 2 = P 2 9009 + 2P COS 2 = P 2 + 2 ⇒ R 2 = P 2 9009 2909. ⇒ R 2 = P 2 + 2PQ COS θ + Q 2 [COS 2 θ + SIN 2 [COS 2 θ + SIN 2 [COS 2 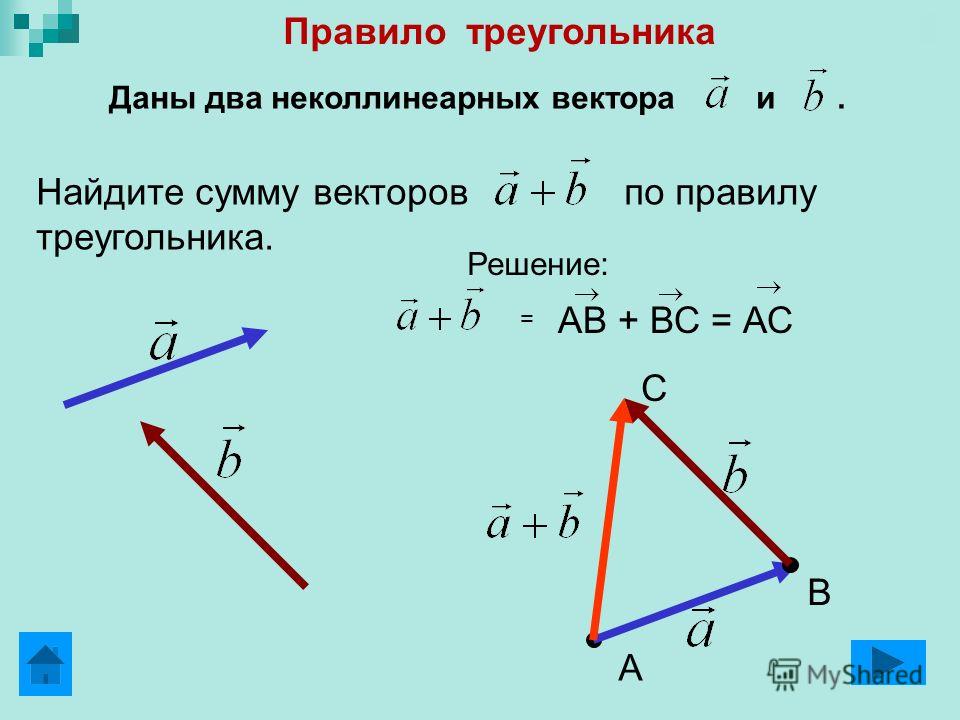 θ + Q 2 (COS 2 θ + SIN 2 θ)
θ + Q 2 (COS 2 θ + SIN 2 θ)
⇒ R = √(P 2 + 2PQ cos θ + Q 2 ) → Величина результирующего вектора R
Теперь, чтобы найти направление R, мы имеем в прямом треугольнике OBC,
tan ϕ = BC/OC
⇒ tan ϕ = Q sin θ/(OA + AC) [Из (2)]
⇒ tan ϕ = Q sin θ/(P + Q cos θ) [Из (2)]
⇒ ϕ = tan -1 [(Q sin θ)/(P + Q cos θ)] → Направление результирующего вектора R
Итак, мы доказали формулы треугольного закона сложения векторов.
Важные замечания о треугольном законе сложения векторов
- Треугольный закон сложения векторов используется для нахождения суммы двух векторов, когда вершина первого вектора соединяется с хвостом второго вектора.
- Величина результирующего вектора суммы R: R = √(P 2 + 2PQ cos θ + Q 2 )
- Направление результирующего вектора R: ϕ = tan -1 [(Q sin θ)/(P + Q cos θ)]
Темы, связанные с важными замечаниями по закону сложения векторов треугольника
- Векторные величины
- Нулевой вектор
- Типы векторов
Часто задаваемые вопросы о законе треугольника сложения векторов
Что такое треугольный закон сложения векторов в математике?
Треугольный закон сложения векторов — это математическая концепция, используемая для нахождения суммы двух векторов.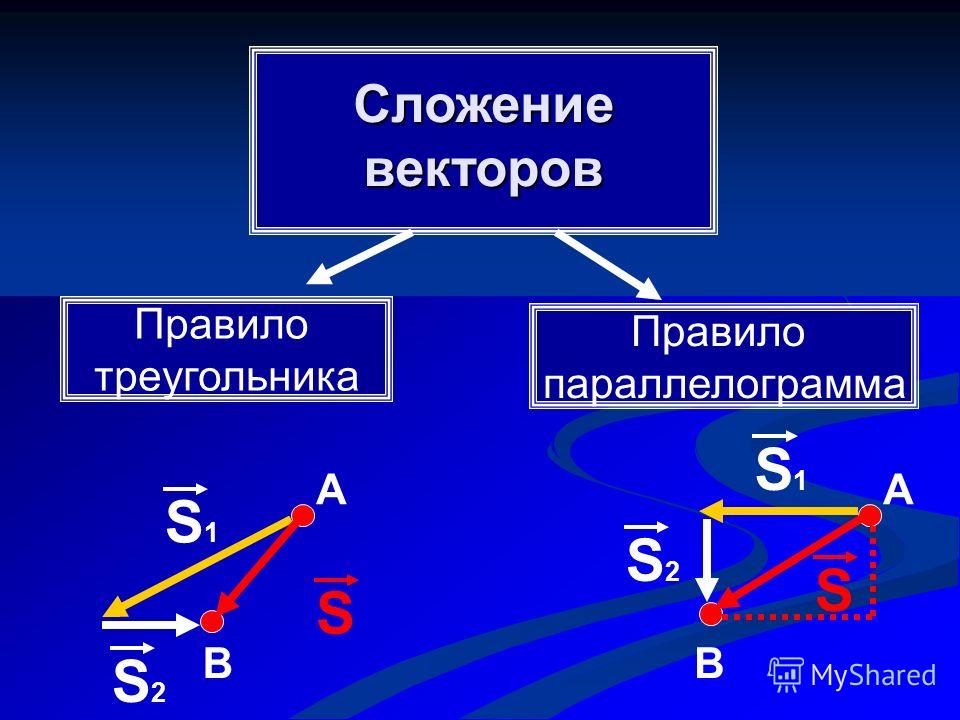 Этот закон используется для сложения двух векторов, когда голова первого вектора соединяется с хвостом второго вектора, а затем присоединяется хвост первого вектора к началу второго вектора, чтобы сформировать треугольник, и, следовательно, получить результирующий вектор суммы .
Этот закон используется для сложения двух векторов, когда голова первого вектора соединяется с хвостом второго вектора, а затем присоединяется хвост первого вектора к началу второго вектора, чтобы сформировать треугольник, и, следовательно, получить результирующий вектор суммы .
Что такое формула треугольного закона сложения векторов?
Сумма двух векторов P и Q с использованием треугольного закона сложения векторов определяется результирующим вектором R, величина и направление которого равны:
- |R| = √(P 2 + Q 2 + 2PQ cos θ)
- ϕ = тангенс -1 [(Q sin θ)/(P + Q cos θ)]
Как сложить векторы, используя закон треугольника для сложения векторов?
При сложении двух векторов P и Q мы складываем векторы и определяем результирующий вектор R по формулам:
- |Р| = √(P 2 + Q 2 + 2PQ cos θ)
- ϕ = тангенс -1 [(Q sin θ)/(P + Q cos θ)]
В чем разница между законом параллелограмма и законом треугольника сложения векторов?
Результирующий вектор суммы определяется диагональю параллелограмма по закону параллелограмма и третьей стороной треугольника по закону сложения векторов треугольника.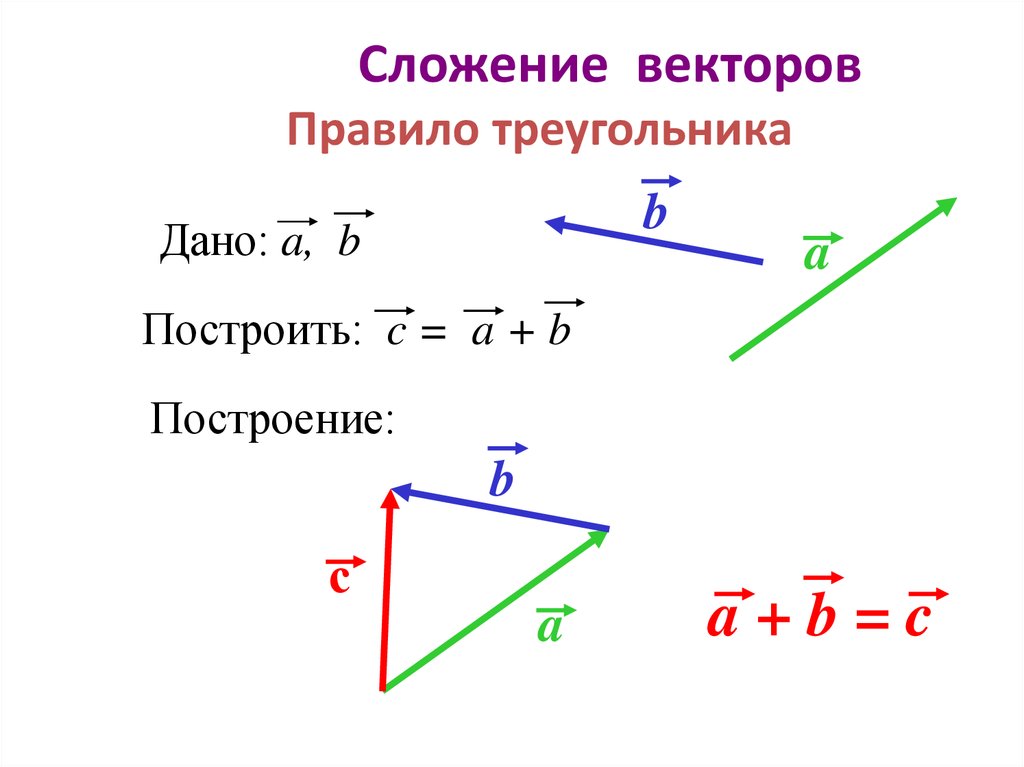

 Физика
Физика