Предел (lim), предел последовательности
Мы уже знаем, что арифметическая и геометрическая прогрессии — это последовательность чисел. Давайте возьмем последовательность an = 1/n, если k
и m натуральные числа, тогда для каждого k k > am, поэтому, чем больше становится
n тем меньше становится an и это число всегда позитивно, но никогда не становится равным нулю. В этом случае, мы говорим, что 0 есть
пределом lim an->∞ если n->∞, или, если записать по-другому: limn->∞ an = 0.
Определение предела
Число a называется пределом последовательности, если для каждого ε > 0 может быть найдено число nε, то для всех членов последовательности an with index n > nε верно, что a — ε n
Основное правило
Если limn->∞ an = a, an -> a an — a -> 0 |an — a| -> 0
Последовательность не всегда имеет предел, а иногда имеет предел бесконечности ( -∞ or +∞ ).
Если обе последовательности an and bn имеют действительные пределы, тогда последовательности
an + bn,
an — bn, an.bn и an / bn также имеют действительный предел и:
limn -> ∞(an + bn) = limn -> ∞an + limn -> ∞bn
limn -> ∞(an — bn) = limn -> ∞an — limn -> ∞bn
limn -> ∞(an . bn) = limn -> ∞an . limn -> ∞bn
limn -> ∞(an/ bn) = limn -> ∞an / lim n -> ∞bn
если bn ≠ 0 and limn->∞bn ≠ 0
Если ann для каждого натурального n
и limn->∞an = a,
limn->∞bn = b
тогда a ≤ b
Если an ≤ bn ≤ cn или каждое действительное
n и если limn->∞an = limn->∞cn = A
тогда limn->∞bn = A.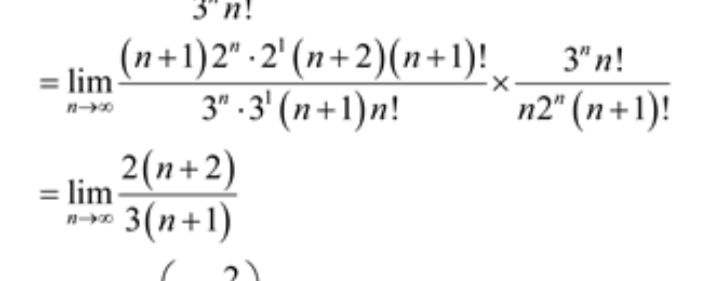
Если an ≥ 0 и limn->∞an = a, тогда последовательность bn = √an также имеет предел и limn->∞√an = √an.
Если an = 1/nk и k ≥ 1 тогда limn->∞an = 0.
Если -1 n->∞qn = 0.
limn->∞(1 — 1/n)
(1+1/n)nn-1
e is the number of Neper.
Если последовательность an имеет предел бесконечность ( -∞ или +∞ ) тогда последовательность 1/an имеет предел и limn->∞1/an = 0
Если последовательности an иbn имеют бесконечные пределы и limn->∞an=+∞, limn->∞bn=+∞ тогда:
limn->∞(an + bn) = +∞
limn->∞(an . bn) = +∞
bn) = +∞
limn->∞ank = +∞ если k > 0
limn->∞ank = 0; если k
limn->∞-an = -∞
Упражнения с пределами
Упражнение 1:
Ответ:
limn->0an = limn->05 . limn->04n = 5 . 40 = 5.1 = 5
Упражнение 2:
| Если an = |
| then limn->∞an = ? |
Ответ:
| limn->∞ |
| = limn->∞ | . |
| = limn->∞ |
| = -3 |
Упражнение 3:
| = ? |
Ответ:
| liman->1 = |
| = | liman->∞ |
| = |
Больше о пределах на страницах математического форума
Для участия в математическом форуме регистрация не требуется!
Как считать пределы.
 2 стремится к нулю.
2 стремится к нулю.Обычно переменная величина x стремится к конечному пределу a, причем, x постоянно приближается к a, а величина a постоянна. Это записывают следующим образом: limx =a, при этом, n также может стремиться как к нулю, так и к бесконечности. Существуют бесконечные функции, для них предел стремится к бесконечности. В других случаях, когда, например, функцией замедление хода поезда, можно о пределе, стремящемся к нулю.
У пределов имеется ряд свойств. Как правило, любая функция имеет только один предел. Это главное свойство предела. Другие их свойства перечислены ниже:
* Предел суммы равен сумме пределов:
lim(x+y)=lim x+lim y
* Предел произведения равен произведению пределов:
lim(xy)=lim x*lim y
* Предел частного равен частному от пределов:
lim(x/y)=lim x/lim y
* Постоянный множитель выносят за знак предела:
lim(Cx)=C lim x
Если дана функция 1 /x, в которой x →∞, ее предел равен нулю. Если же x→0, предел такой функции равен ∞.
Для тригонометрических функций имеются исключения из этих правил. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
lim sin x/x=1
В ряде задач встречаются функции, при вычислении пределов которых возникает неопределенность — ситуация, при которой предел невозможно вычислить. Единственным выходом из такой ситуации становится применение правила Лопиталя. Существует два вида неопределенностей:
* неопределенность вида 0/0
* неопределенность вида ∞/∞
К примеру, дан предел следующего вида: lim f(x)/l(x), причем, f(x0)=l(x0)=0. В таком случае, возникает неопределенность вида 0/0. Для решения такой задачи обе функции подвергают дифференцированию, после чего находят предел результата. Для неопределенностей вида 0/0 предел равен:
lim f(x)/l(x)=lim f»(x)/l»(x) (при x→0)
Это же правило справедливо и для неопределенностей типа ∞/∞. Но в этом случае справедливо следующее равенство: f(x)=l(x)=∞
С помощью правила Лопиталя можно находить значения любых пределов, в которых фигурируют неопределенности. (n-1)
(n-1)
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что «скучная теория» должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
Примеры решений
| Пример 1 |
| Вычислить а) $ \lim_{x \to 0} \frac{1}{x} $; б)$ \lim_{x \to \infty} \frac{1}{x} $ |
| Решение |
а) $$ \lim \limits_{x \to 0} \frac{1}{x} = \infty $$ б)$$ \lim_{x \to \infty} \frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. |
Алгоритм вычисления лимитов
Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:
- Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: «ноль делить на ноль» или «бесконечность делить на бесконечность» и переходим к следующим пунктам инструкции.
- Чтобы устранить неопределенность «ноль делить на ноль» нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
- Если неопределенность «бесконечность делить на бесконечность», тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!
Пример 4
Найти предел
Это более простой пример для самостоятельного решения. В предложенном примере снова неопределённость ( более высокого порядка роста, чем корень ).
Если «икс» стремится к «минус бесконечности»Призрак «минус бесконечности» уже давно витал в этой статье. Рассмотрим пределы с многочленами, в которых . Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.
Рассмотрим 4 фишки, которые потребуются для решения практических заданий:
1) Вычислим предел
Значение предела зависит только от слагаемого , поскольку оно обладает самым высоким порядком роста. Если , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени , в данном случае – в четвёртой, равно «плюс бесконечности»: . Константа («двойка») положительна , поэтому:
Если , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени , в данном случае – в четвёртой, равно «плюс бесконечности»: . Константа («двойка») положительна , поэтому:
2) Вычислим предел
Здесь старшая степень опять чётная , поэтому: . Но перед расположился «минус» (отрицательная константа –1), следовательно:
3) Вычислим предел
Значение предела зависит только от . Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное число в НЕЧЁТНОЙ степени равно «минус бесконечности», в данном случае: .
Константа («четвёрка») положительна , значит:
4) Вычислим предел
Первый парень на деревне снова обладает нечётной степенью, кроме того, за пазухой отрицательная константа, а значит: Таким образом:
.
Пример 5
Найти предел
Используя вышеизложенные пункты, приходим к выводу, что здесь неопределённость . Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
Решение тривиально:
Пример 6
Найти предел
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
А сейчас, пожалуй, самый тонкий из случаев:
Пример 7
Найти предел
Рассматривая старшие слагаемые, приходим к выводу, что здесь неопределённость . Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:
Решаем:
Разделим числитель и знаменатель на
Пример 15
Найти предел
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
Ещё пара занятных примеров на тему замены переменной:
Пример 16
Найти предел
При подстановке единицы в предел получается неопределённость .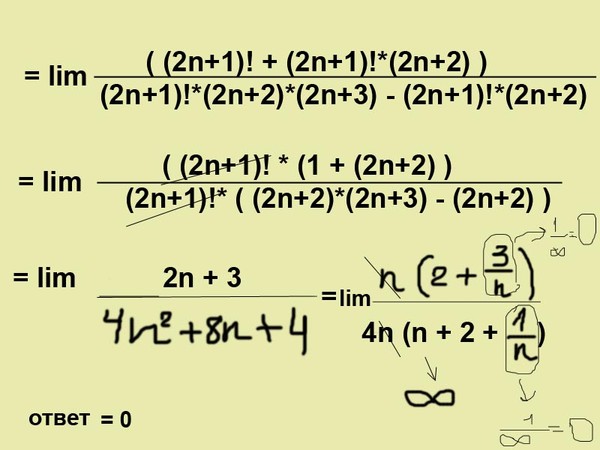 Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле . Действительно, зачем нам тангенс?
Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле . Действительно, зачем нам тангенс?
Заметьте, что , поэтому . Если не совсем понятно, посмотрите значения синуса в тригонометрической таблице . Таким образом, мы сразу избавляемся от множителя , кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.
Проведем замену:
Если , то
Под косинусом у нас находится «икс», который тоже необходимо выразить через «тэ».
Из замены выражаем: .
Завершаем решение:
(1) Проводим подстановку
(2) Раскрываем скобки под косинусом.
(4) Чтобы организовать первый замечательный предел , искусственно домножаем числитель на и обратное число .
Задание для самостоятельного решения:
Пример 17
Найти предел
Полное решение и ответ в конце урока.
Это были несложные задачи в своём классе, на практике всё бывает хуже, и, помимо формул приведения , приходится использовать самые разные тригонометрические формулы , а также прочие ухищрения. В статье Сложные пределы я разобрал пару настоящих примеров =)
В статье Сложные пределы я разобрал пару настоящих примеров =)
В канун праздника окончательно проясним ситуацию ещё с одной распространённой неопределённостью:
Устранение неопределённости «единица в степени бесконечность»Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-й замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёт только о неопределённости и никакой другой .
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы , которые относятся ко 2-му замечательному пределу. Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-й замечательный предел.
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а .
Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim — от английского limit — предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача — найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
математический-анализ / Вычислить предел $%\lim_{n \rightarrow \infty} (\frac{n^3-3n+1}{n^3+2n^2+1})^n$% / Математика
|
Проходим последовательности, их пределы (неравенство Бернулли, фундаментальная константа $%e$%), было показано задание вычисления пределов через формулу $%\lim_{n \rightarrow \infty} (1+\frac{A}{n})^n=e^A$%, я попробовал дома решить пару примеров из задачника на эту тему, решил все, которые хотел, кроме одного: пределы вычислить математический-анализ задан 11 Сен ’14 20:32 ratchet изменен 12 Сен ’14 10:53 Виталина |
старыеновыеценные
|
То выражение, которое у Вас прибавлено к 1, если взять старшие члены в числителе и знаменателе, превращается в $%-\frac2n$%. ссылка отвечен 11 Сен ’14 20:45 ratchet изменен 11 Сен ’14 21:05 |
Ваш ответ
Если вы не нашли ответ, задайте вопрос.
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
регистрация »
отмечен:
математический-анализ
×4,181
пределы
×836
вычислить
×42
задан
11 Сен ’14 20:32
показан
1631 раз
обновлен
12 Сен ’14 0:27
Связанные исследования
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Предел последовательности свойства пределов раскрытие неопределенностей второй замечательный предел число e вычисление пределов числовых последовательностей
| Справочник по математике | Элементы математического анализа | Числовые последовательности |
Содержание
| Предел числовой последовательности |
| Свойства пределов числовых последовательностей |
| Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессии |
Примеры вычисления пределов последовательностей. Раскрытие неопределенностей Раскрытие неопределенностей |
| Число e. Второй замечательный предел |
Предел числовой последовательности
ОПРЕДЕЛЕНИЕ 1. Число a называют пределом числовой последовательности
a1 , a2 , … an , …
если для любого положительного числа ε найдется такое натуральное число N , что при всех n > N выполняется неравенство
| an – a | < ε .
Условие того, что число a является пределом числовой последовательности
a1 , a2 , … an , … ,
записывают с помощью обозначения
и произносят так: «Предел an при n , стремящемся к бесконечности, равен a ».
То же самое соотношение можно записать следующим образом:
an → a при .
Словами это произносится так: «an стремится к a при n , стремящемся к бесконечности».
ЗАМЕЧАНИЕ. Если для последовательности
a1 , a2 , … an , …
найдется такое число a , что an → a при , то эта последовательность ограничена.
ОПРЕДЕЛЕНИЕ 2. Говорят, что последовательность
a1 , a2 , … an , …
стремится к бесконечности, если для любого положительного числа C найдется такое натуральное число N , что при всех n > N выполняется неравенство
| an| > C .
Условие того, что числовая последовательность
a1 , a2 , … an , … ,
стремится к бесконечности, записывают с помощью обозначения
или с помощью обозначения
при .
ПРИМЕР 1. Для любого числа k > 0 справедливо равенство
ПРИМЕР 2 . Для любого числа k > 0 справедливо равенство
ПРИМЕР 3. Для любого числа a такого, что | a | < 1, справедливо равенство
ПРИМЕР 4. Для любого числа a такого, что | a | > 1, справедливо равенство
ПРИМЕР 5 . Последовательность
– 1 , 1 , – 1 , 1 , … ,
заданная с помощью формулы общего члена
an = (– 1)n ,
предела не имеет.
Свойства пределов числовых последовательностей
Рассмотрим две последовательности
a1 , a2 , … an , … , и b1 , b2 , … bn , … .
Если при существуют такие числа a и b , что
и ,
то при существуют также и пределы суммы, разности и произведения этих последовательностей, причем
Если, кроме того, выполнено условие
то при существует предел дроби
причем
Для любой непрерывной функции f (x) справедливо равенство
Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессии
Рассмотрим геометрическую прогрессию
b1 , b2 , … bn , … ,
знаменатель которой равен q .
Для суммы первых n членов геометрической прогрессии
Sn = b1 + b2 + … + bn , n = 1, 2, 3, …
справедлива формула
Если для суммы всех членов бесконечно убывающей геометрической прогрессии ввести обозначение
S = b1 + b2 + … + bn + … ,
то будет справедлива формула
В случае бесконечно убывающей геометрической прогрессии знаменатель q удовлетворяет неравенству
| q | < 1 ,
поэтому, воспользовавшись cвойствами пределов числовых последовательностей и результатом примера 3, получаем
Итак,
Примеры вычисления пределов последовательностей.
 Раскрытие неопределенностей
Раскрытие неопределенностейОПРЕДЕЛЕНИЕ 3. Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к , то вычисление такого предела называют раскрытием неопределенности типа .
Часто неопределенность типа удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменателе дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.
ПРИМЕР 6. Найти предел последовательности
РЕШЕНИЕ. Сначала преобразуем выражение, стоящее под знаком предела, воспользовавшись свойствами степеней:
Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби, а также, используя cвойства пределов последовательностей и результат примера 3, получаем
Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби и сокращая дробь, получаем
Используя cвойства пределов последовательностей и результат примера 3, находим
ОТВЕТ.
ПРИМЕР 7 . Найти предел последовательности
РЕШЕНИЕ. Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби, а также, используя cвойства пределов последовательностей и результат примера 1, получаем
РЕШЕНИЕ. Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби:
Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем
ОТВЕТ.
В следующих двух примерах показано, как можно раскрыть неопределенности типа.
ПРИМЕР 8 . Найти предел последовательности
РЕШЕНИЕ. Сначала преобразуем выражение, стоящее под знаком предела, приводя дроби к общему знаменателю:
Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в каждой из скобок знаменателя дроби, а также, используя cвойства пределов последовательностей и результат примера 1, получаем
Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в каждой из скобок знаменателя дроби:
Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем
ОТВЕТ.
ПРИМЕР 9. Найти предел последовательности
РЕШЕНИЕ. В рассматриваемом примере неопределенность типа возникает за счет разности двух корней, каждый из которых стремится к . Для того, чтобы раскрыть неопределенность, умножим и разделим выражение, стоящее под знаком предела, на сумму этих корней и воспользуемся формулой сокращенного умножения «разность квадратов».
Из-за большого размера формул подробные вычисления видны только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах). На Вашем мобильном устройстве отображается только результат описанных операций.
Вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое из-под каждого корня в знаменателе дроби, а также, используя cвойства пределов последовательностей и результат примера 1, получаем
Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое из-под каждого корня в знаменателе дроби, а затем сокращая дробь на n2:
Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем
ОТВЕТ.
ПРИМЕР 10. Найти предел последовательности
РЕШЕНИЕ. Замечая, что для всех k = 2, 3, 4, … выполнено равенство
,
получаем
ОТВЕТ. 1 .
Число e. Второй замечательный предел
Рассмотрим последовательность
| (1) |
В дисциплине «Математический анализ», которую студенты естественнонаучных и технических направлений высших учебных заведений изучают на 1 курсе, доказывают, что последовательность (1) монотонно возрастает и ограничена сверху. Из теоремы Вейерштрасса о монотонных и ограниченных последовательностях, доказательство которой выходит за рамки школьного курса математики, вытекает, что последовательность (1) имеет конечный предел. Этот предел принято обозначать буквой e.
Таким образом, справедливо равенство
| (2) |
причем расчеты показывают, что число
e = 2,718281828459045…
и является иррациональным и трансцендентным числом.
Число e играет исключительно важную роль в естествознании и, в частности, служит основанием натуральных логарифмов и основанием показательной функции
y = e x,
которую называют «экспонента».
Число e также является пределом последовательности
| (3) |
что позволяет вычислять число e с любой точностью. Конечно же, доказательство формулы (3) выходит за рамки школьного курса математики.
ЗАМЕЧАНИЕ. Предел (2), в котором для последовательностей раскрывается неопределенность типа , называют вторым замечательным пределом. В разделе нашего справочника «Пределы функций» можно ознакомиться со вторым замечательным пределом для функций.
{1/n}/n$ как $n\to\infty$Задавать вопрос
спросил
Изменено 1 год, 4 месяца назад
Просмотрено 46 тысяч раз
$\begingroup$
(необходимо доказательство) 9{\frac{1}{n}}}{n}$$
У меня пока нет ответа, но я знаю, что он существует и стоит меньше $1$.
Редакт. Ответ Винтера самый правильный. Я не понимаю, как он прыгает от (log(n!) — nlog(n)) к нему, равному сумме от k=1 до n из log(k/n). Не думайте, что это неправильно, мне нужно идти, и я продолжу смотреть на него, когда вернусь
Любая помощь приветствуется
исчисление ограничивает факториал
$\endgroup$ 9n$, то $a_{2n} = 2$ и $a_{2n+1} = 0$. Поскольку подпоследовательности $a_{2n}$ и $a_{2n+1}$ имеют разные пределы ($\lim a_{2n} = 2$ и $\lim a_{2n+1} = 0$), предел $ \lim a_n$ не существует.
$\endgroup$
$\begingroup$
Предела не существует, и это можно доказать несколькими способами.
Заметим, как утверждает @kobe, что мы можем найти две сходящиеся подпоследовательности в разных пределах, и, таким образом, у нас есть не сходящаяся последовательность. Это могут быть состояния с точки зрения верхнего предела и нижнего предела и отмечая, что они разные.
Еще один способ доказать это — использовать противоречие. Поскольку последовательность принимает только два значения $0$ и $2$, можно тривиально увидеть (и доказать), что любое значение, кроме этих двух, не может быть пределом. Предполагая $l=0$ и беря $\varepsilon<2$, мы видим, что предел не может существовать, так как $|x_n-x_{n+1}|=2>\varepsilon$. Аналогично доказываем для $l=2$.
КЭД.
$\endgroup$
$\begingroup$
Увы, этого предела не существует. 9n$ не существует.
Ура!
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
MySQL LIMIT
Сводка : В этом руководстве вы узнаете, как использовать предложение MySQL LIMIT для ограничения количества строк, возвращаемых запросом.
Введение в MySQL LIMIT
Предложение Предложение LIMIT используется в операторе SELECT для ограничения количества возвращаемых строк. Предложение LIMIT принимает один или два аргумента. Значения обоих аргументов должны быть нулевыми или целыми положительными числами.
Ниже показан синтаксис предложения LIMIT с двумя аргументами:
Язык кода: SQL (язык структурированных запросов) (sql)
SELECT select_list ИЗ имя_таблицы LIMIT [смещение,] row_count;
В этом синтаксисе:
- Смещение
смещениепервой строки равно 0, а не 1. - Параметр
row_countуказывает максимальное количество возвращаемых строк.
Следующий рисунок иллюстрирует предложение LIMIT :
Когда вы используете предложение LIMIT с одним аргументом, MySQL будет использовать этот аргумент для определения максимального количества строк, возвращаемых из первой строки результирующего набора.
Следовательно, эти два предложения эквивалентны:
Язык кода: SQL (язык структурированных запросов) (sql)
LIMIT row_count;
И
LIMIT 0 , row_count;
В дополнение к приведенному выше синтаксису MySQL предоставляет следующий альтернативный синтаксис предложения LIMIT :
Язык кода: SQL (Structured 016 The
LIMIT row_count OFFSET offsetThe
) и предложения ORDER BY
По умолчанию
SELECT 9Оператор 0348 возвращает строки в неопределенном порядке.Когда вы добавляете предложение
LIMITв инструкциюSELECT, возвращаемые строки непредсказуемы.Поэтому, чтобы гарантировать, что предложение
LIMITвозвращает ожидаемый результат, вы всегда должны использовать его с предложениемORDER BYследующим образом:Язык кода: SQL (язык структурированных запросов) (sql)
SELECT select_list ИЗ имя_таблицы СОРТИРОВАТЬ ПО sort_expression LIMIT смещение, row_count;На следующем рисунке показан порядок оценки предложения
LIMITв оператореSELECT:Примеры предложения MySQL LIMIT
Для демонстрации мы будем использовать таблицу
customersиз примера базы данных.1) Использование MySQL LIMIT для получения самых высоких или самых низких строк
В этом операторе используется предложение
LIMITдля получения первых пяти клиентов с самым высоким кредитом:Кодовый язык: SQL (язык структурированных запросов) (sql)
ВЫБЕРИТЕ номер клиента, Имя Клиента, кредитный лимит ИЗ клиенты ЗАКАЗАТЬ ПО кредитному лимиту DESC ПРЕДЕЛ 5;Попробуйте
В этом примере:
- Во-первых, предложение
ORDER BYсортирует клиентов по количеству кредитов от большего к меньшему.
- Затем предложение
LIMITвозвращает первые 5 строк.
Аналогично, в этом примере используется ПРЕДЕЛ 9.0348, чтобы найти пять клиентов с наименьшим кредитом:
Язык кода: SQL (язык структурированных запросов) (sql)
ВЫБЕРИТЕ номер клиента, Имя Клиента, кредитный лимит ИЗ клиенты ЗАКАЗАТЬ ПО кредитному лимиту ПРЕДЕЛ 5;
Попробуйте
В этом примере:
- Во-первых, предложение
ORDER BYсортирует клиентов по кредитам в порядке возрастания. - Затем предложение
LIMITвозвращает первые 5 строк.
Поскольку существует более 5 клиентов с нулевым кредитом, результат запроса выше может привести к противоречивому результату.
Чтобы устранить эту проблему, вам нужно добавить дополнительные столбцы в предложение ORDER BY , чтобы ограничить строку в уникальном порядке:
Язык кода: SQL (язык структурированных запросов) (sql)
SELECT номер клиента, Имя Клиента, кредитный лимит ИЗ клиенты СОРТИРОВАТЬ ПО кредитный лимит, номер клиента ПРЕДЕЛ 5;
Попробуйте
2) Использование предложения MySQL LIMIT для разбиения на страницы
Когда вы отображаете данные на экране, вы часто хотите разделить строки на страницы, где каждая страница содержит ограниченное количество строк, например 10 или 20.
Чтобы рассчитать количество страниц, нужно разделить общее количество строк на количество строк на странице. Для выборки строк определенной страницы вы можете использовать предложение LIMIT .
Этот запрос использует агрегатную функцию COUNT(*) , чтобы получить общее количество строк из клиентов таблица:
Язык кода: SQL (язык структурированных запросов) (sql)
ВЫБЕРИТЕ СЧИТАТЬ(*) ИЗ клиенты;
Язык кода: JavaScript (javascript)
+----------+ | СЧЕТ(*) | +----------+ | 122 | +----------+ 1 строка в наборе (0,00 сек)
Предположим, что каждая страница имеет 10 строк; чтобы отобразить 122 клиентов, у вас есть 13 страниц. Последняя 13-я страница содержит только две строки.
Последняя 13-я страница содержит только две строки.
Этот запрос использует предложение LIMIT для получения строк страницы 1, содержащих первых 10 клиентов, отсортированных по имени клиента:
Язык кода: SQL (язык структурированных запросов) (sql)
SELECT номер клиента, Имя Клиента ИЗ клиенты ЗАКАЗАТЬ ПО customerName ПРЕДЕЛ 10;
Попробуйте
В этом запросе используется предложение LIMIT для получения строк второй страницы, содержащих строки 11–20:
Язык кода: SQL (язык структурированных запросов) (sql)
ВЫБЕРИТЕ номер клиента, Имя Клиента ИЗ клиенты ЗАКАЗАТЬ ПО customerName ПРЕДЕЛ 10, 10;
Попробуйте
В этом примере предложение LIMIT 10, 10 возвращает 10 строк для строки 11–20. Использование
Использование
3) MySQL LIMIT для получения n
th самого высокого или самого низкого значения Чтобы получить n th самого высокого или самого низкого значения, вы используете следующие LIMIT пункт:
Язык кода: SQL (язык структурированных запросов) (sql)
SELECT select_list ОТ имя_таблицы ORDER BY sort_expression ПРЕДЕЛ n-1, 1;
Предложение LIMIT n-1, 1 возвращает 1 строку, начинающуюся со строки n .
Например, следующий код находит клиента со вторым по величине кредитом:
Язык кода: SQL (язык структурированных запросов) (sql)
ВЫБЕРИТЕ Имя Клиента, кредитный лимит ИЗ клиенты СОРТИРОВАТЬ ПО кредитный лимит DESC ПРЕДЕЛ 1,1;
Попробуйте
Давайте еще раз проверим результат. Этот запрос возвращает всех клиентов, отсортированных по количеству кредитов от большего к меньшему:
Этот запрос возвращает всех клиентов, отсортированных по количеству кредитов от большего к меньшему:
Язык кода: SQL (язык структурированных запросов) (sql)
SELECT Имя Клиента, кредитный лимит ИЗ клиенты СОРТИРОВАТЬ ПО кредитный лимит DESC;
Попробуйте
Как видно из вывода, результат оказался правильным, как и ожидалось.
Обратите внимание, что этот метод работает, когда нет двух клиентов с одинаковыми кредитными лимитами. Чтобы получить более точный результат, следует использовать оконную функцию DENSE_RANK().
Предложения MySQL LIMIT и DISTINCT
Если вы используете предложение LIMIT с предложением DISTINCT , MySQL немедленно прекращает поиск, когда находит количество уникальных строк, указанное в предложении LIMIT .
В примере используется ПРЕДЕЛ 9Предложение 0348 с предложением : DISTINCT для возврата первых пяти уникальных состояний в таблице клиентов
Язык кода: SQL (язык структурированных запросов) (sql)
SELECT DISTINCT государство ИЗ клиенты КУДА состояние НЕ НУЛЕВОЕ ПРЕДЕЛ 5;
Попробуйте
Сводка
- Используйте предложение MySQL
LIMIT, чтобы ограничить количество строк, возвращаемых оператором 90 SELECT.
Было ли это руководство полезным?
4.1: Последовательности — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14700
Эта страница является черновиком и находится в активной разработке.
В этом разделе мы вводим последовательности и определяем, что означает сходимость или расхождение последовательности. Мы покажем, как находить пределы сходящихся последовательностей, часто используя свойства пределов для функций, обсуждавшихся ранее. Мы завершаем этот раздел теоремой о монотонной сходимости — инструментом, который мы можем использовать для доказательства сходимости определенных типов последовательностей.
Терминология последовательностей
Для работы с этой новой темой нам понадобятся некоторые новые термины и определения. Во-первых, бесконечная последовательность — это упорядоченный список чисел вида 9∞_n=1,\]
или просто \(\displaystyle {a_n}\) для обозначения этой последовательности. Подобное обозначение используется для наборов, но последовательность — это упорядоченный список, тогда как набор не является упорядоченным. Поскольку для каждого положительного целого числа \(\displaystyle n\) существует определенное число \(\displaystyle a_n\), мы также можем определить последовательность как функцию, областью определения которой является множество положительных целых чисел.
Рассмотрим бесконечный упорядоченный список
\[\displaystyle 2,4,8,16,32,….\]
Это последовательность, в которой первый, второй и третий члены задаются \( \displaystyle a_1=2, a_2=4,\) и \(\displaystyle a_3=8.\) Вероятно, вы видите, что термины в этой последовательности имеют следующий шаблон: 9n}.\]
В качестве альтернативы мы можем описать эту последовательность по-другому. Поскольку каждый термин в два раза больше предыдущего, эту последовательность можно определить рекурсивно, выразив \(\displaystyle nth\) термин \(\displaystyle a_n\) через предыдущий термин \(\displaystyle a_{n−1}\ ). В частности, мы можем определить эту последовательность как последовательность \(\displaystyle {a_n}\), где \(\displaystyle a_1=2\) и для всех \(\displaystyle n≥2\) каждый член an определяется повторение отношение
\[\displaystyle a_n=2a_{n−1}.\]
Определение: бесконечная последовательность
Бесконечная последовательность \(\displaystyle {a_n}\) представляет собой упорядоченный список чисел вида
\(\displaystyle a_1,a_2,…,a_n,…. \)
\)
Нижний индекс \(\displaystyle n\) называется индексной переменной последовательности. Каждое число \(\displaystyle a_n\) является членом последовательности. Иногда последовательности определяются явными формулами, в этом случае \(\displaystyle a_n=f(n)\) для некоторой функции \(\displaystyle f(n)\), определенной над положительными целыми числами. В других случаях последовательности определяются с помощью рекуррентное отношение . В рекуррентном отношении один член (или более) последовательности задается явно, а последующие члены определяются в терминах более ранних членов последовательности.
Обратите внимание, что индекс не обязательно должен начинаться с \(\displaystyle n=1\), но может начинаться с других целых чисел. Например, последовательность, заданная явной формулой \(\displaystyle a_n=f(n)\), может начинаться с \(\displaystyle n=0\), и в этом случае последовательность будет
\[\displaystyle a_0, а_1, а_2,…. n}\). 9п\)}.
n}\). 9п\)}.
Часто встречаются два типа последовательностей, которым даются специальные названия: арифметические последовательности и геометрические последовательности. В арифметической последовательности разница между каждой парой последовательных членов одинакова. Например, рассмотрим последовательность
\[\displaystyle 3,7,11,15,19, \ldots\]
. Вы можете видеть, что разница между каждой последовательной парой терминов равна \(\displaystyle 4\). Предполагая, что этот шаблон продолжается, эта последовательность является арифметической последовательностью. Его можно описать с помощью рекуррентного соотношения
\[\displaystyle \begin{cases}a_1=3\\a_n=a_{n−1}+4&for n≥2\end{case}.\]
Обратите внимание, что
\[\displaystyle a_2=3 +4\]
\[\displaystyle a_3=3+4+4=3+2⋅4\]
\[\displaystyle a_4=3+4+4+4=3+3⋅4.\]
Таким образом, последовательность также может быть описана с помощью явной формулы (\displaystyle a_n=cn+b.\)
В геометрической последовательности , отношение каждой пары последовательных терминов одинаково. Например, рассмотрим последовательность
Например, рассмотрим последовательность
\[\displaystyle 2,−\dfrac{2}{3},\dfrac{2}{9},−\dfrac{2}{27},\dfrac{2}{81 },….\]
Мы видим, что отношение любого члена к предыдущему равно \(\displaystyle −\dfrac{1}{3}\). Предполагая, что этот шаблон продолжается, эта последовательность является геометрической последовательностью. Его можно определить рекурсивно как
\[ a_1=2\]
\[a_n=−\dfrac{1}{3}⋅a_{n−1}\]
для \([\displaystyle n≥2 .\) 9н\).
Пример \(\displaystyle \PageIndex{1}\): поиск явных формул
Для каждой из следующих последовательностей найдите явную формулу для \(\displaystyle n-го\) члена последовательности.
- \(\displaystyle −\dfrac{1}{2},\dfrac{2}{3},−\dfrac{3}{4},\dfrac{4}{5},−\dfrac{5 {6},…\)
- \(\displaystyle \dfrac{3}{4},\dfrac{9}{7},\dfrac{27}{10},\dfrac{81}{13},\dfrac{243}{16}, …\).
Раствор :
а. Во-первых, обратите внимание, что последовательность чередуется с отрицательной на положительную. n\). Далее рассмотрим последовательность числителей \(\displaystyle {1,2,3,…}\) и последовательность знаменателей \(\displaystyle {2,3,4,…}\). Мы можем видеть, что обе эти последовательности являются арифметическими последовательностями. Термин \(\displaystyle nth\) в последовательности числителей равен \(\displaystyle n\), а член \(\displaystyle nth\) в последовательности знаменателей равен \(\displaystyle n+1\). Следовательно, последовательность может быть описана явной формулой 9п}\).
n\). Далее рассмотрим последовательность числителей \(\displaystyle {1,2,3,…}\) и последовательность знаменателей \(\displaystyle {2,3,4,…}\). Мы можем видеть, что обе эти последовательности являются арифметическими последовательностями. Термин \(\displaystyle nth\) в последовательности числителей равен \(\displaystyle n\), а член \(\displaystyle nth\) в последовательности знаменателей равен \(\displaystyle n+1\). Следовательно, последовательность может быть описана явной формулой 9п}\).
Упражнение \(\PageIndex{2}\)
Найдите явную формулу для рекурсивно определенной последовательности, такой что \(\displaystyle a_1=−4\) и \(\displaystyle a_n=a_{n−1}+6 \).
- Подсказка
Это арифметическая последовательность.
- Ответить
\(\displaystyle a_n=6n−10\)
Ограничение последовательности
Фундаментальный вопрос, возникающий в отношении бесконечных последовательностей, заключается в поведении членов при увеличении \(\displaystyle n\). Поскольку последовательность — это функция, определенная для положительных целых чисел, имеет смысл обсудить предел терминов в виде \(\displaystyle n→∞\). Например, рассмотрим следующие четыре последовательности и их различное поведение как \(\displaystyle n→∞\) (рис. \(\PageIndex{2}\)): 9n}{n}→0\) as \(\displaystyle n→∞.\)
Поскольку последовательность — это функция, определенная для положительных целых чисел, имеет смысл обсудить предел терминов в виде \(\displaystyle n→∞\). Например, рассмотрим следующие четыре последовательности и их различное поведение как \(\displaystyle n→∞\) (рис. \(\PageIndex{2}\)): 9n}{n}→0\) as \(\displaystyle n→∞.\)
Из этих примеров мы видим несколько возможностей поведения членов последовательности как \(\displaystyle n→∞\). В двух последовательностях члены приближаются к конечному числу, поскольку \(\displaystyle n→∞. \) В двух других последовательностях члены не приближаются. Если члены последовательности приближаются к конечному числу \(\displaystyle L\) при \(\displaystyle n→∞\), мы говорим, что последовательность является сходящейся последовательностью, а действительное число L является пределом последовательности. Здесь мы можем дать неформальное определение.
\) В двух других последовательностях члены не приближаются. Если члены последовательности приближаются к конечному числу \(\displaystyle L\) при \(\displaystyle n→∞\), мы говорим, что последовательность является сходящейся последовательностью, а действительное число L является пределом последовательности. Здесь мы можем дать неформальное определение.
Определение: сходящиеся и расходящиеся последовательности
Для данной последовательности \(\displaystyle {a_n},\), если члены an становятся сколь угодно близкими к конечному числу \(\displaystyle L\), когда n становится достаточно большим, мы говорим \ (\displaystyle {a_n}\) — сходящаяся последовательность , а \(\displaystyle L\) — предел последовательности . В этом случае мы пишем
\[\lim_{n→∞}a_n=L.\]
Если последовательность \(\displaystyle {a_n}\) не сходится, мы говорим, что это 9n}\) — сходящаяся последовательность, предел которой равен \(\displaystyle 1\). Напротив, на рисунке видно, что члены последовательности \(\displaystyle 1+3n\) не приближаются к конечному числу, когда \(\displaystyle n\) становится больше. Мы говорим, что \(\displaystyle {1+3n}\) — расходящаяся последовательность.
Мы говорим, что \(\displaystyle {1+3n}\) — расходящаяся последовательность.
В неформальном определении предела последовательности мы использовали термины «сколь угодно близкие» и «достаточно большие». Хотя эти фразы помогают проиллюстрировать значение сходящейся последовательности, они несколько расплывчаты. Чтобы быть более точным, мы теперь представляем более формальное определение предела для последовательности и показываем эти идеи графически на рисунке.
Определение: сходимость
Последовательность \(\displaystyle {a_n}\) сходится к действительному числу \(\displaystyle L\), если для всех \(\displaystyle ε>0\) существует целое число \(\ displaystyle N\) такой, что \(\displaystyle |a_n−L|<ε\), если \(\displaystyle n≥N\). Число \(\displaystyle L\) является пределом последовательности, и мы пишем
\[\lim_{n→∞}a_n=Lora_n→L.\]
В этом случае мы говорим, что последовательность \(\ displaystyle {a_n}\) — сходящаяся последовательность. Если последовательность не сходится, то это расходящаяся последовательность, и мы говорим, что предела не существует.
Заметим, что сходимость или расхождение последовательности \(\displaystyle {a_n}\) зависит только от того, что происходит с членами \(\displaystyle a_n\) при \(\displaystyle n→∞\). Следовательно, если конечное число терминов \(\displaystyle b_1,b_2,…,b_N\) помещено перед \(\displaystyle a_1\) для создания новой последовательности
\[\displaystyle b_1,b_2,…,b_N, a_1,a_2,…,\]
эта новая последовательность будет сходиться, если \(\displaystyle {a_n}\) сходится, и расходиться, если \(\displaystyle {a_n}\) расходится. Кроме того, если последовательность \(\displaystyle {a_n}\) сходится к \(\displaystyle L\), эта новая последовательность также сходится к \(\displaystyle L\). 9n}\) расходится, потому что термины чередуются между \(\displaystyle 1\) и \(\displaystyle −1\), но не приближаются к одному значению как \(\displaystyle n→∞\). С другой стороны, последовательность \(\displaystyle {1+3n}\) расходится, потому что члены \(\displaystyle 1+3n→∞\) как \(\displaystyle n→∞\). Мы говорим, что последовательность \(\displaystyle {1+3n}\) расходится к бесконечности, и пишем \(\displaystyle \lim_{n→∞}(1+3n)=∞\). Важно понимать, что это обозначение не означает, что предел последовательности \(\displaystyle {1+3n}\) существует. На самом деле последовательность расходится. Написание того, что предел равен бесконечности, предназначено только для предоставления дополнительной информации о том, почему последовательность расходится. Последовательность также может расходиться к отрицательной бесконечности. Например, последовательность \(\displaystyle {−5n+2}\) расходится к отрицательной бесконечности, потому что \(\displaystyle −5n+2→−∞\) как \(\displaystyle n→−∞\). Мы запишем это как \(\displaystyle \lim_{n→∞}(−5n+2)=→−∞.\)
Мы говорим, что последовательность \(\displaystyle {1+3n}\) расходится к бесконечности, и пишем \(\displaystyle \lim_{n→∞}(1+3n)=∞\). Важно понимать, что это обозначение не означает, что предел последовательности \(\displaystyle {1+3n}\) существует. На самом деле последовательность расходится. Написание того, что предел равен бесконечности, предназначено только для предоставления дополнительной информации о том, почему последовательность расходится. Последовательность также может расходиться к отрицательной бесконечности. Например, последовательность \(\displaystyle {−5n+2}\) расходится к отрицательной бесконечности, потому что \(\displaystyle −5n+2→−∞\) как \(\displaystyle n→−∞\). Мы запишем это как \(\displaystyle \lim_{n→∞}(−5n+2)=→−∞.\)
Поскольку последовательность — это функция, областью определения которой является множество положительных целых чисел, мы можем использовать свойства пределов функций, чтобы определить, сходится ли последовательность. Например, рассмотрим последовательность \(\displaystyle {a_n}\) и связанную с ней функцию \(\displaystyle f\), определенную для всех положительных действительных чисел, такую, что \(\displaystyle f(n)=a_n\) для всех целых чисел \ (\ Displaystyle п ≥ 1 \). Поскольку домен последовательности является подмножеством домена \(\displaystyle f\), если \(\displaystyle \lim_{x→∞}f(x)\) существует, то последовательность сходится и имеет тот же предел . Например, рассмотрим последовательность \(\displaystyle {\dfrac{1}{n}}\) и связанную с ней функцию \(\displaystyle f(x)=\dfrac{1}{x}\). Поскольку функция \(\displaystyle f\), определенная для всех действительных чисел, \(\displaystyle x>0\), удовлетворяет \(\displaystyle f(x)=\dfrac{1}{x}→0\) при \(\ displaystyle x→∞\), последовательность \(\displaystyle {\dfrac{1}{n}}\) должна удовлетворять \(\displaystyle \dfrac{1}{n}→0\) как \(\displaystyle n→ ∞.\) 9n}\) сходится к \(\displaystyle 0+0=0\). Точно так же, как мы смогли оценить предел, включающий алгебраическую комбинацию функций \(\displaystyle f\) и \(\displaystyle g\), взглянув на пределы \(\displaystyle f\) и \(\displaystyle g\ ) (см. Введение в пределы), мы можем оценить предел последовательности, члены которой являются алгебраическими комбинациями \(\displaystyle a_n\) и \(\displaystyle b_n\), вычислив пределы \(\displaystyle {a_n }\) и \(\displaystyle {b_n}\).
Поскольку домен последовательности является подмножеством домена \(\displaystyle f\), если \(\displaystyle \lim_{x→∞}f(x)\) существует, то последовательность сходится и имеет тот же предел . Например, рассмотрим последовательность \(\displaystyle {\dfrac{1}{n}}\) и связанную с ней функцию \(\displaystyle f(x)=\dfrac{1}{x}\). Поскольку функция \(\displaystyle f\), определенная для всех действительных чисел, \(\displaystyle x>0\), удовлетворяет \(\displaystyle f(x)=\dfrac{1}{x}→0\) при \(\ displaystyle x→∞\), последовательность \(\displaystyle {\dfrac{1}{n}}\) должна удовлетворять \(\displaystyle \dfrac{1}{n}→0\) как \(\displaystyle n→ ∞.\) 9n}\) сходится к \(\displaystyle 0+0=0\). Точно так же, как мы смогли оценить предел, включающий алгебраическую комбинацию функций \(\displaystyle f\) и \(\displaystyle g\), взглянув на пределы \(\displaystyle f\) и \(\displaystyle g\ ) (см. Введение в пределы), мы можем оценить предел последовательности, члены которой являются алгебраическими комбинациями \(\displaystyle a_n\) и \(\displaystyle b_n\), вычислив пределы \(\displaystyle {a_n }\) и \(\displaystyle {b_n}\).
Законы алгебраического предела
Даны последовательности \(\displaystyle {a_n}\) и \(\displaystyle {b_n}\) и любое действительное число \(\displaystyle c\), если существуют константы \(\displaystyle A\) и \(\displaystyle B\) такие, что \(\displaystyle \lim_{n→∞}a_n=A\) и \(\displaystyle \lim_{n→∞}b_n=B\), то
- \( \displaystyle \lim_{n→∞}c=c\)
- \(\displaystyle \lim_{n→∞}ca_n=c\lim_{n→∞}a_n=cA\)
- \(\displaystyle \lim_{n→∞}(a_n±b_n)=\lim_{n→∞}a_n±\lim_{n→∞}b_n=A±B\)
- \(\displaystyle \lim_{n→∞}(a_n⋅b_n)=(\lim_{n→∞}a_n)⋅(\lim_{n→∞}b_n)=A⋅B\)
- \(\displaystyle \lim_{n→∞}(\dfrac{a_n}{b_n})=\dfrac{\lim_{n→∞}a_n}{\lim_{n→∞}b_n}=\dfrac{A {B}\), если \(\displaystyle B≠0\) и каждый \(\displaystyle b_n≠0.\)
Доказательство
Докажем часть III.
Пусть \(\displaystyle ϵ>0\). Поскольку \(\displaystyle \lim_{n→∞}a_n=A\), существует постоянное натуральное число \(\displaystyle N_1\) такое, что для всех \(\displaystyle n≥N_1\). Поскольку \(\displaystyle \lim_{n→∞}b_n=B\), существует константа \(\displaystyle N_2\) такая, что \(\displaystyle |b_n−B|<ε/2\) для всех \( \displaystyle n≥N_2\). Пусть \(\displaystyle N\) будет наибольшим из \(\displaystyle N_1\) и \(\displaystyle N_2\). Следовательно, для всех \(\displaystyle n≥N\), \(\displaystyle |(a_n+b_n)−(A+B)|≤|a_n−A|+|b_n−B|<\dfrac{ε}{ 2}+\dfrac{ε}{2}=ε\). 9x]=\lim_{x→∞}xln(1+\dfrac{4}{x})\).
Поскольку \(\displaystyle \lim_{n→∞}b_n=B\), существует константа \(\displaystyle N_2\) такая, что \(\displaystyle |b_n−B|<ε/2\) для всех \( \displaystyle n≥N_2\). Пусть \(\displaystyle N\) будет наибольшим из \(\displaystyle N_1\) и \(\displaystyle N_2\). Следовательно, для всех \(\displaystyle n≥N\), \(\displaystyle |(a_n+b_n)−(A+B)|≤|a_n−A|+|b_n−B|<\dfrac{ε}{ 2}+\dfrac{ε}{2}=ε\). 9x]=\lim_{x→∞}xln(1+\dfrac{4}{x})\).
Поскольку правая часть этого уравнения имеет неопределенный вид \(\displaystyle ∞⋅0\), перепишем ее в виде дроби, чтобы применить правило Лопиталя. Напишите
\(\displaystyle \lim_{x→∞}xln(1+\dfrac{4}{x})=\lim_{x→∞}\dfrac{ln(1+4/x)}{1/ Икс}\).
Поскольку правая часть теперь представлена в неопределенной форме 0/0, мы можем применить правило Лопиталя. Мы заключаем, что
\(\displaystyle \lim_{x→∞}\dfrac{ln(1+4/x)}{1/x}=\lim_{x→∞}\dfrac{4}{1+4 /х}=4.\) 9n}.\) Определить, сходится ли последовательность. Если оно сходится, найти его предел.
- Подсказка
Используйте правило Лопиталя.
 2}→5\). Поскольку \(\displaystyle \sqrt{x}\) является непрерывной функцией в точке \(\displaystyle x=5\), 92})}=\sqrt{5}.\]
2}→5\). Поскольку \(\displaystyle \sqrt{x}\) является непрерывной функцией в точке \(\displaystyle x=5\), 92})}=\sqrt{5}.\]Непрерывные функции, определенные на сходящихся последовательностях
Рассмотрим последовательность \(\displaystyle {a_n}\) и предположим, что существует действительное число \(\displaystyle L\), такое что последовательность \(\displaystyle {a_n}\) сходится к \(\displaystyle L\). Предположим, что \(\displaystyle f\) является непрерывной функцией в точке \(\displaystyle L\). Тогда существует целое число \(\displaystyle N\), такое что \(\displaystyle f\) определено для всех значений an для \(\displaystyle n≥N\), и последовательность \(\displaystyle {f(a_n) }\) сходится к \(\displaystyle f(L)\) (рис. \(\PageIndex{4}\)).
Рисунок \(\PageIndex{4}\): Поскольку \(\displaystyle f\) является непрерывной функцией, поскольку входные параметры \(\displaystyle a_1,a_2,a_3,…\) приближаются к \(\displaystyle L\), выходы \(\displaystyle f(a_1),f(a_2),f(a_3),…\) приближаются \(\displaystyle f(L)\).
Доказательство
Пусть \(\displaystyle ϵ>0.\) Поскольку \(\displaystyle f\) непрерывна в \(\displaystyle L\), существует \(\displaystyle δ>0\) такое, что \(\ displaystyle |f(x)−f(L)|<ε\), если \(\displaystyle |x−L|<δ\). Поскольку последовательность \(\displaystyle {a_n}\) сходится к \(\displaystyle L\), существует \(\displaystyle N\) такая, что \(\displaystyle |a_n−L|<δ\) для всех \( \displaystyle n≥N\). Следовательно, для всех \(\displaystyle n≥N\), \(\displaystyle |a_n−L|<δ\), откуда следует \(\displaystyle |f(a_n)−f(L)|<ε\). Мы заключаем, что последовательность \(\displaystyle {f(a_n)}\) сходится к \(\displaystyle f(L)\). 92})=cos(0)=1.\)
Упражнение \(\PageIndex{4}\)
Определите, является ли последовательность \(\displaystyle {\sqrt{\dfrac{2n+1}{3n+5 }}}\) сходится. Если оно сходится, найти его предел.
- Подсказка
Рассмотрим последовательность \(\displaystyle {\dfrac{2n+1}{3n+5}}.\)
- Ответить
Последовательность сходится, и ее предел равен \(\displaystyle \sqrt{2/3}\).

Другая теорема, касающаяся пределов последовательностей, является расширением теоремы о сжатии для пределов, обсуждавшейся во введении к пределам.
Теорема сжатия для последовательностей
Рассмотрим последовательности \(\displaystyle {a_n}, {b_n},\) и \(\displaystyle {c_n}\). Предположим, что существует целое число \(\displaystyle N\), такое что
\[\displaystyle a_n≤b_n≤c_n\) для всех \(\displaystyle n≥N.\]
Если существует действительное число \(\ displaystyle L\) такой, что
\[\displaystyle \lim_{n→∞}a_n=L=\lim_{n→∞}c_n,\]
, тогда \(\displaystyle {b_n}\) сходится и \(\displaystyle \lim_{n→∞}b_n=L\) (рис. \(\PageIndex{5}\)).
Рисунок \(\PageIndex{5}\): каждый терм bn удовлетворяет условию \(\displaystyle a_n≤b_n≤c_n\), а последовательности \(\displaystyle {a_n}\) и \(\displaystyle {c_n}\) сходятся к тому же пределу, поэтому последовательность \(\displaystyle {b_n}\) также должна сходиться к тому же пределу.
Доказательство
Пусть \(\displaystyle ε>0.\) Поскольку последовательность \(\displaystyle {a_n}\) сходится к \(\displaystyle L\), существует целое число \(\displaystyle N_1\) такое, что \(\displaystyle |a_n−L|<ε\) для всех \(\displaystyle n≥N_1\). Точно так же, поскольку \(\displaystyle {c_n}\) сходится к \(\displaystyle L\), существует целое число \(\displaystyle N_2\), такое что \(\displaystyle |c_n−L|<ε\) для всех \(\displaystyle n≥N_2\). По условию существует целое число \(\displaystyle N\), такое что \(\displaystyle a_n≤b_n≤c_n\) для всех \(\displaystyle n≥N\). Пусть \(\displaystyle M\) будет наибольшим из \(\displaystyle N_1,N_2\) и \(\displaystyle N\). Мы должны показать, что \(\displaystyle |b_n−L|<ε\) для всех \(\displaystyle n≥M\). Для всех \(\displaystyle n≥M\),
\[\displaystyle −ε<−|a_n−L|≤a_n−L≤b_n−L≤c_n−L≤|c_n−L|<ε\]
Следовательно, \(\displaystyle −ε
□
Пример \(\displaystyle \PageIndex{5}\): Использование теоремы о сжатии
Используйте теорему о сжатии, чтобы найти предел каждой из следующих последовательностей.
9n}\) расходится \text{ если } \displaystyle r≤−1\]Ограниченные последовательности
Обратимся теперь к одной из наиболее важных теорем, касающихся последовательностей: теореме о монотонной сходимости. Прежде чем сформулировать теорему, нам необходимо ввести некоторую терминологию и мотивацию. Начнем с определения того, что означает ограниченность последовательности.
Определение: связанные последовательности
Последовательность \(\displaystyle {a_n}\) ограничена выше , если существует действительное число \(\displaystyle M\), такое что
\(\displaystyle a_n≤M\)
для всех положительных целых чисел \(\displaystyle n\).
Последовательность \(\displaystyle {a_n}\) ограничена ниже , если существует действительное число \(\displaystyle M\) такое, что
\(\displaystyle M≤a_n\)
для всех положительных целых чисел \(\displaystyle п\).

Последовательность \(\displaystyle {a_n}\) является ограниченной последовательностью , если она ограничена сверху и снизу.
Если последовательность не ограничена, это 9n}\) — неограниченная последовательность.
Обсудим теперь связь между ограниченностью и сходимостью. Предположим, что последовательность \(\displaystyle {a_n}\) неограничена. Тогда оно не ограничено сверху, или не ограничено снизу, или и то, и другое. В любом случае существуют термины an, величина которых сколь угодно велика по мере того, как \(\displaystyle n\) становится больше. В результате последовательность \(\displaystyle {a_n}\) не может сходиться. Следовательно, ограниченность является необходимым условием сходимости последовательности.
Сходящиеся последовательности ограничены 9n}\) ограничено, но последовательность расходится, потому что последовательность колеблется между \(\displaystyle 1\) и \(\displaystyle −1\) и никогда не приближается к конечному числу. Обсудим теперь достаточное (но не необходимое) условие сходимости ограниченной последовательности.

Рассмотрим ограниченную последовательность \(\displaystyle {a_n}\). Предположим, что последовательность \(\displaystyle {a_n}\) возрастает. То есть \(\displaystyle a_1≤a_2≤a_3….\) Поскольку последовательность возрастает, члены не колеблются. Следовательно, есть две возможности. Последовательность может расходиться до бесконечности, а может и сходиться. Однако, поскольку последовательность ограничена, она ограничена сверху, и последовательность не может расходиться до бесконечности. Мы заключаем, что \(\displaystyle {a_n}\) сходится. Например, рассмотрим последовательность
\[\displaystyle {\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{4},\dfrac{4}{5},…}.\]
Поскольку эта последовательность возрастающая и ограниченная сверху, она сходится. Далее рассмотрим последовательность
\[\displaystyle {2,0,3,0,4,0,1,−\dfrac{1}{2},−\dfrac{1}{3},−\dfrac{ 1}{4},…}.\]
Несмотря на то, что последовательность возрастает не для всех значений \(\displaystyle n\), мы видим, что \(\displaystyle −1/2<−1/3<− 1/4<⋯\).
 Следовательно, начиная с восьмого члена, \(\displaystyle a_8=−1/2\), последовательность увеличивается. В этом случае мы говорим, что последовательность в конечном счете возрастает. Поскольку последовательность ограничена сверху, она сходится. Также верно, что если последовательность убывает (или в конце концов убывает) и ограничена снизу, она также сходится.
Следовательно, начиная с восьмого члена, \(\displaystyle a_8=−1/2\), последовательность увеличивается. В этом случае мы говорим, что последовательность в конечном счете возрастает. Поскольку последовательность ограничена сверху, она сходится. Также верно, что если последовательность убывает (или в конце концов убывает) и ограничена снизу, она также сходится.Определение
Последовательность \(\displaystyle {a_n}\) возрастает для всех \(\displaystyle n≥n_0\), если
\(\displaystyle a_n≤a)n+1\) для всех \(\ стиль отображения n≥n_0\).
Последовательность \(\displaystyle {a_n}\) убывает для всех \(\displaystyle n≥n_0\), если
\(\displaystyle a_n≥a_{n+1}\) для всех \(\displaystyle n ≥n_0\).
Последовательность \(\displaystyle {a_n}\) является монотонной последовательностью для всех \(\displaystyle n≥n_0\), если она возрастает для всех \(n≥n_0\) или убывает для все \(\displaystyle n≥n_0\).
Теперь у нас есть необходимые определения для формулировки теоремы о монотонной сходимости, которая дает достаточное условие сходимости последовательности.

Определение: теорема о монотонной сходимости
Если \(\displaystyle {a_n}\) является ограниченной последовательностью и существует натуральное число n0 такое, что \(\displaystyle {a_n}\) является монотонным для всех \(\displaystyle n ≥n_0\), то \(\displaystyle {a_n}\) сходится.
Доказательство этой теоремы выходит за рамки этого текста. Вместо этого мы приводим график, чтобы наглядно показать, почему эта теорема имеет смысл (рис. \(\PageIndex{6}\)).
Рисунок \(\PageIndex{6}\): Поскольку последовательность \(\displaystyle {a_n}\) возрастает и ограничена сверху, она должна сходиться.В следующем примере мы покажем, как можно использовать теорему о монотонной сходимости для доказательства сходимости последовательности.
Пример \(\displaystyle \PageIndex{6}\): Использование теоремы о монотонной сходимости
Для каждой из следующих последовательностей используйте теорему о монотонной сходимости, чтобы показать, что последовательность сходится, и найти ее предел.
 n}{n!}}\) 9n}{n!}=\dfrac{4}{n+1}⋅a_n≤a_n\) if \(\displaystyle n≥3.\)
n}{n!}}\) 9n}{n!}=\dfrac{4}{n+1}⋅a_n≤a_n\) if \(\displaystyle n≥3.\)Следовательно, последовательность убывает для всех \(\displaystyle n≥ 3\). Кроме того, последовательность ограничена снизу \(\displaystyle 0\), потому что \(\displaystyle 4n/n!≥0\) для всех положительных целых чисел \(\displaystyle n\). Следовательно, по теореме о монотонной сходимости последовательность сходится.
Чтобы найти предел, мы используем тот факт, что последовательность сходится, и пусть \(\displaystyle L=\lim_{n→∞}a_n\). Теперь обратите внимание на это важное наблюдение. Рассмотрим \(\displaystyle \lim_{n→∞}a_{n+1}\). С
\(\displaystyle {a_{n+1}}={a_2,a_3,a_4,…},\)
единственная разница между последовательностями \(\displaystyle {a_{n+1}}\) и \(\displaystyle {a_n}\) заключается в том, что в \(\displaystyle {a_{n+1}}\) отсутствует первый член. Поскольку конечное число членов не влияет на сходимость последовательности,
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}a_n=L.
 \)
\)Объединив этот факт с уравнением
\(\displaystyle a_{n+1}=\dfrac{4}{n+1}a_n\)
и взяв предел обеих частей уравнения
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}\dfrac{4}{n+1}a_n\),
можно сделать вывод, что
\ (\displaystyle L=0⋅L=0.\)
б. Записав первые несколько терминов,
\(\displaystyle {2,\dfrac{5}{4},\dfrac{41}{40},\dfrac{3281}{3280},…}.\)
мы можем предположить, что последовательность убывает и ограничена снизу \(\displaystyle 1\). Чтобы показать, что последовательность ограничена снизу \(\displaystyle 1\), мы можем показать, что
\(\displaystyle \dfrac{a_n}{2}+\dfrac{1}{2a_n}≥1.\) 92_н\).
Разделив обе части на \(\displaystyle 2a_n\), получим
\(\displaystyle \dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n.\)
Используя определение \(\displaystyle a_{n+1}\), мы заключаем, что
\(\displaystyle a_{n+1}=\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n\) .
Поскольку \(\displaystyle {a_n}\) ограничено снизу и убывает, по теореме о монотонной сходимости оно сходится.

Чтобы найти предел, пусть \(\displaystyle L=\lim_{n→∞}a_n\). Затем, используя рекуррентное соотношение и тот факт, что \(\displaystyle \lim_{n→∞}a_n=\lim_{n→∞}a_{n+1}\), мы имеем 92=1\), что подразумевает \(\displaystyle L=±1\). Поскольку все члены положительны, предел \(\displaystyle L=1\).
Упражнение \(\PageIndex{6}\)
Рассмотрим последовательность \(\displaystyle {a_n}\), определенную рекурсивно так, что \(\displaystyle a_1=1\), \(\displaystyle a_n=a_{n− 1}/2\). Используйте теорему о монотонной сходимости, чтобы показать, что эта последовательность сходится, и найти ее предел.
- Подсказка
Показать, что последовательность убывает и ограничена снизу.
- Ответить
\(\displaystyle 0\).
Определение: числа Фибоначчи. 2,\)
\(\displaystyle F_n=F_{n−1}+F_{n−2}.\)
Здесь мы рассмотрим свойства чисел Фибоначчи.

1. Запишите первые двадцать чисел Фибоначчи. 9н\). Используя начальные условия \(\displaystyle F_0\) и \(\displaystyle F_1\), определите значения констант \(\displaystyle c_1\) и \(\displaystyle c_2\) и запишите замкнутую формулу \(\displaystyle Ф_н\).
3. Используйте ответ в 2 c. чтобы показать, что
\[\displaystyle \lim_{n→∞}\dfrac{F_{n+1}}{F_n}=\dfrac{1+\sqrt{5}}{2}.\]
число \(\displaystyle ϕ=(1+\sqrt{5})/2\) известно как золотое сечение (рисунок и рисунок).
Рисунок \(\PageIndex{7}\): Семена подсолнуха имеют спиральные узоры, изгибающиеся влево и вправо. Количество спиралей в каждом направлении всегда является числом Фибоначчи — всегда. (кредит: модификация работы Эссдраса Кальдерана, Wikimedia Commons) Рисунок \(\PageIndex{8}\): пропорция золотого сечения встречается во многих известных образцах искусства и архитектуры. Древнегреческий храм, известный как Парфенон, был спроектирован с учетом этих пропорций, и это соотношение снова проявляется во многих мелких деталях. (кредит: модификация работы TravelingOtter, Flickr).
(кредит: модификация работы TravelingOtter, Flickr).Ключевые понятия
- Чтобы определить сходимость последовательности, заданной явной формулой \(\displaystyle a_n=f(n)\), мы используем свойства пределов для функций.
- Если \(\displaystyle {a_n}\) и \(\displaystyle {b_n}\) — сходящиеся последовательности, которые сходятся к A и B соответственно, а c — любое действительное число, то последовательность \ (\displaystyle {ca_n} \)сходится к c⋅A, последовательности {an±bn} сходятся к A±B, последовательность {an⋅bn} сходится к A⋅B, а последовательность {an/bn} сходится к A/B при условии B≠0. 9n}\) сходится тогда и только тогда, когда \(\displaystyle |r|<1\) или \(\displaystyle r=1\).
Глоссарий
- арифметическая последовательность
- последовательность, в которой разница между каждой парой последовательных членов одинакова, называется арифметической последовательностью
- ограниченный выше
- последовательность \(\displaystyle {a_n}\) ограничена сверху, если существует константа \(\displaystyle M\) такая, что \(\displaystyle a_n≤M\) для всех натуральных чисел \(\displaystyle n\)
- ограниченный снизу
- последовательность \(\displaystyle {a_n}\) ограничена снизу, если существует константа \(\displaystyle M\) такая, что \(\displaystyle M≤a_n\) для всех положительных целых чисел \(\displaystyle n\)
- ограниченная последовательность
- последовательность \(\displaystyle {a_n}\) является ограниченной, если существует константа \(\displaystyle M\) такая, что \(\displaystyle |a_n|≤M\) для всех положительных целых чисел \(\displaystyle n\)
- сходящаяся последовательность
- сходящаяся последовательность — это последовательность \(\displaystyle {a_n}\), для которой существует действительное число \(\displaystyle L\), такое что \(\displaystyle a_n\) сколь угодно близко к \(\displaystyle L\) пока \(\displaystyle n\) достаточно большой
- расходящаяся последовательность
- последовательность, которая не сходится, является расходящейся
- явная формула
- последовательность может быть определена явной формулой, такой что \(\displaystyle a_n=f(n)\)
- геометрическая последовательность
- последовательность \(\displaystyle {a_n}\), в которой отношение \(\displaystyle a_{n+1}/a_n\) одинаково для всех натуральных чисел \(\displaystyle n\), называется геометрической последовательностью
- индексная переменная
- нижний индекс, используемый для определения терминов в последовательности, называется индексом
- предел последовательности
- действительное число LL, к которому сходится последовательность, называется пределом последовательности
- монотонная последовательность
- возрастающая или убывающая последовательность
- рекуррентное соотношение
- рекуррентное отношение — это отношение, в котором термин \(a_n\) в последовательности определяется в терминах более ранних терминов в последовательности
- последовательность
- упорядоченный список чисел вида \(\displaystyle a_1,a_2,a_3,…\) является последовательностью
- срок
- число \(\displaystyle a_n\) в последовательности \(\displaystyle {a_n}\) называется \(\displaystyle n-м\) членом последовательности
- неограниченная последовательность
- последовательность, которая не ограничена, называется неограниченной
Авторы и авторство
4.


 2-1}{x+1} = \infty $$
2-1}{x+1} = \infty $$ Точка а принадлежит интервалу, на котором определена функция.
Точка а принадлежит интервалу, на котором определена функция.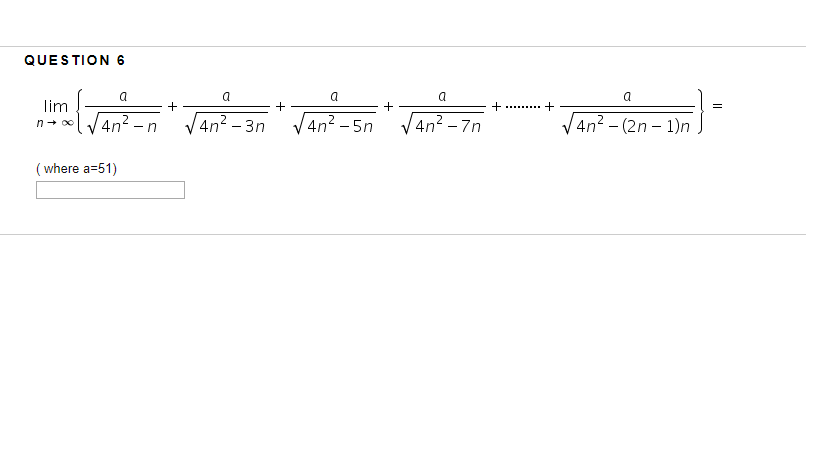 $$ Но дальше не знаю, что можно сделать, дайте хотя бы подсказку, кто увидит, спасибо.
$$ Но дальше не знаю, что можно сделать, дайте хотя бы подсказку, кто увидит, спасибо. {-2}$$
Я решил не удалять вопрос, если у кого-то возникнут трудности с этой или похожей задачей, ну и жалко уже было удалять.
{-2}$$
Я решил не удалять вопрос, если у кого-то возникнут трудности с этой или похожей задачей, ну и жалко уже было удалять.