Контрольные работы по «Макроэкономике» для студентов Филиала УдГУ в г
%PDF-1.5 % 1 0 obj > /Metadata 2 0 R /Pages 3 0 R /StructTreeRoot 4 0 R /Type /Catalog /Lang (ru-RU) >> endobj 5 0 obj /Creator /Producer /ModDate (D:20180326095227+04’00’) /Title >> endobj 2 0 obj > stream 2018-03-19T11:36:10+04:00Microsoft® Word 20102018-03-26T09:52:27+04:002018-03-26T09:52:27+04:00application/pdf



 32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
28 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
29 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
30 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
31 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
32 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
33 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
34 0 obj
>
/MediaBox [0 0 595.
32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
28 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
29 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
30 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
31 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
32 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
33 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
34 0 obj
>
/MediaBox [0 0 595.
 32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
42 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
43 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
44 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
45 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
46 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
47 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
48 0 obj
>
/MediaBox [0 0 595.
32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
42 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
43 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
44 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
45 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
46 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
47 0 obj
>
/MediaBox [0 0 595.32 842.04]
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/ExtGState >
>>
/Type /Page
>>
endobj
48 0 obj
>
/MediaBox [0 0 595.
6rg816N447Ȳųۑ]iIMDˬ6U#b-5Rg%-$䂓{‘ΛΛ\HL>gR}tm8pdvnLҵR_N`
Тесты . Экономическая теория: макроэкономика
1. Макроэкономика, как область экономической науки изучает:
а) роль государства в экономике;
б) глобальные тенденции экономического развития человечества;
в) процессы, происходящие в национальной экономике, взятой в целом;
г) процессы, происходящие в домашнем хозяйстве.
2. Укажите среди пар экономических целей противоречивую:
а) социально-экономическая стабильность и экономический рост;
б) ускорение экономического роста и охрана окружающей среды;
в) социально-экономическая стабильность и полная занятость;
г) экономический рост и ускорение НТП.
3. Предположим, что ВНП увеличился с 500 млрд. долл. до 600 млрд. долл., а дефлятор ВНП со 125 до 150. При таких условиях величина реального ВНП:
а) не изменится;
б) увеличится;
в) уменьшится;
г) все ответы неверны.
4. Для расчета вклада фирмы в созданный ВНП, исчисленного по сумме произведенной работниками добавленной стоимости, необходимо из рыночной стоимости созданной продукции вычесть: а) стоимость использованных ею сырья, материалов и полуфабрикатов;
б) все косвенные налоги, которые она выплачивает государству;
в) нераспределенную прибыль;
г) амортизацию;
д) объем продаж другим фирмам.
5. Если объем реального ВНП снизился на 6 %, а численность населения в том же году сократилась на 3 %, то:
а) реальный ВНП на душу населения снизился;
б) реальный ВНП на душу населения увеличился;
в) реальный ВНП увеличился, а номинальный снизился;
г) номинальный ВНП не изменился;
д) цены упали на 3 %.
6. Заработная плата учитывается при расчете:
а) ВНП по методу потока доходов;
б) ВНП по методу расходов;
в) чистого экспорта;
г) чистых субсидий государственным предприятиям.
7. Общая сумма доходов, приходящаяся на факторы производства в экономике – это:
а) личный располагаемый доход;
б) реальный валовой национальный продукт;
в) национальный доход;
г) национальное богатство;
д) чистый национальный продукт.
8. Трансфертные платежи – это:
а) коммунальные платежи;
б) рентные платежи;
в) выплаты домашним хозяйствам, не обусловленные предоставлением с их стороны товаров и услуг;
г) платежи при перевозке товаров.
9. Валовые частные инвестиции учитываются при расчете:
а) ВНП по методу потока доходов;
б) ВНП по методу потока расходов;
в) ЧНП по методу потока расходов;
г) располагаемого дохода;
д) личного дохода.
10. Чистый национальный продукт (ЧНП) – это:
а) стоимость произведенных за год товаров и услуг;
б) рыночная цена произведенных товаров минус стоимость потребленного сырья;
в) сумма всех доходов, полученных от производства продукции данного года;
г) валовой национальный продукт, уменьшенный на сумму амортизационных отчислений;
д) товары и услуги, покупаемые для конечного пользования.
11. Чистый национальный продукт минус косвенные налоги:
а) личный располагаемый доход;
б) реальный валовой национальный продукт;
в) национальный доход;
г) национальное богатство;
д) чистый национальный продукт.
12. В ВВП, подсчитанный по потоку расходов, не входят:
а) потребительские расходы;
б) чистый экспорт товаров и услуг
в) прибыль корпораций
г) государственные закупки товаров и услуг;
д) валовые частные инвестиции.
13. В ВНП, подсчитанный по потоку доходов, не входят:
а) заработная плата;
б) процент и другие доходы от собственности;
в) валовые частные инвестиции;
г) рентные платежи;
д) амортизационные отчисления.
14. Номинальный ВВП пересчитывается в реальный с помощью:
а) индекса потребительских цен;
б) индекса оптовых цен;
в) дефлятора ВВП;
г) всех вышеперечисленных индексов.
15. Все нижеперечисленное относится к проблемам макроэкономики, кроме:
а) инфляции;
б) дефицита государственного бюджета;
в) государственной налоговой политики;
г) размеров средних издержек производства.
Данный текст является ознакомительным фрагментом.
Преобразование номинального ВВП в реальный
Цели обучения
- Расчет реального ВВП на основе значений номинального ВВП
- Рассчитайте реальный темп роста ВВП
Теперь мы можем ответить на вопрос, который мы задавали ранее: учитывая номинальный ВВП для экономики США с 1960 по 2010 год, насколько фактически увеличился реальный ВВП?
Чтобы увидеть, насколько на самом деле увеличилось производство, нам нужно извлечь влияние более высоких цен на номинальный ВВП, чтобы у нас остался реальный ВВП, увеличение количества произведенных товаров и услуг. Это можно легко сделать, используя концепцию, известную как дефлятор ВВП. Дефлятор ВВП – это индекс цен, измеряющий среднюю цену всех товаров и услуг, включенных в экономику. Мы подробно изучим индексы цен и то, как они рассчитываются, когда узнаем больше об инфляции, но пока этого определения достаточно. Данные для дефлятора ВВП приведены в таблице 1 и показаны графически на рисунке 1.
Данные для дефлятора ВВП приведены в таблице 1 и показаны графически на рисунке 1.
| 1960 | 19,0 | Рисунок 1. Дефлятор ВВП США, 1960–2010 гг. Как и номинальный ВВП, дефлятор ВВП экспоненциально рос с 1960 по 2010 год. (Источник: BEA). |
| 1965 | 20,3 | |
| 1970 | 24,8 | |
| 1975 | 34,1 | |
| 1980 | 48,3 | |
| 1985 | 62,3 | |
| 1990 | 72,7 | |
| 1995 | 81,7 | |
| 2000 | 89,0 | |
| 2005 | 100,0 | |
| 2010 | 110,0 | |
| Источник: www.bea.gov, Национальные счета | ||
На рисунке 1 показано, что уровень цен, измеряемый дефлятором ВВП, резко вырос с 1960 года. Используя простую формулу темпов роста, которую мы объясняли на предыдущей странице, мы видим, что уровень цен в 2010 году составлял почти шесть раз выше, чем в 1960 (дефлятор на 2010 г. составил 110 против уровня 19 в 1960 г.). Ясно, что большая часть видимого роста номинального ВВП была обусловлена инфляцией, а не фактическим изменением количества произведенных товаров и услуг, иными словами, не реальным ВВП. Напомним, что номинальный ВВП может расти по двум причинам: увеличение объема производства и/или повышение цен. Что необходимо, так это извлечь рост цен из номинального ВВП, чтобы измерить только изменения выпуска . В конце концов, доллары, использовавшиеся для измерения номинального ВВП в 1960 долларов стоят больше, чем доллары, надутые в 1990 году, и индекс цен точно показывает, насколько больше. Эту корректировку легко выполнить, если вы используете формулу преобразования номинального значения в действительное, которую мы объясняли ранее:
Используя простую формулу темпов роста, которую мы объясняли на предыдущей странице, мы видим, что уровень цен в 2010 году составлял почти шесть раз выше, чем в 1960 (дефлятор на 2010 г. составил 110 против уровня 19 в 1960 г.). Ясно, что большая часть видимого роста номинального ВВП была обусловлена инфляцией, а не фактическим изменением количества произведенных товаров и услуг, иными словами, не реальным ВВП. Напомним, что номинальный ВВП может расти по двум причинам: увеличение объема производства и/или повышение цен. Что необходимо, так это извлечь рост цен из номинального ВВП, чтобы измерить только изменения выпуска . В конце концов, доллары, использовавшиеся для измерения номинального ВВП в 1960 долларов стоят больше, чем доллары, надутые в 1990 году, и индекс цен точно показывает, насколько больше. Эту корректировку легко выполнить, если вы используете формулу преобразования номинального значения в действительное, которую мы объясняли ранее:
[латекс]\текст{Номинальная стоимость выпуска}=\text{Цена}\times\text{Количество выпуска}[ /latex]
Взяв форму ВВП из этого уравнения:
[latex]\text{Номинальный ВВП}=\text{Дефлятор ВВП}\times\text{Реальный ВВП}[/latex]
Разделите обе части на Дефлятор ВВП:
[латекс]\displaystyle\text{Реальный ВВП}=\frac{\text{Номинальный ВВП}}{\text{Дефлятор ВВП}}[/latex]
По причинам, которые будут объяснены более подробно ниже, математически, индекс цен (например, дефлятор ВВП) – это двузначное десятичное число, например 1,00, 0,85 или 1,25. Поскольку некоторым людям трудно работать с десятичными дробями, когда публикуется индекс цен, его традиционно умножают на 100, чтобы получить целые числа, такие как 100, 85 или 125. Это означает, что когда мы «дефлируем» номинальные цифры, чтобы получить реальные цифры (путем деления номинала на индекс цен), нам также нужно помнить о том, чтобы разделить опубликованный индекс цен на 100, чтобы математика работала. Таким образом, формула становится:
Поскольку некоторым людям трудно работать с десятичными дробями, когда публикуется индекс цен, его традиционно умножают на 100, чтобы получить целые числа, такие как 100, 85 или 125. Это означает, что когда мы «дефлируем» номинальные цифры, чтобы получить реальные цифры (путем деления номинала на индекс цен), нам также нужно помнить о том, чтобы разделить опубликованный индекс цен на 100, чтобы математика работала. Таким образом, формула становится:
[латекс]\displaystyle\text{Реальный ВВП}=\frac{\text{Номинальный ВВП}}{\frac{\text{Дефлятор ВВП}}{100}}[/latex]
Вычисление реального ВВП
Давайте попрактикуемся в определении реального ВВП, взглянув на фактические данные о номинальном ВВП и дефляторе ВВП.
| Таблица 2. Номинальный ВВП США и дефлятор ВВП | ||
|---|---|---|
| Год | Номинальный ВВП (млрд долларов) | Дефлятор ВВП (2005 г. = 100) |
| 1960 | 543,3 | 19,0 |
| 1965 | 743,7 | 20,3 |
| 1970 | 1 075,9 | 24,8 |
| 1975 | 1 688,9 | 34,1 |
| 1980 | 2 862,5 | 48,3 |
| 1985 | 4 346,7 | 62,3 |
| 1990 | 5 979,6 | 72,7 |
| 1995 | 7 664,0 | 81,7 |
| 2000 | 10 289,7 | 89,0 |
| 2005 | 13 095,4 | 100,0 |
| 2010 | 14 958,3 | 110,0 |
Источник: www. bea.gov bea.gov | ||
Шаг 1. Посмотрите в Таблицу 2, чтобы увидеть, что в 1960 году номинальный ВВП составлял 543,3 миллиарда долларов, а индекс цен (дефлятор ВВП) равнялся 19..0.
Шаг 2. Для расчета реального ВВП в 1960 г. используйте формулу:
[латекс]\begin{array}{l}\text{Реальный ВВП}=\frac{\text{Номинальный ВВП}}{ \frac{\text{Индекс цен}}{100}}\\\text{Реальный ВВП}=\frac{543,3\text{миллиард}}{\frac{19}{100}}=\$2859,5\text{миллиард }\end{array}[/latex]
Мы сделаем это в двух частях, чтобы было понятно. Сначала настройте индекс цен: 19 разделить на [латекс]100 = 0,19[/латекс]. Затем разделите на номинальный ВВП:
[латекс]\frac{\$543,3\text{млрд}}{0,19}=\2859,5$\текст{млрд}[/латекс].
Шаг 3. Используйте ту же формулу для расчета реального ВВП в 1965 году.
[латекс]\begin{array}{l}\text{Реальный ВВП}=\frac{\text{Номинальный ВВП}}{ \frac{\text{Индекс цен}}{100}}\\\text{Реальный ВВП}=\frac{743,7\text{миллиард}}{\frac{20,3}{100}}=\$3663,5\text{миллиард }\end{array}[/latex]
Шаг 4. Продолжайте использовать эту формулу для расчета всех значений реального ВВП с 1960 по 2010 год. Расчеты и результаты показаны в таблице 3.
Продолжайте использовать эту формулу для расчета всех значений реального ВВП с 1960 по 2010 год. Расчеты и результаты показаны в таблице 3.
| Таблица 3. Преобразование номинального ВВП в реальный | ||||
|---|---|---|---|---|
| Год | Номинальный ВВП (млрд долларов) | Дефлятор ВВП (2005 г. = 100) | Расчеты | Реальный ВВП (млрд долларов 2005 г.) |
| 1960 | 543,3 | 19,0 | [латекс]\displaystyle\frac{543.3}{(\frac{19.0}{100})}[/latex] | Показать ответ |
| 1965 | 743,7 | 20,3 | 743,7 / (20,3/100) [латекс]\displaystyle\frac{743.7}{(\frac{20,3}{100})}[/latex] | Показать ответ |
| 1970 | 1075,9 | 24,8 | 1075,9 / (24,8/100) [латекс]\displaystyle\frac{1075,9}{(\frac{24,8}{100})}[/latex] | Показать ответ |
| 1975 | 1688,9 | 34,1 | 1688,9 / (34,1/100) [латекс]\displaystyle\frac{1688,9}{(\frac{34. 1}{100})}[/латекс] 1}{100})}[/латекс] | Показать ответ |
| 1980 | 2862,5 | 48,3 | 2862,5 / (48,3/100) [латекс]\displaystyle\frac{2862,5}{(\frac{48,3}{100})}[/latex] | Показать ответ |
| 1985 | 4346.7 | 62,3 | 4346,7 / (62,3/100) [латекс]\displaystyle\frac{4346,7}{(\frac{62,3}{100})}[/latex] | Показать ответ |
| 1990 | 5979,6 | 72,7 | 5979,6 / (72,7/100) [латекс]\displaystyle\frac{5979,6}{(\frac{72,7}{100})}[/latex] | Показать ответ |
| 1995 | 7664.0 | 82,0 | 7664 / (82,0/100) [латекс]\displaystyle\frac{7664,0}{(\frac{82,0}{100})}[/latex] | Показать ответ |
| 2000 | 10289. 7 7 | 89,0 | 10 289,7 / (89,0/100) [латекс]\displaystyle\frac{10 289,7}{(\frac{89,0}{100})}[/latex] | Показать ответ |
| 2005 | 13095.4 | 100,0 | 13 095,4 / (100,0/100) [латекс]\displaystyle\frac{13 095,4}{(\frac{100,0}{100})}[/latex] | Показать ответ |
| 2010 | 14958.3 | 110,0 | 14 958,3 / (110,0/100) [латекс]\displaystyle\frac{14,958.3}{(\frac{110.0}{100})}[/латекс] | Показать ответ |
| Источник: Бюро экономического анализа, www.bea.gov | ||||
Здесь следует отметить пару вещей. Всякий раз, когда вы вычисляете реальную статистику, один год (или период) играет особую роль. Он называется базовым годом (или базисным периодом). Базовый год — это год, цены которого используются для расчета реальной статистики (как мы показали на предыдущей странице). Например, когда мы рассчитываем реальный ВВП, мы берем количество товаров и услуг, произведенных за каждый год (например, 1960 или 1973 г.) и умножить их на их цены в базовом году (в данном случае 2005 г.), таким образом, мы получим показатель ВВП, в котором используются цены, не меняющиеся из года в год. Вот почему реальный ВВП помечен как «постоянные доллары» или «доллары 2005 года», что означает, что реальный ВВП построен с использованием цен, существовавших в 2005 году. Используемая формула:
Например, когда мы рассчитываем реальный ВВП, мы берем количество товаров и услуг, произведенных за каждый год (например, 1960 или 1973 г.) и умножить их на их цены в базовом году (в данном случае 2005 г.), таким образом, мы получим показатель ВВП, в котором используются цены, не меняющиеся из года в год. Вот почему реальный ВВП помечен как «постоянные доллары» или «доллары 2005 года», что означает, что реальный ВВП построен с использованием цен, существовавших в 2005 году. Используемая формула:
[латекс]\displaystyle\text{дефлятор ВВП}= \frac{\text{Номинальный ВВП}}{\text{Реальный ВВП}}\times{100}[/latex]
Преобразование формулы и использование данных за 2005 год:
[латекс]\begin{array}{l}\text{Реальный ВВП}=\frac{\text{Номинальный ВВП}}{\frac{\text{Индекс цен}}{100}}\\\text{ Реальный ВВП}=\frac{13 095,4\text{ миллиард}}{\frac{100}{100}}=\$13 095,4\text{ миллиард}\end{array}[/latex]
Сравнение реального ВВП и номинального ВВП для 2005, вы видите, что они одинаковы. Это не случайно. Это связано с тем, что 2005 год был выбран в качестве «базового года» в этом примере. Поскольку индекс цен в базовом году всегда имеет значение 100 (по определению), номинальный и реальный ВВП в базовом году всегда одинаковы. Посмотрите на данные за 2010 год.
Это не случайно. Это связано с тем, что 2005 год был выбран в качестве «базового года» в этом примере. Поскольку индекс цен в базовом году всегда имеет значение 100 (по определению), номинальный и реальный ВВП в базовом году всегда одинаковы. Посмотрите на данные за 2010 год.
[латекс]\begin{array}{l}\text{Реальный ВВП}=\frac{\text{Номинальный ВВП}}{\frac{\text{Индекс цен}}{100}}\\\text{ Реальный ВВП}=\frac{14 958,3\text{ миллиард}}{\frac{110}{100}}=\$13 598,5\text{ миллиард}\end{array}[/latex]
Используйте эти данные, чтобы сделать еще одно наблюдение : Пока инфляция положительна, то есть цены в среднем растут из года в год, реальный ВВП должен быть меньше номинального ВВП в любой год после базисного. Причина этого должна быть ясна: значение номинального ВВП «раздувается» инфляцией. Точно так же, пока инфляция положительна, реальный ВВП должен быть больше номинального ВВП в любой год, предшествующий базовому году.
Попробуйте
На рисунке 2 показаны номинальный и реальный ВВП США с 1960 года. Поскольку 2005 год является базовым, номинальные и реальные значения в этом году точно совпадают. Однако с течением времени рост номинального ВВП выглядит намного большим, чем рост реального ВВП (то есть линия номинального ВВП растет более круто, чем линия реального ВВП), потому что рост номинального ВВП преувеличен наличием инфляции. , особенно в 1970-е гг.
Поскольку 2005 год является базовым, номинальные и реальные значения в этом году точно совпадают. Однако с течением времени рост номинального ВВП выглядит намного большим, чем рост реального ВВП (то есть линия номинального ВВП растет более круто, чем линия реального ВВП), потому что рост номинального ВВП преувеличен наличием инфляции. , особенно в 1970-е гг.
Рисунок 2. Номинальный и реальный ВВП США, 1960–2012. Красная линия показывает ВВП США в номинальных долларах. Черная линия измеряет ВВП США в реальных долларах, где все долларовые значения были конвертированы в доллары 2005 года. Поскольку реальный ВВП выражается в долларах 2005 г., две линии пересекаются в 2005 г. Однако реальный ВВП окажется выше номинального ВВП в годы до 2005 г., поскольку доллары в 2005 г. стоили меньше, чем в предыдущие годы. И наоборот, реальный ВВП окажется ниже после 2005 г., поскольку в 2005 г. доллары стоили больше, чем в последующие годы.
Вернемся к изначально заданному вопросу: насколько вырос ВВП в реальном выражении? Какими были темпы роста реального ВВП с 1960 по 2010 г. ? Чтобы найти реальный темп роста, мы применяем формулу процентного изменения:
? Чтобы найти реальный темп роста, мы применяем формулу процентного изменения:
[латекс]\displaystyle\frac{2010\text{реальный ВВП}-1960\text{реальный ВВП}}{1960\text{реальный ВВП}} \times{100}=\text{ процентное изменение}[/latex]
[латекс]\displaystyle\frac{13 598,5–2 859,5}{2 859,5}\times{100}=376\text{ процент}[/latex]
Другими словами, экономика США увеличила реальное производство товаров и услуг почти в четыре раза (т.е. на 376%) с 1960. Конечно, это занижает материальное улучшение, поскольку оно не отражает улучшения качества продуктов и изобретения новых продуктов.
Для коротких периодов времени есть более быстрый способ приблизительно ответить на этот вопрос, используя еще один математический прием. Помните, что номинальный ВВП увеличивается по двум причинам: во-первых, из-за роста цен, а во-вторых, из-за увеличения реального ВВП. Другими словами, процентное увеличение номинального ВВП (приблизительно) равно процентному увеличению цен плюс процентное увеличение реального ВВП.
Выразив это уравнением,
[латекс]\%{\text{изменение номинального ВВП}}=\%{\text{изменение цен}}+\%{\text{изменение реального ВВП}} [/latex]
Вычитание % изменения цен с обеих сторон дает:
[латекс]\%{\text{изменение номинального ВВП}}-\%{\text{изменение цен}}=\%{\ text{ изменение реального ВВП}}[/latex]
Таким образом, темп роста (процентное изменение) реального ВВП равен темпу роста номинального ВВП (процентное изменение стоимости) минус темп роста цен (процентное изменение ВВП дефлятор).
Два способа расчета темпов роста
Давайте посмотрим на нижние числа из следующей таблицы:
| Год | Номинальный ВВП | Дефлятор ВВП | Реальный ВВП |
| 2005 | $13095,4 | 100 | $13095,4 |
| 2010 | 14958,3 $ | 110 | 13598,5 $ |
Метод 1: использование формулы простого темпа роста
(реальный ВВП в 2010 г. – реальный ВВП в 2005 г.) / реальный ВВП в 2005 г. = рост реального ВВП / $13 095,5 = 4%
– реальный ВВП в 2005 г.) / реальный ВВП в 2005 г. = рост реального ВВП / $13 095,5 = 4%
Метод 2: использование математического трюка
Рост номинального ВВП – Рост ВВП Дефлятор = Рост реального ВВП
Подстановка чисел и использование формулы простого темпа роста дает
]\frac{($14,958,3-$13 095,4)}{$13095,4}-(\frac{(110-100)}{100})=14,2\%-10\%=4,2\%[/latex]
Обратите внимание, что метод 2 является лишь быстрым приближением к методу 1.
Попробуйте
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Ответы на задание 4
Ответы на задание 4Проблема 1:
мпс = ДЦ/ДДИ = изменение потребительских расходов, деленное на изменение реальных располагаемых доход.
C — потребительские расходы
DI — реальный располагаемый доход
Для этой проблемы обратите внимание на таблицу, что каждое изменение одноразовых
доход 10 приводит к изменению
в потреблении 5. Следовательно, ПДК = 5/10 = 0,50
Следовательно, ПДК = 5/10 = 0,50
Понимая, что C линейна, мы знаем наклон и точку пересечения. Так, используя линейную зависимость
C = a + mpcDI получаем уравнение C = 5 + 0,5DI
а — автономное потребление или потребление, не зависящее от ЦИ.
mpc — предельная склонность к потреблению.
Помните,
ДИ = С+С. Следовательно, S = DI-C . Книга просит вас
создайте таблицу, как показано ниже:
| ДИ (млн долларов США) | C (млн долларов) | С (млн долларов) |
S = -a+mpsDI где а — автономное потребление, а -a = автономные сбережения
или S = -5+0,5DI
для этого набора данных.
mps = предельная склонность к сбережению = DS/DDI
Примечание. 1 = [DC/DDI] + [ДС/ДДИ]
1 = мпс+мпс
Следовательно, для этой задачи м/с = 1-0,5 = 0,5.
Обратите внимание, мы также можем прочитать это из таблицы.
Задача 2:
Помните, что AE = А 0 + mpcY
где A 0 = точка пересечения линии AE = все автономные
расходы. В этом случае I и G равны .
автономный. mpc = наклон линии AE.
Кроме того, без налогов DI = Y. Все в миллиардах долларов.
А. От график, А 0 = 2,0 миллиарда долларов.
Б. На графике наклон линии AE составляет 3,6/6,0. = 0,6
К. От график, когда ВВП составляет 6 миллиардов долларов, AE = 5,6 долларов. миллиард.
Д.
Из этой информации мы знаем уравнение для AE: AE = $2+0,6Y 90 567.
Следовательно, если Y = 4 доллара, то AE = 4,4 доллара [поскольку AE(4) = 2 доллара + 0,6 (4 доллара) = 2$+2,4$ = 4,4$]
Это означает, что AE больше, чем Y, когда Y = $4. Итак, есть незапланированное сокращение запасов.
Е. Если Y = 6 долларов, тогда AE = 2 + 0,6 (6 долларов) = 5,6 долларов, как мы видели. Произошло незапланированное увеличение складских запасов.
F. Множитель: где k = [DY/DA 0 ].
Мультипликатор расходов измеряет эффект на равновесии Y изменения автономных расходов.
Числовое значение k = 1/[1-mpc] = 1/mps.
Для нашей задачи k = 1/[1-0,6] = 1/0,4 = 2,5
Проблема 3
У нас есть следующая информация (в миллиардах долларов):
автономное потребление = a = $100
ПДК = 0,9
I = 460 долларов
G = 400 долларов США
Tx = 400 долларов (нам говорят, что эти
являются самостоятельными налогами, поскольку они не зависят от дохода.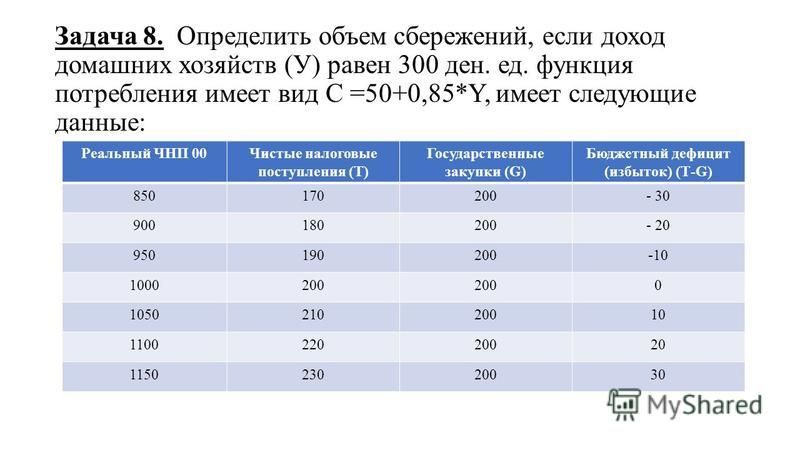 )
)
А. Таким образом, C = 100 долл. США + 0,9 DI , где DI = Y–Tx. DI — располагаемый доход, Y — реальный ВВП
заменив DI, а затем Tx, C = 100 долларов + 0,9 (Y-Tx) = 100–0,9 долларов США (400 долларов США) + 0,9 Y 90 567
или C = -260 долл. США + 0,9 года 90 567.
Б. Мы также знаем, что AE = C+I+G или, в данном случае, AE = -260$+0,9Y+460$+400$ .
упрощение: AE = 860-260 долларов + 0,9 года
вычитание AE = 600 долларов США + 0,9 Y 90 567
C. В равновесии AE = Y. Итак, получаем:
600 долларов + 0,9 Y = 90 567 Y
Равновесие Y = 600 долл. США/(1-0,1) = 600 долл. США (10) = 6000 долларов
Альтернативный подход: Рассчитайте общие автономные расходы: = 600 долларов
Рассчитайте значение множителя: k = 1/(1-mpc). Для этой проблемы к = 10,
Равновесие Y = kA = 10 (600 долл. США) = 6000 долл. США
США) = 6000 долл. США
D. Если я упаду с от 460 до 360 долларов, но больше ничего не меняется, мы можно переделать функцию AE, а затем решить для равновесия:
AE = C+I+G = -260$+0,9Y+360$+400$ = 500$+0,9Y
Найдите равновесие: AE = Y 90 567.
500 долларов + 0,9 Y = 90 567 Y
Равновесие Y = $500/(1-0,9) = 10 (500 долларов США) = 5000 долларов США. Поэтому 100 долларов падение I приводит к падению на 1000 долларов в Equilibrium Y.
Альтернативный подход: $100
снижение I приводит к снижению общих автономных расходов на 100 долларов. Поэтому,
так как мы знаем, что
множитель k = 10, мы знаем:
DEравновесие Y=k DA = k(-100$)=10(-100$)= -1000$ . Следовательно, равновесие Y выпадает из от 6000 до 5000 долларов.
Проблема 4
Ответ на этот вопрос свяжет анализ АЭ в задаче 3 с
диаграмма AD-AS, которую мы использовали ранее.
Мы начнем с ответа на Задачу 3, часть C. В этот момент у нас было равновесие Y, равное 6000 долларов, при I = 460 долларов.
Теперь, если I поднимется с 460 до 560 долларов, мы можем пересчитать AE и найти
равновесие. Но, мы уже знаем, используя альтернативный подход
изложено в
Задача 3, часть D: увеличение I на 100 долларов приведет к увеличению на 1000 долларов.
в равновесии Y за счет эффекта мультипликатора.
DEравновесие Y=k DA = k(100$)=10(100$)= 1000$. Следовательно, Equilibrium Y поднимается с 6000 долларов. до 7000 долларов.
Мы можем увидеть результаты этого на диаграмме AE ниже.
Как показано на графике, равновесие повышается
от Y = 6000 долларов в точке E до Y = 7000 долларов в точке F.
Сдвиг линий от AE(Y) до AE(Y)’ вызван
увеличение I, о чем свидетельствует увеличение автономных расходов от
от А до А’.
Поскольку AE смещается на приведенной выше диаграмме, AD смещается вправо на диаграмме AD-AS, как показано ниже:
Точка F на схеме AD-AS выше соответствует
к точке F на диаграмме АЭ. Обратите внимание, что новое равновесное значение
на схеме АЭ
Обратите внимание, что новое равновесное значение
на схеме АЭ
не является краткосрочным равновесием в AD-AS
схема; равновесие AE=Y показывает точку совокупного спроса, а не полного
равновесие в пространстве AD-AS.
A. Объем спроса на реальный ВВП
поднимается до 7000 долларов.
B. В краткосрочной перспективе реальный ВВП не
подняться до 7000 долларов, но до уровня в точке G на приведенной выше диаграмме.
Начинается рост цен, и это сокращает величину спроса на реальный ВВП.
несколько больше, чем это было бы, 7000 долларов, если бы уровень цен был
постоянная при P = 100.
C. В долгосрочной перспективе цены будут расти
экономика достигает долгосрочного равновесия в точке H, при этом уровень цен
выше, чем P = 100, но такой же реальный ВВП, как у нас
изначально стоил 6000 долларов.
D. Уровень цен растет в краткосрочной перспективе
до уровня в точке G.
E. Уровень цен растет в долгосрочной перспективе
до уровня в точке H. В точке H реальная заработная плата такая же, как
это было первоначально, в точке Е.
В точке H реальная заработная плата такая же, как
это было первоначально, в точке Е.
ПРИМЕЧАНИЕ. Хотя вы
не спрашивали об этом, вы должны понимать, что горизонтальная ось на обоих
вышеприведенных диаграмм в том же реальном ВВП.
Следовательно, для достижения краткосрочного равновесия при
точка G на нижней диаграмме, мы должны иметь AE(Y)’ на верхней диаграмме
несколько сместится назад по мере роста уровня цен.
Чем выше уровень цен, тем больше объем спроса.
немного понизить, от F до G.
Глава 12:
Задача 1:
Данные для задачи: mpc = 0,9
I = 50 долларов
G = $40
Пересылка = 40 долл. США 90 567
Мы знаем приведенную форму уравнения для нахождения равновесия реальный ВВП:
Равновесие Y = кА и что DY = кДА
Если ПДК=0,9, то k = 1/(1-0,9) = 10
A. Если G упадет с 40 до 30 миллиардов долларов,
A упал на 10 миллиардов долларов с 90 567
Если G упадет с 40 до 30 миллиардов долларов,
A упал на 10 миллиардов долларов с 90 567
A = a+I+G-mpcTx для этой задачи; падение в G является падением в A.
Таким образом, линия AE в этом случае смещается вниз на 10 миллиардов долларов.
B. Множитель по-прежнему k = 10.
Следовательно, уменьшение A на 10 миллиардов долларов приведет к падению 90 567.
равновесия Y на 100 миллиардов долларов, поскольку DY = kDA.
[100 долларов = 10 [10 миллиардов долларов]]
C. В этом случае, если G сохраняется в 40 миллиардов долларов, но Tx сократился до 30 миллиардов долларов, мы имеем:
DA = -mpcDTx = -0,9[-$10 миллиард] = 9 миллиардов долларов
Падение налогов на 10 миллиардов долларов приводит к увеличению автономных
расходы в размере 9 миллиардов долларов, как
потребители увеличивают свои потребительские расходы. Линия AE смещается до на 9 миллиардов долларов.
D. Используя обычную формулу, DY = кДА, имеем ДГ = 10[$9миллиард] = 90 миллиардов долларов.
Книга запрашивает мультипликатор паушального налога. Это можно найти таким образом:
DY = kDA = k[-mpcDTx] = [-mpc/(1-mpc)]DTx
Таким образом, мультипликатор единовременного налога равен -mpc/(1-mpc) = -0,9/(1-0,9) = 9 .
На самом деле нет необходимости вычислять этот срок, так как использование DY
= кДА мы можем
получить результат. Нам просто нужно помнить, как меняется A при изменении Tx.
E. Если
правительство сокращает Tx на 10 миллиардов долларов и G на 10 миллиардов долларов одновременно
время, мы получаем
мультипликативный эффект сбалансированного бюджета .
Обратите внимание: если G и Tx изменяются, то изменение A будет: .
DA= DG-mpcDTx
но DG = DTx = -$10
миллиарда в данном случае.
Таким образом, DA = -(1-mpc)10 миллиардов долларов = -1 миллиард долларов.
Таким образом, чистый эффект на совокупные расходы равен 90 567.
падение на 1 миллиард долларов, когда и Tx, и G сокращаются на 10 миллиардов долларов.
Обратите внимание, что это подразумевает [заменив DA а затем к]:
DY = kDA = k[(1-mpc)(-$10
миллиард)] = [1/(1-mpc)][1-mpc][-10 миллиардов долларов] = — 10 миллиардов долларов.
Это эффект мультипликатора сбалансированного бюджета : с единовременной выплатой
только налоги, если мы изменим G и Tx
на ту же величину, то Y изменится на эту же величину. Множитель
эффект снижен до
1 = (1-мпк)/(1-мпк).
Задача 2:
A. и B. Как мы видели выше, DY
= kDA, поэтому, если A упадет на 10 миллиардов долларов, Y
упадет на 100 миллиардов долларов. Следовательно, линия AE сдвинется вниз на
10 миллиардов долларов. Это означает, что кривая AD сдвинется влево на
100 миллиардов долларов за счет эффекта мультипликатора.
Это означает, что кривая AD сдвинется влево на
100 миллиардов долларов за счет эффекта мультипликатора.
C. С восходящим краткосрочным кривая совокупного предложения, реальный ВВП увеличится менее чем на 100 млрд долл. при новом краткосрочном равновесии.
D. В долгосрочной перспективе реальный ВВП вернуться к исходному уровню, поскольку владельцы ресурсов завышают номинальную заработную плату до восстановить реальную заработную плату.
E. В краткосрочном периоде уровень цен поднимается.
F. В долгосрочной перспективе уровень цен поднимается.
Задача 3:
A. В точке a, P = 150, реальный ВВП = 600
B. Немедленным эффектом является ход к пункту b, P = 160, реальный ВВП = около 650.
C. Система перемещается в точку d, более низкая цена, чем в b, более высокий реальный ВВП, чем в b.
D. Продолжение сдвига
кривых SAS приводит систему к точке e, более низкому уровню цен, чем
в
Продолжение сдвига
кривых SAS приводит систему к точке e, более низкому уровню цен, чем
в
точка а, и более высокий реальный ВВП, чем в точке а.
Однако это предполагает большой побочный эффект предложения от
снижение налогов.
3. 3. Нам дано следующее данные о потребительских расходах в простой экономике.
Располагаемый доход
Потребление Расходы Экономия
0
$1,0 млн — $1,0 млн 90 567
1 миллион долларов
1,75 млн долларов США -0,75 млн долларов США 90 567
2 миллиона долларов
2,5
-0,50
3 миллиона долларов
3,25
-0,25
4 миллиона долларов
4.0
0,0
5 миллионов долларов
4,75
0,25
6 миллионов долларов
5,50
0,50
7 миллионов долларов
6,25
0,75
8 миллионов долларов
7.00
1.0
9 миллионов долларов
7,75
1,25
10 миллионов долларов
8. 50
1,50
50
1,50
A. Определение ПДК. Предполагая, что она постоянна, рассчитать его и использовать для заполнения остальной части таблицы. Определять множитель. Какова его ценность для этого примера?
Предельная склонность к потребителю: изменение потребительских расходов, вызванное изменением располагаемого доход.
ПДК = 0,75
B. Налоги и переводы не взимаются. платежи или амортизация в этой модели, на данный момент. Но, у нас есть следующие дополнительные данные:
Инвестиционные расходы = 2 миллиона долларов
Государственные расходы = 0,5 миллиона долларов {только
Федеральный, без штата и
Местный}
Экспорт = $3 млн
Импорт = 1 миллион долларов
Учитывая эту информацию, каково равновесие
уровень ВВП?
Автономные расходы = А = а+I+G+X-IM
a = расходы на автономное потребление = 1 миллион долларов, из таблицы. Поэтому,
используя другие данные
Поэтому,
используя другие данные
дано в задаче:
А = 1+2+0,5+3-1 = 5,5
k = 1/(1-mpc) = 1/(1-0,75) = 4
Равновесие Y = kA = 4[5,5] = 22 миллиона долларов.
C. Экономисты, работающие в Департаменте Министерства торговли прогнозируют, что в следующем году импорт вырастет на 2 млн долларов, а экспорт вырастет всего на 0,5 млн долларов. Предполагая, что инвестиции государственные расходы остаются прежними, а функция потребления остается прежним:
а. Каким будет новое равновесие уровень ВВП в следующем году, если эти экономисты правильно спрогнозировали?
DA = DX — DIM = 0,5 -2,0 = -1,5 миллиона долларов.
Поскольку DY = kDA = 4[-1,5 миллиона долларов] = -6 миллионов долларов. Поэтому новый уровень реального Требуемый ВВП составляет
22 миллиона долларов — 6 миллионов долларов = 16 миллионов долларов.
б. Какой будет уровень потребительских расходов при этом новом равновесном ВВП? Что будет новый уровень сбережений? Верно ли, что сбережения равны инвестициям? Объяснять.
C = 1+0,75Y = 1 + 0,75 (16 миллионов долларов) = 13 миллионов долларов.
S = -1+0,25Y = -1 + 0,25 (16 миллионов долларов) = 3 миллиона долларов.
Нет, I = S+(Tx-G)-(X-IM), как и раньше. Но в этой задаче Tx = 0.
I = 3 доллара — 0,5 -0,5 = 2 доллара, как мы видим выше.
S+(Tx-G)-(X-IM) равняется ресурсам, доступным для использования инвесторами; т.е.
общая экономия на открытом воздухе
экономика. В равновесии инвестиции равны этому общему уровню сбережений.
D. [Чтобы ответить на этот вопрос, мы начните с данных и результатов в (B) и игнорируйте то, что происходило в (С).]
Большинство членов Конгресса
согласны с тем, что федеральное правительство уже достаточно долго имеет дефицит, и
что необходимо принять меры для его ликвидации. Обсуждались два плана.
Один говорит о сокращении государственных расходов с нынешнего уровня в 0,5 миллиона долларов.
до нуля. Другой говорит, что налоги должны быть повышены до тех пор, пока бюджет не будет
сбалансированный; предполагая только автономные налоги (иногда называемые паушальными
налоги), это означало бы, что налоги должны быть повышены с их нынешнего уровня.
от нуля до 0,5 млн долларов.
Обсуждались два плана.
Один говорит о сокращении государственных расходов с нынешнего уровня в 0,5 миллиона долларов.
до нуля. Другой говорит, что налоги должны быть повышены до тех пор, пока бюджет не будет
сбалансированный; предполагая только автономные налоги (иногда называемые паушальными
налоги), это означало бы, что налоги должны быть повышены с их нынешнего уровня.
от нуля до 0,5 млн долларов.
а. Протестируйте каждый
политики путем нахождения нового равновесного уровня ВВП, который будет достигнут каждым из них.
Почему равновесные уровни ВВП различаются?
Если G вырезать
от 0,5 доллара до нуля, тогда DA = 0,5 миллиона долларов, и
ДЯ
= kDA = 4[0,5] = 2 миллиона долларов.
Таким образом, новое равновесие составит 20 миллионов долларов.
Если Tx поднимается из от 0 до 0,5 млн долларов, тогда DA = -mpcDTx = -0,75[0,5 миллиона долларов] = -0,375 миллиона долларов.
Следовательно, ДГ
= kDA = 4[-0,375 млн долларов] = — 1,5 млн долларов.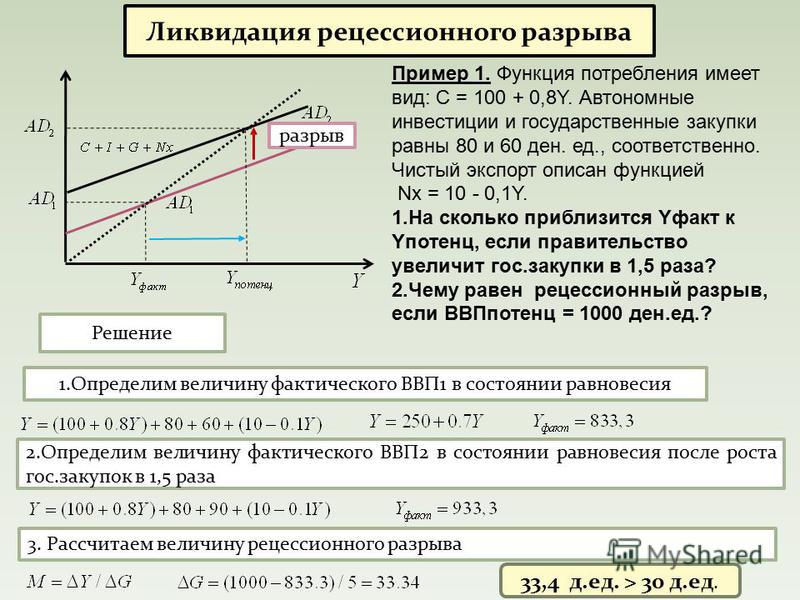 Таким образом, новое равновесие составит 20,5 млн долларов.
Таким образом, новое равновесие составит 20,5 млн долларов.
Равновесия отличаются потому что налоги действуют через ПДК на потребление. Увеличение налогов в размере 0,5 млн долларов приводит к сокращению автономных расходов всего на 0,375 млн долларов, или 75% от увеличения налогов.
б. Обсудить последствия каждой политики для состава равновесного ВВП, т. е. как изменяется доля различных товаров, произведенных и проданных, при каждая схема, и кто их покупает?.
В первом случае, когда G падает до нуля, у нас есть: C = 1 + 0,75 Y = 1 + 0,75 [20 миллионов долларов] = 16 миллионов долларов.
Во втором случае, когда Tx увеличен до 0,5 миллиона долларов, C = 1 + 0,75 [Y-Tx} = 1 + 0,75 [20,5 доллара — 0,5 доллара] = 16 миллионов долларов.
Следовательно, потребители
иметь одинаковый уровень расходов в каждом случае. Но во втором случае,
правительство
покупает $0,5 млн в
продукции, оплаченной налогами. Во втором случае правительство
никакой роли в экономике.
Во втором случае правительство
никакой роли в экономике.
4. Нам предоставлены следующие данные для простая экономия.
[В миллионах долларов]
Расходы на потребление = C = a(r)+0,8*DI
a(r)= 100-5r где r — проценты
ставка в процентах
[a(r), расходы на автономное потребление, является компонентом потребления
расходы , которые не зависят от DI, , но
зависит от процентной ставки.]
Инвестиции = I(r) = 200 — 10r
Расходы автономного правительства = G = 100
Автономные налоги = Tx = 50
Автономный экспорт = X = 200
Автономный импорт = IM = 175
r = 10 процентов
A. За каждый процент увеличения в процентной ставке, насколько изменятся потребительские расходы? В каком направлении? Приведите два примера такого типа потребления. расходы.
Каждый раз r
увеличивается на 1, a(r) падает на 5 миллионов долларов.
Автомобили, Бытовая техника.
B. Используйте приведенную выше информацию, чтобы
Запишите общие автономные расходы как функцию процентной ставки.
Укажите его значение при r = 10.
A(r) = a(r)+I(r)+G+X-IM-mpcTx = 100-5r + 200-10r
+100+200-175-0,8(50)
= 385-15р
А(r=10) = 385-150 = 235
C. Рассчитайте равновесный уровень
ВВП.
Y=kA(r) = kA(r=10) = 5[235] = $1175
D. Если процентные ставки вырастут с 10 процентов до 12 процентов, найти новый уровень автономного потребления, новый уровень инвестиций и новой стоимости автономных расходов? Что новый равновесный уровень ВВП?
а(r=12) = 100-5(12) = 40
I(r-12) = 200-10(12) = 80
А(r=12) = 385-15(12) = 180 = 205
Y = кА(r=12) = 5[205] = 1025 долл. США
E. Если процентные ставки упадут до 8 процентов,
найти новый уровень автономного потребления, новый уровень инвестиций,
и новый уровень автономных
расходы. Каков новый равновесный уровень ВВП?
Каков новый равновесный уровень ВВП?
а(г=8) = 100 -5(8) = 60
I(r=8) = 200 — 10(8) = 120
А(r=8) = 385-15(8) = 265
Д = кА(r=8) = 5[265] = $1325
5. Нам предоставляется следующая информация
об хозяйстве:
[В миллионах долларов]
Расходы на потребление = C = a(r)+0,8*DI
a(r)= 200-10r где r —
процентная ставка в процентах
[a(r), автономное потребление
расходы – это составляющая потребительских расходов, которая не зависит
на ДИ, но зависит от процентной ставки.]
Инвестиционные расходы = I(r) = 300 — 15r
Расходы автономного правительства = G = 500
Автономные налоги = T0 = 50
Автономный экспорт = X = 200
Автономный импорт = IM = 175
r = 10 процентов
DI = Y — Налоги
Y = реальный ВВП
A. Найти равновесный реальный ВВП для
данные приведены выше.
Найти равновесный реальный ВВП для
данные приведены выше.
A(r) = a(r)+I(r)+G+X-IM-mpcTx = 200-10r+300-15r+500+200-175-0,8(50)
= 985-25р
A(r=10) = 985-250 = 735
Y = кА(r=10) = 5[735] = 3675 долл. США
B. В каком состоянии находится правительство? бюджет? Рассчитайте профицит или дефицит.
Tx-G = 50-500 = -450. Там дефицит составляет 450 миллионов долларов.
C. Конгресс принимает решение учредить
подоходный налог в этой экономике, чтобы сбалансировать государственный бюджет.
Государственные расходы не изменятся, а вместо
наличия только автономных налогов уровень налога будет
определяется по следующему уравнению:
Налоги = T 0 + т*г
Где T 0 = 50, как указано выше, и налоговая ставка, t = 0,25
а.
Запишите уравнение для мультипликатора с подоходным налогом.
При подоходном налоге мультипликатор расходов становится k’ = 1/[1-mpc(1-t)] .
б. Для этой конкретной проблемы, каково значение мультипликатора расходов после введения налога на прибыль?
k’ = 1/[1-mpc(1-t)] = 1/[1-0,8+0,2]=2,5 В этой задаче мультипликатор расходов уменьшается вдвое за счет подоходного налога.
c. Найдите равновесный реальный ВВП после введения налога на прибыль.
Y = k’A(r) = 2,5[735] = 1837,5 миллионов долларов. Нет никаких изменений ни в
автономные переменные, но наклон AE
линия уменьшается.
d. Как изменило ли введение подоходного налога сальдо государственного бюджета; соответствовал ли подоходный налог цель политики, поставленная Конгрессом? Объяснять.
При подоходном налоге Y = 1837,5 долл. США, поэтому Tx = 50 + 0,25 (1837,5 долл. США). = 50 + 459,375 = 509,375 долларов США.
Незначительного профицита нет, так что цель почти достигнута.
