Преобразуйте выражение sin a ctg a: Ответы: Преобразуйте выражение:sin a ctg a…

Внеклассный урок — Формулы приведения для тригонометрических функций

Формулы приведения для тригонометрических функций

Формулы приведения – это формулы, позволяющие упростить сложные выражения тригонометрической функции.

Выражения типа π + t,  3π/2 – t,  π/2 + t и т.п. можно упростить настолько, что они будут состоять лишь из одного аргумента t. В предыдущих разделах мы имели дело с несколькими такими упрощениями – например, sin (π + t) = –sin t.

Формул приведения очень много. Запомнить их трудно – но самое главное, в этом нет необходимости. Достаточно запомнить одно-единственное правило – и вы легко сможете самостоятельно выводить формулы и упрощать выражения.

 

Правило приведения:

Для выражений π + t,   π – t,   2π + t,   2π – t	Для выражений π/2 + t,   π/2 – t,   3π/2 + t,  3π/2 – t
1) В приведенном выражении следует сохранить тригонометрическую функцию преобразуемого выражения. 2) Перед полученной функцией следует поставить тот знак, который имела бы преобразуемая функция при условии, что 0 < t < π/2.	1) В приведенном выражении следует изменить тригонометрическую функцию преобразуемого выражения на противоположную. 2) Перед полученной функцией следует поставить тот знак, который имела бы преобразуемая функция при условии, что 0 < t < π/2.

Обратите внимание: в левом и правом столбцах различаются только первые пункты правила. Вторые пункты абсолютно идентичны.

 

Пример 1: Надо преобразовать выражение cos (π + t).

Решение.

Следуем правилу:

1) Выражение не имеет дроби – значит, применяем левое правило. То есть функция после приведения остается прежней:

cos (π + t) = cos t.

2) Осталось определиться со знаком полученной функции.
Если предположить, что аргумент t больше нуля и меньше π/2, то π + t – это аргумент третьей четверти (то есть отмерили полукруг от точки А, а потом еще прошли дугу t длиной меньше π/2 и оказались в третьей четверти).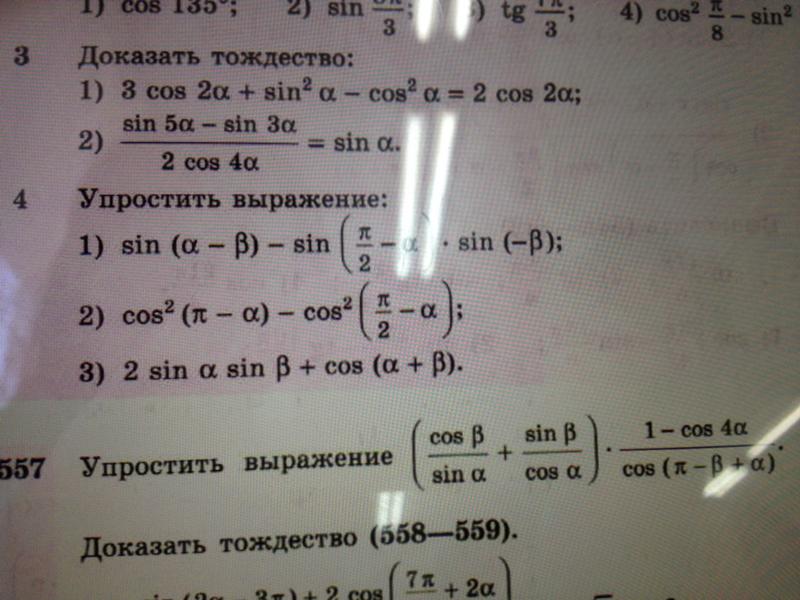 А в третьей четверти косинус имеет знак минус. Значит, после преобразования наша функция обрела следующий тождественный вид:

cos (π + t) = –cos t.

Пример решен.

 

Пример 2: Надо преобразовать выражение sin (3π/2 – t).

Решение.

Следуем правилу:

1) Выражение имеет дробь – поэтому применяем правое правило. То есть функция меняется на обратную:

sin (3π/2 – t) = cos t

2) Теперь выясним, с каким знаком должно быть наше приведенное выражение. Снова предположим, что 0 < t < π/2. Тогда аргумент 3π/2 – t находится в третьей четверти. А в третьей четверти преобразуемая функция синус имеет знак минус. Значит, наше новое тождественное выражение тоже со знаком минус:

sin (3π/2 – t) = –cos t.

Пример решен.

Следуя этому правилу, можно составить другие формулы приведения.

Формулы приведения.

cos (π + t) = –cos t	sin (π + t) = –sin t	tg (π + t) = tg t	ctg (π + t) = ctg t
cos (π – t) = –cos t	sin (π – t) = sin t	tg (π – t) = –tg t	ctg (π – t) = –ctg t
cos (2π + t) = cos t	sin (2π + t) = sin t	tg (2π + t) = tg t	ctg (2π + t) = ctg t
cos (2π – t) = cos t	sin (2π – t) = –sin t	tg (2π – t) = –tg t	ctg (2π – t) = –ctg t
cos (π/2 + t) = –sin t	sin (π/2 + t) = cos t	tg (π/2 + t) = –ctg t	ctg (π/2 + t) = –tg t
cos (π/2 – t) = sin t	sin (π/2 – t) = cos t	tg (π/2 – t) = ctg t	ctg (π/2 – t) = tg t
cos (3π/2 + t) = sin t	sin (3π/2 + t) = –cos t	tg (3π/2 + t) = –ctg t	ctg (3π/2 + t) = –tg t
cos (3π/2 – t) = –sin t	sin (3π/2 – t) = –cos t	tg (3π/2 – t) = ctg t	ctg (3π/2 – t) = tg t

Примечание:

Часто встречаются более сложные выражения, но они не меняют правила.
Например, если cos (2π + t) = cos t, то cos (2π + 3t) = cos 3t.

 

Основные тригонометрические формулы — Мегаобучалка

ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ

Тригонометрический круг

1.Углом какой четверти является угол α, если:

а) α = 283˚ б) α = 190˚

в) α = 100˚ г) α = –20˚

д) α = –110˚ е) α = 4200˚

ж)α = 179˚ з) α = 325˚

и) α = –150˚ к) α = –10˚

л) α = 800˚ м) α = 10 000˚

 

а		б
в		г
д		е
ж		з
и		к
л		м

 

 

Радианная мера угла

180˚ = π рад

Преобразование углов из градусной меры в радианную:

α рад =

Преобразование углов из радианной меры в градусную:

α˚ =

2. Выразите в радианной мере величины углов:

а) 45˚, 36˚, 180˚; б) 120˚, 310˚, 360˚;

в) 60˚, 72˚, 270˚; г) 150˚, 216˚, 90˚.

а		б
в		г

3. Выразите в градусной мере величины углов:
а) ; б) ;

в) ; г)

а		б
в		г

Тригонометрические функции в прямоугольном треугольнике

Если а и b — катеты, с — гипотенуза прямоугольного треугольника ABC, то выполняются следующие равенства:

Линии тригонометрического круга

Основные тригонометрические формулы

I группа.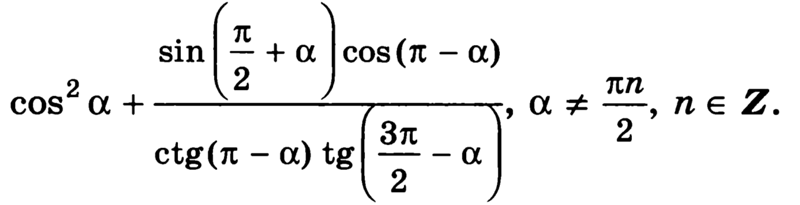 Соотношения между тригонометрическими функциями одного и того же аргумента:

 

 

4. Какой знак имеет выражение:

а) ; б) ; в) ;

г) ; д) ; е) ;

ж) ; з) ; и)

к) ; л) ; н) ;

о) ; п.) ; р)tg(-10°).

 

а	+	б	+	в	–
г	+	д	+	е	–
ж	–	з	–	и	–
к	+	л	+	н	–
о	+	п	+	р	–

 

5. Какой знак имеет выражение:

а) ; б) ; в) ; г)

д) _; е) ; ж) ; з)

и) ; к) ; л) ; м)

н) ; о) ; п) ; р) .

 

а	+	б	–	в	–	г	–
д	–	е	+	ж	–	з	+
и	–	к	–	л	–	м	+
н	–	о	+	п	–	р	–

 

6. Определите знак выражения:

а) ; ;

б) ;

 

а	+	в	+
б	–	г	–

 

7. Определите знак выражения:

а) б)

в) г)

д) е)

ж) з)

и)

к)

а	–	б	–
в	+	г	–
д	–	е	+
ж	+	з	+
и	+	к	–

 

8. По заданному значению функции найдите значения осталь­ных тригонометрических функций:

а) б)

в) г)

д) е)

з)

и) к)

л) м)

 

а
б
в
г
д
е
ж
з
и
к
л
м
н
о
п
р

 

 

II группа. Формулы приведения:

 

формулы приведения для преобразования выражений вида

Для запоминания этих формул удобно пользоваться та­ким мнемоническим правилом:

а) перед приведенной функцией ставится тот знак, который имеет исходная функция, если ;

б) функция меняется на «кофункцию», если пнечетно; функция не меняется, если

пчетно.

(Кофункциями синуса, косинуса, тангенса и котан­генса называются соответственно косинус, си­нус, котангенс и тангенс.)

 

 

 

 

9. Замените тригонометрической функцией угла :

а) б) в)

г) д) е)

ж) з) и)

к) л) м)

н) о) п)

р) с) т)

у) ф) х)

 

 

а	cosα	б	sinα	в	ctgα
г	ctgα	д	cosα	е	sinα
ж	–tgα	з	– sinα	и	– ctgα
к	sinα	л	– cosα	м	– ctgα
н	cosα	о	– sinα	п	tgα
р	cosα	с	– ctgα	е	– sinα
у	sinα	ф	– sinα	х	ctgα

 

10. Приведите к тригонометрической функции угла из проме­жутка : а) б)

в) г)

 

а	;	б	;
в	;	г

 

 

11. Приведите к тригонометрической функции угла от 0° до 90°:а) б)

в) г)

а	;	б	;
в	;	г	.

 

12. Найдите значение выражения:

а)в)д)

б) г) е)

ж)и)л)

з) к) м)

а	;	в	;	д	;
б	;	г	;	е	.
ж	а) ;	и	в) ;	л	д) ;
з	б) ;	к	г) ;	м	е) .

 

14. Выразите через тригонометрическую функцию угла от 0° до 90°, если:

а) б)

в) г)

 

а	sin130˚=cos40˚ cos130˚=–sin40˚ tg130˚=–ctg40˚ ctg130˚=–tg40˚	б	sin190˚=–sin10˚ cos190˚=–cos10˚ tg190˚=tg10˚ ctg190˚=ctg10˚
в	sin(–320˚)=sin40˚ cos(–320˚)=cos40˚ tg(–320˚)=tg40˚ ctg(–320˚)=ctg40˚	г	sin(–590˚)=sin50˚ cos(–590˚)=–cos50˚ tg(–590˚)=–tg50˚ ctg(–590˚)=–ctg50˚

 

15. Найдите если:

а) б) в)

а	sin cos tg ctg
б	sin cos tg ctg
в	sin cos tg ctg

 

16.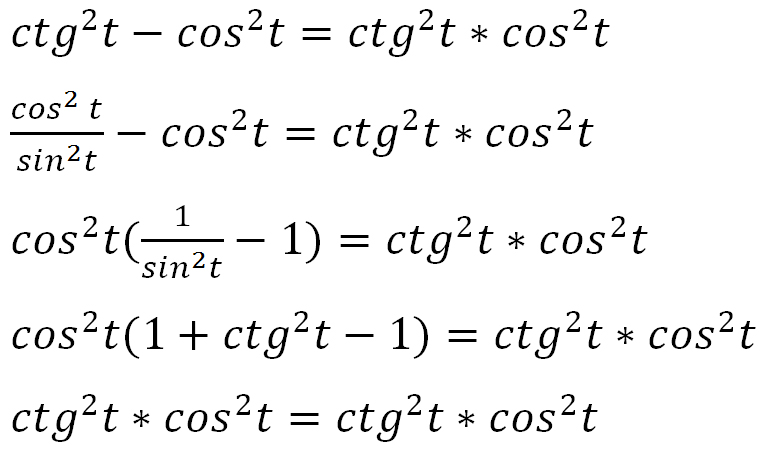 Преобразуйте выражение:

а) в)

б) г)

д)

е)

 

а	sin2α	в	sin2α	д
б	ctg2α	г	ctg2α	е	2cosα

 

17. Упростите выражение:

а)в)

б) г)

д)

е)

ж)з)

и)

к)

 

л) н)

м) о)

п)

р)

 

а	;	д
б	;	е
в	;	ж
г	.	з
и	;	н	;
к	.	о	.
л		п	;
м		р

 

18. Вычислите с помощью формул приведения:

а) в)

б) г)

д) е)

ж)

з)

а		д	;
б		е	;
в		ж	;
г		з	.

 

 

III группа. Формулы сложения:

 

19. С помощью формул сложения преобразуйте выражение:

а) в)

б) г)

д) е)

а		в
б		г
д		е

 

20. Представив 105° как сумму 60° + 45°, вычислите:

а) sin 105°; б) cos 105°.

 

а

;

б

.

21.Представив 75° как сумму 30°+45°, вычислите:
а) sin 75°; б) cos 75°.

 

а

;

б

 

22. Упростите выражение:

а) в)

б) г)

д) ж)

е) з)

и)л)

к) м)

н) о)

 

 

а		в
б		г
д	;	ж	;
е	;	з	.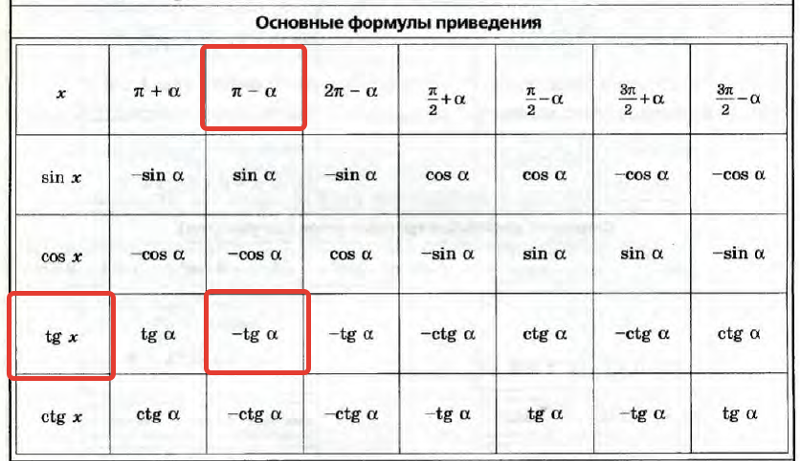
и	;	л	;
к	;	м	.
н	;	о	.

 

23. Найдите значение выражения:
а)
б)

в) г)

д)
е)

 

а		в
б		г	.
д		е

 

24.Упростите выражение:

а)

б)

в) г)

д) е)

 

а		г
б		д
в		е

 

25. Зная, что sin , , и —углы I четверти,

найдите значение выражения:

а) б) в)

 

 

26.Известно, что и — углы II четверти и ,

. Найдите:

а) б)

в) г)

 

а		б
в		г

 

27. Вычислите: а) б)

 

а

б

 

28. Известно, что , . Найдите:

а) 6)

 

а

б

 

Калькулятор опорного угла

| Квадранты графика

Базовый угол для 1°: 1°

Базовый угол для 2°: 2°

Базовый угол для 3°: 3°

Базовый угол для 4°: 4°

Базовый угол для 5°: 5°

Базовый угол для 6°: 6°

Базовый угол для 7°: 7°

Базовый угол для 8°: 8°

Базовый угол для 9°: 9°

Базовый угол для 10°: 10°

Базовый угол для 15°: 15°

Базовый угол для 20°: 20°

Базовый угол для 25°: 25°

Базовый угол для 30°: 30° (π / 6)

Базовый угол для 35°: 35°

Базовый угол для 40°: 40°

Базовый угол для 45°: 45° (π / 4)

Базовый угол для 50°: 50°

Базовый угол для 55°: 55°

Базовый угол для 60°: 60° (π / 3)

Базовый угол для 65°: 65°

Базовый угол для 70°: 70°

Базовый угол для 75°: 75°

Базовый угол для 80°: 80°

Опорный угол для 85°: 85°

Базовый угол для 90°: 90° (π / 2)

Базовый угол для 95°: 85°

Базовый угол для 100°: 80°

Базовый угол для 105°: 75°

Базовый угол для 110°: 70°

Базовый угол для 115°: 65°

Опорный угол для 120°: 60° (π / 3)

Базовый угол для 125°: 55°

Базовый угол для 130°: 50°

Базовый угол для 135°: 45° (π / 4)

Базовый угол для 140°: 40°

Базовый угол для 145°: 35°

Базовый угол для 150°: 30° (π / 6)

Базовый угол для 155°: 25°

Базовый угол для 160°: 20°

Базовый угол для 165°: 15°

Базовый угол для 170°: 10°

Базовый угол для 175°: 5°

Базовый угол для 180°: 0°

Базовый угол для 185°: 5°

Базовый угол для 190°: 10°

Базовый угол для 195°: 15°

Базовый угол для 200°: 20°

Базовый угол для 205°: 25°

Базовый угол для 210°: 30° (π / 6)

Базовый угол для 215°: 35°

Базовый угол для 220°: 40°

Базовый угол для 225°: 45° (π / 4)

Базовый угол для 230°: 50°

Базовый угол для 235°: 55°

Опорный угол для 240°: 60° (π / 3)

Базовый угол для 245°: 65°

Базовый угол для 250°: 70°

Базовый угол для 255°: 75°

Базовый угол для 260°: 80°

Базовый угол для 265°: 85°

Базовый угол для 270°: 90° (π / 2)

Базовый угол для 275°: 85°

Опорный угол для 280°: 80°

Базовый угол для 285°: 75°

Базовый угол для 290°: 70°

Базовый угол для 295°: 65°

Базовый угол для 300°: 60° (π / 3)

Базовый угол для 305°: 55°

Базовый угол для 310°: 50°

Базовый угол для 315°: 45° (π / 4)

Базовый угол для 320°: 40°

Базовый угол для 325°: 35°

Базовый угол для 330°: 30° (π / 6)

Базовый угол для 335°: 25°

Базовый угол для 340°: 20°

Базовый угол для 345°: 15°

Базовый угол для 350°: 10°

Базовый угол для 355°: 5°

Опорный угол для 360°: 0°

PhraseExpress — Программирование

Фраза ссылки

Эта функция макроса вставляет содержимое другой фразы:

Первая рекомендуемая опция позволяет выбрать фразу по ее описанию. Затем связь устанавливается с помощью внутреннего идентификатора.

Кроме того, вы можете адресовать фразу по ее автотексту (классический метод).

Если вы выберете фразу папку (вместо фразы), PhraseExpress предложит вам выбрать элемент в определенной папке фразы.

Вы также можете перетаскивать фразы из дерева фраз прямо в поле содержания фразы, чтобы связать его с редактируемой в данный момент фразой. PhraseExpress автоматически создает макрос вставки фразы в том месте, где вы перетаскиваете фразу.

Преимущества использования вложенных фраз

• Вложенные фразы работают как система шаблонов. Изменения текста нижнего колонтитула автоматически вступают в силу для всех фраз, которые к нему относятся, и вам не нужно вводить фразы по отдельности. Это хорошо, если, например. необходимо обновить только номер телефона в нижнем колонтитуле или если вы хотите добавить временное объявление о специальном предложении в нижний колонтитул.
• Вы экономите место для хранения, так как вам нужно только добавить ссылку на вложенную фразу, а не вводить ее содержимое в каждую отдельную фразу.

If-Then-Else

Макрос If-Then-Else позволяет изменить ход фразы на основе оценки одного или нескольких условий.

Каждую оценку можно настроить так, чтобы она сочеталась с логикой «или» или «и».

Вычислить выражение

Эта макрофункция выводит результат математического выражения. 9, ln(x), sin(x), cos(x), tan(x), ctg(x), abs(x), sqrt(x), modulo(x % y), round(x), floor( x), trunc(x), frac(x)

Можно ввести шестнадцатеричное число, используя символ $, например $ 1F.

Сообщение об ошибке появляется в случае непоследовательного форматирования ввода (например, непоследовательное использование десятичных разделителей или разделителей тысяч).

Для вычисления даты PhraseExpress предлагает отдельную функцию макроса.

Переменные

Видеоруководство

Временные переменные хранят любые текстовые или числовые данные для повторного использования в одной или нескольких фразах. Если содержимое пусто, временная переменная не удаляется, а очищается, чтобы вы могли проверить это состояние с помощью макроса условного оператора.

Содержимое временных переменных будет удалено при выходе из программы.

В отличие от функции макроса для создания/изменения фразы, временные переменные не запускают операцию записи файла фразы.

Связанные страницы

Задать переменную

Эта макрофункция устанавливает содержимое переменной с указанным содержимым. Если пусто, переменная будет очищена.

Содержимое переменной может быть дополнительно выведено сразу после определения ее содержимого.

Если содержимое пусто, переменная не удаляется, поэтому ее можно проверить на наличие пустого содержимого для операций сравнения.

Содержимое сохраняется до тех пор, пока оно не будет переопределено или, альтернативно, пока программа PhraseExpress не будет завершена.

Выходная переменная

Эта макрофункция выводит содержимое переменной с указанным именем.

При вводе имени ранее определенной переменной в поле ввода содержимого фразы PhraseExpress предлагает автоматически преобразовать его в функцию макроса для вывода переменных с таким именем.