Примеры на плюс минус умножение и деление: Порядок действий в Математике

Умножения и деление отрицательных чисел. Решение примеров.

Дарим в подарок бесплатный вводный урок!

 

 

В этой статье мы будем изучать умножение и деление отрицательных чисел. Существуют определенные правила умножения отрицательных чисел.

• \(«—«-\) при умножении минус на минус результат становится положительным;
• \(«-+»-\) при умножении минуса на плюс результат становится отрицательным;
•  \(«+-«-\) при умножении плюса на минус результат становится отрицательным;
• \(«++»-\)  при умножении плюса на плюс результат становится положительным.

---

Примеры умножения отрицательных чисел. 

Задача 1. Вычислить: \((-4)*(-4)\) и \((-6)*(-5).\)

Решение.

Отрицательное число при умножении на отрицательное станет положительным согласно правилу.

1. \((-4)*(-4)=16\)
2. \((-6)*(-5)=30\)

Ответ: \(16;30. \)

Задача

2. Вычислить: \((-10)*12\) и \((-7)*4.\)

Решение.

Отрицательное при умножении на положительное число станет отрицательным согласно правилу.

-10 * 12= -120

(-7)*4=-28

 

Ответ: \(-120; -28\)

---

Задача 3. Вычислить: \(11*(-11)\) и \(13*(-6).\)

Решение.

Положительное при умножении на отрицательное число станет отрицательным согласно правилу.

1. \(11*(-11)=-121\)
2. \(13*(-6)=-78\)

Ответ: \(-121;-78.\)

Деление отрицательных чисел

 

При делении действуют те же правила знаков, что и при умножении. Делить на ноль нельзя.

• ​\(«—«-\)​ при делении минус на минус результат становится положительным;
•  ​\(«-+»-\)​при делении минуса на плюс результат становится отрицательным;
•  \(«+-«-\)при делении плюса на минус результат становится отрицательным;
• \(«++»-\) при делении плюса на плюс результат становится положительным.

Задача 4. Вычислить: \((-16)*(-4)\) и \((-6)*(-2)\).

Решение.

1. \(-16:(-4)=4\)
2. \((-6):-2=3\)

Ответ: \(4;3.\)

Задача 5. Вычислить: \((-10):5\) и \((-12):6\).

Решение.

1.  \((-10):5=-2\)
2. \((-12):6=-2\)

Ответ: \(-2;-2.\)

Задача 3. Вычислить:  \(121:(-11)\) и  \(169:(-13)\).

Решение.

1.  \(121:(-11)=-11\)
2.  \(169:(-13)=-13\)

Ответ: \(-11;-13.\)

 

 

 

 

 

 

 

 

 

 

Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Порядок действий.

Правила и примеры — Kid-mama

Мы рассмотрим в этой статье три варианта примеров:

1. Примеры со скобками (действия сложения и вычитания)

2. Примеры со скобками (сложение, вычитание, умножение, деление)

3. Примеры, в которых много действий

 Примеры со скобками (действия сложения и вычитания)

Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:

Мы видим, что порядок действий  в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.

Запомните правило: Если в примере нет скобок, мы выполняем все действия по порядку, слева направо. Если  в примере есть скобки, то сначала мы выполняем действия в скобках, и лишь потом все остальные действия, начиная слева направо.

*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи. 

Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем  все действия по порядку, слева направо:

В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.

 

Примеры со скобками (сложение, вычитание, умножение, деление)

Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.

Сначала рассмотрим примеры без скобок:

Запомните правило: Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо. Если  в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.

Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий  полученные результаты.  Затем выполняем сложение и вычитание по порядку:

Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:

Примеры, в которых много действий

Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно.  Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).

Эти знаки и будут делить наш пример на блоки:

 Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.

Сложение, вычитание, умножение и деление (видео и практика)

TranscriptPractice

Привет, ребята! Сегодня мы рассмотрим математические операции: сложение , вычитание , умножение и деление . Эти четыре операции служат фундаментальными строительными блоками для всей математики, поэтому крайне важно иметь четкое представление о том, на чем можно основываться. Давайте углубимся.

Сложение и вычитание

Мы используем сложение и вычитание для решения многих реальных ситуаций. Сложение и вычитание — это просто математические термины, используемые для описания «объединения» и «удаления». Когда мы к добавляем , мы объединяем или увеличиваем. Когда мы вычитаем , мы отнимаем или уменьшаем.

Напоминаем:

• Для сложения используется символ \(+\)
• Ответ на задачу на сложение называется суммой
• Для вычитания используется символ \(–\)
• Ответ на задачу на вычитание называется разностью

 
По существу, сложение и вычитание — противоположные операции. Один добавляет стоимость, а другой вычитает стоимость. Одна из стратегий визуализации этих двух операций — использование числовой прямой. Мы будем использовать числовую прямую, чтобы проиллюстрировать следующие примеры.

Давайте представим ситуацию, связанную с продажей попкорна. Для этого сценария предположим, что вы пытаетесь собрать деньги, продавая пакеты с попкорном, и вы начинаете с 20 пакетов.

Когда придет ваш первый покупатель, он захочет купить 4 пакета попкорна. Это означает, что ваше оставшееся количество сумок уменьшится. Мы можем представить эту ситуацию с помощью простого уравнения, включающего вычитание. Мы начали с 20 мешков и «уменьшили на 4» или вычли 4. Наше уравнение вычитания записывается как \(20-4=16\).

На числовой прямой мы можем представить это вычитание, начав с 20 и затем переместившись на четыре единицы назад в отрицательном направлении. Каждый прыжок назад представляет собой вычитание на 1.

Предположим, вы начали с 20 пакетов попкорна, а к концу дня у вас осталось 6 пакетов. Вам нужно пополнить свой запас, чтобы поддерживать продажи, поэтому вы делаете еще 4 пакета попкорна. Сколько пакетов попкорна у вас сейчас есть в наличии для продажи? Для этого сценария, поскольку мы рассматриваем увеличение мешков на , мы будем использовать сложение.

Эту ситуацию можно описать уравнением \(6+4=10\). Изначально у вас было 6 мешков, а затем «объединили» это количество еще с 4 мешками. Всего у вас 10 мешков. На числовой прямой сложение представлено скачками вправо в положительном направлении. Каждый прыжок вправо представляет собой добавление одной единицы. Так что в этом примере мы бы начали с 6 и прыгнули бы на 4 единицы вправо. Мы видим, что мы приземлились на 10.

Важно отметить, что при использовании сложения порядок значений не имеет значения. Например, \(10+30\) равносильно \(30+10\). Размещение или расположение значений не влияет на результат. Обе схемы будут равны 40. Однако то же самое не верно для вычитания . Означает ли \(30-10\) то же самое, что и \(10-30\)? Явно нет. Мы видим, что порядок имеет значение при работе с ситуацией, связанной с вычитанием. Технический термин для этого качества известен как 9.0005 коммутативное свойство . По сути, это свойство верно для операций, в которых значения могут перемещаться, «коммутировать», а результат выражения или уравнения не изменится. Коммутативность применима к сложению, но не к вычитанию.

Умножение и деление

Еще одна операция, которая также обладает свойством коммутативности, — это умножение. Давайте обсудим умножение вместе с делением, как мы делали сложение и вычитание. Умножение и деление похожи на сложение и вычитание тем, что выполняют противоположные функции. Функция умножение предназначено для представления нескольких групп определенного значения, тогда как деление предназначено для отображения разделения или подразделения значения на более мелкие группы.

Напоминаем:

• Символ, который мы используем для умножения, это \(\times\)
• Ответ на задачу на умножение называется произведением
• Символ, который мы используем для деления, это \(\div \)
• Ответ на задачу о делении называется числом 9.0005 частное

 

Умножение — это удобный и быстрый способ показать то, что называется «повторяющимся сложением». Например, если вам нужно заполнить 30 мешков попкорна, а в каждом мешке требуется 60 зерен, может потребоваться несколько часов, чтобы подсчитать, сколько всего зерен вам нужно, просто используя сложение. Более быстрый и эффективный способ сделать это вычисление — использовать повторное сложение. Вместо того, чтобы считать каждое семя независимо, мы сгруппировали их и сложили группы вместе. Тогда расчет будет состоять из 30 групп по 60. Эта группировка с целью повторного сложения является по своей сути процессом умножения. 30 групп по 60 записывается как \(30\х60=1800\). Таким образом, для заполнения 30 мешков попкорна требуется 1800 ядер.

И сложение, и умножение коммутативны, потому что порядок не влияет на ответ. 30 групп по 60 дают нам тот же результат, что и 60 групп по 30. противоположный. Когда мы используем деление, мы, по сути, делим большую группу на более мелкие подгруппы. В нашем примере с попкорном мы можем использовать деление, чтобы ответить на следующий вопрос:

Сколько пакетов попкорна я могу приготовить из 1800 ядер, если для каждого пакета требуется 60 семян?

 

Эта ситуация требует, чтобы мы разделили большое значение 1800 на группы по 60. Каждая меньшая подгруппа теперь будет представлять пакет попкорна. 1800, разделенных на группы по 60, представлены как \(1800\div 60\). В данном случае ответ равен 30, значит, из наших 1800 ядер можно приготовить 30 пакетов попкорна. Как видите, деление не является коммутативным, потому что порядок значений играет решающую роль в определении ответа. \(1800\div 60\) — это не то же самое, что \(60\div 1800\).

Хорошо, это все для этого обзора математических операций! Спасибо за просмотр и удачной учебы!

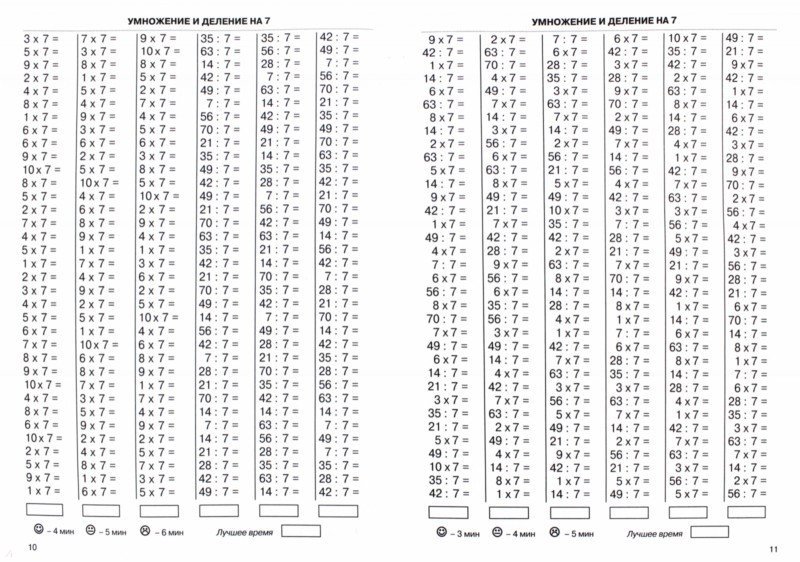
Таблица умножения и печатные формы

 

Практические вопросы

Вопрос №1:

 
Ответ на задачу на вычитание называется …

3 004 Сумма

Частное

Продукт

Показать Ответ:

Ответ:

A — правильный ответ. Поскольку вычитание — это разница между меньшим числом и большим числом, ответ на задачу на вычитание называется разницей.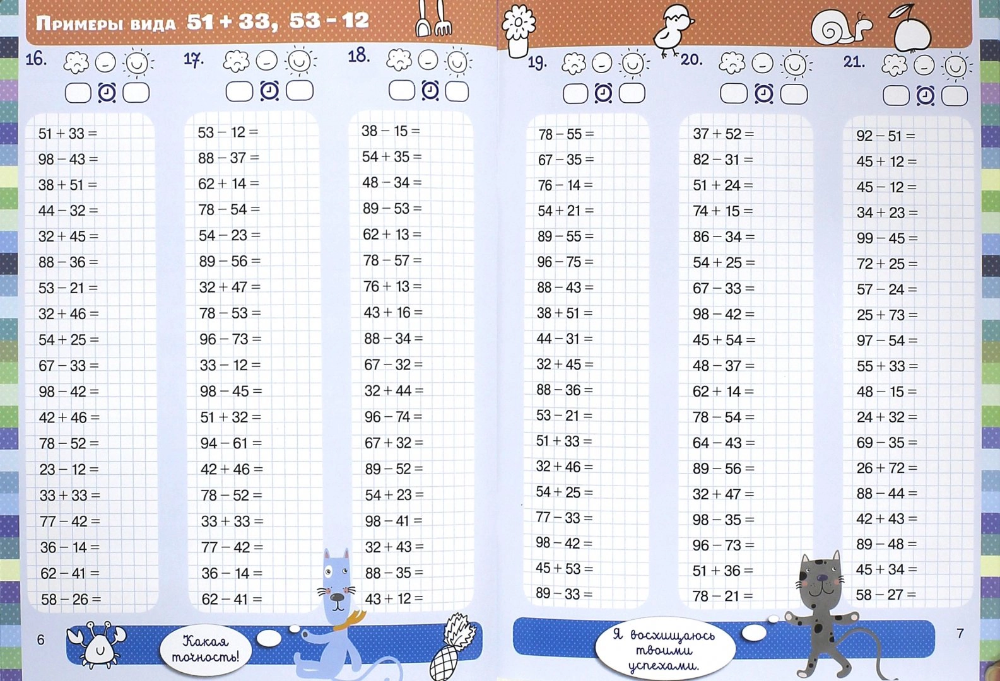

Скрыть ответ

Вопрос № 2:

 
Какое утверждение верно?

Вычитание и умножение — противоположные операции.

Вычитание и деление — противоположные операции.

Умножение и сложение — противоположные операции.

Умножение и деление — противоположные операции.

Показать ответ

Ответ:

D — правильный ответ. Деление разбивает большую группу на более мелкие подгруппы, а умножение представляет собой многократное сложение меньших подгрупп, чтобы найти общее количество в большой группе. Следовательно, эти операции выполняют противоположные функции.

Скрыть ответ

Вопрос №3:

 
Джейми арендует велосипед за 8 долларов в час. Всего у него велосипед на 4 часа. Какое уравнение можно использовать, чтобы узнать, сколько денег Джейми тратит на аренду велосипеда?

\(8+4=12\)

\(8-4=4\)

\(8\times4=32\)

\(8÷4=2\)

Показать ответ

Ответ:

C — правильный ответ. Поскольку Джейми тратит 8 долларов за каждый час пользования велосипедом, он тратит 8 долларов + 8 долларов + 8 долларов + 8 долларов, что равно 8 долларов ✕ 4, или 32 доллара.

Скрыть ответ

Вопрос № 4:

 
Какое утверждение лучше всего иллюстрирует свойство коммутативности?

\(12÷3=3÷12\)

\(12\times3=3\times12\)

\(12-3=3-12\)

\(12+3=15\)

Показать ответ

Ответ:

B — правильный ответ. Свойство коммутативности гласит, что числа в математической задаче можно перемещать или менять местами, и результат уравнения не изменится. Коммутативное свойство применяется к сложению и умножению, но не работает для деления или вычитания.

Скрыть ответ

Вопрос № 5:

 
В Mike’s Deli индейка стоит 4 доллара за фунт. Кейт покупает индейку, чтобы приготовить бутерброды на обед. Если Кейт тратит 80 долларов, какое уравнение показывает, сколько фунтов индейки она купила?

\(80+4=84\)

\(4÷80=20\)

\(80÷4=20\)

\(80-4=76\)

Показать ответ

Ответ:

C — правильный ответ. Кейт знает, что общая потраченная сумма составила 80 долларов. Она также знает, что каждый фунт стоил ей 4 доллара. Кате нужно знать, на сколько равных групп разбито 80 долларов, если в каждой группе по 4 доллара. Чтобы решить эту проблему, Кате нужно разделить. Поскольку 80 — это число, которое делится, оно стоит первым в задаче на деление. B неверно, потому что \(4÷80\) не совпадает с \(80÷4\). 9Скрыть ответ 0258 Цели обучения

• Использовать сложение, вычитание, умножение и деление при вычислении целого числа выражения

Работа с целыми числами и выполнение основных вычислений — основа всей математики. Мы предполагаем, что вы помните, как выполнять сложение, вычитание, умножение и деление однозначных чисел. Вы часто будете иметь под рукой калькулятор для выполнения этих расчетов, но быстрое освежение знаний поможет вам лучше понять, как работать с числами, чтобы сложные уравнения не вызывали у вас затруднений.

Дополнение

пример

Добавление: [латекс]28+61[/латекс]

Решение
Чтобы складывать числа, состоящие из более чем одной цифры, часто проще писать числа вертикально в столбцах.

Напишите числа так, чтобы единицы и десятки располагались вертикально.	[латекс]\begin{array}{c}\hfill 28\\ \\ \hfill \underset{\text{____}}{+61}\end{array}[/latex]
Затем добавьте цифры в каждом разряде. Добавьте единицы: [латекс]8+1=9[/латекс] Добавьте десятки: [латекс]2+6=8[/латекс]	[латекс]\begin{array}{c}\hfill 28\\ \\ \hfill \underset{\text{____}}{+61}\\ \hfill 89\end{array}[/latex]

 

В предыдущем примере сумма единиц и сумма десятков были меньше [латекс]10[/латекс]. Но что произойдет, если сумма [latex]10[/latex] или больше? Давайте воспользуемся нашей моделью base-[latex]10[/latex], чтобы выяснить это.

На приведенном ниже рисунке показано добавление [латекс]17[/латекс] и [латекс]26[/латекс].

 

 

Когда мы добавляем единицы, [латекс]7+6[/латекс], мы получаем [латекс]13[/латекс] единиц. Поскольку у нас их больше, чем [латекс]10[/латекс], мы можем обменять [латекс]10[/латекс] из них на [латекс]1[/латекс] десять. Теперь у нас есть [латекс]4[/латекс] десятки и [латекс]3[/латекс] единицы. Не используя модель, мы показываем это как маленький красный [латекс]1[/латекс] над цифрами в разряде десятков.

Когда сумма в столбце разряда больше, чем [latex]9[/latex], мы переносимся в следующий столбец слева. Перенос — это то же самое, что перегруппировка путем обмена. Например, [latex]10[/latex] единиц для [latex]1[/latex] десяти или [latex]10[/latex] десятков для [latex]1[/latex] сотен.

Сложите целые числа

1. Запишите числа так, чтобы каждый разряд располагался вертикально.
2. Добавьте цифры в каждое разрядное значение. Работайте справа налево, начиная с места единиц. Если сумма в разряде больше, чем [latex]9[/latex], выполняется перенос к следующему разряду.
3. Продолжайте добавлять каждое разрядное значение справа налево, добавляя каждое разрядное значение и перенося при необходимости.

пример

Добавить: [латекс]43+69[/латекс]

Показать ответ

попробуй

попробуй

Если слагаемые имеют разное количество цифр, будьте осторожны, чтобы выровнять соответствующие разрядные значения, начиная с единиц и двигаясь влево.

Пример

Добавить: [латекс]1,683+479[/латекс].

Показать ответ

попробуй

Вычитание

Сложение и вычитание являются обратными операциями. Сложение отменяет вычитание, а вычитание отменяет сложение.
Мы знаем [латекс]7 — 3=4[/латекс], потому что [латекс]4+3=7[/латекс]. Знание всех фактов сложения чисел поможет с вычитанием. Затем мы можем проверить вычитание, сложив. В приведенных выше примерах наши вычитания можно проверить сложением.

[латекс]7-3=4[/латекс]	потому что	[латекс]4+3=7[/латекс]
[латекс]13-8=5[/латекс]	потому что	[латекс]5+8=13[/латекс]
[латекс]43-26=17[/латекс]	потому что	[латекс]17+26=43[/латекс]

Чтобы вычесть числа, состоящие из более чем одной цифры, обычно проще записывать числа вертикально в столбцы, как мы это делали для сложения. Выровняйте цифры по разрядности, а затем вычтите каждый столбец, начиная с единиц, и затем работайте влево.

Упражнение

Вычтите, а затем проверьте, добавив: [латекс]89 — 61[/латекс].

Показать ответ

ПОПРОБУЙТЕ 

Вычтите целые числа

1. Запишите числа так, чтобы каждое разрядное значение располагалось вертикально.
2. Вычтите цифры из каждого разряда. Работайте справа налево, начиная с места единиц. Если цифра сверху меньше, чем цифра снизу, заимствуйте по мере необходимости.
3. Продолжайте вычитать значение каждого разряда справа налево, при необходимости заимствуя.
4. Проверить добавлением.

упражнение

Вычесть: [латекс]43 — 26[/латекс].

Показать ответ

В приведенном выше примере, если мы моделируем вычитание [латекс]26[/латекс] из [латекс]43[/латекс], мы заменим [латекс]1[/латекс] десять на [латекс]10[/латекс] те. Когда мы делаем это без моделей, мы говорим, что заимствуем [латекс]1[/латекс] из разряда десятков и добавляем [латекс]10[/латекс] к разряду единиц.

попробуйте

Упражнение

Вычтите и затем проверьте, добавив: [латекс]207 — 64[/латекс].

Показать ответ

попробуйте

Упражнение

Вычтите и затем проверьте, добавив: [латекс]2,162 — 479[/латекс].

Показать ответ

попробуйте

 

Посмотрите видео ниже, чтобы увидеть еще один пример вычитания целых чисел путем выстраивания разрядных значений.

Умножение

Чтобы умножать без использования моделей, вам нужно знать все факты умножения одной цифры. Убедитесь, что вы знаете их бегло, прежде чем продолжить изучение этого раздела. В таблице ниже показаны факты умножения.

Каждое поле показывает произведение числа в левом столбце и числа в верхней строке. Если вы не уверены в продукте, смоделируйте его. Важно, чтобы вы запомнили любые факты о числах, которые вы еще не знаете, чтобы вы были готовы умножать большие числа.

[латекс]х[/латекс]	[латекс]0[/латекс]	[латекс]1[/латекс]	[латекс]2[/латекс]	[латекс]3[/латекс]	[латекс]4[/латекс]	[латекс]5[/латекс]	[латекс]6[/латекс]	[латекс]7[/латекс]	[латекс]8[/латекс]	[латекс]9[/латекс]
[латекс]0[/латекс]	[латекс]0[/латекс]	[латекс]0[/латекс]	[латекс]0[/латекс]	[латекс]0[/латекс]	[латекс]0[/латекс]	[латекс]0[/латекс]	[латекс]0[/латекс]	[латекс]0[/латекс]	[латекс]0[/латекс]	[латекс]0[/латекс]
[латекс]1[/латекс]	[латекс]0[/латекс]	[латекс]1[/латекс]	[латекс]2[/латекс]	[латекс]3[/латекс]	[латекс]4[/латекс]	[латекс]5[/латекс]	[латекс]6[/латекс]	[латекс]7[/латекс]	[латекс]8[/латекс]	[латекс]9[/латекс]
[латекс]2[/латекс]	[латекс]0[/латекс]	[латекс]2[/латекс]	[латекс]4[/латекс]	[латекс]6[/латекс]	[латекс]8[/латекс]	[латекс]10[/латекс]	[латекс]12[/латекс]	[латекс]14[/латекс]	[латекс]16[/латекс]	[латекс]18[/латекс]
[латекс]3[/латекс]	[латекс]0[/латекс]	[латекс]3[/латекс]	[латекс]6[/латекс]	[латекс]9[/латекс]	[латекс]12[/латекс]	[латекс]15[/латекс]	[латекс]18[/латекс]	[латекс]21[/латекс]	[латекс]24[/латекс]	[латекс]27[/латекс]
[латекс]4[/латекс]	[латекс]0[/латекс]	[латекс]4[/латекс]	[латекс]8[/латекс]	[латекс]12[/латекс]	[латекс]16[/латекс]	[латекс]20[/латекс]	[латекс]24[/латекс]	[латекс]28[/латекс]	[латекс]32[/латекс]	[латекс]36[/латекс]
[латекс]5[/латекс]	[латекс]0[/латекс]	[латекс]5[/латекс]	[латекс]10[/латекс]	[латекс]15[/латекс]	[латекс]20[/латекс]	[латекс]25[/латекс]	[латекс]30[/латекс]	[латекс]35[/латекс]	[латекс]40[/латекс]	[латекс]45[/латекс]
[латекс]6[/латекс]	[латекс]0[/латекс]	[латекс]6[/латекс]	[латекс]12[/латекс]	[латекс]18[/латекс]	[латекс]24[/латекс]	[латекс]30[/латекс]	[латекс]36[/латекс]	[латекс]42[/латекс]	[латекс]48[/латекс]	[латекс]54[/латекс]
[латекс]7[/латекс]	[латекс]0[/латекс]	[латекс]7[/латекс]	[латекс]14[/латекс]	[латекс]21[/латекс]	[латекс]28[/латекс]	[латекс]35[/латекс]	[латекс]42[/латекс]	[латекс]49[/латекс]	[латекс]56[/латекс]	[латекс]63[/латекс]
[латекс]8[/латекс]	[латекс]0[/латекс]	[латекс]8[/латекс]	[латекс]16[/латекс]	[латекс]24[/латекс]	[латекс]32[/латекс]	[латекс]40[/латекс]	[латекс]48[/латекс]	[латекс]56[/латекс]	[латекс]64[/латекс]	[латекс]72[/латекс]
[латекс]9[/латекс]	[латекс]0[/латекс]	[латекс]9[/латекс]	[латекс]18[/латекс]	[латекс]27[/латекс]	[латекс]36[/латекс]	[латекс]45[/латекс]	[латекс]54[/латекс]	[латекс]63[/латекс]	[латекс]72[/латекс]	[латекс]81[/латекс]

Мы знаем, что изменение порядка сложения не меняет сумму. Мы видели, что [латекс]8+9=17[/латекс] совпадает с [латекс]9+8=17[/латекс].

Верно ли это и для умножения? Рассмотрим несколько пар факторов.

[латекс]4\cdot 7=28\quad 7\cdot 4=28[/латекс]
[латекс]9\cdot 7=63\quad 7\cdot 9=63[/latex]
[latex]8\cdot 9=72\quad 9\cdot 8=72[/latex]

При обратном порядке множителей произведение не меняется. Это называется коммутативным свойством умножения.

Коммутативное свойство умножения

Изменение порядка множителей не меняет их произведения.

[латекс]a\cdot b=b\cdot a[/латекс]

пример

Умножить:

[латекс]8\cdot 7[/латекс]
[латекс]7\cdot 8[/латекс]

Показать ответ

попробуй

Чтобы умножать числа, состоящие из более чем одной цифры, обычно проще записывать числа вертикально в столбцы, как мы это делали для сложения и вычитания.

[латекс]\begin{array}{c}\hfill 27\\ \hfill \underset{\text{___}}{\times 3}\end{array}[/latex]

Начнем с умножения [ латекс]3[/латекс] от [латекс]7[/латекс].

[латекс]3\раз 7=21[/латекс]

Мы пишем [латекс]1[/латекс] в единицах продукта. Мы переносим [латекс]2[/латекс] десятки, написав [латекс]2[/латекс] над разрядом десятков.

Затем мы умножаем [латекс]3[/латекс] на [латекс]2[/латекс] и прибавляем [латекс]2[/латекс] выше разряда десятков к произведению. Итак, [латекс]3\умножить на 2=6[/латекс] и [латекс]6+2=8[/латекс]. Напишите [латекс]8[/латекс] в разряде десятков продукта.

Продукт [латекс]81[/латекс].

 

Когда мы умножаем два числа с разным количеством цифр, обычно проще написать меньшее число внизу. Можно было бы написать и по-другому, но с этим проще работать.

пример

Умножить: [латекс]15\cdot 4[/латекс]

Показать ответ

попробовать

пример

Умножить: [латекс]286\cdot 5[/латекс]

Показать ответ

попробуй

Когда мы умножаем на число, состоящее из двух и более цифр, мы умножаем на каждую цифру отдельно, работая справа налево. Каждое отдельное произведение цифр называется частичным произведением. Когда мы пишем частичные произведения, мы должны убедиться, что разрядные значения выровнены.

Умножение целых чисел

1. Запишите числа так, чтобы каждый разряд располагался вертикально.
2. Умножьте цифры в каждом разряде.
   • Работайте справа налево, начиная с разряда единиц в нижнем ряду.
     • Умножьте нижнее число на разряд единиц в верхнем числе, затем на разряд десятков и так далее.
     • Если продукт в разрядном значении больше, чем [latex]9[/latex], перенос на следующее разрядное значение.
     • Напишите частичные произведения, выровняв цифры разрядов с числами выше.
   • Повторите для разряда десятков в нижнем числе, разряда сотен и так далее.
   • Вставьте ноль в качестве заполнителя для каждого дополнительного частичного продукта.
3. Добавьте частичные произведения.

пример

Умножить: [латекс]62\влево(87\вправо)[/латекс]

Показать ответ

попробуй

 

Когда множителей три или более, мы умножаем первые два, а затем умножаем их произведение на следующий множитель. Например:

умножить	[латекс]8\cdot 3\cdot 2[/латекс]
первое умножение [латекс]8\cdot 3[/латекс]	[латекс]24\cdot 2[/латекс]
затем умножьте [латекс]24\cdot 2[/латекс]	[латекс]48[/латекс]

В видео ниже мы обобщаем концепции, представленные на этой странице, включая свойство умножения нуля, свойство идентичности умножения и свойство перестановочности умножения.m

Деление

Мы сказали, что сложение и вычитание являются обратными операциями, потому что одно отменяет другое. Точно так же деление является обратной операцией умножения. Мы знаем [латекс]12\дел 4=3[/латекс], потому что [латекс]3\cdot 4=12[/латекс]. Знание всех фактов числа умножения очень важно при делении.

Мы проверяем наш ответ на деление, умножая частное на делитель, чтобы определить, равно ли оно делимому. Мы знаем, что [латекс]24\дел 8=3[/латекс] правильный, потому что [латекс]3\cdot 8=24[/латекс].

Пример

Разделить. Затем проверьте умножением.

1. [латекс]42\дел 6[/латекс]
2. [латекс]\фракция{72}{9}[/латекс]
3. [латекс]7\overline{)63}[/латекс]

Решение:

1.
	[латекс]42\дел 6[/латекс]
Разделите [латекс]42[/латекс] на [латекс]6[/латекс].	[латекс]7[/латекс]
Проверить умножением. [латекс]7\cdot 6[/латекс]
[латекс]42\quad\галочка [/латекс]

2.
	[латекс]\фракция{72}{9}[/латекс]
Разделите [латекс]72[/латекс] на [латекс]9[/латекс].	[латекс]8[/латекс]
Проверить умножением. [латекс]8\cdot 9[/латекс]
[латекс]72\quad\галочка [/латекс]

3.
	[латекс]7\overline{)63}[/латекс]
Разделите [латекс]63[/латекс] на [латекс]7[/латекс].	[латекс]9[/латекс]
Проверить умножением. [латекс]9\cdot 7[/латекс]
[латекс]63\quad\галочка [/латекс]

попробуй

Чему равно частное при делении числа само на себя?

[латекс]\frac{15}{15}=1\text{ потому что }1\cdot 15=15[/latex]

Деление любого числа [латекс]\текст{(кроме 0)}[/латекс] сам по себе дает частное [latex]1[/latex]. Кроме того, любое число, деленное на [latex]1[/latex], дает частное от числа. Эти две идеи изложены в Свойствах Разделения Единого.

Раздел Свойства одного

Любое число (кроме 0), деленное само на себя, равно единице.	[латекс]а\дел а=1[/латекс]
Любое число, деленное на единицу, равно числу.	[латекс]а\дел 1=а[/латекс]

Пример

Разделить. Затем проверьте умножением:

1. [латекс]11\дел 11[/латекс]
2. [латекс]\фракция{19}{1}[/латекс]

Показать ответ

попробуйте

Предположим, у нас есть [латекс]\текст{\$0}[/латекс], и мы хотим разделить его между [латекс]3[/латекс] людьми. Сколько получит каждый? Каждый человек получит [латекс]\текст{\$0}[/латекс]. Ноль, разделенный на любое число, равен [латекс]0[/латекс].

Теперь предположим, что мы хотим разделить [латекс]\текст{\$10}[/латекс] на [латекс]0[/латекс]. Это означает, что нам нужно найти число, которое мы умножим на [latex]0[/latex], чтобы получить [latex]10[/latex]. Этого не может быть, потому что [латекс]0[/латекс], умноженное на любое число, равно [латекс]0[/латекс]. Говорят, что деление на ноль равно undefined .

Эти две идеи составляют Свойства Разделения Зеро.

Свойства разделения Зеро

Ноль, разделенный на любое число, равен [латекс]0[/латекс].	[латекс]0\дел а=0[/латекс]
Деление числа на ноль не определено.	[латекс]а\дел 0[/латекс] не определено

Другой способ объяснить, почему деление на ноль не определено, состоит в том, чтобы вспомнить, что деление на самом деле представляет собой многократное вычитание. Сколько раз мы можем отнять [латекс]0[/латекс] от [латекс]10?[/латекс] Поскольку вычитание [латекс]0[/латекс] никогда не изменит итоговое значение, мы никогда не получим ответ. Поэтому мы не можем разделить число на [latex]0[/latex].

Пример

Разделить. Проверить умножением:

1. [латекс]0\дел 3[/латекс]
2. [латекс]\фракция{10}{0}[/латекс]

Показать ответ

попробуйте

Когда делитель или делимое содержит более одной цифры, обычно проще использовать запись [latex]4\overline{)12}[/latex]. Этот процесс называется длинным делением. Давайте рассмотрим этот процесс, разделив [латекс]78[/латекс] на [латекс]3[/латекс].

The next line reads » data-label=»»>

Разделите первую цифру делимого [латекс]7[/латекс] на делитель [латекс]3[/латекс].
Делитель [латекс]3[/латекс] может входить в [латекс]7[/латекс] два раза, так как [латекс]2\раз 3=6[/латекс] . Напишите [латекс]2[/латекс] над [латекс]7[/латекс] в частном.
Умножьте [латекс]2[/латекс] в частном на [латекс]2[/латекс] и запишите произведение [латекс]6[/латекс] под [латекс]7[/латекс].
Вычтите это произведение из первой цифры делимого. Вычтите [латекс]7 — 6[/латекс] . Запишите разницу 1 под первой цифрой делимого.
Сократите следующую цифру делимого. Опусти [латекс]8[/латекс].
Разделите [латекс]18[/латекс] на делитель [латекс]3[/латекс]. Делитель [латекс]3[/латекс] входит в [латекс]18[/латекс] шесть раз.
Напишите [латекс]6[/латекс] в частном над [латекс]8[/латекс].
Умножьте [латекс]6[/латекс] в частном на делитель и запишите произведение [латекс]18[/латекс] под делимым. Вычтите [латекс]18[/латекс] из [латекс]18[/латекс].

Мы будем повторять процесс до тех пор, пока в делимом не останется цифр, которые нужно уменьшить. В этой задаче больше не осталось цифр, поэтому деление закончено.

[латекс]\текст{Так} 78\дел 3=26[/латекс].

Проверьте, умножив частное на делитель, чтобы получить делимое. Умножьте [латекс]26\умножить на 3[/латекс], чтобы убедиться, что произведение равно делимому, [латекс]78[/латекс].

[латекс]\begin{array}{c}\hfill \stackrel{1}{2}6\\ \hfill \underset{\text{___}}{\times 3}\\ \hfill 78 \end{ массив}[/латекс]

Да, значит, наш ответ правильный. [latex]\checkmark[/latex]

Деление целых чисел

1. Разделить первую цифру делимого на делитель. Если делитель больше первой цифры делимого, разделить первые две цифры делимого по делителю и так далее.
2. Запишите частное над делимым.
3. Умножьте частное на делитель и запишите произведение под делимым.
4. Вычтите этот продукт из дивиденда.
5. Сократите следующую цифру делимого.
6. Повторяйте с шага 1 до тех пор, пока в делимом не останется цифр, которые нужно уменьшить.
7. Проверьте, умножив частное на делитель.

В видео ниже мы показываем еще один пример использования деления в длину.

пример

Разделить [латекс]2,596\дел 4[/латекс]. Проверить умножением:

Показать ответ

попробуйте

пример

Разделите [латекс]4,506\дел 6[/латекс]. Проверить умножением:

Показать ответ

попробуй

Посмотрите это видео, чтобы увидеть еще один пример использования деления в длину для деления целого четырехзначного числа на целое двузначное число.

До сих пор все задачи на деление решались равномерно. Например, если бы у нас было [латекс]24[/латекс] печенья и мы хотели сделать пакеты из [латекс]8[/латекс] печенья, у нас было бы [латекс]3[/латекс] пакетов. Но что, если бы было [латекс]28[/латекс] печенья, и мы хотели бы сделать пакеты из [латекс]8?[/латекс] Начните с [латекс]28[/латекс] печенья.

Попробуйте разложить печенье по восемь штук.

Остались группы [latex]3[/latex] из восьми файлов cookie и еще [latex]4[/latex] cookie. Мы называем файлы cookie [latex]4[/latex], которые остались поверх остальных, и показываем их, записывая R4 рядом с [latex]3[/latex]. (R означает остаток.) ​​

Чтобы проверить это деление, мы умножаем [латекс]3[/латекс] на [латекс]8[/латекс], чтобы получить [латекс]24[/латекс], а затем складываем остаток [латекс]4[/латекс].

[латекс]\begin{array}{c}\hfill 3\\ \hfill \underset{\text{___}}{\times 8}\\ \hfill 24\\ \hfill \underset{\text{___ }}{+4}\\ \hfill 28\end{массив}[/latex]

пример

Разделить [латекс]1,439\дел 4[/латекс]. Проверьте умножением.

Показать ответ

попробуй

пример

Раздели и проверь умножением: [латекс]1,461\дел 13[/латекс].

Показать ответ

попробуйте

Посмотрите видео ниже, чтобы увидеть еще один пример того, как использовать деление в длинную сторону для деления целых чисел, когда есть остаток.

 

Внесите свой вклад!

У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.