Примеры пересечения множеств: Пересечение и объединение множеств — урок. Алгебра, 9 класс.

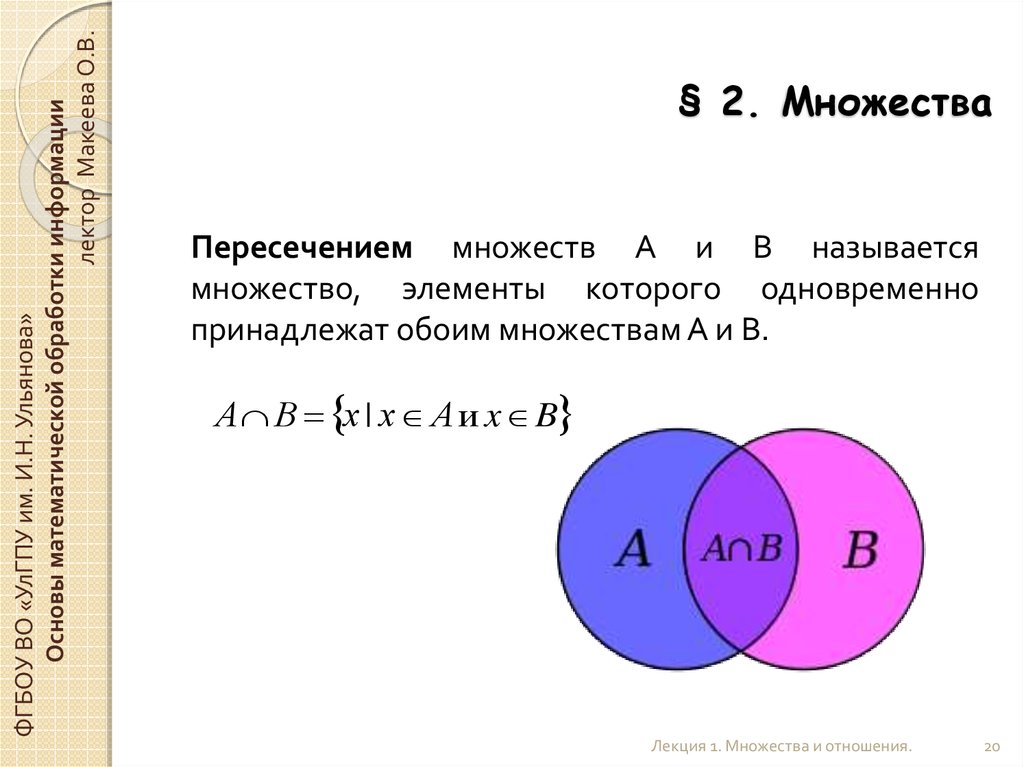
Пересечение множеств чисел – примеры, определение, формула (8 класс, информатика)

4.1

Средняя оценка: 4.1

Всего получено оценок: 109.

4.1

Средняя оценка: 4.1

Всего получено оценок: 109.

Математическая логика занимается изучением логических законов, применяемых в теории множеств. Основы алгебры логики рассматриваются в курсе информатики 8 класса. Над множествами можно выполнять различные действия, одним из которых является пересечение.

Пересечение множеств

Важным разделом в информатике является алгебра логики. Знание логических законов и правил дает возможность быстро решать сложные задачи в любой области деятельности — в области правовых и экономических наук, в технике и технологии.

Множество чисел

Множеством называется совокупность определенных и различных между собой объектов, воспринимаемых как единое целое.

Например, совокупность учеников класса, совокупность целых положительных чисел.

Множества могут быть конечными и бесконечными. Количество учеников в классе — это конечное множество, можно четко назвать конкретное число учеников. Количество целых положительных чисел — бесконечное множество оно может быть бесконечно большим.

В математике множество обозначают прописными латинскими буквами.

Например, множество А={1,5,12,6,7} и множество В={2,4,12,3,7} конечные множества целых положительных чисел

С множествами можно выполнять различные действия. Одним из таких действий является пересечение множеств чисел.

Пересечение множеств чисел

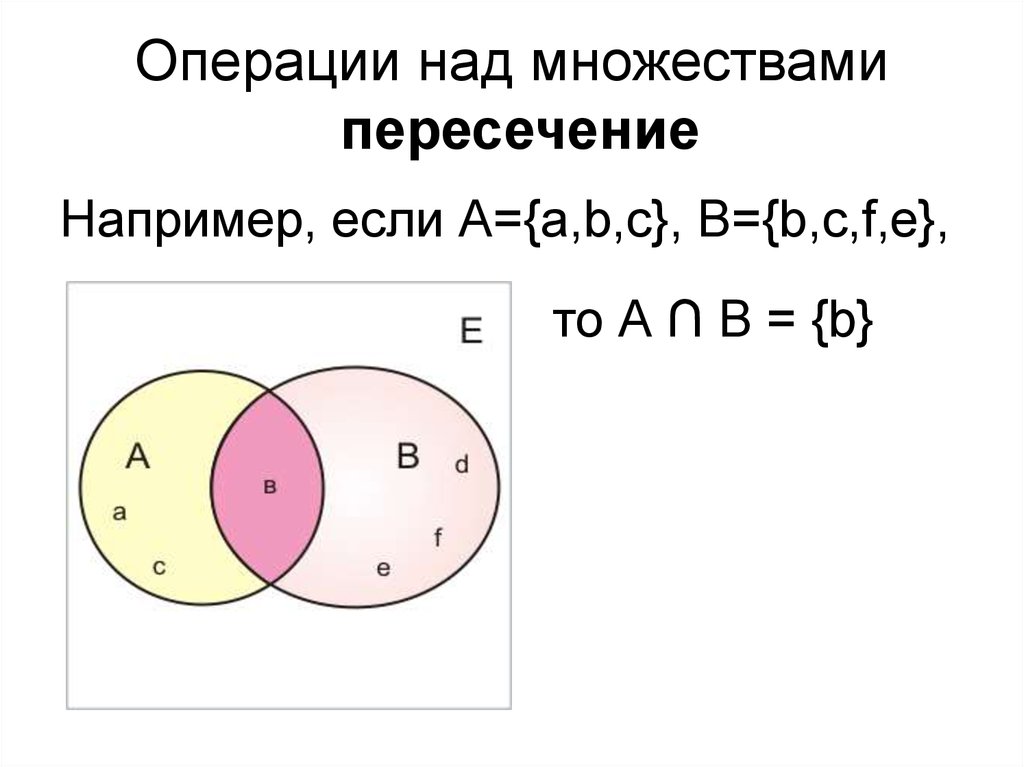
С точки зрения математики, пересечением двух множеств Х и Y является третье множество Z, в состав которого входят элементы, как первого, так и второго множеств. Приведем примеры пересечения множеств чисел.

Для множеств чисел Х={1, 2,4,5,6,8} и Y={2,3,4,6,7,9} пересечением будет третье множество Z={2, 4, 6}.

В качестве элементов множеств могут выступать не только числа.

Для множеств А={А, Б, В, Г, Д, Е} и B={Г, Д, Е, Ё, Ж} пересечением будет третье множество, элементы которого — буквы, одинаковые в исходных множествах C={Г, Д, Е}.

Обозначение пересечения

Операцию пересечения называют и обозначают по-разному, но суть от этого не меняется. В теории множеств для обозначения пересечения используется знак ∩, а формула выглядит так: А ∩ B = C

Пересечение также называют произведением множеств, и для обозначения операции используют знак умножения: А ∙ В = С

В математической логике, работающей с высказываниями, используют понятие «конъюнкция». Для ее обозначения используют символ &: А & В = С. Допустимо конъюнкцию обозначать буквой И: А И В = С.

Визуальное представление пересечения

Для визуального отображения действий с множествами используют диаграммы Эйлера, которые представляют собой две окружности, частично наложенные друг на друга. Окружности — это множества. Закрашенная область, принадлежащая одновременно каждой окружности, образованная путем наложения — это область пересечения.

Рис. 1. Диаграмма Эйлера для пересечения множеств.

Круги Эйлера представляют собой простой инструмент, который доходчиво объясняет суть основ теории множеств. Широко известен цикл работ Леонарда Эйлера под названием «Письма к немецкой принцессе о разных физических и философских материях», написанный для дочерей маркграфа Бранденбург-Шведт. В письмах 102 – 104 второго тома этого произведения использован данный графический метод.

Рис. 2. Портрет Леонарда Эйлера.

Определение результатов операций над множествами с использованием кругов Эйлера значительно облегчает решение логических задач.

Таблица истинности

В алгебре логики объектом, к которому применяются логические операции, является высказывание. Оно представляет собой некоторое повествовательное предложение, содержание которого можно однозначно определить как истинное или ложное. Если высказывание истинно, то его обозначают единицей, если ложно — то это ноль.

Например, высказывание «Москва — столица РФ» истинное высказывание. «Площадь квадрата определяется как сумма его сторон» — это ложное высказывание.

Высказывание не может быть вопросительным или побудительным предложением, числовые выражения, которые не содержат логических операций, или содержащие переменные, также не являются высказываниями.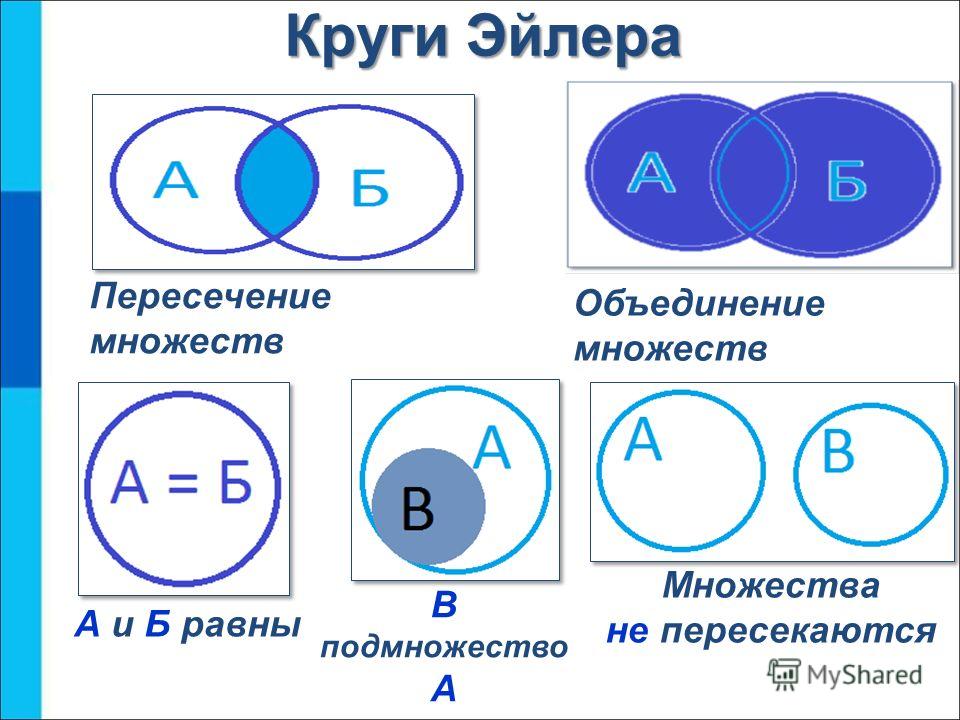

Для обозначения всех возможных вариантов высказываний используются таблицы истинности.

Рис. 3. Таблица истинности для конъюнкции.

По таблице видно, что в результате операции конъюнкции (пересечения) истинное выражение (равно 1) тогда и только тогда, когда оба исходные выражения истинны. Во всех других случаях результат равен нулю (ложь).

Что мы узнали?

Пересечение двух множеств представляет собой третье множество, содержащее элементы общие для исходных множеств. Операцию пересечения можно обозначать по-разному. Пересечение также называется произведением множеств и конъюнкцией. Визуально пересечение удобно представлять с помощью диаграмм Эйлера. Для отображения всех вариантов высказываний используют таблицы истинности. Для пересечения результат принимает значение истина только в случае, когда истинны оба операнда.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Алексей Беляев

  10/10

Оценка статьи

4. 1

Средняя оценка: 4.1

Всего получено оценок: 109.

---

А какая ваша оценка?

примеры определения по алгоритму и применение в 8 классе на уроке информатики

Математика

12.11.21

10 мин.

Математика тесно связана с различными дисциплинами, одной из которых является информатика. В последней применяются массивы, состоящие из чисел, букв и слов. Чтобы научиться работать с этим типом данных, необходимо разобрать объединение и пересечение множеств, примеры которых разбираются на уроках по алгебре в 8 классе средних образовательных школах. Однако для начала нужно изучить теорию.

Оглавление:

• Общие сведения
• Правила чтения
• Пересечение множеств
• Объединение объектов

Общие сведения

Множеством (массивом) называется математический объект или тип данных (в программировании), состоящий из определенного количества простых элементов. Примером является квартира, в которой находится различная техника, мебель и другие элементы. Следует отметить, что множества также бывают и сложными, однако в 8 классе они не рассматриваются.

Обозначается оно двумя способами:

1. Заглавной литерой, после которой идут элементы: D = {1, 2, 3, 4}.
2. Только в фигурных скобках.

Первый случай применяется при решении задач с несколькими различными массивами, чтобы их не перепутать между собой. Если в задании используется только одна последовательность, то короткая запись включает только фигурные скобки.

Исключением считается массив информатики в 8 классе, формулы записи которого предусматривают только поименованные объекты, т. е. любая переменная должна иметь определенный идентификатор (имя).

Правила чтения

Очень важно научиться правильно читать множества. Для примера следует разобрать массив чисел-делителей числа 20, имеющий следующий вид: F = {1, 2, 4, 5, 10, 20}. Принадлежность заданного элемента объекту обозначается символом «∈». Например, запись «5 ∈ F» читается таким образом: элемент «5» принадлежит F. Если число не принадлежит, то знак «∈» перечеркивается, т. е. 7

∉ F.

В программировании массив обозначается заглавной буквой, и указываются все его элементы. В Турбо Паскале, который изучается в школах и профильных училищах на базе 8 классов, используется для записи ключевое слово «array», т. е. var а: array [ 1, 2, 4, 5, 10, 20 ] of integer.

Сочетание слов «of integer» обозначает тип элементов. Читается строка таким образом: тип данных в виде массива «а», содержащего целые числа (integer). Последние указываются в квадратных скобках. Именно ключевое слово «array» и указывает на принадлежность переменной к этому типу данных.

В учебных заведениях с физико-математическим уклоном изучаются в 3 классе примеры пересечения множеств.

Учителя дают только общие понятия в виде презентаций, чтобы постепенно перейти к усиленной программе обучения.

Пересечение множеств

В математике, как и информатике, пересечение множеств является важной операцией. Она позволяет из двух объектов определить только общие элементы, которые в них содержатся. Для обозначения процесса используется специальный знак «∩».

Чтобы не путаться в терминах, математики рекомендуют разобрать основные определения. Пересечение множеств — массив, состоящий только из общих их элементов. Например, дано два объекта S = {1, 2, 4, 6, 7, 8} и I = {3, 4, 7, 12, 18, 20}.

Алгоритм определения

Для определения их пересечения необходимо перебрать все их элементы. Конечный результат «R» вычисляется по такой формуле перебора:

1. Записать пустое множество: R = {}.
2. Акцентировать внимание на S.
3. Первый элемент отсутствует в I, тогда он не записывается в R.
4. Второго также нет.
5. Третий компонент присутствует в S и I. В этом случае число «4» записывается в R, т. е. R = {4}.
6. Четвертого нет в I.
7. Пятый: есть. R = {4, 7}.
8. Последний — отсутствует.
9. Запись результата: {1, 2, 4, 6, 7, 8} ∩ {3, 4, 7, 12, 18, 20} = {4, 7}. Краткая запись имеет следующий вид: S ∩ I = R.

В программировании примером пересечения множеств является объединение двух массивов в один с уникальными элементами. Язык программирования Турбо Паскаль не применяется в написании современных приложений. Он изучается в ознакомительных целях, которые дают базовые знания.

Современные профессиональные языки программирования могут осуществлять доступ к базе данных или к другим массивам информации, в которые не записывается одинаковая информация для экономии оперативной и дисковой памяти компьютера или интернет-ресурса.

Основные свойства

Для решения задач на пересечение объектов, состоящих из числовых или символьных элементов, могут быть полезны свойства. К ним относятся следующие:

1. Бинарность.
2. Коммутативность.
3. Ассоциативность.
4. Нейтральность.
5. Идемпотентность.
6. С пустым объектом.

В первом случае результатом, с точки зрения логической алгебры, являются только 2 значения (пересекает или не пересекает). Коммутативность обусловлена тем, что можно брать первый или второй массив, т. е. S ∩ I = R или I ∩ S = R. Результат от этого не изменится. При рассмотрении трех и более составных объектов справедливо свойство ассоциативности: (S ∩ I) ∩ T = S ∩ (I ∩ T) = (S ∩ T) ∩ I = R.

Четвертое свойство предусматривает существование некоторого нейтрального множества, которое не учитывается при решении.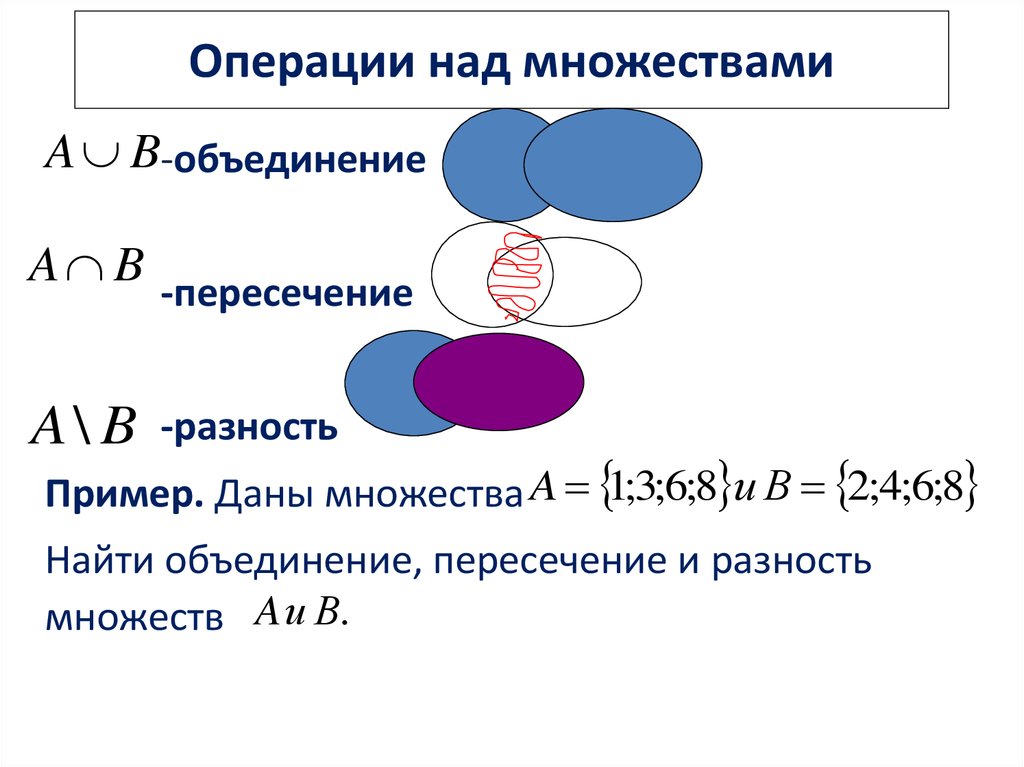 Например, в квартире установлена следующая техника: телевизор, компьютер, кондиционер и т. д. Массивом является «техника», а его компоненты — телевизор, компьютер и другие виды приборов. «Квартира» — нейтральный объект, поскольку он не рассматривается, но включает «технику» и другие группы элементов.

Идемпотентность — пересечение идентичных множеств, т. е. все элементы первого совпадают со вторым. Результатом является искомый объект. Свойство записывается математически таким образом: S ∩ S = S.

Последнее свойство — пересечение объекта с пустым массивом, который обозначается символом «∅». Результатом является ∅, поскольку оно не содержит общих элементов с исходным.

Объединение объектов

Объединение множеств — математическая операция, которая предусматривает создание массива из всех их элементов. Например, даны два объекта S = {1, 2, 4, 6, 7, 8} и I = {3, 4, 7, 12, 18, 20}. Чтобы их объединить необходимо воспользоваться следующей методикой:

1. Записать результирующий массив: R = {}.
2. Добавить в R все элементы: R = {1, 2, 4, 6, 7, 8, 3, 4, 7, 12, 18, 20}.
3. Выполнить сортировку элементов по возрастанию: R = {1, 2, 3, 4, 4, 6, 7, 7, 8, 12, 18, 20}.
4. Исходя из условия задачи, убрать повторяющиеся элементы: R = {1, 2, 3, 4, 6, 7, 8, 12, 18, 20}.

Операция довольно простая, поскольку разобраться с ней не составит труда. При написании программы на языке программирования высокого уровня (например, python) необходимо избегать дублирования элементов. Перед записыванием информации в файл или базу данных нужно убрать одинаковые компоненты при помощи встроенных функций.

Таким образом, изучать операции над множествами необходимо, поскольку эти знания пригодятся при решении сложных задач по высшей математике, а также написании программ на высокоуровневых языках программирования.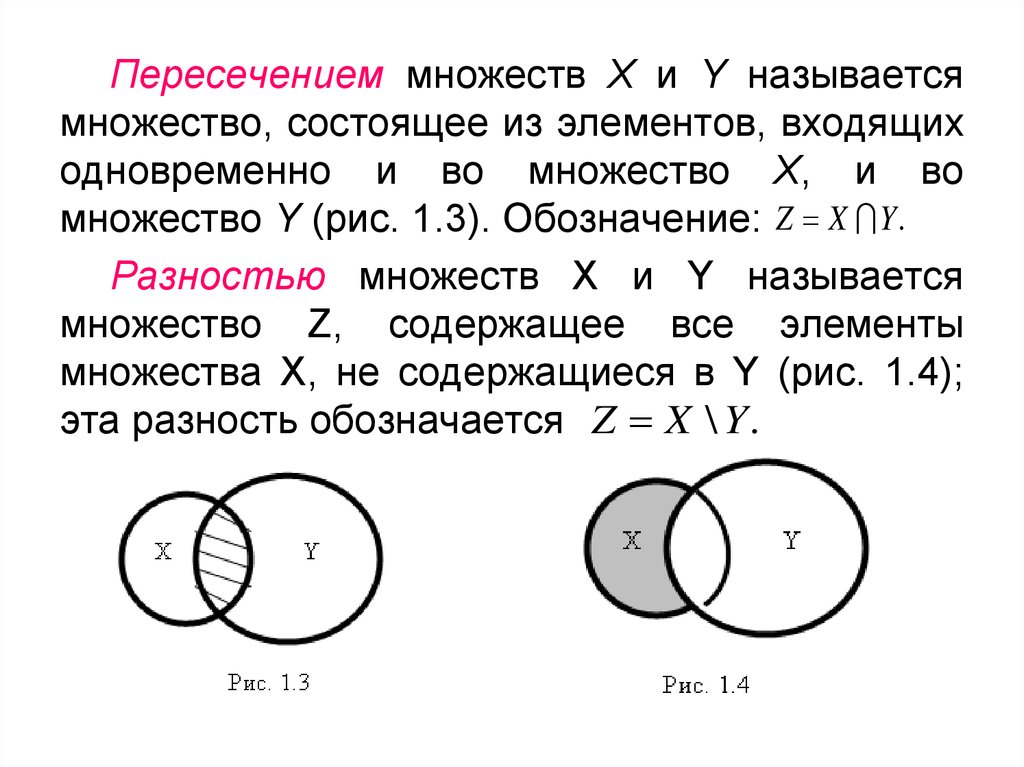

Пересечение множеств – определение и примеры

Понятие пересечения не ограничивается только теорией множеств. На самом деле это широко распространенное математическое понятие. Это одно из распространенных понятий евклидовой геометрии и теории множеств. Интуитивно говоря, всякий раз, когда мы пересекаем два или более объектов, это обычно приводит к меньшему объекту.

Однако в теории множеств пересечение — это другая операция. Мы знаем, что можем комбинировать разные наборы различными способами, чтобы получить больше наборов. Эти комбинации называются операцией. Операция — это действие, в котором мы можем комбинировать разные наборы для формирования нового набора с определенными свойствами.

В этой лекции мы обсудим операцию, известную как Пересечение множеств.

Пересечение множеств A и B можно определить как новое множество, содержащее общие элементы A и B.

В этой статье мы рассмотрим следующие темы:

• наборов?
• Обозначение пересечения множеств.
• Представление пересечения множеств с помощью диаграмм Венна.
• Пересечение Против. Непересекающиеся множества.
• Свойства пересекающихся множеств.
• Examples
• Practice Problems

Before moving forward, you may consider refreshing your knowledge on the following prerequisites:

• Describing Sets
• Sets Notation
• Subset
• Universal Set

What is the Intersection наборов?

Всякий раз, когда мы говорим о пересечении двух множеств, имеется в виду результирующее множество, содержащее все общие элементы между этими двумя множествами. В качестве альтернативы мы также можем сказать, что он содержит все элементы одного множества, которые также принадлежат другому множеству.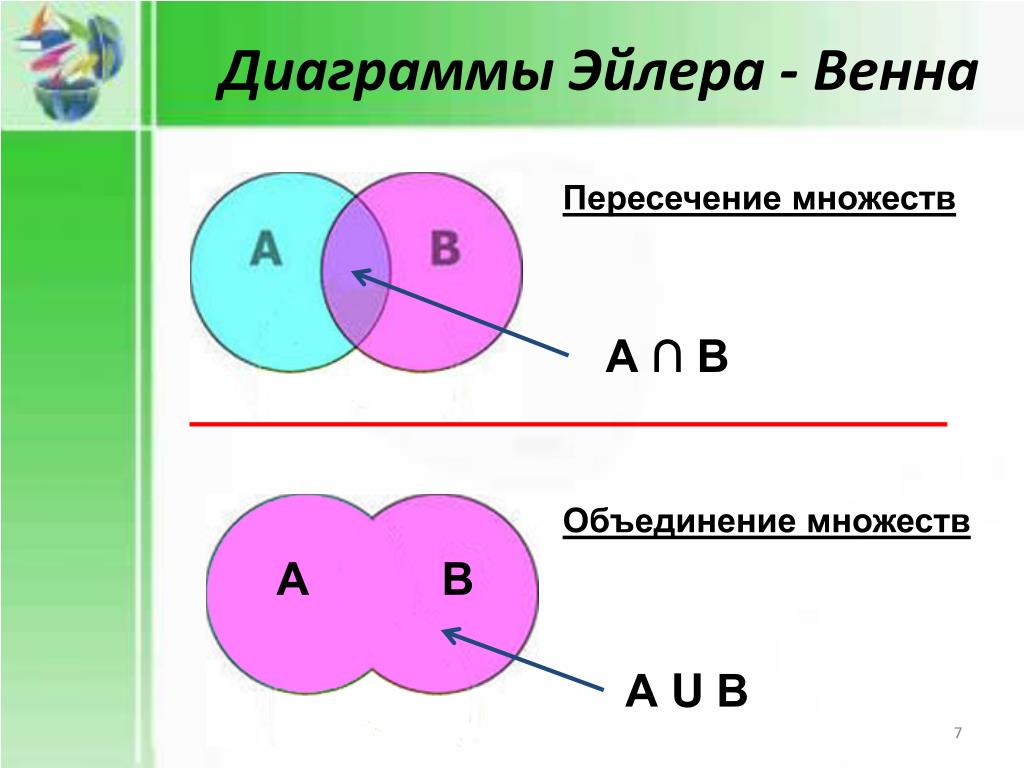

Предположим, что у нас есть два множества, A и B, тогда их пересечение приводит к новому множеству, содержащему все общие элементы между A и B.

Если мы говорим с точки зрения математики, любой элемент является частью пересечения тогда и только тогда, когда он является элементом обоих вовлеченных множеств (или более).

Мы будем обсуждать свойства пересечения далее в лекции, а пока давайте придерживаться понимания того, что пересечение является ассоциативной и коммутативной операцией. 9Пример 1 пересечение множеств.

Решение:

Как известно, пересечением двух множеств является множество, содержащее общие элементы обоих множеств; таким образом, наш новый набор будет иметь вид:

{4, 9}

Мы можем заметить, что 4 и 9 являются единственными общими элементами как для A, так и для B. Таким образом, множество, содержащее оба этих элемента, будет пересечением наборы.

Обозначение пересечения множеств

Углубившись в пересечение множеств, наш следующий шаг — поговорить об обозначениях, используемых для представления пересечения множеств. Пересечение между любыми двумя множествами, A и B, представлено символом «∩» . Подобно символу, используемому для объединения наборов, этот символ используется между операндами. Операндами в данном случае являются имена, обозначающие наборы.

Этот метод записи называется «инфиксной записью». В этой записи оператор окружен операндами. Оператор в нашем случае ‘∩’. Чаще всего используется для обозначения бинарных операций. Мы знаем, что пересечение, как объединение множеств, также является бинарной операцией.

Примером этого может быть следующее:

A = {0, 0, 0, 4}

B = {2, 6, 9}

Тогда пересечение этих множеств обозначается:

A ∩ B

Итак, всякий раз, когда мы хотим выразить пересечение между двумя множествами, мы делаем это символически следующим образом. Это выражение множества A, пересекающего множество B. 

Давайте решим несколько примеров, чтобы понять пересечение множеств.

Пример 2

Если множества A и B определены как:

A = {1, 12, 14, 11, 13, 7, 9, 17, 19}

15 , 14, 2, 1, 6, 9, 0}

Найдите пересечение множества A и B.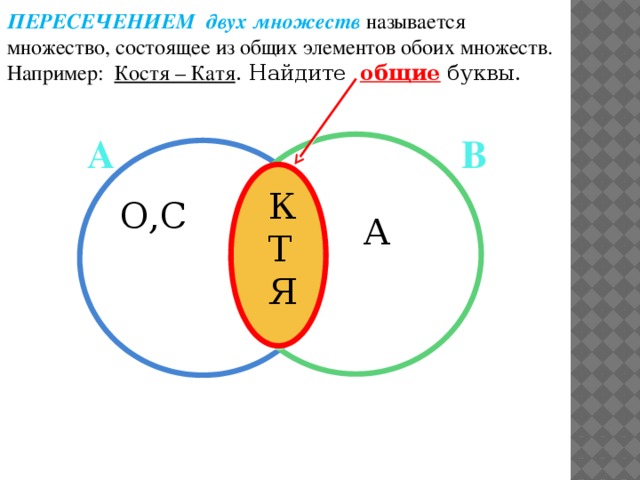

Решение:

Пересечение двух множеств определяется как множество, содержащее элементы множества A, которые также присутствуют в наборе Б; другими словами, общие элементы.

Как мы видим, 12, 14, 1, 9 — это элементы, присутствующие как в множестве A, так и в множестве B. Таким образом, мы имеем пересечение множеств, равное:

A ∩ B = {12, 14, 1, 9}

Представление пересечения с помощью диаграммы Венна

Как мы неоднократно подчеркивали, насколько важны диаграммы Венна для визуализации множеств и различных операций, которые мы можем выполнять над ними.

Итак, давайте кратко расскажем о диаграммах Венна. Диаграмма Венна является наиболее подходящим инструментом для всестороннего понимания операций над множествами. Они используются только для представления конечных множеств. Вся область, охватываемая кривой, представляется как одно множество. Принимая во внимание, что элементы этого конкретного набора представлены точками внутри области диаграммы.

Допустим, U представляет универсальное множество, множества A и B являются подмножествами этого универсального множества. Например, если A = {a, b, c, d, e} и B = {a, e, i, o, u}, то их пересечение таково:

A ∩ B = {a, e}

A’ и ‘e’ — единственные два общих элемента между множествами A и B.

Чтобы изобразить их на диаграмме Венна, мы будем использовать две окружности, одну для множества A и одну для множества B. универсальное множество U , в данном случае — это множество алфавитов, которым принадлежат оба множества A и B. Ниже приведено представление перекрестка на диаграмме Венна:

Заштрихованная синяя область представляет собой пересечение между A и B.

Здесь мы показываем только два набора. Диаграмму Венна для любой операции можно построить, используя несколько наборов, если они конечны.

Давайте решим несколько примеров, чтобы научиться строить нашу собственную диаграмму Венна.

Пример 3

Рассмотрим набор A = {3, 6, 9, 12} и набор B = {0, 3, 5, 8, 12}. Покажите пересечение между A и B через диаграмму Венна. Пусть множество U = {множество целых чисел до 20}.

Решение:

Пересечение между двумя множествами A и B можно определить как:

A = {3, 6, 9, 12}

And,

B = {0, 3, 5, 8, 12}

Пересечение:

A ∩ B = {3, 12}

Представление диаграммы Венна для пересечения множеств A и B:

Пересекающиеся и непересекающиеся множества

Пересечение двух множеств также является другим способом использования логики «И». Это означает, что вы также можете использовать слово «И» для обозначения пересечения. Но как это отразится на реальных примерах?

Предположим, вы должны найти вероятность одного события и другого события; это выражается с помощью пересечения множеств. Если вероятность того, что оба события произойдут вместе, отлична от нуля, мы можем сказать, что множества пересекаются. Наоборот, если вероятность того, что оба события произойдут вместе, равна нулю, мы говорим, что это непересекающиеся множества.

Рассмотрим понятие непересекающихся множеств более ясно.

Если у нас есть два набора и некоторые элементы, присутствующие в одном наборе, которые также присутствуют в другом наборе, мы называем наборы пересекаются.

Однако, если между множествами нет общего элемента, они называются непересекающимися множествами. На пересечении наборов нет элементов. Например, {4, 9, 10} и {1, 5} являются непересекающимися множествами, поскольку между ними нет общих элементов. Следовательно, их пересечение является нулевым множеством.

A ∩ B = Ⲫ

Свойства пересечения множеств

Мы изучили несколько свойств других операций над множествами; теперь мы рассмотрим свойства пересечения множеств:

Коммутативность Свойство:

Любая операция считается коммутативной, если изменить порядок операндов, но это изменение не влияет на результат.

Это одно из самых фундаментальных свойств нескольких бинарных операций. Эффект этого свойства заключается в том, что мы можем изменить положение операндов, не беспокоясь о каких-либо расхождениях в результате.

Коммутативный закон пересечения утверждает, что:

На результат не влияет порядок операционных наборов.

Итак, если у нас есть два множества, A и B, то математически коммутативность будет следующей:

A ∩ B = B ∩ A

Давайте решим пример, чтобы понять это.

Пример 4

Учитывая, что множества A и B: что для них выполняется свойство коммутативности пересечения.

Решение:

Наш первый шаг состоит в том, чтобы найти левую часть уравнения:

A ∩ B = {3, 6, 9, 10}  ∩  {1, 3, 5, 8, 10}

A ∩ B = {3, 10}

Затем находим правую часть уравнения:

B ∩ A = {1, 3, 5, 8, 10}  ∩ {3, 6, 9, 10}

B ∩ A = {3, 10}

Из приведенных выше правой и левой частей уравнения мы можем доказать, что свойство коммутативности выполняется для пересечения, поскольку обе стороны равны .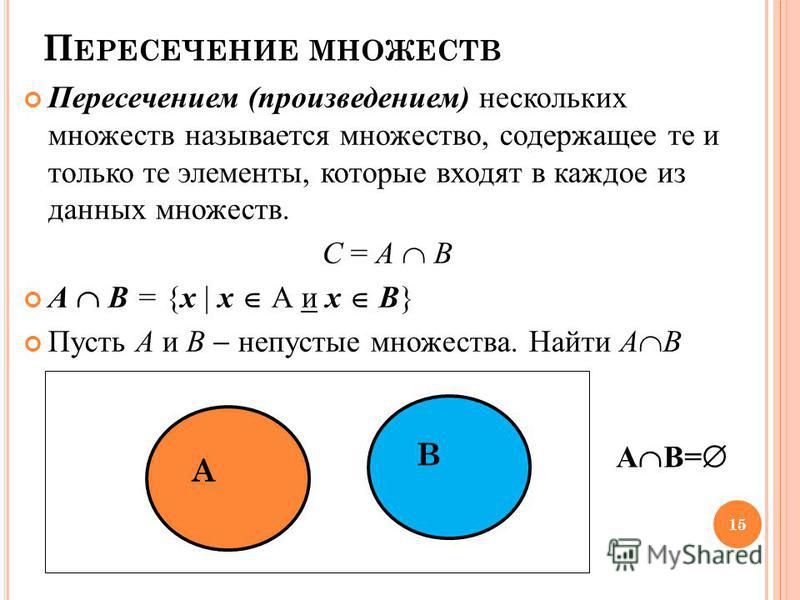

Ассоциативное свойство:

Это свойство означает, что вы можете сдвигать или переставлять скобки, не беспокоясь об изменении результатов уравнения.

Как обсуждалось для свойства коммутативности, ассоциативность также является более широкой математической концепцией и не ограничивается только теорией множеств. Подобно коммутативному свойству, оно также является одним из фундаментальных свойств бинарных операций. Он в основном используется в доказательствах, где требуется перестановка каких-либо символов. По сути, ассоциативность связана с расположением любых операндов в любом уравнении.

Однако ассоциативный закон пересечения утверждает, что изменение положения скобок в любом выражении множеств, включающем операцию пересечения, никоим образом не повлияет на результаты.

Группировка наборов для пересечения не повлияет на результат.

Аналогично, если у нас есть три множества, а именно A, B и C, на которых должно быть выполнено пересечение Математически, свойство ассоциативности пересечения записывается как:

(A ∩ B) ∩ C = A ∩ (B ∩ C)

Давайте решим пример, чтобы понять это.

Пример 5

Докажите, что свойство ассоциативности пересечения выполняется для следующих множеств: = {1, 8, 9}

Решение:

Решая сначала левую часть уравнения:

(A ∩ B) = {1, 5, 8}  ∩  {2, 5, 8, 9} = {5, 8}

(A ∩ B) ∩ C = {5, 8} ∩ {1, 8, 9} = {8}

Теперь решим правую часть уравнения: 

(B ∩ C) = {2, 5, 8, 9}  ∩  {1, 8, 9} = {8, 9}

A ∩ (B ∩ C) = {1, 5, 8} ∩ {8, 9} = {8} 

Из левой и правой частей уравнений можно доказать, что свойство ассоциативности выполняется для множеств A , B и C.

Свойство идемпотента:

Свойство идемпотента утверждает, что пересечение любого множества с самим собой даст само множество. Допустим, у нас есть множество A; то свойство идемпотента утверждает, что:

A ∩ A = A

Мы знаем, что общие элементы между двумя идентичными множествами будут исходными элементами множества.

Свойство U:

Свойство универсального множества утверждает, что пересечение A с универсальным множеством приведет к A .

Это можно понять, если представить А как подмножество универсального множества, поскольку элементы А будут присутствовать в универсальном множестве. Мы можем с уверенностью сказать, что их пересечение даст A как пересекающееся множество.

A ∩ U = A

Свойство Ⲫ:

Свойство нулевого множества гласит, что пересечение любого множества A с нулевым множеством приведет к нулевому множеству. Математически это можно записать так:

A ∩ Ⲫ = Ⲫ

Практические задачи

1. Найдите пересечение следующих множеств: A = {множество натуральных чисел}, B = {множество натуральных чисел}, B = {множество натуральных чисел}, целые числа}.
2. Нарисуйте диаграмму Венна пересечения точек A = {0, 3, 5, 7, 9, 10} и В = {2, 4, 6}.
3. Объясните, являются ли приведенные выше множества непересекающимися или пересекающимися множествами. Назови причины.
4. Использование U = множество натуральных чисел и A = {1, 2, 3, 4, 5, 6, 7, 8} удовлетворяют свойству U.
5. Если A = {a, b, e, g, j }, B = {d, h, e, g} и C = {c, g, h}. Найдите пересечение между:

1. A и C
2. B и C
3. A, B и C.

Ответы

1. {множество натуральных чисел}
2. Оставлено читателю
3. Непересекающиеся множества, без общих элементов
4. Оставлено читателю
5. (1): {g}, (2): {g, h}, (3): {g}

Предыдущий урок | Главная страница | Следующий урок

Перекресток | Математические вкусности

Форма поиска

Поиск

В предыдущих уроках мы использовали диаграммы Венна для представления отношений между множествами. Давайте посмотрим на взаимосвязь множеств, описанных в примере 1 ниже.

Пример 1: Пусть X  = {1, 2, 3} и пусть Y  = {3, 4, 5}. Что общего между элементами X и Y ?

Анализ: Мы нарисуем диаграмму Венна из двух перекрывающихся кругов. Элементы, общие для обоих наборов, будут размещены в средней части, где круги перекрываются.

Решение:

Объяснение: Кружок слева представляет набор X , а кружок справа представляет набор Д . Заштрихованная область посередине — это то, что у них общего. Это их пересечение. Пересечение множеств X и Y равно 3.

Диаграмма Венна в примере 1 позволяет легко увидеть, что число 3 является общим для обоих множеств. Таким образом, пересечение X и Y равно 3, и это записывается как:

X ∩ Y = {3}

Пересечение двух множеств, X и Y, — это набор элементов, общих для X и Y . Он обозначается как X ∩ Y, и читается как « X пересекает Y ».

Таким образом, пересечение двух множеств — это множество элементов, общих для обоих множеств. Давайте рассмотрим еще несколько примеров пересечения.

Пример 2: Let  = {число чисел},  P  = {кратное 3 меньше 20} и  Q  = {четные числа меньше 20}. Нарисуйте и подпишите диаграмму Венна, чтобы показать пересечение P и Q .

Анализ: начните с заполнения элементов на пересечении. Поскольку P  = {3, 6, 9, 12, 15, 18} и  Q  = {2, 4, 6, 8, 10, 12, 14, 16, 18}, мы знаем, что 6, 12 и 18 будет заполнен первым.

Решение:

Обозначение: P ∩ Q = {6, 12, 18}

---

Другой способ определения пересечения двух множеств выглядит следующим образом:

A   ∩   B  = { x | x A и x B }

Процедура для рисования для рисования двух сетей.

Процедура рисования пересечения двух перекрывающихся множеств

Шаг 1:

Шаг 2:

Шаг 3:

Давайте посмотрим на пересечение других типов множеств. В примере 3 ниже данные наборы не перекрываются.

Пример 3: Пусть  = {животные},  A  = {собаки} и  B  = {кошки}. Нарисуйте и подпишите диаграмму Венна, чтобы показать пересечение A и B .

Анализ: наборы A и B не пересекаются. Эти множества не пересекаются и не имеют общих элементов.

Решение:

Обозначение: A ∩ B = Ø

---

Два набора a и B — это, если их интерс. Это обозначается как A ∩ B = Ø , , где Ø    – нулевое или пустое множество .

Напомним, что a Универсальное множество — это множество всех рассматриваемых элементов, обозначаемое прописной буквой. Все остальные множества являются подмножествами универсального множества. Таким образом, в каждом приведенном выше примере кружки являются подмножествами универсального набора.  Мы рассмотрели пересечение перекрывающихся множеств и непересекающихся множеств. Давайте посмотрим на пересечение одного множества, содержащегося внутри другого.

Пример 4:  Пусть C = {a, r, e} и D = {f, a, i, r, e, s, t}. Нарисуйте и подпишите диаграмму Венна, чтобы показать пересечение множеств C и D.

Анализ: C является подмножеством D. Напомним, что это обозначается CD D.

Решение:

Объяснение. Оказывается, C ∩ D = {a, r, e}, равное множеству C.

In example 4, since  C     D   , we get that   C   ∩   D  =  C . Это отношение определено ниже.

Ниже показана процедура рисования пересечения одного множества, содержащегося в другом.

Процедура рисования пересечения одного множества, содержащегося внутри другого
Шаг 1:	Нарисуйте один круг внутри другого круга.
Шаг 2:	Запишите элементы во внутреннем круге.
Шаг 3:	Запишите оставшиеся элементы во внешнем круге.

Давайте посмотрим, сможете ли вы выполнить задание, представленное в примере 5.

Пример 5:  Учитывая приведенную ниже диаграмму Венна, назовите участника Band, который не входит ни в Band, ни в Chorus.

Анализ: эта задача требует от нас найти участника группы, который не находится на пересечении группы и хора.

Решение: 

Объяснение: Сэм, Лорри и Рауль являются членами только группы Band. Кроме того, эти студенты не в оркестре и хоре.

---

Резюме: Пересечение двух множеств A и B, обозначаемое A ∩ B, представляет собой множество элементов, общих для A и B. Формальное определение пересечения показано ниже.

A ∩ B  = {  x  | x   A  и x B }

---

Упражнения

Подпишите ответ на каждый вопрос и подпишите его. Выберите свой ответ, нажав на соответствующую кнопку. Обратная связь по вашему ответу представлена ​​в ОКНО РЕЗУЛЬТАТЫ. Если вы допустили ошибку, обдумайте свой ответ еще раз, а затем выберите другую кнопку.

1.	Given   = {apples, oranges, bananas, pears} and   = {oranges, pears, grapes}, what is   ∩   ?
	P ∩ Q = Ø  P ∩ Q = {апельсины, груши}  P ∩ Q = {яблоки, апельсины}  Все вышеперечисленное. ЯЩИК РЕЗУЛЬТАТОВ:

2.	Учитывая  = {четные целые числа} и  = {простые числа}, что такое 9 ∩ ?
	A ∩ B = Ø  A ∩ B = {0, 2, 4}  A ∩ B = {2}  Ничего из вышеперечисленного. ЯЩИК РЕЗУЛЬТАТОВ:

3.	Указано = {13, 21, 34, 55, 89} и = {однозначные цифры}, что является }14141414141414141412?
	X ∩ Y = Ø   X  ∩ Y = {13, 34, 55}   X  ∩ Y = {13, 21, 34, 55, 89}  Ничего из вышеперечисленного. ЯЩИК РЕЗУЛЬТАТОВ:

4.	Дано   = {суббота, воскресенье} и   = {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}, чему равно  ?
	C ∩ D = {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}  C ∩ D = {понедельник, вторник, среда, четверг, пятница}  C ∩ D = {суббота, воскресенье}  Все выше. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт