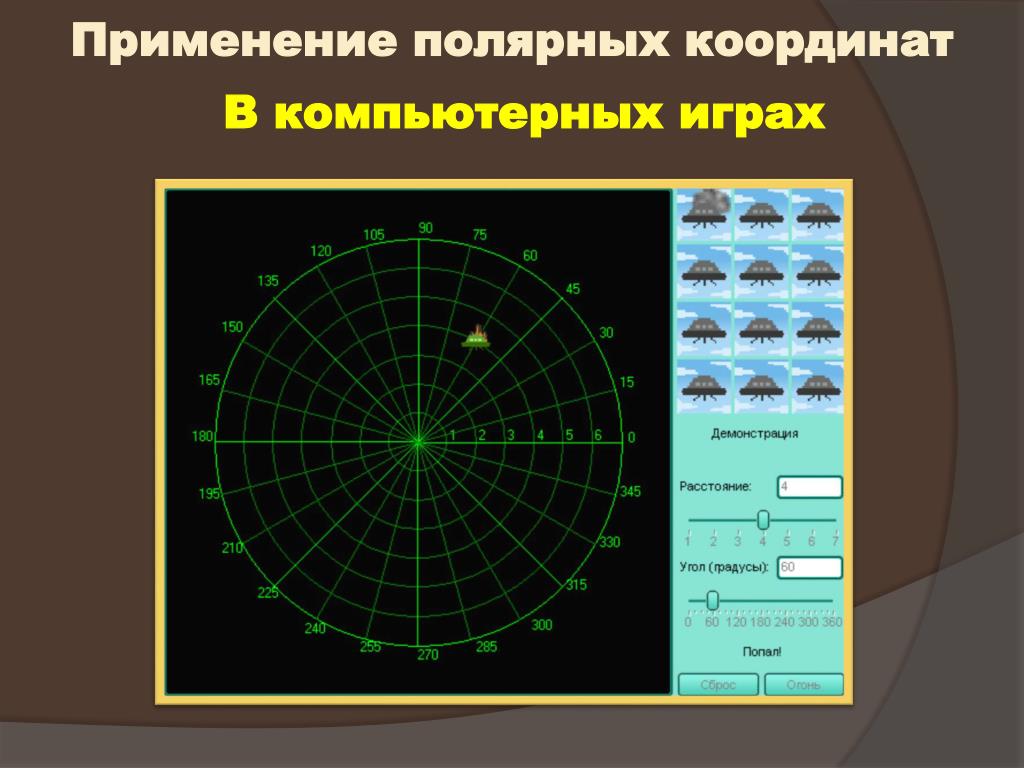
Полярная система координат с примерами и образцами решения
Оглавление:
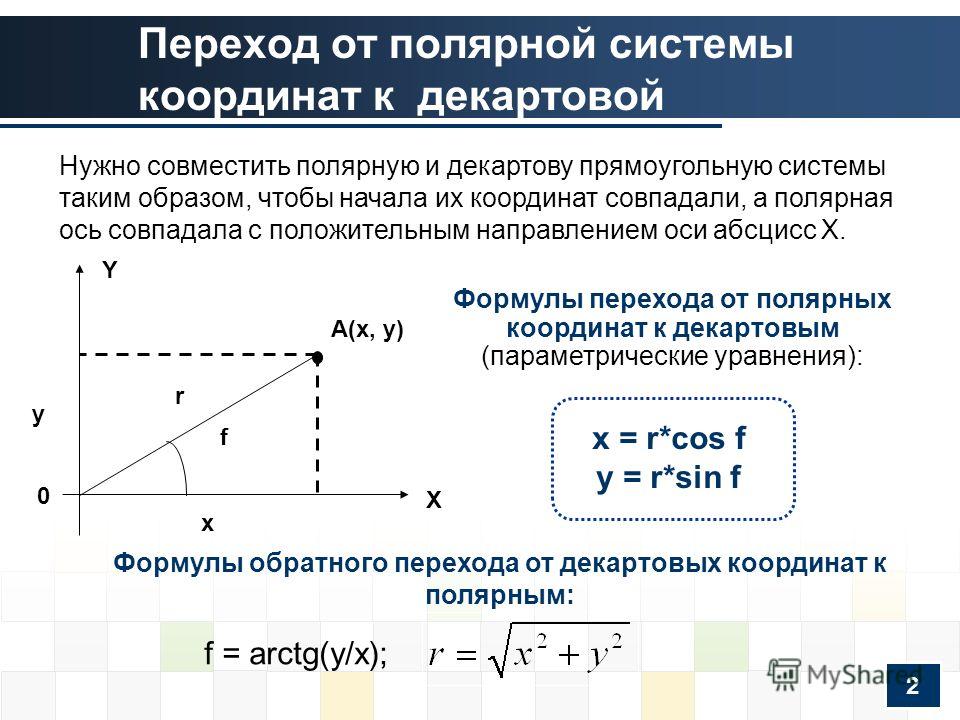
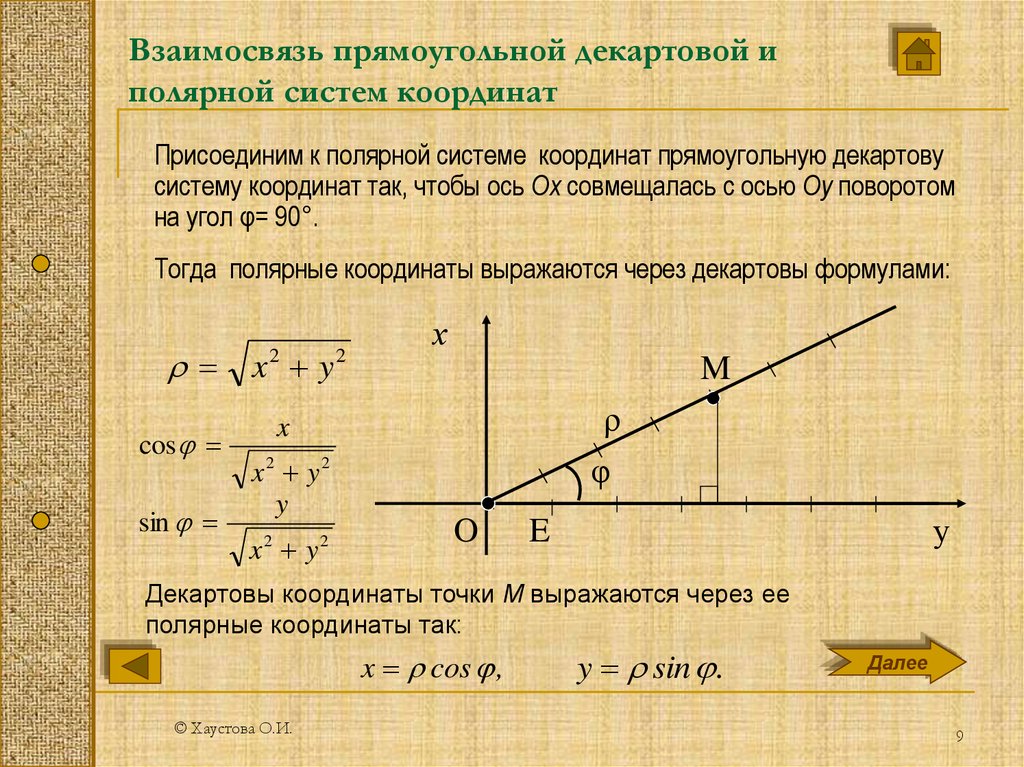
Полярная система координатОпределение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат . Пусть — точка на плоскости, . Полярными координатами точки М называются числа — длина ее радиус-вектора (полярный радиус) и — угол, образованный радиус-вектором с положительным направлением оси (полярный угол), . Точка О при этом называется полюсом, а полуось — полярной осью.
Замечание. Зависимость между прямоугольными и полярными координатами точки М задается в виде:
Рис. 1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя прямоугольную систему координат:
Задача №83
Построим на плоскости линию, заданную уравнением: — лемниската.
Решение:
.
Вычислим значения при различных значениях
Проводим лучи из начала координат под углами к оси и на них откладываем отрезки длины , получим :
Рис. З. Лемниската
З. Лемниската
Задача №84
а) Построим кривую — кардиоида. Рассуждая, как в примере 1 получим:
Рис.4. Кардиоида .
б) — окружность.
Рис.5. Окружность .
в) — спираль Архимеда.
Рис.6. Спираль Архимеда .
г) — трехлепестковая роза.
Рис.7. Трехлепестковая роза .
Упражнение 1. Построить графики из примеров 1 и 2 в системе Mathematica (использовать функцию PolarPlot, см.пример 10 § 17).
Замечание. Если в определении 1 отбросить требование и не требовать , то формулы (1) будут задавать непрерывное отображение точек плоскости на точки плоскости .
При этом, если , то векторы сопаправлены, если , то — противоположно направлены:
Тогда, с учетом (1), кривую можно рассматривать как заданную параметрически в виде: — параметр.
В этом случае па кривой получаются два дополнительных лепестка, когда , соответствующие случаю (см.пример 10 § 17). Фактически, такая кривая — это параметрическая кривая:
(см.пример 9 § 30).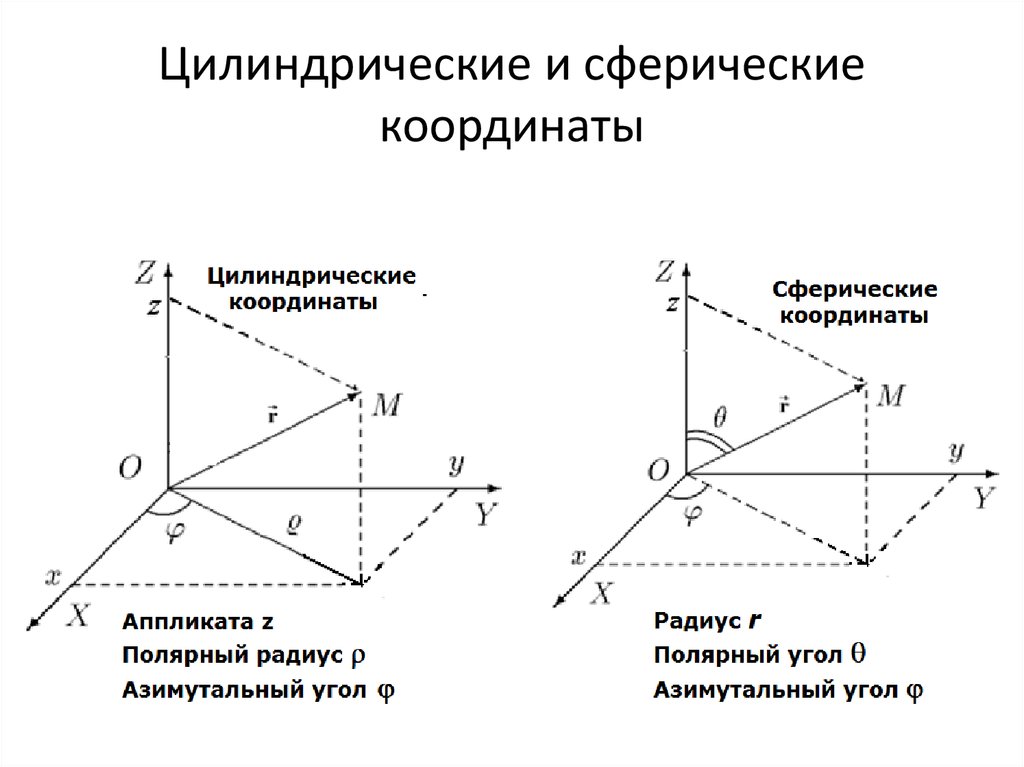
На кривой каждый из лепестков проходится дважды и задается параметрически формулами:
(см.пример 10 § 30).
Упражнение 2. Используя команду PolarPlot построить графики , (сравни с примерами 9 — 11 § 30).
Пусть — кривая в полярной системе координат, — непрерывна при . Рассмотрим на плоскости криволинейный сектор Найдем его площадь. Заметим, что сектору Ф соответствует обычная криволинейная трапеция па плоскости
Разобьем фигуру Ф на n частичных фигур лучами На плоскости получаем обычное разбиение трапеции:
Рассмотрим, например, нижние суммы Дарбу:
Рис.8. Нижняя сумма Дарбу .
Каждое слагаемое в нижней сумме равно площади обычного кругового сектора радиуса , где ,
таким образом,
для нижних сумм и
для верхних сумм Дарбу, где Суммы (2) и (3) — суммы Дарбу для функции (см.формулы (5) § 24), поэтому
Задача №85
Найти площадь ограниченную лемнискатой (см.пример 1).
Решение:
По формуле (4):
площадь одного лепестка.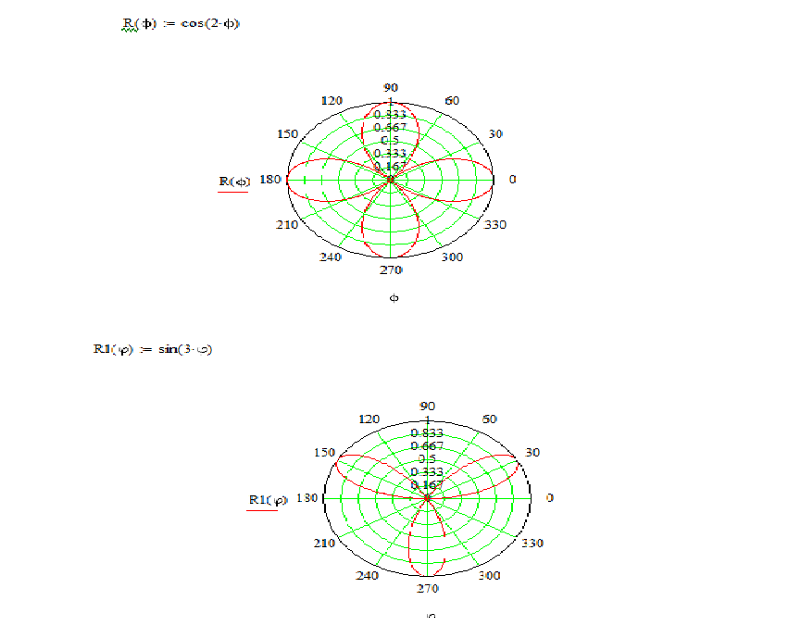
Поэтому
Задача №86
Найти площадь фигуры ограниченной линиями: и (вне круга).
Рис.8. Фигура .
Решение:
Найдем точки пересечения кривых: ; . По формуле (4):
Задача №87
. Вычислим
Преобразуем уравнение — окружность радиуса 1 с центром в точке (1; 0).
Рис.9. Окружность .
При изменении от 0 до окружность проходится дважды и оба раза против часовой стрелки, поэтому (см. § 30) найденное значение интеграла задает удвоенную площадь круга.
Упражнение 3. Пусть
Проверить, что (см. (7) §30):
Упражнение 4. Используя формулу (4), найти площади фигур, ограниченных линиями: (сравнить с примерами 9 — 11 § 30).
Упражнение 5. Найти площадь петли кривой — (Декартов лист).
Рис. 10. Кривая и наклонная асимптота .
Указание. Перейти в полярную систему координат.
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет.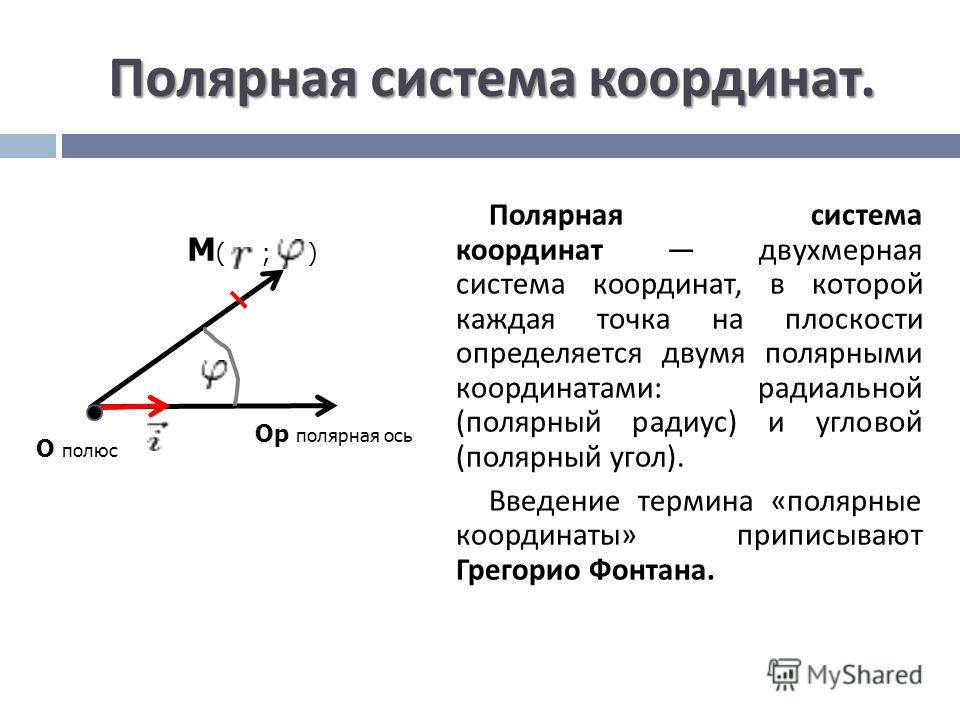 На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа?Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню.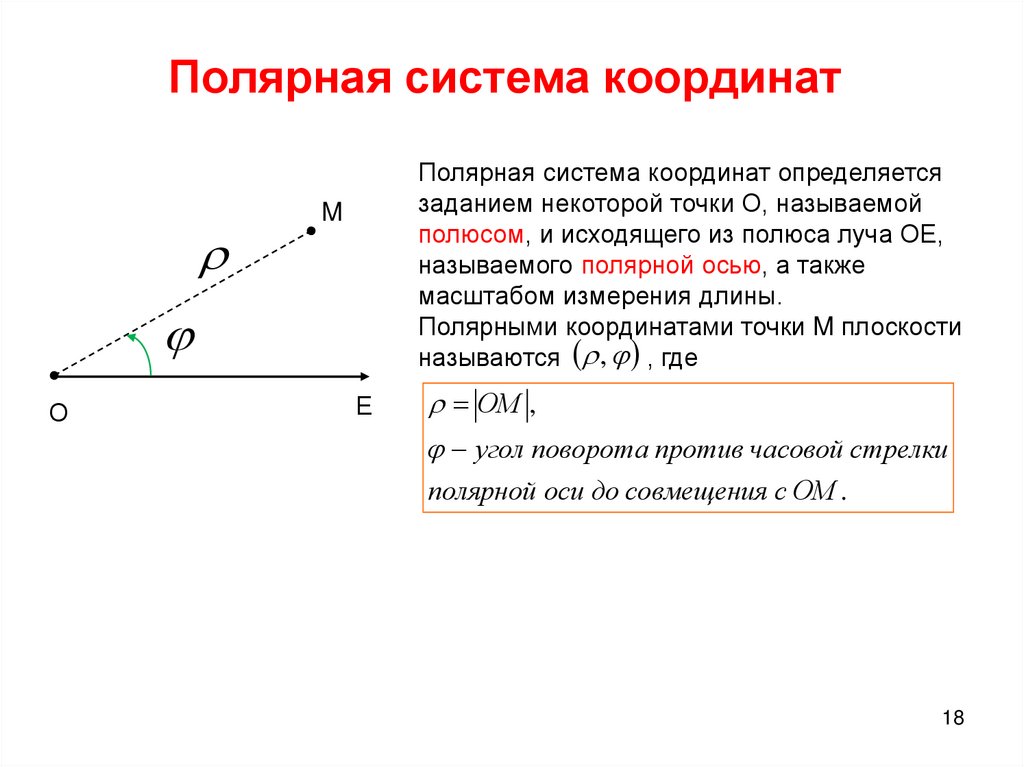
youtube.com/embed/vOuj6t2Zyeg» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/ElMEic2MJ-U» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.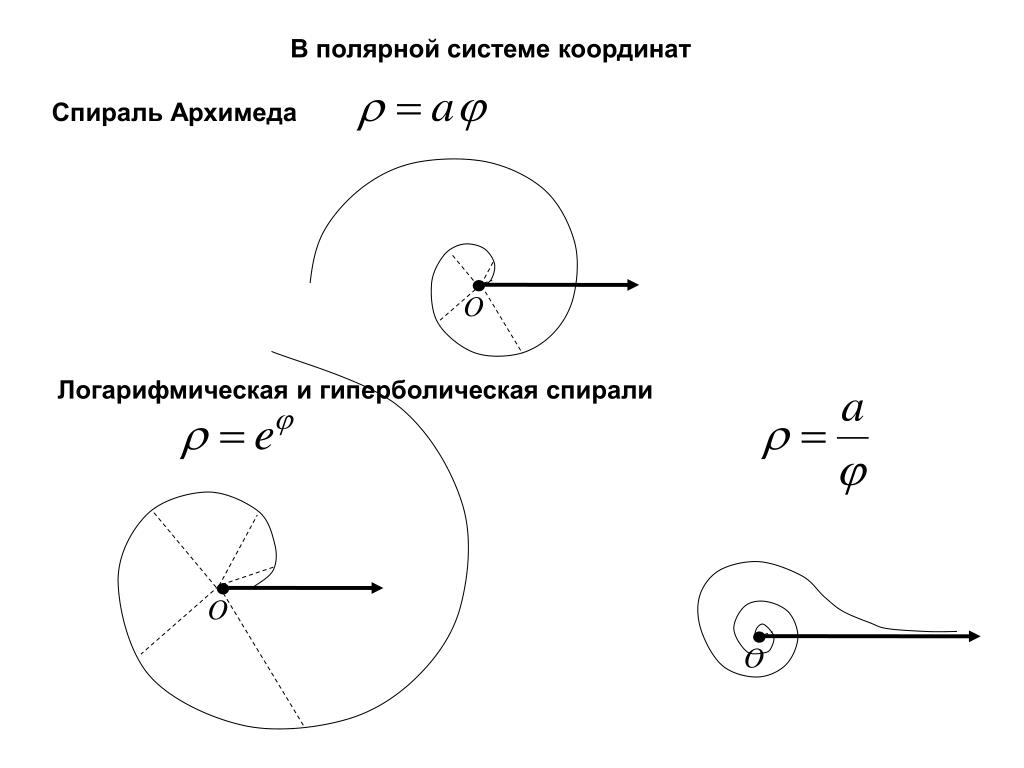
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
5.4: Полярная система координат
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7127
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley State University
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
- Как определяются полярные координаты точки на плоскости?
- Как преобразовать полярные координаты в прямоугольные?
- Как нам преобразовать прямоугольные координаты в полярные?
- Как правильно построить графики полярных уравнений как вручную, так и с помощью калькулятора?
Начало действия
На диаграмме нанесена точка с координатами \((\sqrt{3}, 1)\). Определите значение \(r\) и угол \(\theta\) в радианах и градусах.
До сих пор в нашем исследовании тригонометрии всякий раз, когда мы рисовали уравнение или определяли точку на плоскости, мы использовали прямоугольные (или декартовы) координаты. Использование этого типа системы координат произвело революцию в математике, поскольку обеспечило первую систематическую связь между геометрией и алгеброй. \circ\).
\circ\).
Полярная система координат
В прямоугольной системе координат мы используем два числа в виде упорядоченной пары для определения точки на плоскости. Мы делаем то же самое для полярных координат, но теперь первое число представляет собой расстояние от точки, а второе число представляет собой угол. В полярной системе координат
- Число \(r\), называемое радиальным расстоянием , — направленное расстояние от полюса до точки \(P\).
- Число \(\theta\), называемое полярным углом , является мерой угла между полярной осью и отрезком линии \(OP\). (Для измерения угла можно использовать как радианы, так и градусы.
 )
)
Условные обозначения для полярных координат
Полярный угол \(\theta\) считается положительным, если он измеряется против часовой стрелки от полярной оси.
Полярный угол \(\theta\) считается отрицательным, если он измеряется по часовой стрелке от полярной оси.
Если радиальное расстояние \(r\) положительно, то точка \(P\) находится в \(r\) единицах от \(O\) вдоль конечной стороны \(\theta\).
Рисунок \(\PageIndex{1}\): Полярные координаты
Если радиальное расстояние \(r\) отрицательно, то точка \(P\) находится в \(|r\) единицах от \(O\) вдоль луча в направлении, противоположном конечной стороне \( \тета\).
Если радиальное расстояние \(r\) равно нулю, то точка \(P\) является точкой \(O\).
Чтобы проиллюстрировать некоторые из этих соглашений, рассмотрим точку \(P(3, \dfrac{4\pi}{3})\), показанную слева на рисунке \(\PageIndex{2}\). (Обратите внимание, что нарисована окружность радиуса \(3\) с центром на полюсе.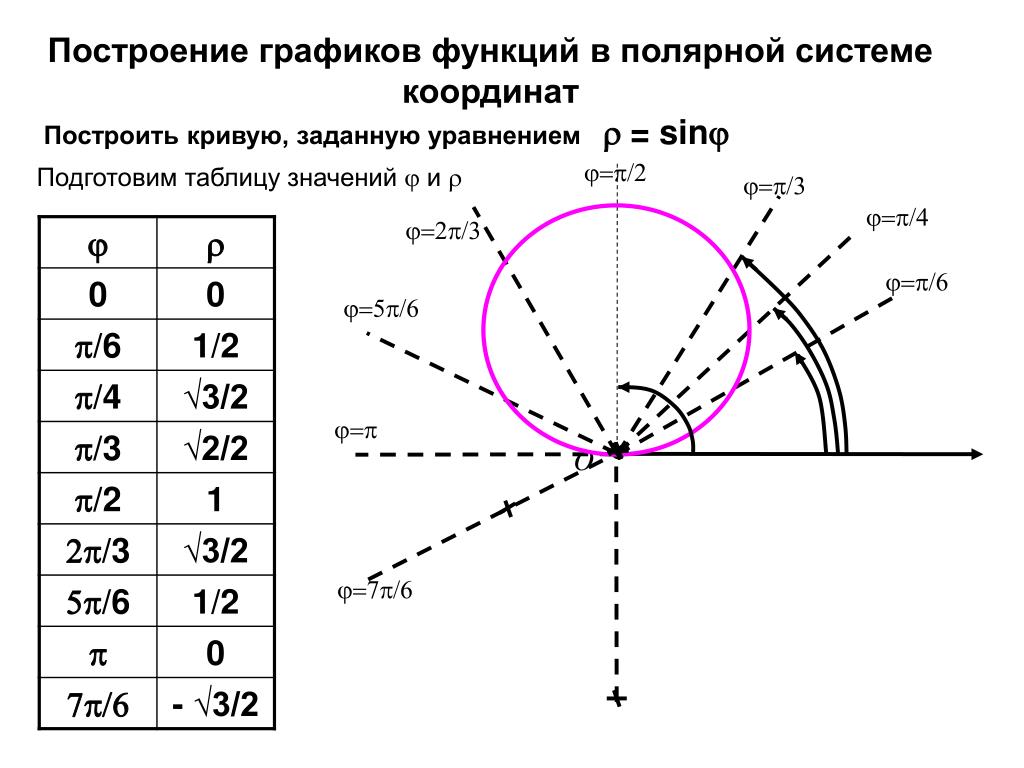
Рисунок \(\PageIndex{2}\): точка с двумя разными наборами полярных координат
Диаграмма справа на рисунке \(\PageIndex{2}\) показывает, что эта точка \(P\) также имеет полярные координаты \(P(-3, \dfrac{\pi}{3})\). Это связано с тем, что когда мы используем полярный угол \(\theta = \dfrac{\pi}{3}\) и радиальное расстояние \(r = -3\), тогда точка \(P\) равна \(3 \) единиц от полюса вдоль луча в направлении, противоположном конечной стороне \(\тета\).
Упражнение \(\PageIndex{1}\)
Поскольку точка с полярными координатами \((r, \theta)\) должна лежать на окружности радиуса r с центром в полюсе, целесообразно размещать точки на сетке концентрических окружностей и лучей, начальная точка которых на столбе, как показано на рисунке \(\PageIndex{3}\). На этой полярной миллиметровке каждое приращение угла равно \(\dfrac{\pi}{12}\) радианам. Например, точка \((4, \dfrac{\pi}{6})\) нанесена на рисунок \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\) : Полярная графическая бумага
Нанесите следующие точки с указанными полярными координатами.
\[(1, \dfrac{\pi}{4}), (5, \dfrac{\pi}{4}), (2, \dfrac{\pi}{3}), (3, \ dfrac{5\pi}{4}), (4, -\dfrac{\pi}{4}), (4, \dfrac{7\pi}{4}), (6, \dfrac{5\pi {6}), (5, \dfrac{9\pi}{4}), (-5, \dfrac{5\pi}{4})\]
- Ответ
В упражнении \(\PageIndex{1}\) мы заметили, что полярные координаты \((5, \dfrac{\pi}{4}), (5, \dfrac{9\pi}{4})\) и \((-5, \dfrac{5\pi}{4})\) определяют одну и ту же точку на плоскости. Это иллюстрирует основное различие между прямоугольными координатами и полярными координатами. В то время как каждая точка имеет уникальное представление в прямоугольных координатах, данная точка может иметь множество различных представлений в полярных координатах. В первую очередь это связано с тем, что полярная система координат использует для своей сетки концентрические окружности, и мы можем начать в точке на окружности, двигаться по окружности и закончить в точке, из которой мы начали. Так как один оборот вокруг окружности соответствует углу \(2\pi\) радиан или \(360^\circ\), мы имеем следующее: 9\круг)\]
Преобразование между полярными и прямоугольными координатами
Теперь у нас есть два способа определения местоположения точек на плоскости. Одна из них — обычная прямоугольная (декартова) система координат, а другая — полярная система координат. В прямоугольной системе координат для нахождения точки используются два расстояния, тогда как в полярной системе координат для нахождения точки используются расстояние и угол. Хотя эти две системы можно изучать независимо друг от друга, мы можем настроить их так, чтобы между двумя типами координат существовала связь. Делаем это следующим образом:
Одна из них — обычная прямоугольная (декартова) система координат, а другая — полярная система координат. В прямоугольной системе координат для нахождения точки используются два расстояния, тогда как в полярной системе координат для нахождения точки используются расстояние и угол. Хотя эти две системы можно изучать независимо друг от друга, мы можем настроить их так, чтобы между двумя типами координат существовала связь. Делаем это следующим образом:
- Мы помещаем полюс полярной системы координат в начало прямоугольной системы координат.
- У нас есть полярная ось полярной системы координат, совпадающая с положительной осью \(x\) прямоугольной системы координат, как показано на рисунке \(\PageIndex{4}\)
Используя тригонометрию прямоугольного треугольника и теорему Пифагора, мы получаем следующие соотношения между прямоугольными координатами \((x, y)\) и полярными координатами \((r, \theta)\): 9{2}\) для определения \(r\) и определения угла \(\theta\), так что
\[\tan(\theta) = \dfrac{y}{x}\], если \(x \ neq 0\)
\[\cos(\theta) = \dfrac{x}{r}\]
\[\sin(\theta) = \dfrac{y}{r}\]
При определении полярные координаты точки, мы обычно выбираем положительное значение для \(г\).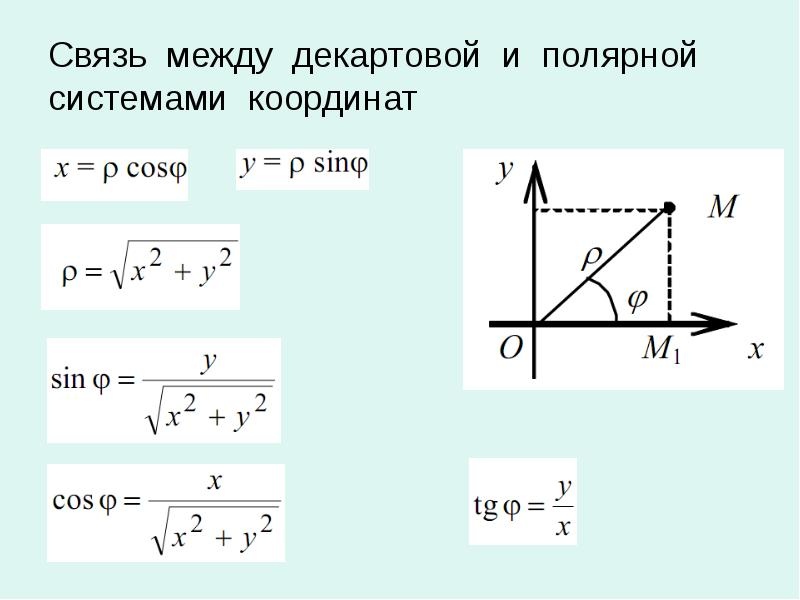 Мы можем использовать обратную тригонометрическую функцию, чтобы помочь определить \(\тета\), но мы должны быть осторожны, чтобы поместить \(\тета\) в правильный квадрант, используя знаки \(х\) и \(у\). Обратите внимание, что если \(x = 0\), мы можем использовать \(\theta = \dfrac{\pi}{2}\) или \(\theta = \dfrac{3\pi}{2}\)
Мы можем использовать обратную тригонометрическую функцию, чтобы помочь определить \(\тета\), но мы должны быть осторожны, чтобы поместить \(\тета\) в правильный квадрант, используя знаки \(х\) и \(у\). Обратите внимание, что если \(x = 0\), мы можем использовать \(\theta = \dfrac{\pi}{2}\) или \(\theta = \dfrac{3\pi}{2}\)
Упражнение \(\PageIndex{3}\)
Определите прямоугольные координаты для каждой из следующих точек в полярных координатах:
\[(3, \dfrac{\pi}{3})\] \[(5 , \dfrac{11\pi}{6})\] \[(-5, \dfrac{3\pi}{4})\]
Когда мы преобразуем прямоугольные координаты в полярные, мы должны быть осторожны и используйте знаки \(x\) и \(y\), чтобы определить правильный квадрант для угла \(\theta\). Во многих ситуациях может быть проще сначала определить опорный угол для угла \(\theta\), а затем использовать знаки \(x\) и \(y\) для определения \(\theta\).
- Ответить
Для каждой точки мы используем уравнения \(x = r\cos(\theta)\) и \(y = r\sin(\theta)\).
 В каждом из этих случаев мы можем определить точные значения \(x\) и \(y\).
В каждом из этих случаев мы можем определить точные значения \(x\) и \(y\).Полярные координаты Прямоугольные координаты 1. \((3, \dfrac{\pi}{3})\) \((\dfrac{3}{2}, \dfrac{3\sqrt{3}}{2})\) 2. \((5, \dfrac{11\pi}{6})\) \((\dfrac{5\sqrt{3}}{2}, -\dfrac{5}{2})\) 3. \((-5, \dfrac{3\pi}{4})\) \((\dfrac{5\sqrt{2}}{2}, -\dfrac{5\sqrt{2}}{2})\)
Пример \(\PageIndex{1}\): (преобразование прямоугольных координат в полярные) 9{2} = 8 \nonumber\]
Поскольку обычно легче работать с положительным значением для \(r\), мы будем использовать \(r = \sqrt{8}\).
Мы также видим, что \(\tan(\theta) = \dfrac{3}{-3} = -1\). Мы можем использовать множество различных значений для \(\theta\), но для простоты мы используем \(\theta\), как показано на диаграмме. Для исходного угла \(\hat{\theta}\) имеем \(\tan(\hat{\theta}) = 1\) и поэтому \(\hat{\theta} = \dfrac{\pi} {4}\). Поскольку \(-2 < 0\) и \(2 > 0\), \(\theta\) находится во втором квадранте, и мы имеем \[\theta = \pi — \dfrac{\pi}{4} = \dfrac{3\pi}{4}\]
Итак, точка \((-2, 2)\) в прямоугольных координатах имеет полярные координаты \((\sqrt{8}, \dfrac{3\pi}{4})\).
Упражнение \(\PageIndex{4}\)
Определите полярные координаты для каждой из следующих точек в прямоугольных координатах:
\[(6, 6\sqrt{3})\] \[(0, -4 )\] \[(-4, 5)\]
В каждом случае используйте положительное радиальное расстояние \(r\) и полярный угол \(\theta\) с \(0 \leq \theta \leq 2 \Пи\).
Для (3) необходимо использовать обратную тригонометрическую функцию. 9{-1}(\dfrac{-4}{\sqrt{21}})\).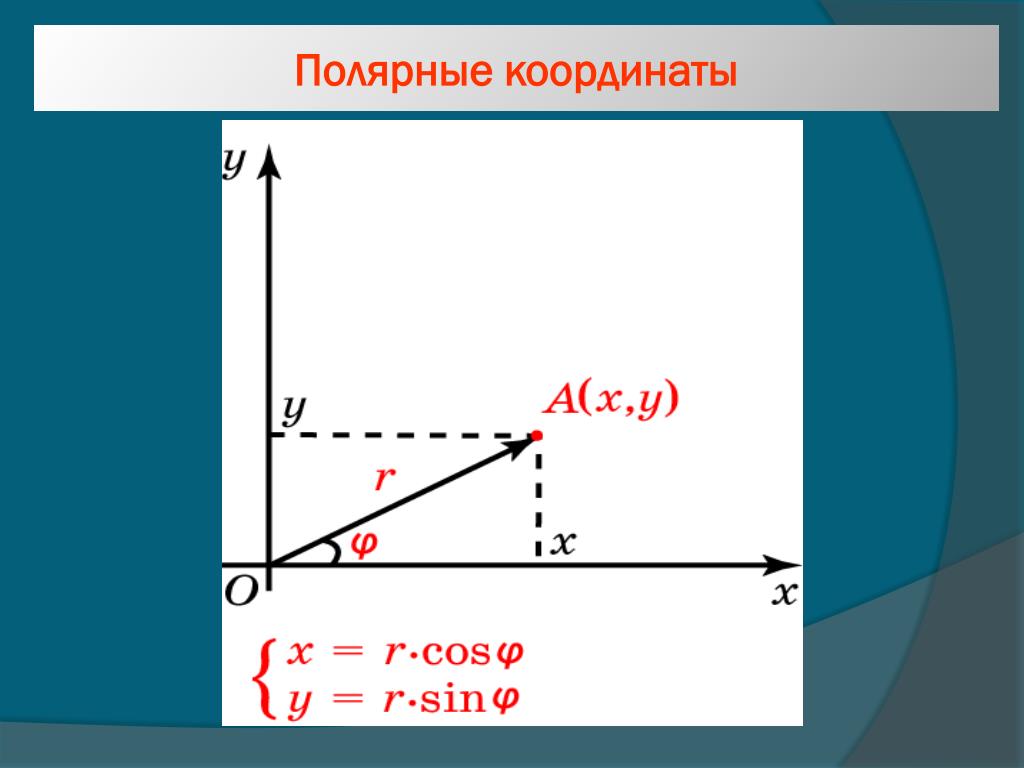
График полярного уравнения
График уравнения в прямоугольной системе координат состоит из всех точек \((x, y)\), которые удовлетворяют уравнению. Уравнение часто можно записать в виде функции типа \(y = f(x)\). В этом случае точка \((a, b)\) находится на графике этой функции тогда и только тогда, когда \(b = f(a)\) Аналогично,
Определение
Уравнение, переменными которого являются полярные координаты (обычно \(r\) и \(\theta\)) называется
.0060 полярное уравнение . График полярного уравнения — это множество всех точек, полярные координаты которых \((r, \theta)\) удовлетворяют данному уравнению.
Примером полярного уравнения является \(r = 4\sin(\theta)\). Для этого уравнения обратите внимание, что
- Если \(\theta = 0\), то \(r = 4\sin(0) = 0\) и, таким образом, точка \((0, 0)\) (в полярной координаты) находится на графике этого уравнения.
- Если \(\theta = \dfrac{\pi}{6}\), то \(r = 4\sin(\dfrac{\pi}{6}) = 4\cdot \dfrac{1}{2} = 2\), поэтому \((2, \dfrac{\pi}{6})\) находится на графике этого уравнения.
 (Помните: для полярных координат значением \(r\) является первая координата.)
(Помните: для полярных координат значением \(r\) является первая координата.)
Самый простой метод рисования графика полярного уравнения состоит в том, чтобы нанести точки, удовлетворяющие полярному уравнению, на миллиметровую бумагу, как показано на рисунке \(\PageIndex{4}\), а затем соединить точки плавной кривой. .
Упражнение \(\PageIndex{5}\)
В следующей таблице показаны значения \(r\) и \(\theta\) для точек, находящихся на графике полярного уравнения \(r = 4\ грех(\тета)\).
| \(r = 4\sin(\тета)\) | \(\тета\) |
|---|---|
| 0 | 0 |
| 2 | \(\dfrac{\pi}{6}\) |
| \(2\кв{2}\) | \(\dfrac{\pi}{4}\) |
| \(2\кв{3}\) | \(\dfrac{\pi}{3}\) |
| 4 | \(\dfrac{\pi}{2}\) |
| \(2\кв{3}\) | \(\dfrac{2\pi}{3}\) |
| \(2\кв{2}\) | \(\dfrac{3\pi}{4}\) |
| 2 | \(\dfrac{5\pi}{6}\) |
| 0 | \(\пи\) |
Нанесите эти точки на полярную диаграмму и проведите гладкую кривую через точки для графика уравнения \(r = 4\sin(\theta)\).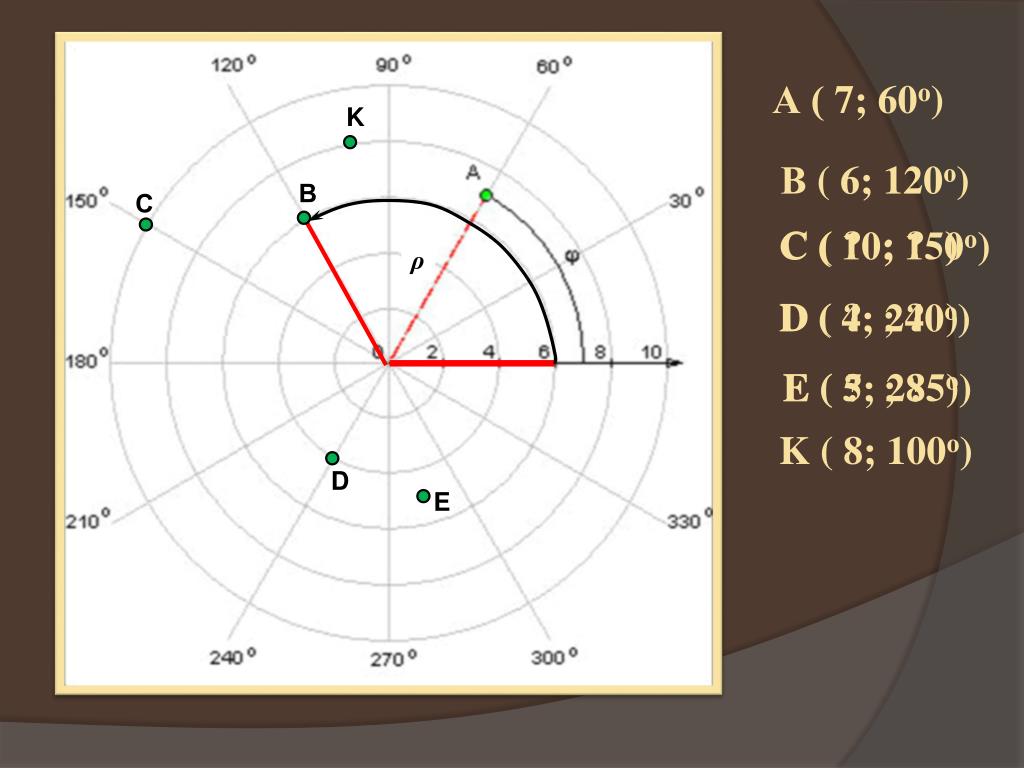
- Ответить
В зависимости от того, насколько тщательно мы нанесем точки и насколько хорошо нарисуем кривую, график в упражнении \(\PageIndex{5}\) может быть кругом. Мы, конечно, можем начертить больше точек. Фактически, в упражнении \(\PageIndex{5}\) мы использовали только значения для \(\theta\) с \(0 \leq \theta \leq \pi\). В следующей таблице показаны значения \(r\) и \(\theta\) для точек, которые находятся на графике полярного уравнения \(r = 4\sin(\theta)\) с \(\pi \leq \тета \leq 2\pi\).
| \(r = 4\sin(\тета)\) | \(\тета\) |
|---|---|
| 0 | \(\пи\) |
| -2 | \(\dfrac{7\pi}{6}\) |
| \(-2\кв{2}\) | \(\dfrac{5\pi}{4}\) |
| \(-2\кв{3}\) | \(\dfrac{4\pi}{3}\) |
| -4 | \(\dfrac{3\pi}{2}\) |
| \(-2\кв{3}\) | \(\dfrac{5\pi}{3}\) |
| \(-2\кв{2}\) | \(\dfrac{7\pi}{4}\) |
| -2 | \(\dfrac{11\pi}{6}\) |
| 0 | \(\пи\) |
Из-за отрицательных значений для \(r\), если мы нанесем эти точки на график, мы получим те же точки, что и в упражнении \(\PageIndex{4}\). {2}\), чем с \(r\). 9{2}\]
{2}\), чем с \(r\). 9{2}\]
Это уравнение (в прямоугольных координатах) окружности с радиусом \(2\) и центром в точке \((0, 2)\). Мы видим, что это согласуется с графиком, полученным в упражнении \(\PageIndex{5}\).
Упражнение \(\PageIndex{7}\)
Преобразуйте уравнение \(r = 6\cos(\theta)\) в уравнение в прямоугольных координатах, а затем объясните, почему график \(r = 6\cos (\тета)\) — круг. Каков радиус этой окружности и каков ее центр?
9{2}\]Таким образом, график \(r = 3\cos(\theta)\) представляет собой окружность с радиусом \(3\) и центром в точке \((3, 0)\).
Полярная сетка
Мы представили полярную миллиметровую бумагу на рис. 5.7. Обратите внимание, что он состоит из концентрических окружностей с центром на полюсе и линий, проходящих через полюс. Эти окружности и линии имеют очень простые уравнения в полярных координатах. Например:
- Рассмотрим уравнение \(r = 3\). Чтобы точка попала на график этого уравнения, она должна лежать на окружности радиуса 3, центром которой является полюс.
 Таким образом, график этого уравнения представляет собой окружность радиуса 3 с центром в полюсе. Мы также можем показать это, приведя уравнение \(r = 3\) к прямоугольной форме следующим образом:{2} = 9\]
Таким образом, график этого уравнения представляет собой окружность радиуса 3 с центром в полюсе. Мы также можем показать это, приведя уравнение \(r = 3\) к прямоугольной форме следующим образом:{2} = 9\]В прямоугольных координатах это уравнение окружности радиуса 3 с центром в начале координат.
- Теперь рассмотрим уравнение \(\theta= \dfrac{\pi}{4}\). Чтобы точка находилась на графике этого уравнения, линия, проходящая через полюс и эту точку, должна составлять угол \(\dfrac{\pi}{4}\) радиан с полярной осью. Если мы допустим только положительные значения для \(r\), график будет лучом с начальной точкой на полюсе, который составляет угол \(\dfrac{\pi}{4}\) радиан с полярной осью. Однако, если мы позволим \(r\) быть любым действительным числом, то мы получим линию через полюс, которая составляет угол \(\dfrac{\pi}{4}\) радиан с полярной осью. Мы можем преобразовать это уравнение в прямоугольные координаты следующим образом:
\[\theta = \dfrac{\pi}{4}\]
\[\tan(\theta) = \tan(\dfrac{\pi}{4})\]
\[\dfrac {y}{x} = 1\]
\[y = x\]
Это уравнение прямой линии, проходящей через начало координат с наклоном 1.

В общем случае:
Определение
- Если \(а\) — положительное действительное число, то график \(г = а\) представляет собой окружность радиуса \(а\), центр которой является полюсом.
- Если \(b\) — действительное число, то график \(\theta = b\) представляет собой линию, проходящую через полюс, которая составляет угол \(b\) радиан с полярной осью.
Заключительные замечания
Мы изучили лишь несколько графиков полярных уравнений. Есть много интересных графиков, которые можно построить с помощью полярных уравнений, которые очень трудно выполнить в прямоугольных координатах. Поскольку полярная система координат основана на концентрических окружностях, неудивительно, что окружности с центром на полюсе будут иметь «простые» уравнения типа \(r = a\).
В упражнении \(\PageIndex{5}\) и \(\PageIndex{7}\) мы видели полярные уравнения, графики которых представляли собой окружности с центрами не на полюсах. Это были частные случаи следующего:
Полярные уравнения, графики которых представляют собой окружности
Если \(a\) — положительное действительное число, то
График \(r = 2a\sin(\theta)\) представляет собой окружность радиусом \(a\) с центром в точке \((0, a)\) в прямоугольных координатах или \((a, \dfrac{\pi}{2})\) в полярных координатах.
График \(r = 2a\sin(\theta)\) представляет собой окружность радиуса \(a\) с центром в точке \((a, 0)\) в прямоугольных координатах или \((a , 0)\) в полярных координатах.
Мы изучим это и графики других полярных уравнений в упражнениях.
Эта страница под названием 5.4: Полярная система координат распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Тедом Сандстромом и Стивеном Шликером (ScholarWorks @Grand Valley State University) через исходный контент. это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Тед Сандстром и Стивен Шликер
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
- источник@https://scholarworks.
 gvsu.edu/books/12
gvsu.edu/books/12
- источник@https://scholarworks.
10.3: Полярные координаты — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2682
- OpenStax
- OpenStax
- Нанесение точек с использованием полярных координат.
- Преобразовать полярные координаты в прямоугольные.
- Преобразовать прямоугольные координаты в полярные.
- Преобразование уравнений между полярной и прямоугольной формами.
- Определите и начертите полярные уравнения, преобразовав их в прямоугольные уравнения.

- Ответить
Рисунок \(\PageIndex{4}\)
- Нанести точку \(\left(2,\dfrac{\pi}{6}\right)\), перемещая dfrac{\pi}{6}\) в направлении против часовой стрелки и продолжение направленного отрезка \(2\) единиц в первый квадрант.
 Затем проследите направленный отрезок обратно через полюс и продолжайте движение на \(2\) единиц в третий квадрант;
Затем проследите направленный отрезок обратно через полюс и продолжайте движение на \(2\) единиц в третий квадрант; - Переместите \(\dfrac{\pi}{6}\) в направлении против часовой стрелки и нарисуйте направленный отрезок от полюса \(2\) единиц в отрицательном направлении в третий квадрант.
- Ответить
Рисунок \(\PageIndex{6}\)
- Учитывая полярную координату \((r,\theta)\, запишите \(x=r \cos \theta\) и \(y=r \sin \theta\).
- Оценить \(\cos \theta\) и \(\sin \theta\).
- Умножьте \(\cos \theta\) на \(r\), чтобы найти \(x\) — координату прямоугольной формы.
- Умножьте \(\sin\theta\) на \(r\), чтобы найти \(y\) — координату прямоугольной формы.
- Ответить
\((x,y)=\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\)
- Измените MODE на POL , представляя полярную форму.
- Нажмите кнопку Y= , чтобы вызвать экран, позволяющий ввести шесть уравнений: \(r_1\), \(r_2\),…, \(r_6\).
- Введите полярное уравнение, установите его равным \(r\).
- Нажмите ГРАФИК .
- Ответить
Мы будем использовать отношения \(x=r \cos \theta\) и \(y=r \sin \theta\).
 92\) в полярной форме.
92\) в полярной форме.- Ответить
\(r=\sqrt{3}\)
Идентификация и построение полярных уравнений путем преобразования в прямоугольные уравнения
Мы научились преобразовывать прямоугольные координаты в полярные координаты и увидели, что точки действительно совпадают. Мы также преобразовали полярные уравнения в уравнения прямоугольной формы и наоборот. Теперь мы продемонстрируем, что их графики, хотя и построенные на разных сетках, идентичны.
Пример \(\PageIndex{6A}\): построение графика полярного уравнения путем преобразования в прямоугольное уравнение
Преобразование полярного уравнения \(r=2 \sec \theta\) в прямоугольное уравнение и построение соответствующего ему графика .
Решение
Преобразование
\[\begin{align*} r &=2 \sec \theta \\ r &= \dfrac{2}{\cos \theta} \\ r \cos \ theta &=2 \\ x &=2 \end{align*}\]
Обратите внимание, что уравнение \(r=2 \sec \theta\), нарисованное на полярной сетке, явно совпадает с вертикальной линией \( x=2\), нарисованный на прямоугольной сетке (см.
 рисунок \(\PageIndex{14}\)). Точно так же, как \(x=c\) является стандартной формой для вертикальной линии в прямоугольной форме, \(r=c \sec \theta\) является стандартной формой для вертикальной линии в полярной форме.
рисунок \(\PageIndex{14}\)). Точно так же, как \(x=c\) является стандартной формой для вертикальной линии в прямоугольной форме, \(r=c \sec \theta\) является стандартной формой для вертикальной линии в полярной форме.Рисунок \(\PageIndex{14}\): (a) Полярная сетка (b) Прямоугольная система координат
Аналогичное обсуждение показало бы, что график функции \(r=2 \csc \theta\) будет горизонтальной линией \(y=2\). На самом деле \(r=c\csc\theta\) является стандартной формой горизонтальной линии в полярной форме, соответствующей прямоугольной форме \(y=c\).
Пример \(\PageIndex{6B}\): переписывание полярного уравнения в декартовой форме 92 \end{align*}\]
Когда все наше уравнение было изменено с \(r\) и \(\theta\) на \(x\) и \(y\), мы можем остановиться, если нас не попросят решить для \(y\) или упростить. См. рисунок \(\PageIndex{15}\).
Рисунок \(\PageIndex{15}\)
График в форме песочных часов называется гиперболой .
 2}. \конец{массив}\) 9{\ гидроразрыва {2} {3}} \)
2}. \конец{массив}\) 9{\ гидроразрыва {2} {3}} \)Media
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики работы с полярными координатами.
- Введение в полярные координаты
- Сравнение полярных и прямоугольных координат
Ключевые уравнения
Формулы преобразования \(\cos\theta=\dfrac{x}{r} \rightarrow x=r \cos\theta\)
\(\sin\theta=\dfrac{y}{r} \rightarrow y=r \sin\theta\) 92\)
\(\тангенс\тета=\dfrac{y}{x}\)
Основные понятия
- Полярная сетка представлена в виде ряда концентрических кругов, исходящих из полюса или источника.
- Чтобы нанести точку в виде \((r,\theta)\), \(\theta>0\), переместитесь против часовой стрелки от полярной оси на угол \(\theta\), а затем продлите направленный отрезок от полюса на длину \(r\) в направлении \(\theta\).

Цели обучения
На расстоянии \(12\) километров от порта парусная лодка попадает в непогоду и сбивается с курса ветром силой \(16\) узлов (см. рисунок \(\PageIndex{1}\)). Как моряк может указать свое местонахождение береговой охране? В этом разделе мы исследуем метод представления местоположения, отличный от стандартной сетки координат.
Рисунок \(\PageIndex{1}\)
Построение точек с использованием полярных координат
Когда мы думаем о построении точек на плоскости, мы обычно думаем о прямоугольных координатах \((x,y)\) в декартовой координатной плоскости . Однако существуют и другие способы записи координатной пары и другие типы сеточных систем. В этом разделе мы познакомимся с полярными координатами, которые представляют собой точки, обозначенные \((r,\theta)\) и нанесенные на полярную сетку. Полярная сетка представлена в виде серии концентрических кругов, исходящих из полюса или начала координатной плоскости.
Полярная сетка масштабируется как единичный круг с положительной осью \(x\) — , которая теперь рассматривается как полярная ось, а начало координат — как полюс. Первая координата \(r\) — это радиус или длина направленного отрезка прямой от полюса. Угол \(\theta\), измеренный в радианах, указывает направление \(r\). Мы перемещаемся против часовой стрелки от полярной оси на угол \(\theta\) и измеряем направленный отрезок длиной \(r\) в направлении \(\theta\). Несмотря на то, что мы сначала измеряем \(\theta\), а затем \(r\), полярная точка сначала записывается с координатой \(r\). Например, чтобы нанести точку \(\left(2,\dfrac{\pi}{4}\right)\), мы должны переместить \(\dfrac{\pi}{4}\) единиц против часовой стрелки. а затем длину \(2\) от полюса. Эта точка нанесена на сетку на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\)
Пример \(\PageIndex{1}\): Нанесение точки на полярную сетку
Нанесение точки \(\left(3, \dfrac{\pi}{2}\right)\) на полярной сетке.
Решение
Угол \(\dfrac{\pi}{2}\) находится путем протягивания против часовой стрелки \(90°\) от полярной оси. Точка расположена на расстоянии \(3\) единиц от полюса в направлении \(\dfrac{\pi}{2}\), как показано на рисунке \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\)
Упражнение \(\PageIndex{1}\)
Постройте точку \(\left(2, \dfrac{\pi}{3 }\right)\) в полярной сетке.
Пример \(\PageIndex{2}\): построение точки в полярной системе координат с отрицательной составляющей
Нанесение точки \(\left(−2, \dfrac{\pi}{6}\right)\ ) на полярной сетке.
Решение
Мы знаем, что \(\dfrac{\pi}{6}\) находится в первом квадранте. Однако \(r=−2\). Мы можем построить точку с отрицательным значением \(r\) двумя способами:
См. рисунок \(\PageIndex{5a}\). Сравните это с графиком полярной координаты \((2,π6)\), показанным на рисунке \(\PageIndex{5b}\).
Рисунок \(\PageIndex{5}\)
Упражнение \(\PageIndex{2}\)
Нанесите точки \(\left(3,−\dfrac{\pi}{6}\right)\) и \(\left(2,\dfrac{9)\pi}{4}\right)\) на той же полярной сетке.
Преобразование полярных координат в прямоугольные координаты
Когда задан набор полярных координат , нам может потребоваться преобразовать их в прямоугольные координаты. Для этого мы можем вспомнить отношения, существующие между переменными \(x\), \(y\), \(r\) и \(\theta\).
Для этого мы можем вспомнить отношения, существующие между переменными \(x\), \(y\), \(r\) и \(\theta\).
\(\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\)
\(\sin \theta=\dfrac{y}{r}\rightarrow y=r \ sin \theta\)
Если опустить перпендикуляр из точки плоскости на ось x-, получится прямоугольный треугольник, как показано на рисунке \(\PageIndex{7}\). Простой способ запомнить приведенные выше уравнения — представить \(\cos\theta\) как примыкающую сторону к гипотенузе и \(\sin\theta\) как противоположную сторону к гипотенузе.
Рисунок \(\PageIndex{7}\)
ПРЕОБРАЗОВАНИЕ ПОЛЯРНЫХ КООРДИНАТ В ПРЯМОУГОЛЬНЫЕ
Преобразование полярных координат \((r, \theta)\) в прямоугольные координаты \((x, y)\) , пусть
\[\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\]
\[\sin \theta=\dfrac{y}{r}\rightarrow y =r \sin\тета\]
Как: преобразовать заданные полярные координаты в прямоугольные.

Пример \(\PageIndex{3A}\): запись полярных координат в виде прямоугольных координат
Запись полярных координат \(\left(3,\dfrac{\pi}{2}\right)\) в виде прямоугольных координат.
Решение
Используйте эквивалентные соотношения.
\[\begin{align*} x&= r \cos \theta\\ x&= 3 \cos \dfrac{\pi}{2}\\ &= 0\\ y&= r \sin \theta\\ y& = 3 \sin \dfrac{\pi}{2}\\ &= 3 \end{align*}\]
Прямоугольные координаты \((0,3)\). См. рисунок \(\PageIndex{8}\).
Рисунок \(\PageIndex{8}\)
Пример \(\PageIndex{3B}\): запись полярных координат в виде прямоугольных координат
Запишите полярные координаты \((−2,0)\) в виде прямоугольных координат.
Решение
См. рисунок \(\PageIndex{9}\). Записав полярные координаты в виде прямоугольника, мы имеем
\[\begin{align*} x&= r \cos \theta\\ x&= -2 \cos(0)\\ &= -2\\ y&= r \sin \theta\\ y&= -2 \sin(0)\\ &= 0 \end{align*}\]
Прямоугольные координаты также равны \((−2,0)\).
Рисунок \(\PageIndex{9}\)
Упражнение \(\PageIndex{3}\)
Запишите полярные координаты \(\left(−1,\dfrac{2\pi}{3}\right)\) в виде прямоугольных координат.
Преобразование прямоугольных координат в полярные координаты
Для преобразования прямоугольных координат в полярные координаты мы будем использовать два других знакомых соотношения. Однако при таком преобразовании мы должны знать, что набор прямоугольных координат даст более одной полярной точки. 92\)
\(\tan \theta=\dfrac{y}{x}\)
Рисунок \(\PageIndex{10}\)
Пример \(\PageIndex{4} \): запись прямоугольных координат в виде полярных координат
Преобразование прямоугольных координат \((3,3)\) в полярные координаты.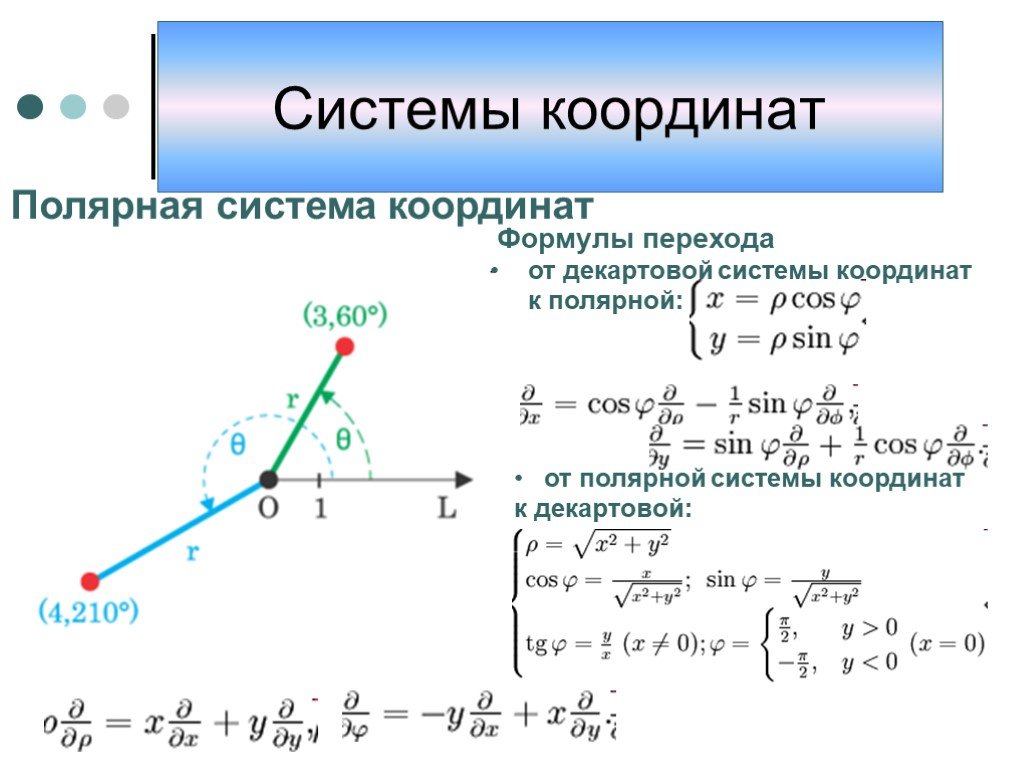
Раствор
Мы видим, что исходная точка \((3,3)\) находится в первом квадранте. Чтобы найти \(\theta\), используйте формулу \(\tan \theta=\dfrac{y}{x}\). Это дает
92}\\ r&= \sqrt{9+9}\\ r&= \sqrt{18}\\ &= 3\sqrt{2} \end{align*}\]Итак, \(r=3\sqrt{2}\) и \(\theta=\dfrac{\pi}{4}\), что дает нам полярную точку \((3\sqrt{2},\dfrac {\pi}{4})\). См. рисунок \(\PageIndex{11}\).
Рисунок \(\PageIndex{11}\)
Анализ
Есть и другие наборы полярных координат, которые будут такими же, как наше первое решение. Например, точки \(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) и \(\left(3\sqrt{2},−\dfrac{ 7\pi}{4}\right)\) будет совпадать с исходным решением \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) указывает на движение против часовой стрелки на \(\pi\), что прямо противоположно \(\ dfrac{\pi}{4}\). Радиус выражается как \(−3\sqrt{2}\).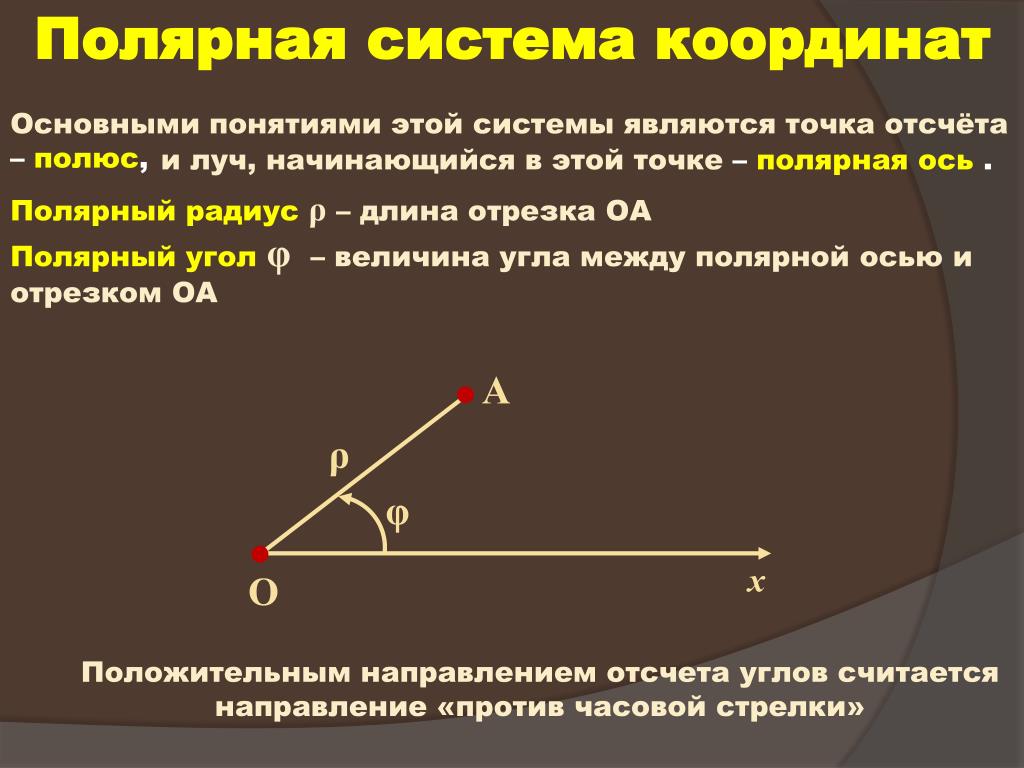 Однако угол \(\dfrac{5\pi}{4}\) расположен в третьем квадранте, и, поскольку \(r\) отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант . Это та же точка, что и \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) – это перемещение по часовой стрелке на \(−\dfrac{7\pi}{4}\ ), из \(\dfrac{\pi}{4}\). Радиус, \(3\sqrt{2}\), такой же.
Однако угол \(\dfrac{5\pi}{4}\) расположен в третьем квадранте, и, поскольку \(r\) отрицательно, мы продолжаем направленный отрезок в противоположном направлении, в первый квадрант . Это та же точка, что и \(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка \(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) – это перемещение по часовой стрелке на \(−\dfrac{7\pi}{4}\ ), из \(\dfrac{\pi}{4}\). Радиус, \(3\sqrt{2}\), такой же.
Преобразование уравнений между полярной и прямоугольной формами
Теперь мы можем преобразовать координаты между полярной и прямоугольной формой. Преобразование уравнений может быть более сложным, но может быть полезно иметь возможность преобразования между двумя формами. Поскольку существует ряд полярных уравнений, которые не могут быть четко выражены в декартовой форме, и наоборот, мы можем использовать те же процедуры, которые мы использовали для преобразования точек между системами координат. Затем мы можем использовать графический калькулятор для построения графика прямоугольной или полярной формы уравнения.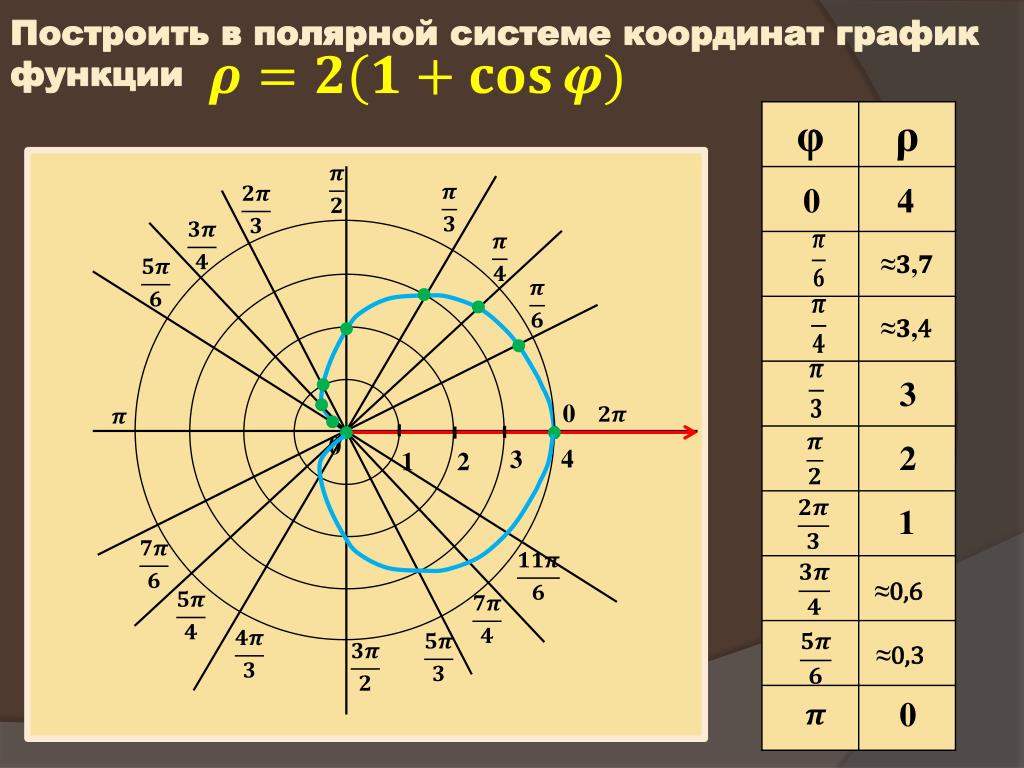
Как: Имея уравнение в полярной форме, начертите его с помощью графического калькулятора
Пример \(\PageIndex{5A}\): запись декартова уравнения в полярной форме 92=6y\) (b) полярная форма \(r=6 \sin \theta\)
Декартово или прямоугольное уравнение наносится на прямоугольную сетку, а полярное уравнение наносится на полярную сетку. Ясно, что графики идентичны.
Упражнение \(\PageIndex{4A}\):
Переписать декартово уравнение в полярной форме
Переписать декартово уравнение \(y=3x+2\) как полярное уравнение.

 )
) В каждом из этих случаев мы можем определить точные значения \(x\) и \(y\).
В каждом из этих случаев мы можем определить точные значения \(x\) и \(y\).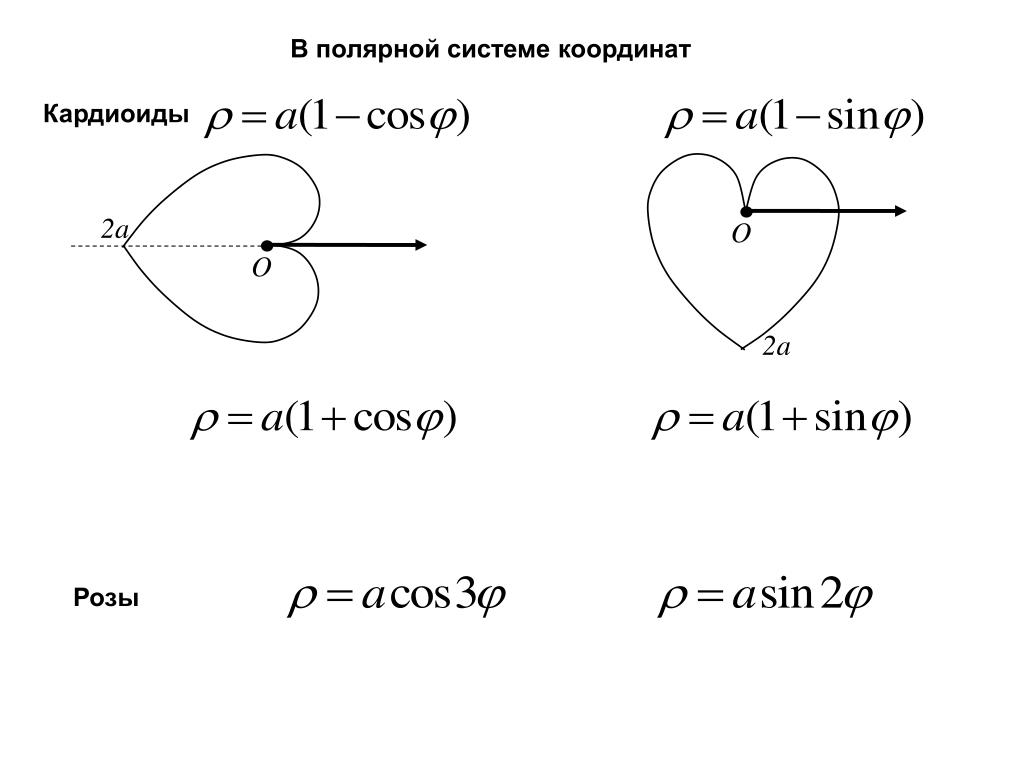 (Помните: для полярных координат значением \(r\) является первая координата.)
(Помните: для полярных координат значением \(r\) является первая координата.) Таким образом, график этого уравнения представляет собой окружность радиуса 3 с центром в полюсе. Мы также можем показать это, приведя уравнение \(r = 3\) к прямоугольной форме следующим образом:{2} = 9\]
Таким образом, график этого уравнения представляет собой окружность радиуса 3 с центром в полюсе. Мы также можем показать это, приведя уравнение \(r = 3\) к прямоугольной форме следующим образом:{2} = 9\]

 gvsu.edu/books/12
gvsu.edu/books/12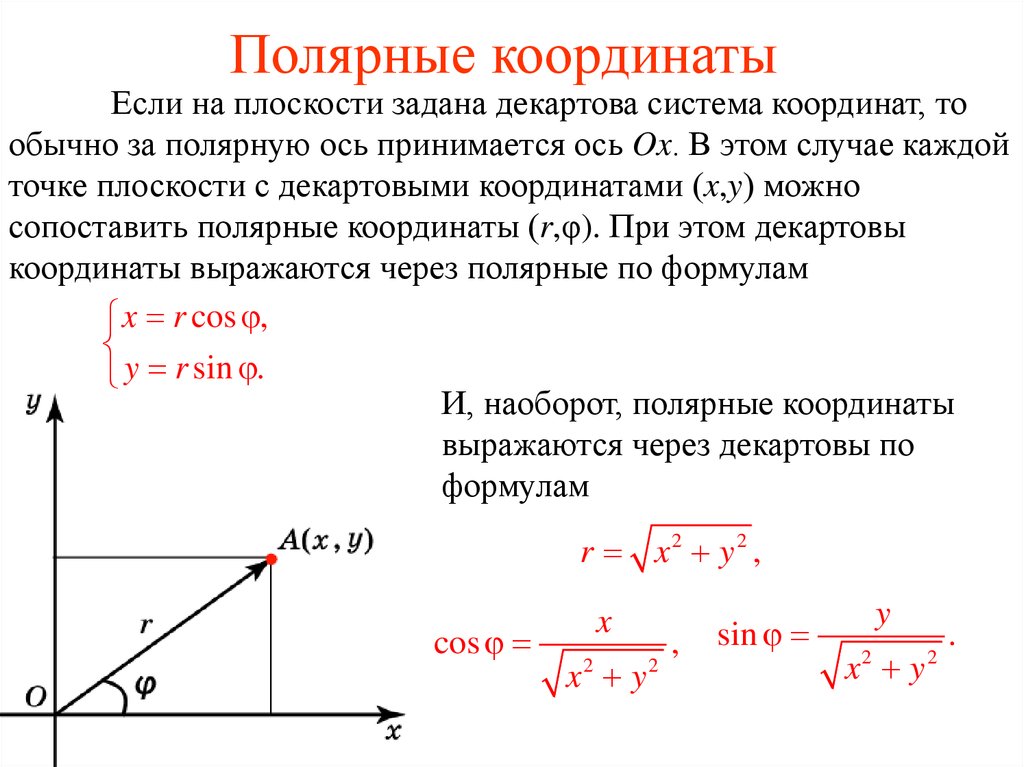
 Затем проследите направленный отрезок обратно через полюс и продолжайте движение на \(2\) единиц в третий квадрант;
Затем проследите направленный отрезок обратно через полюс и продолжайте движение на \(2\) единиц в третий квадрант;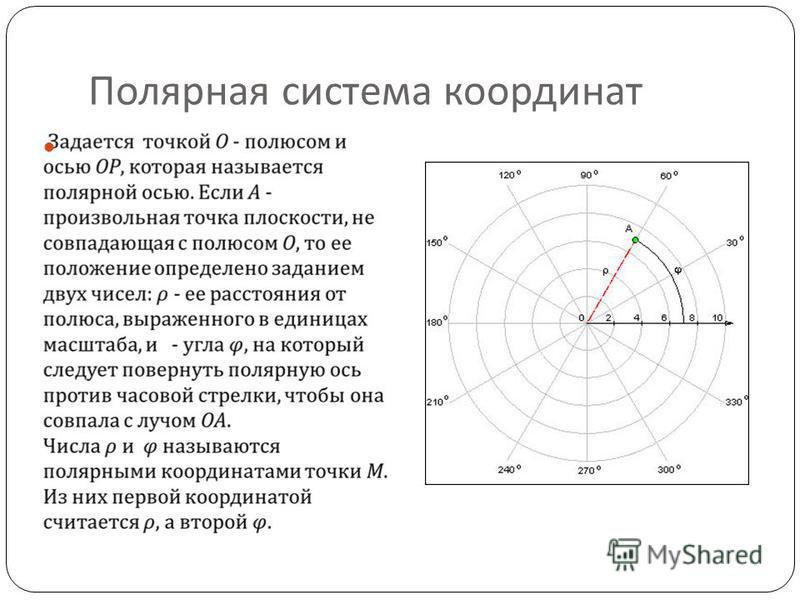 92\) в полярной форме.
92\) в полярной форме. рисунок \(\PageIndex{14}\)). Точно так же, как \(x=c\) является стандартной формой для вертикальной линии в прямоугольной форме, \(r=c \sec \theta\) является стандартной формой для вертикальной линии в полярной форме.
рисунок \(\PageIndex{14}\)). Точно так же, как \(x=c\) является стандартной формой для вертикальной линии в прямоугольной форме, \(r=c \sec \theta\) является стандартной формой для вертикальной линии в полярной форме. 2}. \конец{массив}\) 9{\ гидроразрыва {2} {3}} \)
2}. \конец{массив}\) 9{\ гидроразрыва {2} {3}} \)