Примеры решения систем линейных уравнений метод гаусса: Метод Гаусса — примеры c решением, теоремы и формулы

Содержание

Метод Гаусса — примеры c решением, теоремы и формулы

Метод Гаусса – идеальный вариант для решения систем линейных алгебраических уравнений (далее СЛАУ). Благодаря методу Гаусса можно последовательно исключать неизвестные путём элементарных преобразований. Метод Гаусса – это классический метод решения СЛАУ, который и рассмотрен ниже.

Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ

Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.

Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений.

Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.

У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.

Определения и обозначения

Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.

Для начала систематизируем знания о системах линейных уравнений.

Обратите внимание!

СЛАУ в зависимости от её элементов может иметь:

Одно решение;
много решений;
совсем не иметь решений.

В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.

Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:

перемена мест уравнений системы;

почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
сложение к обеим частям одного из уравнений определённых частей другого уравнения.

Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.

Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:

где а, в, с – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.

Если = = = , тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.

Множественные числа , , называются решением СЛАУ, если при подстановке , , в СЛАУ получим числовые тождества.

Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:

– это основная матрица СЛАУ.

– матрица столбец неизвестных переменных.

– матрица столбец свободных членов.

Если к основной матрице добавить в качестве – ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой , а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов. То есть, расширенная матрица выглядит так:

Если квадратная матрица равна нулю, она называется вырожденная, а если – матрица невырожденная.

Обратите внимание!

Если с системой уравнений:

Произвести такие действия:

умножать обе части любого из уравнений на произвольное и отличное от нуля число ;
менять местами уравнения;
к обеим частям любого из уравнений прибавить определённые части другого уравнения, которые умножаются на произвольное число ,

тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.

Теперь можно перейти непосредственно к методу Гаусса.

Нужна работа? Есть решение!

Более 70 000 экспертов: преподавателей и доцентов вузов готовы помочь вам в написании работы прямо сейчас.

Подробнее Гарантии Отзывы

Простейшие преобразования элементов матрицы

Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:

Из уравнения запишем расширенную матрицу:

Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.

Определение

Матрица системы – это матрица, которая составляется исключительно с коэффициентами при неизвестных. Что касается расширенной матрицы системы, так, это такая матрица, в которой кроме коэффициентов записаны ещё и свободные члены. Любую из этих матриц называют просто матрицей.

На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:

1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:

2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).

3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.

4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.

5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:

Для удобства умножаем первую строку на (-3):

Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:

В итоге получилось такое преобразование:

Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:

В матрице верхняя строка преобразовалась:

Первую строку делим на и преобразовалась нижняя строка:

И верхнюю строку поделили на то же самое число :

Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась.

ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты.

Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:

Обратите внимание!

Если в примере приведены десятичные дроби, метод Гаусса в этом случае также поможет решить систему линейных алгебраических уравнений. Однако, не стоит забывать, что следует избегать приближённых вычислений, так как ответ будет неверным. Лучше всего использовать десятичные дроби, а от них переходить к обыкновенным дробям.

Алгоритм решения методом Гаусса пошагово

После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:

Шаг 1. Переписываем систему в виде матрицы

Записываем матрицу:

Шаг 2.

Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю

Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на .

Шаг 3. Приводим матрицу к ступенчатому виду

Теперь вторую строку можно поделить на 2 и получается:

Верхнюю строку делим на и приводим матрицу к ступенчатому виду:

Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.

Шаг 4. Записываем эквивалентную систему

После наших элементарных преобразований получилась эквивалентная система:

Шаг 5. Производим проверку (решение системы обратным путём)

Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки.

находим : ,

После находим :

Тогда:

Как видим, уравнение решено правильно, так как ответы в системе совпадают.

Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений

Как мы уже упоминали, невырожденная матрица бывает тогда, когда . Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.

Дана система уравнений:

Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.

Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную :

Из последнего, третьего уравнения мы видим, что . Из второго уравнения находим . И последнее, находим первое уравнение .

Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.

Когда выражается через и в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:

берём второе уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на ,
берём третье уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на .

И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:

Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:

В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно , чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.

Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.

В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.

Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.

Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений

Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.

Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.

В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:

1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.

Например, вам попалась подобная система:

У нас получается такая ситуация

Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.

Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.

2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где – число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:

Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:

В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных , и , и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.

3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной . Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной . Если же уже исключались, тогда переходим к , и т. д.

Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :

Такая система уравнений после преобразования выглядит так:

Вы наверное уже обратили внимание, что вместе с исключились и . Поэтому решение методом Гаусса продолжаем исключением переменной из всех уравнений системы, а начнём мы с третьего уравнения:

Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:

Допусти, что система уравнений стала:

В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:

В нашем примере это , и . В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:

Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: , , , где , , – произвольные числа.

Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.

В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении: , а из первого уравнения получаем:

= =

В итоге, получился результат, который можно и записать.

Ответ

Примеры решения методом Гаусса

Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.

Пример 1

Задача

Решить систему линейных алгебраических уравнений методом Гаусса:

Решение

Выписываем матрицу, куда добавляем столбец свободных членов:

Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:

Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой превратился в . Для этого можно ко второй строке прибавить первую строку и умножить на .Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на (разрешающий элемент данного шага).

Соответственно, первая строка остаётся неизменной, а вторая поменяется:

Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на и только после этого ко второй строке прибавить изменённую после умножения на вторую строку. Вот что получилось:

. Теперь прибавляем со второй строки первую строку . У нас получился , который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:

Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.

Итак, у нас получился ступенчатый вид матрицы:

Записываем новую систему уравнений:

Для проверки решаем систему обратным ходом. Для этого находим сначала :

Так как найден, находим :

Подставляем в изначальную нашу систему уравнений найденные и :

и .

Как видите из решения, система уравнений решена верно. Запишем ответ.

Ответ

Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.

Пример 2

Задача

Решить систему уравнений методом Гаусса:

Решение

Составляем матрицу, куда вписываем и свободные члены:

Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку: . В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем , и . Аналогично, и . И умножаем свободный член . Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:

Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:

Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:

В результате получилась ступенчатая система уравнений:

Сначала находим : ,

Обратный ход:

Итак, уравнение системы решено верно.

Ответ

Пример 3

Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.

Задача

Решите систему уравнений методом Гаусса:

Решение

В уравнении , то есть – ведущий член и пусть ≠ 0

Из данного уравнения составим расширенную матрицу:

Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: , , . Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в теперь стоит 0.

Поменяем вторую и третью строку местами и получим:

Получилось так, что = b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную из третьей и четвёртой строк:

Получилась такая матрица:

Также, учитывая, что = , умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную и получаем новую систему уравнений:

Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,

из третьего: = = =

второе уравнение находим: = = = 2,

из первого уравнения: = .

Значит, решение системы такое: (1, 2, -1, -2).

Ответ

Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.

Пример 4

Задача

Решить систему уравнений методом Гаусса:

Решение

Записываем расширенную матрицу системы:

Сначала смотрим на левое верхнее число:

Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:

Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:

Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:

Получился ступенчатый вид уравнения:

Проверяем:

Ответ

Заключение

Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.

Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.

Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.

Литература для общего развития:

Умнов А. Е. Аналитическая геометрия и линейная алгебра, изд. 3: учеб. пособие – М. МФТИ – 2011 – 259 с.

Карчевский Е. М. Лекции по линейной алгебре и аналитической геометрии, учеб. пособие – Казанский университет – 2012 – 302 с.

Метод Гаусса – теорема, примеры решений обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру

Метода Гаусса: примеры решения СЛАУ: понятия, определения, примеры задач

Найти решение этого же примера методом Гаусса в матричной форме записи:

3×1+2×2+x3+x4=-2×1-x2+4×3-x4=-1-2×1-2×2-3×3+x4=9×1+5×2-x3+2×4=4

Как решать?

Расширенная матрица системы представлена в виде:

x1 x2 x3 x432111-14-1-2-2-3115-12-2-194

Прямой ход метода Гаусса в данном случае предполагает приведение расширенной матрицы к трапецеидальному виду при помощи элементарных преобразований. Этот процесс очень поход на процесс исключения неизвестных переменных в координатном виде.

Преобразование матрицы начинается с превращения всех элементов нулевые. Для этого к элементам 2-ой, 3-ей и 4-ой строк прибавляем соответствующие элементы 1-ой строки, которые умножены на -a21a11=-13, -a31a11=—23=23 и на -а41а11=-13.

Дальнейшие преобразования происходит по такой схеме: все элементы во 2-ом столбце, начиная с 3-ей строки, становятся нулевыми. Такой процесс соответствует процессу исключения переменной . Для того, чтобы выполнить этой действие, необходимо к элементам 3-ей и 4-ой строк прибавить соответствующие элементы 1-ой строки матрицы, которая умножена на -а32(1)а22(1)=-23-53=-25 и -а42(1)а22(1)=-133-53=135:

x1 x2 x3 x43211|-20-53113-43|-130-23-7353|2330133-4353|143~

x1 x2 x3 x4~3211|-20-53113-43|-130-23+(-25)(-53)-73+(-25)11353+(-25)(-43)|233+(-25)(-13)0133+135(-53)-43+135×11353+135(-43)|143+135(-13)~

x1 x2 x3 x4~3211|-20-53113-43|-1300-195115|39500415-95|195

Теперь исключаем переменную x3 из последнего уравнения — прибавляем к элементам последней строки матрицы соответствующие элементы последней строки, которая умножена на а43(2)а33(2)=-415-195=4119.

x1 x2 x3 x43211|-20-53113-43|-1300-195115|39500415-95|195~

x1 x2 x3 x4~3211|-20-53113-43|-1300-195115|39500415+4119(-195)-95+4119×115|195+4119×395~

x1 x2 x3 x4~3211|-20-53113-43|-1300-195115|3950005619|39219

Теперь применим обратных ход метода. В матричной форме записи такое преобразование матрицы, чтобы матрица, которая отмечена цветом на изображении:

x1 x2 x3 x43211|-20-53113-43|-1300-195115|3950005619|39219

стала диагональной, т.е. приняла следующий вид:

x1 x2 x3 x43000|а10-5300|а200-1950|а30005619|39219, где а1, а2, а3 — некоторые числа.

Такие преобразования выступают аналогом прямому ходу, только преобразования выполняются не от 1-ой строки уравнения, а от последней. Прибавляем к элементам 3-ей, 2-ой и 1-ой строк соответствующие элементы последней строки, которая умножена на

-1155619=-209280, на —435619=1942 и на -15619=1956.

x1 x2 x3 x43211|-20-53113-43|-1300-195115|3950005619|39219~

x1 x2 x3 x4~3211+(-1956)5619|-2+(-1956)392190-53113-43+1942×5619|-13+1942×3921900-195115+(-209280)5619|395+(-209280)392190005619|39219~

x1 x2 x3 x4~3210|-90-531130|900-1950|-3850005619|39219

Далее прибавляем к элементам 2-ой и 1-ой строк соответствующие элементы 3-ей строки, которые умножены на

-113-195=5557 и на -1-195=519.

x1 x2 x3 x43210|-90-531130|900-1950|-3850005619|39219~

x1 x2 x3 x4~321+519(-195)0|-9+519(-385)0-53113+5557(-195)0|9+5557(-385)00-1950|-3850005619|39219~

x1 x2 x3 x4~3210|-110-5300|5300-1950|-3850005619|39219

На последнем этапе прибавляем элементы 2-ой строки к соответствующим элементам 1-ой строки, которые умножены на -2-53=65.

x1 x2 x3 x43210|-110-5300|5300-1950|-3850005619|39219~

x1 x2 x3 x4~32+65(-53)00|-11+65×53)0-5300|5300-1950|-3850005619|39219~

x1 x2 x3 x4~3000|-90-5300|5300-1950|-3850005619|39219

Полученная матрица соответствует системе уравнений

3×1=-9-53×2=53-195×3=-3855619×4=39219, откуда находим неизвестные переменные.

Ответ: x1=-3, x2=-1,x3=2,x4=7.

в чем суть, решение системы уравнений, примеры с объяснением

Благодаря великим ученым было открыто множество эффективных теорем для работы со сложными математическими задачами. Один из таких примеров — метод Гаусса.

Метод Гаусса — что это такое

Метод Гаусса представляет собой методику эквивалентного преобразования исходной системы линейных уравнений в систему, решаемую существенно проще, чем исходный вариант.

Метод Гаусса используют для решения систем линейных алгебраических формул. Такой способ обладает рядом важных преимуществ:

Нет необходимости сравнивать уравнения для оценки совместимости.
Решение систем равенств, в которых число определителей совпадает или не совпадает с количеством неизвестных переменных.
Поиск решений для уравнений с нулевым определителем.
Сравнительно небольшое количество вычислительных операций для получения результата.

Основные определения и обозначения

Матрицы: определение и свойства

Такие системы являются наиболее удобным способом представления данных, с которыми впоследствии производят манипуляции. Матрица имеет вид прямоугольника для удобства расчетов. При использовании метода Гаусса работа осуществляется с треугольными матрицами, при записи которых применяется прямоугольник с нулями на тех местах, где числа отсутствуют. Часто нули не записывают, а только подразумевают.

Важным параметром матрицы является размер:

ширина — это количество строк, обозначают буквой m;
длину выражают числом столбцов, записывают буквой n.

Источник: bigpicture.ru

Размер матрицы будет записан в формате А m*n. В случае, когда m=n, матрица является квадратной, а m=n служит ее порядком. Номера строк и столбцов изменяются.

Определитель

Матрица обладает крайне важной характеристикой. Таким параметром является определитель. Данную величину рассчитывают с помощью диагонали. Для этого в матрице необходимо провести воображаемые диагональные линии. Затем следует найти произведение элементов, которые располагаются на этих диагоналях, а полученные значения суммировать таким образом:

Если диагональ обладает наклоном в правую сторону, то знак «+».
Для диагоналей, наклоненных влево, знак «–».

Источник: wp.com

Рассчитать определитель представляется возможным лишь в случае работы с квадратной матрицей.

Если необходимо определить данный параметр для прямоугольной матрицы, то следует выполнить следующие манипуляции:

из числа строк и числа столбцов выбрать наименьшее и обозначить его k;
отметить в матрице произвольным образом k столбцов и k строк.

Элементы, которые расположены на пересечении отмеченных столбцов и строк, образуют новую квадратную матрицу. В случае, когда определитель является числом, не равным нулю, то данный параметр будет обозначен как базисный минор первоначальной прямоугольной матрицы. Перед решением систем уравнений методом Гаусса полезно рассчитать определитель. Если данная характеристика равна нулю, то матрица имеет бесконечное множество решений либо не имеет их вовсе. В таком случае потребуется определить ранг матрицы.

Классификация систем

Ранг матрицы является распространенным понятием. Он обозначает максимальный порядок ее определителя, который не равен нулю. По-другому можно сказать, что ранг матрицы представляет собой порядок базисного минора. Исходя из данного критерия, СЛАУ классифицируют на несколько типов. В совместных системах, которые состоят лишь из коэффициентов, ранг основной матрицы совпадает с рангом расширенной. Для подобных систем характерно одно или множество решений. По этой причине совместные системы подразделяют на следующие типы:

определенные, обладающие одним решением, в которых наблюдается равенство ранга матрицы и количество неизвестных;
неопределенные;
обладающие бесконечным числом решений с рангом матрицы, который меньше количества неизвестных.

В несовместных системах ранги, характеризующие основную и расширенную матрицы, отличаются. С помощью метода Гаусса в процессе решения можно прийти либо к однозначному доказательству несовместности системы, либо к решению общего вида для системы, обладающей бесконечным количеством решений.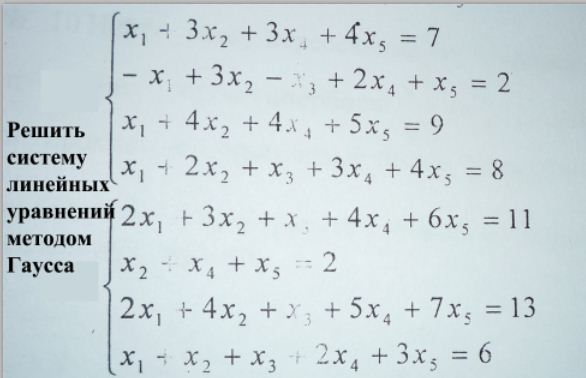

Источник: asiaplustj.info

Основные правила и разрешаемые преобразования при использовании метода Гаусса

Перед тем, как решать систему, необходимо ее упростить. На данном этапе выполняют элементарные преобразования, которые не влияют на конечный результат. Определенные манипуляции справедливы лишь в случае матриц, исходниками которых являются СЛАУ. Список элементарных преобразований:

Перестановка строк. При перемене записей в системе местами ее решение не меняется. Можно менять место строк в матрице, учитывая столбец со свободными членами.
Произведение всех элементов строк и некоторого коэффициента. Сокращаются большие числа в матрице, и исключаются нули. При этом множество решений сохраняется без изменений, а дальнейшие манипуляции существенно упрощаются. Важным условием является отличие от нуля коэффициента.
Удаление строк, которые содержат пропорциональные коэффициенты. Данное преобразование следует из предыдущего пункта. При условии, что две или более строк в матрице обладают пропорциональными коэффициентами, то при произведении или делении одной из строк на коэффициент пропорциональности получают две или более абсолютно одинаковые строки. В этом случае лишние строки исключают, оставляя только одну.
Удаление нулевой строки. Бывают случаи, когда в процессе манипуляций с уравнениями возникает строка, все элементы которой, в том числе свободный член, равны нулю. Нулевую строку допустимо исключать из матрицы.
Суммирование элементов одной строки с элементами другой, умноженными на некоторый коэффициент, в соответствующих столбцах. Данное преобразование имеет наиболее важное значение из всех перечисленных.

Особенности использования метода Гаусса для решения СЛАУ

На первом этапе система уравнений записывается в определенном виде. Пример выглядит следующим образом:

Источник: wp.com

Коэффициенты необходимо представить в виде таблицы. С правой стороны в отдельном столбце записаны свободные члены. Данный блок отделен для удобства решения. Матрицу со столбцом со свободными членами называют расширенной.

Источник: wp.com

Затем основная матрица с коэффициентами приводится к верхней треугольной форме. Данное действие является ключевым моментом при решении системы уравнений с помощью метода Гаусса. По итогам преобразований матрица должна приобрести такой вид, чтобы слева внизу находились одни нули:

Источник: wp.com

При записи новой матрицы в виде системы уравнений можно отметить, что последняя строка уже содержит значение одного из корней, которое в дальнейшем подставляется в уравнение выше для нахождения следующего корня и так далее. Подобное описание позволяет разобраться в методе Гаусса в общих чертах.

Обратный и прямой ход метода Гаусса

В первом случае необходимо представить запись расширенной матрицы системы. При выполнении обратного метода Гаусса далее в главную матрицу добавляют столбец со свободными членами.

Источник: wp.com

Суть такого способа заключается в выполнении элементарных преобразований, по итогам которых данная матрица приводится к ступенчатому или треугольному виду. В этом случае над или под главной диагональю матрицы располагаются только нули.

Источник: wp.com

Варианты дальнейших действий:

перемена строк матрицы местами, при наличии одинаковых или пропорциональных строк их можно исключить, кроме одной;
деление либо умножение строки на любое число, не равное нулю;
удаление нулевых строк;
добавление строки, умноженной на число, не равное нулю, к другой строке.

Имея преобразованную систему с одной неизвестной Xn, которая становится известной, можно выполнить поиск в обратном порядке остальных неизвестных с помощью подстановки известных х в уравнения системы, вплоть до первого. Данный способ называют обратным методом Гаусса.

Примеры решений с объяснением

Пример 1

Требуется решить с помощью метода Гаусса систему линейных уравнений, которая выглядит следующим образом:

Источник: wp.

com

Решение

Необходимо записать расширенную матрицу:

Источник: wp.com

Затем нужно выполнить преобразования. В результате матрица должна приобрести треугольный вид. Для этого следует умножить первую строку на (3) и умножить вторую строку на (-1). В результате суммирования второй и первой строк получается следующее:

Источник: wp.com

Далее следует умножить третью строку на (-1). После добавления третьей строки ко второй получаем следующие преобразования:

Источник: wp.com

После этого необходимо умножить первую строку на (6) и вторую строку на (13). Далее следует добавить вторую строку к первой:

Источник: wp.com

После того, как система преобразована, остается вычислить неизвестные:

$x_{3}=\frac{98}{49}=2$

$x_{2}=\frac{14-7x_{3}}{6}=\frac{14-7*2}{6}=0$

$x_{3}=\frac{-9+5x_{2}+6x_{3}}{3}=\frac{-9+5*0+6*2}{3}=1$

Данный пример демонстрирует единственное решение системы.

Источник: supertics.

com

Пример 2

Необходимо решить систему уравнений, которая выглядит следующим образом:

Источник: wp.com

Решение

Необходимо составить матрицу:

Источник: wp.com

Согласно методу Гаусса уравнение первой строки по итогам преобразований не меняется. Удобнее, когда левый верхний элемент матрицы обладает наименьшим значением. В таком случае первые элементы остальных строк после преобразований будут равны нулю. Таким образом, составленная матрица будет решаться проще, если на место первой строки поставить вторую:

вторая строка:

$k = (-a_{21} /a_{11}) = (-3/1) = -3$

$a»_{21} = a_{21} + k×a_{11} = 3 + (-3)×1 = 0$

$a» _{22} = a_{22} + k×a _{12} = -1 + (-3)×2 = -7$

$a»_{ 23} = a_{23} + k×a_{13} = 1 + (-3)×4 = -11$

b» 2 = b 2 + k×b 1 = 12 + (-3)×12 = -24

третья строка:

$k = (-a_{31} /a_{11}) = (-5/1) = -5$

$a»_{31} = a_{31} + k×a_{11} = 5 + (-5)×1 = 0$

$a»_{32} = a_{32} + k×a_{12} = 1 + (-5)×2 = -9$

$ a»_{33} = a_{33} + k×a_{13} = 2 + (-5)×4 = -18$

$ b»_3 = b_3 + k×b_1 = 3 + (-5)×12 = -57$

Матрица с промежуточными результатами манипуляций будет иметь следующий вид:

Источник: wp.

com

Благодаря некоторым операциям можно придать матрице наиболее удобный вид. К примеру, вторую строку можно избавить от всех «минусов» путем умножения каждого элемента на «-1». Можно заметить, что для третьей строки характерны все элементы, кратные трем. В этом случае строка сокращается с помощью произведения каждого элемента на «-1/3». Минус позволит удалить отрицательные значения.

Источник: wp.com

Далее следует приступить к манипуляциям со второй и третьей строками. Необходимо суммировать третью и вторую строки. Вторая строка при этом умножается на такой коэффициент, при котором элемент а 32 будет равен нулю.

$k = (-a_{32} /a_{22}) = (-3/7) = -3/7$

В случае, когда некоторые преобразования приводят в результате к получению не целого числа, следует оставить его в этом виде. Таким образом, вычисления будут более точными. Затем при получении ответов можно определиться с его дальнейшем округлением или переводом в другую форму записи.

$a»_{32} = a_{32} + k×a_{22} = 3 + (-3/7)×7 = 3 + (-3) = 0$

$a»_{33} = a_{33} + k×a_{23} = 6 + (-3/7)×11 = -9/7$

$b»_3 = b_3 + k×b_2 = 19 + (-3/7)×24 = -61/7$

Преобразованная матрица будет иметь следующий вид:

Матрица обладает ступенчатым видом. Дальнейшие преобразования с помощью метода Гаусса нецелесообразны. В этом случае можно удалить из третьей строки общий коэффициент «-1/7».

Источник: wp.com

Затем необходимо представить запись матрицы в виде системы уравнений для вычисления корней.

x + 2y + 4z = 12 (1)

7y + 11z = 24 (2)

Найти корни можно обратным методом Гаусса. Уравнение (3) содержит значение z:

y = (24 — 11×(61/9))/7 = -65/9

С помощью первого уравнения можно определить х:

x = (12 — 4z — 2y)/1 = 12 — 4×(61/9) — 2×(-65/9) = -6/9 = -2/3

Подобная система является совместной и определенной, для которого характерно единственное решение. Ответ будет следующим:

x 1 = -2/3, y = -65/9, z = 61/9.

Метод Гаусса предполагает последовательное исключение неизвестных. Методика справедлива в случае решения квадратных систем линейных алгебраических уравнений. Несмотря на простоту метода, многие студенты сталкиваются с некоторыми трудностями в процессе поиска правильного решения. Это связано с наличием знаков «+» и «-». Поэтому для решения СЛАУ требуется проявить внимательность. А получить квалифицированную помощь можно на ресурсе Феникс.Хелп.

Методы решения систем линейных уравнений. Метод Гауса.

Линейными называются такие уравнения, в которых все переменные находятся в первой степени. Так же в высшей математике переменные могут обозначаться не просто x, y, z и т.д., а переменными с индексами —

Решить систему уравнений означает найти такие значения переменных, при которых каждое уравнение системы превращается в верное равенство. Это правило применимо к любым системам уравнений с любым количеством неизвестных.

Существует несколько методов решения систем линейных уравнений:

метод подстановки («школьный метод»), или, как его еще называют, методом исключения неизвестных;
метод почленного сложения (вычитания) уравнений системы;
метод Гаусса;
метод Крамера;
метод обратной матрицы.

Рассмотрим некоторые из вышеуказанных методов.

Pешение системы уравнений методом Гаусса

Метод Гаусса является самым универсальным и эффективным и заключается в последовательном исключении переменных.

Пример.

Необходимо решить систему:

Решение:

Прямой ход.

Представим исходную систему в следующем виде:

На каждом этапе решения будем располагать с правой стороны расширенную матрицу,
эквивалентную системе уравнений. Расширенная матрица представляет собой несколько иную
форму записи исходной системы уравнений. Это позволит нам вести решение более наглядно.

Исключим переменную x₁ из последнего уравнения.

Для удобства переведем систему уравнений в целые числа, для этого умножим коэффициенты
первого уравнения на 3, а коэффициенты второго уравнения на -2:

Умножим коэффициенты первого уравнения на -1.

Обычно, данное преобразование системы выполняется в уме и не указывается при решении.

Прибавим получившееся уравнение ко второму уравнению.

Первое уравнение при этом не изменится в исходной системе.

Обратный ход.

Рассмотрим второе уравнение получившейся системы:

Рассмотрим первое уравнение получившейся системы:

Найдем значение переменной x₁

Найдем значение переменной x₂, подставив найденное значение x₁.

Ответ :

Если решили построить дом, то проекты коттеджей (http://www.intexhome.ru/projects/) вам будут необходимы.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Решение систем линейных уравнений

Определение и формула решения систем линейных уравнений

Школьные методы решения систем описаны в статье (\textbf{ссылка на статью «Решение систем уравнений» выше}).

Метод Гаусса для решения систем линейных уравнений

Метод Гаусса — это метод последовательного исключения переменных, когда расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к матрице (системе) треугольного вида, из которой последовательно, начиная с последней, находятся все остальные неизвестные системы. Метод назван в честь немецкого математика, механика, физика, астронома и геодезиста Иоганна Карла Фридриха Гаусса (1777-1855), хотя первое известное описание метода встречается уже в китайском трактате «Математика в девяти книгах» (10-2 в.в. до н.э.).

Метод Крамера для решения систем линейных уравнений

Матричный метод (метод обратной матрицы)

Матричный метод или метод обратной матрицы базируется на следующем алгоритме:

1. Система (1) записывается в матричной форме , где

2. Из матричного уравнения получаем, что

где матрица — это обратная матрица к матрице системы . Обратная матрица находится по формуле:

Матрица называется союзной матрицей к матрице , ее элементами есть алгебраические дополнения к соответствующим элементам матрицы .

Необходимым и достаточным условием применимости матричного метода является неравенство нулю определителя матрицы .

Понравился сайт? Расскажи друзьям!

Метод Гаусса для решения систем линейных уравнений | Математика

Пусть задана система из линейных уравнений с неизвестными:

(1.27)

Допустим, что в системе коэффициент при в первом уравнении Разделив обе части этого уравнения на , получим равносильную данной систему:

(1.28)

где

Получить решение

Исключим с помощью первого уравнения системы (1. 28) неизвестное из всех оставшихся уравнений этой системы. Для этого умножим первое уравнение этой системы последовательно на и в том же порядке вычтем полученное из второго, третьего и последующих уравнений системы (1.28). В результате получим равносильную систему вида

(1.29)

где

Допустим, что коэффициент при во втором уравнении системы (1.29) отличен от нуля. В противном случае переставим местами уравнения этой системы, записав вторым другое уравнение с подходящим вторым коэффициентом.

Исключим неизвестное с помощью второго уравнения из всех последующих уравнений. Для этого разделам второе уравнение на . Затем умножим последовательно полученное второе уравнение на и вычтем эти результаты из третьего, четвертого и всех оставшихся уравнений.

В итоге получим очередную систему уравнений:

где

Продолжая этот процесс исключения неизвестных, получим либо несовместную, либо совместную систему уравнений. В первом случае в системе будет содержаться уравнение, в котором все коэффициенты левой части равны нулю, а свободный член отличен от нуля, т.е. уравнение вида , где . Во втором случае получим либо систему треугольной формы

(1.30)

либо систему трапециевидной (ступенчатой) формы

(1.31)

В случае треугольной системы из последнего уравнения (1.30) следует, что Подставляя это значение в предпоследнее уравнение системы (1.30), найдем неизвестное . Подставляя значения и в предыдущее уравнение, найдем значение неизвестного и т.д.

Таким образам, если данная система (1.27) с помощью элементарных преобразований приводится к системе треугольной формы, то система имеет единственное решение (т.е. система совместна и определенна).

В случае системы ступенчатой формы (1.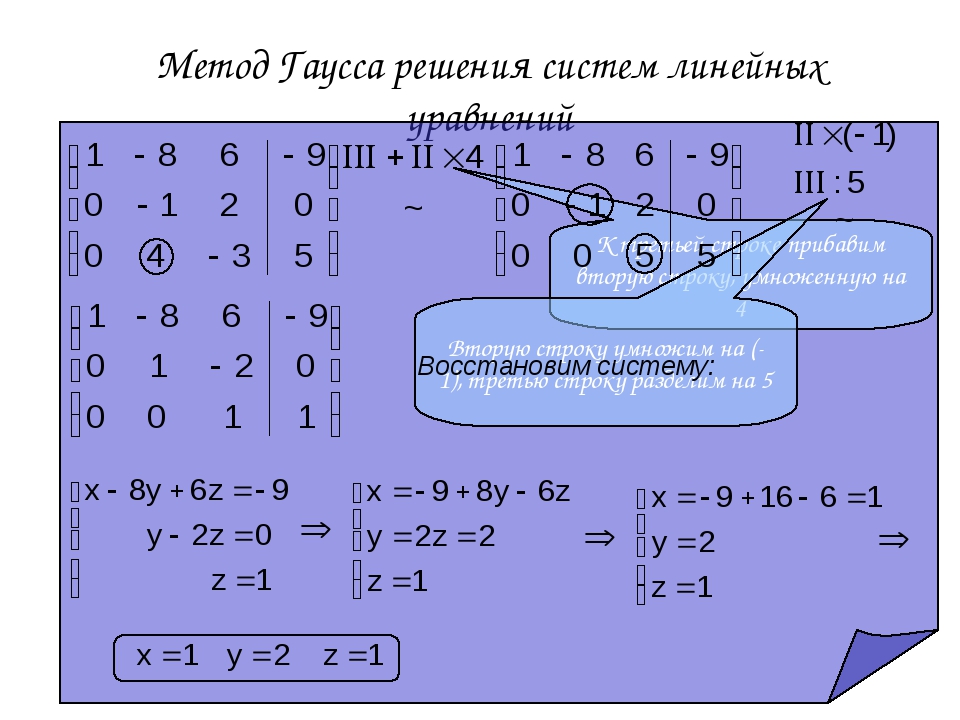 31), перенося все слагаемые, содержащие неизвестные в правую часть уравнений, получим систему вида

(1.32)

Из (1.32) следует, что значения неизвестных выражаются через значения неизвестных . Так как последним неизвестным, называемым свободными неизвестными, можно придавать любые произвольные значения, то система (1.32), а вместе с ней и данная система (1.27), имеет бесконечное множество решений.

Итак, если данная система приводится к трапециевидной форме, то она имеет бесконечное множество решений (т.е. система совместна и неопределенна). Найденные решения, записанные в форме

где любые числа, называются общими решениями системы. Решения, полученные из общих решений при конкретных значениях свободных неизвестных , называются частными решениями.

Заключение

Матричный способ решения систем линейных уравнений, как и решение методом Крамера, применим только для особых систем линейных уравнений, в которых количество неизвестных совпадает с количеством уравнений. Метод Гаусса применим для решения произвольных систем линейных уравнений и, следовательно, является универсальным методом. Этот метод позволяет существенно упростить и сам процесс поиска решений, если все промежуточные преобразования осуществить над специальной матрицей составленной из коэффициентов системы (1.27) и ее свободных членов.

Матрица В называется расширенной матрицей системы. Она позволяет заменить элементарные преобразования системы уравнений на соответствующие элементарные преобразования над своими строками, что существенно сокращает процесс поиска решении.

Примеры решения методом Гаусса

ПРИМЕР 1.1.15

Решить систему уравнений методом Гаусса.

Построим расширенную матрицу системы

Исключая с помощью первой строки неизвестное из всех оставшихся строк матрицы , получим

где символ есть символ элементарного преобразования матрицы.

Исключая с помощью второй строки неизвестное из всех последующих строк матрицы , получим

Исключая с помощью третьей строки неизвестное из четвертой строки, получим:

Матрица имеет треугольную форму. Следовательно, заданная система эквивалентна системе

Последовательно вычисляя из последнего уравнения, далее из третьего, из второго и из первого уравнения этой системы найдем, что =2, =1, =0, =1. Итак, заданная система имеет единственное решение =1, =0, =1, =2.

ПРИМЕР 1.1.16

Решить систему уравнений

Построим расширенную матрицу системы

Таким образом, заданная система эквивалентна системе,

которая имеет ступенчатый вид, и, следовательно, имеет бесконечное множество решений. Выразим переменные через :

;

Итак, общим решением данной системы будет

любое число.

Полагая, в частности, найдем, что . Тогда , будет одним из частных решений системы.

Страница не найдена — ПриМат

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Валентин Малявко (8), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Олег Шпинарев (7), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2),

Системы линейных уравнений: исключение Гаусса

Решение линейной системы с матрицами с использованием исключения Гаусса

После нескольких уроков, в которых мы неоднократно упоминали, что мы охватываем основы, необходимые для последующего изучения того, как решать системы линейных уравнений, пришло время для нашего урока сосредоточиться на полной методологии, которой нужно следовать, чтобы найти решения. для таких систем.

Что такое элиминация по Гауссу

Исключение Гаусса — это название метода, который мы используем для выполнения трех типов операций со строками матрицы над расширенной матрицей, полученной из линейной системы уравнений, чтобы найти решения для такой системы.Этот метод также называется сокращением строк и состоит из двух этапов: прямого исключения и обратной замены.

Эти два шага метода исключения Гаусса различаются не операциями, которые вы можете использовать с их помощью, а результатом, который они производят. Шаг прямого исключения относится к сокращению строки, необходимому для упрощения рассматриваемой матрицы до ее эшелонированной формы. Такой этап имеет целью продемонстрировать, имеет ли система уравнений, изображенная в матрице, единственное возможное решение, бесконечное множество решений или просто отсутствие решения.Если обнаружено, что система не имеет решения, то нет причин продолжать сокращение строки матрицы на следующем этапе.

Если возможно получить решения для переменных, входящих в линейную систему, то выполняется этап исключения Гаусса с обратной подстановкой. На этом последнем шаге будет получена сокращенная форма матрицы, которая, в свою очередь, дает общее решение системы линейных уравнений.

Правила исключения Гаусса такие же, как правила для трех элементарных операций со строками, другими словами, вы можете алгебраически оперировать строками матрицы следующими тремя способами (или комбинацией):

Перестановка двух рядов
Умножение строки на константу (любую константу, отличную от нуля)
Добавление строки к другой строке

Итак, решение линейной системы с матрицами с использованием исключения Гаусса оказывается структурированным, организованным и довольно эффективным методом.

Как выполнить гауссовское исключение

На самом деле это не установленный набор шагов исключения Гаусса, которым нужно следовать, чтобы решить систему линейных уравнений, это все о матрице, которая у вас есть в ваших руках, и необходимых операциях со строками для ее упрощения. Для этого давайте поработаем над нашим первым примером исключения Гаусса, чтобы вы могли начать изучать весь процесс и интуицию, которая необходима при работе с ними:

Пример 1

Обратите внимание, что в этот момент мы можем заметить, что эта система линейных уравнений разрешима с единственным решением для каждой из ее переменных.То, что мы выполнили до сих пор, — это первый этап сокращения строк: прямое исключение. Мы можем продолжить упрощение этой матрицы еще больше (что приведет нас ко второму этапу обратной подстановки), но нам это действительно не нужно, поскольку на этом этапе система легко разрешима. Таким образом, мы смотрим на получившуюся систему, чтобы решить ее напрямую:

Уравнение 5: Полученная линейная система уравнений для решения

Из этого набора мы можем автоматически заметить, что значение переменной z равно: z = -2.Мы используем это знание, чтобы подставить его во вторые уравнения для решения относительно y, и подставить значения y и z в первые уравнения для решения относительно x:

В последний раздел этого урока добавлено больше задач исключения Гаусса. Обязательно проработайте их, чтобы практиковаться.

Разница между устранением гаусса и устранением гаусса иордана

Разница между гауссовым исключением и гауссовым методом исключения Жордана состоит в том, что один создает матрицу в форме эшелона строк, а другой — матрицу в форме уменьшенного эшелона строки.Матрица формы эшелона строк имеет верхнюю треугольную композицию, где любые нулевые строки находятся внизу, а ведущие члены находятся справа от ведущего члена из строки выше. Уменьшенная форма эшелона выходит за рамки еще большего упрощения (иногда даже достигая формы единичной матрицы).

Уравнение 8: Разница между формой эшелона и формой ряда эшелонов

История исключения Гаусса и его названия весьма интересны, вы будете удивлены, узнав, что название «Гауссовский» было присвоено этой методологии по ошибке в прошлом веке.В действительности было обнаружено, что алгоритм одновременного решения системы линейных уравнений с использованием матриц и редукции строк записан в той или иной форме в древних китайских текстах, которые датируются еще до нашей эры. Затем в конце 1600-х годов Исаак Ньютон провел по этому поводу урок, чтобы заполнить то, что он считал пробелом в книгах по алгебре. После того, как название «Гауссиан» было уже установлено в 1950-х годах, термин Гаусса-Иордана был принят, когда геодезист У. Джордан усовершенствовал технику, чтобы он мог использовать такие вычисления для обработки своих наблюдаемых данных топографической съемки.Если вы хотите продолжить чтение увлекательной истории математиков исключения Гаусса, не бойтесь щелкнуть ссылку и прочитать.

На самом деле нет никакой физической разницы между исключением Гаусса и исключением Гаусса Джордана, оба процесса следуют одному и тому же типу операций со строками и их комбинациям, их различие зависит от результатов, которые они производят. Многие математики и учителя во всем мире будут относиться к исключению Гаусса и исключению Гаусса Джордана как к методам создания матрицы эшелонированной формы по сравнению с методом создания матрицы уменьшенной эшелонированной формы, но на самом деле они говорят о двух стадиях сокращения строк. мы объяснили это в самом первом разделе этого урока (прямое исключение и обратная подстановка), и поэтому вы просто применяете операции со строками, пока не упростите рассматриваемую матрицу.Если вы дойдете до формы эшелона, вы обычно можете решить с ней систему линейных уравнений (до сих пор это то, что называлось бы исключением Гаусса). Если вам нужно продолжить упрощение такой матрицы, чтобы напрямую получить общее решение для системы уравнений, над которой вы работаете, в этом случае вы просто продолжаете работать с матрицей по строкам, пока не упростите ее до сокращенной формы эшелона. (это будет то, что мы называем частью Гаусса-Жордана, и которую можно также рассматривать как поворотное исключение Гаусса).

Мы оставим подробное объяснение форм сокращения строк и эшелонирования для следующего урока, поскольку сейчас вам нужно знать это, если у вас нет единичной матрицы в левой части расширенной матрицы, которую вы решаете (в этом случае вы не используете не нужно ничего делать для решения системы уравнений, относящейся к матрице), метод исключения Гаусса (регулярное сокращение строк) всегда будет использоваться для решения линейной системы уравнений, которая была записана в виде матрицы.

Примеры исключения Гаусса

В качестве последнего раздела давайте поработаем еще несколько упражнений по исключению Гаусса (сокращение строк), чтобы вы могли больше практиковаться в этой методологии.На протяжении многих будущих уроков этого курса линейной алгебры вы обнаружите, что сокращение строк является одним из самых важных инструментов при работе с матричными уравнениями. Поэтому убедитесь, что вы понимаете все этапы решения следующих проблем.

Пример 2

Пример 3

Мы знаем, что для этой системы мы получим расширенную матрицу с тремя строками (поскольку система содержит три уравнения) и тремя столбцами слева от вертикальной линии (поскольку есть три разных переменных).В этом случае мы перейдем непосредственно к сокращению строк, и поэтому первая матрица, которую вы увидите в этом процессе, — это та, которую вы получите, преобразовав систему линейных уравнений в расширенную матрицу.

Уравнение 15: Строка, уменьшающая расширенную матрицу

Обратите внимание, как мы можем сразу сказать, что переменная z равна нулю для этой системы, поскольку третья строка результирующей матрицы показывает уравнение -9z = 0 . Мы используем это знание и проверяем вторую строку матрицы, которая предоставит уравнение 2y — 6z = 0 , подставив в это уравнение значение z = 0 \, в результате получится y \, также равное нулю.Таким образом, мы наконец подставляем оба значения y и z \ в уравнение, которое получается из первой строки матрицы: x + 4y + 3z = 1 , поскольку и y , и z \ , равны нулю, то это дает нам x = 1 . Итак, окончательное решение этой системы уравнений выглядит следующим образом:

Уравнение 16: Окончательное решение системы уравнений

Пример 4

Из чего видно, что последняя строка дает уравнение: 6z = 3 и, следовательно, z = 1/2.Мы подставляем это в уравнения, полученные во второй и первой строках (в указанном порядке), чтобы вычислить значения переменных x и y:

Пример 5

Решите следующую линейную систему, используя метод исключения Гаусса: Уравнение 21: Система линейных уравнений с двумя переменными
Транскрипция линейной системы в виде расширенной матрицы и редукции строк: Уравнение 22: Строка, уменьшающая расширенную матрицу
Что автоматически говорит нам y = 8 . Итак, подставляя это значение в уравнение из первой строки, получаем: 4x — 5y = 4x — 5 (8) = 4x — 40 = -6 4x = 34 \, и поэтому значение x равно: x = 172 \ frac {\ small17} {\ small2} 217 . И окончательное решение этой системы уравнений:
Уравнение 23: Окончательное решение системы уравнений

Пример 6

Чтобы завершить наш урок на сегодня, у нас есть рекомендация по ссылке, чтобы дополнить ваши исследования: Исключение Гаусса — статья, которая содержит некоторую дополнительную информацию о сокращении строк, включая введение в тему и еще несколько примеров.Как мы упоминали ранее, будьте готовы продолжать использовать сокращение строк почти на всем протяжении этого курса линейной алгебры, так что до встречи на следующем уроке!

Системы линейных уравнений: исключение Гаусса

Системы линейных уравнений:
Решение методом исключения Гаусса (стр. 6 из 7)

Разделы: Определения, Решение по графику, Подстановка, Исключение / добавление, исключение по Гауссу.

Решение трех переменных, линейных систем с тремя уравнениями сложнее, по крайней мере, на начальном этапе, чем решение систем с двумя переменными, потому что требуемые вычисления более грязный. Вам нужно будет очень аккуратно работать, и вам следует планируйте использовать много бумаги для заметок. Метод решения этих систем является расширением метода сложения двух переменных, поэтому сделайте конечно ты знаешь это метод хорошо и может использовать его последовательно правильно.

Хотя метод решения основан на добавлении / исключении, попытка выполнить фактическое добавление имеет тенденцию становится очень запутанным, поэтому существует систематизированный метод решения трех или более переменных системы. Этот метод называется «исключением по Гауссу» (с уравнения заканчиваются тем, что называется «строковой формой»).

Начнем с простого, и работаем над более сложными примерами.

Решите следующие проблемы система уравнений.

Довольно легко увидеть как действовать в этом случае. Я просто подставлю обратно значение z -value из третьего уравнения во второе, решите результат для л , а затем вставьте z и y в первое уравнение и решите результат для x .

10 л 3 (3) = 11
10 y 9 = 11
10 y = 20
y = 2

5 х + 4 (2) (3) = 0
5 x + 8 3 = 0
5 x + 5 = 0
5 x = 5
x = 1

Тогда решение ( х , y , z ) = (1, 2, 3).

Причина, по которой эта система была Легко решить, что система была «треугольной»; это относится к уравнениям, имеющим форму треугольника, из-за нижних уравнений содержащий только более поздние переменные.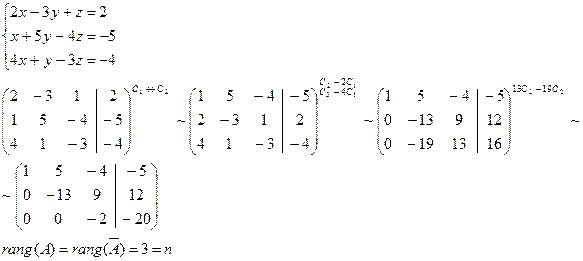

Дело в том, что в этом формат, система проста в решении. И гауссовское исключение — это метод, который мы будем использовать для преобразования систем в эту верхнетреугольную форму, используя операции со строками, которые мы изучили, когда применили метод сложения.

Решите следующие проблемы система уравнений с использованием исключения Гаусса.

Ни одно уравнение не решается для переменной, поэтому мне нужно будет выполнить умножение и сложение чтобы упростить эту систему. Чтобы отслеживать свою работу, напишу вниз на каждом шагу, когда я иду. Но я сделаю свои вычисления на бумаге для заметок. Вот как я это сделал:

Первое, что нужно сделать избавиться от ведущих терминов x в два ряда.А пока я просто посмотрю, какие строки будут легко расчистить; Я могу поменять строки позже, чтобы перевести систему в «верхний треугольной «формы. Нет правила, которое гласит, что я должен использовать x — срок из первой строки, и в этом случае, думаю, будет проще используйте термин x из третьей строки, так как его коэффициент просто «1». Я умножу третью строку на 3, и добавьте его в первую строку.Я делаю вычисления на бумаге для заметок:

… а потом записываю результатов:

(Когда мы решали системы с двумя переменными, мы могли умножить строку, переписав систему в сторону, а затем добавить. Для этого нет места в система с тремя переменными, поэтому нам и нужна бумага для заметок.)

Предупреждение: поскольку я не на самом деле ничего не делаю с третьей строкой, я скопировал ее без изменений, в новую матрицу уравнений.Я б / у третий ряд, но на самом деле я не менял Это. Не путайте «использование» с «изменением».

Чтобы получить меньшие числа для коэффициентов умножу первую строку на половину:

Теперь умножу третий ряд на 5 и добавьте это ко второму строка. Работаю на бумаге для заметок:

Я ничего не делал с первым рядом, поэтому я скопировал его без изменений. Я работал с третий ряд, но я работал только на вторая строка, поэтому вторая строка обновляется, а третья строка копируется более без изменений.

Хорошо, теперь x — столбец удаляется, за исключением ведущего члена в третьей строке.Так что дальше Приходится работать с колонкой y .

Предупреждение: С третьего уравнение имеет член x , Я больше не могу использовать его ни в одном из двух других уравнений (или я отменить мой прогресс). Я могу работать с по уравнению , но не с с Это.

Если я добавлю в два раза больше первого строки во вторую строку, это даст мне ведущую 1 во втором ряду.Я не буду избавились от ведущего y -термина во втором ряду, но я его преобразовал (не вмешиваясь дробями) в более простую форму. (Вы должны сохранить обратите внимание на такого рода упрощения.) Сначала я делаю царапину работа:

… а потом записываю результатов:

Теперь могу использовать второй ряд, чтобы очистить y -term в первом ряду.Вторую строку умножу на 7 и добавить. Сначала я царапаю работа:

… а потом записываю результатов:

Я могу сказать что z сейчас, но для большей точности я разделю первую строку на 43. Затем я переставляю ряды в верхнетреугольную форму:

Теперь я могу начать процесс обратного решения:

Тогда решение ( х , y , z ) = ( 2, 3, 1 ) .

Примечание: нет ничего священного о шагах, которые я использовал при решении указанной выше системы; там ничего не было особенно о том, как я решил эту систему. Вы могли бы работать в другом упорядочивайте или упрощайте разные строки, и все равно получите правильный ответ. Эти системы достаточно сложны, поэтому вряд ли один правильный способ вычисления ответа. Так что не беспокойтесь о том, «как она знала, что делать дальше? », потому что здесь нет правила.я просто делал все, что пришло мне в голову; Я делал то, что казалось самым простым или что-то еще пришла в голову первая. Не волнуйтесь, если бы вы использовали совершенно другой шаги. Если каждый шаг на пути верен, вы придумаете Такой же ответ.

В приведенном выше примере я мог пошли дальше в своих вычислениях и более тщательно проработали строковые операции, очищая все термины y кроме этого во втором ряду и во всех терминах z кроме того, что в первой строке.Это то, что процесс тогда выглядело так:

Так я могу просто читать от значений x , л , и z , и мне не нужно заморачиваться с обратной заменой. Это более полное метод решения называется «методом исключения Гаусса-Жордана» (с уравнения, попадающие в так называемый «пониженный ряд-эшелон» форма»).Многие тексты доходят до исключения Гаусса, но я всегда было легче продолжать и делать Гаусс-Джордан.

Обратите внимание, что я выполнил две строковые операции сразу на этом последнем шаге перед переключением строк. Пока я не работа с и работа с в той же строке на том же шаге, это нормально. В этом случае я работал с первой строкой и рабочий по второй и третий ряды.

<< Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Вернуться к указателю Далее >>

Цитируйте эту статью как:

Стапель, Елизавета. «Системы линейных уравнений, решаемые методом исключения Гаусса». Purplemath
Доступно с https: // www.purplemath.com/modules/systlin6.htm .
Дата обращения [Дата] [Месяц] 2016 г.

Решение системы с исключением Гаусса

Результаты обучения

Используйте метод исключения Гаусса для решения системы уравнений, представленной в виде расширенной матрицы.
Интерпретировать решение системы уравнений в виде расширенной матрицы.

Мы видели, как написать систему уравнений с расширенной матрицей , а затем как использовать строковые операции и обратную подстановку для получения строковой формы .Теперь мы будем использовать метод исключения Гаусса как инструмент для решения системы, записанной в виде расширенной матрицы. В нашем первом примере мы покажем вам процесс использования исключения Гаусса в системе двух уравнений с двумя переменными.

Пример: решение системы 2 X 2 методом исключения Гаусса

Решите данную систему методом исключения Гаусса.

[латекс] \ begin {array} {l} 2x + 3y = 6 \ hfill \\ \ text {} x-y = \ frac {1} {2} \ hfill \ end {array} [/ latex]

Показать решение

Сначала мы запишем это как расширенную матрицу.

[латекс] \ left [\ begin {array} {rr} \ hfill 2 & \ hfill 3 \\ \ hfill 1 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 6 \\ \ hfill \ frac {1} {2} \ end {array} \ right] [/ latex]

Нам нужна 1 в строке 1, столбце 1. Этого можно добиться, поменяв местами строку 1 и строку 2.

[латекс] {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 2 & \ hfill 3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 6 \ end {array} \ right] [/ latex]

Теперь у нас есть 1 как первая запись в строке 1, столбце 1.Теперь давайте получим 0 в строке 2, столбце 1. Это можно сделать, умножив строку 1 на [latex] -2 [/ latex], а затем прибавив результат к строке 2.

[латекс] -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill 5 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 5 \ end {массив } \ right] [/ latex]

У нас есть только один шаг, чтобы умножить строку 2 на [latex] \ frac {1} {5} [/ latex].

[латекс] \ frac {1} {5} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \ \ \ hfill 0 & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {cc} & \ frac {1} {2} \\ & 1 \ end {array} \ right] [/ latex]

Использовать обратную замену. Вторая строка матрицы представляет [латекс] y = 1 [/ латекс]. Подставьте обратно [latex] y = 1 [/ latex] в первое уравнение.

[латекс] \ begin {array} {l} x- \ left (1 \ right) = \ frac {1} {2} \ hfill \\ \ text {} x = \ frac {3} {2} \ hfill \ end {array} [/ latex]

Решение — точка [латекс] \ left (\ frac {3} {2}, 1 \ right) [/ latex].

Попробуйте

Решите данную систему методом исключения Гаусса.

[латекс] \ begin {массив} {l} 4x + 3y = 11 \ hfill \\ \ text {} \ text {} \ text {} x — 3y = -1 \ hfill \ end {array} [/ latex]

Показать решение

[латекс] \ влево (2,1 \ вправо) [/ латекс]

В нашем следующем примере мы решим систему двух уравнений с двумя зависимыми переменными.Напомним, что зависимая система имеет бесконечное количество решений, и результатом операций со строками в ее расширенной матрице будет уравнение, такое как [latex] 0 = 0 [/ latex]. Мы также рассмотрим написание общего решения для зависимой системы.

Пример: решение зависимой системы

Решите систему уравнений.

[латекс] \ begin {array} {l} 3x + 4y = 12 \\ 6x + 8y = 24 \ end {array} [/ latex]

Показать решение Выполните строковые операции в расширенной матрице, чтобы попытаться получить строковой формы .

[латекс] A = \ left [\ begin {array} {llll} 3 \ hfill & \ hfill & 4 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 12 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] [/ latex]

[латекс] \ begin {array} {l} \ hfill \\ \ begin {array} {l} — \ frac {1} {2} {R} _ {2} + {R} _ {1} = { R} _ {1} \ to \ left [\ begin {array} {llll} 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end { array} | \ begin {array} {ll} \ hfill & 0 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] \ hfill \\ {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {llll} 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \\ 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 24 \ hfill \\ \ hfill & 0 \ hfill \ end {array} \ right] \ hfill \ end {array} \ hfill \ end {array} [/ latex]

Матрица заканчивается всеми нулями в последней строке: [latex] 0y = 0 [/ latex].Таким образом, существует бесконечное количество решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и решите для [latex] y [/ latex].

[латекс] \ begin {array} {l} 3x + 4y = 12 \ hfill \\ \ text {} 4y = 12 — 3x \ hfill \\ \ text {} y = 3- \ frac {3} {4} x \ hfill \ end {array} [/ latex]

Итак, решение этой системы — [латекс] \ left (x, 3- \ frac {3} {4} x \ right) [/ latex].

Теперь мы перейдем на ступенчатую форму, чтобы решить систему линейных уравнений 3 на 3.Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.

Пример: решение системы линейных уравнений с использованием матриц

Решите систему линейных уравнений с помощью матриц.

[латекс] \ begin {массив} {c} \ begin {array} {l} \ hfill \\ \ hfill \\ x-y + z = 8 \ hfill \ end {array} \\ 2x + 3y-z = -2 \\ 3x — 2y — 9z = 9 \ end {array} [/ latex]

Показать решение

Сначала мы пишем расширенную матрицу.

[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill -1 \\ \ hfill 3 & \ hfill -2 & \ hfill -9 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 8 \\ \ hfill -2 \\ \ hfill 9 \ end {array} \ right] [/ latex]

Затем мы выполняем строковые операции, чтобы получить форму «строка-эшелон».

[латекс] \ begin {array} {rrrrr} \ hfill -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} { rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 3 & \ hfill & \ hfill -2 & \ hfill & \ hfill -9 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill 9 \ end {массив} \ right] & \ hfill & \ hfill & \ hfill & \ hfill -3 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill -15 \ end {array} \ right] \ end {array} [/ latex]

Самый простой способ получить 1 в строке 2 столбца 1 — это поменять местами [латекс] {R} _ {2} [/ latex] и [latex] {R} _ {3} [/ latex].

[латекс] \ text {Interchange} {R} _ {2} \ text {и} {R} _ {3} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill — 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 8 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill & \ hfill -15 \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill & \ hfill -18 \ end {array} \ right] [/ latex]

Затем

[латекс] \ begin {array} {l} \\ \ begin {array} {rrrrr} \ hfill -5 {R} _ {2} + {R} _ {3} = {R} _ {3} \ в \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 57 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \\ \ hfill & \ hfill 57 \ end {array} \ right] & \ hfill & \ hfill & \ hfill & \ hfill — \ frac {1} {57} {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \ \ \ hfill & \ hfill 1 \ end {array} \ right] \ end {array} \ end {array} [/ latex]

Последняя матрица представляет собой эквивалентную систему.

[латекс] \ begin {массив} {l} \ text {} x-y + z = 8 \ hfill \\ \ text {} y — 12z = -15 \ hfill \\ \ text {} z = 1 \ hfill \ end {array} [/ latex]

Используя обратную подстановку, мы получаем решение как [latex] \ left (4, -3,1 \ right) [/ latex].

Напомним, что есть три возможных исхода решений для линейных систем. В предыдущем примере решение [латекс] \ left (4, -3,1 \ right) [/ latex] представляет точку в трехмерном пространстве. Эта точка представляет собой пересечение трех плоскостей.В следующем примере мы решаем систему, используя операции со строками, и обнаруживаем, что она представляет зависимую систему. Зависимая система в 3-х измерениях может быть представлена двумя идентичными плоскостями, как в 2-х измерениях, где зависимая система представляет две идентичные линии.

Пример: решение зависимой системы 3 x 3

Решите следующую систему линейных уравнений, используя метод исключения Гаусса.

[латекс] \ begin {array} {r} \ hfill -x — 2y + z = -1 \\ \ hfill 2x + 3y = 2 \\ \ hfill y — 2z = 0 \ end {array} [/ latex]

Показать решение

Запишите расширенную матрицу.

[латекс] \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill -2 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill -2 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill 2 \\ \ hfill 0 \ end {array} \ right] [/ latex]

Сначала умножьте строку 1 на [latex] -1 [/ latex], чтобы получить 1 в строке 1, столбце 1. Затем выполните операции со строками , чтобы получить форму строки-эшелон.

[латекс] — {R} _ {1} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 & \ hfill & \ hfill 2 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill & \ hfill 0 \ end {array} \ справа] [/ латекс]

[латекс] {R} _ {2} \ leftrightarrow {R} _ {3} \ to \ left [\ begin {array} {rrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 \ \ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 \ end {array} \ text {} | \ begin {array} { rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 2 \ end {array} \ right] [/ latex]

[латекс] -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -1 & \ hfill & \ hfill 2 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]

[латекс] {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 0 & \ hfill \ end { array} | \ begin {array} {rr} \ hfill & \ hfill 2 \\ \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]

Последняя матрица представляет следующую систему.

[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y — 2z = 0 \ hfill \\ \ text {} 0 = 0 \ hfill \ конец {array} [/ latex]

По тождеству [latex] 0 = 0 [/ latex] мы видим, что это зависимая система с бесконечным числом решений. Затем мы находим общее решение. Решив второе уравнение для [latex] y [/ latex] и подставив его в первое уравнение, мы можем решить для [latex] z [/ latex] через [latex] x [/ latex].

[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y = 2z \ hfill \\ \ hfill \\ x + 2 \ left (2z \ справа) -z = 1 \ hfill \\ \ text {} x + 3z = 1 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \ end {array} [/ latex]

Теперь мы подставляем выражение для [latex] z [/ latex] во второе уравнение, чтобы решить для [latex] y [/ latex] через [latex] x [/ latex].

[латекс] \ begin {массив} {l} \ text {} y — 2z = 0 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \\ \ hfill \\ y — 2 \ left (\ frac {1-x} {3} \ right) = 0 \ hfill \\ \ text {} y = \ frac {2 — 2x} {3} \ hfill \ end {array} [/ latex ]

Общее решение — [latex] \ left (x, \ frac {2 — 2x} {3}, \ frac {1-x} {3} \ right) [/ latex].

Общее решение для зависимой системы 3 X 3

Напомним, что когда вы решаете зависимую систему линейных уравнений с двумя переменными с использованием исключения или подстановки, вы можете записать решение [latex] (x, y) [/ latex] через x, потому что существует бесконечно много (x, y) пары, которые будут удовлетворять зависимой системе уравнений, и все они попадают на линию [латекс] (x, mx + b) [/ latex].Теперь, когда вы работаете в трех измерениях, решение будет представлять собой плоскость, поэтому вы должны записать его в общей форме [латекс] (x, m_ {1} x + b_ {1}, m_ {2} x + b_ { 2}) [/ латекс].

Попробуйте

Решите систему методом исключения Гаусса.

[латекс] \ begin {array} {c} x + 4y-z = 4 \\ 2x + 5y + 8z = 15 \ x + 3y — 3z = 1 \ end {array} [/ latex]

Показать решение

[латекс] \ левый (1,1,1 \ правый) [/ латекс]

Вопросы и ответы

Можно ли решить любую систему линейных уравнений методом исключения Гаусса?

Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.

Как: решить систему уравнений с помощью матриц с помощью калькулятора

Сохраните расширенную матрицу как матричную переменную [latex] \ left [A \ right], \ left [B \ right], \ left [C \ right] \ text {,} \ dots [/ latex].
Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.

Пример: решение систем уравнений с помощью калькулятора

Решите систему уравнений.

[латекс] \ begin {array} {r} \ hfill 5x + 3y + 9z = -1 \\ \ hfill -2x + 3y-z = -2 \\ \ hfill -x — 4y + 5z = 1 \ end { array} [/ latex]

Показать решение

Напишите расширенную матрицу для системы уравнений.

[латекс] \ left [\ begin {array} {rrr} \ hfill 5 & \ hfill 3 & \ hfill 9 \\ \ hfill -2 & \ hfill 3 & \ hfill -1 \\ \ hfill -1 & \ hfill -4 & \ hfill 5 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill -2 \\ \ hfill 1 \ end {array} \ right] [/ latex]

На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную [latex] \ left [A \ right] [/ latex].

[латекс] \ left [A \ right] = \ left [\ begin {array} {rrrrrrr} \ hfill 5 & \ hfill & \ hfill 3 & \ hfill & \ hfill 9 & \ hfill & \ hfill -1 \\ \ hfill — 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill -1 & \ hfill & \ hfill -2 \\ \ hfill -1 & \ hfill & \ hfill -4 & \ hfill & \ hfill 5 & \ hfill & \ hfill 1 \ end {массив } \ right] [/ latex]

Используйте функцию ref ( в калькуляторе, вызывая матричную переменную [latex] \ left [A \ right] [/ latex].

[латекс] \ text {ref} \ left (\ left [A \ right] \ right) [/ латекс]

Оценить.

[латекс] \ begin {array} {l} \ hfill \\ \ left [\ begin {array} {rrrr} \ hfill 1 & \ hfill \ frac {3} {5} & \ hfill \ frac {9} {5 } & \ hfill \ frac {1} {5} \\ \ hfill 0 & \ hfill 1 & \ hfill \ frac {13} {21} & \ hfill — \ frac {4} {7} \\ \ hfill 0 & \ hfill 0 & \ hfill 1 & \ hfill — \ frac {24} {187} \ end {array} \ right] \ to \ begin {array} {l} x + \ frac {3} {5} y + \ frac {9} {5} z = — \ frac {1} {5} \ hfill \\ \ text {} y + \ frac {13} {21} z = — \ frac {4} {7} \ hfill \\ \ text {} z = — \ frac {24} {187} \ hfill \ end {array} \ hfill \ end {array} [/ latex]

При использовании обратной подстановки решение: [latex] \ left (\ frac {61} {187}, — \ frac {92} {187}, — \ frac {24} {187} \ right) [/ latex] .

Приложения систем уравнений

Теперь обратимся к приложениям, для которых используются системы уравнений. В следующем примере мы определяем, сколько денег было инвестировано по двум разным ставкам, учитывая сумму процентов, полученных на обоих счетах.

Пример: применение матриц 2 × 2 к финансам

Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов.Сколько было вложено по каждой ставке?

Показать решение

У нас есть система двух уравнений с двумя переменными. Пусть [latex] x = [/ latex] сумма, инвестированная под 10,5% годовых, и [latex] y = [/ latex] сумма, инвестированная под 12% годовых.

[латекс] \ begin {массив} {l} \ text {} x + y = 12 000 \ hfill \\ 0,105x + 0,12y = 1,335 \ hfill \ end {array} [/ latex]

В качестве матрицы имеем

[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0.105 & \ hfill 0.12 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 12,000 \\ \ hfill 1,335 \ end {array} \ right] [/ latex]

Умножить строку 1 на [латекс] -0.105 [/ latex] и добавьте результат в строку 2.

[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0 & \ hfill 0.015 \ end {array} \ text {} | \ text {} \ begin {array} {r } \ hfill 12,000 \\ \ hfill 75 \ end {array} \ right] [/ latex]

Затем,

[латекс] \ begin {array} {l} 0,015y = 75 \ hfill \\ \ text {} y = 5,000 \ hfill \ end {array} [/ latex]

Итак [латекс] 12 000 — 5 000 = 7 000 [/ латекс].

Таким образом, 5000 долларов были инвестированы под 12% и 7000 долларов под 10,5%.

Пример: применение матриц 3 × 3 к финансам

Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5% годовых, другой — 8%, а третий — 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?

Показать решение

У нас есть система трех уравнений с тремя переменными. Пусть [latex] x [/ latex] будет сумма, инвестированная под 5% годовых, пусть [latex] y [/ latex] будет суммой, инвестированной под 8%, и пусть [latex] z [/ latex] будет инвестированной суммой. под 9% годовых. Таким образом,

[латекс] \ begin {array} {l} \ text {} x + y + z = 10 000 \ hfill \\ 0.05x + 0,08y + 0,09z = 770 \ hfill \\ \ text {} 2x-z = 0 \ hfill \ end {array} [/ latex]

В качестве матрицы имеем

[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 1 & \ hfill 1 \\ \ hfill 0,05 & \ hfill 0,08 & \ hfill 0,09 \\ \ hfill 2 & \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 10,000 \\ \ hfill 770 \\ \ hfill 0 \ end {array} \ right] [/ latex]

Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.

[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ -0.05 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 2 & \ hfill & \ hfill 0 & \ hfill & \ hfill -1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill 0 \ end {array} \ right] \ hfill \ end {array} \ hfill \\ -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ \ frac {1} {0.03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ 2 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill — \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end {array} \ right] \ hfill \ end {array} [/ latex]

Третья строка сообщает нам [латекс] — \ frac {1} {3} z = -2,000 [/ latex]; таким образом [латекс] z = 6,000 [/ латекс].

Вторая строка сообщает нам [латекс] y + \ frac {4} {3} z = 9000 [/ latex].

Подставляя [латекс] z = 6,000 [/ латекс], получаем

[латекс] \ begin {array} {r} \ hfill y + \ frac {4} {3} \ left (6000 \ right) = 9000 \\ \ hfill y + 8000 = 9000 \\ \ hfill y = 1000 \ end {array} [/ latex]

Первая строка сообщает нам [латекс] x + y + z = 10,000 [/ latex]. Подставляя [latex] y = 1,000 [/ latex] и [latex] z = 6,000 [/ latex], мы получаем
[latex] \ begin {array} {l} x + 1,000 + 6,000 = 10,000 \ hfill \\ \ text {} x = 3,000 \ text {} \ hfill \ end {array} [/ latex]

Ответ: 3000 долларов вложены под 5%, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.

Попробуйте

Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своего ассортимента. Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов. Используйте матрицы, чтобы найти сумму, заимствованную по каждой ставке.

Показать решение

150 000 долларов США под 7%, 750 000 долларов США под 8%, 600 000 долларов США под 10%

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

систем линейных уравнений: исключение Гаусса

Решать нелинейные системы уравнений довольно сложно, а линейные системы довольно легко изучать. Существуют численные методы, которые помогают аппроксимировать нелинейные системы линейными в надежде, что решения линейных систем достаточно близки к решениям нелинейных систем. Мы не будем здесь это обсуждать.Вместо этого мы сосредоточим наше внимание на линейных системах.

Для простоты мы ограничимся тремя, максимум четырьмя неизвестными. Читатель, интересующийся случаем большего количества неизвестных, может легко развить следующие идеи.

Определение. Уравнение

a x + b y + c z + d w = h

где a , b , c , d и h — известные числа, а x , y , z и w — неизвестные числа. называется линейным уравнением .Если h = 0, линейное уравнение называется однородным . Линейная система представляет собой набор линейных уравнений, а однородная линейная система представляет собой набор однородных линейных уравнений.

Например,

а также

линейные системы, а

является нелинейной системой (из-за y ²). Система

является однородной линейной системой.

Матричное представление линейной системы

Матрицы помогают переписать линейную систему в очень простой форме.Затем для решения систем можно использовать алгебраические свойства матриц. Сначала рассмотрим линейную систему

Установите матрицы

Используя матричное умножение, мы можем переписать линейную систему выше как матричное уравнение

Как видите, это намного лучше, чем уравнения. Но иногда стоит решить систему напрямую, минуя матричную форму. Матрица A называется матричным коэффициентом линейной системы.Матрица C называется неоднородным членом . Когда , линейная система однородна. Матрица X — это неизвестная матрица. Его записи являются неизвестными линейной системы. Расширенная матрица , связанная с системой, является матрицей [ A | C ], где

В общем, если линейная система имеет n уравнений с m неизвестными, то матричный коэффициент будет матрицей nxm, а расширенная матрица — матрицей nx (m + 1).Теперь обратим внимание на решения системы.

Определение. Две линейные системы с n неизвестными называются эквивалентными тогда и только тогда, когда они имеют одинаковый набор решений.

Это определение важно, поскольку идея решения системы состоит в том, чтобы найти эквивалентную систему, которую легко решить. Вы можете задаться вопросом, как мы придумаем такую систему? Легко, мы делаем это с помощью элементарных операций . Действительно, ясно, что если мы поменяем местами два уравнения, новая система все равно будет эквивалентна старой.Если мы умножим уравнение на ненулевое число, мы получим новую систему, по-прежнему эквивалентную старой. И, наконец, заменив одно уравнение суммой двух уравнений, мы снова получим эквивалентную систему. Эти операции называются элементарными операциями над системами. Посмотрим, как это работает в конкретном случае.

Пример. Рассмотрим линейную систему

Идея состоит в том, чтобы сохранить первое уравнение и поработать над двумя последними. При этом мы попытаемся убить одного из неизвестных и решить два других.Например, если мы сохраним первое и второе уравнение и вычтем первое из последнего, мы получим эквивалентную систему

Затем мы сохраняем первое и последнее уравнение и вычитаем первое из второго. Получаем эквивалентную систему

Теперь мы сосредоточимся на втором и третьем уравнениях. Повторяем ту же процедуру. Попробуйте убить одного из двух неизвестных ( y или z ). Действительно, мы сохраняем первое и второе уравнение и добавляем второе к третьему, умножив его на 3.Мы получили

Это, очевидно, означает z = -2. Из второго уравнения мы получаем y = -2, и, наконец, из первого уравнения мы получаем x = 4. Следовательно, линейная система имеет одно решение.

Переход от последнего уравнения к первому при решении для неизвестных называется обратным решением .

Имейте в виду, что линейные системы, для которых матричный коэффициент является верхнетреугольным, легко решить. Это особенно верно, если матрица имеет эшелонированную форму.Таким образом, фокус состоит в том, чтобы выполнить элементарные операции по преобразованию исходной линейной системы в другую, для которой матрица коэффициентов имеет эшелонированную форму.
Используя наши знания о матрицах, можем ли мы в любом случае переписать то, что мы сделали выше, в матричной форме, которая упростит нашу нотацию (или представление)? Действительно, рассмотрим расширенную матрицу

Выполним над этой матрицей несколько элементарных операций со строками. Действительно, если мы сохраним первую и вторую строки и вычтем первую из последней, мы получим

Затем мы сохраняем первую и последнюю строки и вычитаем первую из второй.Мы получили

Затем мы сохраняем первую и вторую строки и добавляем вторую к третьей, умножив ее на 3, чтобы получить

Это треугольная матрица, не имеющая эшелонированной формы. Линейная система, для которой эта матрица является расширенной, есть

Как видите, мы получили ту же систему, что и раньше. Фактически мы следовали тем же элементарным операциям, что и выше. На каждом этапе новая матрица была в точности расширенной матрицей, связанной с новой системой.Это показывает, что вместо того, чтобы писать системы снова и снова, легко поиграться с элементарными операциями со строками, и как только мы получим треугольную матрицу, напишем связанную линейную систему, а затем решим ее. Это известно как исключения Гаусса . Подведем итоги процедуры:

Исключение Гаусса. Рассмотрим линейную систему.

1.: Построить расширенную матрицу для системы;
2.: Используйте элементарные операции со строками, чтобы преобразовать расширенную матрицу в треугольную;
3.: Запишите новую линейную систему, для которой треугольная матрица является связанной с ней расширенной матрицей;
4.: Решите новую систему. Вам может потребоваться присвоить некоторые параметрические значения некоторым неизвестным, а затем применить метод обратной подстановки для решения новой системы.

Пример. Решите следующую систему методом исключения Гаусса

Расширенная матрица

Мы используем элементарные операции со строками, чтобы преобразовать эту матрицу в треугольную.Мы сохраняем первую строку и используем ее для получения всех нулей в любом месте первого столбца. У нас есть

Далее мы сохраняем первую и вторую строки и стараемся, чтобы во втором столбце были нули. Мы получили

Далее сохраняем первые три ряда. Добавляем последний к третьему, чтобы получить

Это треугольная матрица. Связанная с ним система

Очевидно, что v = 1. Установите z = s и w = t , тогда мы имеем

Из первого уравнения следует Используя алгебраические манипуляции, получаем
x = — — с — т .
Собрав все вместе, у нас есть

Пример. Используйте метод исключения Гаусса для решения линейной системы

Соответствующая расширенная матрица

Сохраняем первую строку и вычитаем первую строку, умноженную на 2, из второй строки. Мы получили

Это треугольная матрица. Связанная система

Ясно, что второе уравнение означает, что эта система не имеет решения. Следовательно, эта линейная система не имеет решения.

Определение. Линейная система называется непоследовательной или переопределенной , если у нее нет решения. Другими словами, набор решений пуст. В противном случае линейная система называется согласованной .

Следуя приведенному выше примеру, мы видим, что если мы выполним элементарные операции со строками над расширенной матрицей системы и получим матрицу с одной из строк, равной , где , тогда система несовместима.

[Назад] [Следующий] [Геометрия] [Алгебра] [Тригонометрия] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра]

С.O.S MATH: Домашняя страница

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.

Автор : М.А.Хамси

Авторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователя онлайн за последний час

7.6 Решение систем с исключением Гаусса — Колледжская алгебра

Цели обучения

В этом разделе вы:

Напишите расширенную матрицу системы уравнений.
Напишите систему уравнений из расширенной матрицы.
Выполняет операции со строками в матрице.
Решите систему линейных уравнений, используя матрицы.

Рисунок 1 Немецкий математик Карл Фридрих Гаусс (1777–1855).

Карл Фридрих Гаусс жил в конце 18-го и начале 19-го веков, но до сих пор считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика.Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.

Мы впервые столкнулись с методом исключения Гаусса в системах линейных уравнений: две переменные. В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.

Запись расширенной матрицы системы уравнений

Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы.Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей.

Например, рассмотрим следующую систему уравнений 2 × 22 × 2.

3x + 4y = 74x − 2y = 53x + 4y = 74x − 2y = 5

Мы можем записать эту систему в виде расширенной матрицы:

[344−2 | 75] [344−2 | 75]

Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов.

Система уравнений три на три, например

3x − y − z = 0 x + y = 5 2x − 3z = 23x − y − z = 0 x + y = 5 2x − 3z = 2

имеет матрицу коэффициентов

[3−1−111020−3] [3−1−111020−3]

и представлен расширенной матрицей

[3−1−111020−3 | 052] [3−1−111020−3 | 052]

Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: x -термов идут в первый столбец, — -члены во втором столбце и z -термы в третьем. столбец.Очень важно, чтобы каждое уравнение было записано в стандартной форме ax + by + cz = dax + by + cz = d, чтобы переменные совпадали. Если в уравнении отсутствует член переменной, коэффициент равен 0.

How To

Для данной системы уравнений напишите расширенную матрицу.

Запишите коэффициенты членов x в виде чисел в первом столбце.
Запишите коэффициенты членов и в виде чисел во втором столбце.
Если имеется z -термов, запишите коэффициенты в виде чисел в третьем столбце.
Нарисуйте вертикальную линию и напишите константы справа от нее.

Пример 1

Написание расширенной матрицы для системы уравнений

Напишите расширенную матрицу для данной системы уравнений.

x + 2y − z = 32x − y + 2z = 6 x − 3y + 3z = 4 x + 2y − z = 32x − y + 2z = 6 x − 3y + 3z = 4

Решение

Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.

[12−12−121−33 | 364] [12−12−121−33 | 364]

Попробуй # 1

Запишите расширенную матрицу данной системы уравнений.

4x − 3y = 113x + 2y = 44x − 3y = 113x + 2y = 4

Написание системы уравнений из расширенной матрицы

Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными. Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным.Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.

Пример 2

Написание системы уравнений из расширенной матричной формы

Найдите систему уравнений из расширенной матрицы.

[1−3−52−5−4−354 | −256] [1−3−52−5−4−354 | −256]

Решение

Когда столбцы представляют переменные x, x, y, y и z, z,

[1−3−52−5−4−354 | −256] → x − 3y − 5z = −22x − 5y − 4z = 5−3x + 5y + 4z = 6 [1−3−52−5−4−354 | −256] → x − 3y − 5z = −22x − 5y − 4z = 5−3x + 5y + 4z = 6

Попробуй # 2

Напишите систему уравнений из расширенной матрицы.

[1−112−13011 | 51−9] [1−112−13011 | 51−9]

Выполнение операций со строками в матрице

Теперь, когда мы можем писать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками, которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.

Выполнение строковых операций над матрицей — это метод, который мы используем для решения системы уравнений. Чтобы решить систему уравнений, мы хотим преобразовать матрицу в форму строки-эшелона, в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали. как показано.

Форма строки-эшелон [1ab01d001] Форма строки-эшелон [1ab01d001]

Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строкам в более простой форме. Вот рекомендации по получению формы рядного эшелона.

В любой ненулевой строке первым ненулевым числом является 1. Оно называется ведущим 1.
Любые нулевые строки помещаются внизу матрицы.
Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.

Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в форму ряда строк и выполнить обратную подстановку, чтобы найти решение.

Поменять ряды местами. (Замечание: Ri↔RjRi↔Rj)
Умножить строку на константу. (Замечание: cRicRi)
Добавить произведение одной строки на константу к другой строке. (Замечание: Ri + cRj) Ri + cRj)

Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными.С помощью этих операций есть несколько ключевых ходов, которые быстро достигнут цели написания матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, так что строку 1 можно использовать для преобразования оставшихся строк.

Исключение по Гауссу

Метод исключения Гаусса относится к стратегии, используемой для получения матрицы в виде строки-эшелона. Цель состоит в том, чтобы записать матрицу AA с номером 1 в качестве записи вниз по главной диагонали и иметь все нули внизу.

A = [a11a12a13a21a22a23a31a32a33] → После исключения по Гауссу A = [1b12b1301b23001] A = [a11a12a13a21a22a23a31a32a33] → После исключения по Гауссу A = [1b12b1301b23001]

Первый шаг 1 этой строки может быть использован в качестве первой стратегии по Гауссу. чтобы изменить строки ниже.

Как к

Учитывая расширенную матрицу, выполните операции со строками для получения формы «строка-эшелон».

Первое уравнение должно иметь старший коэффициент 1.При необходимости поменяйте местами строки или умножьте на константу.
Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.
Используйте операции со строками, чтобы получить 1 в строке 2, столбце 2.
Используйте операции со строками, чтобы получить нули в нижнем столбце 2, ниже записи 1.
Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу будут только нули.
Если какие-либо строки содержат все нули, поместите их внизу.

Пример 3

Решение системы 2 × 22 × 2 методом исключения Гаусса

Решите данную систему методом исключения Гаусса.

2x + 3y = 6 x − y = 122x + 3y = 6 x − y = 12

Решение

Сначала мы запишем это как расширенную матрицу.

[231−1 | 612] [231−1 | 612]

Нам нужна 1 в строке 1, столбце 1. Этого можно добиться, поменяв местами строку 1 и строку 2.

R1↔R2 → [1−123 | 126] R1↔R2 → [1−123 | 126]

Теперь у нас есть 1 как первая запись в строке 1, столбце 1.Теперь давайте получим 0 в строке 2, столбце 1. Это можно сделать, умножив строку 1 на −2, −2 и затем добавив результат к строке 2.

−2R1 + R2 = R2 → [1−105 | 125 | ] −2R1 + R2 = R2 → [1−105 | 125]

У нас есть только один шаг, чтобы умножить строку 2 на 15,15.

15R2 = R2 → [1−101 | 121] 15R2 = R2 → [1−101 | 121]

Использовать обратную замену. Вторая строка матрицы представляет y = 1. y = 1. Подставьте обратно y = 1y = 1 в первое уравнение.

x− (1) = 12 x = 32x− (1) = 12 x = 32

Решением является точка (32,1).(32,1).

Попробуй # 3

Решите данную систему методом исключения Гаусса.

4x + 3y = 11 x − 3y = −14x + 3y = 11 x − 3y = −1

Пример 4

Использование исключения Гаусса для решения системы уравнений

Используйте метод исключения Гаусса, чтобы решить данную 2 × 22 × 2 система уравнений.

2x + y = 14x + 2y = 6 2x + y = 14x + 2y = 6

Решение

Запишите систему как расширенную матрицу.

[2142 | 16] [2142 | 16]

Получите 1 в строке 1, столбце 1.Этого можно добиться, умножив первую строку на 12,12.

12R1 = R1 → [11242 | 126] 12R1 = R1 → [11242 | 126]

Затем нам нужен 0 в строке 2, столбце 1. Умножим строку 1 на −4−4 и прибавим строку 1 к строке 2.

−4R1 + R2 = R2 → [11200 | 124] −4R1 + R2 = R2 → [11200 | 124]

Вторая строка представляет уравнение 0 = 4,0 = 4. Следовательно, система непоследовательна и не имеет решения.

Пример 5

Решение зависимой системы

Решите систему уравнений.

3x + 4y = 126x + 8y = 243x + 4y = 126x + 8y = 24

Решение

Выполните операции со строками в расширенной матрице, чтобы попытаться получить форму строки-эшелона.

A = [3468 | 1224] A = [3468 | 1224] −12R2 + R1 = R1 → [0068 | 024] R1↔R2 → [6800 | 240] −12R2 + R1 = R1 → [0068 | 024] R1↔ R2 → [6800 | 240]

Матрица заканчивается всеми нулями в последней строке: 0y = 0,0y = 0. Таким образом, существует бесконечное количество решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и решите относительно y.y.

3x + 4y = 12 4y = 12−3x y = 3−34x3x + 4y = 12 4y = 12−3x y = 3−34x

Итак, решение этой системы — (x, 3−34x).(x, 3−34x).

Пример 6

Выполнение операций со строками в расширенной матрице 3 × 3 для получения формы Row-Echelon

Выполняет строковые операции с заданной матрицей для получения формы «строка-эшелон».

[1−342−56−334 | 366] [1−342−56−334 | 366]

Решение

В первой строке уже есть 1 в строке 1, столбце 1. Следующим шагом будет умножение строки 1 на −2−2 и прибавление ее к строке 2. Затем замените строку 2 результатом.

−2R1 + R2 = R2 → [1−3401−2−334 | 306] −2R1 + R2 = R2 → [1−3401−2−334 | 306]

Затем получите ноль в строке 3, столбце 1.

3R1 + R3 = R3 → [1−3401−20−616 | 3015] 3R1 + R3 = R3 → [1−3401−20−616 | 3015]

Затем получаем ноль в строке 3, столбце 2.

6R2 + R3 = R3 → [1−3401−2004 | 3015] 6R2 + R3 = R3 → [1−3401−2004 | 3015]

Последний шаг — получить 1 в строке 3, столбце 3.

14R3 = R3 → [1−3401−2001 | 3−6154] 14R3 = R3 → [1−3401−2001 | 3−6154]

Попробуй # 4

Запишите систему уравнений в виде ряда.

x − 2y + 3z = 9 − x + 3y = −42x − 5y + 5z = 17 x − 2y + 3z = 9 − x + 3y = −42x − 5y + 5z = 17

Решение системы линейных уравнений с использованием матриц

Мы увидели, как написать систему уравнений с расширенной матрицей, а затем как использовать строковые операции и обратную подстановку для получения строчно-эшелонированной формы.Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.

Пример 7

Решение системы линейных уравнений с использованием матриц

Решите систему линейных уравнений с помощью матриц.

x − y + z = 82x + 3y − z = −23x − 2y − 9z = 9x − y + z = 82x + 3y − z = −23x − 2y − 9z = 9

Решение

Сначала мы пишем расширенную матрицу.

[1−1123−13−2−9 | 8−29] [1−1123−13−2−9 | 8−29]

Затем мы выполняем строковые операции для получения формы «строка-эшелон».

−2R1 + R2 = R2 → [1−1105−33−2−9 | 8−189] −3R1 + R3 = R3 → [1−1105−301−12 | 8−18−15] −2R1 + R2 = R2 → [1−1105−33−2−9 | 8−189] −3R1 + R3 = R3 → [1−1105−301−12 | 8−18−15]

Самый простой способ получить 1 в строке 2 столбец 1 предназначен для замены R2R2 и R3.R3.

Обмен R2 и R3 → [1−11801−12−1505−3−18] Обмен R2andR3 → [1−11801−12−1505−3−18]

Тогда

−5R2 + R3 = R3 → [1−1101−120057 | 8−1557] −157R3 = R3 → [1−1101−12001 | 8−151] −5R2 + R3 = R3 → [1−1101−120057 | 8− 1557] −157R3 = R3 → [1−1101−12001 | 8−151]

Последняя матрица представляет собой эквивалентную систему.

x − y + z = 8 y − 12z = −15 z = 1x − y + z = 8 y − 12z = −15 z = 1

Используя обратную подстановку, мы получаем решение как (4, −3,1) . (4, −3,1).

Пример 8

Решение зависимой системы линейных уравнений с использованием матриц

Решите следующую систему линейных уравнений, используя матрицы.

−x − 2y + z = −1 2x + 3y = 2y − 2z = 0 − x − 2y + z = −1 2x + 3y = 2y − 2z = 0

Решение

Запишите расширенную матрицу.

[−1−2123001−2 | −120] [- 1−2123001−2 | −120]

Сначала умножьте строку 1 на −1−1, чтобы получить 1 в строке 1, столбце 1.Затем выполните операции со строками, чтобы получить форму эшелона строк.

−R1 → [12−123001−2 | 120] −R1 → [12−123001−2 | 120] R2↔R3 → [12−101−2230 | 102] R2↔R3 → [12−101−2230 | 102] −2R1 + R3 = R3 → [12−101−20−12 | 100] −2R1 + R3 = R3 → [12−101−20−12 | 100] R2 + R3 = R3 → [12−101−2000 | 210] R2 + R3 = R3 → [12−101−2000 | 210]

Последняя матрица представляет следующая система.

x + 2y − z = 1 y − 2z = 0 0 = 0x + 2y − z = 1 y − 2z = 0 0 = 0

Мы видим из тождества 0 = 00 = 0, что это зависимая система с бесконечным числом решений.Затем мы находим общее решение. Решив второе уравнение для yy и подставив его в первое уравнение, мы можем решить для zz через x.x.

x + 2y − z = 1 y = 2zx + 2 (2z) −z = 1 x + 3z = 1 z = 1 − x3x + 2y − z = 1 y = 2zx + 2 (2z) −z = 1 x + 3z = 1 z = 1 − x3

Теперь мы подставляем выражение для zz во второе уравнение, чтобы решить относительно yy через xx

y − 2z = 0z = 1 − x3y − 2 (1 − x3) = 0y = 2−2x3y − 2z = 0z = 1 − x3y − 2 (1 − x3) = 0y = 2−2×3

Общее решение: ( x, 2−2×3,1 − x3).(х, 2−2×3,1 − x3).

Попробуй # 5

Решите систему, используя матрицы.

x + 4y − z = 42x + 5y + 8z = 15x + 3y − 3z = 1x + 4y − z = 42x + 5y + 8z = 15x + 3y − 3z = 1

Вопросы и ответы

Можно ли решить любую систему линейных уравнений методом исключения Гаусса?

Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.

Как к

Дана система уравнений, решите с помощью матриц с помощью калькулятора.

Сохранить расширенную матрицу как матричную переменную [A], [B], [C],….[A], [B], [C],….
Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.

Пример 9

Решение систем уравнений с матрицами с помощью калькулятора

Решите систему уравнений.

5x + 3y + 9z = −1−2x + 3y − z = −2 − x − 4y + 5z = 1 5x + 3y + 9z = −1−2x + 3y − z = −2 − x − 4y + 5z = 1

Решение

Напишите расширенную матрицу для системы уравнений.

[539−23−1−1−45 | −1−2−1] [539−23−1−1−45 | −1−2−1]

На странице матриц калькулятора введите расширенную матрицу выше в качестве матричной переменной [A].[А].

[A] = [539−1−23−1−2−1−451] [A] = [539−1−23−1−2−1−451]

Используйте ref (функцию в калькуляторе, вызов матричной переменной [A]. [A].

Оценить.

[1359515011321−47001−24187] → x + 35y + 95z = −15y + 1321z = −47z = −24187 [1359515011321−47001−24187] → x + 35y + 95z = −15y + 1321z = −47z = −24187

Использование обратная подстановка, решение будет (61187, −92187, −24187). (61187, −92187, −24187).

Пример 10

Применение матриц 2 × 2 к финансам

Кэролайн инвестирует в общей сложности 12000 долларов в две муниципальные облигации, одна из которых выплачивает 10.5% годовых, а другой — 12% годовых. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?

Решение

У нас есть система двух уравнений с двумя переменными. Пусть x = x = сумма, инвестированная под 10,5%, а y = y = сумма, инвестированная под 12%.

x + y = 12,0000,105x + 0,12y = 1,335 x + y = 12,0000,105x + 0,12y = 1,335

В качестве матрицы мы имеем

[110.1050.12 | 12,0001,335] [110.1050.12 | 12,0001,335]

Умножьте строку 1 на −0,105−0,105 и прибавьте результат к строке 2.

[1100.015 | 12,00075] [1100.015 | 12,00075]

Тогда

0,015y = 75 y = 5,0000,015y = 75 y = 5,000

Итак, 12,000-5,000 = 7,000. 12,000-5,000 = 7,000.

Таким образом, 5000 долларов были инвестированы под 12% и 7000 долларов под 10,5%.

Пример 11

Применение матриц 3 × 3 к финансам

Решение

У нас есть система трех уравнений с тремя переменными. Пусть xx будет суммой, инвестированной под 5%, пусть yy будет суммой, инвестированной под 8%, и пусть zz будет суммой, инвестированной под 9%. Таким образом,

x + y + z = 10,0000,05x + 0,08y + 0,09z = 770 2x − z = 0 x + y + z = 10,0000.05x + 0,08y + 0,09z = 770 2x − z = 0

В качестве матрицы имеем

[1110.050.080.0920−1 | 10,0007700] [1110.050.080.0920−1 | 10,0007700]

Теперь мы выполняем исключение по Гауссу, чтобы получить форму строки-эшелон.

−0.05R1 + R2 = R2 → [11100.030.0420−1 | 10,0002700] −2R1 + R3 = R3 → [11100.030.040−2−3 | 10,000270−20,000] 10.03R2 = R2 → [01101430−2 −3 | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 | 10,0009,000−2,000] −0,05R1 + R2 = R2 → [11100.030.0420−1 | 10,0002700] — 2R1 + R3 = R3 → [11100.030.040−2−3 | 10,000270−20,000] 10.03R2 = R2 → [01101430−2−3 | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 | 10,0009,000−2,000]

Третья строка сообщает нам -13z = −2,000; −13z = −2,000; таким образом, z = 6000. z = 6000.

Вторая строка говорит нам, что y + 43z = 9000.y + 43z = 9000. Подставляя z = 6000, z = 6000, мы получаем

y + 43 (6000) = 9000y + 8000 = 9000y = 1000y + 43 (6000) = 9000y + 8000 = 9000y = 1000

. х + у + г = 10,000. х + у + г = 10,000. Подставив y = 1,000y = 1,000 и z = 6,000, z = 6,000, мы получим

x + 1,000 + 6,000 = 10,000 x = 3,000x + 1,000 + 6,000 = 10,000 x = 3,000

Ответ: 3,000 долларов вложены под 5% годовых, 1000 долларов инвестировано под 8%, а 6000 долларов — под 9%.

Попробуй # 6

7.6 Упражнения по разделам

Устные

Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет.Объясните, как написать эту расширенную матрицу.

Можно ли любую матрицу записать в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.

Есть только один правильный метод использования строк в матрице? Попытайтесь объяснить две различные операции со строками, которые можно использовать для решения расширенной матрицы [931−2 | 06]. [931−2 | 06].

Можно ли решить матрицу с нулевым элементом на диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?

Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.

Алгебраический

Для следующих упражнений напишите расширенную матрицу линейной системы.

8x − 37y = 82x + 12y = 38x − 37y = 82x + 12y = 3

16y = 49x − y = 2 16y = 49x − y = 2

3x + 2y + 10z = 3−6x + 2y + 5z = 13 4x + z = 183x + 2y + 10z = 3−6x + 2y + 5z = 13 4x + z = 18

x + 5y + 8z = 1912x + 3y = 43x + 4y + 9z = −7 x + 5y + 8z = 1912x + 3y = 43x + 4y + 9z = −7

10.

6x + 12y + 16z = 4 19x − 5y + 3z = −9 x + 2y = −86x + 12y + 16z = 4 19x − 5y + 3z = −9 x + 2y = −8

Для следующих упражнений запишите линейную систему из расширенной матрицы.

11.

[−256−18 | 526] [- 256−18 | 526]

12.

[341017 | 10439] [341017 | 10439]

13.

[320−1−94857 | 3−18] [320−1−94857 | 3−18]

14.

[8291−175003 | 433810] [8291−175003 | 433810]

15.

[45−2015887−3 | 122−5] [45−2015887−3 | 122−5]

Для следующих упражнений решите систему методом исключения Гаусса.

16.

[1000 | 30] [1000 | 30]

17.

[1010 | 12] [1010 | 12]

18.

[1245 | 36] [1245 | 36]

19.

[−124−5 | −36] [- 124−5 | −36]

20.

[−2002 | 1−1] [- 2002 | 1−1]

21.

2x − 3y = −95x + 4y = 58 2x − 3y = −95x + 4y = 58

22.

6x + 2y = −43x + 4y = −176x + 2y = −43x + 4y = −17

23.

2x + 3y = 12 4x + y = 142x + 3y = 12 4x + y = 14

24.

−4x − 3y = −2 3x − 5y = −13−4x − 3y = −2 3x − 5y = −13

25.

−5x + 8y = 310x + 6y = 5−5x + 8y = 310x + 6y = 5

26.

3x + 4y = 12−6x − 8y = −24 3x + 4y = 12−6x − 8y = −24

27.

−60x + 45y = 12 20x − 15y = −4−60x + 45y = 12 20x − 15y = −4

28.

11x + 10y = 4315x + 20y = 6511x + 10y = 4315x + 20y = 65

29.

2x − y = 23x + 2y = 172x − y = 23x + 2y = 17.

30.

−1.06x − 2.25y = 5.51−5.03x − 1.08y = 5.40−1.06x − 2.25y = 5.51−5.03x − 1.08y = 5,40

31.

34x − 35y = 414x + 23y = 134x − 35y = 414x + 23y = 1

32.

14x − 23y = −112x + 13y = 314x − 23y = −112x + 13y = 3

33.

[100011001 | 314587] [100011001 | 314587]

34.

[101110011 | 5020−90] [101110011 | 5020−90]

35.

[123056008 | 479] [123056008 | 479]

36.

[−0.10.3−0.1−0.40.20.10.60.10.7 | 0.20.8−0.8] [- 0.10.3−0.1−0.40.20.10.60.10.7 | 0,20,8−0,8]

37.

−2x + 3y − 2z = 3 4x + 2y − z = 94x − 8y + 2z = −6−2x + 3y − 2z = 3 4x + 2y − z = 94x − 8y + 2z = −6

38.

x + y − 4z = −4 5x − 3y − 2z = 0 2x + 6y + 7z = 30 x + y − 4z = −4 5x − 3y − 2z = 0 2x + 6y + 7z = 30

39.

2x + 3y + 2z = 1 −4x − 6y − 4z = −210x + 15y + 10z = 5 2x + 3y + 2z = 1 −4x − 6y − 4z = −210x + 15y + 10z = 5

40.

x + 2y − z = 1 − x − 2y + 2z = −23x + 6y − 3z = 5 x + 2y − z = 1 − x − 2y + 2z = −23x + 6y − 3z = 5

41.

x + 2y − z = 1 − x − 2y + 2z = −23x + 6y − 3z = 3 x + 2y − z = 1 − x − 2y + 2z = −23x + 6y − 3z = 3

42.

x + y = 2 x + z = 1 − y − z = −3 x + y = 2 x + z = 1 − y − z = −3

43.

x + y + z = 100 x + 2z = 125 − y + 2z = 25x + y + z = 100 x + 2z = 125 − y + 2z = 25.

44.

14x − 23z = −1215x + 13y = 4715y − 13z = 2914x − 23z = −1215x + 13y = 4715y − 13z = 29

45.

−12x + 12y + 17z = −5314 12x − 12y + 14z = 3 14x + 15y + 13z = 2315−12x + 12y + 17z = −5314 12x − 12y + 14z = 3 14x + 15y + 13z = 2315

46.

−12x − 13y + 14z = −296 15x + 16y − 17z = 431210−18x + 19y + 110z = −4945−12x − 13y + 14z = −296 15x + 16y − 17z = 431210−18x + 19y + 110z = — 4945

Расширения

Для следующих упражнений используйте метод исключения Гаусса для решения системы.

47.

x − 17 + y − 28 + z − 34 = 0x + y + z = 6x + 23 + 2y + z − 33 = 5x − 17 + y − 28 + z − 34 = 0x + y + z = 6x. + 23 + 2у + г — 33 = 5

48.

x − 14 − y + 14 + 3z = −1 x + 52 + y + 74 − z = 4 x + y − z − 22 = 1x − 14 − y + 14 + 3z = −1 x + 52 + y + 74-г = 4 х + у-г-22 = 1

49.

x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 8x + y + z = 1x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 8x + y + z = 1

50.

x − 310 + y + 32−2z = 3x + 54 − y − 18 + z = 32x − 14 + y + 42 + 3z = 32x − 310 + y + 32−2z = 3x + 54 − y − 18 + z = 32x − 14 + y + 42 + 3z = 32

51.

x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 7x + y + z = 1x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 7x + y + z = 1

Реальные приложения

Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.

52.

Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если вкус шоколада в 3 раза популярнее, чем аромат ванили, сколько кексов продается в день?

53.

В конкурирующем магазине кексов ежедневно продаются кексы на 4520 долларов. Шоколадные кексы стоят 2,25 доллара, а кексы из красного бархата — 1,75 доллара. Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?

54.

Вы вложили 10 000 долларов в два счета: один с простой процентной ставкой 3%, а другой — с процентной ставкой 2,5%. Если ваша общая выплата процентов по истечении одного года составила 283,50 доллара, какая сумма была на каждом счете по истечении года?

55.

Вы вложили 2300 долларов на счет 1 и 2700 долларов на счет 2.Если общая сумма процентов через год составляет 254 доллара, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.

56.

Bikes’R’Us производит велосипеды по 250 долларов. Он стоит производителю 180 долларов за велосипед плюс стартовый взнос в размере 3500 долларов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?

57.

Крупный магазин бытовой техники рассматривает возможность покупки пылесосов у небольшого производителя. Магазин сможет приобрести пылесосы по цене 86 долларов каждый, с оплатой доставки в размере 9 200 долларов, независимо от того, сколько пылесосов будет продано.Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать за пылесосы?

58.

Три самых популярных вкуса мороженого — это шоколад, клубника и ваниль, составляющие 83% вкусов, продаваемых в магазине мороженого. Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?

59.

В магазине мороженого растет спрос на три вкуса.В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы — на 20%. Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте, какой процент продаж мороженого было произведено каждым отдельным мороженым в прошлом году.

60.

Пакет с ореховой смесью содержит кешью, фисташки и миндаль.Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек. Кешью весит 3 г, фисташки — 4 г, миндаль — 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.

61.

Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Изначально кешью было на 100 штук больше, чем миндаля.Для начала выясните, сколько орехов каждого типа было в пакете.

Гаусс Джордан Устранение — Объяснение и примеры

Метод исключения Гаусса-Жордана — это алгоритм для решения линейной системы уравнений. Мы также можем использовать его, чтобы найти обратную матрицу. Давайте сначала посмотрим на определение:

Метод исключения Гаусса Джордана, или исключение Гаусса, представляет собой алгоритм для решения системы линейных уравнений, представляя ее в виде расширенной матрицы, сокращая ее с помощью операций со строками и выражая систему в сокращенной строке. -эшелонированная форма для нахождения значений переменных.

В этом уроке мы увидим детали метода исключения Гаусса и того, как решить систему линейных уравнений с помощью метода исключения Гаусса-Жордана. Примеры и практические вопросы будут приведены ниже.

Что такое метод исключения Гаусса?

Метод исключения Гаусса — это структурированный метод решения системы линейных уравнений. Таким образом, это алгоритм, который легко запрограммировать для решения системы линейных уравнений. Основная цель исключения Гаусса-Джордана:

представить систему линейных уравнений в форме расширенной матрицы
затем выполнить операции строки $ 3 $ до тех пор, пока не будет получена сокращенная форма эшелона строк (RREF) достигнуто
Наконец, мы можем легко распознать решения из RREF

Давайте посмотрим, что такое расширенная матричная форма, операции со строками стоимостью 3 доллара, которые мы можем выполнять с матрицей, и сокращенная форма эшелона строк матрицы.

Расширенная матрица

Система линейных уравнений показана ниже:

$ \ begin {align *} 2x + 3y & = \, 7 \\ x — y & = 4 \ end {align *} $

We запишет расширенную матрицу этой системы, используя коэффициенты уравнений и записав ее в стиле , показанном ниже:

$ \ left [\ begin {array} {rr | r} 2 & 3 & 7 \\ 1 & -1 & 4 \ end {array} \ right] $

Пример использования одновременных уравнений $ 3 $ показан ниже:

$ \ begin {align *} 2x + y + z & = \, 10 \\ x + 2y + 3z & = 1 \\ — x — y — z & = 2 \ end {align *} $

Представление этой системы в виде расширенной матрицы:

$ \ left [\ begin {array} {rrr | r} 2 & 1 & 1 & 10 \\ 1 & 2 & 3 & 1 \\ — 1 & — 1 & — 1 & 2 \ end {array} \ right] $

Операции со строками в матрице

Есть $ 3 $ элементарных операций со строками , которые мы можем выполнять с матрицами.Это не изменит решения системы. Это:

Обмен $ 2 $ строк
Умножить строку на ненулевой ($ \ neq 0 $) скаляр
Добавить или вычесть скалярное кратное одной строки из другой строки.

Форма сокращенного эшелона строк

Основная цель исключения Гаусса Джордана — использовать операции элементарной строки стоимостью 3 доллара в расширенной матрице, чтобы привести ее к форме сокращенного эшелона строк (RREF). Считается, что матрица находится в сокращенной форме эшелона строк , также известной как каноническая форма строки , если выполняются следующие условия $ 4 $:

строк с нулевыми записями (все элементы этой строки равны $ 0 $. s) находятся внизу матрицы.
ведущая запись (первая ненулевая запись в строке) каждой ненулевой строки соответствует правой ведущей записи строки непосредственно над ней.
Начальная запись в любой ненулевой строке — 1 доллар.
Все записи в столбце, содержащем начальную запись ($ 1 $), нулевые.

Как выполнить исключение Гаусса-Джордана

В методе исключения Гаусса-Джордана нет каких-либо определенных шагов, но алгоритм ниже описывает шаги, которые мы выполняем, чтобы прийти к сокращенной форме эшелона строк расширенной матрицы.

Поменяйте местами строки так, чтобы все строки с нулевыми записями находились внизу матрицы.
Поменяйте местами строки так, чтобы строка с самой большой левой цифрой находилась наверху матрицы.
Умножьте верхнюю строку на скаляр, который преобразует ведущую запись верхней строки в $ 1 $ (если ведущей записью верхней строки является $ a $, умножьте ее на $ \ frac {1} {a} $, чтобы получить $ 1 $).
Сложите или вычтите значения, кратные верхней строке, из других строк, чтобы все записи в столбце ведущей записи верхней строки были нулями.
Выполните шаги $ 2 — 4 $ для следующей крайней левой ненулевой записи , пока все ведущие записи каждой строки не будут равны 1 $.
Поменяйте местами строки так, чтобы ведущая запись каждой ненулевой строки находилась справа от ведущей записи строки непосредственно над ней

На первый взгляд, запомнить / запомнить шаги не так просто. Это вопрос решения нескольких проблем, пока вы не освоитесь с процессом. Существует также фактор интуиции , который играет B-I-G роль в выполнении исключения Гаусса Джордана.

Давайте рассмотрим несколько примеров, чтобы пояснить процесс решения системы линейных уравнений с помощью метода исключения Гаусса-Джордана .

Пример 1

Решите систему, показанную ниже, используя метод исключения Гаусса Джордана:

$ \ begin {align *} {- x} + 2y & = \, {- 6} \\ { 3x} — 4y & = {14} \ end {align *} $

Решение

Первый шаг — написать расширенную матрицу системы.Мы показываем это ниже:

$ \ left [\ begin {array} {r r | r} — 1 & 2 & — 6 \\ 3 & -4 & 14 \ end {array} \ right] $

Теперь наша задача состоит в том, чтобы преобразовать матрицу в сокращенную форму эшелона строк (RREF), выполнив команду $ 3 $ элементарные операции со строками.

У нас есть расширенная матрица:

$ \ left [\ begin {array} {r r | r} — 1 & 2 & — 6 \\ 3 & — 4 & 14 \ end {array} \ right] $

Шаг 1:

Мы можем умножить первую строку на $ — 1 $, чтобы получить ведущий вход $ 1 $.Показано ниже:

$ \ left [\ begin {array} {r r | r} 1 & — 2 & 6 \\ 3 & — 4 & 14 \ end {array} \ right] $

Шаг 2:

Теперь мы можем умножить первую строку на 3 $ и вычесть ее из второй ряд. Показано ниже:

$ \ left [\ begin {array} {r r | r} 1 & -2 & 6 \\ {3 — (1 \ times 3)} & {-4 — (-2 \ times 3)} & {14 — (6 \ times 3)} \ end {array} \ справа] $

$ = \ left [\ begin {array} {rr | r} 1 & — 2 & 6 \\ 0 & 2 & — 4 \ end {array} \ right] $

У нас есть $ 0 $ как первая запись во второй строке.

Шаг 3:

Чтобы сделать вторую запись второй строки $ 1 $, мы можем умножить вторую строку на $ \ frac {1} {2} $. Показано ниже:

$ \ left [\ begin {array} {r r | r} 1 & — 2 & 6 \\ {\ frac {1} {2} \ times 0} & {\ frac {1} {2} \ times 2} & {\ frac {1} {2} \ times — 4} \ end {array} \ right] $

$ = \ left [\ begin {array} {rr | r} 1 & — 2 & 6 \\ 0 & 1 & — 2 \ end {array} \ right] $

Шаг 4:

Мы почти у цели!

Вторая запись первой строки должна быть $ 0 $.Для этого мы умножаем вторую строку на $ 2 $ и добавляем ее к первой строке. Показано ниже:

$ \ left [\ begin {array} {r r | r} {1 + (0 \ times 2)} & {- 2 + (1 \ times 2)} & {6 + (- 2 \ times 2)} \\ 0 & 1 & — 2 \ end {array} \ справа] $

$ = \ left [\ begin {array} {rr | r} 1 & 0 & 2 \\ 0 & 1 & — 2 \ end {array} \ right] $

Это сокращенный эшелон строки формы . Из расширенной матрицы мы можем написать два уравнения (решения):

$ \ begin {align *} x + 0y & = \, 2 \\ 0x + y & = -2 \ end {align *} $

$ \ begin {align *} x & = \, 2 \\ y & = — 2 \ end {align *} $

Таким образом, решение системы уравнений: $ x = 2 $ и $ y = — 2 $.

Пример 2

Решите систему, показанную ниже, используя метод исключения Гаусса Джордана:

$ \ begin {align *} x + 2y & = \, 4 \\ x — 2y & = 6 \ end { align *} $

Решение

Запишем расширенную матрицу системы уравнений:

$ \ left [\ begin {array} {rr | r} 1 & 2 & 4 \\ 1 & — 2 & 6 \ end {array} \ right] $

Теперь мы выполняем элементарные операции со строками с этой матрицей, пока не получим сокращенную форму эшелона строк.

Шаг 1:

Умножаем первую строку на $ 1 $, а затем вычитаем ее из второй строки. По сути это вычитание первой строки из второй:

$ \ left [\ begin {array} {r r | r} 1 & 2 & 4 \\ 1 — 1 & — 2 — 2 & 6 — 4 \ end {array} \ right] $

$ = \ left [\ begin {array} {r r | r} 1 & 2 & 4 \\ 0 & — 4 & 2 \ end {array} \ right] $

Шаг 2:

Мы умножаем вторую строку на $ — \ frac {1} {4} $, чтобы получить вторая запись строки, $ 1 $:

$ \ left [\ begin {array} {rr | r} 1 и 2 и 4 \\ 0 \ times — \ frac {1} {4} & — 4 \ times — \ frac {1} {4} и 2 \ times — \ frac {1} {4} \ end {массив} \ right] $

$ = \ left [\ begin {array} {rr | r} 1 & 2 & 4 \\ 0 & 1 & — \ frac {1} {2} \ end {array} \ right] $

Шаг 3:

Наконец, мы умножаем вторую строку на $ — 2 $ и добавьте его в первую строку, чтобы получить уменьшенную форму эшелона строк этой матрицы:

$ \ left [\ begin {array} {rr | r} 1 + (- 2 \ times 0) & 2+ (- 2 \ times 1) & 4 + (- 2 \ times — \ frac {1} {2}) \\ 0 & 1 & — \ frac {1 } {2} \ end {array} \ right] $

$ = \ left [\ begin {array} {rr | r} 1 & 0 & 5 \\ 0 & 1 & — \ frac {1} {2} \ end {array} \ right] $

Это сокращенный эшелон строки формы .Из расширенной матрицы мы можем написать два уравнения (решения):

$ \ begin {align *} x + 0y & = \, 5 \\ 0x + y & = — \ frac {1} {2} \ end {align *} $

$ \ begin {align *} x & = \, 5 \\ y & = — \ frac {1} {2} \ end {align *} $

Таким образом, решение системы уравнений составляет $ x = 5 $ и $ y = — \ frac {1} {2} $.

Практические вопросы

Решите систему, показанную ниже, используя метод исключения Гаусса Джордана:
$ \ begin {align *} 2x + y & = \, — 3 \\ — x — y & = 2 \ end {align *} $
Решите систему, показанную ниже, используя метод исключения Гаусса Джордана:
$ \ begin {align *} x + 5y & = \, 15 \\ — x + 5y & = 25 \ end {align *} $

Ответы

Начнем с написания расширенной матрицы системы уравнений:
$ \ left [\ begin {array} {rr | r} 2 & 1 & — 3 \\ — 1 & — 1 & 2 \ end {array} \ right] $
Теперь мы выполняем элементарные операции со строками, чтобы прийти к нашему решению.
Первый,
Инвертируем знаки второй строки и меняем строки местами. Итак, имеем:
$ \ left [\ begin {array} {r r | r} 1 & 1 & — 2 \\ 2 & 1 & — 3 \ end {array} \ right] $
Во-вторых,
Мы дважды вычитаем первую строку из второй строки:
$ \ left [\ begin {array} { rr | r} 1 & 1 & — 2 \\ 2 — (2 \ times 1) & 1 — (2 \ times 1) & — 3 — (2 \ times — 2) \ end {array} \ right] $
$ = \ left [\ begin {array} {rr | r} 1 & 1 & — 2 \\ 0 & — 1 & 1 \ end {array} \ right] $
В-третьих,
Мы инвертируем вторую строку, чтобы получить:
$ = \ left [\ begin {array} {rr | r} 1 & 1 & — 2 \\ 0 & 1 & — 1 \ end {array} \ right] $
Наконец,
Мы вычитаем вторую строку из первой и получаем:
$ = \ left [\ begin { массив} {rr | r} 1 & 0 & — 1 \\ 0 & 1 & — 1 \ end {array} \ right] $
Из этой расширенной матрицы мы можем написать два уравнения (решения):
$ \ begin {align *} x + 0y & = \, — 1 \\ 0x + y & = — 1 \ end {align *} $
$ \ begin {align *} x & = \, — 1 \\ y & = — 1 \ end {align *} $
Таким образом, решение системы уравнений: $ x = — 1 $ и $ y = — 1 $.
Расширенная матрица системы:
$ \ left [\ begin {array} {rr | r} 1 & 5 & 15 \\ — 1 & 5 & 25 \ end {array} \ right] $
Давайте приведите эту матрицу к приведенной форме эшелона строк и найдите решение системы.

Сначала
Отмените первую строку, затем вычтите ее из второй строки, чтобы получить:
$ \ left [\ begin {array} {rr | r} 1 & 5 & 15 \\ — 1 — (- 1) & 5 — (- 5) & 25 — (- 15) \ end {array} \ right] $
$ = \ left [\ begin {array} {rr | r} 1 & 5 & 15 \\ 0 & 10 & 40 \ end {array} \ right] $
Во-вторых,
Разделите вторую строку на $ 10 $, чтобы получить:
$ \ left [\ begin {array} {rr | r} 1 & 5 & 15 \\ 0 & 1 & 4 \ end {array} \ right] $
Затем
Умножьте вторую строку на $ 5 $ и вычтите ее из первой строки, чтобы получить окончательное решение:
$ \ left [\ begin {array} {rr | r} 1 — (5 \ times 0) & 5 — (5 \ times 1) & 15 — (5 \ times 4) \\ 0 & 1 & 4 \ end {array} \ right] $
$ = \ left [ \ begin {array} {rr | r} 1 & 0 & — 5 \\ 0 & 1 & 4 \ end {array} \ right] $
Это сокращенная форма эшелона строк (RREF).Из этой расширенной матрицы мы можем написать два уравнения (решения):
$ \ begin {align *} x & = \, — 5 \\ y & = 4 \ end {align *} $
Таким образом, решение системы уравнений $ x = — 5 $ и $ y = 4 $.

Предыдущий урок | Главная страница | Следующий урок. K ] { u } = { F }.В операциях с матрицами существует три распространенных типа манипуляций, которые служат для создания новой матрицы, обладающей теми же характеристиками, что и исходная:
1.
Поменять местами любые две строки.
2.
Умножьте каждую запись в любой строке на ненулевое постоянное значение.
3.
Добавьте значения из каждой записи одной строки к каждой записи другой строки.
Цель использования исключения Гаусса — создать новую матрицу с теми же свойствами, что и исходная [ K ], но в формате, в котором только верхний треугольник имеет ненулевые элементы.Используя предыдущую матрицу 5 × 5 в качестве примера, верхний треугольник состоит из элементов в правом верхнем треугольнике матрицы и включает элементы в правой диагональной строке в виде
[m11m12m13m14m150m22m23m24m2500m33m34m35000m44m450000m55].
Мы достигаем цели исключения Гаусса, правильно применяя одну из трех вышеупомянутых операций за раз. После того, как верхняя треугольная матрица сформирована, мы используем метод обратной подстановки , чтобы сначала найти последнюю переменную.Причина, по которой этот метод называется «обратной заменой», заключается в том, что последняя строка верхней треугольной матрицы должна быть решена первой. Поскольку в последней строке верхней треугольной матрицы имеется только одна ненулевая запись, мы можем найти неизвестную переменную простым арифметическим делением, то есть из
[K] {u2v2u3u4v4} = [m11m12m13m14m150m22m23m24m2500m33m34m35000m44m40000m55] {u2v2v4vf3fu3fu4fu2 } → v4 = F4Vm55.
Имея значение v ₄, мы решаем от второй до последней переменной.Поскольку m ₄₄ u ₄ + m ₄₅ v ₄ = F _{4 H}, мы можем решить для u _{4 = F4H − m45v4m44. Мы многократно применяем один и тот же набор процедур, пока не будут найдены значения всех переменных.}
Мы будем использовать типичный 64-битный компьютер, чтобы проиллюстрировать критическую проблему при использовании исключения Гаусса. Хорошо известно, что такой компьютер хранит действительное (десятичное) число в формате с плавающей запятой, используя 64 бита: 1 бит для представления знака (плюс или минус), 52 бита для представления числа точных цифр (мантисса), и 11 бит для представления экспоненты.При делении числа на другое очень маленькое число имеющихся цифр в мантиссе может быть недостаточно для поддержания необходимой точности, то есть может возникнуть ошибка округления. В исключении Гаусса точка поворота или позиция поворота — это позиция в строке, которая совпадает с правой диагональной линией. Значения в точках поворота используются в качестве знаменателя при формировании верхней треугольной матрицы. Чтобы исключить ошибки округления, возникающие при делении на очень маленькое число, используется первый тип манипуляции для перемещения строки с очень маленьким числом в точке поворота в другую строку.Это достигается простым перестановкой рядов так, чтобы большие числа располагались в точках поворота. Мы используем вторую и третью операции для получения нулей в левой нижней части матрицы, что необходимо для получения верхней треугольной матрицы.
Модифицированной версией метода исключения Гаусса является метод исключения Гаусса – Жордана. Цель исключения Гаусса – Жордана — получить матрицу, которая имеет правую диагональную линию всех единиц (единиц), а все остальные позиции матрицы содержат нули.Это достигается с помощью тех же трех типов матричных манипуляций, что и в методе исключения Гаусса. Поскольку квадратная матрица состоит только из единичных значений в диагональных элементах, решения для всех неизвестных становятся легко доступными. Один из недостатков метода Гаусса – Жордана заключается в том, что он более затратен в вычислительном отношении, чем метод исключения Гаусса. Таким образом, он полезен только для решения проблем путем ручного расчета, когда есть небольшое количество одновременных уравнений.Используя метод исключения Гаусса, а не метод Гаусса – Жордана, мы избегаем многих дополнительных шагов. Поскольку метод FE обычно включает большую систему, чаще используется метод исключения Гаусса.
В следующем разделе мы шаг за шагом продемонстрируем процессы в методе исключения Гаусса. Конечно, вместо ручных вычислений следует написать и использовать компьютерную программу. Используя предыдущий пример в качестве отправной точки, уравнение. (1.68) повторяется ниже.
[K] {u2v2u3u4v4} = 108 [100−50006.6700−6.67−506.44−1.441.9200−1.44400−6.671.92010.67] {u2v2u3u4v4} = {F2HF2VF3HF4HF4−500} = {0002004–9004). все, кроме первой записи в первом столбце, равны 0. Мы заметили, что третья строка в этом столбце содержит единственное ненулевое значение. Чтобы манипулировать третьей строкой, чтобы сделать ведущее число 0, мы должны умножить существующее число (-5) на такое значение, чтобы добавление результата к первой записи в строке один (10) давало 0. Используя правило два, мы умножаем каждая запись в третьей строке по 2:
108 [100-50006.6700−6.67−10012.88−2.883.8400−1.44400−6.671.92010.67] {u2v2u3u4v4} = {00020000−50000}.
Затем мы добавляем строку 1 к строке 3, но мы не затрагиваем строку 1:
108 [100−50006.6700−6.67007.88−2.883.8400−1.44400−6.671.92010.67] {u2v2u3u4v4} = {00020000−50000 }.
Теперь, когда все значения в первом столбце, кроме первого, равны 0, мы применяем аналогичный процесс ко второму столбцу. Мы хотим, чтобы все значения во втором столбце, кроме второго, равнялись 0, а это означает, что мы должны адресовать −6,67 в последней строке. Его можно изменить на 0, просто добавив значения из строки 2.
108 [100−50006.6700−6.67007.88−2.883.8400−1.4440001.9204] {u2v2u3u4v4} = {00020000−50000}
Две операции, правила два и три, необходимы для преобразования записи в четвертой строке столбца три на 0. Сначала умножаем четвертую строку на 7,881,44 (обратите внимание, что эта операция также применяется к вектору силы):
108 [100-50006,6700-6,67007,88-2,883,8400-7,8821,8 ,9204] {u2v2u3u4v4} = { 0001.094 × 105−50000},
, а затем добавьте значения из третьей строки к этим результатам, чтобы сформировать новую четвертую строку:
108 [100−50006.6700−6.67007.88−2.883.8400019.013.84001.9204] {u2v2u3u4v4} = {0001.094 × 105−50000}.
Аналогичным образом мы умножаем пятую строку на -7,881,92, а затем складываем значения из третьей строки, чтобы сформировать новую пятую строку:
108 [100-50006,6700-6,67007,88-2,883,8400019,013,84000-2,88-12,58 ] {u2v2u3u4v4} = {0001,094 × 1052,052 × 106}.
К этому моменту должно быть очевидно, что умножение на значение в другой строке и последующее деление на значение в текущей строке дает результат, который можно вычесть из этой другой строки и получить 0.Чтобы еще раз увидеть этот процесс, мы умножаем пятую строку на 19.012.88, затем складываем значения из четвертой строки, чтобы получить новую пятую строку:
108 [100-50006.6700-6.67007.88-2.883.8400019.013.840000-79.20] {u2v2u3u4v4} = {0001,094 × 1051,464 × 106}.
Теперь матрица имеет форму верхней треугольной матрицы, что означает, что все значения ниже и слева от правой диагональной линии являются нулями. На этом этапе мы применяем метод обратной замены для определения узловых смещений.
Начнем с последней строки, которая содержит 108 [0000−79.20], и мы умножаем последовательные значения в этой строке на последовательные значения в векторе узлового смещения:
108 ((0) (u2) + (0) (v2) + (0) (u3) + (0) ( u4) + (- 79.20) (v4)) = 1.464 × 106
Мы можем сделать это проще, признав, что только последнее значение в строке не равно нулю, и поэтому v ₄ — это просто конечное значение в вектор силы, деленный на последнюю запись в верхней треугольной матрице [ K ]:
v4 = (1,464 × 106) (- 79,2 × 108) = — 1,849 × 10−4
Мы можем использовать v ₄, чтобы найти u ₄ и т.
No related posts.