Так как \( \displaystyle \sin \left( \frac{\pi }{2} \right)=1\)
Но ты же внимательно читал мои пространные рассуждения, не так ли? И ты ведь не напишешь такую чушь? И ты понял, в чем здесь подвох?
А подвох вот в чем:
\( \displaystyle \frac{\pi }{2}\approx \frac{3,14}{2}>1\)
А мы помним, что если правая часть тригонометрического уравнения больше \( \displaystyle 1\) (или меньше \( \displaystyle -1\)), то такое уравнение решений не имеет в принципе!!
Второе рассуждение тем более ересь: \( \displaystyle \arcsin \left( \frac{\pi }{2} \right)\) надо понимать как угол, синус которого равен \( \displaystyle \frac{\pi }{2}\).
А ну-ка попытайся в таблице найти такой угол, синус которого равен \( \displaystyle \frac{\pi }{2}\)?!
Не нашёл? То-то же!
В общем, из того, что \( \displaystyle \sin \left( \frac{\pi }{2} \right)=1\) никак не следует, что и \( \displaystyle \arcsin \left( \frac{\pi }{2} \right)=1\)!!
Из этого только следует, что \( \displaystyle \arcsin 1=\frac{\pi }{2}\)!
4.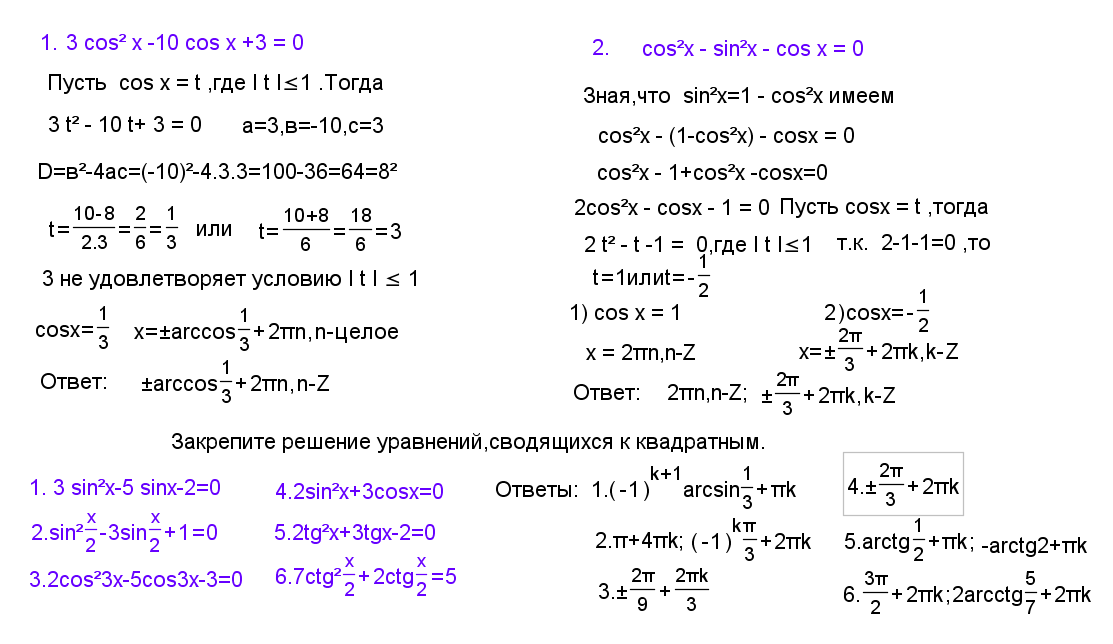 {n+1}}\arcsin \left( 0,1 \right)+\pi n,~n\in Z\)
{n+1}}\arcsin \left( 0,1 \right)+\pi n,~n\in Z\)
5. \( \displaystyle cos\left( x \right)=1\)
И снова по определению (теперь для уравнения другого вида)
\( \displaystyle x=\pm arccos1+2\pi n,~n\in Z\)
Чему равен угол, косинус которого равен \( \displaystyle 1\)?
Этот угол равен\( \displaystyle 0\)!
\( \displaystyle x=\pm 0+2\pi n,~n\in Z\)
Тогда нет смысла прибавлять или вычитать ноль, всё равно это ноль.
\( \displaystyle x=2\pi n,~n\in Z\)
Получили формулу, которая есть в таблице решений тригонометрических уравнений!
Ответ: \( \displaystyle x=2\pi n,~n\in Z\)
6. \( \displaystyle cos\left( x \right)=-\frac{1}{\sqrt{2}}\)
По определению:
\( \displaystyle x=\pm \arccos \left( -\frac{1}{\sqrt{2}} \right)+2\pi n,~n\in Z\)
Прежде всего вынесем «минус» по правилам для арккосинуса:
\( \displaystyle x=\pm \left( \pi -\arccos \left( \frac{1}{\sqrt{2}} \right) \right)+2\pi n,~n\in Z\)
Вот так и никак иначе выносится минус, запомни это!
Теперь арккосинус.
Не во всех таблицах есть значение \( \displaystyle \frac{1}{\sqrt{2}}\), но во всех есть \( \displaystyle \frac{\sqrt{2}}{2}\)!!!
А теперь, внимание, ловкость рук и никакого мошенничества!
\( \displaystyle \frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{\sqrt{2}\cdot \sqrt{2}}=\frac{\sqrt{2}}{2}\)Единица деленная на корень из двух равно корень из двух деленное на два!
Я не зря выделил это замечание жирным шрифтом, запомни это тождество хорошенько! Оно спасёт тебя в очень многих случаях!!
Итак, чему же равен угол, косинус которого равен \( \displaystyle \frac{1}{\sqrt{2}}\)(или одно и то же \( \displaystyle \frac{\sqrt{2}}{2}\))?
Верно, это угол \( \displaystyle \frac{\pi }{4}\).
Тогда:
\( \displaystyle x=\pm \left( \pi -\text{ }\!\!~\!\!\text{ }\frac{\pi }{4} \right)+2\pi n,~n\)
\( \displaystyle x=\pm \left( \frac{4\pi }{4}-\text{ }\!\!~\!\!\text{ }\frac{\pi }{4} \right)+2\pi n,~n\in Z\)
\( \displaystyle x=\pm \frac{3\pi }{4}+2\pi n,~n\in Z\)
Ответ: \( \displaystyle x=\pm \frac{3\pi }{4}+2\pi n,~n\in Z\)
7. \( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
\( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
\( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
Ещё один пример-обманка! Хотя данное уравнение решения имеет, ибо:
\( \displaystyle \frac{\pi }{4}=\frac{3,14}{4}<1\)
Тогда по определению:
\( \displaystyle x=\pm \arccos \left( \frac{\pi }{4} \right)+2\pi n,~n\in Z\)
Но из этого никак не следует, что \( \displaystyle \arccos \left( \frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)=\frac{\sqrt{2}}{2}\)!!!!!!
Запомни, арккосинус – это угол, его аргумент (начинка) – это число, а выход – угол!!!
Ты когда-нибудь встречал в своей практике такой странный угол как \( \displaystyle \frac{\sqrt{2}}{2}\)?!
Вот и я нет. Поэтому оставим как есть!
Поэтому оставим как есть!
Ответ: \( \displaystyle x=\pm \arccos \left( \frac{\pi }{4} \right)+2\pi n,~n\in Z\)
8. \( \displaystyle cos\left( x \right)=-\sqrt{2}\)
Всё просто: \( \displaystyle -\sqrt{2}<-1\)
… и решений данное уравнение не имеет.
9. \( \displaystyle tg\left( x \right)=\sqrt{2}\)
Запишем по определению:
\( \displaystyle x=arctg\sqrt{2}+\pi n,~n\in Z\)
\( \displaystyle arctg\sqrt{2}\) – не табличное значение, поэтому ответ сохраняем неизменным.
Обрати внимание, что в отличие от уравнений с синусом и косинусом, здесь мне не уже важно, какое у меня число стоит в правой части уравнения.
10. \( \displaystyle ctg\left( x \right)=-\sqrt{3}\)
Снова по определению:
\( \displaystyle x=arсctg\left( -\sqrt{3} \right)+\pi n,~n\in Z\)
Без проблем выносим минус из арккотангенса:
\( \displaystyle x=\pi-arcctg\left( \sqrt{3} \right)+\pi n,~n\in Z\)
Вычисляем: котангенс какого угла равен \( \displaystyle \sqrt{3}\)?
Это угол \( \displaystyle \frac{\pi }{6}\).
Ответ: \( \displaystyle x=\pi-\frac{\pi }{6}+\pi n = \frac{5\pi}{6}+\pi n,~n\in Z\).
11. \( \displaystyle ctg\left( x \right)=1\)
По формуле: \( \displaystyle x=arcctg1+\pi n,~n\in Z\).
Котангенс какого угла равен \( \displaystyle 1\)?
Это угол \( \displaystyle \frac{\pi }{4}\).
Ответ: \( \displaystyle x=\frac{\pi }{4}+\pi n,~n\in Z\).
Ну как, материал не кажется тебе слишком сложным? Я надеюсь, что нет. Теперь давай порешаем для закрепления чуть более сложные задачки.
Тригонометрические уравнения в 10 классе, примеры и решения
Дата публикации: .
Урок и презентация на тему: «Решение простейших тригонометрических уравнений»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать: Тригонометрические уравнения (PPTX)
Что будем изучать:
1. Что такое тригонометрические уравнения?
2. Простейшие тригонометрические уравнения.
3. Два основных метода решения тригонометрических уравнений.
4. Однородные тригонометрические уравнения.
5. Примеры.
Что такое тригонометрические уравнения?
Ребята, мы с вами изучили уже арксинуса, арккосинус, арктангенс и арккотангенс. Теперь давайте посмотрим на тригонометрические уравнения в общем.
Тригонометрические уравнения – уравнения в котором переменная содержится под знаком тригонометрической функции.Повторим вид решения простейших тригонометрических уравнений:
1)Если |а|≤ 1, то уравнение cos(x) = a имеет решение:
x= ± arccos(a) + 2πk
2) Если |а|≤ 1, то уравнение sin(x) = a имеет решение:
3) Если |а| > 1, то уравнение sin(x) = a и cos(x) = a не имеют решений
4) Уравнение tg(x)=a имеет решение: x=arctg(a)+ πk
5) Уравнение ctg(x)=a имеет решение: x=arcctg(a)+ πk
Для всех формул k- целое число
Простейшие тригонометрические уравнения имеют вид: Т(kx+m)=a, T- какая либо тригонометрическая функция.
 n – минус один в степени n.
n – минус один в степени n.Ещё примеры тригонометрических уравнений.
Решить уравнения: а) cos(x/5)=1 б)tg(3x- π/3)= √3
Решение:
а) В этот раз перейдем непосредственно к вычислению корней уравнения сразу:
x/5= ± arccos(1) + 2πk. Тогда x/5= πk => x=5πk
Ответ: x=5πk, где k – целое число.
б) Запишем в виде: 3x- π/3=arctg(√3)+ πk. Мы знаем что: arctg(√3)= π/3
3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3
Ответ: x=2π/9 + πk/3, где k – целое число.
Решить уравнения: cos(4x)= √2/2. И найти все корни на отрезке [0; π].
Решение:
Решим в общем виде наше уравнение: 4x= ± arccos(√2/2) + 2πk
4x= ± π/4 + 2πk;
x= ± π/16+ πk/2;
Теперь давайте посмотрим какие корни попадут на наш отрезок. При k
При k=0, x= π/16, мы попали в заданный отрезок [0; π].
При к=1, x= π/16+ π/2=9π/16, опять попали.

Ответ: x= π/16, x= 9π/16
Два основных метода решения.
Мы рассмотрели простейшие тригонометрические уравнения, но существуют и более сложные. Для их решения применяют метод ввода новой переменной и метод разложения на множители. Давайте рассмотрим примеры.
Решим уравнение:
Решение:
Для решения нашего уравнения воспользуемся методом ввода новой переменной, обозначим: t=tg(x).
В результате замены получим: t2 + 2t -1 = 0
Найдем корни квадратного уравнения: t=-1 и t=1/3
Тогда tg(x)=-1 и tg(x)=1/3, получили простейшее тригонометрическое уравнение, найдем его корни.
x=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.
Ответ: x= -π/4+πk; x=arctg(1/3) + πk.
Пример решения уравнения
Решить уравнений: 2sin2(x) + 3 cos(x) = 0
Решение:
Воспользуемся тождеством: sin2(x) + cos2(x)=1
Наше уравнение примет вид:2-2cos2(x) + 3 cos (x) = 0
2 cos2(x) — 3 cos(x) -2 = 0
введем замену t=cos(x): 2t2 -3t — 2 = 0
Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2
Тогда cos(x)=2 и cos(x)=-1/2.
Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней.
Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk
Ответ: x= ±2π/3 + 2πk
Однородные тригонометрические уравнения.
Определение: Уравнение вида a sin(x)+b cos(x) называются однородными тригонометрическими уравнениями первой степени. Уравнения вида
однородными тригонометрическими уравнениями второй степени.
Для решения однородного тригонометрического уравнения первой степени разделим его на cos(x): Делить на косинус нельзя если он равен нулю, давайте убедимся что это не так:
Пусть cos(x)=0, тогда asin(x)+0=0 => sin(x)=0, но синус и косинус одновременно не равны нулю, получили противоречие, поэтому можно смело делить на ноль.
Решить уравнение:
Пример: cos2(x) + sin(x) cos(x) = 0
Решение:
Вынесем общий множитель: cos(x)(c0s(x) + sin (x)) = 0
Тогда нам надо решить два уравнения:
cos(x)=0 и cos(x)+sin(x)=0
cos(x)=0 при x= π/2 + πk;
Рассмотрим уравнение cos(x)+sin(x)=0 Разделим наше уравнение на cos(x):
1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk
Ответ: x= π/2 + πk и x= -π/4+πk
Однородные тригонометрические уравнения второй степени
Как решать однородные тригонометрические уравнения второй степени?1.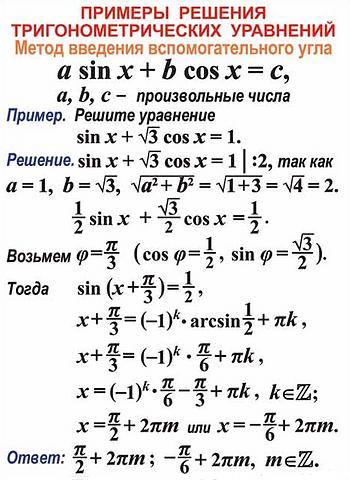 Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде
Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде
2. Если a≠0, то нужно поделить обе части уравнения на косинус в квадрате, получим:
Делаем замену переменной t=tg(x) получаем уравнение:
Решить пример №:3
Решить уравнение:
Решение:
Разделим обе части уравнения на косинус квадрат:
Делаем замену переменной t=tg(x): t2 + 2 t — 3 = 0
Найдем корни квадратного уравнения: t=-3 и t=1
Тогда: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk
tg(x)=1 => x= π/4+ πk
Ответ: x=-arctg(3) + πk и x= π/4+ πk
Решить пример №:4
Решить уравнение:
Решение:
Преобразуем наше выражение:
Решать такие уравнение мы умеем: x= — π/4 + 2πk и x=5π/4 + 2πk
Ответ: x= — π/4 + 2πk и x=5π/4 + 2πk
Решить пример №:5
Решить уравнение:
Решение:
Преобразуем наше выражение:
Введем замену tg(2x)=t:22 — 5t + 2 = 0
Решением нашего квадратного уравнения будут корни: t=-2 и t=1/2
Тогда получаем: tg(2x)=-2 и tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2
2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2
Ответ: x=-arctg(2)/2 + πk/2 и x=arctg(1/2)/2+ πk/2
Задачи для самостоятельного решения.

1) Решить уравнение
а) sin(7x)= 1/2 б) cos(3x)= √3/2 в) cos(-x) = -1 г) tg(4x) = √3 д) ctg(0.5x) = -1.7
2) Решить уравнения: sin(3x)= √3/2. И найти все корни на отрезке [π/2; π ].
3) Решить уравнение: ctg2(x) + 2ctg(x) + 1 =0
4) Решить уравнение: 3 sin 2(x) + √3sin (x) cos(x) = 0
5) Решить уравнение:3sin2(3x) + 10 sin(3x)cos(3x) + 3 cos2(3x) =0
6)Решить уравнение:cos2(2x) -1 — cos(x) =√3/2 -sin2(2x)
Простейшие тригонометрические уравнения и их решение
К простейшим тригонометрическим уравнениям относятся уравнения вида
Решение простейших тригонометрических уравнений
Рассмотрим подробнее каждое из этих уравнений и их решение.
Уравнение вида . Так как для любого x, то при и уравнение не имеет корней. При , корни этого уравнения находятся по формуле
Особые случаи
Примеры решения задач
Уравнение вида . Так как для любого x, то при и уравнение корней не имеет. При , корни этого уравнения находятся по формуле
Так как для любого x, то при и уравнение корней не имеет. При , корни этого уравнения находятся по формуле
Особые случаи:
ПРИМЕР 4| Задание | Решить уравнение — |
| Решение | Косинус – функция ограниченная и лежит в пределах , поэтому данное равенство не имеет смысла. |
| Ответ | Решений нет. |
Простейшие тригонометрические уравнения с тангенсами и котангенсами
Уравнение вида . Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
ПРИМЕР 5
| Задание | Решить уравнение |
| Решение | Выразим из этого равенства тангенс
В последнем равенстве положив , получим простейшее тригонометрическое уравнение , корни которого вычисляются по формуле
Тогда
Сделаем обратную замену
и выразим из полученного уравнения x:
поделим обе части последнего равенства на 2, тогда окончательно получим
|
| Ответ |
Уравнение вида . Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
ПРИМЕР 6
| Задание | Решить уравнение
|
| Решение | Ведем замену , тогда исходное уравнение преобразуется в простейшее тригонометрическое уравнение , корни которого вычисляются по формуле
Тогда
Сделаем обратную замену
и выразим из полученного уравнения x:
поделим обе части последнего равенства на 5, тогда окончательно получим
|
| Ответ |
Приведение тригонометрических уравнений к простейшим
Примеры тригонометрических уравнений, которые приводятся к простейшим тригонометрическим уравнениям с помощью элементарных преобразований или тригонометрических формул.
| Задание | Решить уравнение |
| Решение | Применим к правой части заданного уравнения формулу суммы синусов:
или
Последнее равенство равносильно совокупности простейших уравнений
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
Решение тригонометрического уравнения. С1. Пример 14
ПОДГОТОВКА К ЕГЭ ПО МАТЕМАТИКЕ.
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ.
ЗАДАНИЕ С1.
ПРИМЕР 14.
(в данном подразделе рассматриваем примеры решения тригонометрических уравнений — задание уровня С1 на ЕГЭ по математике; подробный ход решения, приведенный в примерах, позволяет наглядно и доступно представить алгоритм действий применяемый для успешного выполнения задания С1 при сдаче ЕГЭ; в этом примере описано решение тригонометрического уравнения, включенного в некоторые тренировочные тесты ЕГЭ, и максимально сходного с уравнениями, включаемыми в реальные варианты экзамена; тип приведенного здесь тригонометрического уравнения, соответствует типам уравнений включенных в демонстрационные варианты ЕГЭ 2011, 2016 и 2017 гг.)
Решить уравнение:
Решение:
Преобразуем уравнение, воспользовавшись формулой приведения:
Так как угол – угол 2 четверти, а cos во 2 четверти принимает отрицательные значения, то в ответе появляется « — ». Для угла название исходной функции «cos» заменяется на «sin».
Для угла название исходной функции «cos» заменяется на «sin».
Тогда уравнение принимает вид:
Выполним замену:
Получаем:
Выполним замену
Решим уравнение через дискриминант:
Выполним обратную замену:
Теперь отберем корни уравнения из промежутка .
Все примеры решения тригонометрических уравнений >>>
| < Предыдущая | Следующая > |
|---|
Примеры решения тригонометрических уравнений и систем уравнений
Решение тригонометрических уравнений и систем тригонометрических уравнений основывается на решении простейших тригонометрических уравнений. 2 – 4*tg(x) +1 = 0.
2 – 4*tg(x) +1 = 0.
tg(x) = 1, x = pi/4+pi*n, для любого целого n
tg(x) = 1/3, x = arctg(1/3) + pi*k, для любого целого k.
Пример 4. Решить систему уравнений
{x-y = 5*pi/3,
{ sin(x) = 2*sin(y)
Из пергового уравнения выразим y,
y = x-5*pi/3.
Тогда получим, 2*sin(y) = 2*sin(x-5*pi/3) = 2*(sin(x)*cos(5*pi/3) — cos(x)*sin(5*pi/3)) = 2*(sin(x)*(1/2) –((√3)/2)*cos(x)) = sinx + √3*cos(x).
Подставляем это во второе уравнение системы получим cos(x) = 0, x = pi/2 + pi*n, для любого целого n.
Теперь находим y,
y = x — 5*pi/3 = pi/2 + pi*n – 5*pi/3 = -7*pi/6 + pi*n, для любого целого n.
Ответ: (pi/2+pi*n; -7*pi/6 + pi*n), для любого целого n.
Нужна помощь в учебе?
Предыдущая тема: Решение простейших тригонометрических неравенств: примеры и алгоритмы
Следующая тема:   Понятие о приращении функции, приращении аргумента: примеры
Презентация — Решение простейших тригонометрических уравнений
Слайды и текст этой онлайн презентации
Слайд 1
“Уравнение —
это золотой ключ, открывающий
все математические сезамы”. Станислав Коваль
Станислав Коваль
ГАПОУ «ЧТТПиК»
Слайд 2
Решение простейших
тригонометрических
уравнений
ГАПОУ «ЧТТПиК»
Слайд 3
Цель:
закрепление умения решать простейшие тригонометрические уравнения вида
sin t = a, cos t = a, tg t = a, ctg t = a
в ходе решения примеров
Слайд 4
Повторение
Когда тригонометрическое уравнение вида
sin t = a, cos t = a, tg t = a, ctg t = a не имеет решений?
Слайд 5
Что необходимо знать, чтобы решить
любое тригонометрическое уравнение?
Слайд 6
Общие формулы решения простейших
тригонометрических уравнений
Слайд 7
Общие формулы решения простейших
тригонометрических уравнений
cos t = a, sin t = a.
Слайд 8
Общие формулы решения простейших
тригонометрических уравнений.
sin t = а, |a|≤1
t =
2. cos t = a, |a|≤1
t =
Если то решений нет
Слайд 9
Общие формулы решения простейших
тригонометрических уравнений
tg t = a, ctg t = a.
Слайд 10
Общие формулы решения простейших
тригонометрических уравнений.
tg t = а,
t =
2. ctg t = a,
t =
Слайд 11
Дайте определение арксинуса, арккосинуса,
арктангенса и арккотангенса
Арксинусом числа a называется такое число
из отрезка [-π/2 ; π/2], синус которого равен a.
Арккосинусом числа a называется такое число
из отрезка [0; π], косинус которого равен a.
Арктангенсом числа a называется такое число
из интервала (-π/2 ; π/2), тангенс которого равен a.
Арккотангенсом числа a называется такое число
из интервала (0; π), котангенс которого равен a.
Слайд 12
Как находят арксинусы, арккосинусы,
арктангенсы и арккотангенсы отрицательных чисел?
arcsin (-a) = — arcsin a
arccos (-a) = — arccos a
arctg (-a) = — arctg a
arcctg (-a) = — arcctg a
Слайд 13
Существуют ли такие случаи, когда решение уравнения находят не по общей формуле?
Слайд 14
Проверка домашнего задания: Заполните таблицу частных решений
a=1 a=0 a = -1
Слайд 15
Математическая эстафета
1 ряд 2 ряд
Sin x =1∕2 Cos x = √3∕2
Sin x = √3∕2 Cos x = 1∕2
Sin x = -√2∕2 Cos x = -√2∕2
tg x = tg x = 0
сtg x = 0 сtg x = -√3
Слайд 16
Математическая эстафета
Проверка
1 ряд 2 ряд
х = (-1) π ∕6 + πк, к Є Z х = π∕6+ 2 π n; n Є Z
х = (-1) π∕3+πк, к Є Z х = π∕3+ 2 π n; n Є Z
х = (-1) π∕4+πn, n Є Z х = 3π∕4+ 2 π n; n Є Z
х = π∕6 + πn, n Є Z х = π n; n Є Z
х не существует х = 5π∕6+ π n; n Є Z
Слайд 17
«Алгебра и начало анализа 10-11 класс. / под ред. А.Н.Колмогоров. – М.: Просвещение, 2010 г.
стр.75 № 146 в), г).
/ под ред. А.Н.Колмогоров. – М.: Просвещение, 2010 г.
стр.75 № 146 в), г).
Решение задач по учебнику
Слайд 18
Выполнение самостоятельной
работы в форме теста
Слайд 19
Эталон ответов:
1 вариант
А 2. В 3.В
2 вариант
Б 2. А 3.А
Критерии выставления оценок
3 верных ответа- «отлично»,
2 — «хорошо»,
1 – «удовлетворительно».
Слайд 20
ДОМАШНЕЕ ЗАДАНИЕ:
№ 146 а) б) № 147 в)
Дополнительное задание
решить уравнение
Тригонометрические уравнения — формулы, решения, примеры. Простейшие тригонометрические уравнения урок решить уравнение синус 2х 1 2
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получим
tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .
Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0. n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда.
 При любом а.
При любом а. Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.
 ) Собственно, для этого и разбираемся. Что, как и откуда.
) Собственно, для этого и разбираемся. Что, как и откуда.В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.) Ученик обязан знать, что arcsin 0,5 = π /6.
 Полноценный ответ будет:
Полноценный ответ будет:х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.
 ) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу.
 Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т.
 п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн.
Если Вам нравится этот сайт… А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
Числовая окружность
Наряду с понятием числовой прямой есть еще и понятие числовой окружности.
 Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A .
Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C.
 Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.
- Два противоположных числа находятся на симметричных относительно оси абсцисс точках окружности.
Проведем вертикальную хорду АВ (рис. 2). Так как точки A и B симметричны относительно оси Ox, то число -x_0 находится на точке B и, значит, все числа точки B задаются формулой: x_B=-x_0+2πk ,k∈Z. Числа на точках A и B запишем одной формулой: x_(A ; B)=±x_0+2πk ,k∈Z. Сделаем вывод: зная одно из чисел на одной из точек A или B вертикальной хорды АВ, мы можем найти все числа на этих точках. Рассмотрим горизонтальную хорду AD и найдем числа точки D (рис. 2). Так как BD – диаметр и число -x_0 принадлежит точке В, то -x_0 + π одно из чисел точки D и, значит, все числа этой точки задаются формулой x_D=-x_0+π+2πk ,k∈Z.
 k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
π/3 на С1 и
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности.
 На рисунке отмечены также и координаты этих точек (опустим описание их получения).
На рисунке отмечены также и координаты этих точек (опустим описание их получения).Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a) простейших уравнений.
Решить уравнения
1) sinx=1⁄(2) .
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2 .
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2 .
Нам надо найти все числа на точках C4 и C3.
3) sinx=1 . На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.
Ответ: x=π/2+2πk , k∈Z .

4) sinx=-1 .
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0 .
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z .
6) cosx=√2⁄2 .
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2 .
Надо найти числа на точках C_2 и C_3 .
Ответ: x=±2π/3+2πk , k∈Z .
10) cosx=0 .
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения.

.Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosxОтвет: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
5. Тригонометрические уравнения
М. Борна
Тригонометрические уравнения могут быть решены с помощью алгебраические методы и тригонометрические тождества и ценности обсуждалось в предыдущих разделах. Возможно, вы захотите вернуться и взглянуть на тригонометрические функции любого угла, где мы видим предысторию следующих решений.
Безболезненный способ решить эти проблемы — использовать график. Там, где график пересекает ось x , вы найдете свои решения (значения x , которые «работают»).
 Графики также помогают понять, почему иногда есть один ответ, а иногда — много ответов. Я использую Scientific Notebook или аналогичную математическую программу для построения графиков функций.
Графики также помогают понять, почему иногда есть один ответ, а иногда — много ответов. Я использую Scientific Notebook или аналогичную математическую программу для построения графиков функций.Вы можете использовать этот онлайн-калькулятор для построения графиков, чтобы решить следующие уравнения (или проверить свои решения).
Пример 1
Решите уравнение 2 cos θ — 1 = 0 для 0 ≤ θ <2 π .
Ответ
Преобразуя приведенное выше уравнение, получаем:
`cos theta = 1 / 2`
Нам известно следующее:
С
`cos (pi / 3) = 1 / 2`
и `cos θ` положителен в первом и четвертом квадрантах, мы имеем:
`тета = пи / 3`
или
`theta = 2pi-pi / 3 = (5pi) / 3`
Итак, `theta = pi / 3` или` theta = (5pi) / 3`
Пример 2
Решите графически уравнение
2 cos 2 x — sin x — 1 = 0
такой, что 0 ≤ θ <2 π .

Ответ
Используя программное обеспечение для построения графиков, мы рисуем кривую y = 2 cos 2 x — sin x — 1 в области 0 ≤ θ <2π. Везде, где кривая пересекает ось x , будет решением нашего уравнения.
Мы видим из графика, что решения примерно:
x = 0,5
x = 2,6
x = 4,7Для более точных решений мы просто увеличим масштаб графика.
На следующем графике я увеличил масштаб до второго корня (около x = 2,6). Мы видим, что этот корень равен x = 2,618 с точностью до 3 знаков после запятой.
Мы могли бы продолжать увеличивать масштаб настолько близко, насколько захотим, чтобы получить требуемую точность.
Решение уравнений, кратных
θПример 3
Решите уравнение sin 2 θ = 0,8 для 0 ≤ θ <2π.
Ответ
Если проблема касается только θ , мы ожидаем 2 решения; один в первом квадранте и один во втором квадранте.

Но здесь наша задача включает в себя `2θ`, поэтому мы должны удвоить домен ( θ значений) для учета всех возможные решения.
Действуем следующим образом:
Решаем
`sin 2θ = 0,8` для 0 ≤ 2 θ <4 π .
Базовый угол
`α = arcsin 0,8 = 0,9273`
Значения для 2 θ будут в квадрантах I, II, V, VI.
2 θ = 0.9273, или π — 0,9273, или 2 π + 0,9273, или 3 π — 0,9273
То есть
`2θ = 0,9273, 2,2143, 7,2105, 8,4975`
Но нам нужны значения для θ , а не 2 θ , поэтому разделим на 2:
`θ = 0,4637, 1,1072, 3,6053, 4,2488`
Наши ответы верны? В виде обычно, мы проверим, построив график исходного выражения:
Из графика видно, что наши 4 значения разумны, так как это единственные 4 значения которые удовлетворяют `sin 2θ = 0.
 2theta = 1/16`
2theta = 1/16`для 0 ≤ θ <2π.
Ответ
Решение для cos θ дает:
`cos theta = + — 1 / 4`
Если cos alpha = 1/4, то ссылка угол α = 1,3181.
Таким образом, для cos theta = 1/4 мы имеем θ в первом и четвертом квадрантах. Итак
`θ = 1,3181 или 4,9651`
Для cos theta = -1 / 4, мы имеем θ во 2-м и 3-м квадрантах.2θ — грех θ — 1 = 0`
`(2 sin θ — 1) (3 sin θ + 1) = 0`
Так либо
`2 sin θ — 1 = 0`
`грех θ = 1 / 2`
θ будет в 1-м и 2-м квадрантах.
`θ = 0,52360, 2,6180` (то есть` пи / 6` или `(5pi) / 6`)
ИЛИ
`3 грех θ + 1 = 0`
`sin θ = — 1 / 3`
θ будет в 3-м и 4-м квадрантах.
`θ = 3. 4814, 5. 9433`
Проверка нашего решения на график:
Итак `θ = 0.
 2 \ х + 3 \ соз х + 1 = 0`
2 \ х + 3 \ соз х + 1 = 0``(2 \ co \ s x + 1) (cos x + 1) = 0`
Решая, получаем
`cos x = — 0,5` или` cos x = — 1`
Теперь `cos x = -1 / 2` дает` x = (2pi) / 3, (4pi) / 3`.
Однако при проверке исходного уравнения , отметим, что
`» LHS «= cos ((4pi) / 3xx1 / 2)` `= cos ((2pi) / 3)` = -1 / 2`
но
«» RHS «= 1 + cos (4pi) / 3 = + 1 / 2`
Таким образом, единственное решение для этой части — `x = (2pi) / 3.`
Кроме того, cos x = -1 дает x = pi.
Итак, решение уравнения: `x = (2pi) / 3or pi.`
Проверка графика y = cos x / 2-1-cos x подтверждает эти результаты:
(2π / 3 ≈ 2,0944 и π ≈ 3,14).
Пример 7
Решите уравнение
загар 2 θ — детская кроватка 2 θ = 0
для 0 ≤ θ <2π.
 2 2θ = 1`
2 2θ = 1``tan 2θ = ± 1`
Поскольку `0 ≤ θ <2π`, нам нужно рассмотреть значения` 2theta` такие, что `0 ≤ 2θ <4π`.Следовательно, решение в приведенном выше уравнении имеем:
`2 theta = pi / 4, (3pi) / 4, (5pi) / 4 (7pi) / 4,` `(9pi) / 4, (11pi) / 4,` (13pi) / 4, (15pi) ) / 4`
Деление на 2 дает нам полный набор решений в требуемой области, `0 <= theta <2pi`:
`theta = pi / 8, (3pi) / 8,` `(5pi) / 8, (7pi) / 8, » (9pi) / 8, (11pi) / 8,` `(13pi) / 8, (15pi) / 8`
Упражнения
Примечание 1: «Аналитически» означает использование методов и формул из предыдущих разделов.Это означает, что для ее решения нельзя просто использовать график.
Примечание 2: Однако я всегда использую график для проверки своей аналитической работы. Я сразу вижу, произошла ли какая-то ошибка. Я призываю вас поступить так же!
1.
 2x) = 0`
2x) = 0`Умножение на `cos x`:
`4 \ sin x \ cos x = 1`
Делим обе стороны на 2:
`2 \ sin x \ cos x = 1 / 2`
Распознавание LHS — это `sin 2x`, от до:
`sin 2x, = 0.5`
При 0 ≤ x <2π нам нужно найти значения 2 x такие, что 0 ≤ 2 x <4π. (В два раза больше исходного домена.)
Значит, 2x:
.`2x = pi / 6, (5pi) / 6, (13pi) / 6, (17pi) / 6`
Если разделить на 2, то получим требуемые значения для `x`:
`x = pi / 12, (5pi) / 12, (13pi) / 12, (17pi) / 12`
или в десятичной форме:
`x = 0,2618, 1,309, 3.403, 4.451`
2. Решите тригонометрическое уравнение аналитически для 0 ≤ x <2 π :
sin 2 x cos x — cos 2 x sin x = 0
Ответ
Мы узнаем, что левая сторона находится в форма:
`sin (a — b) =` sin a cos b — cos a sin b, `
, где `a = 2x` и` b = x`.

Так
`sin 2x \ cos x — cos 2x \ sin x`
`= грех (2x — x)`
`= грех x`
Теперь мы знаем решения `sin x = 0` быть:
`x = 0, π`.
[Почему?]
3. Решите данное тригонометрическое уравнение. аналитически и графическим методом (для 0 ≤ x <2 π ):
sin 4 x — cos 2 x = 0
Ответ
sin 4 x — cos 2 x = 0
2sin 2 x cos 2 x — cos 2 x = 0
Факторинг дает:
cos 2 x (2 sin 2 x — 1) = 0
ЛИБО
`cos 2x = 0`
`2x = pi / 2, (3pi) / 2, (5pi) / 2, (7pi) / 2`
`x = pi / 4, (3pi) / 4, (5pi) / 4, (7pi) / 4`
ИЛИ
`грех 2x = 1/2`
`2x = pi / 6, (5pi) / 6, (13pi) / 6, (17pi) / 6`
`x = pi / 12, (5pi) / 12, (13pi) / 12, (17pi) / 12`
Или в десятичной форме:
`х = 0.
 26, 0,79, «1,31, 2,36,« 3,40, 3,93,
«4.45, 5.50.»
26, 0,79, «1,31, 2,36,« 3,40, 3,93,
«4.45, 5.50.»График y = sin 4x — cos 2x выглядит следующим образом. Мы можем видеть, откуда график пересекает ось x , что наши ответы разумны.
6.1: Решение тригонометрических уравнений — Математика LibreTexts
Уравнение, включающее тригонометрические функции, называется тригонометрическим уравнением . Например, уравнение типа
\ [\ nonumber
\ tan \; A ~ = ~ 0,75 ~,
\]
, с которым мы столкнулись в главе 1, является тригонометрическим уравнением.\ circ k \ quad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\]
Это является наиболее общим решением уравнения. Часто часть, в которой говорится «для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)», опускается, поскольку обычно понял, что \ (k \) изменяется для всех целых чисел. Общее решение в радианах будет:
\ [\ nonumber
A ~ = ~ 0.6435 \; + \; \ pi k \ quad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (. .. \)}
.. \)}
\]Пример 6.1
Решите уравнение \ (\; 2 \, \ sin \; \ theta \; + \; 1 ~ = ~ 0 \).2 \; \ theta ~ = ~ \ frac {1} {2} \ quad \ Rightarrow \ quad \ cos \; \ theta ~ = ~ \ pm \, \ frac {1} {\ sqrt {2}}
\ quad \ Rightarrow \ quad \ theta ~ = ~ \ frac {\ pi} {4} \ ;, ~ \ frac {3 \ pi} {4} \ ;, ~ \ frac {5 \ pi} {4} \ ;, ~
\ frac {7 \ pi} {4} ~,
\]
и поскольку период косинуса равен \ (2 \ pi \), мы бы добавили \ (2 \ pi k \) к каждому из этих углов, чтобы получить общее решение. Но обратите внимание, что указанные выше углы различаются кратно \ (\ frac {\ pi} {2} \). Итак, поскольку каждое кратное \ (2 \ pi \) также кратно \ (\ frac {\ pi} {2} \), мы можем объединить эти четыре отдельных ответа в один:
\ [\ nonumber
\ boxed { \ theta ~ = ~ \ frac {\ pi} {4} \; + \; \ frac {\ pi} {2} \, k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ ( … \)}
\]Пример 6.3
Решите уравнение \ (\; 2 \, \ sec \; \ theta ~ = ~ 1 \).
 2 \; + \; Икс \;-\; 1 ~ = ~ 0 \ quad \ Rightarrow \ quad x ~ = ~ \ frac {-1 \; \ pm \; \ sqrt {1 — (4) \, (- 1)}} {
2 \; + \; Икс \;-\; 1 ~ = ~ 0 \ quad \ Rightarrow \ quad x ~ = ~ \ frac {-1 \; \ pm \; \ sqrt {1 — (4) \, (- 1)}} {
2 \, (1)} ~ = ~ \ frac {-1 \; \ pm \; \ sqrt {5}} {2} ~ = ~ -1.618 \ ;, ~ 0.618
\]
по квадратичной формуле элементарной алгебры. Но \ (- 1.618 <-1 \), поэтому невозможно, чтобы \ (\; \ sin \ theta = x = -1.618 \). Таким образом, мы должны иметь \ (\; \ sin \; \ theta = x = 0,618 \). Следовательно, есть два возможных решения: \ (\ theta = 0,666 \) рад в QI и его отражение \ (\ pi - \ theta = 2,475 \) рад вокруг оси \ (y \) - в QII. Добавление к ним кратных \ (2 \ pi \) дает нам общее решение:
\ [\ nonumber
\ boxed {\ theta ~ = ~ 0.666 \; + \; 2 \ пи к \ квад \ текст {и} \ квад 2.475 \; + \; 2 \ pi k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\ ]Пример 6.5
Решите уравнение \ (\; \ sin \; \ theta ~ = ~ \ tan \; \ theta \).
Решение:
Используя тот же метод, что и в предыдущем примере, мы получаем
\ [\ nonumber \ begin {align *}
\ sin \; \ theta ~ & = ~ \ tan \; \ theta \\ \ nonumber
\ sin \; \ theta ~ & = ~ \ frac {\ sin \; \ theta} {\ cos \; \ theta} \\ \ nonumber
\ sin \; \ theta ~ \ cos \; \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
\ sin \; \ theta ~ \ cos \; \ theta \; — \; \ sin \; \ theta ~ & = ~ 0 \\ \ nonumber
\ sin \; \ theta ~ (\ cos \; \ theta \; — \; 1) ~ & = ~ 0 \\ \ nonumber
& \ Rightarrow \ quad \ sin \; \ theta ~ = ~ 0 \ quad \ text {или} \ quad \ cos \; \ theta ~ = ~ 1 \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ 0 \ ;, ~ \ pi \ quad \ text {или} \ quad \ theta ~ = ~ 0 \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ 0 \ ;, ~ \ pi ~,
\ end {align *} \ ]
плюс число, кратное \ (2 \ pi \). Итак, поскольку указанные выше углы кратны \ (\ pi \), а каждое кратное \ (2 \ pi \) кратно \ (\ pi \), мы можем объединить два ответа в один для общего решения:
Итак, поскольку указанные выше углы кратны \ (\ pi \), а каждое кратное \ (2 \ pi \) кратно \ (\ pi \), мы можем объединить два ответа в один для общего решения:
\ [\ nonumber
\ boxed {\ theta ~ = ~ \ pi k} \ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \ ), \ (… \)}
\]Пример 6.6
Решите уравнение \ (\; \ cos \; 3 \ theta ~ = ~ \ frac {1} {2} \).
Решение:
Идея здесь состоит в том, чтобы сначала решить для \ (3 \ theta \), используя наиболее общее решение, а затем разделить это решение на \ (3 \).{-1} \ frac {1} {2} = \ frac {\ pi} {3} \), есть два возможных решения для \ (3 \ theta \): \ (3 \ theta = \ frac {\ pi } {3} \) в QI и его отражение \ (- 3 \ theta = — \ frac {\ pi} {3} \) вокруг оси \ (x \) — в QIV. Добавление к ним кратных \ (2 \ pi \) дает нам:
\ [\ nonumber
3 \ theta ~ = ~ \ pm \, \ frac {\ pi} {3} \; + \; 2 \ pi k \ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\]
Таким образом, разделив все на \ (3 \), мы получим общее решение для \ (\ theta \):
\ [\ nonumber
\ boxed {\ theta ~ = ~ \ pm \, \ frac {\ pi} {9} \ ; + \; \ frac {2 \ pi} {3} k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\]Пример 6.7
Решите уравнение \ (\; \ sin \; 2 \ theta ~ = ~ \ sin \; \ theta \).
Решение:
Здесь мы используем формулу двойного угла для синуса:
Рисунок 6.1.1
\ [\ nonumber \ begin {align *}
\ sin \; 2 \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
2 \, \ sin \ theta ~ \ cos \; \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
\ sin \; \ theta ~ (2 \, \ cos \; \ theta \ ; — \; 1) ~ & = ~ 0 \\ \ nonumber
& \ Rightarrow \ quad \ sin \; \ theta ~ = ~ 0 \ quad \ text {или} \ quad \ cos \; \ theta ~ = ~ \ frac {1} {2} \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ 0 \ ;, ~ \ pi \ quad \ text {или} \ quad \ theta ~ = ~ \ pm \, \ frac { \ pi} {3} \\ \ nonumber
& \ Rightarrow \ quad \ boxed {\ theta ~ = ~ \ pi k \ quad \ text {и} \ quad \ pm \, \ frac {\ pi} {3} \ ; + \; 2 \ pi k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\ end {align *}
\]Решение:
Мы будем использовать технику, которую мы обсуждали в главе 5, для нахождения амплитуды комбинации синусоидальных и косинусных функций. Возьмите коэффициенты \ (2 \) и \ (3 \) при \ (\; \ sin \; \ theta \) и \ (\; — \ cos \; \ theta \), соответственно, в приведенном выше уравнении и сделайте им ноги прямоугольного треугольника, как на рисунке 6.1.1. Пусть \ (\ phi \) будет углом, показанным в прямоугольном треугольнике. Нога длиной \ (3> 0 \) означает, что угол \ (\ phi \) находится выше оси \ (x \) -, а нога длиной \ (2> 0 \) означает, что \ (\ phi \) находится справа от оси \ (y \).Следовательно, \ (\ phi \) должен находиться в QI. Гипотенуза имеет длину \ (\ sqrt {13} \) по теореме Пифагора, и, следовательно, \ (\; \ cos \; \ phi = \ frac {2} {\ sqrt {13}} \) и \ (\; \ sin \; \ theta = \ frac {3} {\ sqrt {13}} \). Мы можем использовать это, чтобы преобразовать уравнение для решения следующим образом:\ [\ nonumber \ begin {align *}
2 \, \ sin \; \ theta \; — \; 3 \, \ cos \; \ theta ~ & = ~ 1 \\ \ nonumber
\ sqrt {13} \, \ left (\ tfrac {2} {\ sqrt {13}} \, \ sin \; \ theta \ ; — \; \ tfrac {3} {\ sqrt {13}} \, \ cos \; \ theta
\ right) ~ & = ~ 1 \\ \ nonumber
\ sqrt {13} \, (\ cos \; \ phi \; \ sin \; \ theta \; — \; \ sin \; \ phi \; \ cos \; \ theta) ~ & = ~ 1 \\ \ nonumber
\ sqrt {13} \, \ sin \ ; (\ theta — \ phi) ~ & = ~ 1 \ quad \ text {(по формуле вычитания синуса)} \\ \ nonumber
\ sin \; (\ theta — \ phi) ~ & = ~ \ tfrac {1 } {\ sqrt {13}} \\ \ nonumber
& \ Rightarrow \ quad \ theta — \ phi ~ = ~ 0.281 \ quad \ text {или} \ quad \ theta — \ phi ~ = ~ \ pi — 0,281 = 2,861 \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ \ phi \; + \; 0.281 \ quad \ text {или} \ quad \ theta ~ = ~ \ phi \; + \; 2.861
\ end {align *} \]Теперь, поскольку \ (\; \ cos \; \ phi = \ frac {2} {\ sqrt {13}} \) и \ (\ phi \) находится в QI , наиболее общим решением для \ (\ phi \) является \ (\ phi = 0.983 + 2 \ pi k \) для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \ , 2 \), \ (… \). Итак, поскольку нам нужно было добавить кратные \ (2 \ pi \) к решениям \ (0.281 \) и \ (2.861 \) в любом случае, наиболее общее решение для \ (\ theta \):
\ [\ begin {align *}
\ theta ~ & = ~ 0.983 \; + \; 0,281 \; + \; 2 \ пи к \ квад \ текст {и} \ квад 0,983 \; + \; 2,861 \; + \; 2 \ pi k \\
& \ Rightarrow \ quad \ boxed {\ theta ~ = ~ 1.264 \; + \; 2 \ пи к \ квад \ текст {и} \ квад 3.844 \; + \; 2 \ pi k}
\ quad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\ конец {выравнивание *} \]Примечание: в примере 6.8, если бы уравнение было \ (\; 2 \, \ sin \; \ theta \; + \; 3 \, \ cos \; \ theta ~ = ~ 1 \), то мы все равно использовали бы прямоугольный треугольник с катетами длины \ (2 \) и \ (3 \), но мы бы использовали формулу сложения синуса вместо формулы вычитания.
Авторы и авторство
Calculus I — Решение триггерных уравнений
Эта проблема очень похожа на другие задачи в этом разделе с очень важным отличием. Приступим к решению этой задачи точно так же, как в первом примере. Итак, сначала получим синус с одной стороны.
\ [\ begin {align *} 2 \ sin (5x) & = — \ sqrt 3 \\ \ sin (5x) & = \ frac {{- \ sqrt 3}} {2} \ end {align *} \]Мы ищем углы, которые дадут \ (- \ frac {{\ sqrt 3}} {2} \) вне синусоидальной функции.Снова вернемся к нашему верному юнитовому кругу.
Итак, в первом квадранте нет углов, для которых синус имеет значение \ (- \ frac {{\ sqrt 3}} {2} \). Однако есть два угла в нижней половине единичной окружности, для которых синус будет иметь значение \ (- \ frac {{\ sqrt 3}} {2} \). Итак, что это за углы?
Обратите внимание, что \ (\ sin \ left ({\ frac {\ pi} {3}} \ right) = \ frac {{\ sqrt 3}} {2} \). Учитывая это, мы теперь знаем, что угол в третьем квадранте будет \ (\ frac {\ pi} {3} \) ниже отрицательной оси \ (x \) или \ (\ pi + \ frac { \ pi} {3} = \ frac {{4 \ pi}} {3} \).Легкий способ запомнить это — заметить, что мы повернемся на половину оборота от положительной оси \ (x \), чтобы перейти к отрицательной оси \ (x \), а затем добавить \ (\ frac {\ pi} {3} \), чтобы достичь искомого угла.
Аналогично, угол в четвертом квадранте будет \ (\ frac {\ pi} {3} \) ниже положительной оси \ (x \). Итак, мы могли бы использовать \ (- \ frac {\ pi} {3} \) или \ (2 \ pi — \ frac {\ pi} {3} = \ frac {{5 \ pi}} {3} \) . Помните, что обычно мы ищем положительные углы между 0 и \ (2 \ pi \), поэтому мы будем использовать положительный угол.Простой способ запомнить положительный угол здесь — это повернуть на один полный оборот от положительной оси \ (x \) (, т.е. \ (2 \ pi \)), а затем отступить (, т.е. вычитание ) \ (\ frac {\ pi} {3} \).
Теперь мы подошли к очень важному различию между этой проблемой и предыдущими задачами в этом разделе. Решение: НЕ
\ [\ begin {align *} x & = \ frac {{4 \ pi}} {3} + 2 \ pi n, \ quad n = 0, \ pm 1, \ pm 2, \ ldots \\ x & = \ frac {{5 \ pi}} {3} + 2 \ pi n, \ quad n = 0, \ pm 1, \ pm 2, \ ldots \ end {align *} \]Это не набор решений, потому что мы НЕ ищем значения \ (x \), для которых \ (\ sin \ left (x \ right) = — \ frac {{\ sqrt 3}} {2} \) , но вместо этого мы ищем значения \ (x \), для которых \ (\ sin \ left ({5x} \ right) = — \ frac {{\ sqrt 3}} {2} \).Обратите внимание на разницу в аргументах синусоидальной функции! Один — это \ (x \), а другой — \ (5x \). Это имеет огромное значение в поиске решения! Таким образом, набор решений составляет
\ [\ begin {align *} 5x & = \ frac {{4 \ pi}} {3} + 2 \ pi n, \ quad n = 0, \ pm 1, \ pm 2, \ ldots \\ 5x & = \ frac {{5 \ pi}} {3} + 2 \ pi n, \ quad n = 0, \ pm 1, \ pm 2, \ ldots \ end {align *} \]Ну, вообще-то, это не совсем решение. Мы ищем значения \ (x \), поэтому разделите все на 5, чтобы получить.
\ [\ begin {align *} x & = \ frac {{4 \ pi}} {{15}} + \ frac {{2 \ pi n}} {5}, \ quad n = 0, \ pm 1, \ pm 2, \ ldots \\ x & = \ frac {\ pi} {3} + \ frac {{2 \ pi n}} {5}, \ quad n = 0, \ pm 1, \ pm 2, \ ldots \ end {align *} \]Обратите внимание, что мы также разделили \ (2 \ pi n \) на 5! Это важно! Если мы этого не сделаем, вы БУДЕТЕ пропустить решения. Например, возьмем \ (n = 1 \).
\ [\ begin {align *} x & = \ frac {{4 \ pi}} {{15}} + \ frac {{2 \ pi}} {5} = \ frac {{10 \ pi}} {{ 15}} = \ frac {{2 \ pi}} {3} & \ hspace {0.25 дюймов} & \ Rightarrow \ hspace {0,5 дюйма} \ sin \ left ({5 \ left ({\ frac {{2 \ pi}} {3}} \ right)} \ right) = \ sin \ left ({\ frac {{10 \ pi}} {3}} \ right) = — \ frac {{\ sqrt 3}} {2} \\ x & = \ frac {\ pi} {3} + \ frac {{2 \ pi}} {5} = \ frac {{11 \ pi}} {{15}} & \ hspace {0,25 дюйма} & \ Rightarrow \ hspace {0,5 дюйма} \ sin \ left ({5 \ left ({\ frac {{11 \ pi}} {{15}}} \ right)} \ right) = \ sin \ left ({\ frac {{11 \ pi}} {3}} \ right) = — \ frac {{\ sqrt 3}} {2} \ end {align *} \]Мы предоставим вам возможность проверить нашу работу, показав, что они являются решениями.Однако в этом есть смысл. Если бы вы не разделили \ (2 \ pi n \) на 5, вы бы пропустили эти решения!
Хорошо, теперь, когда мы получили все возможные решения, пора найти решения на заданном интервале. Сделаем это так же, как и в предыдущей задаче. Выберите значения \ (n \) и получите решения.
\ (п = 0 \). \ [\ begin {align *} x & = \ frac {{4 \ pi}} {{15}} + \ frac {{2 \ pi \ left (0 \ right)}} {5} = \ frac {{ 4 \ pi}} {{15}} 2 \ pi \\ x & = \ frac {\ pi} {3} + \ frac {{2 \ pi \ left (5 \ right)}} {5} = \ frac {{35 \ pi}} {{15}}> 2 \ pi \ end {align *} \]Итак, мы наконец-то прошли правильную конечную точку нашего интервала, поэтому нам больше не нужно положительное значение n .Теперь давайте посмотрим на отрицательный \ (n \) и посмотрим, что у нас получилось.
\ (п = –1 \). \ [\ begin {align *} x & = \ frac {{4 \ pi}} {{15}} + \ frac {{2 \ pi \ left ({- 1} \ right)}} {5} = — \ frac {{2 \ pi}} {{15}}> — \ pi \\ x & = \ frac {\ pi} {3} + \ frac {{2 \ pi \ left ({- 1} \ right) }} {5} = — \ frac {\ pi} {{15}}> — \ pi \ end {align *} \] \ (п = –2 \). \ [\ begin {align *} x & = \ frac {{4 \ pi}} {{15}} + \ frac {{2 \ pi \ left ({- 2} \ right)}} {5} = — \ frac {{8 \ pi}} {{15}}> — \ pi \\ x & = \ frac {\ pi} {3} + \ frac {{2 \ pi \ left ({- 2} \ right) }} {5} = — \ frac {{7 \ pi}} {{15}}> — \ pi \ end {align *} \] \ (п = –3 \).\ [\ begin {align *} x & = \ frac {{4 \ pi}} {{15}} + \ frac {{2 \ pi \ left ({- 3} \ right)}} {5} = — \ frac {{14 \ pi}} {{15}}> — \ pi \\ x & = \ frac {\ pi} {3} + \ frac {{2 \ pi \ left ({- 3} \ right) }} {5} = — \ frac {{13 \ pi}} {{15}}> — \ pi \ end {align *} \] \ (п = –4 \). \ [\ begin {align *} x & = \ frac {{4 \ pi}} {{15}} + \ frac {{2 \ pi \ left ({- 4} \ right)}} {5} = — \ frac {{4 \ pi}} {3}И теперь мы прошли левую конечную точку интервала.Иногда будет много решений, как в этом примере. Объединение всего этого дает следующий набор решений, лежащих в заданном интервале.
\ [\ begin {align *} & \ frac {{4 \ pi}} {{15}}, \ frac {\ pi} {3}, \ frac {{2 \ pi}} {3}, \ frac { {11 \ pi}} {{15}}, \ frac {{16 \ pi}} {{15}}, \ frac {{17 \ pi}} {{15}}, \ frac {{22 \ pi} } {{15}}, \ frac {{23 \ pi}} {{15}}, \ frac {{28 \ pi}} {{15}}, \ frac {{29 \ pi}} {{15} } \\ & — \ frac {\ pi} {{15}}, — \ frac {{2 \ pi}} {{15}}, — \ frac {{7 \ pi}} {{15}}, — \ frac {{8 \ pi}} {{15}}, — \ frac {{13 \ pi}} {{15}}, — \ frac {{14 \ pi}} {{15}} \ end {align *} \]Решение тригонометрических уравнений алгебраическими методами
Уравнение, содержащее тригонометрические функции называется тригонометрическое уравнение .
Пример:
грех 2 Икс + потому что 2 Икс знак равно 1 2 грех Икс — 1 знак равно 0 загар 2 2 Икс — 1 знак равно 0
Решение тригонометрических уравнений
Чтобы решить тригонометрическое уравнение, мы используем правила алгебры, чтобы изолировать тригонометрическую функцию по одну сторону от знака равенства.Затем мы используем наши знания о значениях тригонометрических функций для определения переменной.
Когда вы решаете тригонометрическое уравнение, которое включает только одно тригонометрическое выражение, начните с выделения выражения.
Если тригонометрические функции не могут быть объединены с одной стороны уравнения, попробуйте разложить уравнение на множители, а затем применить свойство нулевого продукта для решения уравнения. Если уравнение имеет квадратную форму, по возможности используйте первый множитель. Если это невозможно, примените квадратичная формула для решения уравнения.
Пример :
Решать 2 грех Икс — 1 знак равно 0 .
Чтобы решить уравнение, мы начинаем его переписывать так, чтобы sin Икс изолирован с левой стороны. Итак, сначала добавьте 1 в каждую сторону, а затем разделите каждую сторону на 2 .
2 грех Икс знак равно 1 грех Икс знак равно 1 2
С грех Икс имеет период 2 π , сначала находим все решения в интервале [ 0 , 2 π ] .
Решения Икс знак равно π 6 а также Икс знак равно 5 π 6 .
Решения на интервале ( — ∞ , ∞ ) затем находятся путем добавления целых кратных 2 π . Добавление 2 п π к каждому из решений получаем общее решение данного уравнения.Следовательно, общий вид решений таков: Икс знак равно π 6 + 2 п π а также Икс знак равно 5 π 6 + 2 п π где п любое целое число.
Решение тригонометрических уравнений — она любит математику
\ (\ displaystyle \ begin {array} {c} 4 \ sin x \ cos x = 2 \ sin x \\\ text {Interval} (0,2 \ pi) \ конец {массив} \) \ (\ displaystyle \ begin {array} {c} 4 \ sin x \ cos x-2 \ sin x = 0 \\ 2 \ sin x \ left ({2 \ cos x- 1} \ right) = 0 \ end {array} \)
\ (\ displaystyle \ begin {align} 2 \ sin x = 0 \, \, \, \, \, \, & \, \, \, \, 2 \ cos x-1 = 0 \\\ sin x = 0 \, \, \, \, \, \, & \, \, \, \, \, \ cos x = \ frac {1 } {2} \\ x = 0, \, \, \ pi \, \, \, \, \, & \, \, \, \, x = \ frac {\ pi} {3}, \, \ гидроразрыв {{5 \ pi}} {3} \ end {align} \)
\ (\ displaystyle x = \ left \ {{0, \ pi, \ frac {\ pi} {3}, \ frac {{ 5 \ pi}} {3}} \ right \} \)
\ (\ displaystyle \ begin {array} {c} 4 {{\ cos} ^ {4}} \ theta -7 {{\ cos} ^ {2}} \ theta + 3 = 0 \\\ text {Общие решения (в градусах)} \ end {array} \) \ (\ displaystyle \ left ({4 {{{\ cos}} ^ {2}} \ theta -3} \ right) \ left ({{{{\ cos}} ^ {2}} \ theta -1} \ right) = 0 \)
\ (\ displaystyle \ begin {align} \ sqrt {{{{{\ cos}} ^ {2}} \ theta}} = \ sqrt {{\ frac {3) } {4}}} \, \, \, \, \, \, & \, \, \, \, \, \ sqrt {{{{{\ cos}} ^ {2}} \ theta}} = \ sqrt {1} \\\, \ cos \ theta = \ pm \ frac {{\ sqrt {3}}} {2} \, \, \, \, \, \, \, & \, \, \ , \, \, \ соз \ theta = \ pm 1 \, \ end {align} \)
\ (\ displaystyle \ begin {array} {c} \ text {(Add} 180 {} ^ \ circ k \ text {вместо} 360 {} ^ \ circ k \ text {из-за} \ pm) \\\, \, \, \ theta = 30 {} ^ \ circ +180 {} ^ \ circ k \, \, \, \, \, \, \, \, \, \, \, \, \ theta = 180 {} ^ \ circ k \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ theta = 330 {} ^ \ circ +180 {} ^ \ circ k \, \, \, \, \, \, \ , \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \\\ left \ {\ begin {array} {l} \ theta | \ theta = 30 {} ^ \ circ +180 {} ^ \ circ k, \, \, \ theta = 330 {} ^ \ circ + 180 {} ^ \ circ k, \\\, \, \, \, \ theta = 180 {} ^ \ circ k \ end {array} \ right \} \ end {array} \)
\ (\ displaystyle \ begin {array} {c} 2 {{\ sec} ^ {2}} x-3 \ sec x = 2 \\\ text {General Solutions} \ end {array} \) \ (\ displaystyle \ begin {array} {c} 2 {{\ sec} ^ {2}} x-3 \ sec x-2 = 0 \\\ left ({2 \ sec x + 1} \ right) \ left ({\ сек х-2} \ справа) = 0 \ конец {массив} \)
\ (\ displaystyle \ begin {align} \ sec x = — \ frac {1} {2} \, \, \, \, \, \, \, \, & \, \, \, \, \, \, \ sec x = 2 \\\ text {(без решения)} \, \, \, \, \, \, \, & \, \, \, \, \, \ left ({\ cos x = \ frac {1} {2}} \ right) \ end {align} \)
\ (\ displaystyle \ left \ {{x | x = \ frac {\ pi} {3} +2 \ pi k, \, x = \ frac {{5 \ pi}} {3} +2 \ pi k \,} \ right \} \)
\ (\ displaystyle \ begin {array} {c} {{\ tan} ^ {4}} x -4 {{\ tan} ^ {2}} x + 3 = 0 \\\ text {General Solutions} \ end {array} \) \ (\ displaystyle \ begin {array} {c} \ left ( {{{{\ tan}} ^ {2}} x-3} \ right) \ left ({{{{{\ tan}}} ^ {2}} x-1} \ right) = 0 \\ {{\ tan} ^ {2}} x-3 = 0 \, \, \, \, \, \, \, \, \, {{\ tan} ^ {2}} x-1 = 0 \ end {array} \)
\ (\ displaystyle \ begin {align} \ sqrt {{{{{\ tan}} ^ {2}} x}} = \ sqrt {3} \, \, \, \, \, \, & \, \, \, \, \ sqrt {{{{{\ tan}} ^ {2}} x}} = \ sqrt {1} \\\ tan x = \ pm \ sqrt {3} \ , \, \, \, \, \, \, & \, \, \, \, \, \ tan x = \ pm \ sqrt {1} \\ x = \ frac {\ pi} {3} + \ pi k \, \, \, \, \, \, \, \, & \, \, \, \, \, \, x = \ frac {\ pi} {4} + \ pi k \\ x = \ frac {{2 \ pi}} {3} + \ pi k \, \, \, \, \, \, \, & \, \, \, \, \, \, x = \ frac {{3 \ pi}} {4} + \ pi k \ end {align} \)
\ (\ displaystyl e \ left \ {\ begin {align} x | x = \ frac {\ pi} {3} + \ pi k, \, \, x = \ frac {{2 \ pi}} {3} + \ pi k , \\\, \, \, \, x = \ frac {\ pi} {4} + \ pi k, \, \, \, x = \ frac {{3 \ pi}} {4} + \ pi к \ конец {align} \ right \} \)
\ (\ displaystyle \ begin {array} {c} 3 {{\ cot} ^ {2}} x + 3 \ cot x- \ sqrt {3} \ cot x = \ sqrt {3} \\\ text {Interval} (0,2 \ pi) \ end {array} \) \ (\ displaystyle \ begin {array} {c} 3 {{\ cot } ^ {2}} x + 3 \ cot x- \ sqrt {3} \ cot x- \ sqrt {3} = 0 \\ 3 \ cot x \ left ({\ cot x + 1} \ right) — \ sqrt {3} \ left ({\ cot x + 1} \ right) = 0 \\\ left ({\ cot x + 1} \ right) \ left ({3 \ cot x- \ sqrt {3}} \ справа) = 0 \ конец {массив} \)
\ (\ Displaystyle \ begin {align} \ cot x = -1 \, \, \, \, \, \, & \, \, \, \ , \ cot x = \ frac {{\ sqrt {3}}} {3} \\\ tan x = -1 \, \, \, \, \, & \, \, \, \, \ tan x = \ frac {3} {{\ sqrt {3}}} = \ sqrt {3} \\ x = \ frac {{3 \ pi}} {4}, \, \, \ frac {{7 \ pi}} {4} \, \, \, \, \, & \, \, \, \, \, x = \ frac {\ pi} {3}, \, \, \ frac {{4 \ pi}} { 3} \ end {align} \)
\ (\ displaystyle x = \ left \ {{\ frac {{3 \ pi}} {4}, \ frac {{7 \ pi}} {4}, \ frac {\ pi} {3}, \ frac {{4 \ pi}} {3}} \ right \} \)
\ (\ displaystyle \ begin {array} {c} \ sqrt {3} \ sin \ left ({2 \ theta} \ right) \ cot \ left ({2 \ theta} \ right) — \ sin \ left ({2 \ theta } \ right) = 0 \\\ текст {Интервал} (0,2 \ pi) \ end {array} \)
\ (\ displaystyle \ sin \ left ({2 \ theta} \ right) \ left ({\ sqrt {3} \ cot \ left ({2 \ theta} \ right) -1} \ right) = 0 \)
\ (\ displaystyle \ begin {align} \ sin \ left ({2 \ theta } \ right) = 0 \, \, \, \, \, \, \, & \, \, \, \, \, \ cot \ left ({2 \ theta} \ right) = \ frac {1} {{\ sqrt {3}}} \\ 2 \ theta = \ pi k \, \, \, \, \, \, \, \, \, & \, \, \, \, \, \, 2 \ theta = \ frac {\ pi} {3} + \ pi k \\\, \, \, \, \, \, \, \, \, \, & \, \, \, \, \, \ , 2 \ theta = \ frac {{4 \ pi}} {3} + \ pi k \\\, \, \, \, \, \ theta = \ frac {{\ pi k}} {2} \, \, \, \, \, \, & \, \, \, \, \, \, \, \ theta = \ frac {\ pi} {6} + \ frac {\ pi} {2} k \\ \, \, \, \, \, \, \, & \, \, \, \, \, \, \, \, \ theta = \ frac {{4 \ pi}} {6} + \ frac { \ pi} {2} k \ end {align} \)
Из-за ограничения домена для cot (где указаны его асимптоты), и учитывая, что \ (\ displaystyle \ cot \ left [{2 \ left ({\ frac {{\ pi k}} {2}} \ right)} \ right] = \ cot \ lef t ({\ pi k} \ right) \) не определено, мы должны удалить \ (\ displaystyle \ frac {{\ pi k}} {2} \).
Решения: \ (\ displaystyle \ theta = \ left \ {{\ frac {\ pi} {6}, \ frac {{2 \ pi}} {3}, \ frac {{7 \ pi}} { 6}, \ frac {{5 \ pi}} {3}} \ right \} \)
Тригонометрические уравнения
Тригонометрические тождества верны для всех значений замены для переменных, для которых определены обе части уравнения . Условные тригонометрические уравнения верны только для некоторых значений замены. Решения в определенном интервале, например 0 ≤ x ≤ 2π, обычно называются первичными решениями .Общее решение — это формула, в которой перечислены все возможные решения.
Процесс решения общих тригонометрических уравнений не является однозначным. Не существует правил, которые всегда приводят к решению. Процедура обычно включает использование тождеств, алгебраические манипуляции и метод проб и ошибок. Следующие рекомендации могут помочь найти решение.
Если уравнение содержит более одной тригонометрической функции, используйте тождества и алгебраические манипуляции (например, разложение на множители), чтобы переписать уравнение в терминах только одной тригонометрической функции.Найдите выражения в квадратичной форме и решите с помощью факторизации. Не все уравнения имеют решения, но те, которые имеют, обычно могут быть решены с использованием соответствующих тождеств и алгебраических манипуляций. Ищите шаблоны. Нет замены опыту.
Пример 1: Найдите точное решение:
Сначала преобразуйте уравнение, используя тождество sin 2 α + cos2α = 1.
Следовательно,
Таким образом,
Пример 2: Решите cos 2 x = 3 (sin x — 1) для всех действительных значений x .
Первый ответ, −2,351, не является решением, поскольку функция синуса должна находиться в диапазоне от -1 до 1. Второй ответ, 0,8508, является допустимым значением. Таким образом, если k — целое число,
В радианах,
По форме
Пример 3 : Найдите точное решение:
Сначала преобразуйте уравнение, используя тождество двойного угла cos 2θ = 2 cos 2 θ — 1. 2y-4 \ cos y +3 = 0cos2y − 4cosy + 3 = 0
Обратите внимание, что в приведенных выше уравнениях используется наш знакомый полиномиальный формат, но с добавлением тригонометрических соотношений синуса и косинуса.Теперь, когда у нас есть представление о том, как выглядят триггерные уравнения, давайте посмотрим, как решать триггерные уравнения!
Решение тригонометрических уравнений
Чтобы решить тригонометрические задачи, которые мы рассмотрим в этой статье, сначала важно убедиться, что вы хорошо знакомы с основными, нетригонометрическими функциями и отношениями, а также с факторизацией многочленов. Чтобы освежить память, вам помогут видеоролики о функциях умножения и факторизации трехчленов!
Имея в виду эти концепции, давайте приступим к решению тригонометрических уравнений.Существует множество различных методов решения триггерных проблем, поэтому в зависимости от того, куда вы посмотрите, вы можете получить много разных ответов! В этой статье дается подробный обзор двух основных методов, которые мы можем использовать для решения триггеров.
Метод 1:
Заменить sin x или cos x другой переменной, решить, а затем заменить эту переменную на sin x или cos x.
Метод 2:
Решите, не выполняя замену. Этот метод требует, чтобы вы хорошо разбирались в тригонометрических функциях и легко упрощали с их помощью выражения!
Сейчас довольно сложно описать эти методы без демонстрационного примера, поэтому давайте попрактикуемся в этих методах с некоторыми реальными проблемами.2 + 3w = 06w2 + 3w = 0
3w (2w + 1) = 03w (2w + 1) = 03w (2w + 1) = 0
Шаг 3: Решите относительно x
Надеюсь, вы помните, как решать разложенные на множители многочлены. В этом случае w = 0 и w = -1/2
Шаг 4. Замените w на sinx и измените решения
Теперь, когда мы решили уравнение для w, мы должны не забыть заменить w обратно на sin x и скорректировать наши решения, чтобы учесть это.
Следовательно: sin x = 0 и sin x = -1/2
Используя наш калькулятор или наши знания о неизменно важном единичном круге, мы приходим к следующим решениям: x = 0 и x = -pi / 6
Чтобы попрактиковаться в решении подобных вычислений, ознакомьтесь с уроком по поиску триггерных значений.
Шаг 5: Найдите решения во всем заданном диапазоне
Хотя мы нашли решения для нашего уравнения, помните, что нас попросили найти все решений в диапазоне 0≤x≤2π0 \ leq x \ leq 2 \ pi0≤x≤2π! Из-за повторяющегося характера функций синуса и косинуса у нас, вероятно, будет несколько значений x, которые могут решить это уравнение. Кроме того, -pi / 6 не решает это уравнение, так как оно выходит за пределы допустимого диапазона.
Опять же, как и в большинстве случаев в математике, есть несколько способов найти другие значения x.Самый простой способ — быстро набросать синусоидальный график от 0 до 2pi и посмотреть, когда pi равно 0 и -1/2.
Взглянув на наше изображение выше, легко заметить, где sinx = 0, дает нам значения x 0, pi и 2pi . Теперь ищем sinx = -1/2, мы знаем из нашего начального решения –pi / 6, что sinx = -1/2 для некоторых кратных pi / 6. Глядя на наш график, становится ясно, что sinx = -1/2 для двух значений между пи и 2 пи, эти значения — пи + пи / 6 и 2 пи — пи / 6. Следовательно, дает нам значения x 7pi / 6 и 11pi / 6 .2 x + 3 \ cos x + 1 = 02cos2x + 3 cosx + 1 = 0
Для этого второго и последнего примера мы будем использовать Method 2 , который был описан ранее. Это означает, что мы не будем делать никакой замены и будем решать тригонометрическое уравнение как есть.
Шаг 1. Разложите на множители и упростите уравнение
(2cosx + 1) (cosx + 1) = 0 (2 \ cos x + 1) (\ cos x +1) = 0 (2cosx + 1) (cosx + 1) = 0
Шаг 2: Решить
Теперь, когда мы разложили на множители наше уравнение, легко решить и определить, что:
cosx = -1/2 и cosx = -1
Решение относительно x дает нам решения: x = 2pi / 3 и pi
Шаг 3. Найдите решения в пределах всего указанного диапазона
В этом примере, в отличие от первого, не указан указанный диапазон.Следовательно, мы должны давать решения, которые учитывают постоянно повторяющийся характер функции косинуса. Кроме того, мы должны учитывать, что могут быть другие значения для x, которые наши калькуляторы не выплюнули. Опять же, лучший способ понять все это — взглянуть на график cosx.
Еще раз взглянув на график выше, легко заметить, когда cosx = -1. Cosx будет равен -1 в пи, повторяя каждый «n-й» (где n = целое) полный цикл (2pi) волны, таким образом, x = pi + n2pi .Для cosx = -1 / 2 решение аналогично тому, как мы нашли наши решения в примере 1 . Кроме того, нам нужно помнить о повторяющейся природе, как мы это делали для решений для cosx = -1 для каждого полного цикла (2pi). Таким образом, функция будет равна -1/2 , когда x = 2pi / 3 = n2pi и когда x = 4pi / 3 + n2pi .
Таким образом, наш окончательный ответ: , таким образом, x = pi + n2pi, x = 2pi / 3 = n2pi и x = 4pi / 3 + n2pi
Вот и все! Чтобы узнать больше о тригонометрических уравнениях и о том, как они связаны с производными, ознакомьтесь с этим уроком о производных тригонометрических функций.

 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
 При любом а.
При любом а.  ) Собственно, для этого и разбираемся. Что, как и откуда.
) Собственно, для этого и разбираемся. Что, как и откуда. Полноценный ответ будет:
Полноценный ответ будет: ) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.) Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.) п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.) Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C). k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D). На рисунке отмечены также и координаты этих точек (опустим описание их получения).
На рисунке отмечены также и координаты этих точек (опустим описание их получения).

 Графики также помогают понять, почему иногда есть один ответ, а иногда — много ответов. Я использую Scientific Notebook или аналогичную математическую программу для построения графиков функций.
Графики также помогают понять, почему иногда есть один ответ, а иногда — много ответов. Я использую Scientific Notebook или аналогичную математическую программу для построения графиков функций.

 2theta = 1/16`
2theta = 1/16` 2 \ х + 3 \ соз х + 1 = 0`
2 \ х + 3 \ соз х + 1 = 0` 2 2θ = 1`
2 2θ = 1` 2x) = 0`
2x) = 0`
 26, 0,79, «1,31, 2,36,« 3,40, 3,93,
«4.45, 5.50.»
26, 0,79, «1,31, 2,36,« 3,40, 3,93,
«4.45, 5.50.» .. \)}
.. \)}  2 \; + \; Икс \;-\; 1 ~ = ~ 0 \ quad \ Rightarrow \ quad x ~ = ~ \ frac {-1 \; \ pm \; \ sqrt {1 — (4) \, (- 1)}} {
2 \; + \; Икс \;-\; 1 ~ = ~ 0 \ quad \ Rightarrow \ quad x ~ = ~ \ frac {-1 \; \ pm \; \ sqrt {1 — (4) \, (- 1)}} { Итак, поскольку указанные выше углы кратны \ (\ pi \), а каждое кратное \ (2 \ pi \) кратно \ (\ pi \), мы можем объединить два ответа в один для общего решения:
Итак, поскольку указанные выше углы кратны \ (\ pi \), а каждое кратное \ (2 \ pi \) кратно \ (\ pi \), мы можем объединить два ответа в один для общего решения: