Геометрия. Урок 3. Треугольники — ЁП
Содержание страницы:
Треугольник – многоугольник с тремя сторонами и тремя углами.
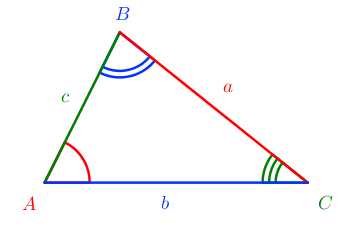
Угол ∠A — угол, образованный сторонами AB и AC и противолежащий стороне BC.
Угол ∠B — угол, образованный сторонами BA и BC и противолежащий стороне AC.
Угол ∠C — угол, образованный сторонами CB и CA и противолежащий стороне AB.
Треугольник остроугольный, если все три угла в треугольнике острые.
Треугольник прямоугольный, если у него один из углов прямой (=90°).
Треугольник тупоугольный, если у него один из углов тупой.
Примеры:
Основные свойства треугольника:
- Против большей стороны лежит больший угол.
- Против равных сторон лежат равные углы.
- Сумма углов в треугольнике равна 180°.
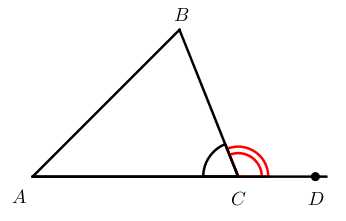
- Если продолжить одну из сторон треугольника, например,
AC,
и взять на продолжении стороны точку
D,
образуется внешний угол
∠BCD
к исходному углу
∠ACB.

Внешний угол равен сумме двух внутренних углов, не смежных с ним. ∠BCD=180°−∠ACB∠BCD=∠A+∠B - Неравенство треугольника: любая из сторон треугольника меньше суммы двух других сторон и больше их разности.
Биссектриса угла — луч, выходящий из вершины угла и делящий его пополам.
Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.
Свойства биссектрис треугольника:
- Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
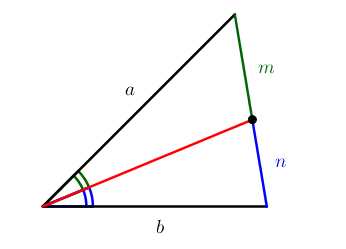
- Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:

ab=mn - Биссектрисы пересекаются в одной точке. Точка пересечения биссектрис – центр вписанной в треугольник окружности.
Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Свойства медиан треугольника:
- Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
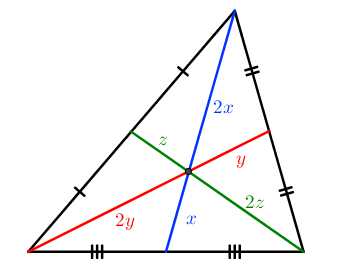
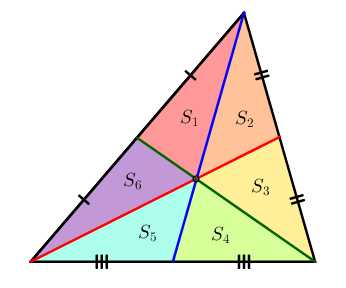
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.


S1=S2=S3=S4=S5=S6
Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.
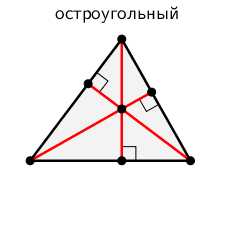
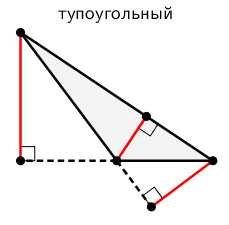
Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.
Пример:
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.
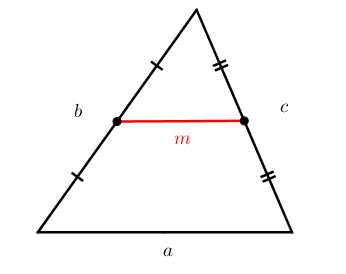
m=a2
Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.
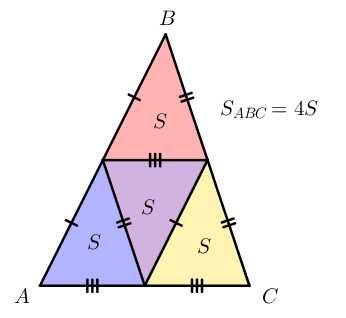
Площадь произвольного треугольника можно найти следующими способами:
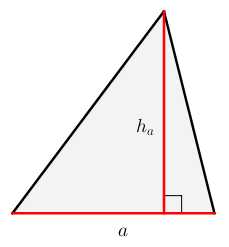
- Полупроизведение стороны на высоту, проведенную к этой стороне.
 S=12a⋅ha
S=12a⋅ha - Полупроизведение двух сторон на синус угла между ними.
 S=12a⋅b⋅sinα
S=12a⋅b⋅sinα - По формуле Герона.

Равнобедренным называется треугольник, у которого две стороны равны.
Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.
Свойства равноберенного треугольника:
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию совпадают.
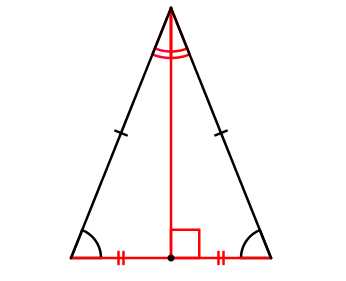
Равносторонним называется треугольник, у которого все стороны и все углы равны.
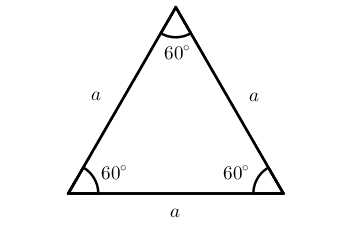
Площадь равностороннего треугольника находится по формуле S=a234
Высота равностороннего треугольника находится по формуле h=a32
Треугольник называется прямоугольным, если у него один из углов равен 90°.
Свойства прямоугольного треугольника:
- Сумма двух острых углов треугольника равна 90°.
- Катет, лежащий напротив угла в 30°, равен половине гипотенузы.
- Если катет равен половине гипотенузы, он лежит напротив угла в
30°.
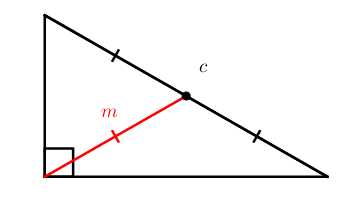
a=c2c=2⋅a - Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
 m=c2
m=c2 - Пропорциональные отрезки в прямоугольном треугольнике
 a=m⋅cb=n⋅ch=m⋅n
a=m⋅cb=n⋅ch=m⋅n
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
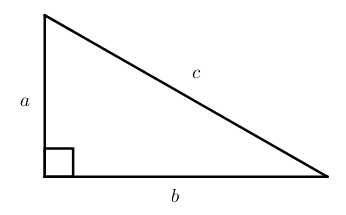
c2=a2+b2
У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:
S=12a⋅b
Модуль геометрия: задания, связанные с треугольниками
Скачать домашнее задание к уроку 3.
epmat.ru
Треугольники — геометрия и искусство
Треугольник — это простейшая фигура: три стороны и три вершины. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы.
Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу. В одном египетском папирусе 4000-летней давности говорится, что площадь равнобедренного треугольника равна произведению половины основания на боковую сторону (а не на высоту).
Через 2000 лет в Древней Греции изучение свойств треугольника ведется очень активно. Пифагор открывает свою теорему. Герон Александрийский находит формулу, выражающую площадь треугольника через его стороны; становится известным, что биссектрисы, как меридианы и высоты, пересекаются в одной точке.
Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру: «Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения, лежат, на одной окружности». Эта окружность получила название «окружности девяти точек». Ее центр оказался в се-редине отрезка, соединяющего точку пересечения высот с центром описанной окружности.
Император Франции Наполеон свободное время посвящал занятиям математикой. Ему приписывает такую красивую, с теорему: «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника». Этот треугольник называется внешним треугольником Наполеона. » Аналогично строится и внутренний треугольник Наполеона.
Тем удивительнее было открытие, сделанное американским математиком Франком Морли. Он доказал, что если в треугольнике провести через вершины лучи, делящие углы на три равные части, то точки пересечения смежных трисектрис углов являются вершинами равностороннего треугольника (1899).
Энц. «Я познаю мир. Математика», 2006
geometry-and-art.ru
Треугольник. Свойства и признаки треугольника.
Треугольник произвольный
Треугольник
– это многоугольник с тремя сторонами (тремя углами).Виды треугольников:+ показать
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).
Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).
Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием.
Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.
Свойства
+ показать
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
3. Сумма углов треугольника равна 180 º .
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:
(Внешний угол образуется в результате продолжения одной из сторон треугольника).
5. Любая сторона треугольника меньше суммы двух других сторон.
Признаки равенства треугольников
+ показать
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.
2. Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.
3. Треугольники равны, если у них соответственно равны три стороны.
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника
Через сторону и высоту
Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где – полупериметр
Формула Герона
, где – полупериметр
Смотрите также площадь треугольника здесь.
И, думаю, будет полезна таблица формул для треугольника.
egemaximum.ru
Формулы, теоремы и свойства элементов треугольника. Справочник репетитора по математике
Теоретичесикие шпаргалки по элементарной геометрии для занятий с репетитором по математике. Базовый школьный уровень. Свойства элементов треугольника. В помощь для решению задач по всему курсу планиметрии. Для тренировки решения задач С4 на ЕГЭ по математике.
1) Определение тригонометрических функций острого угла в прямоугольном треугольнике и теорема Пифагора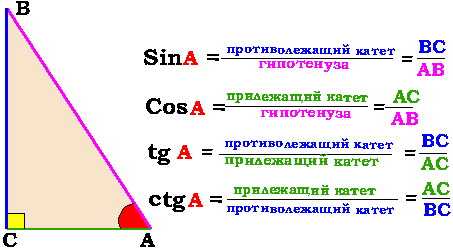
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов, то есть
2) Формулы площади треугольника
,
где (Формула Герона)
, где r- вписанной окружности
, где R — радиус описанной окружности
3) Подобие треугольников
Определение: два треугольника называются подобными, если у них соответствующие углы равны и соответствующие стороны пропорциональны, то есть
и
Обозначение:
4) Признаки подобия двух треугольников
1-й признак: Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Коротко: если , то
2-й признак:если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны
Коротко: если и , то
3-й признак:если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны, то есть
Коротко: если , то
5) Свойства подобных треугольников
если , то
, где
и — любые соответствующие медианы (проведенные к соответствующим сторонам)
и — любые соответствующие биссектрисы (проведенные к соответствующим сторонам)
и — любые соответствующие высоты (проведенные к соответствующим сторонам)
6) Подобие прямоугольных треугольников. Высота, проведенная из вершины прямого угла
Теорема: высота в прямоугольном треугольнике, поведенная из вершины прямого угла образует два треугольника, подобных исходному. Для катетов и высоты исходного треугольника верны следующие формулы:
7) Свойство медиан в треугольнике.
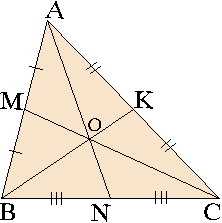
Теорема 1: Все медианы треугольника пересекаются в одной точке (центр тяжести треугольника) и делятся этой точкой в отношении 2:1, считая от вершин. То есть
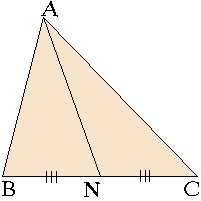 Теорема 2: Каждая медиана, проведенная в треугольнике делит этот треугольник на две равновеликие части (на два треугольника с равными площадями),
Теорема 2: Каждая медиана, проведенная в треугольнике делит этот треугольник на две равновеликие части (на два треугольника с равными площадями),
То есть
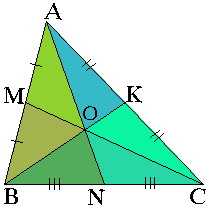
Теорема 3: все три медианы делят треугольник на 6 равновеликих треугольников, то есть
8) Свойство биссектрис в треугольнике 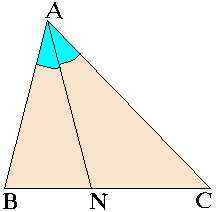 Теорема 1: Каждая биссектриса угла в треугольнике делит его противолежащую сторону на отрезки, пропорциональные к двум другим сторонам треугольника.
Теорема 1: Каждая биссектриса угла в треугольнике делит его противолежащую сторону на отрезки, пропорциональные к двум другим сторонам треугольника.
То есть
Теорема 2: Все биссектрисы в треугольнике пересекаются в одной точке, которая является центром вписанной с треугольник окружности. В любой треугольник можно вписать окружность и только одну.
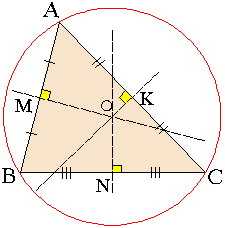
9) Свойство точки пересечения серединных перпендикуляров к сторонам треугольника:
Теорема: все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке и эта точка является центром описанной около треугольника окружности. Вокруг любого треугольника можно описать окружность и только одну.
10) Теорема о разделительном отрезке в треугольнике
Теорема: Отрезок, соединяющий вершину треугольника с противоположной стороной делит ее на отрезки, пропорциональные площадям образованных треугольников.
То есть
11) Средняя линия треугольника
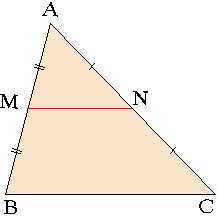
Теорема: Средняя линия треугольника, соединяющая середины двух его сторон параллельна третьей стороне и равна ее половине.
То есть и
12) Теорема синусов и теорема косинусов
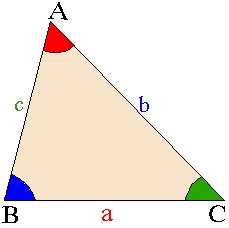
Теорема синусов: Cтороны треугольника пропорциональны синусам противолежащих углов и каждое отношение стороны к синусу равно диаметру описанной около треугольника окружности.
То есть
Теорема косинусов: Квадрат стороны треугольника равне сумме квадратов двух других сторон минус удвоенное произведение этих сторон на синус угла между ними, то есть
13) Теорема Менелая
Теорема: Произведение отношений отрезков, на которые произвольная прямая делит стороны треугольника (или их продолжения) равно единице
То есть
Комментарий репетитора по математике: несправедливо выброшенная теорема из школьного курса геометрии. Рекомендую репетиторам включить ее в подготовку, по крайней мере к вузовским олимпиадам и вступительным экзаменам по математике в МГУ. В программу ЕГЭ теорема Менелая не входит, но несколько типов задач без нее решаются очень сложно.
14) Теорема Чевы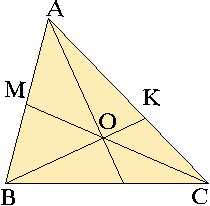
Теорема:если через вершины треугольника и произвольную внутреннюю точку провести отрезки к противоположным сторонам (чевианы), то их точки пересечения разделят стороны на отрезки, произведение отношений которых равно единице.
То есть
Колпаков А.Н. Репетитор по математике.
Метки: Геометрия, Справочник репетитора, Ученикам
ankolpakov.ru
Свойства треугольников, формулы и примеры
Все свойства треугольников
В любом треугольнике три угла и три стороны.
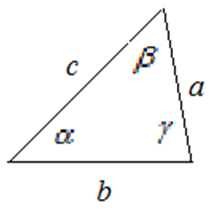
Сумма углов любого треугольника равна .
Против большего угла треугольника лежит большая сторона.
Треугольники бывают остроугольными (если все его углы острые), тупоугольными (если один из его углов тупой), прямоугольными (если один из его углов прямой).
Основные линии треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.
В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.
Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.
Признаки равенства треугольников
I признак. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
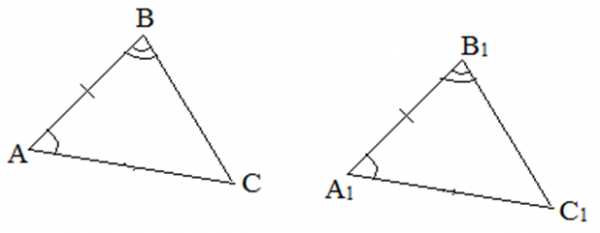
II признак. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
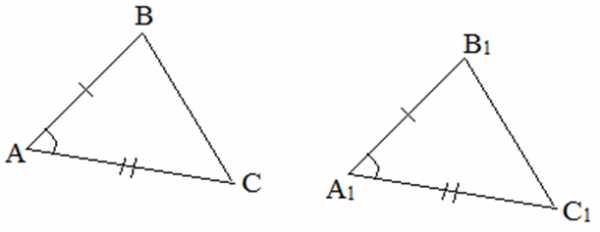
III признак. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
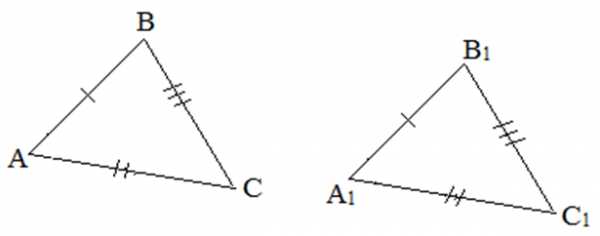
Треугольники называются подобными, если их стороны пропорциональны.
Признаки подобия треугольников
- Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.

- Если три стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники подобны.
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Подробнее про теорему косинусов по ссылке.
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности (обобщенная теорема синусов):
Подробнее про теорему синусов по ссылке.
Площадь треугольника можно вычислить по формулам
1. Через высоту и основание
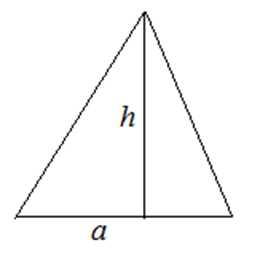
2. По двум сторонам и углу между ними
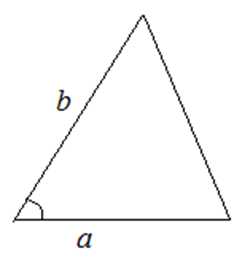
3. По формуле Герона
где – полупериметр треугольника
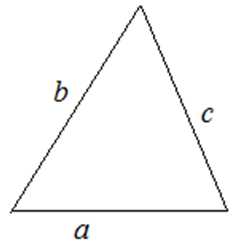
4. Через радиусы вписанной и описанной окружностей
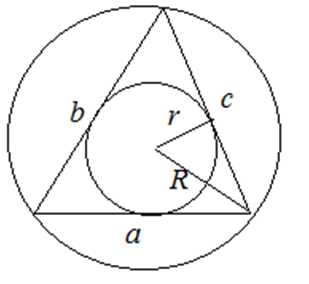
где – полупериметр треугольника, – радиус вписанной окружности;
– радиус описанной окружности.
Примеры решения задач
ru.solverbook.com
Основные факты о треугольниках, теория в ЕГЭ по математике
\[{\Large{\text{Основные сведения}}}\]
Определения
Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от \(0^\circ\) до \(180^\circ\) включительно.
Угол \(\alpha\) называется острым, если \(0^\circ<\alpha<90^\circ\), прямым – если \(\alpha=90^\circ\), тупым – если \(90^\circ<\alpha<180^\circ\), и развернутым – если \(\alpha=180^\circ\).
Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.
Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.
Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.
Теорема
Смежные углы \(\alpha\) и \(\beta\) в сумме дают \(180^\circ\).
Вертикальные углы равны: \(\alpha=\gamma\).
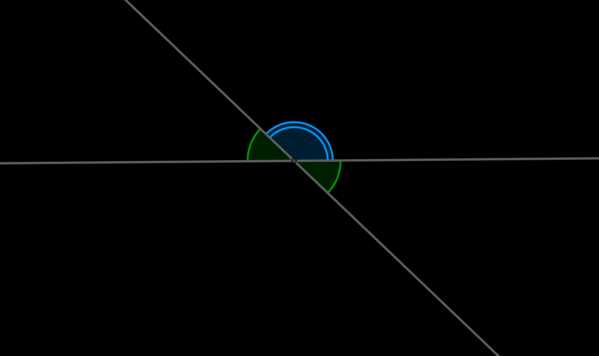
Определения
Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.
Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.

Теоремы: признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Определение
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Две прямые называются перпендикулярными, если угол между ними равен \(90^\circ\).
Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом \(90^\circ\).
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Замечание
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
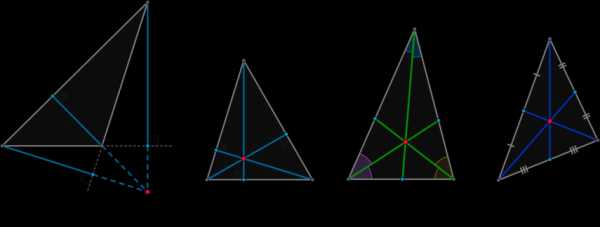
\[{\Large{\text{Параллельные прямые}}}\]
Определение
Две различные прямые на плоскости называются параллельными, если они не пересекаются.
Замечание
Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.
Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.
Следствия из аксиомы
1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.
2. Две прямые, параллельные третьей прямой, параллельны.
Теоремы: признаки параллельности прямых
1. Если при пересечении двух прямых \(a\) и \(b\) секущей \(c\) накрест лежащие углы равны: \(\angle 1=\angle 2\), то такие прямые параллельны.
2. Если при пересечении двух прямых \(a\) и \(b\) секущей \(c\) сумма односторонних углов \(\angle 1\) и \(\angle 3\) равна \(180^\circ\), то такие прямые параллельны.
3. Если при пересечении двух прямых \(a\) и \(b\) секущей \(c\) соответственные углы равны: \(\angle 1=\angle 4\), то такие прямые параллельны.
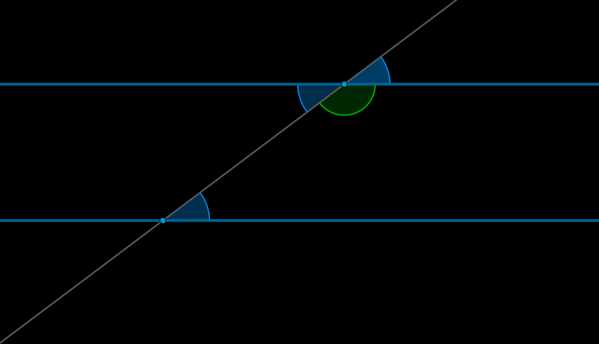
Теоремы: свойства параллельных прямых
1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна \(180^\circ\).
3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
\[{\Large{\text{Углы треугольника}}}\]
Определения
Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).
Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).
Теорема
Сумма внутренних углов треугольника равна \(180^\circ\).
Доказательство
Рассмотрим произвольный треугольник \(ABC\) и покажем, что \(\angle A + \angle B + \angle C = 180^\circ\).
Проведём через вершину \(B\) прямую \(a\), параллельную стороне \(AC\).
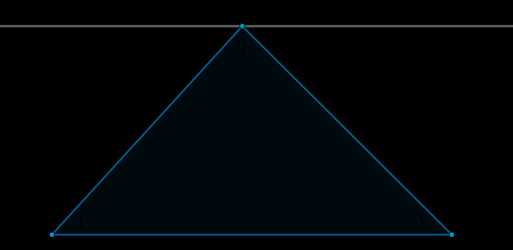
Углы \(1\) и \(4\) являются накрест лежащими углами при пересечении параллельных прямых \(a\) и \(AC\) секущей \(AB\), а углы \(3\) и \(5\) – накрест лежащими углами при пересечении тех же параллельных прямых секущей \(BC\). Поэтому \[\begin{aligned} &\angle 4 = \angle 1, \ \angle 5 = \angle 3. \qquad \qquad \qquad (1) \end{aligned}\]
Очевидно, сумма углов \(4, \ 2\) и \(5\) равна развёрнутому углу с вершиной \(B\), то есть \(\angle 4 + \angle 2 + \angle 5 = 180^\circ\). Отсюда, учитывая равенства \((1)\), получаем: \(\angle 1 + \angle 2 + \angle 3 = 180^\circ\).
Определение
Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.
Теорема
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: \(\angle BCD=\angle BAC+\angle ABC\).
Доказательство
Рассмотрим рисунок.
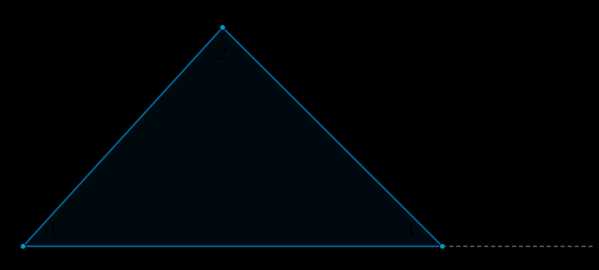
Угол \(4\) – внешний угол треугольника, смежный с углом \(3\). Так как \(\angle 4 + \angle 3 = 180^\circ\), а по теореме о сумме углов треугольника \(\angle 1 + \angle 2 + \angle 3 = 180^\circ\), то \(\angle 4 = \angle 1 + \angle 2\), что и требовалось доказать.
\[{\Large{\text{Равнобедренный треугольник}}}\]
Определения
Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.
Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Доказательство
Пусть \(ABC\) – равнобедренный треугольник, \(AB = BC\), \(BD\) – биссектриса (проведённая к основанию).
Рассмотрим треугольники \(ABD\) и \(BCD\): \(AB = BC\), \(\angle ABD = \angle CBD\), \(BD\) – общая. Таким образом, \(\triangle ABD = \triangle BCD\) по двум сторонам и углу между ними.
Из равенства этих треугольников следует, что \(AD = DC\), следовательно, \(BD\) – медиана.
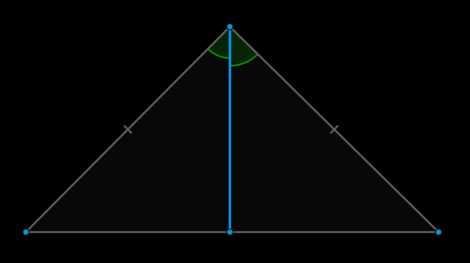
Кроме того, в равных треугольниках против равных сторон лежат равные углы, а \(AB = BC\), следовательно, \[\begin{aligned} &\angle ADB = \angle CDB, \qquad \qquad \qquad (2) \end{aligned}\] но \(\angle ADB + \angle CDB = \angle ADC\) – развёрнутый, следовательно, \(\angle ADB + \angle CDB = 180^\circ\), откуда при учёте \((2)\): \(\angle ADB = 90^\circ = \angle CDB\), то есть \(BD\) – высота.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
В равнобедренном треугольнике углы при основании равны.
Доказательство
Проведем биссектрису \(BD\) (см. рисунок из предыдущей теоремы). Тогда \(\triangle ABD=\triangle CBD\) по первому признаку, следовательно, \(\angle A=\angle C\).
Теоремы: признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то треугольник равнобедренный.
2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.
Теорема о соотношении между сторонами и углами треугольника
В треугольнике против большей стороны лежит больший угол.
В треугольнике против большего угла лежит большая сторона.
Теорема: неравенство треугольника
В треугольнике сумма любых двух сторон больше третьей стороны.
Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.
\[{\Large{\text{Прямоугольный треугольник}}}\]
Определения
В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.
Теоремы: свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна \(90^\circ\).
2. В прямоугольном треугольнике катет, лежащий против угла \(30^\circ\), равен половине гипотенузы.
Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла \(30^\circ\).

shkolkovo.net
Прямоугольный треугольник, формулы и примеры
Определение и формулы прямоугольного треугольника
Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.
Для прямоугольного треугольника справедливы следующие утверждения:
Признаки равенства прямоугольных треугольников
- По двум катетам: если два катета одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
- По стороне и острому углу: Если сторона и прилежащий к ней острый угол одного прямоугольного треугольника соответственно равны стороне и прилежащему к ней острому углу другого прямоугольного треугольника, то такие треугольники равны
Подробнее про признаки равенства треугольников читайте по ссылке.
Тригонометрические соотношения в прямоугольном треугольнике
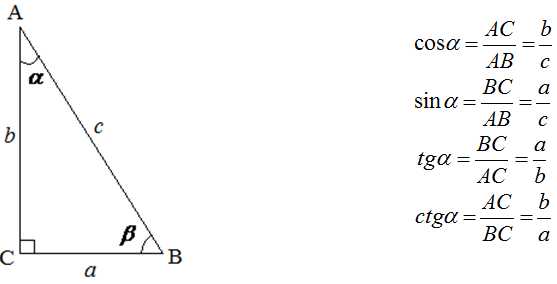
Площадь прямоугольного треугольника равна половине произведения катетов и вычисляется по формуле
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com

 S=12a⋅ha
S=12a⋅ha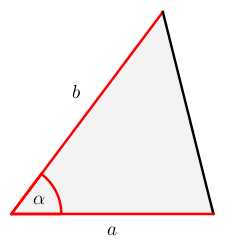 S=12a⋅b⋅sinα
S=12a⋅b⋅sinα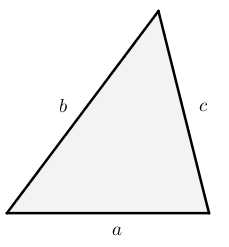
 m=c2
m=c2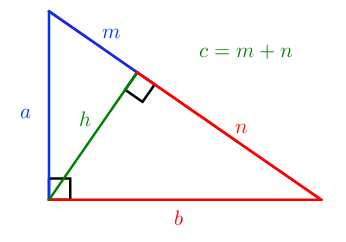 a=m⋅cb=n⋅ch=m⋅n
a=m⋅cb=n⋅ch=m⋅n