Примеры с дискриминантом по алгебре: Дискриминант квадратного уравнения. Формулы дискриминанта

Примеры на нахождение дискриминанта квадратного уравнения онлайн – skills4u

Первичное тестирование для определения вашего уровня знаний — бесплатно.

Советуем пройти тестирование за весь 8 класс по алгебре, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.

После регистрации вы получите 7 дней бесплатного доступа, чтобы увидеть первые результаты занятий и оценить эффективность тренажеров.

Вопросов в тесте: 10

Среднее время прохождения: ~10:00

Зарегистрироваться и пройти тестирование

Как работает платформа Skills4u

Платформа определит, насколько хорошо сформирован навык. Если тема усвоена плохо, предложит «прокачать» ее до 100%.

Не забудьте, что для формирования стойкого навыка нужно выполнить 5 коротких повторений по несколько минут в течение ближайших 4 дней.

Платформа пришлет своевременное напоминание.

Содержание каждого из последующих вопросов будет подстраиваться под ваши индивидуальные особенности с учетом уже выполненных заданий.

Почему нужно пройти общее тестирование по алгебре за 8 класс, а не по отдельной теме «Нахождение дискриминанта полного квадратного уравнения.»

Пройдя тестирование за класс вы получите ПОЛНУЮ КАРТИНУ ЗНАНИЙ ПО ВСЕМ ТЕМАМ.
Такой подход позволит глубинно проанализировать знания, вывести успеваемость и понимание предмета на качественно новый уровень.

Пройдя тестирование по одной теме вы получите РЕЗУЛЬТАТ ЗНАНИЙ ТОЛЬКО ЭТОЙ ТЕМЫ, которая, возможно, плохо изучена. Такой метод не является комплексным и дает лишь точечное понимание знаний по предмету.

Представляем интерактивный тест на нахождение дискриминанта квадратного уравнения по алгебре за 8 класс. Он поможет запомнить формулу и выполнить задание без ошибок и в короткие сроки. Тест создан на базе интеллектуальной образовательной платформы Skills4u и предлагает примеры на нахождение корней через дискриминант, сформированные с учетом подготовки каждого конкретного ученика. Сейчас мы расскажем, как это работает.

Всего в тесте 10 вопросов. Каждый раз предлагается вычислить дискриминант квадратного уравнения и записать полученный ответ в выделенной строке. При этом на экране появляется формула нахождения дискриминанта квадратного уравнения, вам нужно только выполнить вычисления. Поначалу задание может показаться сложным, но с каждым разом вы будете справляться с ним все быстрее. В среднем прохождение теста занимает не более 5-10 минут.

Если вы правильно выполнили нахождение корней дискриминанта, вы автоматически переходите к следующему вопросу. Если же ответ неправильный, загорается красный свет, и одновременно вы видите на экране правильный ответ. Это заставляет задуматься и найти причину, по которой вы ошиблись. В следующий раз вы внимательнее будете выполнять вычисления, а нахождение через дискриминант займет уже меньше времени. Так постепенно формируется стойкий учебный навык решения задач по этой теме.

В первый раз каждый может пройти тестирование совершенно бесплатно. По итогам тестирования система определяет ваш уровень подготовки и формирует рейтинг ученика. Кроме того, вы получите инструкции для продолжения занятий на тренажере по теме «Нахождение дискриминанта полного квадратного уравнения» за 8 класс. Необходимо вернуться к выполнению теста через несколько часов в тот же день, а затем регулярно тренироваться в течение последующих 4-5 дней, чтобы сформировать устойчивый учебный навык. Так сложная формула нахождения дискриминанта прочно закрепится в вашей памяти, и вы будете с легкостью решать любые примеры. Если в контрольной работе по алгебре вам попадутся задания на решение уравнений такого рода, вы вспомните примеры нахождения дискриминанта и без проблем вычислите его.

Для того чтобы получить возможность тренировать навык решения задач на нахождение дискриминанта онлайн, необходимо зарегистрироваться на сайте и оплатить подписку на месяц, полгода или целый учебный год. Как показывает практика, это позволяет существенно улучшить оценки по основным школьным предметам. Многочисленные положительные отзывы учеников и их родителей подтверждают эффективность самостоятельных занятий на тренажере, созданном на базе интеллектуальной образовательной платформы Skills4u.

Первичный Тест «Нахождение дискриминанта полного квадратного уравнения.» по алгебре за 8 класс онлайн и бесплатно предоставляется всем желающим.

Советуем пройти тестирование за весь 8 класс по алгебре, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.

После регистрации вы получите 7 дней бесплатного доступа, чтобы увидеть первые результаты занятий и оценить эффективность тренажеров.

Зарегистрироваться и пройти тестирование

Как растут результаты учеников
после занятий на тренажерах Skills4u

Занятия
на Skills4u

Занятия
с учебником

Успеваемость

Мотивация

Внимательность

Скорость

Самостоятельность

Запоминание

Присоединяйтесь к нам! Мы поможем повысить успеваемость и быстро подготовиться к контрольным работам.

А для комплексного результата пройдите общее тестирование за
класс! Узнайте пробелы в знаниях по всем темам

Ученик

Занимайся 20 минут в день и прокачай знания по школьной программе за месяц!

Родитель

Наслаждайтесь прогрессом вашего ребенка в школе и на платформе

Учитель/
репетитор

Задавайте и проверяйте домашние задания прямо на платформе

Зарегистрироваться и пройти тестирование

55538

---

учеников уже занимаются с нами

нахождение корней по формуле, теореме Виета; алгоритм решения с примерами

Алгебра

12. 11.21

11 мин.

При вычислении точек пересечения квадратичной функции с осью абсцисс требуется решить квадратное уравнение. Нахождение через дискриминант корней тождества является наиболее распространенным способом, но не во всех случаях практичным. Математики разработали специальный алгоритм, позволяющий выбрать оптимальный расчетный метод. Однако для этого нужно изучить теорию.

Оглавление:

• Общие сведения
• Понятие о дискриминанте
• Формула корней
• Теорема Виета
• Примеры решения

Общие сведения

Перед изучением методики нахождения дискриминанта квадратного уравнения нужно ознакомиться с теоретическими основами. Они включают в себя следующие положения:

1. Определение термина.
2. Формула дискриминанта.
3. Соотношения для вычисления корней.

Квадратным уравнением называется некоторая квадратичная функция вида «Wm ² +Qm+P», которая приравнивается к нулевому значению с обязательным наличием второй степени при неизвестной (переменной) величине.

Геометрический смысл квадратичного тождества с нулевым значением — пересечение заданной функции оси абсцисс. Теперь нужно ознакомиться с составляющими квадратного уравнения «Wm ² +Qm+P=0»:

1. W — константа при высшей степени переменной.
2. m — неизвестная величина.
3. Q — постоянный коэффициент при первой степени.
4. P — свободный член.

Следует отметить, что коэффициентов Q и P может не быть. На основании этого уравнения квадратичного вида делятся на следующие два типа:

1. Полные (присутствуют все коэффициенты).
2. Неполные (отсутствует Q и/или Р).

Однако не допускается отсутствие «W», поскольку выражение не удовлетворяет условию квадратичности. Далее необходимо разобрать, что означает дискриминант и как его найти.

Понятие о дискриминанте

Дискриминант — определенная промежуточная величина, позволяющая вычислить значения корней или доказать, что решений не существует. 2−4W (-P)=Q ² +4WP.

После нахождения значения дискриминанта можно сразу выяснить, сколько корней имеет квадратичная функция. Для выяснения их количества требуется разобрать три основных условия:

1. Если величина «D» меньше нуля (отрицательное числовое значение), то решения отсутствуют, т. е. перед ней стоит знак «минус».
2. При дискриминанте, который эквивалентен нулевому значению, можно сделать вывод о существовании только одного корня.
3. Переменная может принимать два значения при условии, что дискриминант больше нуля.

Следует отметить, что дискриминант рекомендуется вычислять при любом методе решения уравнения квадратичной формы. Это поможет избежать лишних временных затрат, поскольку можно сразу найти количество корней.

Формула корней

После нахождения величины промежуточного параметра по формуле дискриминанта квадратного уравнения требуется воспользоваться специальной формулой для вычисления корней уравнения (при D=0 или D>0).

(½)]/(2W)» можно править таким образом: m=[-Q-0]/(2W)=[-Q]/(2W).

Теорема Виета

В некоторых случаях при равенстве единице коэффициента при высшей степени можно воспользоваться теоремой Виета. Она позволяет очень быстро найти решения квадратного уравнения. Такой прием часто применяется в алгебре для оптимизации вычислений.

Формулировка утверждения имеет такой вид: сумма корней квадратичной функции противоположна коэффициенту при переменной в первой степени (-Q), а значение свободного члена «P» эквивалентно их произведению. В математической форме теорема записывается следующим образом:

1. -(m1+m2)=-Q.
2. (m1)*(m2)=P.

Однако бывают случаи, когда очень сложно подобрать значения переменных. Это очень часто происходит при наличии только одного корня или отсутствия решений вообще. Специалисты рекомендуют всегда высчитывать дискриминант, поскольку это позволяет существенно сэкономить время.

Например, на контрольной работе требуется решить 20 уравнений, десять из которых являются приведенными, т. 2−2m2+3=0.

Сравнить выражение в шестом пункте и первоначальное: они являются разными, следовательно, корни у уравнения отсутствуют.

Далее специалисты рекомендуют рассмотреть функцию «5m ² −15m+10» и найти точки пересечения с абсциссами. Алгоритм нахождения корней выглядит таким образом:

1. Записать квадратичную функцию, приравняв ее к нулю: 5m ² −15m+10=0.
2. Вынести общий множитель: 5 (m ² −3m+2)=0.
3. Сократить обе части на 5: m ² −3m+2=0.
4. Найти дискриминант: D=9−4*2=1.
5. Вычислить корни, воспользовавшись теоремой Виета: m1=1 и m2=2.

Следует отметить, что приведенные уравнения квадратичной формы нужно решать при помощи теоремы Виета. Однако для начала нужно найти величину дискриминанта. На основании последнего пункта (пятого) можно сделать вывод, что функция пересекает ось абсцисс в точках (1;0) и (2;0).

Таким образом, нахождение корней квадратичного тождества через дискриминант позволяет не только вычислить количество корней, но и избежать лишних вычислений, существенно оптимизировав расчетный процесс.

примеры решений. Как решать квадратные уравнения через дискриминант

Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.

О каких уравнениях пойдет речь?

На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.

Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.

Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.

Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.

Способы решения уравнений второго порядка

Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:

• с помощью факторизации;
• используя формулу для полного квадрата;
• применяя график соответствующей квадратичной функции;
• используя уравнение дискриминанта.

Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.

Формула для получения корней уравнения

Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).

Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.

В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).

Как только усвоен описанный выше шаг, далее, следует научиться различать коэффициенты. Здесь все просто: при x² всегда стоит a, при x1 находится b, свободный член c представляет собой не связанное с x число.

В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.

Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.

Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»). Для этого в него достаточно подставить коэффициенты b, c, и a.

Понятие о дискриминанте

В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.

Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:

1. D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
2. D
3. D=0: у уравнения всего один корень, и он является действительным числом.

Далее в статье приведены примеры с дискриминантом квадратных уравнений и дано их решение.

Задача на определение дискриминанта

Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.

Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.

Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.

Пример неравенства через дискриминант

Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.

В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.

Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0.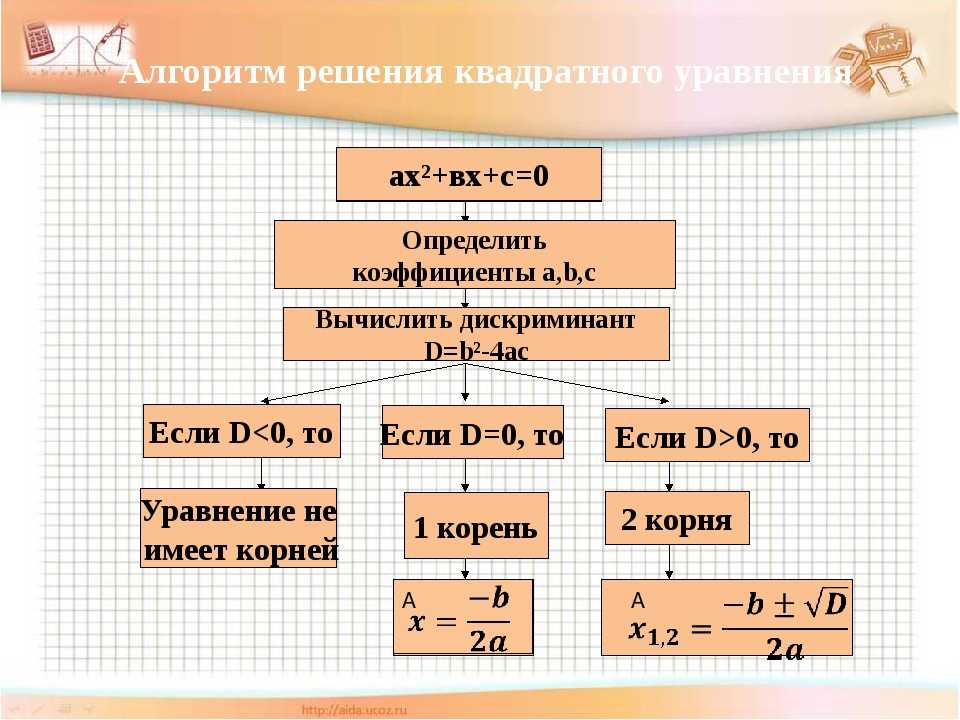 В свою очередь, число -4 не удовлетворяет неравенству (-4

Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.

Пример решения уравнения

Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.

В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.

Геометрическая задача

Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.

У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.

Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.

Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.

Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см.

Квадратичный дискриминант | Brilliant Math & Science Wiki

Содержание

• Объяснение
• Нахождение дискриминанта квадратного числа
• Повторяющиеся корни
• Диапазон решений
92 — 4ас}}{2а}. х=2а-b±b2-4ас.

Теперь заметьте, что дискриминант равен выражению в пределах квадратного корня квадратной формулы.

Поскольку квадратичная формула дает все корни квадратного многочлена, мы имеем следующие случаи:

• Если Δ>0, \Delta > 0 ,Δ>0, то многочлен имеет два различных действительных корня;
• Если Δ=0, \Delta = 0, Δ=0, то многочлен имеет ровно один действительный корень, который является повторяющимся корнем ; 92 — 4с = 1-4с.Δ=12-4с=1-4с.

  Из приведенной выше характеристики корней с помощью дискриминанта мы имеем следующее:

  • Если 1−4c>0, 1−4c > 0 ,1−4c>0, то многочлен имеет два различных действительных корня. Это происходит при c<14c< \frac{1}{4}c<41​.
  • Если 1−4c=0, 1-4c = 0, 1−4c=0, то многочлен имеет повторяющийся корень. Это происходит для c=14c=\frac{1}{4}c=41​.
  • Если 1−4c<0,1-4c < 0, 1−4c<0, то оба корня не являются действительными комплексными корнями. Это происходит для c>14c> \frac{1}{4}c>41​. □_\квадрат□​ 9{2}-12x+40f(x)=x2−12x+40 определено для всех действительных чисел.

    Процитировать как: Квадратичный дискриминант. Brilliant.org . Извлекаются из

    Дискриминант квадратного уравнения – формула и примеры

    Квадратные уравнения – это алгебраические уравнения, имеющие вид . Учитывая эту форму, дискриминантом квадратного уравнения является значение б ²-4 ак . Это значение входит в квадратный корень из общей квадратичной формулы и определяет тип решений, которые у нас будут.

    В этой статье мы узнаем все, что связано с дискриминантом квадратного уравнения. Кроме того, мы будем использовать его формулу для решения некоторых практических задач.

    АЛГЕБРА

    Актуально для …

    Изучение дискриминанта квадратного уравнения.

    См. примеры 92-4ac}}{2a}$$

    Таким образом, мы видим, что дискриминант представляет собой выражение внутри квадратного корня общей формулы. 2+4x+5=0$. 92+2x-10=0$.

    Выберите ответ

    ---

    $латекс D=-14$

    ---

    $латекс D=42$

    ---

    $латекс D=-51$

    ---

    $latex D=84$

    ---

    ---

    См. также

    Хотите узнать больше о квадратных уравнениях? Взгляните на эти страницы:

    • Калькулятор квадратных уравнений
    • Решение квадратных уравнений с помощью квадратичной формулы
    • Неполные квадратные уравнения с примерами
    • Решение квадратных уравнений с помощью факторинга
    • 10 примеров квадратных уравнений с ответами

    Изучайте математику с помощью наших дополнительных ресурсов по различным темам

    УЗНАТЬ БОЛЬШЕ

    Объяснение урока: Дискриминанты квадратного уравнения

    В этом объяснении мы узнаем, как найти дискриминант квадратного уравнения и использовать его для определения числа и типа его корней (решения), не решая его.

    Напомним, что общее квадратное уравнение имеет вид

    𝑎𝑥+𝑏𝑥+𝑐=0,

    ()1

    где 𝑎, 𝑏 и 𝑐 — действительные числа, а 𝑥 — искомая переменная. Чтобы это уравнение было квадратным, мы требуем, чтобы 𝑎≠0, но мы не накладываем такое же ограничение на 𝑏 или 𝑐. Это уравнение «решается», когда найдено значение 𝑥 такое, что равенство (1) верно. Для квадратного уравнения может быть максимум 90 548 двух 90 549 действительных чисел. решений уравнения (1), в отличие от единственного действительного решения линейного уравнения. Чтобы быть более конкретным, для любого квадратного уравнения с действительными коэффициентами будет либо 0, либо 1, либо 2 действительных решения.

    Хорошо известно, что решение квадратного уравнения дается формулой квадратного корня,

    𝑥=−𝑏±√𝑏−4𝑎𝑐2𝑎,

    ()2

    с двумя возможными решениями, обозначенными знаком ±. Справедливость любого из этих двух решений может можно проверить алгебраически, подставив любое выражение в уравнении (2) в уравнение (1).

    Формула квадратного корня намекает на то, что может быть 0, 1 или 2 действительных решения общего квадратичного уравнения уравнение, потому что символ ± предполагает, что есть два возможных вычисления, чтобы найти 𝑥. Если выражение внутри квадратного корня положительное, то проблем с поиском решения нет. Однако, если выражение внутри квадратного корня отрицательно, то мы будем пытаться извлечь квадратный корень из отрицательного числа, для которые не имеют решений в действительных числах. Наконец, если выражение внутри корневого символа равно нулю, то оба вычисления будут равны, поэтому у нас будет только один корень. Следовательно, число действительных решений определяется знаком выражение 𝑏−4𝑎𝑐, известное как дискриминант.

    Определение: Дискриминант квадратного уравнения

    Рассмотрим квадратное уравнение 𝑎𝑥+𝑏𝑥+𝑐=0, где 𝑎, 𝑏 и 𝑐 — действительные числа, а 𝑎≠0. Затем «дискриминант» квадратичного обозначается Δ=𝑏−4𝑎𝑐.

    Если Δ положительно, то у квадратного уравнения есть два действительных решения. Если Δ=0, то существует одно (повторяющееся) действительное решение. А если Δ отрицательно, то реальных решений нет.

    Сделав это определение, мы можем увидеть, как можно записать формулу квадратного корня через дискриминант в виде 𝑥=−𝑏±√Δ2𝑎, что дополнительно проясняет связь с числом решений квадратичного уравнения. Мы продемонстрируем эту идею на примере, рассматривая квадратное уравнение 4𝑥−1+4𝑥=0. Было бы полезно думать вместо этого с точки зрения функция 𝑓(𝑥)=4𝑥+4𝑥−1, а затем спросите значения 𝑥, которые дают 𝑓(𝑥)=0. Другими словами, мы тогда пытаясь найти корни функции 𝑓(𝑥). Начнем с построения графика функции, как показано ниже, это показывает, что есть два корня, один из которых отрицательный, а другой положительный.

    Теперь мы подтвердим это, обратившись к нашему определению дискриминанта. Чтобы решить уравнение 4𝑥−1+4𝑥=0, сначала следует отметить, что это квадратное уравнение относительно 𝑥 с коэффициентами 𝑎=4, 𝑏=4 и 𝑐=−1. Тогда дискриминант вычисляется как ∆=𝑏−4𝑎𝑐=4−4×4×(−1)=32.

    Следовательно, имеем ∆>0, что, согласно приведенному выше определению, означает наличие двух действительных решения. На это также указывает график, который мы построили выше. Затем мы можем использовать квадратное выражение, чтобы напрямую вычислить эти значения. корни следующим образом: 𝑥=−𝑏±√Δ2𝑎=−4±√322×4=−1±√22.

    Мы можем проверить, что эти два реальных решения численно соответствуют решениям, показанным на графике выше.

    Давайте рассмотрим другой пример, на этот раз для квадратичного 4𝑥+1+4𝑥=0, что означает, что мы установили 𝑔(𝑥)=4𝑥+4𝑥+1, которая является квадратичной функцией, где 𝑎=4, 𝑏=4 и 𝑐=1. По сравнению с функция 𝑓(𝑥), функция 𝑔(𝑥) будет иметь ровно та же фигура после переноса на две единицы в положительном вертикальном направлении. График этой функции выглядит следующим образом:

    кажется так, как будто существует только одно действительное решение этого уравнения при 𝑥=−12, которое, как мы покажем, равно точно так же, как с использованием дискриминанта. Рассчитываем дискриминант следующим образом: Δ=𝑏−4𝑎𝑐=4−4×4×1=0. 

    Тот факт, что Δ=0 означает, что существует один действительный (повторяющийся) корень, как видно из графика нанесено выше. Затем по квадратичной формуле вычисляются решения как 𝑥=−𝑏±√Δ2𝑎=−4±√02×4=−12.

    В этом случае член ± не имеет значения, поскольку добавление нуля равносильно вычитанию нуля. в отличие от В предыдущем сценарии нет необходимости выполнять дальнейшие вычисления, чтобы найти (повторяющийся) действительный корень.

    Последний пример, который мы приведем, будет для квадратного уравнения, у которого нет действительных решений. Мы возьмем предыдущий пример и немного изменить его, чтобы получить квадратное уравнение 3+4𝑥+4𝑥=0. Чтобы помочь в нашем процессе, мы определим функцию ℎ(𝑥)=4𝑥+4𝑥+3, которая является квадратичной функцией с 𝑎=4, 𝑏=4 и 𝑐=3. Этот график ℎ(𝑥) совпадает с графиком 𝑔(𝑥), переведенным на две единицы в положительном вертикальном направлении, результат которого показан ниже.

    Из этого графика видно, что действительных решений квадратного уравнения нет, что мы можем показать, вычислив дискриминант следующим образом: Δ=𝑏−4𝑎𝑐=4−4×4×3=−32.

    Это показывает, что Δ0, что означает отсутствие реальных решений, тем самым подтверждая наш прогноз после построения графика. Попытка использовать формулу квадратного корня даст следующую работу: 𝑥=−𝑏±√Δ2𝑎=−4±√−322×4.

    Эта работа показывает, что мы пытаемся вычислить квадратный корень из отрицательного числа, что не дает результата это реальное число. Это означает, что не существует реальных решений исходного квадратного уравнения, как это предсказывает формула значение дискриминанта. В этой ситуации для понимания решений потребуется понимание воображаемых и комплексные числа, которые выходят за рамки этого объяснения.

    Теперь давайте посмотрим на несколько примеров того, как дискриминант используется для определения числа действительных корней квадратного уравнения. уравнение.

    Пример 1. Использование знака дискриминанта для определения числа комплексных корней квадратного уравнения

    Сколько невещественных корней будет иметь квадратное уравнение, если его дискриминант отрицателен?

    Ответ

    Напомним, что если мы имеем квадратное уравнение 𝑎𝑥+𝑏𝑥+𝑐=0, где 𝑎, 𝑏, и 𝑐 — действительные числа и 𝑎≠0, то мы знаем, что формула квадратного корня 𝑥=−𝑏±√𝑏−4𝑎𝑐2𝑎, что дает нам корни квадратного. Дискриминант определяется как Δ=𝑏−4𝑎𝑐, что позволяет формула квадратного корня вместо этого должна быть записана как 𝑥=−𝑏±√Δ2𝑎.

    Если дискриминант отрицательный, то мы попытаемся вычислить квадратный корень из отрицательного числа, которое имеет нет решений в действительных числах. Это означает, что у данного квадратного уравнения нет действительных решений, т.е. означает, что должно быть два невещественных корня.

    Пример 2. Использование знака дискриминанта для определения числа комплексных корней квадратного уравнения

    Какое условие является правильным для квадратного уравнения 𝑎𝑥+𝑏𝑥+𝑐=0 с вещественными коэффициентами не иметь невещественных корней?

    1. Дискриминант 𝑏−4𝑎𝑐 положителен.
    2. Дискриминант 𝑏−4𝑎𝑐 равен нулю.
    3. Дискриминант 𝑏−4𝑎𝑐 отрицателен.
    4. Дискриминант 𝑏−4𝑎𝑐 неотрицательный.
    5. Дискриминант 𝑏−4𝑎𝑐 является целым числом.

    Ответ

    При работе с квадратным числом мы помним, что знак дискриминанта говорит нам о количестве действительных корней. Существует три возможных количества действительных корней:

    • Два действительных корня, когда Δ=𝑏−4𝑎𝑐>0
    • Один действительный (повторяющийся) корень, когда Δ=𝑏−4𝑎𝑐=0
    • Нет действительных корней, когда Δ=𝑏−4𝑎𝑐0

    Нам говорят, что мы ищем, чтобы не было недействительных корней задан квадратичный. Это означает, что должны быть по крайней мере одно действительное решение квадратного уравнения, максимум два. Чтобы было одно реальное решение, мы требуем, чтобы дискриминант был равен нулю, а для того, чтобы было два действительных решения, мы требуем, чтобы дискриминант положителен. Для выполнения любого из этих условий требуется, чтобы дискриминант был больше больше или равно нулю. Это соответствует варианту D из приведенного выше списка, означающему, что дискриминант должен быть неотрицательным.

    Два приведенных выше примера демонстрируют, как можно классифицировать количество корней, просто используя дискриминант. При попытке найти точные корни квадратного уравнения, поэтому полезным упреждающим шагом является вычисление дискриминанта, а затем используйте это, чтобы понять количество корней, прежде чем мы их вычислим. Например, если дискриминант квадратичного отрицательно, то действительных корней нет и, следовательно, нет необходимости использовать квадратную формулу для их нахождения. мы дадим пример этого в следующем вопросе.

    Пример 3. Нахождение дискриминанта квадратного уравнения и его использование для определения числа действительных корней

    1. Найдите дискриминант квадратного уравнения 2𝑥+3𝑥+4=0.
    2. Сколько действительных корней имеет уравнение 2𝑥+3𝑥+4=0?
    3. Следовательно, решите, сколько раз график 𝑦=2𝑥+3𝑥+4 пересечет ось 𝑥.

    Ответ

    Часть 1

    Начнем с того, что приведенное выше квадратное уравнение можно классифицировать обычным способом, записав коэффициенты как 𝑎=2, 𝑏=3 и 𝑐=4. Напомним, что дискриминант квадратичного уравнения равен Δ=𝑏−4𝑎𝑐, которое мы можем вычислить для этого квадратичного уравнения следующим образом: Δ=𝑏−4𝑎𝑐=3−4×2×4=−23,

    Часть 2

    Напомним, что знак дискриминанта квадратного числа говорит нам о количестве действительных корней, которое имеет квадратное число. В частности, если его знак отрицательный, то действительных корней нет. Учитывая, что ∆0, это означает, что у данного квадратного уравнения нет действительных корней, поэтому ответ равен нулю действительных корней.

    Часть 3

    Функция имеет корень, когда график этой функции пересекает ось 𝑥. Учитывая, что эта функция имеет нет действительных корней, это означает, что график функции не пересекает ось 𝑥. Это может быть подтверждено графически с использованием приведенного ниже графика функции 𝑓(𝑥)=2𝑥+3𝑥+4.

    Мы видим, что график функции никогда не пересечет ось 𝑥, как и предсказывалось.

    Мы уже видели, что формула квадратного корня может быть выражена через дискриминант как 𝑥=−𝑏±√Δ2𝑎.

    Прежде чем вычислять корни квадратного числа, нам нужно будет вычислить квадратный корень из дискриминанта Δ. Это означает, что если Δ является квадратным числом, то квадратный корень вернет целое число. При условии, что 𝑎 и 𝑏 оба рациональны, в этом конкретном случае значения 𝑥, следовательно, будет рациональным. Однако, как правило, Δ не является квадратное число, что означает, что квадратный корень этого значения будет иррациональным числом. Когда это так, будет подразумевают, что значения 𝑥 будут иррациональными, поскольку они будут комбинацией иррационального числа и два рациональных числа с помощью сложения и деления. Заметим, что это свойство имеет место только в предположении, что 𝑎 и 𝑏 оба рациональны. Если они оба не рациональны, то нам нужно будет рассмотреть вопрос несколько более деликатный, как мы увидим в следующем примере.

    Пример 4. Определение рациональности корней квадратного уравнения с помощью дискриминанта

    Определить, рациональны или нет корни уравнения 𝑥−√5𝑥−1=0, не решая его.

    Ответ

    Зададим коэффициенты этого квадратного уравнения стандартным образом, зафиксировав 𝑎=1, 𝑏=−√5 и 𝑐=−1. Напомним, что дискриминант квадратичного 𝑎𝑥+𝑏𝑥+𝑐=0 равен Δ=𝑏−4𝑎𝑐, и квадратичная формула говорит нам, что корни этого квадратного числа равны 𝑥=−𝑏±√Δ2𝑎.

    Затем мы можем вычислить дискриминант квадратичного уравнения следующим образом: Δ=𝑏−4𝑎𝑐=−√5−4×1×(−1)=5+4=9.

    Мы знаем, что, поскольку это число положительное, существует два действительных корня. Мы также можем видеть, что в квадратичной формуле 2𝑎 рационально, и √Δ=√9=3 также рационально. Однако −𝑏 иррационально; следовательно, корни будут иррациональными.

    В нашем следующем примере мы исследуем поведение квадратичных уравнений, рассматривая коэффициент 𝑐 быть параметром.

    Пример 5. Нахождение интервала, которому принадлежит переменная в квадратном уравнении, зная тип его корней содержит 𝑘.

    Ответ

    Начнем с того, что обработаем этот квадрат обычным образом. Обозначим параметры как 𝑎=4, 𝑏=−12, и 𝑐=𝑘. Напомним, что знак дискриминанта квадратичного числа 𝑎𝑥+𝑏𝑥+𝑐=0 дает нам количество корней квадратного. В этом вопросе нам нужны два различных действительных корня, что происходит, когда дискриминант положительный. Мы вычисляем дискриминант Δ следующим образом: Δ=𝑏−4𝑎𝑐=(−12)−4×4×𝑘=144−16𝑘=16(9−𝑘).

    Вопрос просил нас найти все возможные значения 𝑘, которые гарантируют, что корни квадратичного настоящие и разные. Другими словами, нас просят найти возможные значения 𝑘 такие, что два действительных корня, а это означает, что ∆>0.

    No related posts.