Сложение и вычитание целых чисел
В данном уроке мы изýчим сложение и вычитание целых чисел.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
−3, −2, −1, 0, 1, 2, 3
Положительные числа легко складываются и вычитаются, умножаются и делятся. К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа и где положительные.
Рассмотрим следующее простейшее выражение
1 + 3
Значение данного выражения равно 4
1 + 3 = 4
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что нужно двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 − 3
Значение данного выражения равно −2
1 − 3 = −2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 − 3 указывает нам, что нужно двигаться влево в сторону уменьшения чисел.
Вообще, если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения −2 + 4
Значение данного выражения равно 2
−2 + 4 = 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2
Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.
Пример 4. Найти значение выражения −1 − 3
Значение данного выражения равно −4
−1 − 3 = −4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.
Пример 5. Найти значение выражения −2 + 2
Значение данного выражения равно 0
−2 + 2 = 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Правила сложения и вычитания целых чисел
Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Можно воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
Пример 1. Найти значение выражения −2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками, потому что −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть ответ будет положительным:
−2 + 5 = 5 − 2 = 3
Обычно записывают покороче: −2 + 5 = 3
Пример 2. Найти значение выражения 3 + (−2)
Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3 + −2.
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:
3 + (−2) = |3| − |−2| = 3 − 2 = 1
Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа, модуль которого больше.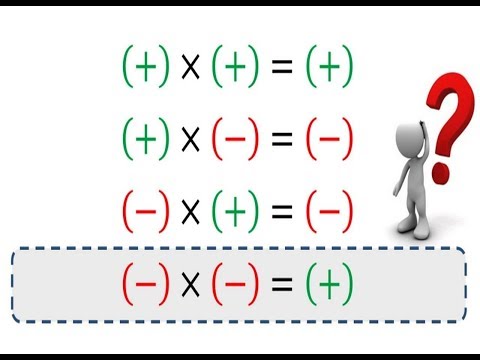 У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
Обычно записывают покороче 3 + (−2) = 1
Пример 3. Найти значение выражения 3 − 7
В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.
3 − 7 = 7 − 3 = −4
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4
Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.
Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 − 7 = − (7 − 3) = − (4) = −4
В этом случае равенство будет соблюдаться на каждом этапе:
После того, как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 − 7 = − (7 − 3) = − (4) = − 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a − b = − (b − a)
Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак, знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:
5 − 3 = 2
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
На примере выражения 5 − 3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того, чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число −3. Записываем новое выражение:
5 + (−3)
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:
5 + (−3) = |5| − |−3| = 5 − 3 = 2
Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.
Это связано с тем, что положительные числа записываются без знака плюс.
Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.
А стало быть, для наглядности данное выражение можно записать следующим образом:
(+3) − (+1)
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.
В выражении (+3) − (+1) вычитаемое это число (+1), а противоположное ему число это (−1).
Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)
(+3) − (+1) = (+3) + (−1)
Дальнейшее вычисление не составит особого труда.
(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.
У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:
(+3) − (+7)
Заменим вычитание сложением:
(+3) − (+7) = (+3) + (−7)
Дальнейшее вычисление не составляет труда:
(+3) − (−7) = (+3) + (-7) = −(|−7| − |+3|) = −(7 − 3) = −(4) = −4
Пример 7. Найти значение выражения −4 − 5
Приведём выражение к понятному виду:
(−4) − (+5)
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).
(−4) − (+5) = (−4) + (−5)
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:
Для таких случаев применяется следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:
(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9
Решение для данного примера можно записать покороче:
−4 − 5 = −(4 + 5) = −9
или ещё короче:
−4 − 5 = −9
Пример 8. Найти значение выражения −3 − 5 − 7 − 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:
(−3) − (+5) − (+7) − (+9)
Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9)
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9) =
= −( |−3| + |−5| + |−7| + |−9| ) = −(3 + 5 + 7 + 9) = −(24) = −24
Решение данного примера можно записать покороче:
−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24
или ещё короче:
−3 − 5 − 7 − 9 = −24
Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7
Приведём выражение к понятному виду:
(−10) + (+6) − (+15) + (+11) − (+7)
Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:
(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)
Соблюдая порядок действий, выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:
(−10) + (+6) = − (10 − 6) = − (4) = − 4
Второе действие:
(−4) + (−15) = − (4 + 15) = − (19) = − 19
Третье действие:
(−19) + (+11) = − (19 − 11) = − (8) = −8
Четвёртое действие:
(−8) + (−7) = − (8 + 7) = − (15) = − 15
Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15
Примечание. Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.
Вычесть одно число из другого означает, прибавить к уменьшаемому такое число, которое противоположно вычитаемому.
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
−50 + 40
Решение
−50 + 40 = −10
Показать решение
Задание 2. Найдите значение выражения:
Найдите значение выражения:
25 + (−5)
Решение
25 + (−5) = 20
Показать решение
Задание 3. Найдите значение выражения:
−20 + 60
Решение
−20 + 60 = 40
Показать решение
Задание 4. Найдите значение выражения:
20 + (−8)
Решение
20 + (−8) = 12
Показать решение
Задание 5. Найдите значение выражения:
30 + (−50)
Решение
30 + (−50) = −20
Показать решение
Задание 6. Найдите значение выражения:
27 + (−19)
Решение
27 + (−19) = 8
Показать решение
Задание 7. Найдите значение выражения:
−17 + (−12) + (−8)
Решение
Показать решение
Задание 8. Найдите значение выражения:
−6 − 4
Решение
−6 − 4 = −6 + (−4) = −10
Показать решение
Задание 9. Найдите значение выражения:
−6 − (−4)
Решение
−6 − (−4) = −6 + 4 = −2
Показать решение
Задание 10. Найдите значение выражения:
−15 − (−15)
Решение
−15 − (−15) = −15 + 15 = 0
Показать решение
Задание 11. Найдите значение выражения:
Найдите значение выражения:
−11 − (−14)
Решение
−11 − (−14) = −11 + 14 = 3
Показать решение
Задание 12. Найдите значение выражения:
−3 + 2 − (−1)
Решение
Показать решение
Задание 13. Найдите значение выражения:
−5 − 6 − 3
Решение
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже Опубликовано Автор
Математика 6 класс темы уроков
Готовимся к школе
В математике 6 класса темы уроков посвящают характерным чертам делимости, делению, умножению, вычитанию и сложению рациональных и натуральных чисел и дробей с различными знаменателями. Изучают положительные и отрицательные числа, а также операции с ними. Заканчивают исследованием координат на плоскости. Кроме того, посвящают время на изучение круга и шара. 6 класс – последний год для математики, поэтому он является подготовкой к алгебре и геометрии.
Заканчивают исследованием координат на плоскости. Кроме того, посвящают время на изучение круга и шара. 6 класс – последний год для математики, поэтому он является подготовкой к алгебре и геометрии.
Делимость чисел
В первую очередь проходят признаки делимости, делители и кратные. Эти знания помогут при решении последующих сложных задач. Можно выделить такие этапы изучения материала:
- Делители, множители и кратные
- Нечётные и чётные числа
- Простые и составные числа.
- Разложение на простые множители и отличия различных способов
- Главная теорема арифметики. Деление на 0 и 10, деление нуля
- Характерные черты делимости на 10, на 5 и на 2
- Характерные черты делимости на 9 и на 3
- Использование нескольких признаков делимости
- Наибольший общий делитель
- Наименьшее общее кратное
Вычитание и сложение дробей с отличающимися знаменателями
Данный раздел поможет вспомнить дроби, а также правила их применения. В темы уроков по математике за 6 класс обязательно включены следующие курсы:
В темы уроков по математике за 6 класс обязательно включены следующие курсы:
- Главное качество дроби. Формулировка и примеры
- Сокращение дробей. Характерные черты сократимости и несократимости
- Сведение дробей к одному знаменателю
- Дополнительный множитель
- Наименьший общий знаменатель
- Сопоставление дробей с отличающимися знаменателями
- Вычитание и сложение дробей с отличающимися знаменателями. Сопоставление дробей
- Вычитание и сложение смешанных чисел
Деление и умножение обыкновенных дробей
Это довольно трудная тема, так что нужно уделить ей особое внимание. Проходят деление и умножение обыкновенных дробей:
- Умножение простых дробей и смешанных чисел
- Произведение дроби на дробь
- Нахождение числа по его дроби
- Распределительная теория её использование при операциях со смешанными дробями
- Обоюдно противоположные числа и методы их поиска
- Деление дробей, натуральных и смешанных чисел
- Три способа поиска числа по его дроби
- Дробные выражения и методы их упрощения
Отношения и пропорции
Эти понятия помогут составить базовые представления о реальном мире, дадут навыки для изучения окружающих предметов.
- Отношения. Поиск корреляции двух чисел без точного значения величин
- Пропорции и математические действия с ними
- Корреляции между размерами и их виды
- Прямые и обратные пропорциональные зависимости
- Изменение площадей и объёмов
- Масштаб, его виды и применение
- Шар и сфера, их математические особенности
- Длина окружности. Площадь круга
Положительные и отрицательные числа
Это один из фундаментальных разделов, который необходим для последующего изучения науки. В математике 6 класса в темы уроков входит исследование положительных и отрицательных чисел:
- Координаты на прямой и плоскости
- Определение позиции точки
- Отрицательные числа. Противоположные числа. Ноль. Знак минус
- Модуль числа и его определение. Модуль переменной величины
- Сопоставление чисел и их порядок
- Изменение величин
Сложение и вычитание положительных и отрицательных чисел
Сначала рассматривают сложение и вычитание положительных и отрицательных чисел:
- Сложение чисел с помощью координатной прямой
- Сложение отрицательных чисел
- Сложение чисел с противоположными знаками
- Вычитание двух отрицательных чисел
Умножение и деление положительных и отрицательных чисел
Позже изучается умножение и деление положительных и отрицательных чисел:
- Умножение положительных и отрицательных чисел
- Умножение чисел с противоположными знаками
- Деление чисел с противоположными знаками
- Рациональные числа.
 Замкнутость их множеств в арифметических операциях
Замкнутость их множеств в арифметических операциях - Изменение периодической дроби
- Характеристика операций с рациональными числами
Решение уравнений
Наиболее важным результатом является умение применять полученные знания на практике, использовать формулы из разных разделов математики. В этом классе много времени уделяется решению уравнений:
- Устранение скобок с плюсом и минусом перед ними
- Коэффициент. Определение и задачи
- Приведение подобных слагаемых и упрощение выражений
Координаты на плоскости
Данный раздел научит проводить классификацию, сформирует понимание о статистике и некоторых закономерностях окружающего мира, а также даст математические инструменты наглядности. В темы уроков по математике за 6 класс входит изучение:
- Параллельных и перпендикулярных прямых, их особенности и вопросы, связанные с ними
- Координатной плоскости, главных определений, координат точки
- Столбчатых и круговых диаграмм
- Графиков, правил построения и применения
Заключение
На этом этапе вы получите многие практические навыки и знания для будущей работы по специальности. Кроме того, многие уроки направлены на развитие логического аппарата и критического мышления. Вы научитесь создавать математические алгоритмы и находить различные пути решения задач. На данном этапе математика даёт знания, необходимые для изучения других школьных предметов.
Кроме того, многие уроки направлены на развитие логического аппарата и критического мышления. Вы научитесь создавать математические алгоритмы и находить различные пути решения задач. На данном этапе математика даёт знания, необходимые для изучения других школьных предметов.
Уравнения и примеры с отрицательными числами и модул…
Все рациональные числа, которые мы можем себе представить, можно разделить на положительные и отрицательные. Изучается данная тема в 5-6 классах. Начиная с этих классов, учащиеся решают примеры, уравнения и задачи, в которых могут быть как положительные, так и отрицательные числа.
Решение примеров с отрицательными числами без ошибок — очень важный математический навык. То же самое касается и решения уравнений с отрицательными числами. В этом контексте в школьном курсе рассматривается и понятие модуля числа.
Давайте сегодня разберем эти вопросы.
Чтобы отличить положительное число от отрицательного, перед отрицательным числом ставят знак минус.
Например:
«5» – положительное число
«-5» — отрицательное число Если рассматривать числа на координатной прямой, то все числа, находящиеся слева от нуля, будут называться отрицательными, а числа, находящиеся справа от нуля – будут, соответственно, положительными.
Правила сложения, вычитания, умножения и деления отрицательных чисел имеют свои особенности.
Например, если нам необходимо выполнить действие:
«7 + 5»
Т.е. сложить два положительных числа, мы механически складываем их величины и получаем результат:
7 + 5 = 12
Если даже у нас будет длинный и трудоемкий пример, принцип его решения будет точно такой же, если числа положительные, то мы механически складываем их:
7 + 5 + 21 + 17 + 19 + 25 = 94
Операция вычитания может быть уже не такой простой.
Если выражение:
7 – 5 = 2
Мы вычисляем легко, то выражение:
5 – 7 = — 2
Это уже серьезная проверка наших знаний в области отрицательных чисел. Здесь важно в ответе правильно поставить знаки «плюс» и «минус».
Здесь перед числом «7» стоит знак «минус». Получается из меньшего числа «5» нужно вычесть большее число «7».
Как не запутаться?
Есть несколько способов. Один из которых вот какой:
Необходимо вспомнить понятие модуля числа.
Модуль числа – это число, записанное в вертикальных скобках:
|5| или |-7|
Когда мы выводим число из модуля, мы оставляем только его значение, а минус убираем:
|5| = 5
|-7| = 7
Записываем наше выражение для модулей этих чисел:
|5| – |7|
Такая запись позволяет нам определить, какое число большее «по модулю», т.е. по своему абсолютному значению, без учета знака «минус» перед числом и стоит правее на числовой оси.
В нашем случае, это число «7».
Поэтому мы из большего «по модулю» числа вычитаем меньшее «по модулю» число и в ответе ставим тот знак (плюс или минус), который стоял в выражении перед большим «по модулю» числом:
|5| – |7| = — |7 — 5| = — |2| = -2
Второй способ вот какой:
Запишем:
5 + (– 7)
Представим каждое слагаемое как выражение двух чисел, с умножением на «-1», получим:
5 = — 1 · (- 5)
— 7 = — 1 · 7
Теперь сложим эти выражения, как в нашем примере, получим:
5 + (– 7) = (- 1 · (- 5)) + (- 1 · 7)
Вынесем за скобки «-1»:
-1·(- 5 + 7) = -1·(7 – 5) = -1· 2 = — 2
Когда мы выносим за скобку «-1», мы получаем возможность вычитать из большего числа меньшее, что гораздо удобнее.
Теперь мы знаем, как решать примеры с отрицательными числами.
Умножение на «-1» помогает нам вспомнить правила умножения и деления, в выражениях с положительными и отрицательными числами. Вот эти правила:
«Если умножать «минус» на «плюс», то получается в ответе «минус».»
«А если умножать «минус» на «минус», то получается в ответе «плюс».»
Проиллюстрируем все возможные варианты применения этих правил:
5 · 7 = 35
5 · (– 7) = — 35
(- 5) · 7 = — 35
(- 5) · (– 7) = 35
Возьмем более сложный случай, вычислим:
7 · (- 5) · 21 · (- 17)
Чтобы было проще, выполним вычисления по действиям:
1) 7 · (- 5) = — 35
2) 21 · (- 17) = — 357
3) (- 35) · (-357) = 12495
Таким образом:
7· (- 5) · 21 · (- 17) = 12495
Теперь рассмотрим, как решать уравнения с отрицательными числами и переменными.
Возьмем пример с уравнением:
3 + 4(5 – х) = 15
Сначала раскроем скобки:
3 + 4 · 5 + 4 · (- х) = 15
Обязательно обращаем внимание на минусы, стоящие перед числами и переменной «х», помним о приведенном выше правиле, получаем:
3 + 20 – 4х = 15
Приведем подобные (3 + 20 = 23) и запишем:
23 – 4х = 15
Переносим слагаемое без переменной «х» из левой части в правую, меняя при этом перед ним знак на противоположный
— 4х = 15 – 23
После приведения подобных в правой части уравнения (15 – 23 = — 8), получим:
— 4х = — 8
Деление отрицательных чисел проводим по тем же правилам, что и умножение:
х = — 8 : (- 4)
«Минус» делим на «минус», получаем «плюс»:
х = 2
Давайте теперь разберем примеры с модулем числа.

Напомню, что, когда мы выводим число из модуля, мы оставляем только его значение, а минус убираем.
Например:
|5| + |-7| = 5 + 7 = 12
|5| — |-7| = 5 — 7 = — 2
|5| · |-7| = 5 · 7 = 35
|-35| : |-7| = 35 : 7 = 5
Как видите, в примерах, где числа стоят под знаком модуля, необходимо следовать правилу:
«Сначала раскрываем скобки модуля, а потом проводим операции сложения, вычитания, умножения или деления».
Конечно, существуют и более сложные примеры с отрицательными числами и модулями. Чтобы познакомиться с правилами их решения, а также вспомнить все, что необходимо, связанное с модулями — следите за нашими уроками или обратитесь к репетитору на нашем сайте.
Примеры по математике 2 класс
Математика 2 класс
- Нестандартные задачи
- Математические диктанты
- Примеры
- Логические примеры
- Тесты
- Диагностические работы
Задачи для 2 класса
- Операции
- Обратные операции
- Прямая, луч, отрезок
- Сложение и вычитание двузначных чисел
- Сотня.
 Счет сотнями.
Счет сотнями. - Метр
Контрольные работы
- Контрольная работа 1
- Контрольная работа 2
- 1 четверть
- 2 четверть
- Итоговая контрольная работа
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Итоговая контрольная работа
Материал для 2 класса. Примеры. Сложение и вычитание чисел от 1 до 100.
| | Математика 2 класс ->> Примеры Первое полугодиеВторое полугодие |
| 61 — 47 = 14 | 16 + 35 = 41 | 77 + 13 = 90 | 56 — 48 = 8 | 89 — 74 = 15 | 64 — 36 = 28 |
| 51 — 24 = 27 | 88 + 6 = 94 | 40 — 22 = 18 | 98 — 79 = 18 | 45 + 19 = 64 | 30 — 17 = 13 |
| 65 — 28 = 37 | 11 — 7 = 4 | 14 + 77 = 91 | 86 + 7 = 93 | 21 — 16 = 5 | 80 — 42 = 38 |
| 16 + 84 = 100 | 43 + 38 = 81 | 62 — 19 = 43 | 30 — 4 = 26 | 38 + 67 = 105 | 27 + 45 = 72 |
| 57 — 19 = 38 | 7 + 19 = 26 | 62 — 48 = 14 | 36 + 67 = 103 | 14 — 6 = 8 | 62 — 14 = 48 |
| 59 + 42 = 101 | 48 + 37 = 85 | 67 + 14 = 81 | 9 + 37 = 46 | 13 + 67 = 80 | |
| 29 + 32 = 61 | 54 — 28 = 26 | 99 — 62 = 37 | 68 + 25 = 93 | 17 — 8 = 9 | 16 + 49 = 65 |
| 35 + 47 = 82 | 60 — 15 = 45 | 42 — 35 = 7 | 48 + 35 = 83 | 30 — 12 = 18 | 45 + 36 = 81 |
| 23 + 29 = 52 | 28 + 4 = 32 | 24 + 18 = 42 | 81 — 48 = 33 | 37 + 46 = 83 | 27 + 38 = 65 |
| 35 + 28 = 63 | 62 + 18 = 80 | 16 + 15 = 31 | 52 + 38 = 90 | 3 + 78 = 81 | 70 — 32 = 38 |
| 48 — 39 = 9 | 27 + 48 = 75 | 8 + 88 = 96 | 18 + 18 = 36 | 83 — 27 = 56 | 65 — 18 = 47 |
| 19 + 14 = 33 | 15 + 18 = 33 | 31 — 5 = 26 | 99 — 43 = 56 | 13 — 7 = 6 | 52 — 19 = 33 |
| 86 + 7 = 93 | 90 — 24 = 66 | 33 — 28 = 5 | 25 + 16 = 41 | 5 + 67 = 73 | 61 — 60 = 1 |
| 350 — 1 = 349 | 41 — 25 = 16 | 92 — 69 = 23 | 32 + 25 = 57 | 61 + 19 = 80 | 73 — 48 = 25 |
| 32 — 25 = 7 | 800 — 70 = 730 | 19 + 65 = 84 | 53 + 38 = 92 | 93 — 47 = 46 | 19 + 34 = 53 |
| 18 + 73 = 91 | 81 + 19 = 100 | 42 + 29 = 71 | 79 + 34 = 113 | 94 — 76 = 18 | 84 — 73 = 11 |
| 26 + 47 = 73 | 37 + 18 = 53 | 46 + 36 = 82 | 90 — 45 = 45 | 46 + 48 = 94 | 79 — 7 = 72 |
| 94 — 64 = 30 | 38 + 26 = 64 | 6 + 65 = 71 | 15 + 15 = 30 | 9 + 4 = 13 | 56 + 41 = 97 |
| 56 — 29 = 85 | 75 — 6 = 69 | 32 — 17 = 15 | 74 + 16 = 90 | 11 — 7 = 4 | 12 + 68 = 80 |
| 50 — 47 = 3 | 17 + 49 = 66 | 94 — 58 = 36 | 36 + 49 = 85 | 15 + 46 = 61 | 97 — 94 = 3 |
| 52 — 17 = 35 | 29 + 41 = 70 | 44 + 37 = 81 | 9 + 15 = 24 | 44 — 17 = 27 | 18 + 47 = 65 |
| 90 — 16 = 74 | 74 + 8 = 82 | 39 + 54 = 93 | 84 — 29 = 55 | 4 + 68 = 72 | 18 + 58 = 76 |
| 27 + 47 = 74 | 60 — 13 = 47 | 31 + 29 = 60 | 58 + 46 = 104 | 72 — 35 = 37 | 66 — 27 = 39 |
| 25 + 37 = 62 | 73 — 18 = 55 | 430 + 60 = 490 | 25 — 17 = 8 | 52 — 48 = 4 | 81 — 26 = 55 |
| 94 — 65 = 29 | 350 — 1 = 349 | 17 — 8 = 9 | 699 + 1 = 700 | 18 — 9 = 9 | 98 — 27 = 71 |
| 63 — 28 = 35 | 14 + 7 = 21 | 70 — 30 = 40 | 350 — 1 = 349 | 32 + 28 = 60 | 14 + 46 = 60 |
| 56 + 8 = 64 | 31 — 15 = 16 | 56 — 49 = 7 | 16 — 8 = 8 | 800 — 70 = 730 | 35 + 35 = 70 |
| 64 + 18 = 82 | 39 + 45 = 84 | 25 — 19 = 6 | 46 + 51 = 97 | 62 — 45 = 17 | 17 + 17 = 34 |
| 40 — 38 = 2 | 39 + 9 = 30 | 38 + 39 = 77 | 96 — 68 = 28 | 9 + 87 = 96 | 31 — 25 = 6 |
| 31 — 14 = 17 | 29 — 19 = 10 | 32 + 59 = 91 | 48 + 37 = 85 | 65 + 27 = 92 | 34 + 67 = 101 |
| _______________ | _______________ | _______________ | _______________ | _______________ | _______________ |
Примеры:
| 34 + 46 | 46 + 29 | 66 + 13 | 39 + 26 | 11 + 38 | 38 + 56 | 50 + 34 | 35 + 64 | 82 + 16 | 15 + 53 | 21 + 52 | 57 + 33 |
| 69 — 24 | 58 — 11 | 21 — 5 | 25 — 24 | 98 — 46 | 81 — 49 | 39 — 21 | 94 — 85 | 18 — 13 | 32 — 18 | 59 — 41 | 19 — 14 |
| 2 + 6 | 3 + 9 | 4 + 2 | 5 + 7 | 3 + 2 | 5 + 8 | 1 + 9 | 8 + 3 | 4 + 4 | 2 + 7 | 9 + 4 | 8 + 7 |
| 4 — 1 | 8 — 5 | 9 — 7 | 6 — 2 | 3 — 1 | 7 — 5 | 8 — 3 | 6 — 4 | 9 — 2 | 5 — 3 | 2 — 1 | 7 — 3 |
| 78 + 21 | 69 + 23 | 45 + 61 | 43 + 11 | 91 + 8 | 53 + 32 | 81 + 16 | 47 + 34 | 73 + 12 | 39 + 31 | 90 + 3 | 22 + 39 |
| 12 — 11 | 47 — 32 | 17 — 8 | 49 — 26 | 58 — 15 | 71 — 39 | 22 — 18 | 93 — 67 | 39 — 27 | 18 — 3 | 69 — 51 | 52 — 51 |
Решение:
34 + 46 = 80 46 + 29 = 75 66 + 13 = 79 39 + 26 = 65 11 + 38 = 49 38 + 56 = 94 50 + 34 = 84 35 + 64 = 99 82 + 16 = 98 15 + 53 = 68 21 + 52 = 73 57 + 33 = 90 69 — 24 = 45 58 — 11 = 47 21 — 5 = 16 25 — 24 = 1 98 — 46 = 52 81 — 49 = 32 39 — 21 = 8 94 — 85 = 9 18 — 13 = 5 32 — 18 = 14 59 — 41 = 18 19 — 14 = 5 2 + 6 = 8 3 + 9 = 12 4 + 2 = 6 5 + 7 = 12 3 + 2 = 5 5 + 8 = 13 1 + 9 = 10 8 + 3 = 11 4 + 4 = 8 2 + 7 = 9 9 + 4 = 13 8 + 7 = 15 4 — 1 = 3 8 — 5 = 3 9 — 7 = 2 6 — 2 = 4 3 — 1 = 2 7 — 5 = 2 8 — 3 = 5 6 — 4 = 2 9 — 2 = 7 5 — 3 = 2 2 — 1 = 1 7 — 3 = 4 78 + 21 = 99 69 + 23 = 92 45 + 51 = 96 43 + 11 = 54 91 + 8 = 99 53 + 32 = 85 81 + 16 = 97 47 + 34 = 81 73 + 12 = 85 39 + 31 = 70 90 + 3 = 93 22 + 39 = 61 12 — 11 = 1 47 — 32 = 15 17 — 8 = 11 49 — 26 = 23 58 — 15 = 43 71 — 39 = 32 22 — 18 = 4 93 — 67 = 26 39 — 27 = 12 18 — 3 = 15 69 — 51 = 18 52 — 51 = 1
Составные задачи
- Задачи на нахождение слагаемого и вычитаемого
- Задачи на нахождение третьего слагаемого
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на нахождение суммы
Простые задачи
- Простые задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Порядок выполнения действий, правила, примеры.
 Порядок выполнения математических действий Примеры в 2 действия без скобок
Порядок выполнения математических действий Примеры в 2 действия без скобокМы рассмотрим в этой статье три варианта примеров:
1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий
1 Примеры со скобками (действия сложения и вычитания)
Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:
Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.
*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:
В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
А теперь — тренажеры!
1) Примеры со скобками в пределах до 20. Онлайн тренажер.
2) Примеры со скобками в пределах до 100. Онлайн тренажер.
3) Примеры со скобками. Тренажер №2
4) Вставь пропущенное число — примеры со скобками. Тренажер
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Эти знаки и будут делить наш пример на блоки:
Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.
А теперь закрепляем решение примеров на порядок действий на тренажерах!
Если у вас не открываются игры или тренажёры, читайте .
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления — это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18:2-2*3+12:3=9-6+4=3+4=7
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30+6*(13-9)=30+6*4=30+24=54
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11 — 5) + 47=
7 * 3 — (16 + 4)=
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18:(11-5)+47=18:6+47=3+47=50
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Festival.1september.ru ().
- Sosnovoborsk-soobchestva.ru ().
- Openclass.ru ().
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Сегодня мы поговорим о порядке выполнения математических действий . Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.
Итак, вспомним о том, что сначала вычисляются выражения в скобках
38 – (10 + 6) = 22 ;
1) в скобках: 10 + 6 = 16 ;
2) вычитание: 38 – 16 = 22 .
Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.
10 ÷ 2 × 4 = 20 ;
Порядок выполнения действий :
1) слева направо, сначала деление: 10 ÷ 2 = 5 ;
2) умножение: 5 × 4 = 20 ;
10 + 4 – 3 = 11
, т. е.:
е.:
1) 10 + 4 = 14 ;
2) 14 – 3 = 11 .
Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.
18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7
Порядок выполнения действий:
1) 18 ÷ 2 = 9 ;
2) 2 × 3 = 6 ;
3) 12 ÷ 3 = 4 ;
4) 9 – 6 = 3 ; т.е. слева направо – результат первого действия минус результат второго;
5) 3 + 4 = 7 ; т.е. результат четвертого действия плюс результат третьего;
Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.
30 + 6 × (13 – 9) = 54 , т.е.:
1) выражение в скобках: 13 – 9 = 4 ;
2) умножение: 6 × 4 = 24 ;
3) сложение: 30 + 24 = 54 ;
Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:
После этого приступать к вычислениям в следующем порядке:
1) действия, заключенные в скобках;
2) умножение и деление;
3) сложение и вычитание.
Если вы хотите получать анонсы наших статей подпишитесь на рассылку “ “.
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Определение 1
В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Пример 1
Условие: вычислите, сколько будет 7 − 3 + 6 .
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
Вот запись всего решения:
7 − 3 + 6 = 4 + 6 = 10
Ответ: 7 − 3 + 6 = 10 .
Пример 2
Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Пример 3
Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
Определение 2
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Определение 3
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Пример 4
Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:
7 − 2 · 3 = 7 − 6 = 1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Пример 5
Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .
Решение
У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .
Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Пример 6
Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .
(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13
Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Рекомендуем вам с ней ознакомиться.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6 .
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Ответ:
7−3+6=10 .
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3
.
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7
.
Ответ:
17−5·6:3−2+4:2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Определение.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3
. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1
. Переходим ко второму выражению в скобках 6−4
. Здесь лишь одно действие – вычитание, выполняем его 6−4=2
.
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Ответ:
5+(7−2·3)·(6−4):2=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3)
. Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5
. Подставив найденное значение, получаем 3+1+4·5
. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24
. Исходное значение, после подстановки этого значения, принимает вид 4+24
, и остается лишь закончить выполнение действий: 4+24=28
.
В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24
. Исходное значение, после подстановки этого значения, принимает вид 4+24
, и остается лишь закончить выполнение действий: 4+24=28
.
Ответ:
4+(3+1+4·(2+3))=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Действия с минусом и плюсом. Сложение чисел с разными знаками — Гипермаркет знаний
формирование знаний о правиле сложения чисел с разными знаками, умений применять его в простейших случаях;
развитие умений сравнивать, выявлять закономерности, обобщать;
воспитание ответственного отношения к учебному труду.
Оборудование: мультимедийный проектор, экран.
Тип урока: урок изучения нового материала.
ХОД УРОКА
1.Организационный момент.
Ровно встали,
Тихо сели.
Прозвенел сейчас звонок,
Начинаем наш урок.
Ребята! Сегодня к нам на урок пришли гости. Давай повернемся к ним и улыбнемся друг другу. Итак, мы начинаем наш урок.
Слайд 2 — Эпиграф урока: «Кто ничего не замечает, тот ничего не изучает.
Кто ничего не изучает, тот вечно хнычет и скучает.»
Роман Сеф (детский писатель)
Слад 3 — Предлагаю поиграть в игру «Наоборот». Правила игры : нужно разделить слова на две группы: выигрыш, ложь,тепло, отдал, правда, добро, проигрыш, взял, зло, холодно, положительное, отрицательное.
Противоречий в жизни много. С их помощью мы определяем окружающую действительность. Для нашего занятия мне необходимо последнее: положительное – отрицательное.
О чем мы говорим в математике, когда употребляем эти слова? (О числах. )
)
Великий Пифагор утверждал: «Числа правят миром». Я предлагаю поговорить о самых загадочных числах в науке – о числах с разными знаками. — Отрицательные числа появились в науке, как противоположность к положительным. Их путь в науку был труден, потому что даже многие ученые не поддерживали идей об их существовании.
Какие понятия и величины люди измеряют положительными и отрицательными числами? (заряды элементарных частиц, температуру, убытки, высоту и глубину и т.д.)
Слайд 4- Слова противоположные по значению – антонимы (таблица).
2.Постановка темы урока.
Слайд 5(работа с таблицей) – Какие числа изучали на предыдущих уроках?
– Какие задания, связанные с положительными и отрицательными числами вы умеете выполнять?
– Внимание на экран. (Слайд 5)
– Какие числа представлены в таблице?
– Назовите модули чисел, записанных по горизонтали.
– Укажите наибольшее число, укажите число с наибольшим модулем.
– Ответьте на те же вопросы для чисел, записанных по вертикали.
– Всегда ли наибольшее число и число с наибольшим модулем совпадают?
– Найдите сумму положительных чисел, сумму отрицательных чисел.
– Сформулируйте правило сложения положительных чисел и правило сложения отрицательных чисел.
– Какие числа осталось сложить?
– Умеете ли вы их складывать?
– Знаете ли вы правило сложения чисел с разными знаками?
– Сформулируйте тему урока.
– Какую цель вы перед собой поставите? .Подумайте, что мы будем делать сегодня? (Ответы детей). Сегодня мы продолжаем знакомиться с положительными и отрицательными числами. Тема нашего урока “Сложение чисел с разными знаками.” А наша цель: научиться без ошибок, складывать числа с разными знаками. Записали в тетрадь число и тему урока .
3.Работа по теме урока .
Слайд 6. – Применяя данные понятия, найдите результаты сложения чисел с разными знаками на экране.
– Какие числа являются результатом сложения положительных чисел, отрицательных чисел?
– Какие числа являются результатом сложения чисел с разными знаками?
– От чего зависит знак суммы чисел с разными знаками? (Слайд 5)
– От слагаемого с наибольшим модулем.
– Это как при перетягивании каната. Побеждает сильнейший.
Слайд 7 – Поиграем. Представьте, что вы перетягиваете канат.. Учитель. Соперники обычно встречаются на соревнованиях. И мы сегодня побываем с вами на нескольких турнирах. Первое, что нас ждет – это финал конкурса по перетягиванию каната. Встречаются Иван Минусов под номером -7 и Петр Плюсов под номером +5. Как вы думаете, кто победит? Почему? Итак, победил Иван Минусов, он действительно оказался сильнее соперника, и смог перетащить его на свою отрицательную сторону ровно на два шага.
Слайд 8.- . А теперь побываем на других соревнованиях. Перед вами финал состязания по стрельбе. Лучшими в этом виде оказались Минус Тройкин с тремя воздушными шарами и Плюс Четвериков, имеющий в запасе четыре воздушных шарика. А здесь ребята, как вы думаете, кто станет победителем?
Слайд 9 — Соревнования показали, что в них побеждает сильнейший. Так и при сложении чисел с разными знаками: -7 + 5 = -2 и -3 + 4 = +1. Ребята, как же складываются числа с разными знаками?Учащиеся предлагают свои варианты.
Ребята, как же складываются числа с разными знаками?Учащиеся предлагают свои варианты.
Учитель формулирует правило, приводит примеры.
10 + 12 = +(12 – 10) = +2
4 + 3,6 = -(4 – 3,6) = -0,4
Учащиеся в процессе демонстрации могут комментировать решение, появляющееся на слайде.
Слайд 10 — Учитель- поиграем ещё в одну игру «Морской бой». К нашему побережью приближается вражеский корабль, его необходимо подбить и потопить. Для этого у нас есть пушка. Но чтобы попасть в цель необходимо произвести точные расчеты. Какие вы сейчас увидите. Готовы? Тогда вперед! Прошу не отвлекаться, примеры меняются ровно через 3 сек. Все готовы?
Учащиеся по очереди выходят к доске и вычисляют примеры, появляющиеся на слайде. – Назовите этапы выполнения задания.
Слайд 11- Работа по учебнику: стр.180 п.33 , прочитать правило сложения чисел с разными знаками. Комментирует правило.
– В чём отличие правила, предложенного в учебнике, от составленного вами алгоритма? Рассмотреть примеры в учебнике с комментарием.
Слайд 12- Учитель-А теперь ребята давайте проведем эксперимент. Но не химический, а математический! Возьмем числа 6 и 8, знаки плюс и минус и все хорошенько перемешаем. Получим четыре примера-опыта. Проделайте их у себя в тетради.(двое учащихся решают на крыльях доски, затем ответы проверяются). Какие выводы можно сделать из этого эксперимента? (Роль знаков). Проведем ещё 2 эксперимента , но с вашими числами (выходят по1 человеку к доске). Придумаем друг другу числа и проверим результаты эксперимента (взаимопроверка).
Слайд 13 .- На экран выводится правило в стихотворной форме .
4.Закрепление темы урока.
Слайд 14 – Учитель- «Знаки всякие нужны, знаки всякие важны!» Сейчас, ребята, мы поделимся с вами на две команды. Мальчики будут в команде Деда Мороза, а девочки – Солнышка. Ваша задача, не вычисляя примеры, определить в каких из них получатся отрицательные ответы, а в каких — положительные и выписать в тетрадь буквы этих примеров. Мальчики соответственно – отрицательные, а девочки – положительные(выдаются карточки с приложения). Проводится самопроверка.
Мальчики соответственно – отрицательные, а девочки – положительные(выдаются карточки с приложения). Проводится самопроверка.
Молодцы! Чутьё на знаки у вас отличное. Это поможет вам выполнить следующее задание
Слайд 15 — Физкульминутка. -10, 0,15,18,-5,14,0,-8,-5 и т. д.(отрицательные числа- приседают, положительные числа- подтягиваются вверх, подпрыгивают)
Слайд 16 -Решить 9 примеров самостоятельно (задание на карточках в приложении). 1человек у доски. Сделать самопроверку. Ответы выводятся на экран, ошибки учащиеся исправляют в тетради. Поднимите руки, у кого верно. (Отметки выставляются только за хороший и отличный результат)
Слайд 17 -Правильно решать примеры нам помогают правила. Давайте их повторим На экране алгоритм сложения чисел с разными знаками.
5.Организация самостоятельной работы.
Слайд 18 -Ф ронтальная работа через игру «Отгадай слово» (задание на карточках в приложении) .
Слайд 19 — Должна получиться оценка за игру — «пятёрочка»
Слайд 20 -А теперь,внимание. Домашнее задание. Домашнее задание не должно вызвать у вас затруднений.
Домашнее задание. Домашнее задание не должно вызвать у вас затруднений.
Слайд 21 — Законы сложения в физических явлениях. Придумайте примеры на сложение чисел с разными знаками и задайте их друг другу. Что нового вы узнали? Достигли ли мы поставленной цели?
Слайд 22 — Вот и кончился урок,подведем сейчас итог. Рефлексия. Учитель комментирует и выставляет оценки за урок.
Слайд 23 — Спасибо за внимание!
Желаю вам, чтобы в вашей жизни было больше положительного и меньше отрицательного, Хочу сказать вам, ребята, спасибо за вашу активную работу. Я думаю, что вы легко сможете применить полученные знания на последующих уроках. Урок окончен. Всем большое спасибо. До свидания!
В этой статье мы детально разберемся с тем, как выполняется сложение целых чисел . Сначала сформируем общее представление о сложении целых чисел, и посмотрим, что представляет собой сложение целых чисел на координатной прямой. Эти знания помогут нам сформулировать правила сложения положительных, отрицательных, а также целых чисел с разными знаками. Здесь же мы подробно разберем применение правил сложения при решении примеров и научимся выполнять проверку полученных результатов. В заключение статьи мы поговорим о сложении трех и большего количества целых чисел.
Здесь же мы подробно разберем применение правил сложения при решении примеров и научимся выполнять проверку полученных результатов. В заключение статьи мы поговорим о сложении трех и большего количества целых чисел.
Навигация по странице.
Общее представление о сложении целых чисел
Приведем примеры сложения целых противоположных чисел. Сумма чисел −5 и 5 равна нулю, сумма 901+(−901) равна нулю, результатом сложения целых противоположных чисел 1 567 893 и −1 567 893 также является нуль.
Сложение произвольного целого числа и нуля
Давайте воспользуемся координатной прямой, чтобы понять, что представляет собой результат сложения двух целых чисел, одно из которых равно нулю.
Прибавление к нулю произвольного целого числа a
означает перемещение из начала отсчета на расстояние a
единичных отрезков. Таким образом, мы оказываемся в точке с координатой a
. Следовательно, результатом сложения нуля и произвольного целого числа является прибавляемое целое число.
С другой стороны, прибавление к произвольному целому числу нуля означает переместиться из точки, координату которой задает данное целое число, на расстояние нуль. Иными словами, мы останемся в исходной точке. Следовательно, результатом сложения произвольного целого числа и нуля является данное целое число.
Итак, сумма двух целых чисел, одно из которых есть нуль, равна другому целому числу . В частности, нуль плюс нуль есть нуль.
Приведем несколько примеров. Сумма целых чисел 78 и 0 равна 78 ; результат сложения нуля и −903 равен −903 ; также 0+0=0 .
Проверка результата сложения
После того, как выполнено сложение двух целых чисел, полезно проверить полученный результат. Нам уже известно, что для проверки результата сложения двух натуральных чисел нужно от полученной суммы отнять любое из слагаемых, при этом должно получиться другое слагаемое. Проверка результата сложения целых чисел выполняется аналогично. Но вычитание целых чисел сводится к прибавлению к уменьшаемому числа, противоположного вычитаемому. Таким образом, чтобы проверить результат сложения двух целых чисел, нужно к полученной сумме прибавить число, противоположное любому из слагаемых, при этом должно получиться другое слагаемое.
Таким образом, чтобы проверить результат сложения двух целых чисел, нужно к полученной сумме прибавить число, противоположное любому из слагаемых, при этом должно получиться другое слагаемое.
Разберемся на примерах с проверкой результата сложения двух целых чисел.
Пример.
При сложении двух целых чисел 13 и −9 было получено число 4 , выполните проверку результата.
Решение.
Прибавим к полученной сумме 4 число −13 , противоположное слагаемому 13 , и посмотрим, получится ли другое слагаемое −9 .
Итак, вычислим сумму 4+(−13) . Это сумма целых чисел с противоположными знаками. Модули слагаемых равны 4 и 13 соответственно. Слагаемое, модуль которого больше, имеет знак минус, который мы и запоминаем. Теперь вычитаем из большего модуля вычитаем меньший: 13−4=9 . Осталось перед полученным числом поставить запомненный знак минус, имеем −9 .
При проверке мы получили число, равное другому слагаемому, следовательно, исходная сумма была вычислена правильно. −19
. Так как мы получили число, равное другому слагаемому, то сложение чисел −35
и −19
было выполнено верно.
−19
. Так как мы получили число, равное другому слагаемому, то сложение чисел −35
и −19
было выполнено верно.
Сложение трех и большего количества целых чисел
До этого момента мы говорили о сложении двух целых чисел. Иными словами, мы рассматривали суммы, состоящие из двух слагаемых. Однако сочетательное свойство сложения целых чисел позволяет нам однозначно определить сумму трех, четырех и большего количества целых чисел.
На основании свойств сложения целых чисел мы можем утверждать, что сумма трех, четырех и так далее чисел не зависит от способа расстановки скобок, указывающих порядок выполнения действий, а также от порядка следования слагаемых в сумме. Эти утверждения мы обосновывали, когда говорили о сложении трех и большего количества натуральных чисел . Для целых чисел все рассуждения полностью совпадают, и мы не будем повторяться.0+(−101) +(−17)+5 . После этого, расставив скобки любым допустимым способом, мы все равно получим число −113 .
Ответ:
5+(−17)+0+(−101)=−113
.
Список литературы.
- Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
В этом уроке мы изучим сложение и вычитание целых чисел , а также правила для их сложения и вычитания.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
−3, −2, −1, 0, 1, 2, 3
Положительные числа легко , и . К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой. Как показывает практика, ошибки сделанные из-за отрицательных чисел, расстраивают обучающихся больше всего.
Содержание урока
Примеры сложения и вычитания целых чисел
Первое чему следует научиться, это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа, и где положительные.
Рассмотрим простейшее выражение: 1 + 3. Значение данного выражения равно 4:
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 − 3.
Значение данного выражения равно −2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 − 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.
Вообще, надо запомнить, что если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения −2 + 4
Значение данного выражения равно 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2.
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.
Знак плюса в выражении −2 + 4 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Пример 4. Найти значение выражения −1 − 3
Значение данного выражения равно −4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.
Знак минуса в выражении −1 − 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.
Пример 5. Найти значение выражения −2 + 2
Значение данного выражения равно 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Знак плюса в выражении −2 + 2 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Правила сложения и вычитания целых чисел
Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Удобнее воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
От этого будет зависеть какое правило применять.
Пример 1. Найти значение выражения −2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками. −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть, ответ будет положительным:
−2 + 5 = 5 − 2 = 3
Обычно записывают покороче: −2 + 5 = 3
Пример 2. Найти значение выражения 3 + (−2)
Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3+−2.
3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3+−2.
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:
3 + (−2) = |3| − |−2| = 3 − 2 = 1
Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа модуль, которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть, ответ положительный.
Обычно записывают покороче 3 + (−2) = 1
Пример 3. Найти значение выражения 3 − 7
В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.
3 − 7 = 7 − 3 = −4
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4
Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.
Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 − 7 = − (7 − 3) = − (4) = −4
В этом случае равенство будет соблюдаться на каждом этапе:
После того, как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 − 7 = − (7 − 3) = − (4) = − 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a − b = − (b − a)
Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак, знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет вычитаемому.
На примере выражения 5 − 3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того, чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число −3. Записываем новое выражение:
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:
Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:
5 + (−3) = |5| − |−3| = 5 − 3 = 2
Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.
Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.
А стало быть, для наглядности данное выражение можно записать следующим образом:
(+3) − (+1)
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.
В таком случае заменить вычитание сложением намного проще.
В выражении (+3) − (+1) в ычитаемое это число (+1), а противоположное ему число это (−1).
Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)
(+3) − (+1) = (+3) + (−1)
Дальнейшее вычисление не составит особого труда.
(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.
У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:
Заменим вычитание сложением:
(+3) − (+7) = (+3) + (−7)
Дальнейшее вычисление не составляет труда:
(+3) − (−7) = (+3) + (-7)
= −(|−7| − |+3|) = −(7 − 3) = −(4) = −4
Пример 7. Найти значение выражения −4 − 5
Найти значение выражения −4 − 5
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).
(−4) − (+5) = (−4) + (−5)
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:
(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9
Решение для данного примера можно записать покороче:
−4 − 5 = −(4 + 5) = −9
или ещё короче:
−4 − 5 = −9
Пример 8. Найти значение выражения −3 − 5 − 7 − 9
Найти значение выражения −3 − 5 − 7 − 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:
(−3) − (+5) − (+7) − (+9)
Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9)
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9) =
= −(|−3| + |−5| + |−7| + |−9|) = −(3 + 5 + 7 + 9) = −(24) = −24
Решение данного примера можно записать покороче:
−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24
или ещё короче:
−3 − 5 − 7 − 9 = −24
Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7
Приведём выражение к понятному виду:
(−10) + (+6) − (+15) + (+11) − (+7)
Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:
Сложение оставляем без изменения, а вычитание заменяем сложением:
(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)
Соблюдая , выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:
(−10) + (+6) = − (10 − 6) = − (4) = − 4
Второе действие:
(−4) + (−15) = − (4 + 15) = − (19) = − 19
Третье действие:
(−19) + (+11) = − (19 − 11) = − (8) = −8
Четвёртое действие:
(−8) + (−7) = − (8 + 7) = − (15) = − 15
Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15
Примечание . Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Сложение отрицательных чисел.
Сумма отрицательных чисел есть число отрицательное. Модуль суммы равен сумме модулей слагаемых .
Давайте разберемся, почему же сумма отрицательных чисел будет тоже отрицательным числом. Поможет нам в этом координатная прямая, на которой мы выполним сложение чисел -3 и -5. Отметим на координатной прямой точку, соответствующее числу -3.
К числу -3 нам нужно прибавить число -5. Куда мы пойдем от точки, соответствующей числу -3? Правильно, влево! На 5 единичных отрезков. Отмечаем точку и пишем число ей соответствующее. Это число -8.
Итак, при выполнении сложения отрицательных чисел с помощью координатной прямой мы все время находимся слева от начала отсчета, поэтому, понятно, что результат сложения отрицательных чисел есть число тоже отрицательное.
Примечание. Мы складывали числа -3 и -5, т.е. находили значение выражения -3+(-5). Обычно при сложении рациональных чисел просто записывают эти числа с их знаками, как бы перечисляют все числа, которые нужно сложить. Такую запись называют алгебраической суммой. Применяют (в нашем примере) запись: -3-5=-8.
Такую запись называют алгебраической суммой. Применяют (в нашем примере) запись: -3-5=-8.
Пример. Найти сумму отрицательных чисел: -23-42-54. (Согласитесь, что эта запись короче и удобнее вот такой: -23+(-42)+(-54))?
Решаем по правилу сложения отрицательных чисел: складываем модули слагаемых: 23+42+54=119. Результат будет со знаком «минус».
Записывают обычно так: -23-42-54=-119.
Сложение чисел с разными знаками.
Сумма двух чисел с разными знаками имеет знак слагаемого с большим модулем. Чтобы найти модуль суммы, нужно из большего модуля вычесть меньший .
Выполним сложение чисел с разными знаками с помощью координатной прямой.
1) -4+6. Требуется к числу -4 прибавить число 6. Отметим число -4 точкой на координатной прямой. Число 6 — положительное, значит от точки с координатой -4 нам нужно идти вправо на 6 единичных отрезков. Мы оказались справа от начала отсчета (от нуля) на 2 единичных отрезка.
Результат суммы чисел -4 и 6 — это положительное число 2:
— 4+6=2. Как можно было получить число 2? Из 6 вычесть 4, т.е. из большего модуля вычесть меньший. У результата тот же знак, что и у слагаемого с большим модулем.
Как можно было получить число 2? Из 6 вычесть 4, т.е. из большего модуля вычесть меньший. У результата тот же знак, что и у слагаемого с большим модулем.
2) Вычислим: -7+3 с помощью координатной прямой. Отмечаем точку, соответствующую числу -7. Идем вправо на 3 единичных отрезка и получаем точку с координатой -4. Мы были и остались слева от начала отсчета: ответ — отрицательное число.
— 7+3=-4. Этот результат мы могли получить так: из большего модуля вычли меньший, т.е. 7-3=4. В результате поставили знак слагаемого, имеющего больший модуль: |-7|>|3|.
Примеры. Вычислить: а) -4+5-9+2-6-3; б) -10-20+15-25.
Что такое обратные операции? — Определение Факты и примеры
Операции
Математическая «операция» относится к вычислению значения с использованием операндов и математического оператора. Числа, используемые для операции, называются операндами. В зависимости от типа операции операндам назначаются разные термины. Операторы — это символы, обозначающие математическую операцию, например:
Операторы — это символы, обозначающие математическую операцию, например:
- + для сложения
- − для вычитания
- × для умножения
- ÷ для деления
- = для равно, указывает на равенство, то есть значение левой части равно значению правой части.
Что такое обратные операции?
Обратное означает обратное. Таким образом, в математике обратная операция может быть определена как операция, которая отменяет то, что было сделано предыдущей операцией. Множество двух противоположных операций называется обратными операциями.
Например: Если мы сложим 5 и 2 ручки, мы получим 7 ручек. Теперь вычтите 7 ручек и 2 ручки, и мы получим 5 обратно. Здесь сложение и вычитание являются обратными операциями.
Ниже приведены примеры обратных операций:
Сложение и вычитание
Сложение и вычитание являются обратными операциями, то есть сложение отменяет вычитание, а вычитание отменяет сложение. Мы можем переставить числа, данные в уравнении сложения, а затем мы можем использовать уравнение сложения, чтобы получить два разных уравнения вычитания.
Например: 15 + 6 = 21
Образуются два уравнения вычитания: 21 – 6 = 15 и 21 – 15 = 6
После этого мы даже можем показать, что если взять число, например 15, прибавить и вычесть то же число до 15, мы снова получим 15.
т. е. 15 + 6 – 6 = 0
Точно так же мы можем переставить числа, данные в уравнении вычитания, и тогда мы можем составить два уравнения сложения.
Например: 30 – 14 = 16
Образуются следующие уравнения сложения: 14 + 16 = 30 и 16 + 14 = 30
Когда мы складываем число и вычитаем его позже, эффект будет обратным.
16 – 4 + 4 = 0
Умножение и деление
Умножение и деление являются обратными операциями, что означает, что умножение отменяет деление, а деление отменяет умножение. Мы можем переставить числа, данные в уравнении умножения, и тогда мы можем сделать два разных уравнения деления.
Например: 7 ✕ 4 = 28
Образуются два уравнения деления: $28\div4=7$ и $28\div7=4$
Кроме того, когда мы умножаем число, а затем делим его позже, эффект обратный.
$12\times4=48; 48\div4=12$
Точно так же мы можем переставить числа, данные в уравнении деления, и тогда мы можем составить два уравнения умножения.
Например: $45\div9=5$
Образуются уравнения умножения: 9 ✕ 5 = 45 и 5 ✕ 9 = 45 перевернуто.
$1\div24=3; 3\times4=12$
Свойства обратных операций
- Обратное аддитивное свойство
Значение, которое при добавлении к исходному числу дает 0, называется аддитивным обратным.
Предположим, что x является исходным числом, тогда его аддитивной инверсией будет минус x, т. е. -x, так что:
$x+(-x)=x-x=0$
Например, $6+(- 6)=0$. Следовательно, –6 является аддитивной величиной, обратной 6, и наоборот.
Предположим, что -x является исходным числом, тогда его аддитивной инверсией будет положительное значение x, т. е. x.
- Свойство обратного умножения
Значение, которое при умножении на исходное число дает 1, называется мультипликативным обратным.
Предположим, что x — исходное число, тогда его мультипликативное обратное число будет обратным $x$, т. е. $\frac{1}{x}$, таким образом, что:
$x\times\frac{1} {x}=1$
Например, $6\times\frac{1}{6}=1$. Следовательно, $\frac{1}{6}$ является мультипликативным, обратным 6, и наоборот.
Предположим, что $\frac{1}{x}$ — исходное число, тогда его мультипликативное обратное число будет обратным $\frac{1}{x}$, т. е. $x$.
Например: мультипликативное обратное значение $\frac{3}{4}$ равно $\frac{4}{3}$.
Решенные примеры
Пример 1. Составьте уравнения вычитания из 24 + 13 = 37.
Решение : 37 – 24 = 13 и 37 – 13 = 24
4 Что является добавкой, обратной
4. –10?
Решение : Поскольку –10 является отрицательным числом, его инверсия по сумме будет положительным числом. Таким образом, аддитивное обратное значение –10 будет равно 10.
3. Чему равно мультипликативное обратное число $(3-\frac{1}{4})$ ?
Чему равно мультипликативное обратное число $(3-\frac{1}{4})$ ?
Ответ: $(3-\frac{1}{4})=\frac{12-1}{4}=\frac{11}{4}$
Мультипликативное значение, обратное $\frac{11} {4}$ равно $\frac{4}{11}$ .
Практические задачи
15 + 3 = 12
12 + 3 = 15
15 — 3 = 12
Ничего из перечисленного
Правильный ответ: 12 + 3 = 15
Уравнение сложения для 15-12=3: 12 + 3 = 15. 12$
Оба A и B
Правильный ответ: Оба A и B
Уравнения деления будут $12\div3=4$ и $12\div4=3$.
$\frac{1}{18}$
$0$
$18$
$-18$
Правильный ответ: $-18$
$3\times6=18$. Аддитивное число, обратное числу 18, равно — 18.
Часто задаваемые вопросы 92=64$, тогда $\sqrt{64}=8$.
Каково назначение обратной операции?
Обратные операции используются для изменения влияния одной операции на другую. Цель обратных операций — понять взаимосвязь между основными математическими операторами +,−,×,÷, чтобы упростить решение уравнения и сэкономить время.
Как используется обратная операция при решении уравнений?
Обратные операции используются при решении уравнений для выделения переменных путем применения обратных операций с обеих сторон.
Целочисленные формулы — Что такое целочисленные формулы? Примеры
Прежде чем изучать формулы для целых чисел, вспомним, что такое целые числа. Целое число — это число, которое не имеет десятичной или дробной части. Термин «целое число» был получен от латинского слова «целое число», что означает «целое». Давайте подробно изучим формулы для целых чисел в следующем разделе. Набор целых чисел представлен буквой «Z» и включает в себя:
- Все натуральные числа
- Отрицательные числа всех натуральных чисел
- Число ноль (0)
Что такое целые формулы?
Целочисленные формулы – это формулы/правила, которые используются для выполнения операций над целыми числами. Формулы целых чисел различаются для нахождения суммы/разности и произведения/частного. Вот формулы.
Вот формулы.
Формулы сложения/вычитания целых чисел
Чтобы сложить два целых числа с одинаковыми знаками, мы просто складываем их абсолютные значения и используем тот же знак, что и заданные целые числа, для результата. Чтобы сложить два целых числа разных знаков, мы вычитаем их абсолютные значения (в порядке большего числа минус меньшее число) и также используем знак большего числа к результату. Мы выполняем вычитание точно так же, как и сложение, но по правилу а — b = а + (-b). Таким образом, формулы сложения/вычитания целых чисел:
- (+) + (+) = +
- (-) + (-) = —
- (+) + (-) = + (абсолютное значение положительного числа больше)
- (+) + (-) = — (абсолютное значение отрицательного числа больше)
Примеры:
- 2 + 3 = 5
- (-2) + (-3) = -5
- 3 + (-2) = +1 (или) 1
- 2 + (-3) = -1
Формулы умножения/деления целых чисел
Произведение/частное двух целых чисел одного знака всегда положительно, а произведение или частное двух целых чисел разных знаков всегда отрицательно. Таким образом, формулы умножения/деления целых чисел:
Таким образом, формулы умножения/деления целых чисел:
- (+) × (+) = +; (+) ÷ (+) = +
- (-) × (-) = +; (-) ÷ (-) = +
- (+) × (-) = -; (+) ÷ (-) = —
- (-) × (+) = -; (-) ÷ (+) = —
Примеры
- 2 × 3 = 6
- -2 × -3 = 6
- 2 × -3 = -6
- -2 × 3 = -6
Примечание: Множество целых чисел замкнуто, ассоциативно и коммутативно относительно сложения и умножения. Аддитивная идентичность 0 и мультипликативная идентичность 1 присутствуют в наборе целых чисел. Все целые числа имеют свои аддитивные инверсии в множестве целых чисел. Ни одно из целых чисел, кроме 1 и -1, не имеет своих мультипликативных инверсий в множестве целых чисел.
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Закажите бесплатный пробный урок
Давайте посмотрим на применение формул для целых чисел в следующих решенных примерах.
Примеры с использованием целочисленных формул
Пример 1: Оцените следующее: a) 12 + (-3) b) 12 × -3
Решение:
а) В 12 + (-3) 12 со знаком + и 3 со знаком -. Итак, мы вычитаем абсолютные значения 12 и -3 (которые равны 12 и 3), вычитаем их (12 — 3 = 9) и присваиваем результату знак наибольшего абсолютного значения (знак 12, который равен +). .
Таким образом, 12 + (-3) = +9 (или) 9
б) 12 × -3
Используя одну из формул для целых чисел, (+) × (-) = — и 12 × 3 = 36.
Таким образом, 12 × -3 = -36.
Ответ: а) 9 б) -36.
Пример 2: Запишите пару целых чисел в каждом из следующих случаев, используя формулы целых чисел: а) сумма которых равна -6 б) произведение которых равно -8.
Решение:
а) Рассмотрим 2 и -8. Их абсолютные значения равны 2 и 8.
Мы знаем, что 8 — 2 = 6, а среди 2 и -8 8 имеет наибольшее абсолютное значение. Таким образом, результат имеет знак минус (поскольку -8 имеет знак минус).
Таким образом, результат имеет знак минус (поскольку -8 имеет знак минус).
Таким образом, 2 + (-8) = -6.
б) Рассмотрим 2 и -4. Поскольку они имеют противоположные знаки, их произведение отрицательно. Таким образом,
2 × -4 = -8.
Ответ: а) 2 и -8; б) 2 и -4.
Пример 3: Оцените следующее: a) (-13) + (-12) + 2 b) -4 + (-2) × (3) + (-4) ÷ 2.
Решение:
Мы будем оценивать данные выражения, используя формулы целых чисел.
а) (-13) + (-12) — 2
= -25 + 2
= -23
б) -4 + (-2) × (3) + (-4) ÷ 2
= -4 + -6 + (-2)
= -10 + (-2)
= -12
Ответ: a) -23 b) -12
Часто задаваемые вопросы о формулах для целых чисел
Что такое формулы для целых чисел?
Целочисленные формулы — это формулы для сложения/вычитания и умножения/деления целых чисел. Эти формулы приведены ниже.
Формулы сложения/вычитания:
- (+) + (+) = +
- (-) + (-) = —
- (+) + (-) = + (абсолютное значение положительного числа больше)
- (+) + (-) = — (абсолютное значение отрицательного числа больше)
Формулы умножения/деления:
- (+) × (+) = +; (+) ÷ (+) = +
- (-) × (-) = +; (-) ÷ (-) = +
- (+) × (-) = -; (+) ÷ (-) = —
- (-) × (+) = -; (-) ÷ (+) = —
Как использовать формулы для целых чисел?
Мы можем использовать формулы целых чисел в зависимости от того, делаем ли мы сложение/вычитание/умножение/деление. Например, если нам нужно найти значение (-3) × (-2), мы используем формулу умножения целых чисел, которая гласит (-) × (-) = +. Используя это, (-3) × (-2) = 6 (поскольку 3 × 2 = 6).
Например, если нам нужно найти значение (-3) × (-2), мы используем формулу умножения целых чисел, которая гласит (-) × (-) = +. Используя это, (-3) × (-2) = 6 (поскольку 3 × 2 = 6).
Что такое -14 + 3 с использованием формул для целых чисел?
Абсолютные значения -14 и 3 равны 14 и 3 соответственно. Используя одну из формул для целых чисел, (-) + (+) = — (абсолютное значение отрицательного числа больше). Используя эту формулу, -14 + 3 = -11.
Что такое (-14) × 3 с помощью формул для целых чисел?
Мы знаем, что 14 × 3 = 42. Теперь, используя одну из формул для целых чисел, (+) × (-) = -. Таким образом, 14 × -3 = -42.
Разница в математике | Обзор, вычитание и примеры — видео и расшифровка урока
Математические курсы / Математика для детей Курс / Математические термины для начальной школы Глава
Элизабет Расмуссен, Т.Дж. Хугстин- Автор Элизабет Расмуссен
- Инструктор Т.
 Дж. Хугстин
Дж. ХугстинТ.Дж. В настоящее время работает учителем 5 класса и заместителем директора. Он имеет степень магистра в области управления образованием и работает над получением степени Ed.D. в образовательном лидерстве.
Посмотреть биографию
Поймите, что означает различие в математике, изучите различные ключевые слова, относящиеся к операции вычитания, и примеры работы. Обновлено: 18.04.2022
Определение различий в математике
Различие между двумя вещами часто используется для изучения того, что у этих двух вещей нет общего. Например, яблоки и апельсины. Яблоки красные и гладкие. С другой стороны, апельсины оранжевые и неровные. Однако понятие разницы в математике отличается. В математике определение числа разность двух чисел есть расстояние между ними по числовой прямой. Например, разница между 10 и 8 равна 2, потому что расстояние по числовой прямой между 10 и 8 равно 2.
Слово «разность» используется в математике по-разному, и, хотя все они используют одно и то же понятие «разность», на практике оно может выглядеть совершенно по-разному.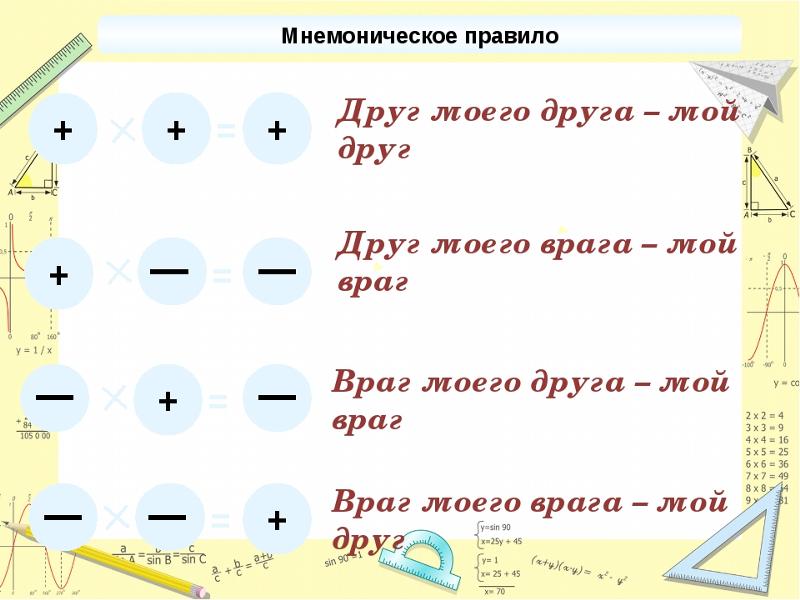
- Разностное уравнение — это уравнение, в котором существует разница между двумя значениями переменной. 92 экв.}.
- Общая разность используется для идентификации и построения арифметических последовательностей.
- В исчислении интеграл использует разницу между функциями для вычисления площади под кривой.
Какая разница?
Глядя на эти две формы, мы замечаем несколько различий, и они, вероятно, очевидны. Один овал, а другой прямоугольник. Один больше другого. Наконец, один зеленый, а другой красный. Когда дело доходит до взгляда на визуальные объекты, такие как фигуры, во многих случаях различия легко увидеть. Но когда дело доходит до математики и чисел, слово «разница» приобретает несколько иной смысл и может быть не столь очевидным на первый взгляд.
Произошла ошибка при загрузке этого видео.
Попробуйте обновить страницу или обратитесь в службу поддержки.
Вы студент или преподаватель?
Присоединяйся сейчас
Больше 84 000 уроков по математике, английскому языку, естественным наукам, истории и многому другому в одном месте!
Более 30 000
Видеоуроки
Практика
Вопросы
Присоединяйся сейчас
Больше 30 000 видеоуроков и учебные ресурсы, все в одном месте!
Более 84 000
Уроки
Викторины и
Рабочие листы
Классная комната
Интеграция
Планы уроков
Далее: Что такое измерение в математике?
пройти викторину Смотреть Следующий урок
Повторить
Просто отмечаюсь. Вы все еще смотрите?
Да! Продолжай играть.Ваш следующий урок будет играть в 10 секунд
- 0:04 Какая разница?
- 0:31 Разница в математике
- 1:56 Итоги урока
Сохранить Сохранить Сохранить
Хронология
Автовоспроизведение
Автовоспроизведение
Скорость
Скорость
Что означает разница в математике?
Итак, что означает различие в математике? Чтобы найти разницу между двумя числами, нужно вычесть одно число из другого. Есть много способов выразить вычитание двух чисел, например:
Есть много способов выразить вычитание двух чисел, например:
- Убрать: Отнять одно число от другого — значит вычесть одно число из другого.
- Меньше: иногда возникает задача найти на одно число меньше другого числа. Это означает, что нужно найти вычесть два числа.
- Минус: одно число минус другое число равносильно вычитанию двух чисел.
Вычитание разницы?
Является ли нахождение разницы тем же самым, что и вычитание? Почти. И нахождение разности, и вычитание относятся к одной и той же математической операции, но при вычитании результат может быть отрицательным. При нахождении разницы между двумя значениями она всегда будет положительной. Если после вычислений разница отрицательна, возьмите абсолютное значение, чтобы найти положительное расстояние.
При вычитании двух чисел друг из друга важно знать, какое число из какого вычитается.
- Уменьшаемое — это значение, из которого вычитается другое значение.

- Вычитаемое — это вычитаемое значение.
Например, найдите разницу между 10 и 4. Для этого вычтите меньшее значение из большего: 10 — 4 = 6. Разница между 10 и 4 равна 6. В этом примере 10 — уменьшаемое, 4 — вычитаемое, а 6 — разность.
Для ясности: найти разницу между 10 и 4 — это то же самое, что найти разницу между 4 и 10. Вычитание 10 из 4 — это не то же самое, что вычитание 4 из 10.
- Вычитание 10 из 4: 4 — 10 = -6
- Вычитание 4 из 10: 10 — 4 = 6
Обращайте особое внимание на знаки при работе со следующими примерами.
- Пример 1: Найдите разницу между 150 и 75.
Решение: возьмите большее число и вычтите меньшее. 150 — 75 = 75. Следовательно, уменьшаемое равно 150, вычитаемое равно 75, а разность равна 75.
- Пример 2. Вычтите 150 из 75.
Решение: Уменьшаемое равно 75, а вычитаемое равно 150, что дает 75 — 150 = -75.
- Пример 3: Найдите разницу между -10 и 3.
Решение: Уменьшаемое равно 3, а вычитаемое равно 3. Таким образом, разность равна 3 — (-10) = 3 + 10 = 13.
- Пример 4: Найдите разницу между -7 и -2.
Решение: -2 является уменьшаемым, так как -2 больше, чем -7. Это означает, что -7 является вычитаемым. Следовательно, -2 — (-7) = -2 + 7 = 5.
- Пример 5. Найдите разницу между {eq}\dfrac{1}{2} {/eq} и {eq}\dfrac{2}{3} {/eq}.
Решение: {eq}\dfrac{2}{3}-\dfrac{1}{2}= \dfrac{4}{6}-\dfrac{3}{6}= \dfrac{1}{6 } {/экв.}.
- Пример 6: В чем разница между 3,5 и 7,25?
Решение: 7,25 — 3,5 = 3,75.
Различия часто встречаются в текстовых задачах реальных приложений.
- Пример 7. В городе рекордно высокая температура 110 F и рекордно низкая температура -10 F.
 В чем разница между этими двумя температурами?
В чем разница между этими двумя температурами?
Решение: 110 — это большая температура, поэтому 110 — уменьшаемое, а -10 — вычитаемое. Разница составляет 110 — (-10) = 110 + 10 = 120 F.
- Пример 8: Элиза хочет испечь партию яблочных пирогов на продажу. Ей нужно 5 фунтов яблок, а сейчас у нее 2 фунта. Сколько еще фунтов яблок нужно Элизе?
Решение: Ей нужно 5 фунтов, а у нее есть 2 фунта, поэтому найдите разницу между 5 и 2. Поскольку 2 — наименьшее значение, оно является вычитаемым, а 5 — уменьшаемым. Таким образом, Элизе нужно еще 5 — 2 = 3 фунта яблок.
Мы также можем найти разницу между полиномами и другими функциями. Поскольку эти функции часто имеют переменные и от того, какое значение принимает переменная, зависит, какая из них является наибольшей, а какая наименьшей, в инструкциях или приложениях должно быть четкое указание, для какой функции является уменьшаемым, а для какой — наименьшим. вычитаемое.
- Пример 9. Найдите разницу: {экв}(2x+3)-(4x-5) {/экв}.

Решение. Распределите отрицательное значение второго полинома: {eq}2x+3-4x+5 {/eq}. Затем сложите как термины: {eq}-2x+8 {/eq}. Результатом является разница между двумя полиномами.
Резюме урока
Таким образом, в математике разность между значениями относится к расстоянию между двумя значениями на числовой прямой. Поскольку разница представляет собой разницу, она всегда должна быть положительной или равной нулю. Чтобы найти разницу, из большего числа вычтите меньшее. При нахождении разницы число, которое вычитается, называется 9.0420 вычитаемое и значение, из которого вычитается вычитаемое .
Разница в математике
Так что же означает слово «разница» в математике? Разность является результатом вычитания одного числа из другого. В то время как мы часто говорим о разнице в том, как вещи выглядят, ощущаются или даже ощущаются на вкус, в математике это показывает, насколько два числа отличаются друг от друга по количеству.
Итак, разность — это то, что останется от одного числа при вычитании из другого. В уравнении вычитания есть три части:
- Уменьшаемое число (от которого вычитается число)
- Вычитаемое (вычитаемое число)
- Разность (результат вычитания вычитаемого из уменьшаемого)
Если бы это было записано в виде уравнения вычитания, то оно выглядело бы так:
- Уменьшаемое — Вычитаемое = Разность
Теперь, если заменить слова цифрами, это будет выглядеть так:
- 9 — 5 = 4
Итак, после выполнения этого уравнения вычитания разница между 9 и 5 равна 4.
Разность слов также может использоваться в текстовых задачах, подобных этой:
- У Джо было две стопки конфет. В одной кучке у него было 23. В другой было 14. Какая разница между двумя кучками?
Слово «проблема» говорит нам об операции, которую нужно решить, и запрашивает разницу между двумя стопками конфет. На самом деле, все текстовые задачи будут использовать определенные слова, чтобы дать подсказку о том, какая операция необходима для ее решения. В этом случае слово «разность» говорит нам о вычитании. Итак, для решения задачи воспользуемся уравнением 23 — 14 = 9.
На самом деле, все текстовые задачи будут использовать определенные слова, чтобы дать подсказку о том, какая операция необходима для ее решения. В этом случае слово «разность» говорит нам о вычитании. Итак, для решения задачи воспользуемся уравнением 23 — 14 = 9.
Резюме урока
В математике слово разность является результатом вычитания одного числа из другого. Это относится к разнице в количестве между двумя числами. В математике мы получаем разницу между двумя числами, вычитая вычитаемое (вычитаемое число) из вычитаемого (число, из которого вычитается).
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свой аккаунт
Какая разница?
Глядя на эти две формы, мы замечаем несколько различий, и они, вероятно, очевидны. Один овал, а другой прямоугольник. Один больше другого. Наконец, один зеленый, а другой красный.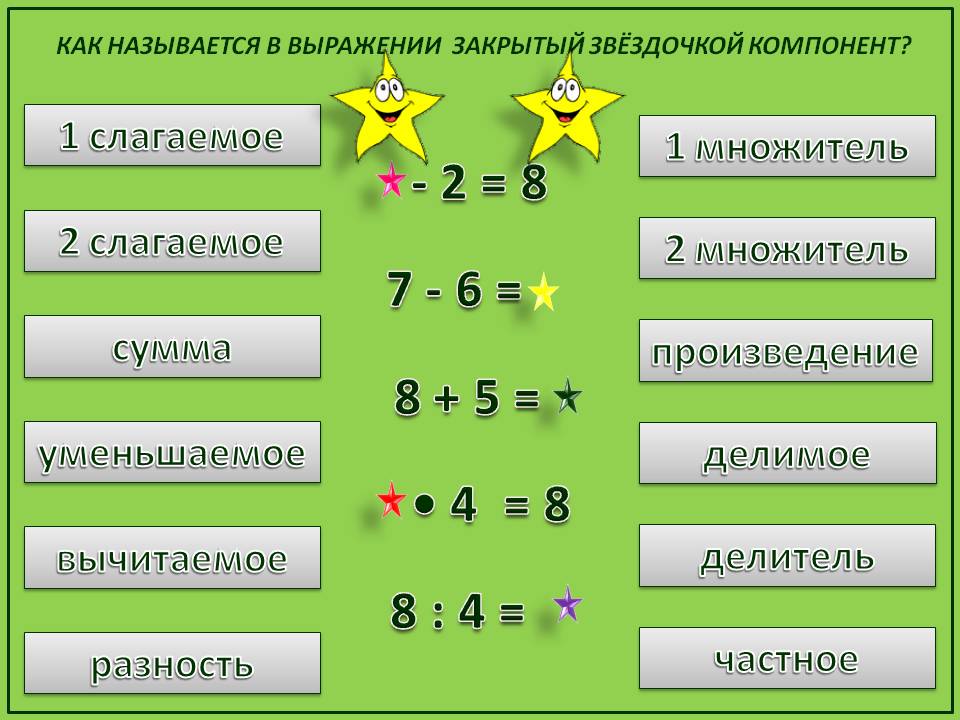 Когда дело доходит до взгляда на визуальные объекты, такие как фигуры, во многих случаях различия легко увидеть. Но когда дело доходит до математики и чисел, слово «разница» приобретает несколько иной смысл и может быть не столь очевидным на первый взгляд.
Когда дело доходит до взгляда на визуальные объекты, такие как фигуры, во многих случаях различия легко увидеть. Но когда дело доходит до математики и чисел, слово «разница» приобретает несколько иной смысл и может быть не столь очевидным на первый взгляд.
Разница в математике
Так что же означает слово «разница» в математике? Разность является результатом вычитания одного числа из другого. В то время как мы часто говорим о разнице в том, как вещи выглядят, ощущаются или даже ощущаются на вкус, в математике это показывает, насколько два числа отличаются друг от друга по количеству.
Итак, разность — это то, что останется от одного числа при вычитании из другого. В уравнении вычитания есть три части:
- уменьшаемое (число, из которого вычитается)
- Вычитаемое (вычитаемое число)
- Разность (результат вычитания вычитаемого из уменьшаемого)
Если бы это было записано в виде уравнения вычитания, то оно выглядело бы так:
- Уменьшаемое — Вычитаемое = Разность
Теперь, если заменить слова цифрами, это будет выглядеть так:
- 9 — 5 = 4
Итак, после выполнения этого уравнения на вычитание разница между 9 и 5 равна 4.
Разность слов также может использоваться в текстовых задачах, подобных этой:
- У Джо было две стопки конфет. В одной кучке у него было 23. В другой было 14. Какая разница между двумя кучками?
Слово «проблема» говорит нам об операции, которую нужно решить, и запрашивает разницу между двумя стопками конфет. На самом деле, все текстовые задачи будут использовать определенные слова, чтобы дать подсказку о том, какая операция необходима для ее решения. В этом случае слово «разность» говорит нам о вычитании. Итак, для решения задачи воспользуемся уравнением 23 — 14 = 9.
Резюме урока
В математике слово разность является результатом вычитания одного числа из другого. Это относится к разнице в количестве между двумя числами. В математике мы получаем разницу между двумя числами, вычитая вычитаемое (вычитаемое число) из вычитаемого (число, из которого вычитается).
Чтобы разблокировать этот урок, вы должны быть участником Study.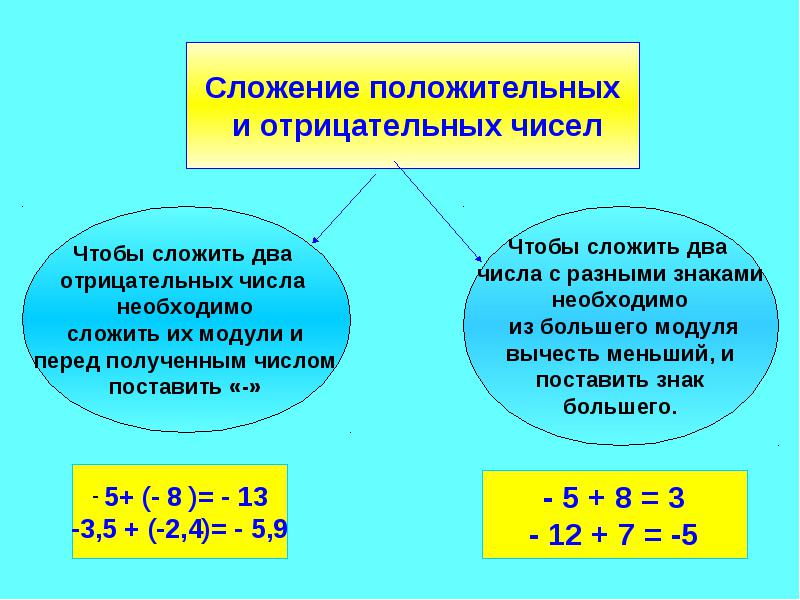 com.
com.
Создайте свой аккаунт
Что является примером различия в математике?
Примером разницы в математике является нахождение разницы между двумя числами. Чтобы найти разницу между двумя числами, возьмите большее из них и вычтите меньшее. Например, разница между 10 и 15 равна 15 — 10 = 5.
Что подразумевается под разницей?
Разница — это расстояние между двумя значениями. Поскольку расстояние всегда неотрицательное расстояние, разница также всегда будет неотрицательной.
Номер со знаком
Номер со знаком Назад в математический центр ПРАВИЛО 1. Если слагаемые имеют один и тот же знак, добавьте два числа и добавьте к их общему знаку префикс.
Если слагаемые имеют один и тот же знак, добавьте два числа и добавьте к их общему знаку префикс.
(+62) + (+14) = +76 (-29) + (-13) = -42
ПРАВИЛО 2. Если слагаемые имеют разные знаки, найдите разницу между двумя числами и поставьте перед ним знак того числа, которое находится на большем расстоянии от нуля.
(+15) + (-8) = +7 (+9) + (-30) = -21
| 1. (-5) + (-6) = 3. (-3) + (-6) = 5. (-2) + (-8) = 7. (-9) + (+10) = 9. (+12) + (+10) = 11. (-29) + (-11) = 13. (+42) + (-19) = 15. (+31) + (-56) = 17. -8 + 10 = 19. 75 + (-25) = 21. 73 + 47 = 23. 78 + (-30) = 25. 75 + (-25) = 27. 200 + 100 = 29. 355 + (-163) = 31. 34 + (-16) = 33. 72 + (-12) = 35. 1/2 + -1/2 = 37.  1/4 + (-1/2) = 1/4 + (-1/2) = 39. 1/4 + -1/2 = 41. 16+16= 43. 3 + (-8) + 7 = 45. 12 + 5 + (-8) + 20 + (-16) = | 2. (+9) + (-4) = 4. (-4) + (-4) = 6. (-7) + (+1) = 8. (-8) + (-5) = 10. (+13) + (-17) = 12. (-36) + (+24) = 14. (-33) + (+42) = 16. (+65) + (+15) = 18. 7 + (-18) = 20. 33 + (-22) = 22. 86 + (-58) = 24. 100 + 50 = 26. 150 + 50 = 28. 132 + (-181) = 30. 900 + 200 = 32. 14 + 43 = 34. 4 + 17 = 36. 7 + (-7) = 38. -1/4 + 1/4 = 40. 17+4= 42. 2436 + (-1064) = 44. 11+5+(-2)= 45. 12 + 5 + (-8) + 20 + (-16) = |
- 11
- 5
- 9
- 8
- 10
- 6
- 1
- 13
- 22
- 4
- 40
- 12
- 23
- 9
- 25
- 80
- 2
- -11
- 50
- 55
- 26
- 28
- 108
- 50
- 100
- 200
- 100
- 49
- 192
- 1100
- 50
- 57
- 60
- 13
- 0
- 0
- 1/4
- 0
- 3/4
- 13
- 0
- 1372
- 2
- 14
- 13
ПРАВИЛО 1. Поскольку каждую задачу на вычитание можно переписать как соответствующую задачу на сложение, используйте следующее правило: Чтобы вычесть целое число, прибавьте его противоположное значение.
Поскольку каждую задачу на вычитание можно переписать как соответствующую задачу на сложение, используйте следующее правило: Чтобы вычесть целое число, прибавьте его противоположное значение.
ПРАВИЛО 1 примеры:
1. (+7) (+4) = (+7) + (-4) = +3
2. (+5) (-6) = (+5) + (+6) = +11
3. (-3) (+8) = (-3) + (-8) = -11
Альтернативное ПРАВИЛО 1. Чтобы вычесть числа со знаком:
- Изменить двойное отрицание на положительное.
- Получить сумму членов с одинаковыми знаками и сохранить заданный знак, используя знак перед числом как знак числа.
- Найдите разницу, когда термины имеют разные знаки, и используйте знак большего числа.
Альтернативное ПРАВИЛО 1 Примеры:
- 7 (-5) = 7 + 5 = 12 (а. Измените двойное отрицание на положительное, используйте правила сложения целых чисел)
- 5 9 = -14 (используя знаки перед цифрами, используйте только правила сложения-знаки одинаковые, добавьте и сохраните знак)
- 6 7 = -1 (используя знаки перед числами, используйте правила сложения-знаки разные, вычтите и возьмите знак наибольшего числительного)
- 6 7 + 3 4 2 = 913 = -4 (Получить сумму членов с одинаковыми знаками, использовать правила сложения)
- 5 (- 8) =
- 7 (+8) =
- 9 (+ 4) =
- 9 (-2) =
- 1 6 =
- 1 (-9) =
- 4 5 =
- 3 10 =
- 8 (-4) =
- 4 6 =
- 8 (-9) =
- 10 10 =
- 10 (-10) =
- 10 10 =
- 25 (-15) =
- 33 (-49) =
- 8 7 =
- 6 8 =
- 3 (-7) =
- 14 (-6) =
- 5 11 =
- 8 6 =
- 11 (-4) =
- 13 (-16) =
- 6 (-10) =
- 7 0 =
- 6 13 =
- 17 81 =
- 10 (7 9) =
- 6 (-9 +7) =
- 6 + (-8 7) =
- 14 (18 40) =
Ключ ответа для вычитания целых чисел
- 13
- 15
- 13
- 11
- 7
- 10
- 9
- 7
- 4
- 2
- 17
- 20
- 20
- 0
- 40
- 16
- 1
- 14
- 4
- 20
- 6
- 14
- 7
- 29
- 4
- 7
- 7
- 98
- 12
- 8
- 9
- 36
Основные математические операции — сложение, вычитание, умножение и деление
Основные математические операции включают четыре основные операции:
● Сложение (+)
● Вычитание (-)
● Умножение (* или x) и
● Деление ( : или /)
арифметических операций . Арифметика — старейшая и наиболее элементарная ветвь математики.
Арифметика — старейшая и наиболее элементарная ветвь математики.
В этом и других связанных уроках мы кратко объясним основные математические операции. Имейте в виду, хотя операции и примеры, показанные здесь, довольно просты, они обеспечивают основу даже для самых сложных операций, используемых в математике.
Сложение
Сложение — это математическая операция, объясняющая общее количество объектов при их объединении в коллекцию.
Например, предположим, что у Джимми 2 яблока, а у Лоры 3 яблока, и мы хотим узнать, сколько яблок у них вместе. Складывая их вместе, мы видим, что у обоих вместе есть 5 яблок (2 яблока Джимми + 3 яблока Лауры = всего 5 яблок). Как видите, добавление обозначается знаком «плюс (+)».
Сложение также можно использовать для выполнения операций с отрицательными числами, дробями, десятичными числами, функциями и т.д. Для сложения характерны несколько арифметических свойств:
1. Коммутативное свойство
2. Ассоциативное свойство
Ассоциативное свойство
3. Свойство идентичности
Вычитание
Вычитание — это арифметическая операция, обратная сложению. Вычитание используется, когда вы хотите узнать, сколько объектов осталось в группе после того, как вы уберете определенное количество объектов из этой группы.
Например, у Мэгги 5 яблок. Она дает 2 яблока своему другу Полу. Сколько яблок у нее? У нее 3 яблока (5 яблок, которые у нее были – 2 яблока, которые она отдала Полу = 3 яблока, которые у нее остались).
Как видите, вычитание определяется «символом минус (-)». Вычитание также можно использовать для выполнения операций с отрицательными числами, дробями, десятичными числами, функциями и т. д.
Умножение
Умножение — третья основная математическая операция. Когда вы умножаете два числа, это то же самое, что прибавлять число к самому себе столько раз, сколько равно значению другого числа. Подумайте об этом так: у вас есть 5 групп яблок, и в каждой группе по 3 яблока. Один из способов узнать, сколько у вас яблок, таков:
Один из способов узнать, сколько у вас яблок, таков:
3 яблока + 3 яблока + 3 яблока + 3 яблока + 3 яблока = всего 15 яблок
Вы можете видеть, что это слишком много работы (особенно если у вас есть большие числа), поэтому вы можете использовать умножение для решения этой задача:
5 групп яблок x 3 яблока в каждой группе = всего 15 яблок
Это может быть еще проще, если использовать таблицу умножения.
Умножение обозначается знаком умножения «x» и часто читается как «умножить» или «умножить на». Таким образом, если бы у вас было выражение типа «3 x 4», вы могли бы прочитать его как «3 умножить на 4» или «3 умножить на 4». Другими словами, выражение умножения означает, сколько раз одно число умножается на другое число.
$\ 3 * 4 = 12$ Число 3 умножается в этом уравнении 4 раза, и при умножении 3 на 4 получается число 12.
Деление
Деление — четвертая основная математическая операция. По сути, можно сказать, что деление означает разделение объектов на равные части или группы.
Например, у вас есть 12 яблок, которые нужно разделить поровну между 4 людьми. Итак, сколько яблок достанется каждому? Каждый получит по 3 яблока (12 яблок / 4 человека = 3 яблока на человека). Деление противоположно умножению:
$\ 3 * 4 = 12$
$\ 4 * 3= 12$
$\frac{12}{4} = 3$
$\frac{12}{3}=4$
Для облегчения понимания деления одного числа на другое используйте таблицу деления:
Основные математические операции
Основные математические операции — сложение, вычитание, умножение и деление. В зависимости от направления математической задачи вы можете увидеть разные слова:
- Дополнение: добавление, добавление
- Вычитание: вычитание, вычитание
- Умножение: умножение, умножение
- Деление: деление, деление
В математике, когда вы выполняете вычислительные действия, вы должны помнить, что существует последовательность, которую необходимо соблюдать, чтобы делайте расчеты правильно.
Сложение и вычитание являются математическими операциями первой степени. Умножение и деление являются математическими операциями второй степени. Это означает:
● Если одинаковые степенных операций , разрешаем их по их порядку (слева направо).
Например:
$\ 18 – 2 + 4 = 16 + 4 = 20$ Это применимо только в том случае, если в уравнении нет скобок. Если есть скобки, сначала разрешаем числа в скобках.
$\ 18 – ( 2 + 4 ) = 18 – 6 = 12 $ Обратите внимание на разницу в результатах даже при одинаковых числах.
● Если имеется операций разной степени , мы разрешаем их в порядке степени – сначала умножение и деление, а потом сложение и вычитание.
Например:
$\ 2 + 3 * 4 = 2 + 12 = 14$
Цифры в скобках в любом случае необходимо решить в первую очередь!
Фундаментальные операции над целыми числами — A Plus Topper Это сложение, вычитание, умножение и деление.
1.
 Сложение целых чисел
Сложение целых чисел Обезьяна сидит на дне пустого резервуара для воды высотой 8 футов. Обезьяна хочет запрыгнуть на верх резервуара с водой. Он подпрыгивает на 3 фута вверх, а затем скользит на 2 фута вниз. За сколько прыжков обезьяна доберется до верха пустой емкости для воды?
Прыжок обезьяны:
Обезьяна достигнет верха пустого резервуара для воды в шестом прыжке.
Два целых числа можно сложить так же, как складывают два целых числа, но при сложении отрицательных целых чисел мы должны двигаться влево по числовой строке.
Подробнее:
- целые числа
- RS Aggarwal Class 6 Solutions Integers
- RS Aggarwal Class 7 Решения
Дополнение целых чисел, имеющих один и тот же знак
1. Сумма двух положительных. сумма их модулей с положительным знаком.
Пример 1: Добавить (+ 6) + (+4).
Решение: На числовой прямой сначала нарисуйте стрелку от 0 до 6, а затем продвиньтесь на 4 шага вперед. Наконечник последней стрелки достигает +10. Итак, (+ 6) + (+ 4) = +10
Наконечник последней стрелки достигает +10. Итак, (+ 6) + (+ 4) = +10
2. Сумма двух отрицательных целых чисел равна сумме их абсолютных значений со знаком минус (-).
Пример 2: Добавьте (-3) + (-4).
Решение: На числовой прямой сначала проводим стрелку слева от нуля от 0 до -3 и далее движемся влево на 4 шага. Наконечник последней стрелки находится на -7. Итак, (-3) + (-4) = (-7)
Сложение целых чисел с противоположными знаками
Сумма двух целых чисел с противоположными знаками равна разности их абсолютных значений со знаком большего абсолютного числа ценность.
Пример 3: Добавить (+6) + (-9).
Решение: На числовой прямой сначала рисуем стрелку от 0 до 6 вправо, а затем делаем 9 шагов влево. Кончик последней стрелки находится на -3. Итак, (+6) + (-9) = (-3)
При вычитании мы меняем знак целого числа, которое нужно вычесть, а затем прибавляем к первому целому числу . Другими словами, если a и b два целых числа, то a – b = a + (-b)
Другими словами, если a и b два целых числа, то a – b = a + (-b)
Пример 4: Вычесть 5 из 12.
Решение: (12) – (5) = (12) + (-5) = 7
Пример 5: Вычесть -7 из -15.
Решение: (-15) – (-7) = (-15) + (7)= -8
Пример 6: Вычесть 6 из -10.
Решение: (-10) -(6) = (-10) + (- 6)
Пример 7: Вычесть (-5) из 4.
Решение: 4 – (-5) = 4 + (5) = 9
Чтобы вычесть (-5) из 4, мы должны найти число, которое при добавлении к (-5) дает нам 4. Итак, на числовой прямой мы начинаем с (-5) и поднимитесь до 4. Теперь найдите, сколько единиц мы переместили. Мы переехали 9единицы.
Итак, 4-(-5) =9
Примечание:
- Сложение целых чисел
(a) Сумма двух целых чисел с одинаковыми знаками равна сумме их абсолютных значений с одинаковым знаком.
(b) Сумма двух целых чисел с разными знаками есть разность их абсолютных значений со знаком большего абсолютного значения. - Вычитание целых чисел
Меняется знак целого числа, которое необходимо вычесть, а затем прибавить к первому целому числу.
Умножение целых чисел одного знака
Когда два целых числа имеют одинаковый знак, их произведение равно произведению их абсолютных значений с положительным знаком.
Примеры
(a) (+6) × (+7) = + 42 или 42
(b) (+5) × (+10) = + 50 или 50
(c) (-3) × ( -5) = + 15 или 15
(d) (-20) × (-6) = 120
(e) (12) × (5) = 60
Умножение целых чисел с противоположными знаками
Произведение двух целых чисел с противоположными знаками равно произведению их абсолютных значений с отрицательным знаком.
Примеры
(a) (-10) × (8) = (- 80)
(b) (- 5) × (7) = (-35)
(c) (12) × (-3) = (-36)
(d) (-6) × (3) = (-18)
(e) 5 × (-4) = (-20)
Примечание:
плюс × минус = минус
минус × плюс = минус
минус × минус = плюс
плюс × плюс = плюс
 Деление целых чисел
Деление целых чисел Деление целых чисел одного знака
Деление двух целых чисел одного знака – это деление их абсолютного значения с положительным знаком. Если оба числа имеют одинаковый знак, то частное будет положительным.
Примеры:
(а) (+9) ÷ (+3) = (3)
(б) (-9) ÷ (-3) = (3)
(в) (-24) ÷ (- 12) = (2)
Деление целых чисел с разными знаками
Если оба целых числа имеют разные знаки, то частное будет отрицательным.
Примеры: (a) 12 ÷ (-3) = (-4)
(b) (-10) ÷ (5) = (-2)
(c) (-18) ÷ (3) = (-6 )
Пример 8: Оценка (-13) – (-7 – 6).
Решение: (-13) – (-7 – 6)
= (-13) -(-13)
= (-13) + (13) (напротив друг друга) = 0
Пример 9 : Вычесть (-5128) из 0.
Решение: 0 – (-5128) = 0 + 5128 = 5128
Пример 10: Разделить (4000) + (- 100).
Решение: \(\frac{4000}{-100}\) = -40
Пример 11: Умножьте (-18) и (-8).
Решение: (-18) × (-8) = 18 × 8 = 144
Примечание:
- Умножение целых чисел
(a) Когда два целых числа имеют одинаковый знак, их произведение произведение их модулей с положительным знаком.
(b) Произведение двух целых чисел с противоположными знаками равно произведению их абсолютных значений с отрицательным знаком. - Деление целых чисел
(a) Если целые числа имеют одинаковый знак, то частное всегда положительно.
(b) Если целые числа имеют противоположные знаки, то частное будет отрицательным.
Примечание:
- Целые числа …, -3,-2,-1, 0,1, 2, 3,…
- 1, 2, 3, 4,… называются положительными целыми числами и — 1,-2,-3,… называются отрицательными целыми числами. 0 не является ни положительным, ни отрицательным.


 Замкнутость их множеств в арифметических операциях
Замкнутость их множеств в арифметических операциях Счет сотнями.
Счет сотнями.
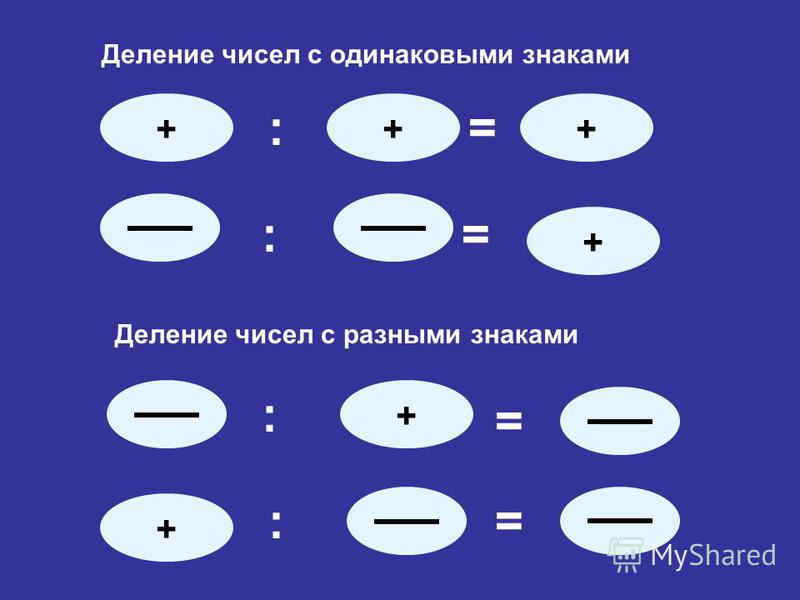 Дж. Хугстин
Дж. Хугстин
 В чем разница между этими двумя температурами?
В чем разница между этими двумя температурами?
