Примеры таблица истинности: Таблицы истинности, с формулами и примерами

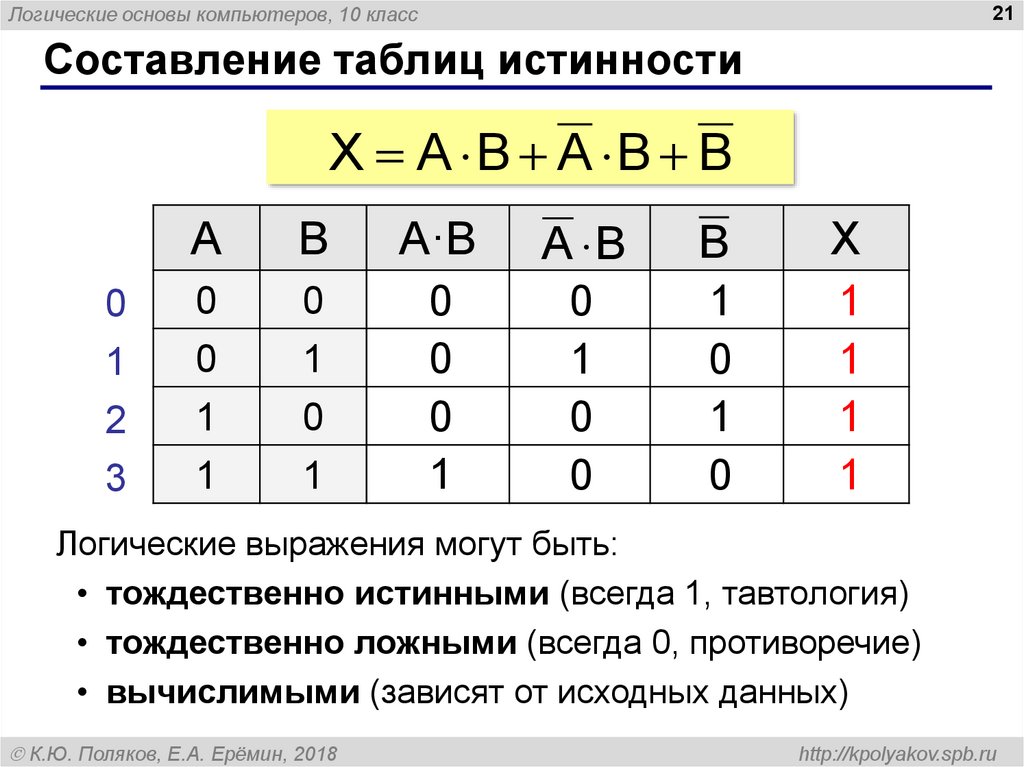
для логических операций и выражений, как строить

Содержание:

• Что такое таблицы истинности
• Логические операции
• Логические выражения
• Инверсия
• Конъюнкция
• Дизъюнкция
• Правила составления таблицы истинности
• Примеры построения таблицы истинности

Содержание

• Что такое таблицы истинности
• Логические операции
• Логические выражения
• Инверсия
• Конъюнкция
• Дизъюнкция
• Правила составления таблицы истинности
• Примеры построения таблицы истинности

Что такое таблицы истинности

Определение

Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов.

Таблица истинности необходима для совершения логических операций. Она включает в себя n+1 столбцы и 2ⁿ строки, где n — число используемых переменных. В первых n столбцах представлены разные значения аргументов функции, а в n+1 столбце представлены значения функции, которые она принимает на данном наборе аргументов.

Набором называется совокупность значений переменных. А = 0, В = 1. В случае, когда количество переменных n, число различных наборов будет равно 2^N. Например, для трех переменных число разных наборов будет равно 2³ = 8.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Для создания таблиц истинности используются обозначения логических значений 0 (ложь) и 1 (истина).

Можно встретить вариацию таблицы, в которой число столбцов равно n + число используемых логических операций. В подобной таблице  в первые n столбцы, так же как и в первом варианте, вписаны наборы аргументов, а остальные столбцы заполнены значениями подфункций, которые входят в запись функции.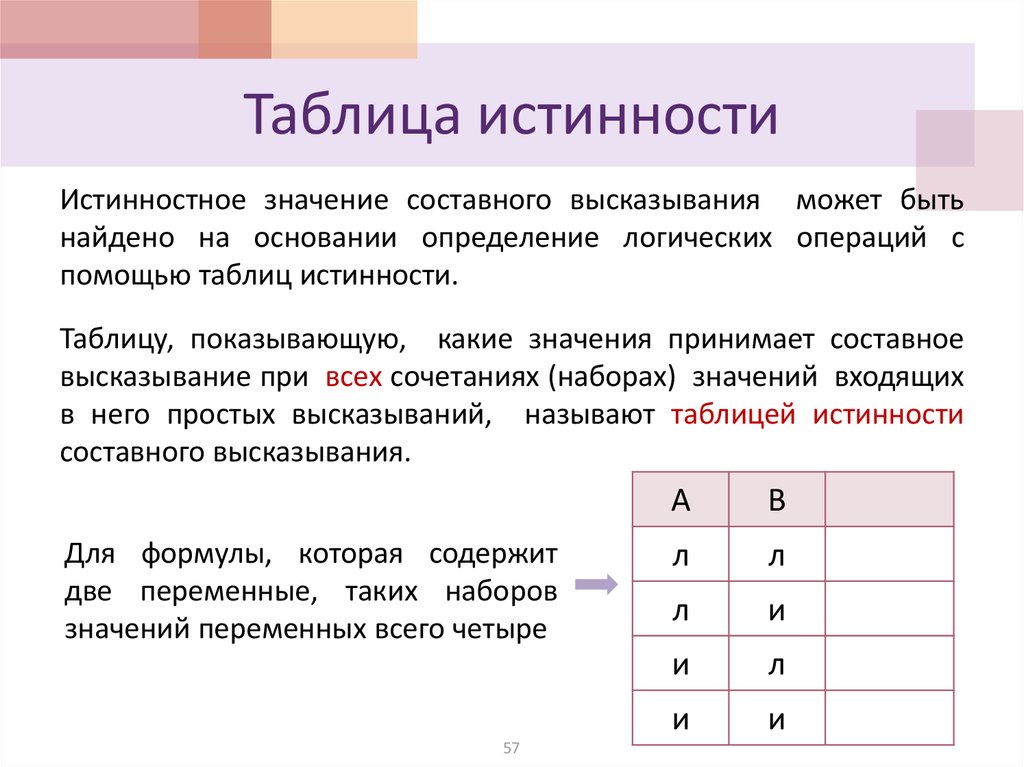 Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.

Применение таблиц истинности чаще всего встречается в булевой алгебре и в цифровой электронной технике для описания работы логических схем.

Логические операции

Определение

Логические операции — построение из одного или нескольких высказываний нового высказывания.

Результатом может являться не только образование нового высказывания, но и изменение содержания или объема уже данных высказываний. В случае логической операции истинность значения нового высказывания всецело определяется истинностью значения исходных высказываний. 

К логическим операциям относятся конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, эквиваленция, антиконъюнкция, антидизъюнкция.

Логические выражения

Определение

Логическое выражение — это запись, принимающая логическое значение «истина» или «ложь».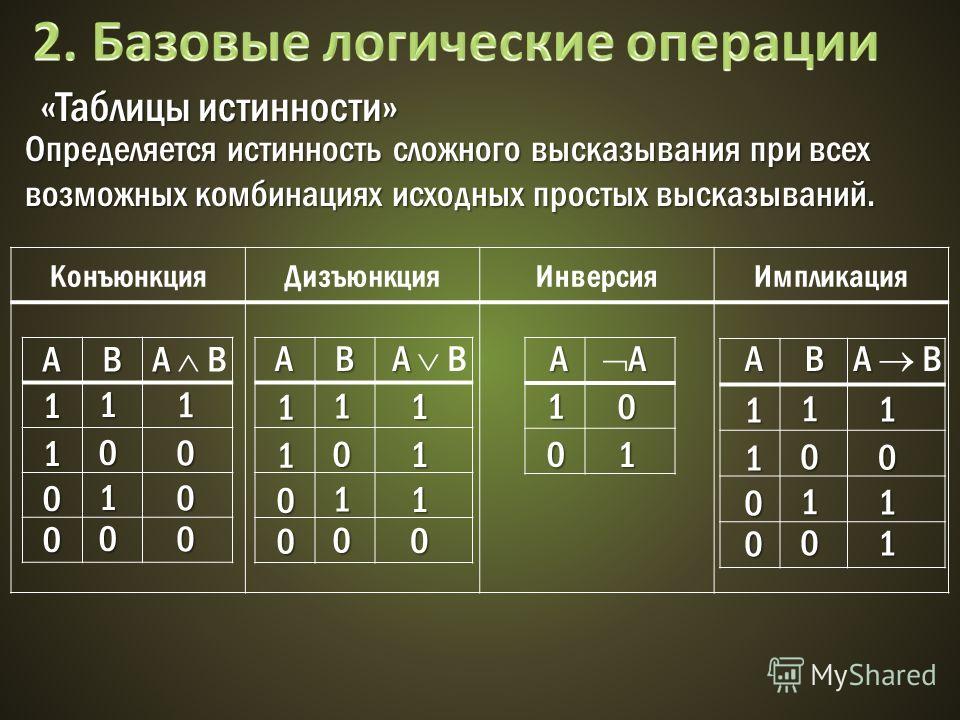

Их можно разделить на два типа:

• выражения, использующие операции сравнения и принимающие логические значения. Например, выражение a < b, где a = 12, а b = 9, равно значению «ложь»;
• логические выражения, которые связаны с логическими величинами и операциями. Например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина.

В логические выражения могут входить функции, алгебраические операции, операции сравнения и логические операции. Для таких случаев существует алгоритм выполнения действий. За исключением тех случаев, когда в логическом выражении присутствуют скобки, влияющие на порядок выполнения операций.

• вычисляется существующие функциональные зависимости;
• вычисляются алгебраические операции в обычном порядке;
• вычисляются операции сравнения в любом порядке;
• вычисляются логические операции начиная с операции отрицания. Следом вычисляется операция логического умножения, логического сложения, в последнюю очередь выполняются операции импликации и эквивалентности.

Инверсия

Определение

Инверсия или логическое отрицание — это логическая операция, при выполнении которой из данного высказывания получается новое высказывание. Это высказывание является отрицанием исходного высказывания.

Если данное высказывание обозначается буквой A, то отрицание исходного высказывания обозначается следующим образом \([\overline{A}]\). Кроме этого возможно использование условного обозначения \(\neg A\). Читаться это будет как «не А», «А ложно», «неверно, что А», «отрицание А».

Унарной в данном случае называется операция, которая используется относительно одной величины.

Конъюнкция

Определение

Конъюнкция — это логическое умножение. Эта операция, для которой требуются два и более логических величины. Конъюнкция соединяет логические высказывания при помощи связки «и».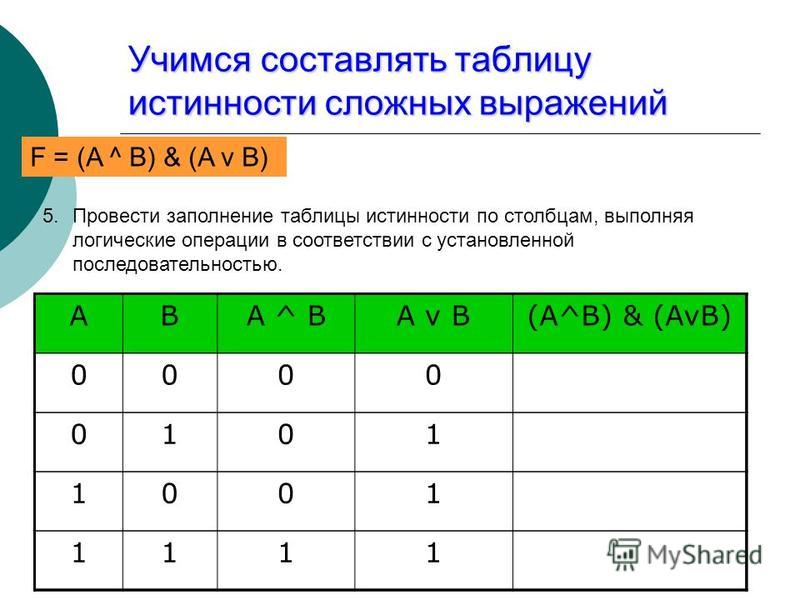

Связка изображается символом ∧.

Конъюнкция может быть истинной только в том случае, если оба высказывания истинны. Например, A ∧ B, если A = ложь, а B = истина, является ложным.

Дизъюнкция

Определение

Дизъюнкция — логическое сложение. Эта логическая операция соединяет два и более высказываний с помощью связки «или». Эта связка обозначается как ∨.

Логическое высказывание будет истинным, если истинно хотя бы одно из условий. Например, A ∨ B истинно, даже если А = истина, а В = ложь. Высказывание будет ложным только в том случае, если ложны и А, и В.

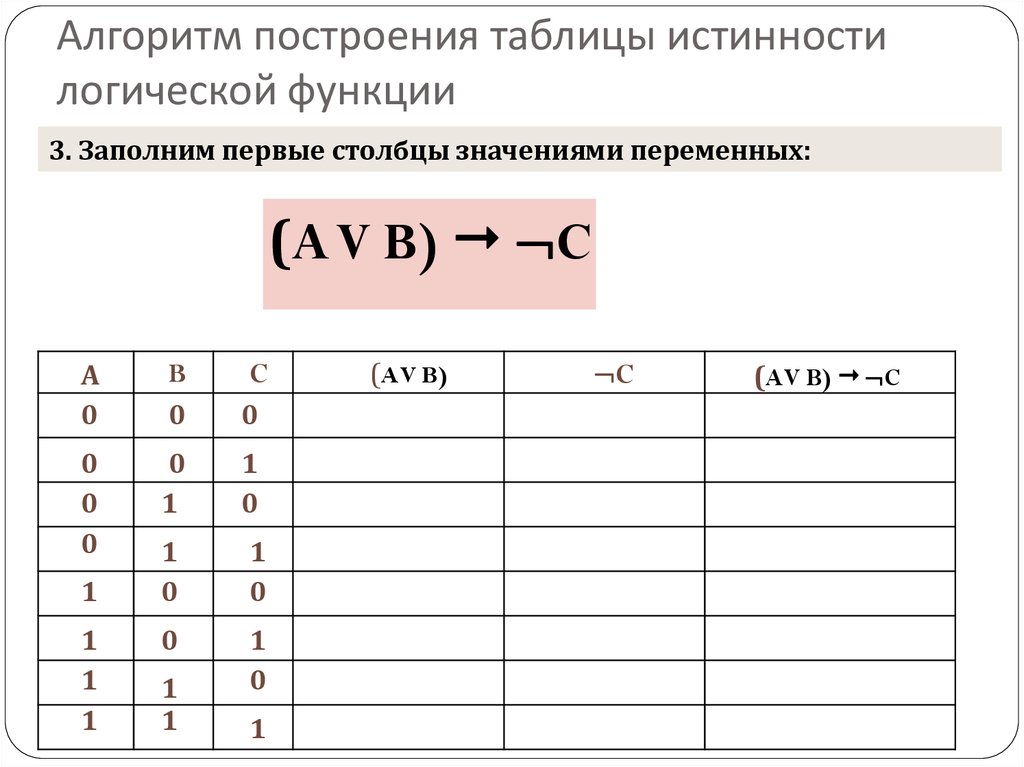
Правила составления таблицы истинности

Таблицу истинности можно построить для любого логического выражения. В этой таблице будут отражены все значения, которые принимает выражение при всех наборах значений входящих в него переменных.

Строить таблицы истинности необходимо по следующему алгоритму:

1. Вычислить число переменных в выражении (n).
2. Вычислить общее количество логических операций в выражении.
3. Определить последовательность, в которой будут выполняться логические операции.
4. Установить количество столбцов в таблице — количество переменных и количество операций.
5. Внести в шапку таблицы переменные и операции, соблюдая последовательность, определенную в пункте 3.
6. Высчитать количество строк в таблице, используя формулу m = 2ⁿ
7. Занести в таблицу наборы входных переменных. Они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2ⁿ−1.
8. Заполнить таблицу, совершая логические операции.

Примеры построения таблицы истинности

Задача

Построим таблицу истинности и решим выражение\( F = (A \vee B) \wedge (¬A \vee ¬B)\). Будем пользоваться приведенным выше алгоритмом.

1. Число переменных в выражении n = 2.
2. Общее количество логических операций в выражении — 5.
3. Последовательность выполнения логических операций — 1, 5, 2, 4, 3.
4. Количество столбцов — 7. Логические переменные (А и В) + логические операции \(\vee\), \(\wedge\), \(¬\), \(\vee\) , \(¬\) = 2 +5 = 7.
5. Количество строк — 5, исходя из m =2ⁿ, таким образом 2² = 4, 4+1 (строка заголовков столбцов) = 5.
6. Заполним таблицу.

Решение

А	В	\(А \vee В\)	¬А	¬В	\(¬А \vee ¬В\)	\((A \vee B) \wedge (¬A \vee ¬B)\)
0	0	0	1	1	1	0
0	1	1	1	0	1	1
1	0	1	0	1	1	1
1	1	1	0	0	0	0

После заполнения таблицы, ответ будет выглядеть следующим образом:

F = 0 при A = B = 0 и A = B = 1

Задача

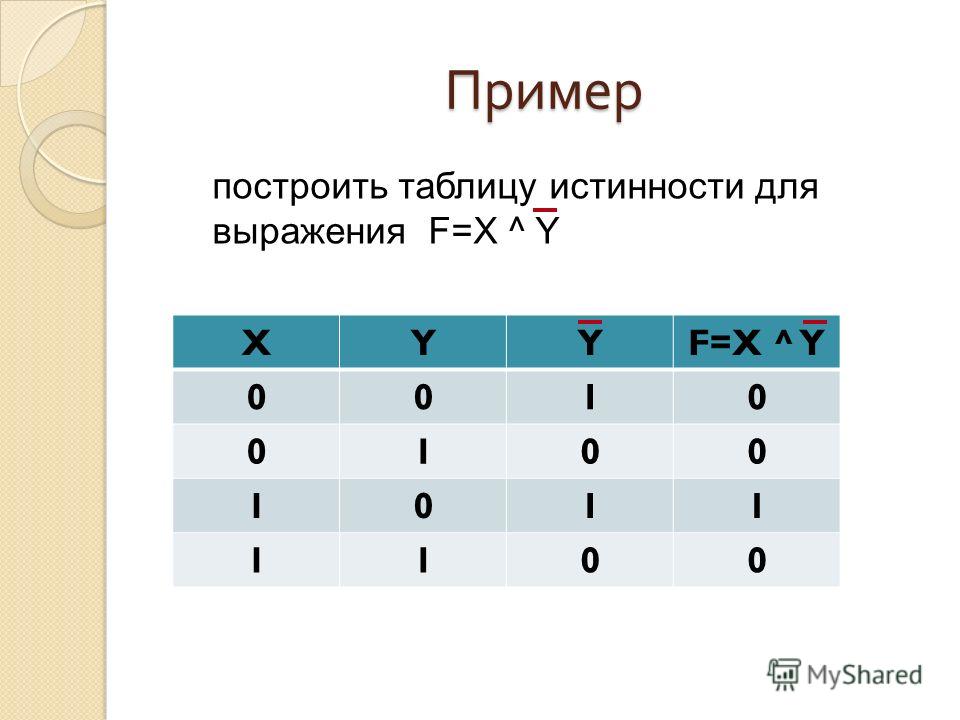
Построим еще одну таблицу истинности и решим выражение \(F = X \vee Y \wedge ¬Z\)

1. Число переменных в выражении n = 3.
2. Общее количество логических операций в выражении — 3.
3. Последовательность выполнения логических операций — 3, 2, 1.
4. Количество столбцов — 6. Логические переменные (X, Y, Z) + логические операции\( \vee\), \(\wedge\), ¬ = 3 + 3 = 6.
5. Количество строк — 9, исходя из m =2ⁿ, таким образом 2³ = 8, 8+1 (строка заголовков столбцов) = 9.
6. Заполним таблицу.

Решение

X	Y	Z	¬Z	\(Y \wedge ¬Z\)	\(X \vee Y \wedge ¬Z\)
0	0	0	q	0	0
0	0	1	0	0	0
0	1	0	1	1	1
1	0	0	1	0	1
1	0	1	0	0	1
1	1	0	1	1	1
1	1	1	0	0	1

После заполнения таблицы, ответ будет выглядеть следующим образом:

F = 0, при X = Y = Z = 0; при X = Y = 0 и Z = 1.

Насколько полезной была для вас статья?

Рейтинг: 2.54 (Голосов: 24)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Таблица истинности логических операций — алгоритм построения » Kupuk.net

Используя таблицы истинности логических операций, можно точно определить, верна ли функция при определённых значениях. В перечень заносят всевозможные комбинации переменных появляющихся на входе и соответствующие им состояния на выходе. Чаще всего таблицы применяют при проектировании и анализе цифровых схем. При этом в интернете существуют сервисы, с помощью которых построить такого рода сводку не составит труда даже слабо разбирающемуся в этой сфере пользователю.

Определения и понятия

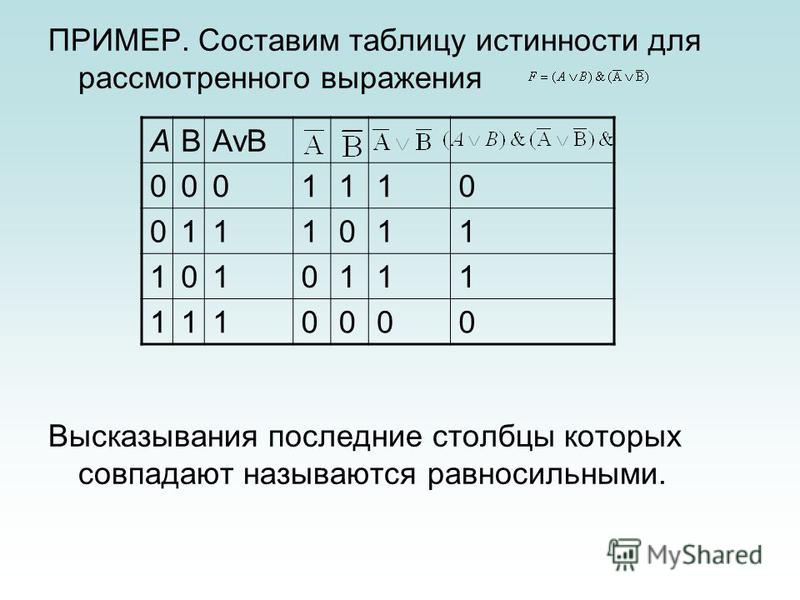
Под таблицей истинности понимают свод значений, которые может принять высказывание при сочетании различных входящих комбинаций.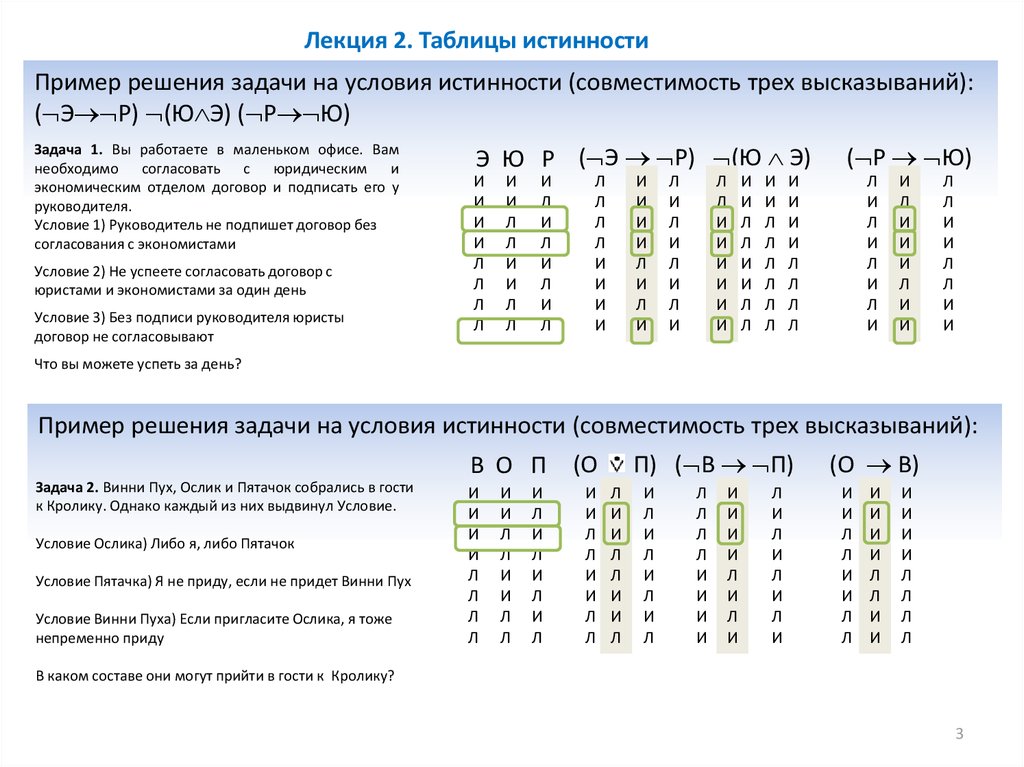 Другими словами, каждому набору функций или сигналам, присутствующим на входе чего-либо, соответствует строго определённые показатели на выходе. Все значения, являющиеся всевозможными высказываниями, называют логическими выражениями. Если в таблице последние столбцы логичных выражений идентичны, то рассматриваемый объект считается равносильным.

Любое выражение можно описать формулой, в которую будут включаться переменные, характеризующие состояния, и обозначающие функции знаки логических операций. Поэтому используя язык математики, в частности, алгебры, любое сложное высказывание можно разделить на несколько простых, а затем объединить логической связью.

Обычно значениями истинности описывают логическую функцию, у которой показатели параметров определяют верность. Раздел математики рассматривающий их на правдивость или ложность называется булевым. В 1854 году английский учёный Джордж Буль предложил метод, позволяющий проводить анализ классов и высказываний. Согласно ему, любое значение может принимать одно из двух состояний — истина или ложь.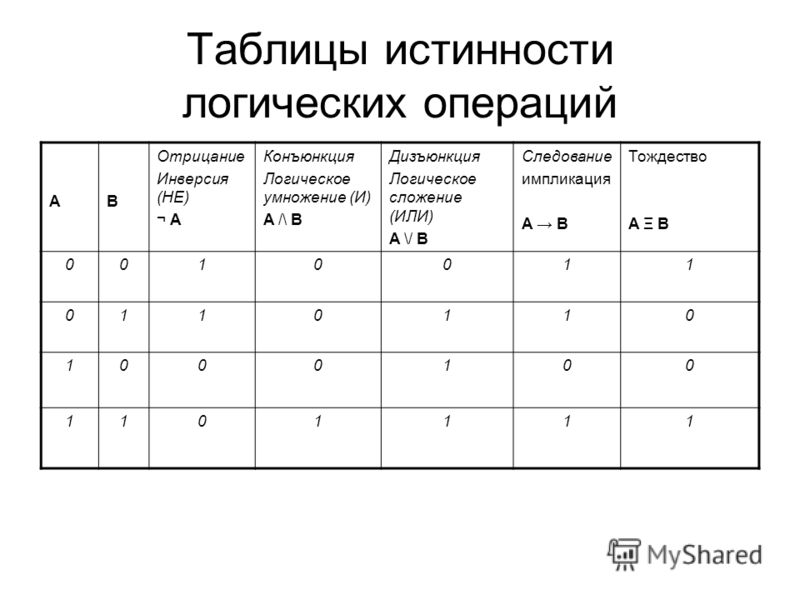

Эти состояния принято обозначать арабскими цифрами один либо ноль или словами true и false. Это возможно из-за того, что для математики важна только истинность высказываний, а конкретное содержание второстепенно. Простые высказывания принято считать логическими переменными, а сложные — функциями логики. Выражения для упрощения записи обозначают латинскими буквами A, B, C.

Применение двух цифр подчёркивает соответствие между двоичной системой счисления и математической логикой. В итоге с помощью последней стало удобным описывать работу цифровых схем радиоэлектронной аппаратуры, алгоритмы в программировании, проводить синтез и анализ результата выполнения операций.

Суждение о правильности построения таблиц истинности для логических выражений основано на учёте всех переменных и операций, последовательно выполняющихся в рассматриваемой функции. Обычно для начертания используют 2n+1 строк, где n обозначает количество входных переменных, и n+m столбцов, m — число значений на выходе.

Виды логических операций

В качестве наименьшей единицы измерения объёма данных принято считать бит. В него заносится одно из двух значений — ложь (0) или правда (1). Каждая ячейка, соответствующая биту, находится лишь в одном из этих состояний. Существуют определённые операции, используемые для действий с ячейками:

AND (И) — применяется для сравнения двух бит. Результатом действия будет единица, но лишь в том случае, если значения двух ячеек одинаковое. При остальных вариантах итог будет иметь устойчивое нулевое состояние.

OR (ИЛИ) — по сути, операция обратная AND. Результат становится нулевым, если содержимое двух сравниваемых бит одинаковое. В остальных случаях он равный единице.

XOR (ИЛИ) — если значения, содержащиеся в двух сравниваемых битах противоположны, при выполнении логического действия результат будет равный единице. Во всех остальных случаях он будет равняться нулю.

NOT (НЕ) — действие, используемое для одного бита. Если первоначально ячейка находилась в нулевом состоянии, то после выполнения над ней операции она станет равной единице и наоборот. Фактические это логическая инверсия.

Эти операции являются основными элементами при составлении таблиц истинности и получения возможного результата. На основании их построена алгебра Буля. Некоторые элементы получаются путём объединения нескольких операций. Так, существует состояние: NAND (И-НЕ) и NOR (ИЛИ-НЕ). Первый элемент является инверсией операции «И», а второй — «ИЛИ». На основании рассмотренных операторов строится работа всех цифровых интегральных схем.

В информатике существует своя терминология, обозначающая то или иное логическое действие. Так, AND называют операцией конъюнкции, OR — дизъюнкции, XOR — сложение по модулю 2, NOT — отрицание. Задача инженера при анализе схем или алгоритма сводится к выполнению булевой арифметики и упрощению выражений. Для этого используют различные правила и положения не требующих доказательства.

Аксиомы и законы

Построение таблиц в удобной форме позволяет определить, когда определённое действие или высказывание принимает верное значение, а в каком случае нет. В верхней строчке записывают логическую форму высказывания, а в столбцах — истинные значения. Некоторые комбинации высказываний всегда будут истинными или ложными, независимо от содержания. Поэтому и были сформулированы следующие законы:

Торжества. Записывается в виде утверждения: А = А. В этом случае таблица будет состоять из двух комбинаций: ложной и правдивой. Бинарная логическая связка «Если А, то А» является материальной импликацией. Для такого варианта всегда можно сказать, что А есть А. Этот закон обозначает то, что нельзя подменять одно понятие другим, иначе возникнут логические ошибки.

Противоречия. Согласно ему, утверждение, что А и НЕ-А, неверно: A & A = 0. Другими словами, если А истинное значение, то его отрицание не может быть ложным. То есть их перемножение будет всегда фальшивой операцией. Этот закон довольно часто применяется для упрощения сложных логических суждений.

Третьего исключённого. Закон записывается в виде A v A = 1 и обозначает, что в один и тот же момент высказывание может быть только правдивым или ложным. То есть третьего не дано.

Эти три закона фундаментальны. Без их соблюдения сделать любое правильное утверждение невозможно.

Для решения логических задач с помощью таблиц истинности используют различные формулы, соответствующие разного вида операциям. Одно из них логическое умножение (конъюнкция). В этом случае считается, что функция истинная лишь тогда, когда оба выражения являются верными: F = A & B. Другое логическое сложение (дизъюнкция). Оно гласит, что если оба выражения ложны, то и логическая функция будет неверной.

Кроме того, используется закон:

• инверсии (отрицания) — если логическое высказывание истинно, то отрицание его будет ложным выражением;
• импликации (следования) — для всегда истинного сложного логического выражения ложь будет тогда, когда из верности следует отрицание;
• эквивалентности (равнозначности) — выражение будет истинным лишь тогда, когда оба высказывания имеют одинаковое значение.

При построении таблиц нужно придерживаться установленного порядка выполнения упрощения операций. Вначале считают инверсию и конъюнкцию, а затем дизъюнкцию, импликацию и эквиваленцию. При изменении же порядка выполнения действий в описании логических операций используют скобки.

Алгоритм построения

Таблицы истинности показывают, какой вид может принять выражение при различных входящих в него значениях переменных.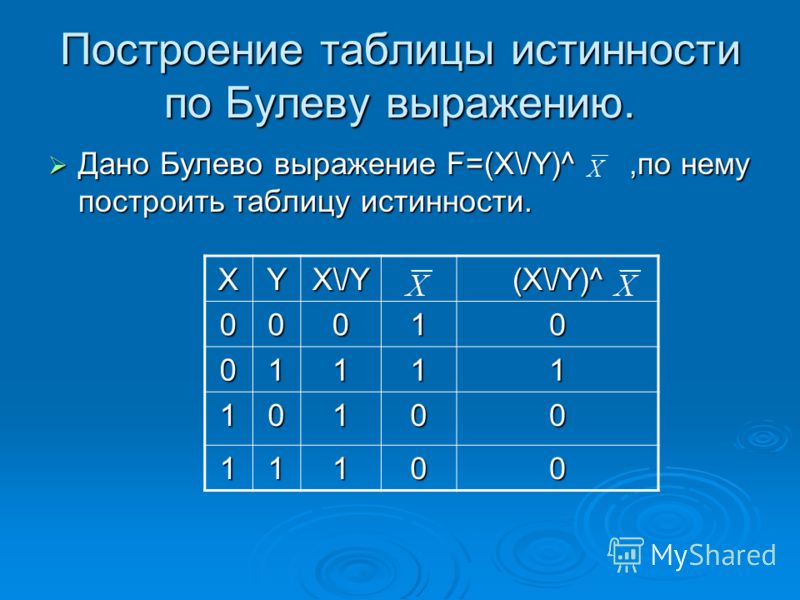 Для того чтобы их правильно построить и выполнить вычисление логического выражения нужно придерживаться установленного алгоритма. Построение таблиц выполняют в следующей последовательности:

• подсчитывают количество переменных n;
• вычисляют число строк для будущей таблицы используя формулу m = 2n+1;
• определяют число логических операций;
• устанавливают порядок выполнения операций в соответствии со скобками и приоритетами;
• строят таблицу с указанием столбцов и наборов значений, заданных логических операций;
• заполняют оставшиеся ячейки в таблице.

Для заполнения таблиц нужно упрощать выражения с учётом последовательности выполнения операций. При этом учитывать, что если значение какого-то из аргументов функции в соответствующей строке таблицы будет равное нулю, то записывать его нужно в виде отрицания.

Пример задания

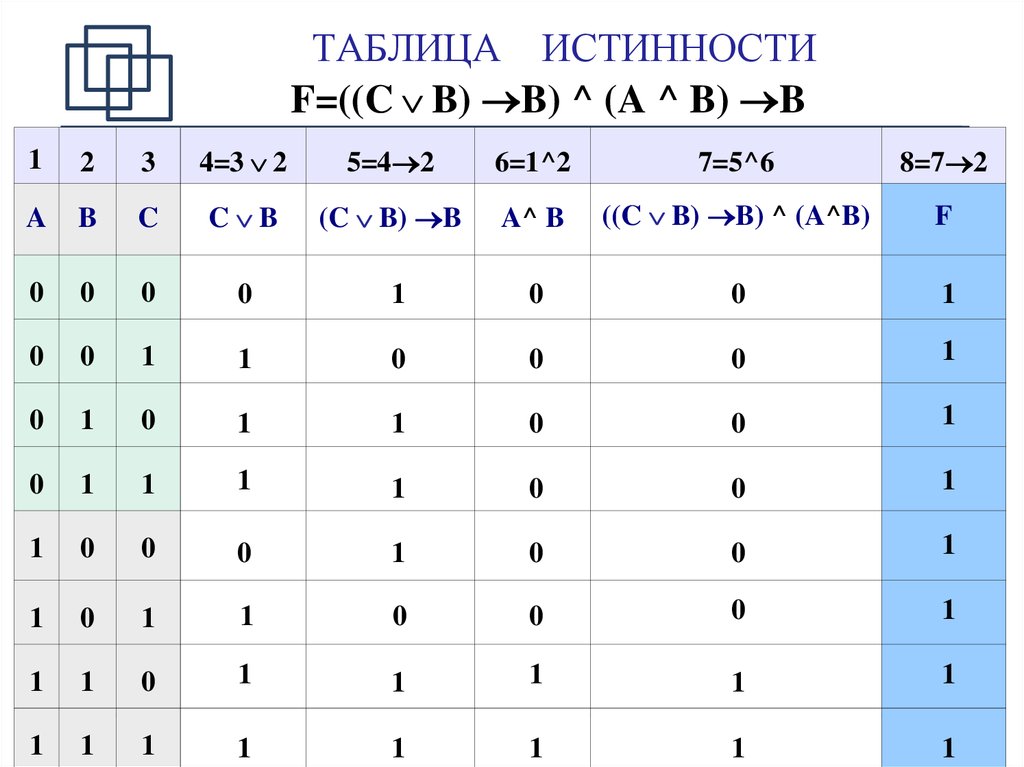
Пусть необходимо построить таблицу для логического выражения F = (A → B) * (A + B). Эта формула состоит из двух логических переменных A и B и нескольких операций. Начинают построение с определения строк. Используя формулу 2n+1 для рассматриваемого примера можно установить, что их число будет: x = 22 + 1 = 5.

Теперь следует определить число столбцов. Для этого используется формула, в которой учитывается количество переменных и операций. Последние можно просто посчитать, сложив количество разных знаков, используемых в записи формулы. Но правильней сначала расставить порядок операций, а затем посчитать. Согласно порядку действия над операциями их нумерацию можно представить в следующей очерёдности:

Импликация в первой скобке.

Инверсия во второй скобке переменной A.

Отрицание во второй скобке неизвестной B.

Сложение во втором члене.

Конъюнкция.

В итоге получится, что столбцов будет: Y = 2 + 5 = 7. Теперь нужно построить таблицу 7Х5. В шапку первого и второго столбца вписывают переменные, а затем операции над ними. Затем в строках, соответствующих A и B нужно записать всё, что с ними может произойти. В итоге останется только правильно посчитать последний столбец.

Для этого нужно использовать законы. Необходимо выполнить логическое умножение значений в скобках. Первой и второй строчке будет соответствовать операция произведения один на один, что в ответе даст единицу. Третьей и четвёртой — ноль на один, что в итоге даст ноль. Последний столбец является главным для рассматриваемой логической функции. По нему можно узнать значение логической функции для любых форм переменных A и B.

Это довольно простая задача, содержащая всего две переменных. Но в реальности, например, в программировании, их может быть намного больше. Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.

Например, заданно выражение (x + y + z) * (x + y). По сути, оно записано в совершенно нормальной конъюнктивной форме. Но для приведения его к этому виду нужно, чтобы во втором выражении стояла z.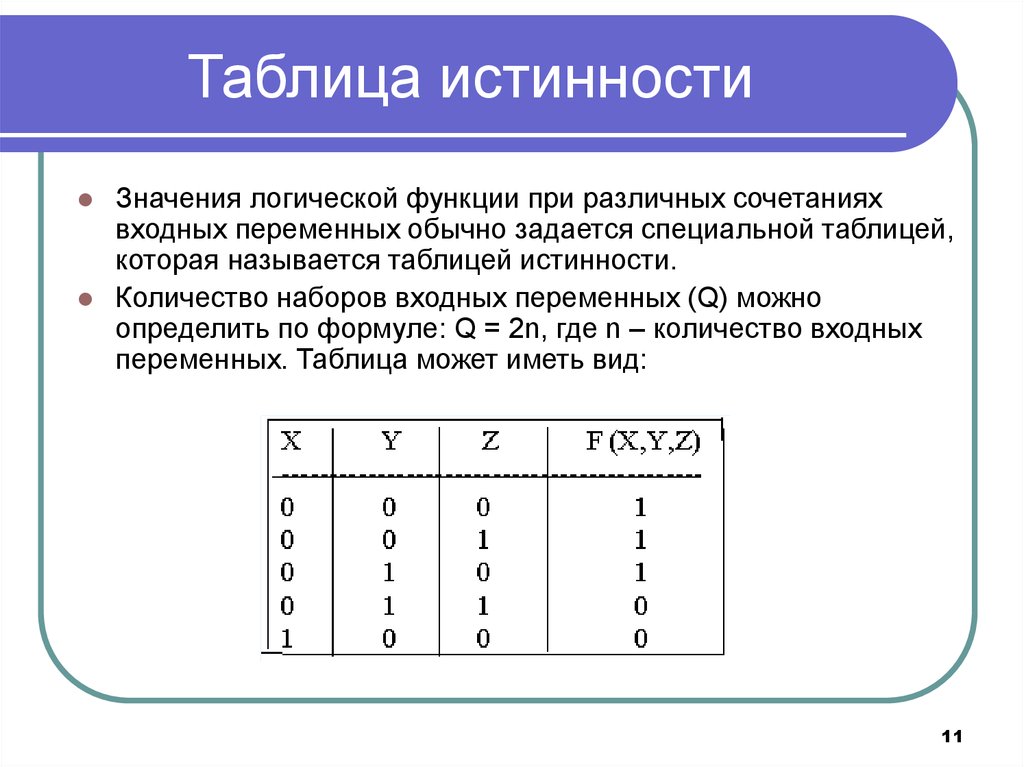 Для того чтобы её добавить необходимо обратить внимание на то, что внутри скобок стоит логическое сложение. Поэтому дописав к нему ноль, результат не изменится. Добавить ноль через z можно, как ноль умножить на НЕ z. В итоге получится выражение (x + y + z) * (x + y + z + z), для которого, используя алгоритм составить таблицу уже не так и сложно.

Вычисления онлайн

В интернете есть сервисы, автоматически строящие таблицы истинности. Такие сайты предлагают свои услуги бесплатно и доступны даже тем, кто слабо ориентируется в теме. С их помощью можно находить таблицы для довольно сложных выражений, решение которых требует скрупулёзности в расчёте. В основе онлайн-вычислений заложены принципы логических законов, поэтому за достоверность результата можно не переживать. Тем более расчёт занимает совсем небольшое количество времени.

Для того чтобы воспользоваться сайтами-калькуляторами пользователю необходимо знать обозначение операций, иметь подключение к интернету и установленный веб-обозреватель, поддерживающий Flash-технологию. Регистрацию, указание личных данных сервисы, предлагающие такого рода услуги, не требуют.

Из различных порталов можно отметить три наиболее популярных калькулятора:

Allcalc.

Programforyou.

Uchim.

Эти сайты имеют интуитивно понятный интерфейс и что довольно полезно, на своих страницах содержат краткую теорию, используемую для составления таблиц истинности и даже примеры решений.

Логические выражения и таблица истинности в примерах решения задач

Теория по этой теме по этой теме Пройти тестирование по этой теме Контрольная по этой теме

 №1.

Докажите, что А <=> В равносильно (A\/ ¬B) /\ (¬A\/ B)

 Для доказательства равносильности двух высказываний достаточно построить таблицу истинности для высказывания (A\/ ) /\ (\/ B) и сравнить ее с таблицей истинности эквивалентности:

А	В	¬B	A\/¬B	¬A	¬AVB	(A\/¬B) /\ (¬A \/B)
0	0	1	1	1	1	1
0	1	0	0	1	1	0
1	0	1	1	0	0	0
1	1	0	1	0	1	1

Последние столбцы этих функций совпадают, значит, они равносильны. ЧТД.

 

№2.

Укажите, какое логическое выражение равносильно выражению 

A /\ ¬ (¬B \/ C)

   1) ¬A \/ ¬B \/ ¬C

   2) A /\ ¬B /\ ¬C  

   3) A /\ B /\ ¬C 

   4) A /\ ¬B /\ C

Ответ:  3

№3.

Постройте таблицу истинности для логического выражения:

1)A=>B<=> ¬А \/  B 

Ответ:

А	В	A=>B	¬А	A → B<=> ¬А	A → B<=> ¬А \/  B
0	0	1	1	1	1
0	1	1	0	0	1
1	0	0	0	1	1
1	1	1	0	0	1

2)F=A<=>B<=>(¬А \/  B) /\ (¬B\/  А)

Ответ:

 

 

 

 

 

№4.

Определите истинность следующего высказывания: «За окном светит солнце, и нет дождя».

Решение:

Нам дано сложное составное высказывание. Выделим из него простые высказывания:

А = «За окном светит солнце»

В = «За окном дождь»

 Составим логическую функцию, соответствующую данному высказыванию.

F(A, B) = A /\ ¬B

построим таблицу истинности для данной логической функции.

A	B	¬B	A /\ ¬B
0	0	1	0
0	1	0	0
1	0	1	1
1	1	0	0

 Ответ: логическое выражение принимает значение истина только при наборе F(1,0)=1.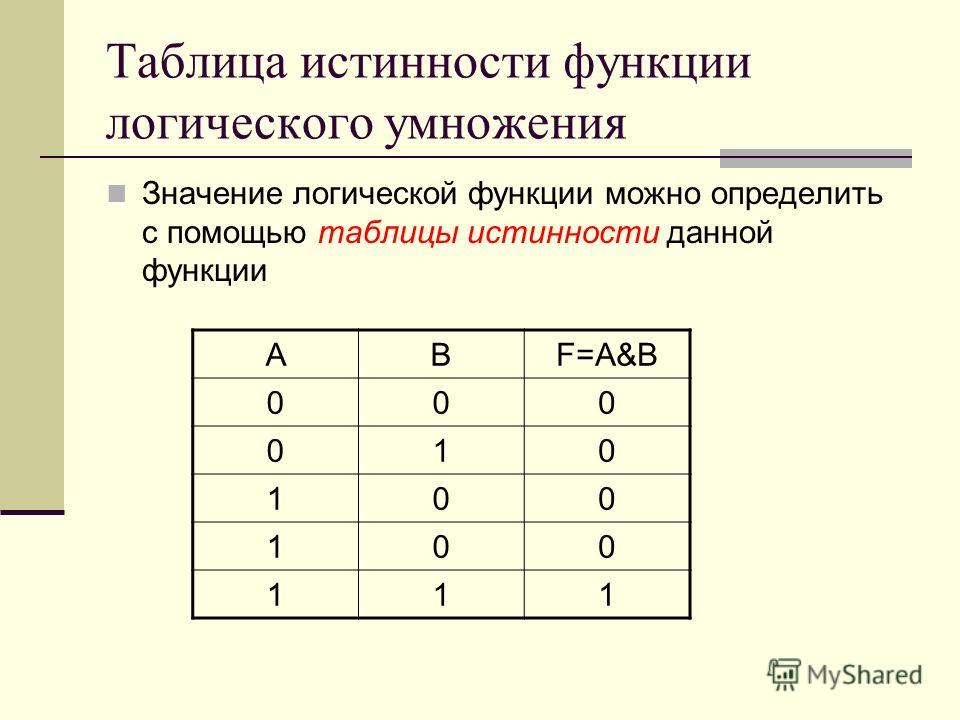 Следовательно, данное нам высказывание истинно только тогда, когда первое простое высказывание истинно, а второе ложно.

 

№5.

Определите истинность следующего высказывания: «Гости смеялись, шутили и не расходились по домам».

Решение:

Выделим из данного сложного высказывания простые высказывания:

А = «Гости смеялись»

В = «Гости шутили»

С = «Гости расходились по домам»

Составим логическую функцию, соответствующую данному высказыванию.

F(A, B, С) = A/\ B /\¬C

Построим таблицу истинности для данной логической функции.

 

A	B	C	¬C	A /\ B/\¬C
0	0	0	1	0
0	0	1	0	0
0	1	0	1	0
0	1	1	0	0
1	0	0	1	0
1	0	1	0	0
1	1	0	1	1
1	1	1	0	0

Ответ: логическое выражение принимает значение истина только при наборе F(1,1,0)=1. Следовательно, данное нам высказывание истинно только тогда, когда первое и второе простые высказывания истинны, а второе ложно.

 

№6.

На языке алгебры логики составьте истинное тождество, соответствующее заданному условию задачи:

Школьника, Миша, остававшийся в классе на перемене, был вызван к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчик ответили следующее: «Я не бил окно, и Коля тоже…»

Известно, что он либо сказал чистую правду, либо в одной части заявления соврал, а другое его высказывание истинно, либо оба факта исказил.

Решение:

Пусть

А = «Окно разбил Миша»

В = «Окно разбил Коля»

Если Миша сказал чистую правду, то¬А /\ ¬В = 1.

Если в одной части заявления Миша соврал, а другое его высказывание истинно, то (¬А /\ В) \/ (А /\¬В) = 1

Если Миша оба факта исказил, то А /\ В = 1.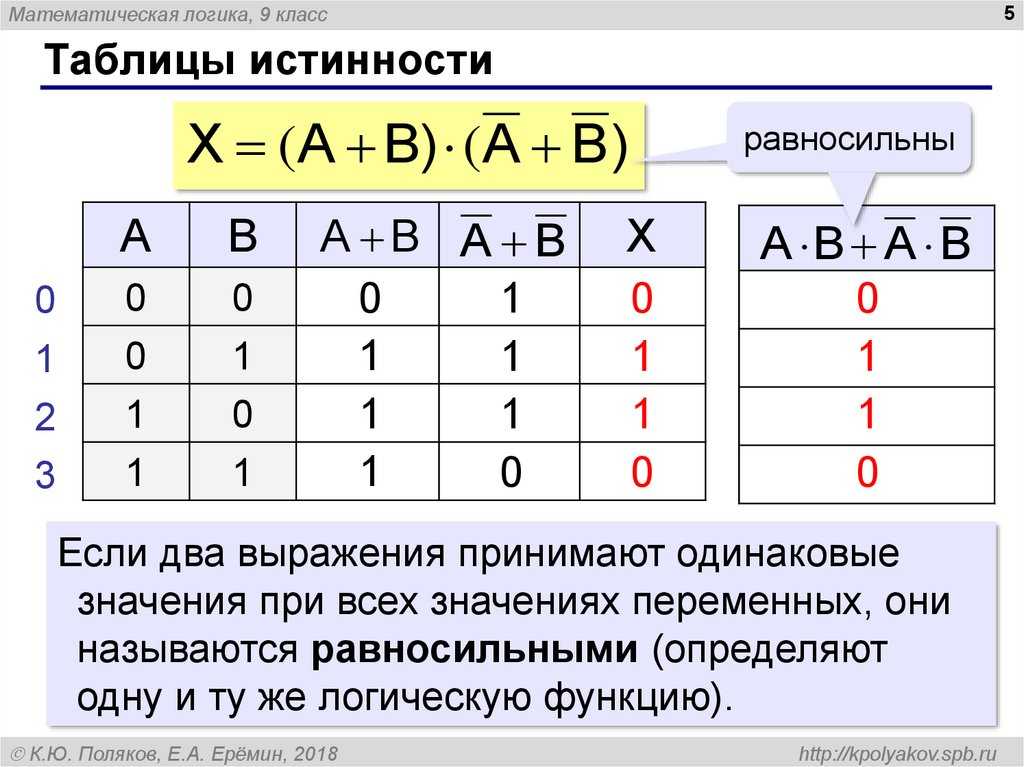

Ответ:

Истинное тождество, соответствующее условию задачи будет выглядеть так: ¬А /\ ¬В  \/¬А /\ В \/А /\ ¬ В \/ А /\ В = 1.

Введение в таблицы истинности, утверждения и связные слова

Поиск

Таблица истинности — это одна из тех вещей в математике, которую гораздо легче понять, когда вы видите, как она выглядит и как она работает, чем изучать ее определение. В любом случае, мы попытаемся дать ему определение, чтобы иметь базовое или базовое понимание того, что это такое.

---

Определение таблицы истинности

В математической логике таблица истинности представляет собой диаграмму строк и столбцов, показывающую истинностное значение (либо «T» для «Истина», либо «F» для «Ложь») каждой возможной комбинации заданные операторы (обычно представленные заглавными буквами P, Q и R), управляемые логическими связками.

---

Два компонента таблицы истинности

I. Утверждение

Определение: Утверждение — это предложение или математическое выражение, которое либо определенно истинно, либо определенно ложно, но не то и другое одновременно. Обычно обозначается заглавной буквой или переменной. Обычными являются P, Q, R и S.

II. Логическая связка

Определение : Логическая связка — это слово, обычно записываемое как символ, который несет определенную логическую инструкцию о том, как выполнять оператор или составной оператор. Логические связки также можно использовать для соединения или объединения двух или более утверждений для формирования нового утверждения.

---

Примеры утверждений

• Утверждения, которые определенно верны.

• Заведомо ложные утверждения.

ОТКРЫТОЕ ПРЕДЛОЖЕНИЕ

Открытое предложение — это предложение, которое является либо истинным, либо ложным в зависимости от значения переменной (переменных). Этот тип предложения НЕ является утверждением, потому что оно должно быть определенно истинным или определенно ложным.

Примеры:

• Число \color{red}k четно. 92=0. Помните, что 0 не является ни положительным, ни отрицательным. Таким образом, это предложение НЕ высказывание, а простой падеж открытого предложения.

  ---

  Общие логические связки

  В этой части урока моя цель состоит в том, чтобы кратко познакомить вас с пятью общими логическими связками , которые также известны как логические операторы. Вы также узнаете символ, используемый для каждого оператора, и что он означает.

  Примечание: \large{P} и \large{Q} являются операторами.

  1) Отрицание

  • Символ: ~ или \neg читается как НЕ
  • Пример: ~P или \neg P переводится как «не P» или «неверно, что P»

  2 ) Соединение

  • Символ: \клин читается как И
  • Пример: P \клин Q переводится как «Р и Q»

  читается как ИЛИ

• Пример: P \vee Q переводится как «P или Q“

4) Импликация или условное обозначение

• Символ: \Стрелка вправо читается как ПОДРАЗУМЕВАЕТ
• Пример: P \Стрелка вправо Q обозначает утверждение «P подразумевает

Q» 90 90 Двойная импликация или биусловие

• Символ: \Leftrightarrow читается как ЕСЛИ И ТОЛЬКО ЕСЛИ
• Пример: P \Leftrightarrow Q означает утверждение «P тогда и только тогда, когда Q»

---

Таблицы истинности для отрицания, соединения , и дизъюнкция

Я намерен охватить только три основных логических оператора, а именно: отрицание , конъюнкция и дизъюнкция . В этой части урока вы познакомитесь с тем, как может выглядеть таблица истинности.

У меня есть отдельный урок, посвященный подробному обсуждению того, как построить таблицы истинности упомянутых здесь логических связок и остальных.

А пока давайте сосредоточим наше внимание на приведенных ниже таблицах истинности:

1. Таблица истинности отрицания

Правило логического оператора отрицания

Значение истинности инвертированного утверждения полностью противоположно истинному значению исходного утверждения.

---

2. Таблица истинности конъюнкции

Правило конъюнкции или логического оператора «И»

Составное высказывание P и Q, записанное как P\wedge Q, является ИСТИННЫМ, если оба высказывания P и Q равны истинный. В противном случае утверждение P\wedge Q является ЛОЖНЫМ.

---

3. Таблица истинности дизъюнкции

Правило дизъюнкции или логический оператор «ИЛИ»

Составное утверждение P или Q, записанное как P \vee Q, является ИСТИННЫМ, если хотя бы одно из утверждений P и Q истинно. Кроме того, поскольку это «включающее ИЛИ», утверждение P \vee Q также ИСТИННО, если оба P и Q истинны. Следовательно, ЛОЖНО только в том случае, если и P, и Q ложны.

---

Вас также могут заинтересовать:

Таблицы истинности пяти (5) общих логических связок или операторов

Обратное, обратное и противоположное условному выражению

17.6: Таблицы истинности: условные, биусловные

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

34287

• Дэвид Липпман
• Колледж Пирса через OpenTextBookStore

Ранее мы обсуждали условные операторы, в которых мы выполняем действие на основе значения условия. Теперь мы рассмотрим другую версию условного предложения, иногда называемую импликацией, в которой говорится, что вторая часть должна логически следовать из первой.

Условное

Условное является логическим составным оператором, в котором оператор \(p\), называемый антецедентом, подразумевает оператор \(q\), называемый консеквентом.

Условное выражение записывается как \(p \rightarrow q\) и переводится как «если \(p\), то \(q\)».

Пример 19

Английское высказывание «Если идет дождь, то облака — это небо» является условным высказыванием. Это имеет смысл, потому что если антецедент «идет дождь» истинен, то и последующее «на небе тучи» также должно быть истинным.

Обратите внимание, что это утверждение ничего не говорит нам о том, чего ожидать, если не идет дождь; на небе могут быть облака, а может и нет. Если антецедент ложен, то консеквент становится нерелевантным.

Пример 20

Предположим, вы заказываете футболку команды онлайн во вторник и хотите получить ее к пятнице, чтобы надеть ее на игру в субботу. На веб-сайте написано, что если вы заплатите за ускоренную доставку, вы получите майку к пятнице. В какой ситуации сайт говорит неправду?

Возможны четыре исхода:

1) Вы платите за ускоренную доставку и получаете футболку к пятнице

2) Вы платите за ускоренную доставку и не получаете футболку к пятнице

3) Вы не платите за ускоренную доставку и получаете футболку к пятнице

4) Вы не платите за ускоренную доставку и не получаете футболку к пятнице

Только один из этих результатов доказывает, что веб-сайт лгал: второй исход, при котором вы платите за ускоренную доставку, но не получаете майку к пятнице. Первый результат — это именно то, что было обещано, так что с этим проблем нет. Третий результат не является ложью, потому что на веб-сайте никогда не говорилось, что произойдет, если вы не оплатите ускоренную доставку; возможно, майка прибудет к пятнице, независимо от того, заплатили вы за ускоренную доставку или нет. Четвертый результат не является ложью, потому что, опять же, веб-сайт не давал никаких обещаний о том, когда джерси прибудет, если вы не оплатите ускоренную доставку.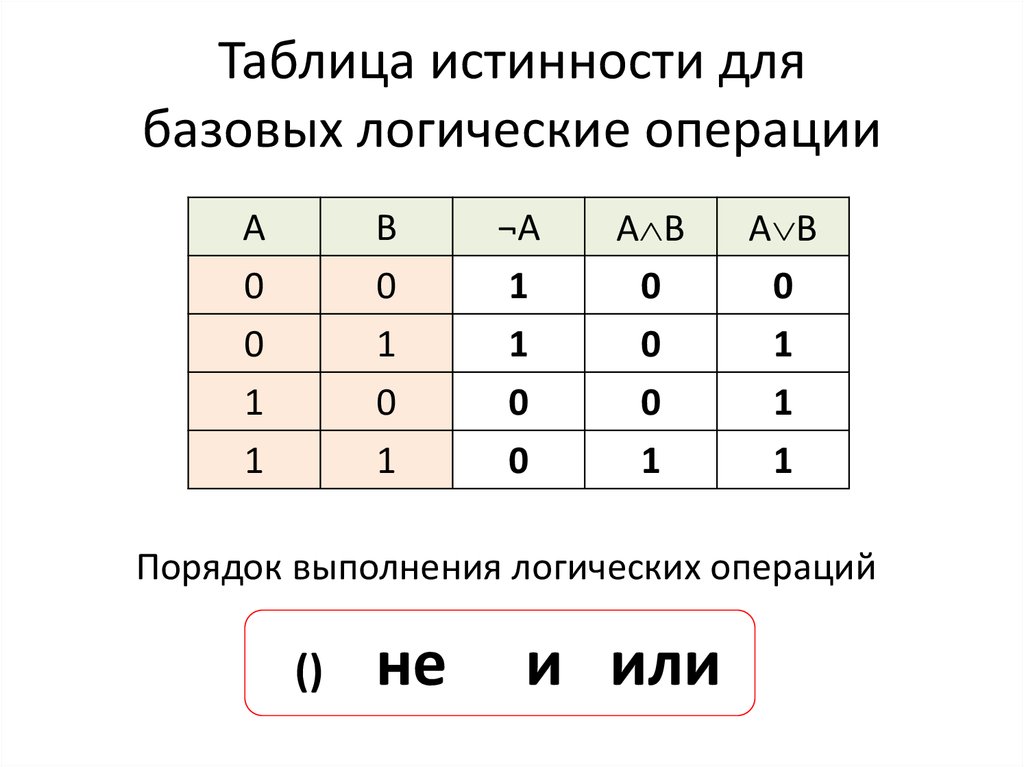

Может показаться странным, что третий результат в предыдущем примере, в котором первая часть ложна, а вторая часть верна, не является ложью. Однако помните, что если антецедент ложен, мы не можем судить о консеквенте. На веб-сайте никогда не говорилось, что оплата ускоренной доставки была единственным способом получить майку к пятнице.

Пример 21

Друг говорит вам: «Если вы загрузите это изображение на Facebook, вы потеряете работу». При каких условиях вы можете сказать, что ваш друг был не прав?

Возможны четыре исхода:

1) Вы загрузите изображение и потеряете работу

2) Вы загрузите изображение и не потеряете работу

3) Вы не загрузите изображение и потеряете работу

4) Вы не загружаете изображение и не теряете работу

Существует только один возможный случай, когда вы можете сказать, что ваш друг был неправ: второй вариант, при котором вы загружаете изображение, но сохраняете свою работу . В последних двух случаях ваш друг ничего не сказал о том, что произойдет, если вы не загрузите картинку, поэтому вы не можете сказать, что его утверждение было неверным. Даже если вы не загрузили картинку и все равно потеряли работу, ваш друг никогда не говорил, что вы гарантированно сохраните свою работу, если не загрузите картинку; вместо этого вы можете потерять работу из-за того, что пропустили смену или ударили своего начальника.

В традиционной логике условное выражение считается истинным, если нет случаев, в которых антецедент истинен, а консеквент ложен.

Таблица истинности условного выражения

\(\begin{array}{|c|c|c|}
\hline p & q & p \rightarrow q \\
\hline \mathrm{T} & \mathrm{T } & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T } \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline
\end{array}\)

Опять же, если антецедент \(p\) ложен, мы не можем доказать, что утверждение ложно, поэтому результат третьей и четвертой строк верен.

Пример 22

Построить таблицу истинности для утверждения \((m \wedge \sim p) \rightarrow r\)

Решение

Начнем с построения таблицы истинности с 8 строками, чтобы охватить все возможные сценарии.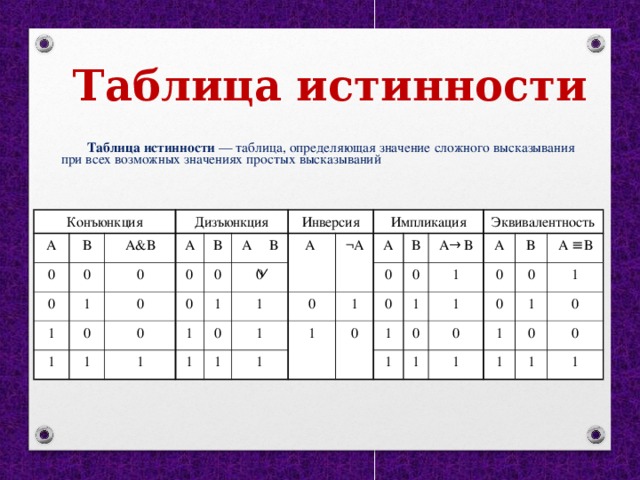 Затем мы можем сосредоточиться на антецеденте, \(m \клин \sim p\).

\(\begin{массив}{|с|с|с|}
\hline m & p & r \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{ F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\ hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline
\end{массив}\)

\(\begin{array}{|c|c|c|c|}
\hline m & p & r & \sim p \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\ hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{ T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{ F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \ mathrm{T} \\
\hline
\end{массив}\)

\(\begin{array}{|c|c|c|c|c|}
\hline m & p & r & \sim p & m \ клин \sim p \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{ T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \ матрм{Т} & \матрм{Т} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \ mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline
\end{массив}\)

Теперь мы можем создать столбец для условного выражения. Поскольку отслеживать все T и \(\mathrm{Fs}\) может быть сложно, почему бы нам не скопировать столбец для \(r\) справа от столбца для \(m \wedge \ дурачок\) ? Это значительно упрощает чтение условного оператора слева направо.

\(\begin{array}{|c|c|c|c|c|c|c|}
\hline m & p & r & \sim p & m \wedge \sim p & r & (m \wedge \sim p) \rightarrow r \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \ mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{ T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \ mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline
\end{массив}\)

Когда \(m\) истинно, \(p\) ложно, а \(r\) ложно — четвертая строка таблицы — тогда антецедент \(m \клин \sim p\) будет true, но последующее false, что приводит к недопустимому условному выражению; каждый другой случай дает действительное условие.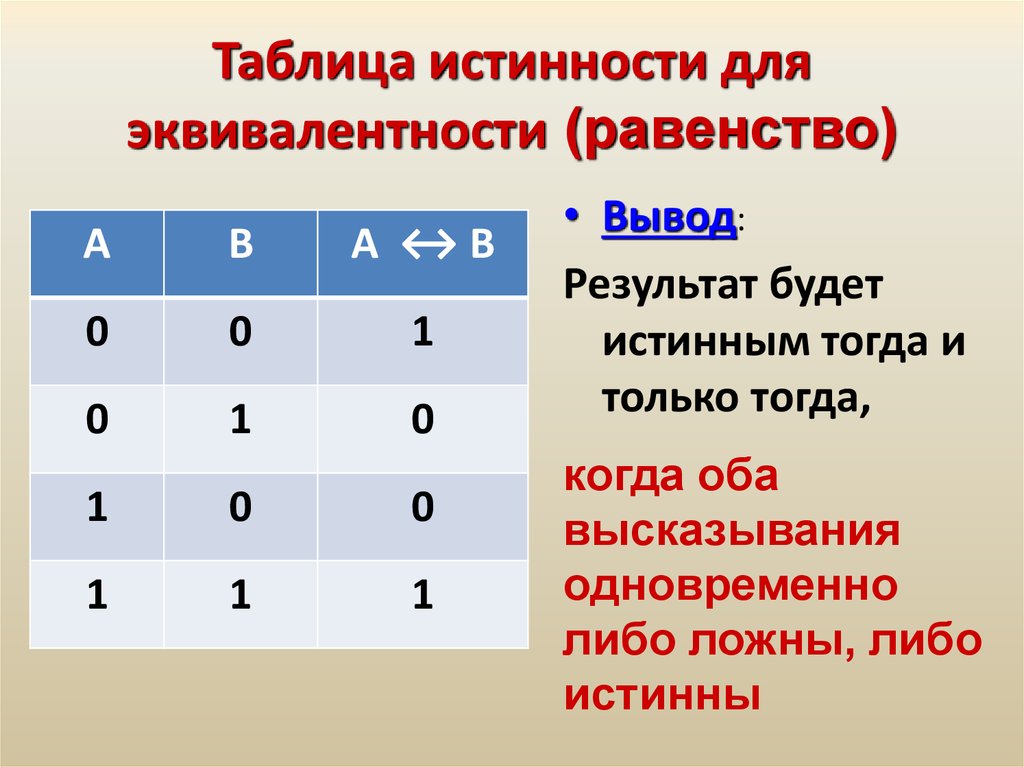

Если вам нужна реальная ситуация, которую можно смоделировать с помощью \((m \клин \sim p) \rightarrow r\), подумайте об этом: пусть \(m=\) мы заказываем фрикадельки, \(p=\ ) мы заказываем пасту, и \(r=\) Роб доволен. Утверждение \((m \wedge \sim p) \rightarrow r\) звучит так: «Если мы закажем фрикадельки и не закажем макароны, Роб будет счастлив». Если \(m\) истинно (мы заказываем фрикадельки), \(p\) ложно (мы не заказываем пасту) и \(r\) ложно (Роб недоволен), то утверждение ложно. , потому что мы удовлетворили антецеденту, а Роб не удовлетворил консеквенту. 9{\prime \prime} \quad \sim q \rightarrow \sim p\)

Пример 23

Рассмотрим снова условное предложение «Если идет дождь, то на небе облака». Кажется разумным предположить, что это правда.

Обратное: «Если на небе облака, значит, идет дождь». Это не всегда правда.

Обратное: «Если не идет дождь, то на небе нет облаков». Точно так же это не всегда верно.

Противоположный вариант: «Если на небе нет облаков, значит, не идет дождь». Это утверждение истинно и эквивалентно исходному условному выражению.

Глядя на таблицы истинности, мы видим, что исходное условное и контрапозитивное логически эквивалентны, а обратное и обратное логически эквивалентны.

Эквивалентность

Условное утверждение и его противоположность логически эквивалентны.

Инверсия и инверсия условного оператора логически эквивалентны.

Другими словами, исходное утверждение и контрапозитив должны согласовываться друг с другом; они оба должны быть истинными, или они оба должны быть ложными. Точно так же обратное и обратное должны согласовываться друг с другом; они оба должны быть истинными, или они оба должны быть ложными.

Имейте в виду, что символическая логика не может идеально представить английский язык. Например, нам может понадобиться изменить время глагола, чтобы показать, что одно событие произошло раньше другого.

Пример 24

Предположим, верно следующее утверждение: «Если я съем это гигантское печенье, меня тошнит». Какое из следующих утверждений также должно быть верным?

1. Если меня тошнит, значит, я съел это гигантское печенье.
2. Если я не съем это гигантское печенье, меня не тошнит.
3. Если меня не тошнит, значит, я не ел это гигантское печенье.

Решение

1. Обратное, что не всегда верно. Я мог чувствовать себя плохо по какой-то другой причине, например, пить кислое молоко.
2. Это обратное, что не обязательно верно. Опять же, я мог чувствовать себя плохо по какой-то другой причине; отказ от куки не гарантирует, что меня не тошнит.
3. Это контрапозитив, что верно, но мы должны мыслить несколько в обратном направлении, чтобы объяснить это. Если бы я съел печенье, меня бы стошнило, но, поскольку меня не тошнит, значит, я не ел печенье.

Еще раз обратите внимание, что исходное утверждение и противопоставленное имеют одинаковое истинностное значение (оба истинны), а обратное и обратное имеют одинаковое истинностное значение (оба ложны).

Попробуйте сейчас 5

«Если вы будете готовить лосося в микроволновой печи на кухне для персонала, я буду на вас зол». Если это утверждение верно, то какое из следующих утверждений также должно быть верным?

1. Если вы не будете готовить лосося в микроволновой печи на кухне для персонала, то я не буду на вас злиться.
2. Если я на тебя не сержусь, значит, ты не приготовила лосося на кухне для персонала.
3. Если я злюсь на тебя, значит, ты приготовил лосося в микроволновой печи на кухне для персонала.

Ответить

Вариант b правильный, потому что он противоположен исходному утверждению.

Рассмотрим утверждение «Если вы припаркуетесь здесь, то получите штраф». Какой набор условий докажет, что это утверждение ложно?

1. Вы не паркуетесь здесь и получаете штраф.
2. Вы не паркуетесь здесь и не получаете штраф.
3. Вы припарковались здесь и не получили штраф.

Первые два утверждения не имеют значения, потому что мы не знаем, что произойдет, если вы припаркуетесь в другом месте. Однако третье утверждение противоречит условному утверждению «Если вы припаркуетесь здесь, то получите билет», потому что вы припарковались здесь, но не получили билет. Этот пример демонстрирует общее правило; отрицание условного предложения может быть записано как союз: «Это не тот случай, что если вы припаркуетесь здесь, то вам дадут билет» эквивалентно «Вы припаркуетесь здесь и вы не получите билет».

Отрицание условного предложения

Отрицание условного утверждения логически эквивалентно соединению антецедента и отрицанию следствия.

\(\sim(p \rightarrow q)\) эквивалентно \(p \wedge \sim q\)

Пример 25

Какое из следующих утверждений эквивалентно отрицанию «Если вы не смажьте сковороду маслом, тогда еда к ней прилипнет» ?

1. Не смазала сковороду маслом и еда к ней не прилипла.
2. Я не смазал сковороду маслом, и продукты прилипли к ней.
3. Я смазал сковороду маслом, и еда к ней не прилипла.

Решение

1. Это верно; это соединение предшествующего и отрицание следствия. Чтобы опровергнуть тот факт, что если не смазывать сковороду маслом, пища прилипает, я должен не смазывать сковороду маслом, и еда не будет прилипать.
2. По сути, это исходное утверждение без отрицания; «если… то» заменено на «и».
3. Это по существу согласуется с первоначальным утверждением и не может его опровергнуть.

Попробуйте прямо сейчас 6

«Если вы пойдете плавать менее чем через час после обеда, у вас начнутся судороги». Какое из следующих утверждений эквивалентно отрицанию этого утверждения?

1. Я пошел плавать более чем через час после обеда, и у меня начались судороги.
2. Я пошел плавать менее чем через час после обеда, и у меня не было судорог.
3. Я пошел плавать более чем через час после обеда, и у меня не было судорог.

Ответить

Вариант b эквивалентен отрицанию; он сохраняет первую часть прежней и отрицает вторую часть.

В повседневной жизни мы часто имеем в виду более сильное значение, когда используем условный оператор. Подумайте: «Если вы отправите свои часы сегодня, вам заплатят в следующую пятницу». На самом деле представитель платежной ведомости имеет в виду следующее: «Если вы отправите свои часы сегодня, вам заплатят в следующую пятницу, а если вы не отправите свои часы сегодня, то вам не заплатят в следующую пятницу». Условный оператор if t , то p также включает обратное утверждение: если не t , то не p . Более компактный способ выразить это утверждение: «В следующую пятницу вам заплатят тогда и только тогда, когда вы отправите свое расписание сегодня». Оператор этой формы называется бикондициональным .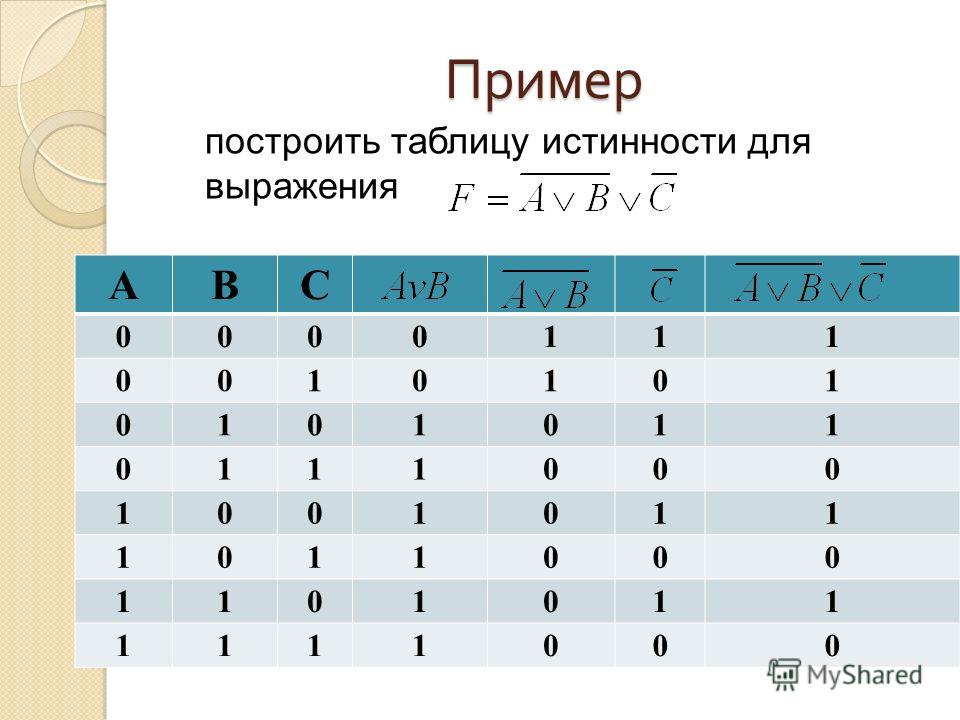 {\prime \prime}\).

Поскольку биусловный оператор \(p \leftrightarrow q\) эквивалентен \((p \rightarrow q) \wedge(q \rightarrow p),\), мы можем думать о нем как об условном операторе, объединенном с его обратным: если \(p\), то \(q\) и , если \(q\), то \(p\). Двунаправленная стрелка показывает, что условный оператор идет слева направо 90 507 и 90 508 справа налево. Бикондиционал считается истинным, пока антецедент и консеквент имеют одинаковое истинностное значение; то есть они либо оба истинны, либо оба ложны.

Таблица истинности для бикондиционала

\(\begin{array}{|c|c|c|}
\hline p & q & p \leftrightarrow q \\
\hline \mathrm{T} & \mathrm{T } & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F } \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline
\end{array}\)

Обратите внимание, что четвертая строка, где оба компонента ложны, правда; если вы не отправите свой табель учета рабочего времени и вам не заплатят, человек из платежной ведомости сказал вам правду.

Пример 26

Предположим, что это утверждение верно: «Мусоровоз проезжает по моей улице тогда и только тогда, когда сегодня утро четверга». Какое из следующих утверждений может быть верным?

1. Сейчас полдень четверга, а мусоровоз сегодня утром не приехал на мою улицу.
2. Сегодня понедельник, и по моей улице едет мусоровоз.
3. Сегодня среда, 23:59, и мусоровоз сегодня не приехал на мою улицу.

Решение

1. Это не может быть правдой. Это похоже на вторую строку таблицы истинности; это правда, что я только что пережил утро четверга, но это ложь, что приехал мусоровоз.
2. Этого не может быть. Это похоже на третью строку таблицы истинности; неверно, что сегодня четверг, но правда, что приехал мусоровоз.
3. Возможно, это правда. Это похоже на четвертую строку таблицы истинности; неверно, что сегодня четверг, но также неверно и то, что приехал мусоровоз, так что все получилось как надо.

Попробуйте сейчас 7

Предположим, верно следующее утверждение: «Я ношу кроссовки тогда и только тогда, когда занимаюсь спортом». Определите, должно ли каждое из следующих утверждений быть истинным или ложным.

1. Я занимаюсь спортом, но не ношу кроссовки.
2. Я ношу кроссовки и не занимаюсь спортом.
3. Я не тренируюсь и не ношу кроссовки.

Ответить

Варианты a и b неверны; с верно.

Пример 27

Создайте таблицу истинности для утверждения \((A \vee B) \leftrightarrow \sim C\)

Решение

Всякий раз, когда у нас есть три утверждения-компонента, мы начинаем с перечисления всех возможных комбинаций значений истинности для \(A, B,\) и \(C.\) После создания этих трех столбцов мы можем создать четвертый столбец для предшествующего, \(A \vee B\). Теперь мы временно проигнорируем столбец для \(C\) и сосредоточимся на \(A\) и \(B\), записывая значения истинности для \(A \vee B\).

\(\begin{array}{|c|c|c|}
\hline A & B & C \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{ T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{ T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{ Ф}\
\hline
\end{array}\)

\(\begin{array}{|c|c|c|c|}
\hline A & B & C & A \vee B \\
\hline \ mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \ mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline
\end{array}\)

Далее мы можем создайте столбец для отрицания \(C\). (Игнорируйте столбец \(A \vee B\) и просто инвертируйте значения в столбце \(C\).)

\(\begin{array}{|c|c|c|c|c|}
\hline A & B & C & A \vee B & \sim C \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{T} & \ mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{ Т}\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \ mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline
\end{array}\)

Наконец, мы находим истинностные значения \((A \vee B) \leftrightarrow \ сим С\). Помните, бикондиционал истинен, когда значения истинности двух частей совпадают, и ложен, когда значения истинности не совпадают.

\(\begin{array}{|c|c|c|c|c|c|}
\hline A & B & C & A \vee B & \sim C & (A \vee B) \leftrightarrow \сим С\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{T} & \ mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{ T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \ mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline
\end{array}\)

Чтобы проиллюстрировать эту ситуацию, предположим, что вашему начальнику нужно, чтобы вы выполнили один из проектов \(A \) или проект \(B\) (или оба, если у вас есть время). Если вы сделаете один из проектов, вы не получите плохой обзор (\(C\) означает плохой). Таким образом, \((A \vee B) \leftrightarrow \sim C\) означает: «Вы не получите плохой обзор тогда и только тогда, когда вы делаете проект \(A\) или проект \(B\)». Глядя на несколько строк таблицы истинности, мы видим, как это работает. В первой строке все \(A, B,\) и \(C\) верны: вы выполнили оба проекта и получили плохой отзыв, а это не то, что ваш начальник сказал вам! Вот почему окончательный результат первой строки ложный. В четвертой строке \(A\) верно, \(B\) ложно, а \(C\) ложно: вы спроектировали \(A\) и не получили плохой отзыв. Это то, что сказал ваш босс, так что окончательный результат этого ряда верен. А в восьмой строке \(A, B\) и \(C\) все ложные: вы не занимались ни одним проектом и не получили плохой отзыв. это , а не , что, по словам вашего босса, произойдет, поэтому окончательный результат этой строки ложен. (Даже если вы можете быть счастливы, что ваш босс не выполнил угрозу, таблица истинности показывает, что ваш босс солгал о том, что произойдет.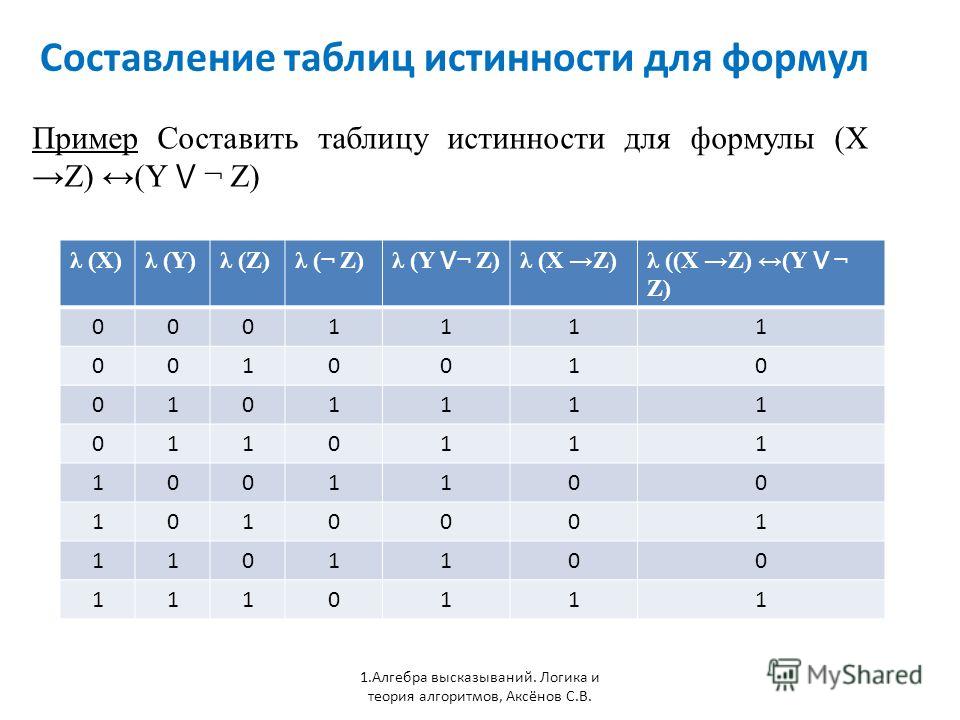 ) лицензия CC BY-SA 3.0, созданная, измененная и/или курируемая Дэвидом Липпманом (The OpenTextBookStore) с помощью исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Дэвид Липпман

   Лицензия

   СС BY-SA

   Версия лицензии

   3,0

   Показать страницу Содержание

   нет

2. Метки

   1. источник@http://www. opentextbookstore.com/mathinsociety

Таблицы истинности и анализ аргументов: примеры | Математика для гуманитарных наук |

Таблицы истинности

Поскольку сложные логические утверждения могут быть сложными для понимания, мы можем создать таблицу истинности , чтобы отслеживать, какие значения истинности для простых утверждений делают сложное утверждение истинным и ложным

Таблица истинности

Таблица, показывающая результирующее истинностное значение сложного утверждения для всех возможных истинностных значений простых утверждений.

Пример 1

Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Получите секционную 9-ку».0090 или что-нибудь с фаэтоном».

Это сложное утверждение состоит из двух более простых условий: «является секционным» и «имеет фаэтон».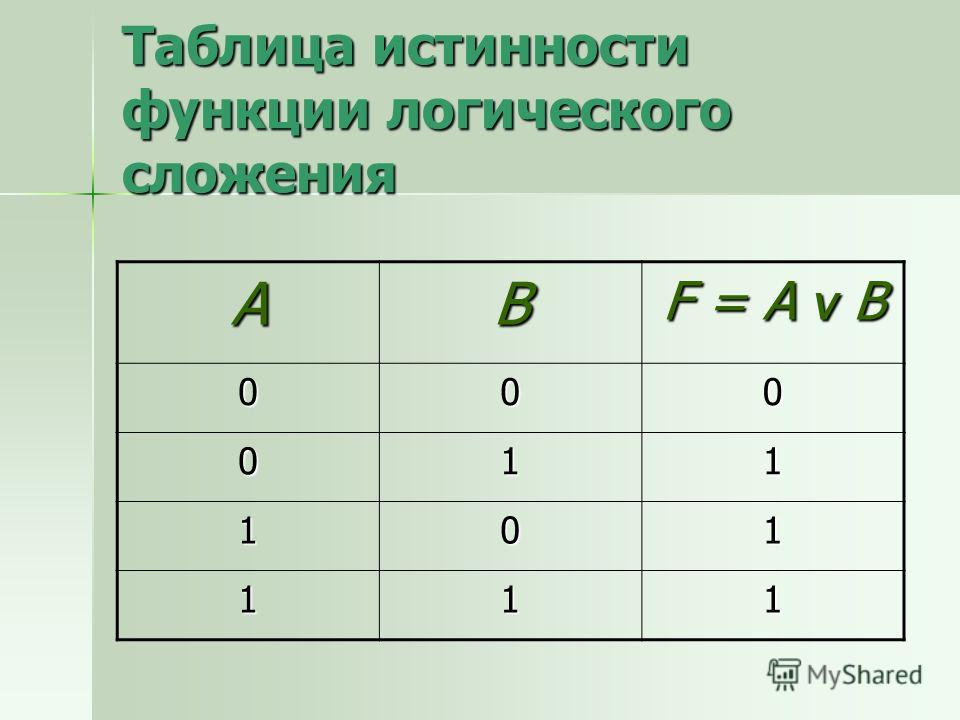 Для простоты давайте использовать S для обозначения «является секционным» и C для обозначения «имеет шезлонг». Условие S верно, если кушетка секционная.

Таблица истинности для этого будет выглядеть так:

S	С	С или C
Т	Т	Т
Т	Ф	Т
Ф	Т	Т
Ф	Ф	Ф

В таблице T используется для true, а F для false. В первой строке, если S верно и C также верно, то сложное утверждение « S или C » верно. Это будет секционная, в которой также есть шезлонг, что соответствует нашему желанию.

Помните также, что или в логике не являются исключительными; если кушетка имеет обе функции, она соответствует условию.

Чтобы еще больше сократить наши обозначения, мы собираемся ввести некоторые символы, которые обычно используются для и , или и вместо .

Символы

Символ ⋀ используется для и : A и B обозначается как A ⋀ B .

Символ ⋁ используется для или : A или B обозначается A ⋁ B

Символ ~ используется для , а не : не A 900 7091 ~ Вы можете запомнить первые два символа, связав их с фигурами объединения и пересечения. A ⋀ B будут элементами, которые существуют в обоих множествах, в A ⋂ B. Аналогично, A ⋁ B будут элементами, которые существуют в любом наборе, в A ⋃ B.

В предыдущем примере таблица истинности на самом деле просто обобщала то, что мы уже знаем о том, как работают операторы или . Ниже показаны таблицы истинности для основных утверждений и , или и , а не .

Основные таблицы истинности

А	Б	А ⋀ Б
Т	Т	Т
Т	Ф	Ф
Ф	Т	Ф
Ф	Ф	Ф

А	Б	А ⋁ В
Т	Т	Т
Т	Ф	Т
Ф	Т	Т
Ф	Ф	Ф

А	~А
Т	Ф
Ф	Т

Таблицы истинности становятся действительно полезными при анализе более сложных логических выражений.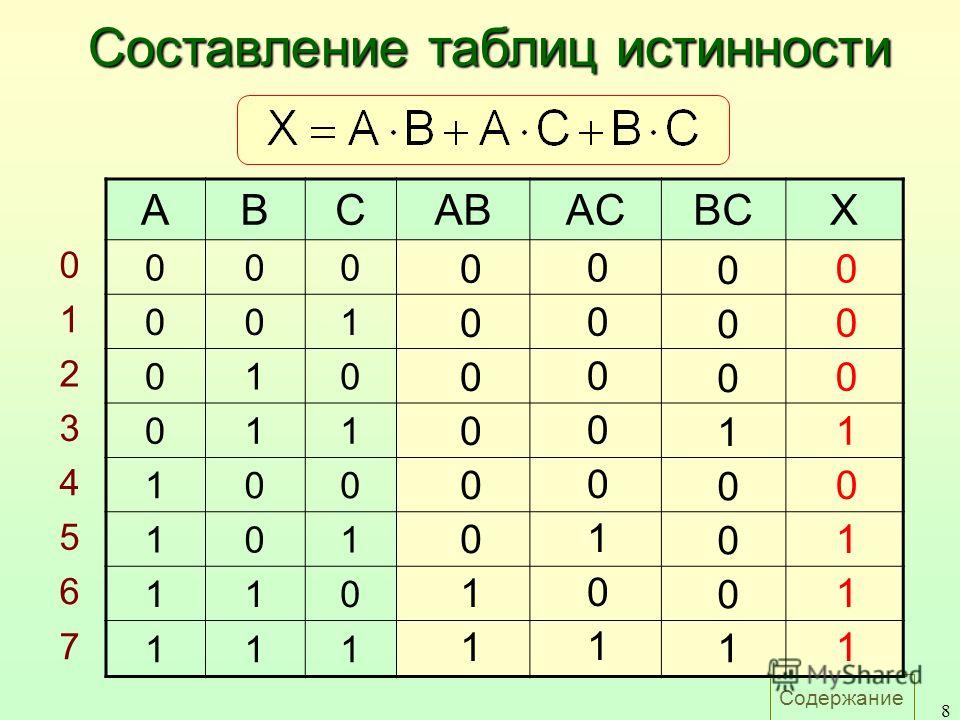

Пример 2

Составьте таблицу истинности для утверждения 9.0090 A ⋀ ~( B ⋁ C )

Помогает работать изнутри наружу при создании таблиц истинности и создавать таблицы для промежуточных операций. Начнем с перечисления всех возможных комбинаций значений истинности для A , B и C . Обратите внимание, что первый столбец содержит 4 T, за которыми следуют 4 F, второй столбец содержит 2 T, 2 F, затем повторяется, а последний столбец чередуется. Этот шаблон гарантирует рассмотрение всех комбинаций. Наряду с этими начальными значениями мы перечислим значения истинности для самого внутреннего выражения, Б ⋁ С .

А	Б	С	В ⋁ С
Т	Т	Т	Т
Т	Т	Ф	Т
Т	Ф	Т	Т
Т	Ф	Ф	Ф
Ф	Т	Т	Т
Ф	Т	Ф	Т
Ф	Ф	Т	Т
Ф	Ф	Ф	Ф

Затем мы можем найти отрицание B ⋁ C , работая с столбцом B ⋁ C , который мы только что создали.

А	Б	С	В ⋁ С	~( Б ⋁ С )
Т	Т	Т	Т	Ф
Т	Т	Ф	Т	Ф
Т	Ф	Т	Т	Ф
Т	Ф	Ф	Ф	Т
Ф	Т	Т	Т	Ф
Ф	Т	Ф	Т	Ф
Ф	Ф	Т	Т	Ф
Ф	Ф	Ф	Ф	Т

Наконец, мы находим значения А и ~( В ⋁ С )

А	Б	С	В ⋁ С	~( Б ⋁ С )	А ⋀ ~( В ⋁ С )
Т	Т	Т	Т	Ф	Ф
Т	Т	Ф	Т	Ф	Ф
Т	Ф	Т	Т	Ф	Ф
Т	Ф	Ф	Ф	Т	Т
Ф	Т	Т	Т	Ф	Ф
Ф	Т	Ф	Т	Ф	Ф
Ф	Ф	Т	Т	Ф	Ф
Ф	Ф	Ф	Ф	Т	Ф

Оказывается, это сложное выражение верно только в одном случае: если А истинно, В ложно и С ложно.

Когда мы обсуждали условия ранее, мы обсуждали тип, при котором мы предпринимаем действие на основе значения условия. Сейчас мы поговорим о более общей версии условного предложения, иногда называемой 9.0003 следствие .

Последствия

Импликации — это логические условные предложения, утверждающие, что утверждение p , называемое антецедентом, подразумевает следствие q .

Импликации обычно записываются как p → q

Последствия аналогичны условным операторам, которые мы рассматривали ранее; p → q обычно записывается как «если p, то q» или «p, следовательно, q». Разница между импликациями и условными предложениями заключается в том, что условные предложения, которые мы обсуждали ранее, предполагают действие — если условие истинно, то в результате мы предпринимаем какое-то действие. Импликации — это логическое утверждение, предполагающее, что следствие должно логически следовать, если антецедент истинен.

Пример 3

Английское высказывание «Если идет дождь, то на небе облака» является логическим следствием. Это правильный аргумент, потому что если антецедент «идет дождь» истинен, то следствие «на небе облака» также должно быть истинным.

Обратите внимание, что утверждение ничего не говорит нам о том, чего ожидать, если не идет дождь. Если антецедент ложен, то импликация становится нерелевантной.

Пример 4

Друг говорит вам, что «если вы загрузите эту фотографию в Facebook, вы потеряете работу». Возможны четыре исхода:

1. Вы загружаете изображение и сохраняете свою работу
2. Вы загрузили картинку и потеряли работу
3. Вы не загружаете картинку и сохраняете свою работу
4. Вы не загрузите картинку и потеряете работу

Есть только один возможный случай, когда ваш друг солгал — первый вариант, когда вы загружаете картинку и сохраняете свою работу. В последних двух случаях ваш друг ничего не сказал о том, что произойдет, если вы не загрузите изображение, поэтому вы не можете заключить, что его заявление недействительно, даже если вы не загрузили изображение и все равно потеряли работа.

В традиционной логике импликация считается достоверной (истинной) до тех пор, пока нет случаев, в которых антецедент истинен, а следствие ложно. Важно помнить, что символическая логика не может охватить все тонкости английского языка.

Значения истинности для следствий

р	q	р → q
Т	Т	Т
Т	Ф	Ф
Ф	Т	Т
Ф	Ф	Т

Пример 5

Постройте таблицу истинности для утверждения ( m ⋀ ~ p ) → r

Начнем с построения таблицы истинности для антецедента.

м	стр	~ р	м ⋀ ~ р
Т	Т	Ф	Ф
Т	Ф	Т	Т
Ф	Т	Ф	Ф
Ф	Ф	Т	Ф

Теперь мы можем построить таблицу истинности для импликации

м	р	~ р	м ⋀ ~ р	р	( м ⋀ ~ р ) → р
Т	Т	Ф	Ф	Т	Т
Т	Ф	Т	Т	Т	Т
Ф	Т	Ф	Ф	Т	Т
Ф	Ф	Т	Ф	Т	Т
Т	Т	Ф	Ф	Ф	Т
Т	Ф	Т	Т	Ф	Ф
Ф	Т	Ф	Ф	Ф	Т
Ф	Ф	Т	Ф	Ф	Т

В этом случае, когда m истинно, p ложно, а r ложно, тогда антецедент m ⋀ ~ p будет истинным, но следствие ложным, что приведет к недопустимому импликации; каждый другой случай дает правильное следствие.

Для любой импликации есть три связанных утверждения: обратное, обратное и контрапозитивное.

Связанные заявления

Первоначальное значение: «Если р Тогда Q »: P → Q

Обратный: «Если Q Тогда P »: Q → P

9000 9000 9000 9000 9000 9000 9000

«Если не р , то не Q »: ~ P → ~ Q

Контрапозитив — «если не Q , то не P »: ~ Q ~ ~ P 95555555 года.

Пример 6

Рассмотрим снова верный вывод: «Если идет дождь, значит, в небе облака».

Обратное: «Если на небе облака, значит, идет дождь». Это, конечно, не всегда верно.

Обратное: «Если не идет дождь, то на небе нет облаков».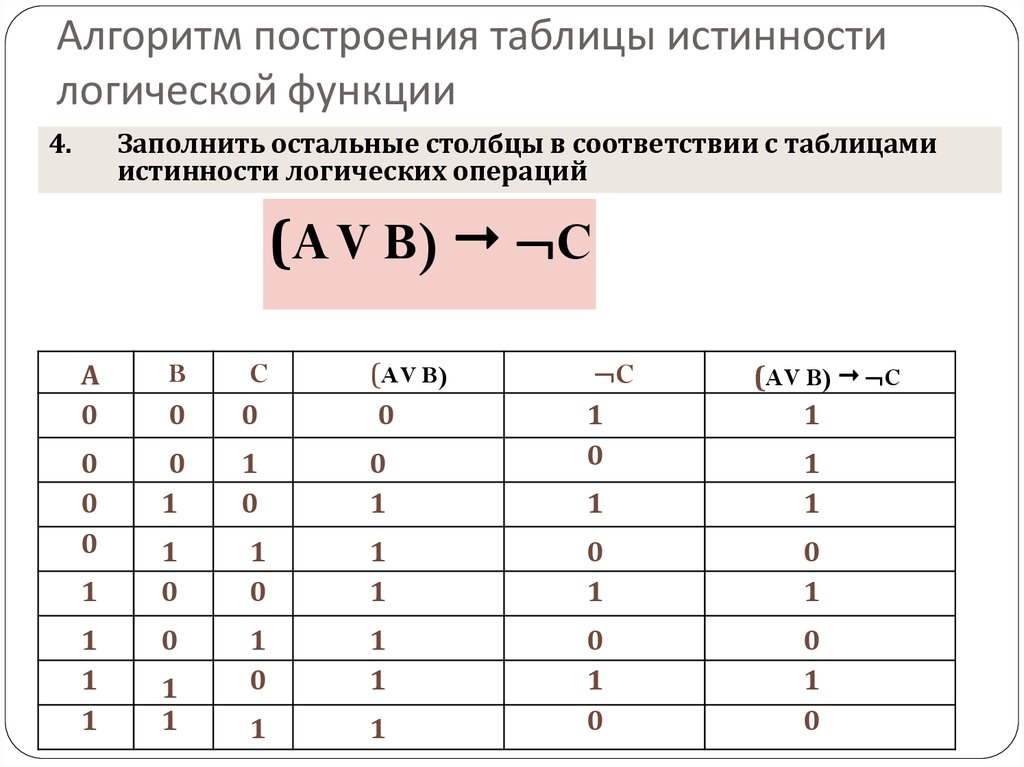 Точно так же это не всегда верно.

Противоположный вариант: «Если на небе нет облаков, значит, не идет дождь». Это утверждение верно и эквивалентно исходному выводу.

Глядя на таблицы истинности, мы видим, что исходное условное и контрапозитивное логически эквивалентны, а обратное и обратное логически эквивалентны.

		Значение	Конверс	Инверсия	Противоположный
р	q	р → q	кв → стр	~ р → ~ q	~ к → ~ к
Т	Т	Т	Т	Т	Т
Т	Ф	Ф	Т	Т	Ф
Ф	Т	Т	Ф	Ф	Т
Ф	Ф	Т	Т	Т	Т

Эквивалентность

Условное утверждение и его противоположность логически эквивалентны.

Обратное и обратное утверждение логически эквивалентны.

Аргументы

Логический аргумент — это утверждение о том, что набор предпосылок поддерживает вывод. Существует два основных типа аргументов: индуктивные и дедуктивные аргументы.

Типы аргументов

Индуктивный 9Аргумент 0004 использует набор конкретных примеров в качестве посылок и использует их, чтобы предложить общий вывод.

дедуктивный аргумент использует набор общих утверждений в качестве своих предпосылок и использует их, чтобы предложить конкретную ситуацию в качестве вывода.

Пример 7

Аргумент «когда я пошел в магазин на прошлой неделе, я забыл свой кошелек, и когда я пошел сегодня, я забыл свой кошелек. Я всегда забываю свою сумочку, когда иду в магазин» — это индуктивный аргумент.

Помещения:

Я забыл свой кошелек на прошлой неделе

Я забыл свой кошелек сегодня

Вывод такой:

Я всегда забываю свой кошелек

Обратите внимание, что посылки — это конкретные ситуации, а заключение — это общее утверждение.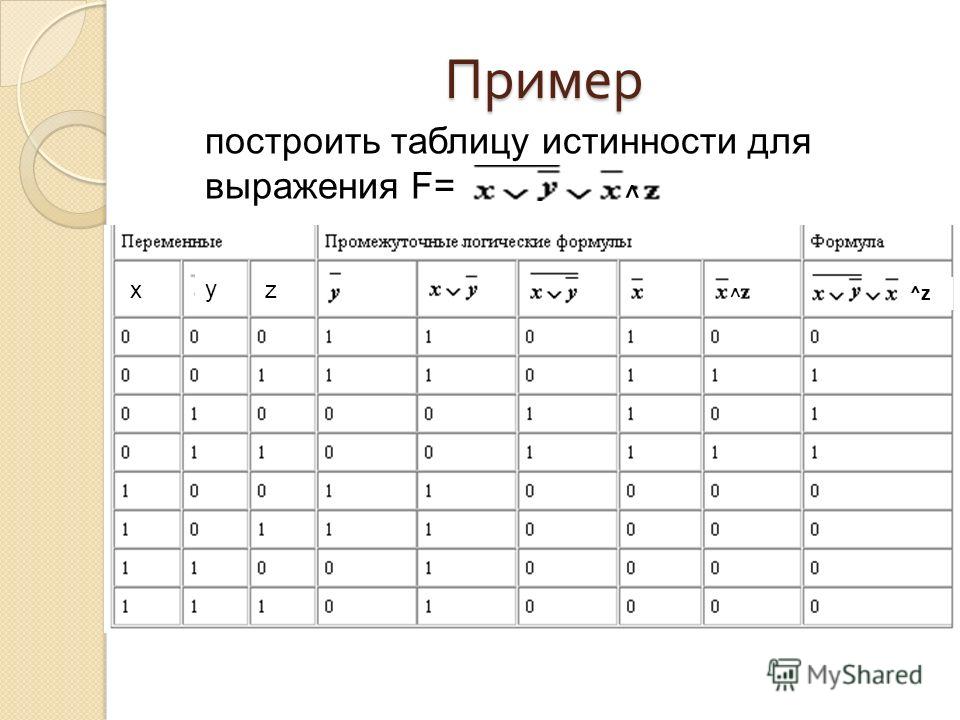 В данном случае это достаточно слабый аргумент, так как он основан всего на двух случаях.

Пример 8

Аргумент «каждый день в течение последнего года самолет пролетает над моим домом в 2 часа дня. Каждый день в 14:00 над моим домом будет летать самолет» — более сильный индуктивный аргумент, поскольку он основан на большем наборе доказательств.

Оценка индуктивных аргументов

Индуктивный аргумент никогда не сможет доказать истинность вывода, но он может предоставить как слабое, так и сильное доказательство того, что оно может быть верным.

Многие научные теории, такие как теория большого взрыва, никогда не могут быть доказаны. Вместо этого они представляют собой индуктивные аргументы, подкрепленные широким спектром доказательств. Обычно в науке идея считается гипотезой до тех пор, пока она не будет тщательно проверена, после чего она становится теорией. Все общеизвестные научные теории, такие как теория гравитации Ньютона, выдержали годы испытаний и доказательств, хотя иногда их необходимо корректировать на основе новых данных. Для гравитации это произошло, когда Эйнштейн предложил общую теорию относительности.

Дедуктивный аргумент является более верным или нет, что облегчает его оценку.

Оценка дедуктивных аргументов

Дедуктивный аргумент считается действительным, если все посылки верны, а вывод логически следует из этих посылок. Другими словами, посылки истинны, и заключение обязательно следует из этих посылок.

Пример 9

Аргумент «Все кошки — млекопитающие, а тигр — кошка, значит, тигр — млекопитающее» — верный дедуктивный аргумент.

Помещения:

Все кошки млекопитающие

Тигр кошка

Вывод:

Тигр — это млекопитающее

Обе посылки верны. Чтобы увидеть, что посылки должны логически вести к заключению, можно использовать диаграмму Венна. Из первой посылки мы можем заключить, что множество кошек является подмножеством множества млекопитающих. Из второй посылки нам говорят, что тигр находится в множестве кошек. Отсюда на диаграмме Венна видно, что тигр также находится внутри множества млекопитающих, так что вывод верен.

Анализ аргументов с помощью диаграмм Венна

^[2]

Чтобы проанализировать аргумент с помощью диаграммы Венна

1. Нарисуйте диаграмму Венна на основе посылок аргумента
2. Если помещения недостаточно для определения того, что определяет расположение элемента, укажите это.
3. Аргумент действителен, если ясно, что вывод должен быть верным

Пример 10

Помещение:          Все пожарные знают CPR

Предпосылка:          Джилл знает СЛР

Вывод:     Джилл — пожарный

Из первой посылки мы знаем, что все пожарные входят в группу тех, кто знает СЛР. Из второй посылки мы знаем, что Джилл является членом этого большего множества, но у нас недостаточно информации, чтобы узнать, является ли она также членом меньшего подмножества, то есть пожарных.

Поскольку вывод не обязательно следует из посылок, это неверный аргумент, независимо от того, действительно ли Джилл является пожарным.

Важно отметить, что для оценки обоснованности аргумента не важно, действительно ли Джилл пожарный; нас интересует только то, достаточно ли посылок для доказательства вывода.

В дополнение к этим категориальным посылкам стиля в форме «все ___», «некоторые ____» и «нет ____», также часто встречаются посылки, являющиеся импликациями.

Пример 11

Помещение:          Если вы живете в Сиэтле, вы живете в Вашингтоне.

Посылка:          Маркус не живет в Сиэтле

Вывод:     Маркус не живет в Вашингтоне

Из первой посылки мы знаем, что множество людей, живущих в Сиэтле, находится внутри множества тех, кто живет в Вашингтоне. Из второй посылки мы знаем, что Маркус не входит в набор Сиэтла, но у нас недостаточно информации, чтобы узнать, живет ли Маркус в Вашингтоне или нет. Это неверный аргумент.

Пример 12

Рассмотрим аргумент «Вы женатый мужчина, поэтому у вас должна быть жена».

Это неверный аргумент, так как есть, по крайней мере, в некоторых частях мира, мужчины, которые женаты на других мужчинах, так что предпосылка не является недостаточной, чтобы подразумевать заключение.

Некоторые аргументы лучше анализировать с помощью таблиц истинности.

Пример 13

Рассмотрим аргумент:

Посылка:          Если вы купили хлеб, то вы пошли в магазин

Посылка:          Вы купили хлеб

Вывод:     Вы пошли в магазин

Хотя мы надеемся, что этот пример является довольно очевидным обоснованным аргументом, мы можем проанализировать его, используя таблицу истинности, представив каждую из предпосылок символически.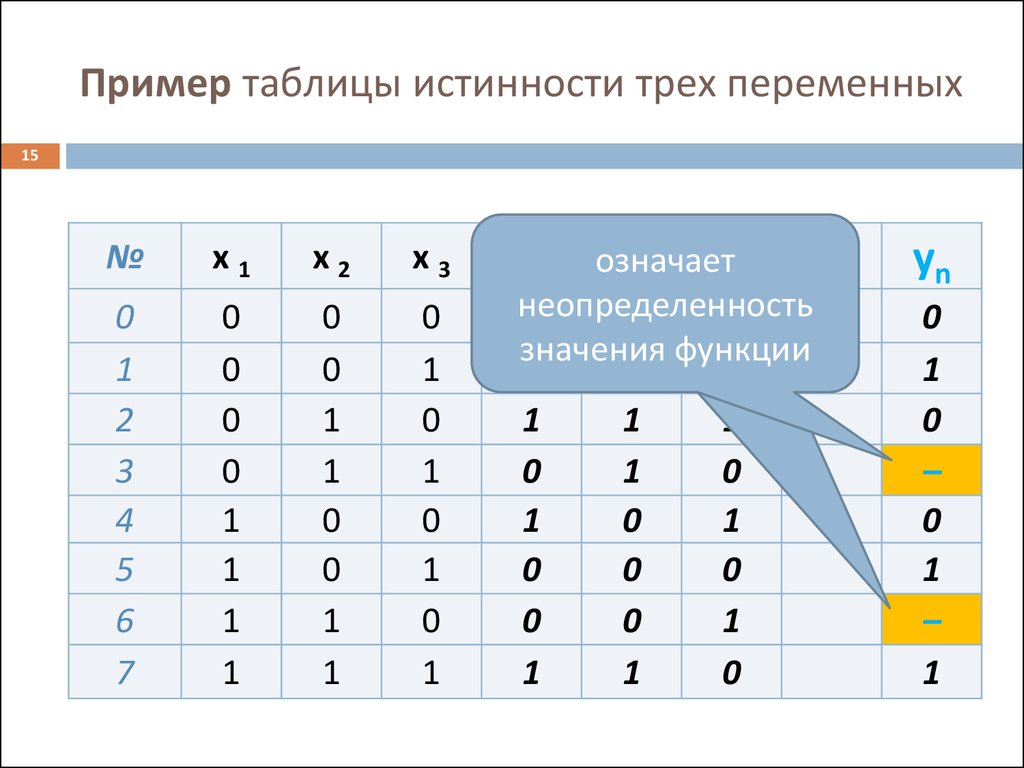 Затем мы можем рассмотреть импликацию о том, что посылки вместе подразумевают вывод. Если таблица истинности является тавтологией (всегда истинной), то аргумент действителен.

Получаем, что B означает «вы купили хлеб», а S — «вы пошли в магазин». Тогда аргумент принимает вид:

Посылка:          B → S

Посылка:          B

Заключение:     S

1 Чтобы проверить достоверность, мы смотрим, подразумевает ли комбинация обеих посылок заключение; правда ли, что [( B → S ) ⋀ B ] → S ?

Б	С	В → С	( Б → С ) ⋀ Б	[( Б → С ) ⋀ Б ] → С
Т	Т	Т	Т	Т
Т	Ф	Ф	Ф	Т
Ф	Т	Т	Ф	Т
Ф	Ф	Т	Ф	Т

Поскольку таблица истинности для [( B → S ) ⋀ B ] → S всегда верна, это правильный аргумент.

Анализ аргументов с использованием таблиц истинности

Чтобы проанализировать аргумент с помощью таблицы истинности:

1. Символически представить каждое из предпосылок
2. Создайте условный оператор, соединив все посылки с помощью и, чтобы сформировать антецедент, и используя заключение в качестве следствия.
3. Создайте таблицу истинности для этого утверждения. Если это всегда истинно, то аргумент действителен.

Пример 14

Предпосылка:         Если я пойду в торговый центр, я куплю новые джинсы

Предпосылка:          Если я куплю новые джинсы, я куплю к ним рубашку

Вывод:     Если мне нужно торговый центр, я куплю рубашку.

Пусть M = я иду в торговый центр, J = я покупаю джинсы и S = я покупаю рубашку.

Посылки и заключение можно сформулировать так:

Предметка: M → J

Предметка: J → S

Заключение: M → S

Мы можем построить таблицу истины для [( м → J ) ⋀ ( J → S )] → ( M → S )

0

0909 900509090 M 209090 M 2

1

09090.

1

09090.

Дж	С	М → Дж	Дж → С	( М → Дж ) ⋀ ( Дж → С )	М → С	[( M → J ) ⋀ ( J → S )] → ( M → S )
Т	Т	Т	Т	Т	Т	Т	Т
Т	Т	Ф	Т	Ф	Ф	Ф	Т
Т	Ф	Т	Ф	Т	Ф	Т	Т
Т	Ф	Ф	Ф	Т	Ф	Ф	Т
Ф	Т	Т	Т	Т	Т	Т	Т
Ф	Т	Ф	Т	Ф	Ф	Т	Т
Ф	Ф	Т	Т	Т	Т	Т	Т
Ф	Ф	Ф	Т	Т	Т	Т	Т

Из таблицы истинности мы видим, что это правильный аргумент.

No related posts.