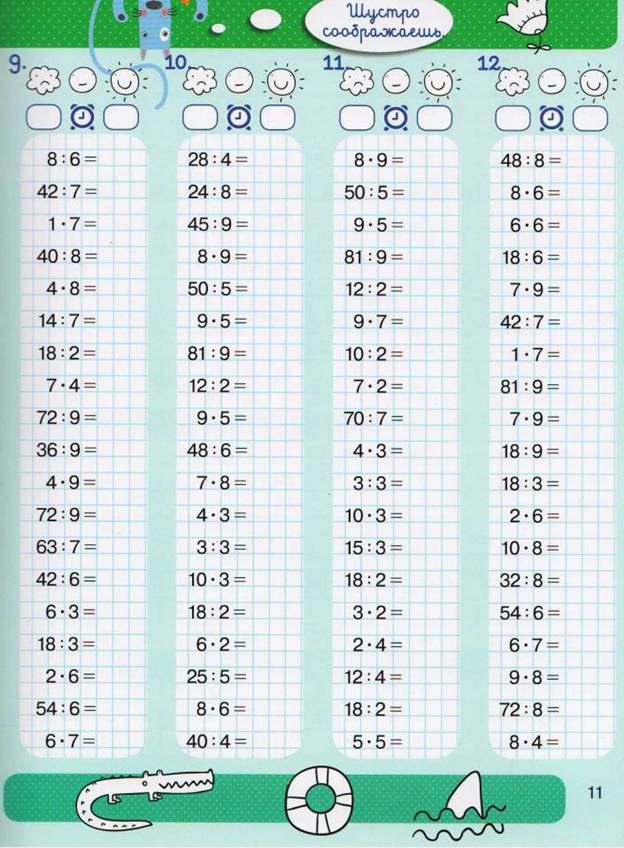
Примеры на умножение 2 класс, распечатать, без ответов
Примеры на умножение эта та же таблица Пифагора (которая является обязательной к изучению).
Такие таблицы (карточки) с примерами на умножения, помогут закрепить и проверить знания этого навыка у вашего второклассника. Это может быть проверкой, как с вашей стороны, так и со стороны ребенка.
Сами таблицы даны без ответов. Распечатать вы их сможете бесплатно.
Ответы находятся под самой таблицей.
Решать примеры можно прямо в самих распечатанных карточках, не записывая примеры на листок бумаги. Всего примеров 46 штук.
Умножение очень необходимый навык для школьника, поэтому развить его необходимо на максимум. Ведь в последующих классах ребенка ждет масса примеров на умножение. Чем больше школьник будет решать такие примеры, тем быстрее освоит умножение.
Ответы 1 таблица:
1 столбик: 2, 21, 18, 30, 20, 49, 5, 42, 8, 28, 54, 16.
2 столбик: 45, 30, 36, 14, 15, 48, 10, 45, 21, 70, 14, 24.
3 столбик: 6, 24, 45, 63, 16, 6, 28, 6, 32, 12, 10.
Ответы 2 таблица:
1 столбик: 1, 8, 24, 100, 12, 35, 20, 7, 9, 27, 60, 63.
2 столбик: 20, 3, 90, 56, 40, 16, 2, 50, 12, 48, 81, 64.
3 столбик: 8, 4, 35, 72, 9, 18, 36, 40, 72, 62, 25.
Сохраните материал в вашей социальной сети, чтобы легко найти его:
Ответы на домашние задания:
- Слова на букву -B в английском языке
- Основные стехиометрические законы по химии
- Формула прямоугольников для вычисления интегралов
- Как найти арифметическую прогрессию формула по математике 9 класс
- Виды правонарушений (и юридическая ответственность) обществознание 9 класс
- Английские слова на темы: «Биржа», «Бизнес», «Экономика».
- Объяснение, почему необходима цифровая безопасность
- Александр 1 характеристика
- Основные разделы генетики
- Как узнать и найти процент от числа
- Образец правильного соединения букв по русскому языку
- Английские слова на тему компьютер
- Таблица вычитания 1 класс «Школа России» — распечатать
- Закон Джоуля-Ленца в виде формулы
org/Article»>Формула нахождения дискриминанта с примерами, алгебра
Таблица умножения на 2 и 3 | Тренажёр по математике (2, 3 класс):
Опубликовано 27.
09.2020 — 23:36 — Велькошевская Екатерина Александровна
Карточки для проверки таблицы умножения на 2 и на 3, примеры даны не по порядку, только на умножение, два вида карточек.(на листе 15 штук)
Скачать:
Предварительный просмотр:
3 х 7 = 3 х 10 = 3 х 9 = 3 х 4 = 3 х 5 = 3 х 8 = 3 х 3 = 3 х 6 = 3 х 2 = 3 х 1 = | 2 х 5 = 2 х 10 = 2 х 9 = 2 х 1 = 2 х 7 = 2 х 2 = 2 х 6 = 2 х 3 = 2 х 8 = 2 х 4 = | 3 х 5 = 3 х 10 = 3 х 9 = 3 х 1 = 3 х 7 = 3 х 2 = 3 х 6 = 3 х 3 = 3 х 8 = 3 х 4 = | 2 х 7 = 2 х 10 = 2 х 9 = 2 х 4 = 2 х 5 = 2 х 8 = 2 х 3 = 2 х 6 = 2 х 2 = 2 х 1 = | 3 х 7 = 3 х 10 = 3 х 9 = 3 х 4 = 3 х 5 = 3 х 8 = 3 х 3 = 3 х 6 = 3 х 2 = 3 х 1 = | 2 х 5 = 2 х 10 = 2 х 9 = 2 х 1 = 2 х 7 = 2 х 2 = 2 х 6 = 2 х 3 = 2 х 8 = 2 х 4 = | 3 х 5 = 3 х 10 = 3 х 9 = 3 х 1 = 3 х 7 = 3 х 2 = 3 х 6 = 3 х 3 = 3 х 8 = 3 х 4 = | 2 х 7 = 2 х 10 = 2 х 9 = 2 х 4 = 2 х 5 = 2 х 8 = 2 х 3 = 2 х 6 = 2 х 2 = 2 х 1 = | 3 х 7 = 3 х 10 = 3 х 9 = 3 х 4 = 3 х 5 = 3 х 8 = 3 х 3 = 3 х 6 = 3 х 2 = 3 х 1 = | 2 х 5 = 2 х 10 = 2 х 9 = 2 х 1 = 2 х 7 = 2 х 2 = 2 х 6 = 2 х 3 = 2 х 8 = 2 х 4 = |
3 х 5 = 3 х 10 = 3 х 9 = 3 х 1 = 3 х 7 = 3 х 2 = 3 х 6 = 3 х 3 = 3 х 8 = 3 х 4 = | 2 х 7 = 2 х 10 = 2 х 9 = 2 х 4 = 2 х 5 = 2 х 8 = 2 х 3 = 2 х 6 = 2 х 2 = 2 х 1 = | 3 х 7 = 3 х 10 = 3 х 9 = 3 х 4 = 3 х 5 = 3 х 8 = 3 х 3 = 3 х 6 = 3 х 2 = 3 х 1 = | 2 х 5 = 2 х 10 = 2 х 9 = 2 х 1 = 2 х 7 = 2 х 2 = 2 х 6 = 2 х 3 = 2 х 8 = 2 х 4 = | 3 х 5 = 3 х 10 = 3 х 9 = 3 х 1 = 3 х 7 = 3 х 2 = 3 х 6 = 3 х 3 = 3 х 8 = 3 х 4 = | 2 х 7 = 2 х 10 = 2 х 9 = 2 х 4 = 2 х 5 = 2 х 8 = 2 х 3 = 2 х 6 = 2 х 2 = 2 х 1 = | 3 х 7 = 3 х 10 = 3 х 9 = 3 х 4 = 3 х 5 = 3 х 8 = 3 х 3 = 3 х 6 = 3 х 2 = 3 х 1 = | 2 х 5 = 2 х 10 = 2 х 9 = 2 х 1 = 2 х 7 = 2 х 2 = 2 х 6 = 2 х 3 = 2 х 8 = 2 х 4 = | 3 х 5 = 3 х 10 = 3 х 9 = 3 х 1 = 3 х 7 = 3 х 2 = 3 х 6 = 3 х 3 = 3 х 8 = 3 х 4 = | 2 х 7 = 2 х 10 = 2 х 9 = 2 х 4 = 2 х 5 = 2 х 8 = 2 х 3 = 2 х 6 = 2 х 2 = 2 х 1 = |
3 х 7 = 3 х 10 = 3 х 9 = 3 х 4 = 3 х 5 = 3 х 8 = 3 х 3 = 3 х 6 = 3 х 2 = 3 х 1 = | 2 х 5 = 2 х 10 = 2 х 9 = 2 х 1 = 2 х 7 = 2 х 2 = 2 х 6 = 2 х 3 = 2 х 8 = 2 х 4 = | 3 х 5 = 3 х 10 = 3 х 9 = 3 х 1 = 3 х 7 = 3 х 2 = 3 х 6 = 3 х 3 = 3 х 8 = 3 х 4 = | 2 х 7 = 2 х 10 = 2 х 9 = 2 х 4 = 2 х 5 = 2 х 8 = 2 х 3 = 2 х 6 = 2 х 2 = 2 х 1 = | 3 х 7 = 3 х 10 = 3 х 9 = 3 х 4 = 3 х 5 = 3 х 8 = 3 х 3 = 3 х 6 = 3 х 2 = 3 х 1 = | 2 х 5 = 2 х 10 = 2 х 9 = 2 х 1 = 2 х 7 = 2 х 2 = 2 х 6 = 2 х 3 = 2 х 8 = 2 х 4 = | 3 х 5 = 3 х 10 = 3 х 9 = 3 х 1 = 3 х 7 = 3 х 2 = 3 х 6 = 3 х 3 = 3 х 8 = 3 х 4 = | 2 х 7 = 2 х 10 = 2 х 9 = 2 х 4 = 2 х 5 = 2 х 8 = 2 х 3 = 2 х 6 = 2 х 2 = 2 х 1 = | 3 х 7 = 3 х 10 = 3 х 9 = 3 х 4 = 3 х 5 = 3 х 8 = 3 х 3 = 3 х 6 = 3 х 2 = 3 х 1 = | 2 х 5 = 2 х 10 = 2 х 9 = 2 х 1 = 2 х 7 = 2 х 2 = 2 х 6 = 2 х 3 = 2 х 8 = 2 х 4 = |
По теме: методические разработки, презентации и конспекты
Конспект урока по математике в 3 классе на тему: «Закрепление таблицы умножения и деления.
Сводная таблица умножения».*…
Обобщение: таблица сложения до20, таблица умножения
Карточки на таблицы сложения в пределах 20, и таблица умножния. Подойдёт на уроки обобщения конец 1 класса, 2класс…
Конспект урока математики в 3 классе по теме:»Таблица умножения 9.Составление таблицы.Установление зависимости между изменяющимся множителем и цифрой в разряде десятков и в разряде единиц».
Конспект урока математики в 3 классе по теме:»Таблица умножения 9.Составление таблицы. Установление зависимости между изменяющимся множителем и цифрой в разряде десятков и в разряде единиц»….
Таблица умножения. Различные приёмы работы, способствующие запоминанию таблицы умножения.
Описаны этапы работы, способствующие более быстрому запоминанию таблицы умножения….
Весёлая таблица ( тренажёр таблицы умножения и деления)
Презентация….
Урок математики во 2-м классе по теме: «Таблица умножения. Составление столбика таблицы умножения на 3»
Закрепление смысла действия умножения, закрепление знания таблицы умножения на 2, составление столбика таблицы умножения на 3.
…
Карточки по математике для закрепления таблицы умножения на 4Карточки по математике для закрепления таблицы умножения на 2
Карточки по математике для закрепления таблицы умножения на 4…
Поделиться:
Рабочие листы по длинному умножению
На этой странице представлены рабочие листы по длинному умножению для учащихся, которые освоили основные факты умножения и учатся умножать 2-, 3-, 4-значные и более числа. Вопросы на этих рабочих листах, которые иногда называют длинным умножением или многозначным умножением, требуют, чтобы учащиеся усвоили факты умножения от 0 до 9. решеточное умножение (которое мы представляем на этой странице), ментальные стратегии, манипулятивное использование, технологии и различные другие алгоритмы бумаги и карандаша. Многозначное умножение может быть разочаровывающим опытом для многих учащихся. Попробуйте научить многозначному умножению, используя более одной стратегии.
Самые популярные длинные рабочие листы по умножению на этой неделе -Digit Numbers (
21 просмотр на этой неделе )Умножение 3-значных чисел на 1-значные числа ( 15 просмотров на этой неделе )Умножение 4-значных чисел на 3-значные числа ( 12 просмотров на этой неделе )Длинные листы умножения
Длинные рабочие листы для практики умножения, включая различные размеры чисел и варианты для различных числовых форматов.
Двузначное умножение является естественным началом после того, как учащиеся усвоили факты умножения. Концепция умножения двузначных чисел требует знания места и значения места, особенно если учащиеся должны полностью понимать, чего они достигают с помощью различных стратегий, которые они используют. Такой вопрос, как 24 × 5, можно рассматривать как (20 + 4) × 5. Умственно это становится намного проще, когда учащиеся умножают 20 на 5, затем 4 на 5 и складывают два произведения. Хороший способ понять значение разряда — использовать блоки с основанием 10.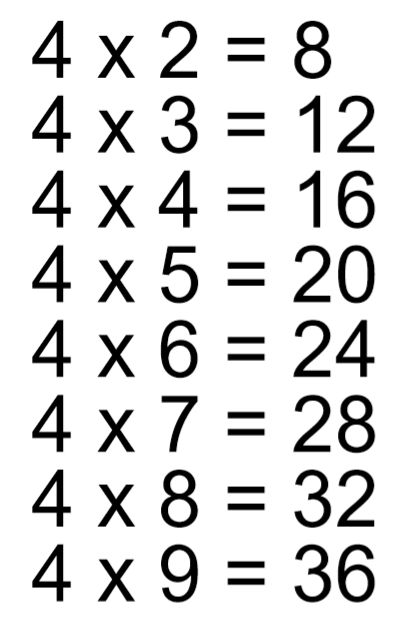
Эти манипуляции также очень хорошо переносятся на бумагу, карандаш и математические стратегии в уме.
Дополнительная цифра может сбить с толку одних учеников, но усложнить задачу другим. Всегда следите за тем, чтобы ученики были готовы к трехзначному умножению, иначе и вы, и ваш ученик будете разочарованы. Рабочие листы для трехзначного умножения требуют овладения фактами однозначного умножения и знания стратегии многозначного умножения, которая позволит учащимся как понять вопрос, так и получить правильный ответ. Четырехзначное умножение было изобретено в 350 г. до н.э. как способ наказания детей, укравших хлеб с рынка. Просто шучу! На самом деле это большая проблема для студентов, которые добились успеха в своих фактах умножения и хорошо разбираются в длинной стратегии умножения. Что вы даете ученикам, которые освоили факты умножения и длинное умножение и которым нравится решать сложные задачи? Не смотрите дальше пяти-восьмизначного умножения. Наслаждаться!
Длинные рабочие листы умножения
В числах на этих листах нет разделителей тысяч.
Это немного усложняет чтение чисел, но иногда лучше не мешать слишком многим вещам, когда учащиеся изучают длинное умножение. Ключи ответов включают ответы с показанными шагами, поэтому учащиеся и учителя могут диагностировать любые проблемы в шагах, которые они предприняли, чтобы ответить на вопросы. В ответах используется алгоритм бумаги и карандаша, который обычно используется в США и других странах. Умножение 2 цифр на 1 цифру Умножение 2-значный на 2-значный Умножение 3-значное на 1-значное Умножение 3-значное на 2-значное Умножение 3-значный на 3-значный Умножение 4-значное на 1-значное Умножение 4-значное на 2-значное Умножение 4-значное на 3-значное Умножение
Длинное умножение с
тысячами, разделенными запятыми Запятые включены в качестве разделителей тысяч для чисел на этих рабочих листах.
Запятые используются в США и других англоязычных странах для облегчения чтения чисел. Как и в других длинных листах умножения на этой странице, ключи ответов включают шаги.
2-значный на 2-значный Умножение (тысячи, разделенные запятыми) 3-значное на 1-значное Умножение (тысячи, разделенные запятыми) 3-значное на 2-значное Умножение (тысячи, разделенные запятыми) 3-значный на 3-значный Умножение (тысячи, разделенные запятыми) 4-значное на 1-значное Умножение (тысячи, разделенные запятыми) 4-значное на 2-значное Умножение (тысячи, разделенные запятыми)
Длинное умножение с
тысячами, разделенными пробелом Разделение тысяч пробелами позволяет избежать путаницы с запятыми и точками.
Различные числовые форматы в разных странах и языках используют запятые и точки как для десятичных знаков, так и для разделителей тысяч, но пробел всегда используется только как разделитель тысяч. Это более распространено в некоторых странах, таких как Канада и Франция, но чаще применяется в других частях мира.
2-значное на 2-значное Умножение (тысячи, разделенные пробелами) 3-значное на 1-значное Умножение (тысячи, разделенные пробелами) 3-значное на 2-значное Умножение (тысячи, разделенные пробелами) 3-значное умножение на 3-значное (тысячи, разделенные пробелами) 4-значное на 1-значное Умножение (тысячи, разделенные пробелами) 4-значное на 2-значное Умножение (тысячи, разделенные пробелами) 4-значное на 3-значное Умножение (тысячи, разделенные пробелами) 4-значное умножение на 4-значное (тысячи, разделенные пробелами) 5-значное на 1-значное Умножение (тысячи, разделенные пробелами) 5-значное на 2-значное Умножение (тысячи, разделенные пробелами) 5-значное на 3-значное Умножение (тысячи, разделенные пробелами) 5-значное на 4-значное Умножение (тысячи, разделенные пробелами) 5-значный на 5-значный Умножение (тысячи, разделенные пробелом) 6-значное на 1-значное Умножение (тысячи, разделенные пробелами) 6-значное на 2-значное Умножение (тысячи, разделенные пробелами) 6-значное на 3-значное Умножение (тысячи, разделенные пробелами) 6-значное на 4-значное Умножение (тысячи, разделенные пробелами) 6-значное на 5-значное Умножение (тысячи, разделенные пробелами) 6-значный по 6-значный Умножение (тысячи, разделенные пробелом) 7-значное на 1-значное Умножение (тысячи, разделенные пробелами) 7-значное на 2-значное Умножение (тысячи, разделенные пробелами) 7-значное на 3-значное Умножение (тысячи, разделенные пробелами) 7-значное на 4-значное Умножение (тысячи, разделенные пробелами) 7-значное на 5-значное Умножение (тысячи, разделенные пробелами) 7-значное на 6-значное Умножение (тысячи, разделенные пробелами) 7-значный на 7-значный Умножение (тысячи, разделенные пробелами) 8-значное на 1-значное Умножение (тысячи, разделенные пробелами) 8-значное на 2-значное Умножение (тысячи, разделенные пробелами) 8-значное на 3-значное Умножение (тысячи, разделенные пробелами) 8-значное на 4-значное Умножение (тысячи, разделенные пробелами) 8-значное на 5-значное Умножение (тысячи, разделенные пробелами) 8-значный на 6-значный Умножение (тысячи, разделенные пробелом) 8-значное на 7-значное Умножение (тысячи, разделенные пробелами) 8-значное на 8-значное Умножение (тысячи, разделенные пробелами) 2-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 3-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 3-значное на 2-значное Умножение ( Крупный шрифт ) (тысячи, разделенные пробелом) 3-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 4-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 4-значное на 2-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 4-значное на 3-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 4-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 5-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 5-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 5-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 5-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 5-значный на 5-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 6-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 6-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 6-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 6-значный на 4-значный Умножение ( Крупный шрифт ) (тысячи, разделенные пробелом) 6-значный на 5-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами) 6-значный на 6-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные пробелами)
Длинное умножение с
тысячами, разделенными точкой В некоторых местах точки используются как разделители тысяч, а запятые — как десятичные дроби.
Это очень сбивает с толку людей, которые привыкли к номерам в формате США.
2-значное на 2-значное Умножение (тысячи, разделенные точкой) 3-значное на 1-значное Умножение (тысячи, разделенные точкой) 3-значное на 2-значное Умножение (тысячи, разделенные точкой) 3-значное на 3-значное Умножение (тысячи, разделенные точкой) 4-значное на 1-значное Умножение (тысячи, разделенные точкой) 4-значное на 2-значное Умножение (тысячи, разделенные точкой) 4-значное на 3-значное Умножение (тысячи, разделенные точкой) 4-значное на 4-значное Умножение (тысячи, разделенные точкой) 5-значное на 1-значное Умножение (тысячи, разделенные точкой) 5-значное на 2-значное Умножение (тысячи, разделенные точкой) 5-значное на 3-значное Умножение (тысячи, разделенные точкой) 5-значное на 4-значное Умножение (тысячи, разделенные точкой) 5-значное на 5-значное Умножение (тысячи, разделенные точкой) 6-значное на 1-значное Умножение (тысячи, разделенные точкой) 6-значное на 2-значное Умножение (тысячи, разделенные точкой) 6-значное на 3-значное Умножение (тысячи, разделенные точкой) 6-значное на 4-значное Умножение (тысячи, разделенные точкой) 6-значное на 5-значное Умножение (тысячи, разделенные точкой) 6-значный на 6-значный Умножение (тысячи, разделенные точкой) 7-значное на 1-значное Умножение (тысячи, разделенные точкой) 7-значное на 2-значное Умножение (тысячи, разделенные точкой) 7-значное на 3-значное Умножение (тысячи, разделенные точкой) 7-значное на 4-значное Умножение (тысячи, разделенные точкой) 7-значное на 5-значное Умножение (тысячи, разделенные точкой) 7-значное на 6-значное Умножение (тысячи, разделенные точкой) 7-значный на 7-значный Умножение (тысячи, разделенные точкой) 8-значное на 1-значное Умножение (тысячи, разделенные точкой) 8-значное на 2-значное Умножение (тысячи, разделенные точкой) 8-значное на 3-значное Умножение (тысячи, разделенные точкой) 8-значное на 4-значное Умножение (тысячи, разделенные точкой) 8-значное на 5-значное Умножение (тысячи, разделенные точкой) 8-значное на 6-значное Умножение (тысячи, разделенные точкой) 8-значное на 7-значное Умножение (тысячи, разделенные точкой) 8-значное на 8-значное Умножение (тысячи, разделенные точкой) 2-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 3-значный на 1-значный Умножение ( Крупный шрифт ) (тысячи, разделенные точкой) 3-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 3-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 4-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 4-значное на 2-значное Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 4-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 4-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 5-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 5-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 5-значный на 3-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 5-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 5-значный на 5-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 1-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 2-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 3-значный Умножение ( Крупный шрифт ) (тысячи, разделенные точкой) 6-значный на 4-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 5-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой) 6-значный на 6-значный Умножение ( Крупный шрифт ) (Тысячи, разделенные точкой)
Решетчатое умножение
Решетчатое умножение Рабочие листы для изучения и использования этой длинной стратегии умножения.
Различные цифры
Умножение на решетку Рабочие листы с включенными решетками Решетчатое или решетчатое умножение — отличная стратегия, которую учащиеся могут использовать для вычисления длинных задач на умножение карандашом и бумагой. Мы упростили первый шаг подготовки решетки, так как на рабочих листах ниже они предварительно нарисованы. Немного попрактиковавшись, учащиеся смогут использовать миллиметровую бумагу или рисовать решетки от руки. Первый фактор разделен разрядным значением в верхней части решетки, что дает каждому разрядному значению собственный столбец. Второй множитель отделяется таким же образом, но по правой стороне с одним разрядным значением в строке. Одноразрядные номера столбца и строки перемножаются, и их произведение записывается в соответствующее поле, разделяя разряды десятков и единиц по обе стороны от диагонали. Наконец, диагональные «строки» суммируются и перегруппировываются, начиная с диагонали в правом нижнем углу, в которой будет только одна цифра.
Ключи ответов, которые мы предоставили, должны дать вам хорошее представление о том, как выполнить решеточное умножение, как профессионал. После того, как учащиеся немного попрактикуются, вы можете обнаружить, что это их предпочтительный метод вычисления произведений больших чисел. Этот метод легко масштабируется, что означает простую задачу умножения 10-значного числа на 10-значное число и т. д.
2-разрядное × 2-разрядное решеточное умножение 2-значное × 3-значное умножение решетки 3-значное × 2-значное умножение решетки 3-разрядное × 3-разрядное решеточное умножение 4-разрядное × 2-разрядное решеточное умножение 4-разрядное × 3-разрядное решеточное умножение 4-разрядное × 4-разрядное решеточное умножение 4-значное × 5-значное решеточное умножение 5-значное × 4-значное решеточное умножение 5-разрядное × 5-разрядное решеточное умножение
Распределительное свойство
Рабочие листы Распределяющее свойство, чтобы помочь учащимся научиться мысленно умножать целые числа, не полагаясь на методы бумаги/карандаша.
Рабочие листы по умножению для изучения распределительного свойства
умножения2-значное × 1-значное умножение 3-значное × 1-значное умножение
Умножение с поддержкой сетки
Умножение на миллиметровой бумаге помогает учащимся «выстраивать» свои числа при выполнении длинных вопросов на умножение. Эти рабочие листы включают настраиваемые сетки, в которых достаточно места для одного вопроса.
Умножение с поддержкой сетки рабочих листов2-разрядный × 1-разрядный Умножение с поддержкой сетки 3-разрядный × 1-разрядный Умножение с поддержкой сетки 4-разрядный × 1-разрядный Умножение с поддержкой сетки 2-разрядный × 2-разрядный Умножение с поддержкой сетки 3-значный × 2-значный Умножение с поддержкой сетки 4 цифры × 2 цифры Умножение с поддержкой сетки 3-значный × 3-значный Умножение с поддержкой сетки 4-разрядный × 3-разрядный Умножение с поддержкой сетки
Умножение с поддержкой сетки Заготовки Если вы или ваши ученики хотите составить свои вопросы, эти поля должны ускорить процесс.
2-разрядный × 1-разрядный Умножение с опорой на сетку Пробелы 3-разрядный × 1-разрядный Умножение с опорой на сетку Пробелы 4-разрядный × 1-разрядный Умножение с опорой на сетку Пробелы 2-значный × 2-значный Умножение с опорой на сетку Пробелы 3-значный × 2-значный Умножение с опорой на сетку Пробелы 4-разрядный × 2-разрядный Умножение с опорой на сетку Пробелы 3-значный × 3-значный Умножение с опорой на сетку Пробелы 4-значный × 3-значный Умножение с пробелами поддержки сетки
Умножение в других системах счисления
Умножение чисел в системах счисления, отличных от десятичных, включая двоичные, четверичные, восьмеричные, двенадцатеричные и шестнадцатеричные числа.
Умножение на другие базовые системыУмножение двоичных чисел (основание 2) Умножение троичных чисел (основание 3) Умножение Четвертичный Числа (Основание 4) Умножение пятеричных чисел (основание 5) Умножение порядковых чисел (основание 6) Умножение восьмеричных чисел на (основание 8) Умножение двенадцатеричных чисел (основание 12) Умножение шестнадцатеричных чисел (основание 16) Умножение десятичных чисел (основание 20) Умножение шестнадцатеричных чисел (основание 36) Умножение различных чисел (различные основания)
Документация Learning with Python 2nd Edition
2.
1. Значения и типы данныхЗначение — это одна из фундаментальных вещей — как буква или число — которыми манипулирует программа. Значения, которые мы видели до сих пор, равны 2 (значение результат, когда мы добавили 1 + 1), и «Hello, World!».
Эти значения относятся к разным типам данных : 2 является целым числом , и «Привет, мир!» это строка , так называемая, потому что она содержит строку буквы. Вы (и интерпретатор) можете идентифицировать строки, потому что они заключено в кавычки.
Оператор печати также работает для целых чисел.
>>> напечатать 4 4
Если вы не уверены, какой тип имеет значение, интерпретатор может указать ты.
>>> type("Привет, мир!")
<тип 'строка'>
>>> тип(17)
<тип 'целое число'>
Неудивительно, что строки относятся к типу str , а целые числа относятся к типу
введите целое число . Менее очевидно, что числа с десятичной точкой принадлежат к типу
называется с плавающей запятой , потому что эти числа представлены в формате, называемом с плавающей запятой .
>>> тип(3.2) <тип 'плавающий'>
Как насчет таких значений, как «17» и «3,2»? Они похожи на числа, но они заключены в кавычки, как строки.
>>> тип("17")
<тип 'строка'>
>>> тип("3.2")
<тип 'строка'>
Это струны.
Строки в Python могут быть заключены либо в одинарные (‘), либо в двойные кавычки («»):
>>> type('Это строка.')
<тип 'строка'>
>>> type("И это тоже.")
<тип 'строка'>
Строки с двойными кавычками могут содержать внутри одинарные кавычки, как в «борода Брюса», а строки в одинарных кавычках могут иметь двойные кавычки. внутри них, как в «Рыцарях, говорящих «Ни!»».
Когда вы вводите большое целое число, у вас может возникнуть соблазн использовать запятые между группы из трех цифр, например, 1 000 000. Это не допустимое целое число в Python, но легально:
>>> напечатать 1 000 000 1 0 0
Ну, это совсем не то, что мы ожидали! Python интерпретирует 1 000 000 как
список из трех пунктов для печати.
Так что не ставьте запятых в
целые числа.
2.2. Переменные
Одной из самых мощных функций языка программирования является возможность управлять переменными . Переменная — это имя, которое ссылается на значение.
Оператор присваивания создает новые переменные и дает им значения:
>>> message = "Как дела, Док?" >>> n = 17 >>> пи = 3,14159
В этом примере выполняются три назначения. Первый присваивает строку «Что up, Doc?» в новую переменную с именем message. Вторая дает целое число 17 в n, а третий дает число с плавающей запятой 3,14159 в Пи.
Оператор присваивания , =, не следует путать со знаком равенства (хотя он использует тот же символ). Операторы присваивания связывают имя , слева от оператора со значением справа. Вот почему вы получите сообщение об ошибке, если введете:
>>> 17 = n
Распространенным способом представления переменных на бумаге является запись имени со стрелкой.
указывая на значение переменной. Такая цифра называется состоянием .
диаграмма , потому что она показывает, в каком состоянии находится каждая из переменных (подумайте об этом
как состояние ума переменной). На этой диаграмме показан результат
операторы присваивания:
Оператор печати также работает с переменными.
>>> распечатать сообщение Что случилось док? >>> напечатать п 17 >>> напечатать пи 3.14159
В каждом случае результатом является значение переменной. Переменные также имеют типы; опять же, мы можем спросить переводчика, каковы они.
>>> тип(сообщение) <тип 'строка'> >>> тип(н) <тип 'целое число'> >>> тип (пи) <тип 'плавающий'>
Тип переменной — это тип значения, на которое она ссылается.
2.3. Имена переменных и ключевые слова
Программисты обычно выбирают для своих переменных осмысленные имена — они документируют, для чего используется переменная.
Имена переменных могут быть произвольно длинными.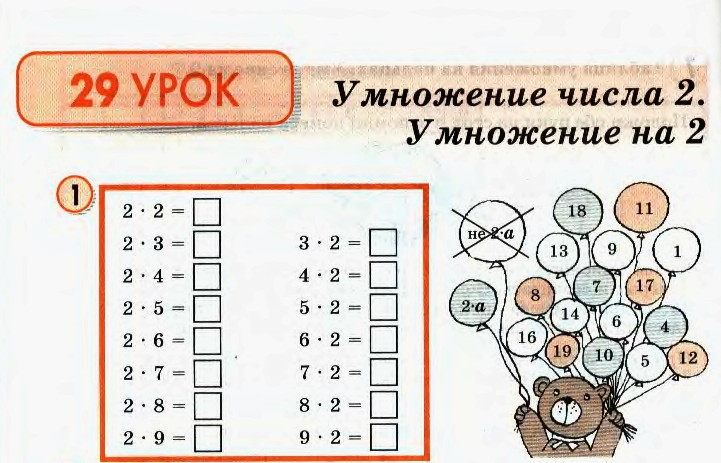
Они могут содержать как буквы, так и
цифры, но они должны начинаться с буквы. Хотя законно использовать
заглавные буквы, по соглашению мы этого не делаем. Если вы это сделаете, помните тот случай
имеет значение. Брюс и Брюс — разные переменные.
Символ подчеркивания (_) может появляться в имени. Он часто используется в названия, состоящие из нескольких слов, например my_name или price_of_tea_in_china.
Если вы дадите переменной недопустимое имя, вы получите синтаксическую ошибку:
>>> 76trombones = "большой парад" SyntaxError: неверный синтаксис >>> больше$ = 1000000 SyntaxError: неверный синтаксис >>> класс = "Информатика 101" SyntaxError: неверный синтаксис
76trombones является незаконным, потому что он не начинается с буквы. больше$ является недопустимым, поскольку содержит недопустимый символ, знак доллара. Но что не так с классом?
Оказывается, этот класс является одним из Python ключевых слов . Ключевые слова определяют
правила и структура языка, и их нельзя использовать в качестве имен переменных.
Python имеет тридцать одно ключевое слово:
| и | как | утверждать | перерыв | класс | продолжить |
| по умолчанию | дел | Элиф | еще | кроме | исполнитель |
| наконец | на | из | глобальный | если | импорт |
| в | это | лямбда | не | или | пройти |
| печать | поднять | вернуть | попробовать | , а | с |
| выход |
Возможно, вы захотите держать этот список под рукой. Если переводчик жалуется на один
ваших имен переменных, и вы не знаете почему, посмотрите, есть ли они в этом списке.
2.5. Вычисление выражений
Выражение представляет собой комбинацию значений, переменных и операторов. если ты введите выражение в командной строке, интерпретатор вычислит его и отображает результат:
>>> 1 + 1 2
вычисление выражения выдает значение, поэтому выражения может появляться в правой части операторов присваивания. Значение по всем само по себе является простым выражением, как и переменная.
>>> 17 17 >>> х 2
Как ни странно, вычисление выражения — это не совсем то же самое, что печать ценность.
>>> message = "Как дела, Док?" >>> сообщение "Что случилось док?" >>> распечатать сообщение Что случилось док?
Когда оболочка Python отображает значение выражения, она использует тот же
формат, который вы использовали бы для ввода значения. В случае строк это означает, что
он включает кавычки. Но оператор печати печатает значение
выражение, которое в данном случае является содержимым строки.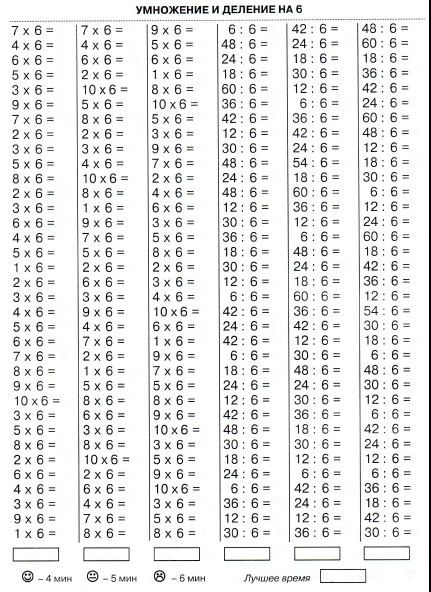
В скрипте выражение само по себе является допустимым утверждением, но оно не Делать что-нибудь. Скрипт
17 3.2 "Привет, мир!" 1 + 1
вообще не выводит. Как бы вы изменили сценарий для отображения значения этих четырех выражений?
2.6. Операторы и операнды
Операторы — это специальные символы, которые представляют такие вычисления, как сложение и умножение. Используемые оператором значения называются операндами .
Ниже приведены все допустимые выражения Python, смысл которых более или менее очистить:
20+32 час-1 час*60+минута минута/60 5**2 (5+9)*(15-7)
Символы +, — и /, а также использование скобок для группировки, означают в Python то, что они означают в математике. Звездочка (*) означает знак умножения, а ** — знак возведения в степень.
Когда вместо операнда появляется имя переменной, оно заменяется на его значение до выполнения операции.
Сложение, вычитание, умножение и возведение в степень делают то, что вы
ожидать, но вы можете быть удивлены разделением.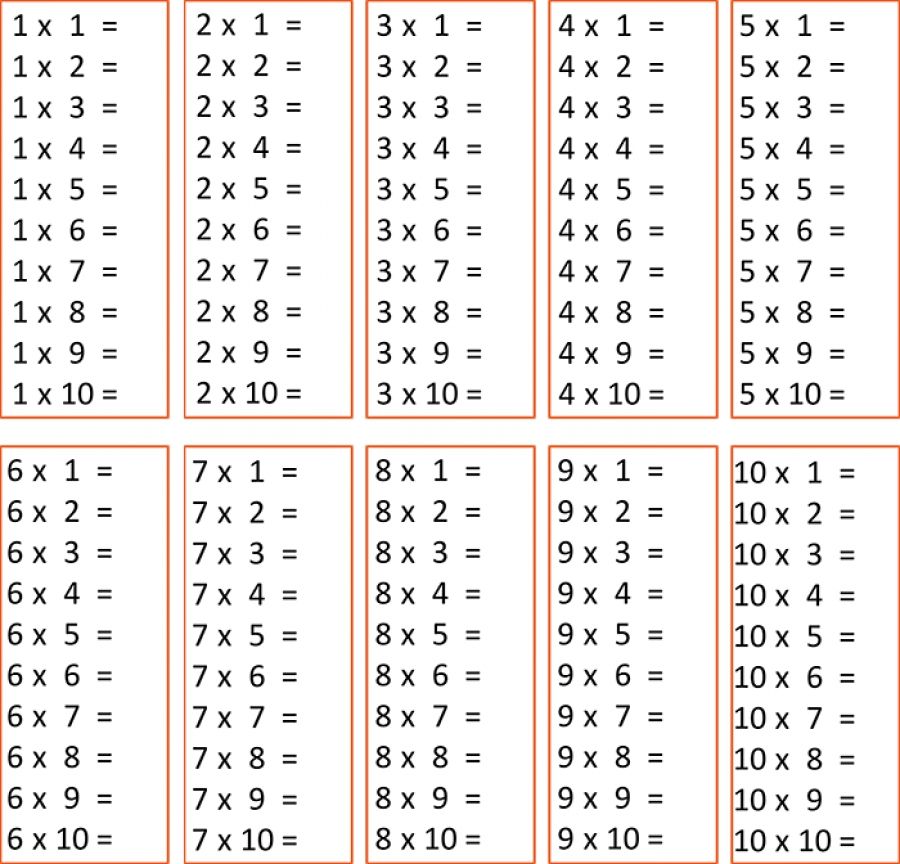
Следующая операция имеет
неожиданный результат:
>>> минута = 59 >>> минут/60 0
Значение минуты равно 59, а 59, деленное на 60, равно 0,98333, а не 0. причина несоответствия в том, что Python выполняет целочисленное деление .
Если оба операнда являются целыми числами, результат также должен быть целым числом, и по соглашению целочисленное деление всегда округляет до вниз , даже в таких случаях где следующее целое число очень близко.
Возможным решением этой проблемы является вычисление процента, а не дробь:
>>> минут*100/60 98
Опять результат округляется в меньшую сторону, но по крайней мере теперь ответ примерно правильный. Другой альтернативой является использование деления с плавающей запятой. мы увидим в глава 4, как преобразовать целые значения и переменные в числа с плавающей запятой ценности.
2.7. Порядок операций
Когда в выражении встречается более одного оператора, порядок вычисления
зависит от правил приоритета .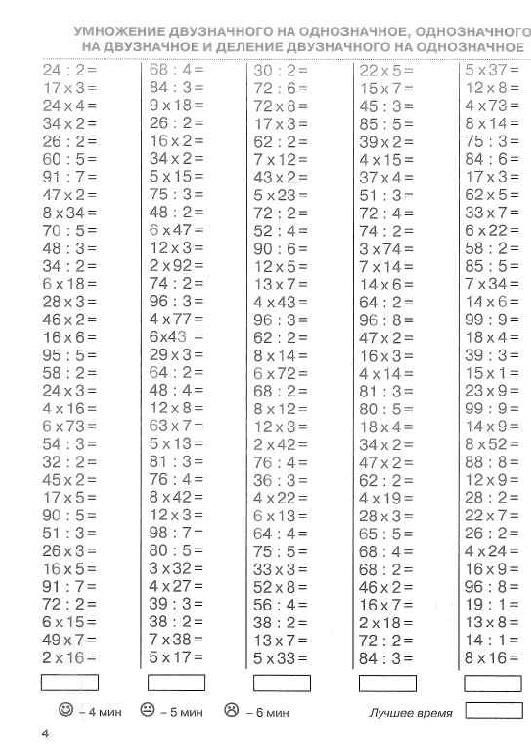
Python следует тому же приоритету
правила для своих математических операторов, которые делает математика. Аббревиатура ПЕМДАС
это полезный способ запомнить порядок операций:
- P арензы имеют наивысший приоритет и могут использоваться для форсирования выражение для оценки в том порядке, в котором вы хотите. Поскольку выражения в скобки оцениваются первыми, 2 * (3-1) равно 4, а (1+1)**(5-2) равно 8. Вы также можете использовать круглые скобки, чтобы упростить чтение выражения, как в (минуты * 100) / 60, хотя это не меняет результат.
- E Возведение в степень имеет следующий наивысший приоритет, поэтому 2**1+1 равно 3 и не 4, а 3*1**3 равно 3, а не 27.
- M умножение и D ivision имеют одинаковый приоритет, т.е.
выше, чем A дополнение и S вычитание, которые также имеют то же самое
приоритет. Таким образом, 2 * 3-1 дает 5, а не 4, а 2/3-1 равно -1, а не 1.
(помните, что при целочисленном делении 2/3=0). - Операторы с одинаковым приоритетом оцениваются слева направо. Итак, в выражение minute*100/60, сначала происходит умножение, что дает 5900/60, что, в свою очередь, дает 98. Если бы операции оценивались из справа налево, результатом было бы 59*1, то есть 59, то есть неправильный.
(помните, что при целочисленном делении 2/3=0).2.8. Операции со строками
В общем, вы не можете выполнять математические операции со строками, даже если строки выглядят как числа. Следующее является незаконным (при условии, что сообщение имеет строку типа):
сообщение-1 "Привет"/123 сообщение*"Привет" "15"+2
Интересно, что оператор + работает со строками, хотя и не делать именно то, что вы могли бы ожидать. Для строк оператор + представляет конкатенация , что означает объединение двух операндов путем их связывания концы с концами. Например:
фрукты = "банан" Baked_good = "ореховый хлеб" распечатать фрукты + запеченное_хорошее
Результатом этой программы является бананово-ореховый хлеб.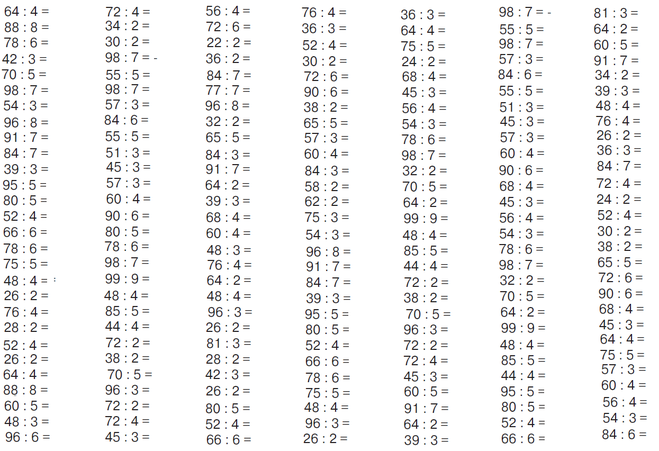
Пробел перед словом
гайка является частью струны и необходима для создания пространства между
объединенные строки.
Оператор * также работает со строками; он выполняет повторение. Например, «Веселье»*3 — это «Веселье, веселье». Один из операндов должен быть строкой; в другое должно быть целым числом.
С одной стороны, такая интерпретация + и * имеет смысл по аналогии с сложение и умножение. Так как 4*3 эквивалентно 4+4+4, мы ожидайте, что «Веселье»*3 будет таким же, как «Веселье»+»Веселье»+»Веселье», и это так. На с другой стороны, существует важный способ, которым конкатенация строк и повторение отличается от целочисленного сложения и умножения. Не могли бы вы подумайте о свойстве, что сложение и умножение имеют эту строку конкатенация и повторение не делают?
2.9. Вход
В Python есть две встроенные функции для получения ввода с клавиатуры:
n = raw_input("Пожалуйста, введите ваше имя: ")
напечатать п
n = input("Введите числовое выражение:")
напечатать п
Пример запуска этого скрипта будет выглядеть примерно так:
$ python tryinput.
py
Пожалуйста, введите ваше имя: Артур, король бриттов
Артур, король бриттов
Введите числовое выражение: 7 * 3
21
Каждая из этих функций позволяет получить подсказку для функции между скобки.
2.10. Композиция
До сих пор мы рассматривали элементы программы — переменные, выражения, и утверждения — по отдельности, не говоря о том, как их сочетать.
Одной из наиболее полезных особенностей языков программирования является их способность возьмите небольшие строительные блоки и составьте из них . Например, мы знаем, как добавляем цифры и умеем печатать; оказывается, мы можем делать и то, и другое одновременно время:
>>> напечатать 17 + 3 20
На самом деле добавление должно произойти до печати, поэтому действия на самом деле происходят не одновременно. Дело в том, что любое выражение включая числа, строки и переменные, могут использоваться внутри оператора печати. Вы уже видели пример этого:
print "Количество минут с полуночи: ", час*60+минута
Вы также можете помещать произвольные выражения в правую часть присваивания выписка:
процент = (минута * 100) / 60
Сейчас эта способность может показаться не впечатляющей, но вы увидите другие примеры, когда
композиция позволяет четко и понятно выражать сложные вычисления.
кратко.
Предупреждение. Существуют ограничения на использование определенных выражений. За Например, левая часть оператора присваивания должна быть имя переменной , а не выражение. Итак, незаконно следующее: минута+1 = час.
2.12. Глоссарий
- оператор присваивания
- = это оператор присваивания Python, который не следует путать с математическим оператором сравнения, использующим тот же символ.
- оператор присваивания
Оператор, который присваивает значение имени (переменной). Слева от оператор присваивания = является именем. Справа от оператор присваивания — это выражение, которое оценивается Python интерпретатор, а затем присвоено имя. Разница между левая и правая части оператора присваивания часто сбивает с толку новых программистов. В следующем задании:
н = н + 1
n играет совершенно разную роль по обе стороны от =. На справа это значение и составляет часть выражения , которое будет быть оценен интерпретатором Python перед тем, как присвоить его имени налево.
- Информация в программе, предназначенная для других программистов (или кого-либо другого). чтение исходного кода) и не влияет на выполнение программа.
- композиция
- Возможность объединять простые выражения и операторы в составные операторы и выражения для представления сложных вычислений кратко.
- объединить
- Чтобы соединить две строки встык.
- тип данных
- Набор значений. Тип значения определяет, как его можно использовать в выражения. До сих пор типы, которые вы видели, были целыми числами (тип int), числа с плавающей запятой (тип float) и строки (тип ул).
- оценить
- Чтобы упростить выражение, выполняя операции, чтобы дают одно значение.
- выражение
- Комбинация переменных, операторов и значений, представляющая единственное значение результата.
- поплавок
- Тип данных Python, который хранит числа с плавающей запятой.
Числа с плавающей запятой хранятся внутри в двух частях: , базовая и
показатель степени . При печати в стандартном формате они выглядят как
десятичные числа. Остерегайтесь ошибок округления при использовании чисел с плавающей запятой.
и помните, что это только приблизительные значения.
- между
- Тип данных Python, содержащий положительные и отрицательные целые числа.
- целочисленное деление
- Операция деления одного целого числа на другое с получением целого числа. Целочисленное деление дает только целое число раз, которое числитель делится на знаменатель и отбрасывает любой остаток.
- ключевое слово
- Зарезервированное слово, используемое компилятором для разбора программы; ты нельзя использовать ключевые слова вроде if, def и while в качестве переменной имена.
- операнд
- Одно из значений, с которыми работает оператор.
- оператор
- Специальный символ, представляющий простое вычисление, такое как сложение, умножение или конкатенация строк.
- правила приоритета
- Набор правил, регулирующих порядок, в котором выражения, включающие
оцениваются несколько операторов и операндов.
- диаграмма состояний
- Графическое представление набора переменных и значений для которые они ссылаются.
- выписка
- Инструкция, которую может выполнить интерпретатор Python. Примеры Операторы включают оператор присваивания и оператор печати.
- ул
- Тип данных Python, содержащий строку символов.
- значение
- Число или строка (или другие элементы, которые будут названы позже), которые можно хранится в переменной или вычисляется в выражении.
- переменная
- Имя, которое ссылается на значение.
- имя переменной
- Имя переменной. Имена переменных в Python состоят из последовательность букв (a..z, A..Z и _) и цифр (0..9), которая начинается с письмом. В передовой практике программирования имена переменных должны быть выбраны так, чтобы они описывали их использование в программе, делая программа самодокументирование .
При печати в стандартном формате они выглядят как
десятичные числа. Остерегайтесь ошибок округления при использовании чисел с плавающей запятой.
и помните, что это только приблизительные значения.
2.13. Упражнения
Запишите, что происходит, когда вы печатаете оператор присваивания:
>>> вывести n = 7
Как насчет этого?
>>> напечатать 7 + 5
Или это?
>>> print 5.
2, "это", 4 - 2, "то", 5/2.0
Можете ли вы придумать общее правило для того, что может следовать за печатью? утверждение? Что возвращает оператор печати?
Возьми предложение: Только работа и отсутствие развлечений делают Джека скучным мальчиком. Сохраните каждое слово в отдельной переменной, затем распечатайте предложение на одну строку с помощью печати.
Добавьте скобки к выражению 6 * 1 — 2, чтобы изменить его значение от 4 до -6.
Поместите комментарий перед строкой кода, которая ранее работала, и запишите, что происходит, когда вы перезапускаете программу.
Разница между input и raw_input заключается в том, что input оценивает входную строку, а raw_input — нет. Попробуйте следующее в интерпретаторе и запишите, что происходит:
>>> х = ввод() 3.14 >>> тип(х)
>>> х = raw_input() 3.14 >>> тип(х)
>>> х = ввод() «Рыцари, которые говорят «ни!» >>> х
Что произойдет, если вы попробуете пример выше без кавычек?
>>> х = ввод() Рыцари, говорящие «ни!» >>> х
>>> х = raw_input() «Рыцари, которые говорят «ни!» >>> х
Опишите и объясните каждый результат.
2, "это", 4 - 2, "то", 5/2.0
