Часть 3. Приведение кривых и поверхностей второго порядка к каноническому виду — FINDOUT.SU
Поможем в ✍️ написании учебной работы
Имя
Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой
Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое
Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности
Уравнение 2- ого порядка определяет на плоскости некоторую кривую 2 – ого порядка (Это может быть эллипс, гипербола, парабола или случаи их вырождения).
Часть слагаемых в этом уравнении есть квадратичная форма с матрицей в ортонормированном базисе .
Существует ортогональное линейное преобразование, которое приводит квадратичную форму к каноническому виду в новом ортонормированном базисе . При этом линейная связь между старыми и новыми координатами такова, что , где — матрица преобразования, элементами столбцов которой являются координаты собственных ортонормированных векторов матрицы . Выразив старые переменные и подставив их вместе с новой квадратичной формой в уравнение (8.1), получим уравнение вида . Если теперь выделить полные квадраты, то получится каноническое уравнение одной из известных кривых в прямоугольной системе координат с базисом , состоящим из собственных ортонормированных векторов матрицы .
Если , уравнение соответствует кривой эллиптического типа, если , то кривой гиперболического типа, если , то уравнение соответствует кривой параболического типа.
Пример 7.3. Построим кривую, заданную уравнением .
Решение. Выпишем квадратичную форму, соответствующую части уравнения . Приведём её к каноническому виду ортогональным преобразованием, которое исходный ортонормированный базис преобразует в новый ортонормированный базис из собственных векторов матрицы . Это преобразование позволит построить кривую в новой прямоугольной системе координат.
Составим матрицу квадратичной формы: .
Определитель Кривая эллиптического типа.
Составим характеристическое уравнение и вычислим собственные значения матрицы:
. Так как , собственные векторы, им соответствующие, ортогональны.
и — нормированные собственные векторы, соответствующие и . Эти векторы образуют новый ортонормированный базис, в котором матрица квадратичной формы принимает канонический вид , а её матрица принимает диагональный вид: .
Матрица перехода к новому базису составляется из координат новых базисных векторов: . Связь между новыми и исходными координатами осуществляется с помощью матрицы перехода по формуле: , откуда получим: .
Подставим в исходное уравнение кривой полученные выражения старых переменных через новые, а также заменим квадратичную форму: .
Приведём подобные слагаемые, выделим полные квадраты и получим каноническое уравнение эллипса в новой системе координат: . Чтобы построить эллипс в исходной системе координат, на координатной плоскости проведём новые координатные оси: ось в направлении собственного вектора , и ось в направлении собственного вектора . В новой системе строим эллипс с центром симметрии в этой системе , с полуосями (см. рис. 2).
Рис.2. Эллипс, заданный уравнением
Пример 7.4. Исследуем уравнение и построим кривую: .
Решение. Выпишем квадратичную форму, соответствующую уравнению:
.
Составим матрицу квадратичной формы: .
Исследуем определитель квадратичной формы: кривая гиперболического типа.
Составим характеристический полином и вычислим собственные числа квадратичной формы:
, .
Собственные (нормированные) векторы: для : , для : .
Из собственных векторов составим базис, в котором квадратичная форма приобретает канонический вид: , а её матрица становится диагональной: . Матрица перехода к новому базису: .
Связь между новыми и исходными координатами осуществляется с помощью матрицы перехода по формуле: , откуда получим: , .
Подставим в исходное уравнение кривой данные выражения, а также заменим квадратичную форму каноническим видом: .
Приведём подобные слагаемые, выделим полные квадраты. Окончательно получим уравнение в каноническом виде: .
Это случай вырождения случай гиперболы в пару пересекающихся прямых .
Чтобы построить полученные прямые, на координатной плоскости проведём новые координатные оси: ось OX1, в направлении собственного вектора , и ось OY1, в направлении собственного вектора .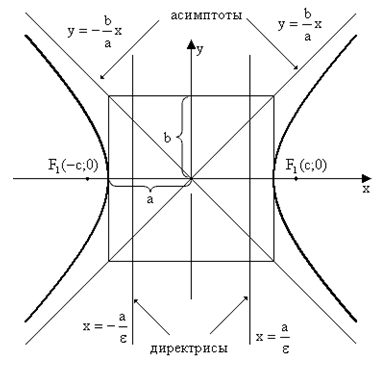
Центра пересечения прямых отмечаем уже в новой системе координат, и строим прямые (см. рис.3).
Рис. 3. Вырожденный случай гиперболы – пара пересекающихся прямых.
Аналогично приводятся к каноническому виду и строятся поверхности второго порядка.
Пример 7.5. Привести к каноническому виду уравнение и построить поверхность: .
Решение. Выпишем квадратичную форму, соответствующую уравнению: .
Матрица квадратичной формы имеет вид: .
Составим характеристический многочлен и вычислим собственные значения квадратичной формы: .
Найдём собственные ортонормированные векторы. для : , для : , для : .
Собственные ортонормированные векторы образуют базис, в котором квадратичная форма имеет канонический вид: , а её матрица становится диагональной: . (В качестве проверки можно вычислить произведение , где — матрица перехода к новому базису, имеющая вид ).
Связь между новыми и исходными координатами осуществляется с помощью матрицы перехода по формуле: , откуда получаем
, , .
Подставим в исходное уравнение кривой данные выражения, а также заменим квадратичную форму каноническим видом: .
Упростим уравнение, выделим полные квадраты и приведём его к каноническому виду:
Мы получили уравнение смещённого эллипсоида. Координаты центра симметрии эллипсоида в новой системе координат O’(1,-2,-1).
Чтобы построить эллипсоид, проведём новые координатные оси так, что ось пойдёт в направлении собственного вектора , ось — в направлении собственного вектора , а ось — в направлении собственного вектора .
Искомый эллипсоид см. на рис. 4
Рис.4. Эллипсоид, заданный уравнением
Самостоятельно решите задачи 4.226, 4.228, 4.231 [3]
Занятие 9 . Контроль по модулю 1.
к каноническому виду уравнение кривой второго порядка онлайн
Вы искали к каноническому виду уравнение кривой второго порядка онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь.
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как к каноническому виду уравнение кривой второго порядка онлайн,как привести к каноническому виду уравнение,как привести к каноническому виду уравнение кривой второго порядка,как привести к каноническому виду уравнение параболы,как привести уравнение к каноническому виду,как привести уравнение к каноническому виду параболы,как привести уравнение кривой второго порядка к каноническому виду,как привести уравнение параболы к каноническому виду,как уравнение кривой второго порядка привести к каноническому виду,как уравнение параболы привести к каноническому виду,как уравнение привести к каноническому виду,калькулятор кривые второго порядка онлайн,калькулятор онлайн кривые второго порядка,канонический вид уравнения,каноническое уравнение параболы онлайн калькулятор,кривые 2 порядка онлайн,кривые второго порядка онлайн,онлайн калькулятор приведение кривой второго порядка к каноническому виду,онлайн каноническое уравнение,онлайн кривые второго порядка,онлайн построение кривых второго порядка,онлайн приведение уравнения к каноническому виду,онлайн привести к каноническому виду уравнение,онлайн привести к каноническому виду уравнение второго порядка,онлайн привести уравнение к каноническому виду,поверхности второго порядка онлайн,построение кривой второго порядка онлайн,построение кривых второго порядка онлайн,построение онлайн кривой второго порядка,построить и привести к каноническому виду,построить кривую,построить кривую второго порядка онлайн,построить кривую заданную уравнением,приведение к каноническому виду,приведение к каноническому виду онлайн,приведение к каноническому виду уравнений второго порядка,приведение к каноническому виду уравнений второго порядка онлайн,приведение к каноническому виду уравнения,приведение к каноническому виду уравнения онлайн,приведение кривой второго порядка к каноническому виду,приведение кривой второго порядка к каноническому виду калькулятор онлайн,приведение кривой второго порядка к каноническому виду онлайн,приведение кривой второго порядка к каноническому виду онлайн калькулятор,приведение уравнений второго порядка к каноническому виду,приведение уравнений второго порядка к каноническому виду онлайн,приведение уравнения к каноническому виду,приведение уравнения к каноническому виду онлайн,приведение уравнения кривой второго порядка к каноническому виду,привести к каноническому виду,привести к каноническому виду и построить,привести к каноническому виду онлайн,привести к каноническому виду онлайн калькулятор,привести к каноническому виду поверхность второго порядка онлайн,привести к каноническому виду уравнение,привести к каноническому виду уравнение второго порядка,привести к каноническому виду уравнение второго порядка онлайн,привести к каноническому виду уравнение кривой,привести к каноническому виду уравнение кривой второго порядка,привести к каноническому виду уравнение кривой второго порядка онлайн,привести к каноническому виду уравнение онлайн,привести к каноническому виду уравнения кривых,привести к каноническому виду уравнения кривых второго порядка,привести к каноническому виду уравнения кривых второго порядка онлайн,привести поверхность второго порядка к каноническому виду онлайн,привести уравнение второго порядка к каноническому виду,привести уравнение второго порядка к каноническому виду онлайн,привести уравнение к каноническому виду,привести уравнение к каноническому виду второго порядка,привести уравнение к каноническому виду онлайн,привести уравнение к каноническому виду онлайн решение,привести уравнение кривой второго порядка к каноническому виду,привести уравнение кривой второго порядка к каноническому виду онлайн,привести уравнение кривой к каноническому виду,привести уравнения кривых второго порядка к каноническому виду,привести уравнения кривых второго порядка к каноническому виду онлайн,уравнение второго порядка привести к каноническому виду,уравнение кривой второго порядка к каноническому виду онлайн,уравнение кривой привести к каноническому виду,уравнение линии привести к каноническому виду построить ее,уравнение привести к каноническому виду онлайн.
Где можно решить любую задачу по математике, а так же к каноническому виду уравнение кривой второго порядка онлайн Онлайн?
Решить задачу к каноническому виду уравнение кривой второго порядка онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.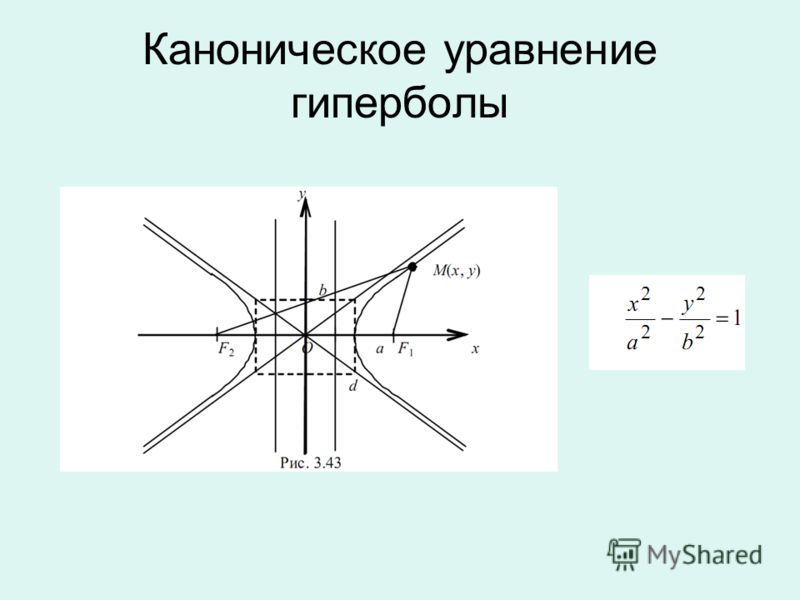
Общее уравнение кривых второго порядка — Студопедия
Поделись
Общее уравнение кривой второго порядка на плоскости имеет вид:
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0, (39)
где A2 + B2 + C2 0, (A, B, C, D, E, F) R. Оно определяет все возможные конические сечения произвольным образом расположенные на плоскости.
Из коэффициентов уравнения (39) составим два определителя:
, , (40)
– называется дискриминантом уравнения (39), а – дискриминантом старших членов уравнения. При 0 уравнение (39) определяет: > 0 – эллипс; < 0 – гиперболу; = 0 – параболу. В случае = 0 кривые вырождаются в точку или прямые линии.
От общего уравнения (39) можно перейти к каноническому уравнению, если исключить линейные и перекрестный члены путем перехода в новую систему координат, совпадающую с осями симметрии фигуры. Заменим в (39) x на x + a и y на y + b, где a, b некоторые константы. Выпишем полученные коэффициенты при х и y и приравняем их к 0
Заменим в (39) x на x + a и y на y + b, где a, b некоторые константы. Выпишем полученные коэффициенты при х и y и приравняем их к 0
(Aa + Bb + D)x = 0, (Cb + Ba + E)y = 0. (41)
В результате уравнение (39) примет вид:
A(x)2 + 2B(x)(y) + C(y)2 + F = 0, (42)
где коэффициенты А, B, C не изменились, а F = / . Решение системы уравнений (41) определит координаты центра симметрии фигуры:
, . (43)
Если B = 0, то a = –D/A, b = –E/C и исключать линейные члены в (39) удобно методом приведения к полному квадрату:
Ax2 + 2Dx = A(x2 + 2xD/A + (D/A)2 – (D/A)2) = A(x + D/A)2 – D2/A.
В уравнении (42) совершим поворот координат на угол a (38). Выпишем полученный коэффициент при перекрестном члене xy и приравняем его к 0
[sin2 (A–C) + 2cos2 B]xy = 0. (44)
Условие (44) определяет необходимый угол поворота осей координат до их совпадения с осями симметрии фигуры и принимает вид:
tg2 = . (45)
Уравнение (42) принимает форму:
A+X2 + C+Y2 + F = 0 (46)
от которой легко перейти к каноническому уравнению кривой:
. (47)
Коэффициенты A+, C+, при условии (45), можно представить как корни вспомогательного квадратного уравнения:
t2 – (A + C)t + = 0. (48)
В результате определены положение и направление осей симметрии фигуры, ее полуоси:
a2 = , b2 =
и она может быть построена геометрически.
В случае = 0 имеем параболу. Если её ось симметрии параллельна оси Ох, то уравнение сводится к виду:
, (49)
если нет, то к виду:
, (50)
где выражения в скобках, приравненные к 0, определяют линии новых осей координат: , .
Решение типичных задачПример 15. Привести уравнение 2x2 + 3y2 – 4x + 6y – 7 = 0 к каноническому виду и построить кривую.
Решение. B = 0, = –72 0, = 6 > 0 эллипс.
Выполним приведение к полному квадрату:
2(x – 1)2 + 3(y + 1)2 – 12 = 0.
Координаты центра симметрии (1; –1), линейное преобразование X = x – 1, Y = y + 1 приводит уравнение к каноническому виду .
Пример 16. Привести уравнение 2xy = a2 к каноническому виду и построить кривую.
Решение. B = 1, = a2 0, = –1 < 0 гипербола.
Центр системы координат находится в центре симметрии кривой, т.к. в уравнении нет линейных членов. Совершим поворот осей на угол a. По формуле (45) имеем tg2a = B/(A – C) = , т.е. a = 45°. Коэффициенты канонического уравнения (46) A+, C+ определяются уравнением (48): t2 = 1 или t1,2 = 1 A+ = 1, C+ = –1, т.е.
X2 – Y2 = a2 или . Таким образом, уравнение 2ху = а2 описывает гиперболу с центром симметрии в (0; 0). Оси симметрии располагаются по биссектрисам координатных углов, асимптотами служат оси координат, полуоси гиперболы равны а.
Пример 17. Привести уравнение x2 + 6х + y + 10 = 0 к каноническому виду и построить кривую.
Решение. B = 0, = –¼ 0, = 0 парабола.
Выполним приведение к полному квадрату:
(x + 3)2 = –(y + 1).
Координаты центра симметрии (–3; –1), линейное преобразование
X = x + 3, Y = y + 1 приводит уравнение к каноническому виду X2 = –Y, где фокальный параметр р = 1/2.
Привести к каноническому виду следующие уравнения и построить соответствующие кривые:
— 4x2 + 9y2 – 16x – 18y – 11 = 0;
— x2 + 2х – y = 0;
— x2 – 9y2 + 6x + 18y – 9 =0;
— 9x2 + y2 – 18x + 2y + 1 = 0;
— 2x2 + 4х + y – 2 = 0;
— 3x2 – 6х – y + 2 = 0;
— x2 + 4y2 – 8x – 9y + 16 = 0;
— 4x2 + 8х – y – 5 = 0;
— 9x2 – y2 + 18x + 2y – 1 = 0;
— 9x2 – 4y2 + 36x + 16y – 16 = 0.
Кривые и поверхности второго порядка (стр. 1 из 3)
Кафедра высшей математики
Курсовая работа
По линейной алгебре и аналитической геометрии
«Кривые и поверхности второго порядка»
Дубна 2002
Оглавление
Введение
Часть I. Исследование кривой второго порядка
1. Определение типа кривой с помощью инвариантов
2. Приведение к каноническому виду
3. Построение графиков
4. Вывод
Часть II. Исследование поверхности второго порядка
1. Определение типа поверхности.
2. Приведение к каноническому виду
3. Исследование формы поверхности методом сечений
4. Графики уравнения поверхности.
5. Вывод
Цель:
Целью данной курсовой работы является исследование кривой и поверхности второго порядка. Закрепление теоретических знаний и практических навыков по изучению и анализу свойств кривых и поверхностей второго порядка.
Постановка задачи:
I) Для данного уравнения кривой второго порядка:
1) Определить тип кривой с помощью инвариантов.
2) При a=0 записать каноническое уравнение прямой и определить расположение центра
3) Привести уравнение к каноническому виду, применяя параллельный перенос и поворот координатных осей.
II) Для данного уравнения плоскости второго порядка:
1) Исследовать форму поверхности методом сечений плоскостями, построить линии, полученные в сечениях.
2) Построить поверхность в канонической системе координат.
1. Определение типа кривой с помощью инвариантов
Для данного уравнения кривой второго порядка:
(5 — a)x2 + 4xy + 3y2 + 8x – 6y +5 = 0 (3.1)
определить зависимость типа кривой от параметра a с помощью инвариантов.
Для данного уравнения кривой второго порядка:
a11 = 5 — a, a12 = 2, a13 = 4, a22 = 2, a23 = -3, a33 = 5
Вычислиминварианты:
I1 = a11 + a22 = (5 — a) +2 = 7 — a
I2 =
=
= (5 — a)2 – 4 = 6 -2a
I2 =
=
= (5 — a)10-24-24-32-9(5 — a)-20 = -a-95
Согласно классификации кривых второго порядка:
I. Если I2 = 0, то данное уравнение (3.1) определяет кривую параболического типа:
Если I2 = 0, то данное уравнение (3.1) определяет кривую параболического типа:
I2 = 6 — 2a = 0, следовательно, при a = 3 уравнение определяет кривую параболического типа.
При a = 3 I3 = — a — 95 = -3 — 95 = 98 ¹ 0. Значит, при a = 3 уравнение (3.1) задаёт параболу.
II. Если I2 ¹ 0, то задаваемая кривая является центральной. Следовательно, при a¹ 3 данное уравнение задаёт центральную кривую.
1. Если I2 > 0, то уравнение задаёт кривую эллиптического типа:
Значит, при a < 3 уравнение (3.1) задаёт кривую эллиптического типа.
a. Если I1I3 < 0, то уравнение определяет эллипс:
I1I3 = — (7 — a)(a+95) = a2+88a-665 < 0, при решении получаем aÎ (-95 , 7). Следовательно, при aÎ (-95 , 3)уравнение (3. 1) задаёт эллипс.
1) задаёт эллипс.
b. Если I1I3 > 0, то уравнение определяет эллипс:
I1I3 = a2+88a-665 > 0, при решении получаем aÎ (-¥, -95). Следовательно, при aÎ (-¥ , -95) уравнение (3.1) задаёт мнимый эллипс.
c. Если I3 = 0, то уравнение определяет две мнимые пересекающиеся прямые:
I3 = -a — 95 = 0, при решении получаем a — 95. Следовательно, при a = — 95 уравнение (3.1) задаёт две мнимые пересекающиеся прямые.
2. Если I2 < 0, то уравнение задаёт кривую гиперболического типа:
Значит, при a > 3 уравнение (3.1) задаёт кривую гиперболического типа.
a. Если I3 ¹ 0, то уравнение определяет гиперболу:
I3 = -a — 95 ¹ 0, получаем a¹ -95. Следовательно, при aÎ (3 , +¥) уравнение (3.1) задаёт гиперболу.
Согласно полученным данным, построим таблицу:
| aÎ(-¥ , -95) | a = -95 | aÎ(-95 , 3) | a = 3 | aÎ(3 , +¥) |
| Мнимый эллипс | Две мнимые пересекающиеся прямые | Эллипс | Парабола | Гипербола |
2. Приведение к каноническому виду
При a = 0 уравнение (3.1) принимает вид:
5x2 + 4xy + 2y2 + 8x — 6y + 5 = 0 (3.2)
Приведем уравнение кривой (3.2) к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. Мы установили, что данная кривая — центральная, поэтому используем методику приведения к каноническому виду для уравнения центральной кривой.
a) Характеристическое уравнения для данной кривой будет иметь вид:
A(x, y) = 5x2 + 4xy + 2y2
Откуда следует, корни характеристического уравнения есть: l1 = 1, l2 = 6.
Расположение эллипса относительно начальной системы координат будет известно, если мы будем знать координаты центра и угловой коэффициент вещественной оси эллипса.
Уравнения для определения координат центра имеют вид:
Откуда мы находим x0 = —
и y0 =
. Следовательно, точка O¢(-
,
) есть центр данной кривой.
Угловой коэффициент оси O¢Xможем определить по формуле:
б) Совершим параллельный перенос начала координат в точкуO¢(x0, y0). При этом координаты x, yпроизвольной точки плоскости в системе координат xOy и координаты x‘, y‘ в новой системе координат x‘O‘y‘ связаны соотношениями:
Подставив данные выражения в уравнение (3.1), получим:
5(x0 + x¢)2 + 4(x0 + x¢)(y0 + y¢) + 2(y0 + y¢)2 + 8(x0 + x¢) — 6(y0 + y¢) + 5=0
Раскрыв скобки и приведя подобные члены, получим:
5x¢2+4x¢y¢+2y¢2+(10x0+4x0 + 8)x¢ + (4x0 + 4y0 — 6)y¢ + (5x02 + 4x0y0 + 2y02 + 8x0 — 6y0 + 5) = 0 (3.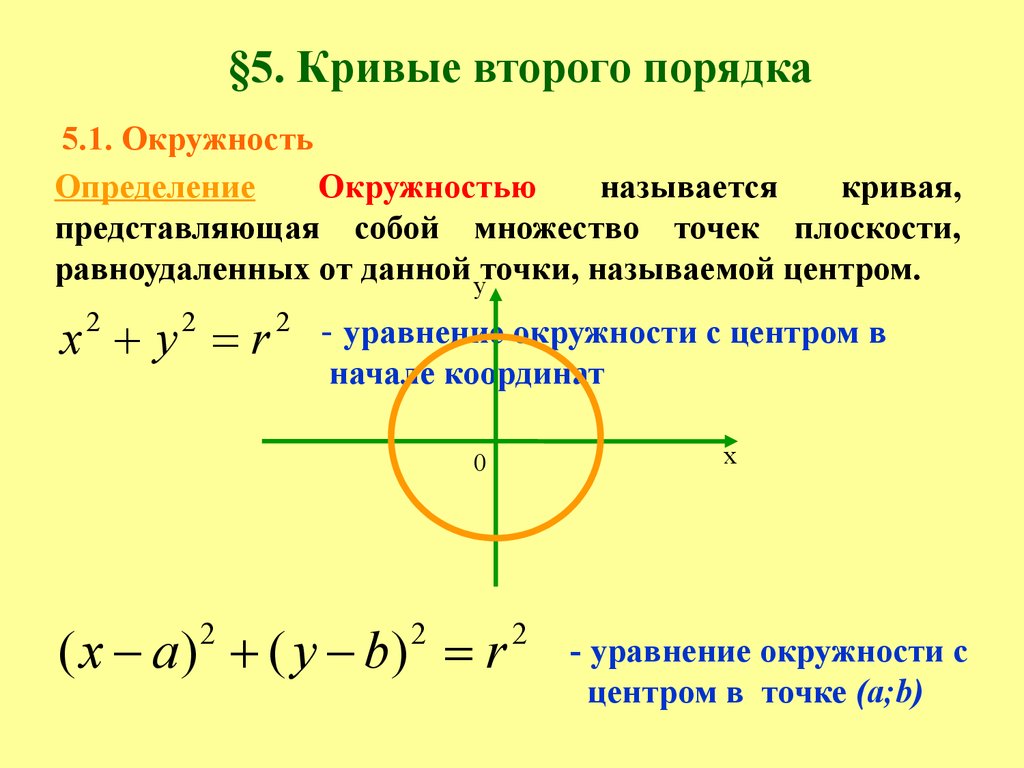 3)
3)
В данном уравнении коэффициенты при x¢ и y¢ приравняем к нулю и получим систему уравнений:
Решив эту систему уравнений, мы получим, найденные уже раннее, координаты центра O¢, x0 = —
и y0 =
. Подставив данные значения в уравнение (3.3), коэффициенты при x¢ и y¢ станут равными нулю, мы получим уравнение в системе координат x‘O‘y‘ :
5x¢2 + 4x¢y¢ + 2y¢2 + (
) = 0
5x¢2 + 4x¢y¢ + 2y¢2 —
= 0 (3.4)
в) Так как a12 = 2 ¹ 0, то для дальнейшего упрощения необходимо произвести поворота осей координат на угол a. При повороте осей координат на уголa координаты x’, y’ произвольной точки М плоскости в системе координат x‘O‘y‘ и координаты X, Y в новой системе координат XO’Y связаны соотношениями:
Подставим данные выражения в уравнение (3. 4), получим:
4), получим:
5(Xcosa — Ysina)2 + 4(Xcosa — Ysina)(Xsina + Ycosa) + 2(Xsina + Ycosa)2 —
= 0
(5cos2a + 4sinacosa + 2sin2a)X2 + (-6sinacosa + 4cos2a — 4sin2a)XY +
(5sin2a — 4sinacosa + 2cos2a)Y2 —
= 0 (3.5)
В полученном выражении найдём такой угол a, чтобы коэффициент при XY стал равен нулю, для этого необходимо:
-6sinacosa + 4cos2a — 4sin2a = 0
2tg2a + 3tga — 2=0
Откуда, при решении, находим два значения tga = -2 и tga =
.
В первом задании мы нашли, что угловой коэффициент вещественной оси O‘X эллипса равен k = -2. Так как угловой коэффициент равен тангенсу, то из двух найдённых значений выберем tga = -2. Следовательно:
cosa =
, sina =
Подставив данные значения для sina и cosa в уравнение (3. 5), коэффициент при XY станет равным нулю, получим:
5), коэффициент при XY станет равным нулю, получим:
(
)X2 + (
)Y2 —
= 0
X2 + 6Y2 —
= 0
(3.6)
— это каноническое уравнение данной кривой (3.1) при a = 0.
| gif»> | 3.2.3. Кривые второго порядка | Высшая математика > 3. Аналитическая геометрия > 3.2. Аналитическая геометрия на плоскости > 3.2.3. Кривые второго порядка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| gif»> | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Кривые и поверхности второго порядка. Методические материалы презентация, доклад
Кривые и поверхности второго порядка
Методические материалы для проведения семинарских занятий с использованием интерактивной электронной доски
О.А. Иванова
Е.Е. Красновский
О.В. Новожилова
Новожилова
Московский государственный технический
университет им. Н.Э. Баумана
Кафедра «Прикладная математика»
Содержание
Основные теоретические сведения
Решение типовых примеров 1 семестра (только
параллельный перенос)
Решение типовых примеров 2 семестра (ортогональные
преобразования и параллельный перенос)
Эллипс
Гипербола
Парабола
Поверхности второго порядка
Кривые второго порядка
Поверхности второго порядка
Кривые второго порядка
Поверхности второго порядка
Содержание
Решение типовых примеров 1 семестра (только
параллельный перенос)
Решение типовых примеров 2 семестра (ортогональные
преобразования и параллельный перенос)
Эллипс
Гипербола
Парабола
Поверхности второго порядка
Кривые второго порядка
Поверхности второго порядка
Кривые второго порядка
Поверхности второго порядка
Основные теоретические сведения
Предисловие
Вариант 2
Метод сечений
Как показывает опыт, при проведении семинарских занятий по изучению кривых и поверхностей второго порядка с использованием традиционных доски и мела преподаватель вынужден тратить много времени на написание формул и, особенно, на создание рисунков.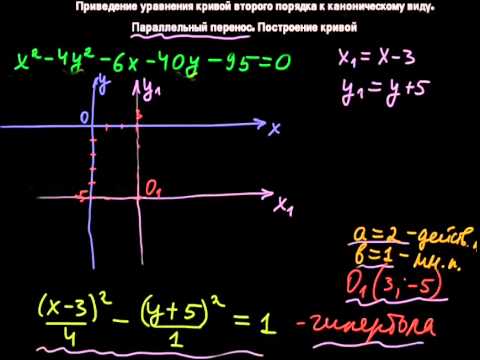 Поэтому сокращается время на объяснение теоретических основ и, самое главное, на разбор типовых задач. В результате студенты испытывают трудности при выполнении домашнего задания и подготовке к контрольным мероприятиям.
Поэтому сокращается время на объяснение теоретических основ и, самое главное, на разбор типовых задач. В результате студенты испытывают трудности при выполнении домашнего задания и подготовке к контрольным мероприятиям.
Сократить время, затрачиваемое преподавателем на подготовку графического представления учебного материала, а также существенно повысить его наглядность можно путём использования интерактивной электронной доски SMARTBOARD. Таким образом, увеличивается как время, которое можно потратить на объяснение, так и число рассматриваемых во время занятия примеров.
Настоящее учебное пособие отражает опыт авторов при проведении занятий в интерактивной форме по дисциплинам «Аналитическая геометрия» и «Линейная алгебра» со студентами 1 курса МГТУ им. Н.Э. Баумана с применением указанной электронной доски.
Содержание пособия отвечает требованиям утвержденных учебных программ, составленных в рамках перехода к блочно-модульному построению учебных курсов и балльно-рейтинговой системе оценки знаний, по следующим дисциплинам: «Аналитическая геометрия» (для факультетов ФН и СМ ),
Предисловие
«Линейная алгебра» (для факультета ФН), «Линейная алгебра и функции нескольких переменных» (для факультета СМ).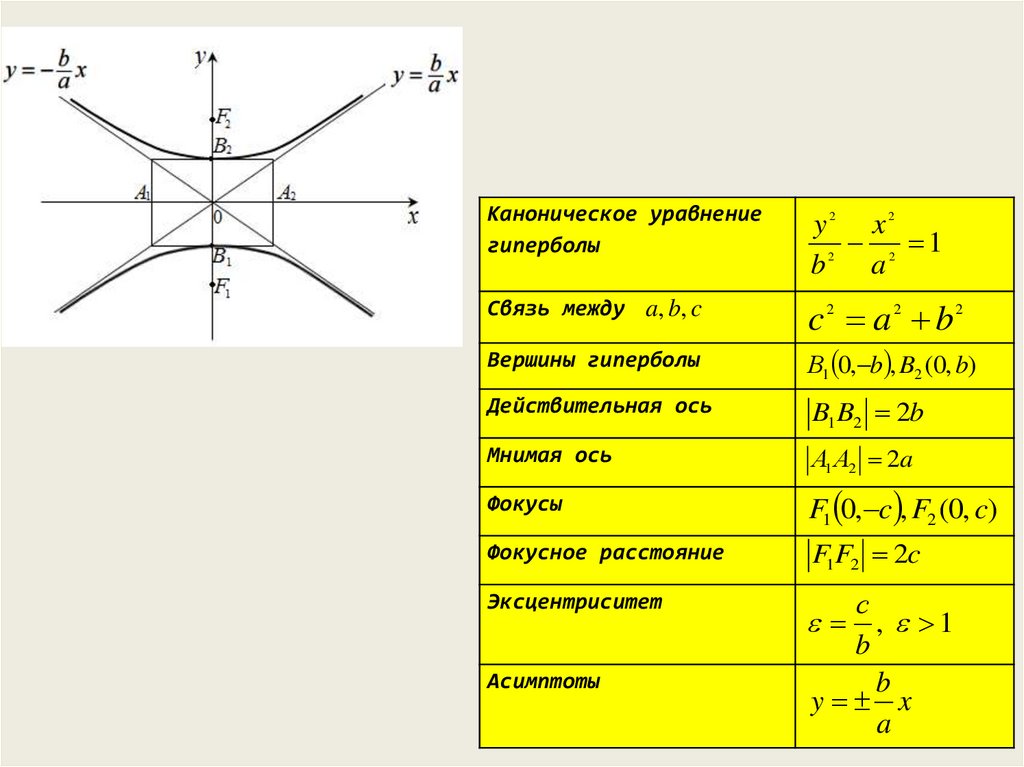
Пособие содержит как теоретический материал по кривым и поверхностям второго порядка, так и 20 примеров решения типовых задач. В большинстве рассмотренных примеров необходимо привести уравнение кривой или поверхности второго порядка к каноническому виду либо с помощью только параллельного переноса (модуль № 2 дисциплины «Аналитическая геометрия»), либо с помощью комбинации ортогонального преобразования и параллельного переноса (модуль № 2 дисциплины «Линейная алгебра» и модуль № 1 дисциплины «Линейная алгебра и функции нескольких переменных»). Оставшиеся примеры посвящены нахождению уравнения кривой по приведенным данным, поскольку такие задачи входят в домашнее задание, предусмотренное модулем № 2 дисциплины «Аналитическая геометрия».
Настоящее электронное учебное пособие можно использовать при проведении занятий в интерактивной форме, при самостоятельной работе студентов, а также при дистанционном обучении, например, с помощью системы MOODLE.
Пособие предназначено для студентов 1 курса факультетов СМ и ФН МГТУ им. Н.Э. Баумана.
Н.Э. Баумана.
Предисловие
Эллипс – геометрическое место точек М плоскости, для которых сумма расстояний до двух заданных точек F1 и F2, называемых фокусами, есть величина постоянная. Возьмем
Отрезок AB, проходящий через фокусы эллипса, с концами, лежащими на эллипсе, называется большой осью эллипса.
Отрезок CD, перпендикулярный большой оси эллипса, с концами, лежащими на эллипсе, и проходящий через центральную точку большой оси, называется малой осью эллипса.
Точка O пересечения большой и малой осей эллипса называется центром эллипса.
Точки A, B, C, D пересечения эллипса с осями называются вершинами эллипса.
Эллипс, основные определения
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях, называются соответственно большой полуосью эллипса и малой полуосью эллипса и обозначаются a и b.
Отрезки F1M и F2M, соединяющие произвольную точку М на эллипсе с его фокусами, называются фокальными радиусами.
Расстояние между фокусами называется фокальным расстоянием и обозначается 2с.
Эллипс, основные определения
Каноническое уравнение эллипса
Выберем прямоугольную систему координат Oxy на плоскости так, чтобы ее начало совпало с центром эллипса, а фокусы находились на оси абсцисс. Такую систему координат называют канонической для рассматриваемого эллипса, а соответствующие переменные – каноническими.
Координаты фокусов в канонической системе координат F1 (c,0) и F2 (–c,0).
Каноническое уравнение эллипса с фокусами на оси Ox
Эксцентриситетом эллипса ε называется отношение расстояния между его фокусами к длине его большой оси. Чем больше эксцентриситет, тем больше вытянут эллипс.
Директрисы – это две прямые d1 и d2, перпендикулярные к большой оси эллипса. Отношение расстояний от любой точки эллипса до фокуса и до соответствующей директрисы постоянно и равно ε.
Отношение расстояний от любой точки эллипса до фокуса и до соответствующей директрисы постоянно и равно ε.
Эксцентриситет и директрисы эллипса с фокусами на оси Ox
Расстояние p от директрисы до ближайшего к ней фокуса называют фокальным параметром эллипса.
Уравнения директрис эллипса
Фокальный параметр
Фокальный параметр эллипса с фокусами на оси Ox
Если b>a, то фокусы эллипса расположены на оси ординат и имеют координаты F1(0,c) и F2(0,–c).
Уравнения директрис эллипса
Каноническое уравнение эллипса с фокусами на оси Oy
Если b=a, тогда
– уравнение окружности с центром
в начале координат, радиуса а.
Фокусы F1 и F2 имеют координаты
то есть F1 и F2 располагаются в начале координат и совпадают друг с другом.
Окружность как эллипс с совпадающими фокусами
Фокусы расположены на оси Ox, a>b.
1. a=2, b=1, ;
2. a=4, b=1, ;
3. a=6, b=1, ;
4. a=6, b=3, .
Форма эллипса при различных соотношениях полуосей
Фокусы расположены на оси Oy, a
1. a=1, b=2, ;
2. a=1, b=3, ;
3. a=3, b=3, ;
4. a=3, b=6, .
Форма эллипса при различных соотношениях полуосей
Если в одном из фокусов эллипса расположить источник света, то все лучи, выходящие из него, концентрируются во втором фокусе .
Оптическое свойство эллипса
Гипербола, основные определения
Гипербола – геометрическое место точек М плоскости, для которых модуль разности расстояний до двух заданных точек F1 и F2, называемых фокусами, есть величина постоянная. Возьмем
Возьмем
Прямая, проходящая через фокусы гиперболы, называется действительной осью гиперболы.
Ось, перпендикулярная действительной оси гиперболы и проходящая через середину отрезка, соединяющего её фокусы, называется мнимой осью гиперболы.
Точка O пересечения действительной и мнимой осей гиперболы называется центром гиперболы.
Точки пересечения гиперболы A и В с её действительной осью называются вершинами гиперболы.
Отрезок, проведённый из центра гиперболы к её вершинам, называется действительной полуосью гиперболы и обозначается a.
Отрезки F1M и F2M, соединяющие произвольную точку М на гиперболе с ее фокусами, называются фокальными радиусами.
Расстояние между фокусами называется фокальным расстоянием и обозначается 2с.
Гипербола, основные определения
Выберем прямоугольную систему координат Oxy на плоскости так, чтобы центр гиперболы находился в начале координат, а фокусы располагались на оси абсцисс.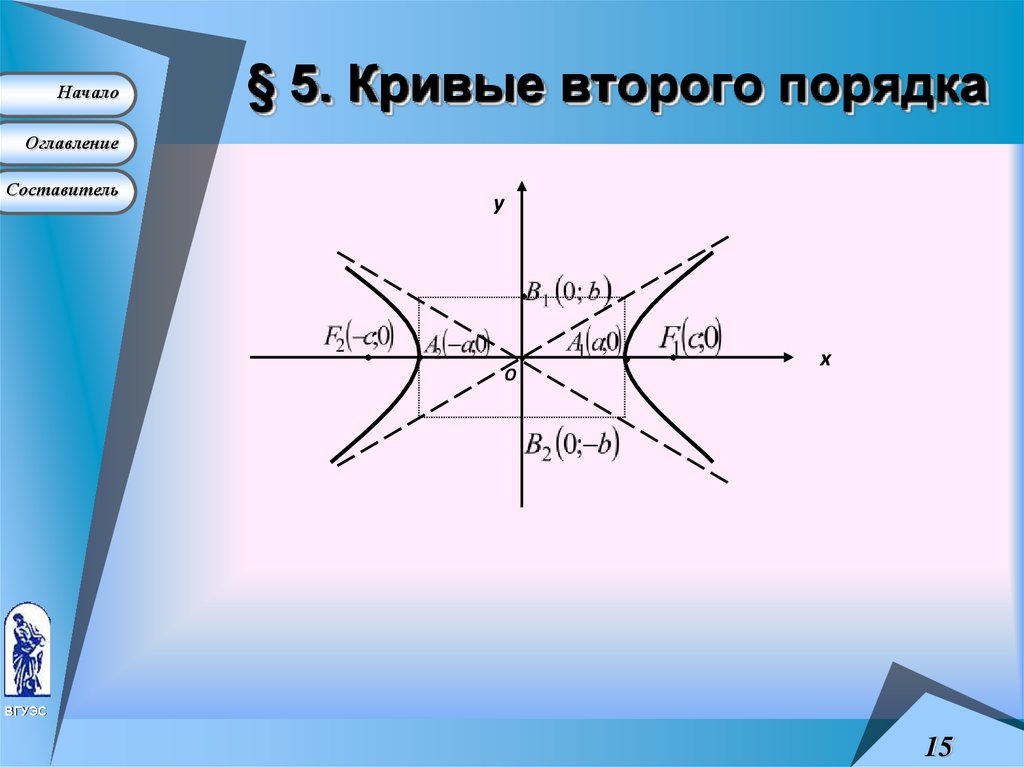 Такую систему координат называют канонической для рассматриваемой гиперболы, а соответствующие переменные – каноническими.
Такую систему координат называют канонической для рассматриваемой гиперболы, а соответствующие переменные – каноническими.
Координаты фокусов в канонической системе координат F1 (c,0) и F2 (–c,0).
Каноническое уравнение
гиперболы
Величину b>0 называют мнимой полуосью гиперболы.
Каноническое уравнение гиперболы с фокусами на оси Ox
Гипербола имеет асимптоты с уравнениями
Эксцентриситетом гиперболы называют отношение ее фокального расстояния к действительной оси. Эксцентриситет обозначают через ε.
Асимптоты и эксцентриситет гиперболы
Директрисы – это две прямые d1 и d2, перпендикулярные к действительной оси гиперболы.
Отношение расстояний от любой точки гиперболы до фокуса и соответствующей директрисы постоянно и равно ε.
Уравнения директрис гиперболы
.
Директрисы гиперболы
Расстояние p от директрисы гиперболы до ближайшего к директрисе фокуса называют фокальным параметром гиперболы.
Фокальный параметр гиперболы
Гипербола, описываемая уравнением
называется сопряженной по отношению
к гиперболе
Сопряженные гиперболы
a=2, b=1,
;
2. a=4, b=1,
;
3. a=6, b=1,
;
4. a=6, b=3,
.
Фокусы расположены на оси Ox.
Форма гиперболы при различных соотношениях полуосей
Лучи, вышедшие из одного фокуса, после отражения от ближайшей ветви гиперболы распространяются так, будто вышли из другого фокуса.
Оптическое свойство гиперболы
Если у гиперболы совпадают действительная и мнимая полуоси, то есть a=b, такую гиперболу называют
равнобочной или равноосной.
В системе координат OXY уравнение равнобочной
гиперболы имеет вид
а в системе координат Oxy уравнение той же гиперболы записывается в виде
Данное уравнение называется уравнением гиперболы в асимптотах.
Гипербола, приведенная к асимптотам
Если у гиперболы совпадают действительная и мнимая полуоси, то есть a=b, такую гиперболу называют равнобочной, или равноосной. Ее асимптоты перпендикулярны, поэтому удобно взять их в качестве координатных осей Ox и Oy. В канонической системе координат уравнение равнобочной гиперболы имеет вид
а в системе координат Oxy уравнение той же гиперболы записывается в виде
Данное уравнение называется уравнением гиперболы в асимптотах.
Гипербола, приведенная к асимптотам – вариант 2
В системе координат
вершины гиперболы имеют координаты А(a,0) и В(-а,0), а фокусы F1(с,0) и F2(-с,0), где
Следовательно, в системе координат Oxy координаты вершин гиперболы
а фокусов
Гипербола, приведенная к асимптотам
Парабола, основные определения
Парабола – геометрическое место точек, равноудаленных от фиксированной точки и от фиксированной прямой.
Фиксированную точку F называют фокусом параболы, а прямую d – директрисой параболы.
Парабола симметрична относи-тельно прямой, перпендикуляр-ной директрисе и проходящей через фокус параболы. Эту прямую называют осью параболы.
Парабола пересекает свою ось в единственной точке O, которую называют вершиной параболы.
Каноническое уравнение параболы
Расстояние от фокуса до директрисы параболы обозначают через p и называют фокальным параметром параболы.
Эксцентриситет параболы равен 1.
Уравнение директрисы
Выберем прямоугольную систему координат Oxy на плоскости так, чтобы вершина параболы находилась в начале координат, а фокус располагался на оси абсцисс. Такую систему координат называют канонической для рассматриваемой параболы, а соответствующие переменные – каноническими.
Каноническое уравнение параболы с осью на оси Ox
1) Фокус расположен на оси Ox.
1. p=4;
2. p=1;
3. p=0.5.
2) Фокус расположен на оси Oy (сопряженная парабола).
1. p=0.25;
2. p=0.5;
3. p=0.125.
Форма параболы в зависимости от фокального параметра
1) Фокус расположен на оси Ox.
2) Фокус расположен на оси Oy.
Другие виды канонических уравнений параболы
Если в фокус параболы поместить источник света, то все световые лучи после отражения от параболы будут параллельны оси параболы.
Оптическое свойство параболы
1. Эллипсоид
Поверхности второго порядка
2. Гиперболоид
а) однополостный
б) двуполостный
Поверхности второго порядка
3. Конус
Конус
Поверхности второго порядка
4. Параболоид
а) эллиптический
б) гиперболический
Поверхности второго порядка
5. Цилиндр второго порядка
а) эллиптический
б) гиперболический
в) параболический
Поверхности второго порядка
1. Сечение плоскостью yOz:
Метод сечений. Построение эллипсоида
2. Сечение плоскостью xOz:
Метод сечений. Построение эллипсоида
3. Сечение плоскостью xOy:
Метод сечений. Построение эллипсоида
Метод сечений. Построение эллипсоида
1. Сечение плоскостью xOy:
Сечение плоскостью xOy:
Метод сечений. Построение однополостного гиперболоида
2. Сечение плоскостью yOz:
Метод сечений. Построение однополостного гиперболоида
3. Сечение плоскостью xOz:
Метод сечений. Построение однополостного гиперболоида
4. Сечения плоскостями z=4 и z=-4 :
Метод сечений. Построение однополостного гиперболоида
Метод сечений. Построение однополостного гиперболоида
1. Сечение плоскостью xOz:
Метод сечений. Построение двуполостного гиперболоида
2. Сечение плоскостью yOz:
Метод сечений. Построение двуполостного гиперболоида
3. Сечения плоскостями z=3 и z=-3 :
Сечения плоскостями z=3 и z=-3 :
Метод сечений. Построение двуполостного гиперболоида
Метод сечений. Построение двуполостного гиперболоида
Задание: Привести уравнение эллипса параллельным переносом к каноническому виду и построить эллипс в системе координат Oxy.
Указать:
канонический вид уравнения;
преобразование параллельного переноса, приводящее к каноническому виду;
полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки
до фокусов;
4) для точки C проверить свойство, характеризующее эллипс как геометрическое место точек.
Решение:
Выделим в уравнении полные квадраты:
Пример 1
Центром эллипса является точка O1(2,2). С помощью параллельного переноса из системы координат Oxy в каноническую систему координат O1x1y1, определяемого соотношениями
приводим уравнение эллипса к виду
Полуоси эллипса равны a=1, b=4; его вершины в системе координат O1x1y1 имеют координаты (–1,0), (1,0), (0,–4), (0,4), а в системе координат Oxy – (1,2), (3,2), (2,–2), (2,6). Так как b>a, фокусы эллипса расположены на оси O1y1.
Так как b>a, фокусы эллипса расположены на оси O1y1.
.
Пример 1
Фокусы эллипса в системе координат O1x1y1
имеют координаты
а в системе координат Oxy
Эксцентриситет эллипса равен
Расстояния от точки до фокусов равны
Поскольку F1C+F2C=8=2b, точка C принадлежит эллипсу.
Пример 1
Задание: Привести уравнение гиперболы параллельным переносом к каноническому виду и построить гиперболу в системе координат Oxy.
Указать:
канонический вид уравнения;
преобразование параллельного переноса, приводящее к каноническому виду;
полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки
до фокусов, уравнения асимптот;
4) для точки C проверить свойство, характеризующее гиперболу как геометрическое место точек.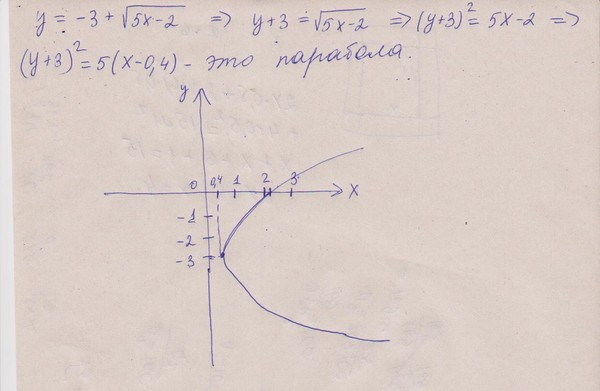
Решение:
Выделим в уравнении полные квадраты:
Пример 2
Центром гиперболы является точка О1(1,2). С помощью параллельного переноса из системы координат Oxy в каноническую систему координат O1x1y1, определяемого соотношениями
приводим уравнение гиперболы к виду
Полуоси гиперболы равны
ее вершины в системе координат O1x1y1 имеют координаты (0,1), (0,–1), а в системе координат Oxy – (1,3), (1,1).
Пример 2
Центром гиперболы является точка О1(1,2). С помощью параллельного переноса из системы координат Oxy в каноническую систему координат O1x1y1, определяемого соотношениями
приводим уравнение гиперболы к виду
Действительная полуось гиперболы равна мнимая полуось равна b=1, ее вершины в системе координат O1x1y1 имеют координаты (0,1), (0,–1), а в системе координат Oxy – (1,3), (1,1).
Пример 2 – вариант 2
Асимптотами гиперболы являются прямые
или
Пример 2
Фокусы гиперболы в системе координат
O1x1y1 имеют координаты
а в системе координат Oxy – координаты
Эксцентриситет гиперболы равен
Расстояния от точки до фокусов равны
Поскольку |F1C-F2C|=2=2b, точка C принадлежит гиперболе.
Пример 2
Задание: Привести уравнение параболы параллельным переносом к каноническому виду и построить параболу в системе координат Oxy.
Указать:
канонический вид уравнения;
преобразование параллельного переноса, приводящее к каноническому виду;
параметр, вершину, фокус, уравнение директрисы, расстояния от точки С(–3,1) до фокуса и директрисы;
4) для точки С проверить свойство, характеризующее параболу как геометрическое место точек.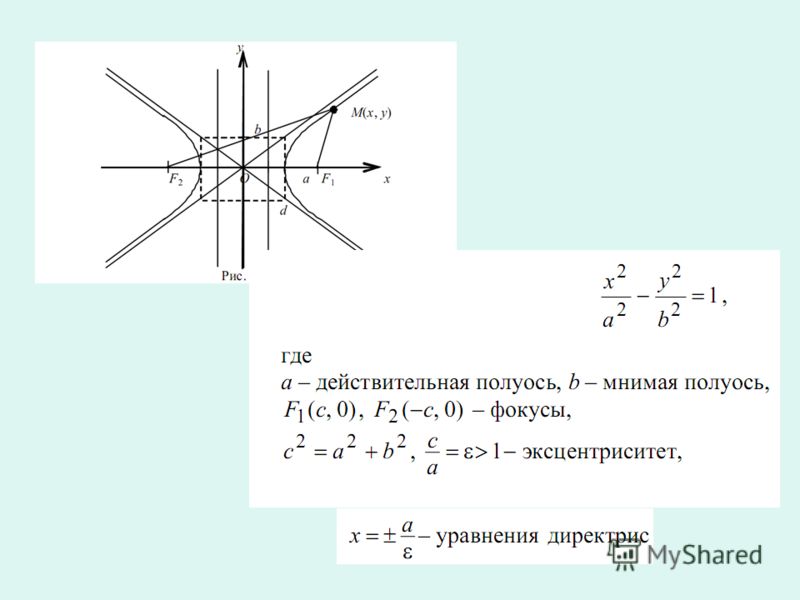
Решение:
Выделим в уравнении полный квадрат по y:
Пример 3
Вершиной параболы является точка O (–2,3).
С помощью параллельного переноса из системы координат Oxy в систему координат O1x1y1, определяемого соотношениями
приводим уравнение параболы к виду
Фокальный параметр параболы равен
а в системе координат Oxy –
Фокус параболы в системе координат O1x1y1 имеет координаты
Пример 3
Директрисой параболы является прямая
или
Расстояние от точки С (-3;1) до фокуса равно
расстояние до директрисы равно
Так как расстояния от точки C до фокуса и до директрисы равны, точка C принадлежит параболе.
Пример 3
Задание: Найти уравнение эллипса, если известно, что он проходит через точку С (0,–1), а его малая ось оканчивается вершинами и
Решение:
Малая полуось эллипса равна а его центр – середина отрезка
AB – имеет координаты О1 (–3,–2).
Пример 4
Следовательно, уравнение эллипса имеет вид
где a – большая полуось эллипса.
Подставив в уравнение эллипса координаты точки C (0,–1), найдем a:
Итак, в исходной системе координат Oxy эллипс задается уравнением
Пример 4
С помощью параллельного переноса из системы координат Oxy в каноническую систему координат O1x1y1, определяемого соотношениями
приводим уравнение эллипса к каноническому виду
Полуоси эллипса равны
его вершины в системе
O1x1y1 имеют координаты
а в системе Oxy – координаты
соответственно.
Пример 4
Фокусы эллипса в системе O1x1y1 имеют координаты F1 (4,0), F2 (–4,0), а в системе координат Oxy – F1 (1,–2), F2 (–7,–2).
эксцентриситет эллипса равен
Расстояния от точки C (0,–1) до фокусов равны
Пример 4
Задание: Найти уравнение равносторонней гиперболы, имеющей асимптоту x=1, пересекающей ось Ox в точке C (–1/3,0), а ось Oy – в точке A (0,1).
Решение:
Поскольку вертикальная асимптота гиперболы – прямая x=1, уравнение гиперболы имеет вид
Подставив в это уравнение координаты
точек C и A, получим
откуда
Искомая гипербола описывается уравнением
Горизонтальной асимптотой гиперболы
является прямая y= –3. Подставив в полученное уравнение гиперболы координаты точки С, найдем const= –4.
Пример 5
Центром гиперболы является точка О1 (1,–3). С помощью параллельного пере-носа из системы координат Oxy в каноническую систему координат O1x1y1, определяемого соотношениями
приводим уравнение к виду
где – полуоси
гиперболы. Ее вершины в системе координат O1x1y1 имеют координаты
а в системе координат Oxy – координаты
соответственно.
Пример 5
Фокусы гиперболы в системе координат O1x1y1 имеют координаты
а в системе координат Oxy – координаты
эксцентриситет гиперболы равен
Расстояния от точки
до фокусов равны
Следовательно,
Пример 5
Задание: Найти уравнение параболы, симметричной относительно прямой x=3, пересекающей ось Oy в точке С (0,11), с вершиной, расположенной в четвертой четверти на расстоянии 3/16 от директрисы.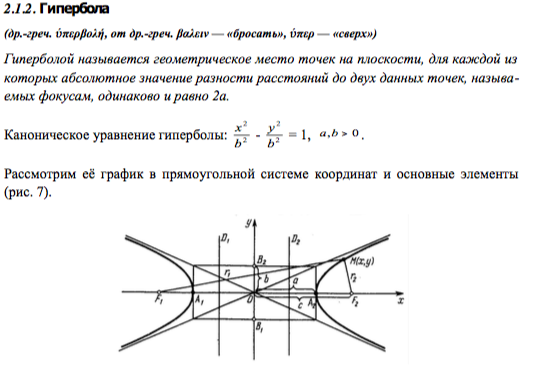
Решение:
Поскольку парабола симметрична относительно прямой x=3, ее вершина лежит на этой прямой и имеет координаты (3,y0), а уравнение имеет вид
Расстояние от вершины до директрисы равно p/2, поэтому фокальный параметр равен
Подставляя в уравнение координаты точки C, получим
Поскольку вершина параболы лежит в четвертой четверти, y0
Пример 6
Вершиной параболы является точка O1 (3,–1). С помощью параллельного переноса из системы координат Oxy в каноническую систему координат O1x1y1, определяемого соотношениями
приводим уравнение параболы к виду
Фокус параболы в системе координат O1x1y1 имеет координаты
а в системе координат Oxy – координаты
Уравнение параболы имеет вид
Пример 6
Директрисой параболы является прямая
или
Расстояние от точки C (0,11) до фокуса
равно
расстояние до директрисы равно
Пример 6
Задание: Найти уравнение гиперболы, имеющей фокусы F1 (1,2) и F2 (11,2) и пересекающей ось Oy в точке
Решение:
Фокусы лежат на прямой y=2; эта прямая является действительной осью гиперболы. Вершина гиперболы – середина отрезка F1F2 – имеет координаты O1(6,2). Так как расстояние между фокусами гиперболы равно 2c=10, то c=5.
Вершина гиперболы – середина отрезка F1F2 – имеет координаты O1(6,2). Так как расстояние между фокусами гиперболы равно 2c=10, то c=5.
Уравнение гиперболы имеет вид
Подставив в уравнение гиперболы координаты точки C и учитывая, что
получим
Пример 7
Уравнение гиперболы имеет вид
Обозначим a2=t, 0
Полуоси гиперболы равны
Пример 7
Асимптотами гиперболы являются прямые
или
С помощью параллельного переноса из системы координат Oxy в каноническую систему координат O1x1y1, определяемого соотно-шениями
приводим исходное уравнение к виду
Пример 7
Фокусы гиперболы в системе координат O1x1y1 имеют координаты
Эксцентриситет гиперболы равен
Расстояния от точки
до фокусов равны
Вершины гиперболы в системе координат O1x1y1 имеют координаты
а в системе координат Oxy –
Пример 7
Задание: Указать преобразование параллельного переноса, приводящее данное уравнение поверхности к каноническому виду, канонический вид уравнения поверхности и тип поверхности. Построить поверхность в канонической системе координат.
Построить поверхность в канонической системе координат.
Решение:
Выделим в уравнении полные квадраты по каждой из переменных:
Пример 8
С помощью параллельного переноса в систему координат O1x1y1z1 с центром O1 (1,–2,2), определяемого соотношениями
приводим уравнение к каноническому виду
Это уравнение описывает двуполостный гиперболоид.
Пример 8
Задание: Указать преобразование параллельного переноса, приводящее данное уравнение поверхности к каноническому виду, канонический вид уравнения поверхности и тип поверхности. Построить поверхность в канонической системе координат.
Решение:
Выделим в уравнении полные квадраты по каждой из переменных:
Пример 9
С помощью параллельного переноса в систему координат O1x1y1z1 с центром O1 (2,–1,–4), определяемого соотношениями
приводим уравнение к каноническому виду
Это уравнение описывает эллипти-ческий параболоид.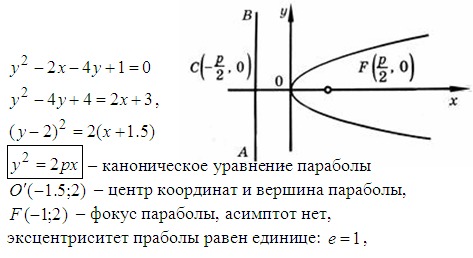
Пример 9
Задание: Указать преобразование параллельного переноса, приводящее данное уравнение поверхности к каноническому виду, канонический вид уравнения поверхности и тип поверхности. Построить поверхность в канонической системе координат.
Решение:
Выделим в уравнении полные квадраты по каждой из переменных:
Пример 10
С помощью параллельного переноса в систему координат O1x1y1z1 с центром
O1 (–2,0,3), определяемого соотношениями
приводим уравнение к каноническому виду
Это уравнение описывает эллипсоид.
Пример 10
Задание: Указать преобразование параллельного переноса, приводящее данное уравнение поверхности к каноническому виду, канонический вид уравнения поверхности и тип поверхности. Построить поверхность в канонической системе координат.
Решение:
Выделим в уравнении полный квадрат по переменной y:
Пример 11
С помощью параллельного переноса в систему координат O1x1y1z1 с центром O1 (–1,–2,0), определяемого соотношениями
приводим уравнение к канони-ческому виду
Это уравнение описывает параболический цилиндр.
Пример 11
Задание: Указать преобразование параллельного переноса, приводящее данное уравнение поверхности к каноническому виду, канонический вид уравнения поверхности и тип поверхности. Построить поверхность в канонической системе координат.
Решение:
Выделим в уравнении полные квадраты по каждой из переменных:
Пример 12
С помощью параллельного переноса в систему координат O1x1y1z1 с центром O1 (4,–1,1), определяемого соотношениями
приводим уравнение к каноническому виду
Это уравнение описывает гиперболический параболоид.
Пример 12
Пример 13
Задание: Привести уравнение кривой второго порядка ортогональным преобразованием и параллельным переносом к каноническому виду, указав преобразования перехода от исходной прямоугольной системы координат Oxy к полученной системе O2x2y2. Начертить кривую на плоскости Oxy, изобразив на чертеже каноническую систему координат O2x2y2.
Решение:
.
Квадратичная форма имеет вид
В матричном виде уравнение этой кривой второго порядка имеет вид
где
Пример 13
Собственному значению λ1=2 соответствует единичный собственный вектор
Собственному значению λ2=8
соответствует единичный собственный вектор
.
Найдём собственные числа и собственные векторы матрицы А квадратичной формы
Пример 13
Матрица ортогонального преобразования, приводящего квадратичную форму к каноническому виду, составлена из столбцов координат собственных векторов. Это преобразование является поворотом.
Это преобразование является поворотом.
Этому ортогональному преобразованию соответствует линейная замена переменных
.
Пример 13
После подстановки x и y в уравнение кривой получаем уравнение с квадратичной формой канонического вида
Пример 13
Отметим, что канонический вид квадратичной формы мы можем записать сразу по известным собственным числам
.
Порядок следования собственных чисел соответствует порядку собственных векторов в матрице ортогонального преобразования – матрице перехода между ортонормированными базисами систем координат Oxy и Ox1y1.
Линейные слагаемые преобразуются следующим образом.
Поскольку , то вектор-строка коэффициентов при линейных слагаемых равен
Свободный член останется прежним.
В результате уравнение поверхности в системе координат Ox1y1 принимает вид
После деления обеих частей уравнения на 2 получаем
Пример 13
приводит к уравнению в системе координат O2x2y2, началом которой является точка O2 (–2,2)
Разделив обе части уравнения на 8, получаем каноническое уравнение эллипса
Преобразование параллельного переноса
По каждой из переменных выделяем полный квадрат:
.
В системе координат O2x2y2 уравнение эллипса имеет канонический вид
Пример 13
Пример 13
1. Изображаем исходную систему Oxy, а в ней векторы и .
Эти векторы откладываем от начала O системы координат, они задают координатные оси новой системы координат Ox1y1.
Для того, чтобы построить эллипс, заданный в исходной системе координат Oxy уравнением
поступаем следующим образом:
Пример 13
2. В системе координат Ox1y1 строим точку O2 (–2,2), которая является началом канонической системы координат O2x2y2. Оси O2x2 и O2y2 параллельны осям Ox1 и Oy1.
Пример 14
Решение:
Задание: Привести уравнение кривой второго порядка ортогональным преобразованием и параллельным переносом к каноническому виду, указав преобразования перехода от исходной прямоугольной системы координат Oxy к полученной системе O2x2y2. Начертить кривую на плоскости Oxy, изобразив на чертеже каноническую систему координат O2x2y2.
Начертить кривую на плоскости Oxy, изобразив на чертеже каноническую систему координат O2x2y2.
.
Квадратичная форма имеет вид
В матричном виде уравнение этой кривой второго порядка имеет вид
где
Пример 14
Собственному значению λ1= –5 соответствует единичный собственный вектор
а собственному значению λ2=5 соответствует еди-ничный собственный вектор
.
Найдём собственные числа и собственные векторы матрицы А квадратичной формы
Пример 14
Матрица ортогонального преобразования, приводящего квадратичную форму к каноническому виду, составлена из столбцов координат собственных векторов. Это преобразование является поворотом.
Этому ортогональному преобразованию соответствует линейная замена переменных
Пример 14
После подстановки x и y в уравнение кривой получаем уравнение с квадратичной формой канонического вида
Пример 14
Отметим, что канонический вид квадратичной формы мы можем записать сразу по известным собственным числам
.
Порядок следования собственных чисел соответствует порядку собственных векторов в матрице ортогонального преобразования – матрице перехода между ортонормированными базисами систем координат Oxy и Ox1y1.
Линейные слагаемые преобразуются следующим образом.
Поскольку , то вектор-строка коэффициентов при линейных слагаемых равен
Свободный член останется прежним.
В результате уравнение поверхности в новых координатах принимает вид
После деления обеих частей уравнения на -5 получаем
Пример 14
По каждой из переменных выделяем полный квадрат
Преобразование параллельного переноса
приводит к уравнению в системе координат O2x2y2, началом которой является точка O2 (2,0)
Разделив обе части уравнения на 8, получаем каноническое уравнение гиперболы
Пример 14
В системе координат O2x2y2 уравнение гиперболы имеет канонический вид
Уравнения асимптот
Пример 14
Для того, чтобы построить гиперболу, заданную в исходной системе координат Oxy уравнением
поступаем следующим образом:
1. Изображаем исходную систему Oxy, а в ней векторы и .
Изображаем исходную систему Oxy, а в ней векторы и .
Эти векторы откладываем от начала O системы координат, они задают координатные оси новой системы координат Ox1y1.
Пример 14
2. В системе координат Ox1y1 строим точку O2 (2,0), которая является началом канонической системы координат O2x2y2. Оси O2x2 и O2y2 параллельны осям Ox1 и Oy1.
Пример 15
Решение:
Задание: Привести уравнение кривой второго порядка ортогональным преобразованием и параллельным переносом к каноническому виду, указав преобразования перехода от исходной прямоугольной системы координат Oxy к полученной системе O2x2y2. Начертить кривую на плоскости Oxy, изобразив на чертеже каноническую систему координат O2x2y2.
.
Квадратичная форма имеет вид
В матричном виде уравнение этой кривой второго порядка имеет вид
где
Пример 15
Собственному значению λ1=0 соответствует единичный собственный вектор
а собственному значению λ2=25 соответствует единич-ный собственный вектор
Найдём собственные числа и собственные векторы матрицы А квадратичной формы
Пример 15
Матрица ортогонального преобразования, приводящего квадратичную форму к каноническому виду, составлена из столбцов координат собственных векторов. Это преобразование является поворотом.
Это преобразование является поворотом.
Этому ортогональному преобразованию соответствует линейная замена переменных
Пример 15
После подстановки x и y в уравнение кривой получаем уравнение с квадратичной формой канонического вида
Пример 15
Отметим, что канонический вид квадратичной формы мы можем записать сразу по известным собственным числам
.
Порядок следования собственных чисел соответствует порядку собственных векторов в матрице ортогонального преобразования – матрице перехода между ортонормированными базисами систем координат Oxy и Ox1y1.
Линейные слагаемые преобразуются следующим образом.
Поскольку , то вектор-строка коэффициентов при линейных слагаемых равен
Свободный член отсутствует.
В результате уравнение поверхности в новых координатах принимает вид
После деления обеих частей уравнения на 25 получаем
Пример 15
Выделяем полный квадрат
Преобразование параллельного переноса
приводит к уравнению в системе координат O2x2y2, началом которой является точка O2 (1/6,–1)
В системе координат O2x2y2 уравнение параболы имеет канонический вид
Пример 15
1. Изображаем исходную систему Oxy, а в ней векторы и
Изображаем исходную систему Oxy, а в ней векторы и
Эти векторы откладываем от начала O системы координат, они задают координатные оси новой системы координат Ox1y1.
Для того, чтобы построить параболу, заданную в исходной системе координат Oxy уравнением
поступаем следующим образом:
Пример 15
2. В системе координат Ox1y1 строим точку O2 (1/6,–1), которая является началом следующей канонической системы координат O2x2y2. Оси O2x2 и O2y2 параллельны осям Ox1 и Oy1.
Задание: Привести уравнение поверхности второго порядка ортогональным преобразованием и параллельным переносом к каноническому виду, указав преобразование перехода от исходной прямоугольной системы координат Oxyz к канонической системе координат O2x2y2z2. Построить поверхность в полученной системе координат O2x2y2z2, используя метод сечений.
Все собственные числа матрицы A квадратичной формы расположить в порядке возрастания, а матрицу ортогонального преобразования U построить так, чтобы det U= +1.
Пример 16
.
В матричном виде уравнение этой поверхности второго порядка имеет вид
где
Решение:
Собственным значениям λ1, λ2, λ3 соответствуют единичные собственные векторы
Пример 16
Найдём собственные числа и собственные векторы матрицы А квадратичной формы
Матрица ортогонального преобразования, приводящего квадратичную форму к каноническому виду, составлена из столбцов координат собственных векторов. Это преобразование является поворотом.
Этому ортогональному преобразованию соответствует линейная замена переменных
Пример 16
Пример 16
Канонический вид квадратичной формы мы можем записать сразу по известным собственным числам
.
Порядок следования собственных чисел соответствует порядку собственных векторов в матрице ортогонального преобразования – матрице перехода между ортонормированными базисами систем координат Oxyz и Ox1y1z1.
Линейные слагаемые преобразуются следующим образом.
Поскольку , то вектор-строка коэффициентов при линейных cлагаемых равен
Свободный член останется прежним.
В результате уравнение поверхности в новых координатах принимает вид
После деления обеих частей уравнения на 3 получаем
Таким образом, в новых координатах уравнение поверхности примет вид
По каждой из переменных выделяем полный квадрат
Параллельный перенос из системы координат Ox1y1z1 в O2x2y2z2 определен соотношениями
Пример 16
Уравнение поверхности в системе координат O2x2y2z2, началом которой является точка O2 (1,2,1) в системе координат Ox1y1z1, имеет вид
Разделив на 2, получаем каноническое уравнение эллипсоида
Пример 16
Задание: Привести уравнение поверхности второго порядка ортогональным преобразованием и параллельным переносом к каноническому виду, указав преобразование перехода от исходной прямоугольной системы координат Oxyz к канонической системе координат O2x2y2z2. Построить поверхность в полученной системе координат O2x2y2z2, используя метод сечений.
Построить поверхность в полученной системе координат O2x2y2z2, используя метод сечений.
Во всех задачах собственные числа матрицы A квадратичной формы расположить в порядке возрастания, а матрицу ортогонального преобразования U построить так, чтобы det U= +1.
Пример 17
.
В матричном виде уравнение этой поверхности второго порядка имеет вид
где
Решение:
Собственным значениям λ1, λ2, λ3 соответствуют единичные собственные векторы
Пример 17
Найдём собственные числа и собственные векторы матрицы А квадратичной формы
Матрица ортогонального преобразования, приводящего квадратичную форму к каноническому виду, составлена из столбцов координат собственных векторов. Это преобразование является поворотом.
Этому ортогональному преобразованию соответствует линейная замена переменных
Пример 17
Пример 17
Канонический вид квадратичной формы мы можем записать сразу по известным собственным числам
Порядок следования собственных чисел соответствует порядку собственных векторов в матрице ортогонального преобразования – матрице перехода между ортонормированными базисами систем координат Oxyz и Ox1y1z1.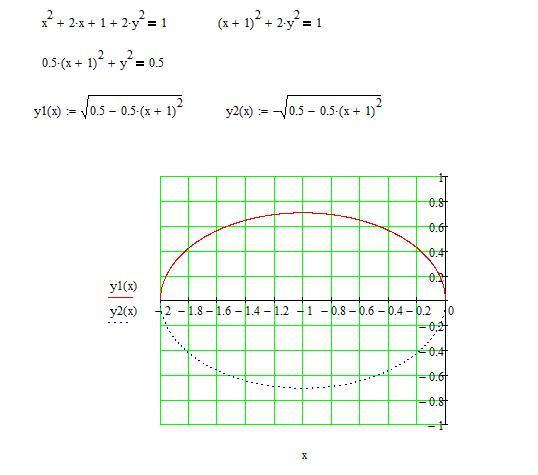
Линейные слагаемые преобразуются следующим образом.
Поскольку , то вектор-строка коэффициентов при линейных слагаемых равен
Свободный член отсутствует.
В результате уравнение поверхности в новых координатах принимает вид
По каждой из переменных выделяем полный квадрат
Пример 17
В итоге мы получили каноническое уравнение однополостного гиперболоида.
Параллельный перенос из системы координат Ox1y1z1 в O2x2y2z2 определен соотношениями
или, что тоже самое
Пример 17
Он приводит к уравнению поверхности в системе координат O2x2y2z2, началом
которой является точка , заданная в системе координат Ox1y1z1,
Пример 17
Однополостный гиперболоид
Задание: Привести уравнение поверхности второго порядка ортогональным преобразованием и параллельным переносом к каноническому виду, указав преобразования перехода от исходной прямоугольной системы координат Oxyz к канонической системе координат O2x2y2z2. Построить поверхность в полученной системе координат O2x2y2z2, используя метод сечений.
Построить поверхность в полученной системе координат O2x2y2z2, используя метод сечений.
Во всех задачах собственные числа матрицы A квадратичной формы расположить в порядке возрастания, а матрицу ортогонального преобразования U построить так, чтобы det U= +1.
Пример 18
.
В матричном виде уравнение этой поверхности второго порядка имеет вид
где
Решение:
Собственным значениям λ1, λ2, λ3 соответствуют единичные собственные векторы
Пример 18
Найдём собственные числа и собственные векторы матрицы А квадратичной формы
Матрица ортогонального преобразования, приводящего квадратичную форму к каноническому виду, составлена из столбцов координат собственных векторов. Это преобразование является поворотом.
Этому ортогональному преобразованию соответствует линейная замена переменных
Пример 18
Пример 18
Канонический вид квадратичной формы мы можем записать сразу по известным собственным числам
Порядок следования собственных чисел соответствует порядку собственных векторов в матрице ортогонального преобразования – матрице перехода между ортонормированными базисами систем координат Oxyz и Ox1y1z1.
Линейные слагаемые преобразуются следующим образом.
Поскольку , то вектор-строка коэффициентов при линейных слагаемых равен
Свободный член остается прежним.
В результате уравнение поверхности в новых координатах принимает вид
По каждой из переменных выделяем полный квадрат
Пример 18
Он приводит к уравнению поверхности в системе координат O2x2y2z2, началом
которой является точка , заданная в системе координат Ox1y1z1,
Параллельный перенос из системы координат Ox1y1z1 в O2x2y2z2 определен соотношениями
Разделив на -4/5, получаем каноническое уравнение двуполостного гиперболоида
Пример 18
Пример 18
Двуполостный
гиперболоид
Задание: Привести уравнение поверхности второго порядка ортогональным преобразованием и параллельным переносом к каноническому виду, указав преобразования перехода от исходной прямоугольной системы координат Oxyz к канонической системе координат O2x2y2z2. Построить поверхность в полученной системе координат O2x2y2z2, используя метод сечений.
Построить поверхность в полученной системе координат O2x2y2z2, используя метод сечений.
Во всех задачах собственные числа матрицы A квадратичной формы расположить в порядке возрастания, а матрицу ортогонального преобразования U построить так, чтобы det U= +1.
Пример 19
.
В матричном виде уравнение этой поверхности второго порядка имеет вид
где
Решение:
Собственным значениям λ1, λ2, λ3 соответствуют единичные собственные векторы
Пример 19
Найдём собственные числа и собственные векторы матрицы А квадратичной формы
Матрица ортогонального преобразования, приводящего квадратичную форму к каноническому виду, составлена из столбцов координат собственных векторов. Это преобразование является поворотом.
Этому ортогональному преобразованию соответствует линейная замена переменных
Пример 19
Пример 19
Канонический вид квадратичной формы мы можем записать сразу по известным собственным числам
Порядок следования собственных чисел соответствует порядку собственных векторов в матрице ортогонального преобразования – матрице перехода между ортонормированными базисами систем координат Oxyz и Ox1y1z1.
Линейные слагаемые преобразуются следующим образом.
Поскольку , то вектор-строка коэффициентов при линейных слагаемых равен
Свободный член останется прежним.
В результате уравнение поверхности в новых координатах принимает вид
Он приводит к уравнению поверхности в системе координат O2x2y2z2, началом
которой является точка O2 (3,0,0), заданная в системе координат Ox1y1z1:
Параллельный перенос из системы координат Ox1y1z1 в O2x2y2z2 определен соотношениями
Разделив на 24, получаем каноническое уравнение эллиптического параболоида
Пример 19
Пример 19
Эллиптический
параболоид
Задание: Привести уравнение поверхности второго порядка ортогональным преобразованием и параллельным переносом к каноническому виду, указав преобразования перехода от исходной прямоугольной системы координат Oxyz к канонической системе координат O2x2y2z2. Построить поверхность в полученной системе координат O2x2y2z2, используя метод сечений.
Построить поверхность в полученной системе координат O2x2y2z2, используя метод сечений.
Все собственные числа матрицы A квадратичной формы расположить в порядке возрастания, а матрицу ортогонального преобразования U построить так, чтобы det U= +1.
Пример 20
.
В матричном виде уравнение этой поверхности второго порядка имеет вид
где
Решение:
Собственным значениям λ1, λ2, λ3 соответствуют единичные собственные векторы
Пример 20
Найдём собственные числа и собственные векторы матрицы А квадратичной формы
Матрица ортогонального преобразования, приводящего квадратичную форму к каноническому виду, составлена из столбцов координат собственных векторов. Это преобразование является поворотом.
Этому ортогональному преобразованию соответствует линейная замена переменных
Пример 20
Пример 20
Канонический вид квадратичной формы мы можем записать сразу по известным собственным числам
.
Порядок следования собственных чисел соответствует порядку собственных векторов в матрице ортогонального преобразования – матрице перехода между ортонормированными базисами систем координат Oxyz и Ox1y1z1.
Линейные слагаемые преобразуются следующим образом.
Поскольку то вектор-строка коэффициентов при линейных слагаемых равен
Свободный член остается прежним.
В результате уравнение поверхности в новых координатах принимает вид
После деления обеих частей уравнения на 9 получаем
По каждой из переменных выделяем полный квадрат
Параллельный перенос из системы координат Ox1y1z1 в O2x2y2z2 определен соотношениями
Пример 20
Уравнение поверхности в системе координат O2x2y2z2, началом которой является точка O2 (1,3,2), заданная в системе координат Ox1y1z1, имеет вид
Разделив на 4, получаем каноническое уравнение гиперболического параболоида
Пример 20
Литература
Основная литература
Канатников А. Н., Крищенко А.П. Аналитическая геометрия: Учеб. для вузов 2-е изд. / Под ред. B.C. Зарубина, А.П. Крищенко. – М., Изд. МГТУ, 2000. – 388 с. (Сер. Математика в техническом университете, вып. III).
Н., Крищенко А.П. Аналитическая геометрия: Учеб. для вузов 2-е изд. / Под ред. B.C. Зарубина, А.П. Крищенко. – М., Изд. МГТУ, 2000. – 388 с. (Сер. Математика в техническом университете, вып. III).
Канатников А.Н., Крищенко А.П. Линейная алгебра: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 336 с. (Сер. Математика в техническом университете, вып. IV).
Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Физматлит, 2003. – 240 с.
Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2003. – 296 с.
Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П. Демидовича. – М.: Интеграл-Пресс, 1997. – 416 с.
Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб. пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с.
Дополнительная литература
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1987. – 336 с.
– М.: Наука, 1987. – 336 с.
2. Беклемишева Л.А., Петрович Ю.А., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре. – М.: Наука, 1987. – 496 с.
Литература
3. Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко и др. – Т. 1. – М.: Эдиториал УРСС, 2000. – 327 с.
4. Клетеник Д.В. Сборник задач по аналитической геометрии. – Спб.: Профессия, 2001. – 240 с.
5. Сборник задач по линейной алгебре / Под ред. С.К. Соболева. – М.: МГТУ, 1991. –154 с.
Методические пособия, изданные в МГТУ
Бархатова О.А., Садыхов Г.С. Поверхности второго порядка. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. – 40 с.
Гришина Г.В., Козлов М.Е., Пашовкин Е.М., Подобряев В.Н. Методические указания к самостоятельной работе студентов по разделам «Математический анализ» и «Линейная алгебра», под ред. Гришиной Г.В. Учеб. пособие. – М.: МГТУ, 1990.–38 с.
Дубограй И. В., Леванков В.И., Максимова Е.В. Методические указания к выполнению домашнего задания по теме «Кривые второго порядка». – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. – 52 с.
В., Леванков В.И., Максимова Е.В. Методические указания к выполнению домашнего задания по теме «Кривые второго порядка». – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. – 52 с.
Пугачев О.В., Стась Г.П., Чередниченко А.В. Квадратичные формы и их геометрические приложения. Методические указания к выполнению типового расчета. – М.: МГТУ, 2004. – 59 с.
Приведение к канонической форме онлайн
- График неявной функции
- Поверхность определяется уравнением
- Каноническая форма эллиптического параболоида
- Каноническая форма двойного гиперболоида
- Каноническая форма воображаемого эллипсоида
- Каноническая форма вырожденного эллипса 92-6х1х2
⚟
График:
x : [ ]
у : [ ]
z : [ ]
Качество:
(Количество точек на оси)
Тип графика:
SurfaceGridLineDot
Что умеет канонический калькулятор?
- Для заданного уравнения находит:
- Каноническая форма уравнения (для линий и поверхностей второго порядка)
- Базис-вектор канонической системы координат (для линий 2-го порядка)
- Центр канонической системы координат (для линий 2-го порядка)
- Подробное решение двумя способами:
- Прямой метод с переходом в новый центр координат и поворотом вокруг нового центра координат (для линий) 92/=1/14
Две параллельные плоскости Поверхность Чтобы увидеть подробное решение, поделитесь им со всеми своими друзьями-студентами
17 канонических форм
17 канонических форм
SolitaryRoad. com
comВладелец сайта: Джеймс Миллер
[ Дом ] [ Вверх ] [ Информация ] [ Почта ]ОБЩЕЕ УРАВНЕНИЕ ВТОРОЙ СТЕПЕНИ, КВАДРИЧНОЕ ПОВЕРХНОСТИ, ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ, 17 КАНОНИЧЕСКИЕ ФОРМЫ, ПРЕОБРАЗОВАНИЕ КООРДИНАТЫ
Общее уравнение второй степени. Общее уравнение второго степень по трем переменным равна
1) f(x, y, z) = ax 2 + by 2 + cz 2 + 2fyz + 2gxz + 2hxy + 2px + 2qy + 2rz + d = 0,
Геометрическим местом этого уравнения является поверхность в пространстве, называемая квадрикой или коникоидом. См. рисунок 1. Квадратичные поверхности состоят из эллипсоидов, гиперболоидов, параболоидов и некоторых предельных или вырожденные их формы.
Упрощение путем изменения система координат. Алгебраический выражение для любой кривой или поверхности в зависимости от расположения и направления система координат. Когда координата система вращается или перемещается каким-либо образом выражение для изменения кривой или поверхности.
 Общее уравнение второй степени
можно значительно упростить, заменив
другая система координат. Подходящий
вращение системы координат будет
исключить все смешанные термины в xy, xz
и ыз. Подходящий перевод устранит большинство или все термины первой степени в x, y и z.
Путем подходящего переноса и поворота системы координат общее уравнение второй степени
можно привести к одной из следующих канонических форм:
Общее уравнение второй степени
можно значительно упростить, заменив
другая система координат. Подходящий
вращение системы координат будет
исключить все смешанные термины в xy, xz
и ыз. Подходящий перевод устранит большинство или все термины первой степени в x, y и z.
Путем подходящего переноса и поворота системы координат общее уравнение второй степени
можно привести к одной из следующих канонических форм:
Сделаем несколько замечаний относительно некоторых поверхностей.
● Эллипсоид можно представить как поверхность, полученную из сферы путем равномерного растяжения (или сжимая) сферу в трех взаимно перпендикулярных направлениях на заданные величины. уравнение сферы с центром в начале координат:
2) x 2 + y 2 + z 2 = 1
, а уравнение эллипсоида с центром в начале координат равно
.Если (x, y, z) — точка, удовлетворяющая уравнению 2), то (ax, by, cz) — точка, удовлетворяющая уравнению 3).
 Таким образом
если P (x, y, z) — точка на сфере 2), то P'(ax, by, cz) — соответствующая точка на эллипсоиде 3).
Таким образом
если P (x, y, z) — точка на сфере 2), то P'(ax, by, cz) — соответствующая точка на эллипсоиде 3).● Гиперболоид одного листа (форма 3), гиперболоид двух листов (форма 4), второго порядка конус (форма 5) и эллиптический параболоид (форма 7) появляются в особых случаях как поверхности революция. Общие формы этих поверхностей можно рассматривать как созданные однородным растяжение их формы поверхности вращения подобно тому, как эллипсоид может быть изготовлен из сферы растяжением. Например, уравнение гиперболоида одного листа
Если a = b, это поверхность вращения с уравнением
Поверхность 4) может быть получена из поверхности 5) растяжением в направлении y на коэффициент b/a. То же самое и с другими поверхностями — гиперболоидом из двух листов, конусом второго порядка и т. д. Мы можем взять поверхность в форме поверхности вращения и растянуть ее в направлении перпендикулярно его оси, в направлении x или y, чтобы получить общий вид.

● Можно многое узнать о таких поверхностях, изучая поперечные сечения. Например, можно исследовать поперечные сечения, перпендикулярные оси z 5), установив z = k, и увидеть, что они являются кругами. Мы также можем посмотреть на поперечное сечение, созданное плоскостью, проходящей через (содержащей) ось Z. Например, если мы подставим y = 0 в 5), мы получим уравнение пересечения поверхность с плоскостью y = 0. Заметим, что это гипербола. Такие кривые, полученные при переходе плоскости, проходящие через ось вращения, называются меридианами. Поверхность вращения может быть получается при вращении меридиана вокруг оси вращения.
● Все формы 9–17 представлены уравнениями только с двумя переменными x и y ( переменная z отсутствует). Таким образом, все они соответствуют цилиндрам, направляющие которых являются соответствующие кривые в плоскости x-y, образующими которых являются прямые, параллельные оси z.
******************************************************* ******
ПРЕОБРАЗОВАНИЕ КООРДИНАТ
******************************************************* ******
Преобразовать уравнение поверхности из старой системы прямоугольных координат (x, y, z) в новую систему прямоугольных координат (x’, y’, z’), замените каждую старую переменную в уравнении поверхности свое выражение через новые переменные.

Перевод системы координат. Пусть начало новой системы x’-y’-z’ находится в точке (h, k, l) старой системы x-y-z с осями новой системы, параллельными соответствующим осям старая система. Затем
х = х’ + ч
у = у’ + к
г = г’ + л
См. рис. 1.
Вращение осей вокруг начала координат. Пусть начало новой системы x’-y’-z’ совпадает с происхождением старой системы и пусть λ 1 , µ 1 , ν 1 – направляющие косинусы оси x, λ 2 , µ 2 , ν 2 — направляющие косинусы оси y’, λ 3 , μ 3 , ν 3 — направляющие косинусы оси z’.
Затем
x = λ 1 x’ + λ 2 y’ + λ 3 z’
1) y = µ 1 x’ + µ 2 y’ + µ 3 из
z = ν 1 x’ + ν 2 y’ + ν 3 z’
x’ = λ 1 x + μ 1 y + ν 1 z
2) y’ = λ 2 x + μ 2 y + ν 2 z
z’ = λ 3 x + μ 3 y + ν 3 z
Мы можем записать эти уравнения в матричной форме как
, где матрицы называются матрицами вращения.
 Умножение на матрицу вращения преобразует
координаты точки из одной системы в другую систему.
Умножение на матрицу вращения преобразует
координаты точки из одной системы в другую систему.Примечание. Уравнение 1) лучше всего понимать в терминах вектора как изменение базиса, где 1) равно эквивалентно
векторов
, представляющие ортогональные единичные базисные векторы.
Уравнения, связывающие координаты исходная и каноническая системы координат квадратичная поверхность. Пусть x, y и z — координаты точка P относительно исходной координаты XYZ системы и x c , y c и z c — координаты точки относительно канонического X c -Y c -Z c система координат. См. рис. 3. Пусть начало координат Canonical X C -Y C -Z C Система (x 0 , Y 0 , Z 0 ) и LET λ 1 , μ 3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333н.
 — направляющие косинусы
ось x c , λ 2 , µ 2 , ν 2 – направляющие косинусы оси y c , λ 3 , µ 3
— направляющие косинусы
ось x c , λ 2 , µ 2 , ν 2 – направляющие косинусы оси y c , λ 3 , µ 3533 3
— направляющие косинусы ось z c относительно системы координат X-Y-Z. Тогда отношения между координаты x, y, z и x c , y c и z c задаются следующими уравнениями:и
Еще от SolitaryRoad.com:
Путь Истины и Жизни
Божье послание миру
Иисус Христос и Его Учение
Мудрые слова
Путь просветления, мудрости и понимания
Путь истинного христианства
Америка, коррумпированная, развратная, бессовестная страна
О честности и ее отсутствии
Критерием христианства человека является то, что он есть
Кто попадет в рай?
Высшее лицо
О вере и делах
Девяносто пять процентов проблем, с которыми большинство людей пришли от личной глупости
Либерализм, социализм и современное государство всеобщего благосостояния
Желание причинить вред, мотив поведения
Учение это:
О современном интеллектуализме
О гомосексуализме
О самодостаточной загородной жизни, приусадебном хозяйстве
Принципы жизни
Тематические пословицы, поучения, Цитаты.
 Общие поговорки. Альманах бедного Ричарда.
Общие поговорки. Альманах бедного Ричарда.Америка сбилась с пути
Действительно большие грехи
Теория формирования характера
Моральное извращение
Ты то, что ты ешь
Люди как радиотюнеры — они выбирают и слушать одну длину волны и игнорировать остальные
Причина черт характера — по Аристотелю
Эти вещи идут вместе
Телевидение
Мы то, что мы едим — живем по дисциплине диеты
Избегание проблем и неприятностей в жизни
Роль привычки в формировании характера.
Истинный христианин
Что такое истинное христианство?
Личные качества истинного христианина
Что определяет характер человека?
Любовь к Богу и любовь к добродетели тесно связаны
Прогулка по одинокой дороге
Интеллектуальное неравенство между людьми и властью в хороших привычках
Инструменты сатаны. Тактика и Уловки, используемые Дьяволом.
О реакции на обиды
Настоящая христианская вера
Естественный путь – неестественный путь
Мудрость, Разум и Добродетель тесно связаны
Знание одно, мудрость другое
Мои взгляды на христианство в Америке
Самое главное в жизни это понимание
Оценка людей
Мы все примеры — хорошо это или плохо
Телевидение — духовный яд
Перводвигатель, который решает, «Кто мы есть»
Откуда берутся наши взгляды, взгляды и ценности?
Грех — дело серьезное.
 Наказание за это настоящее. Ад реален.
Наказание за это настоящее. Ад реален.Самостоятельная дисциплина и регламентация
Достижение счастья в жизни — вопрос правильных стратегий
Самодисциплина
Самообладание, сдержанность, самодисциплина — основа стольких вещей в жизни.
Мы наши привычки
Что формирует нравственный характер?
[ Дом ] [ Вверх ] [ Информация ] [ Почта ]Каноническая форма линейных УЧП второго порядка — ESE Jupyter Material
Математика для ученых и инженеров 2
Здесь мы рассматриваем общий УЧП второго порядка функции \(u(x, y)\): 92 — 4ас < 0\)
Любое эллиптическое, параболическое или гиперболическое УЧП можно привести к следующим каноническим формам с помощью подходящего преобразования координат \(\xi = \xi(x, y), \qquad \eta = \eta(x,y)\ )
Каноническая форма для гиперболических УЧП: \(u_{\xi \eta} = \phi(\xi, \eta, u, u_{\xi}, u_{\eta}) \) или \( u_{\ xi \xi} — u_{\eta \eta} = \phi(\xi, \eta, u, u_{\xi}, u_{\eta})\)
Каноническая форма для параболических УЧП: \(u_{\eta \eta} = \phi(\xi, \eta, u, u_{\xi}, u_{\eta}) \) или \( u_{\xi \xi} = \phi(\xi, \eta, u, u_{\xi}, u_{\eta})\)
Каноническая форма для эллиптических УЧП: \(u_{\xi \xi} + u_{\eta \eta} = \phi(\xi, \eta, u, u_{\xi}, u_{\eta})\ )
Находим преобразование координат
\[\begin{split} u_x = u_\xi \xi_x + u_\eta \eta_x, \qquad u_y = u_\xi \xi_y + u_\eta \eta_y \\ \text{и аналогично для } u_{xx}, u_{xy}, u_{yy} \end{split}\]
Подключив это обратно к (26), мы получим
.
(27)\[ A u_{\xi \xi} + B u_{\xi \eta} + C u_{\eta \eta} = F(\xi, \eta, u, u_\xi, u_\eta ) \] 92 — 4ac > 0\) мы знаем, что это будут два различных действительных числа.
Но что на самом деле представляют величины \(\xi_x / \xi_y \) и \( \eta_x / \eta_y\)? Это наклоны характеристик \(\xi(x, y) = \text{const.}\) и \(\eta(x, y) = \text{const.}\) Обратите внимание, что если мы если бы мы не разделили уравнения на \(\xi_y\) и \(\eta_y\), мы получили бы
\[ \xi_x = \lambda_1 \xi_y, \qquad \eta_x = \lambda_2 \eta_y \]
, характеристические кривые которых удовлетворяют ОДУ
\[ \frac{dy}{dx} = -\lambda_1, \qquad \frac{dy}{dx} = -\lambda_2 \]
Решения этих ОДУ:
\[ у + \лямбда_1 х = с_1, \qquad у + \лямбда_2 х = с_2 \]
, где \(c_1, c_2\) — константы интегрирования, поэтому мы выбираем \(\xi\) и \(\eta\), чтобы они были равны
\[ \xi = y + \lambda_1 x, \qquad \eta = y + \lambda_2 x \]
Наконец, возвращаясь к канонической форме
\[ u_{\xi \eta} = F \]
интегрируем w.
 r.t. \(\eta\) и \(\xi\), чтобы получить решение 92 + б\лямбда + с = 0 \]
r.t. \(\eta\) и \(\xi\), чтобы получить решение 92 + б\лямбда + с = 0 \]имеет два равных корня
\[ \lambda = \lambda_1 = \xi_x / \xi_y = \eta_x / \eta_y = \lambda_2 \]
, но нам по-прежнему нужно, чтобы \(\xi\) и \(\eta\) были независимыми, чтобы преобразование имело смысл. Итак, пусть \(\xi\) будет решением
.\[ \frac{dy}{dx} = -\лямбда \]
т.е.
\[ \xi = у + \лямбда х \]
и мы можем выбрать
\[ \эта = х \]
, так что \(\xi\) и \(\eta\) независимы. Тогда, возвращаясь к каноническому виду и дважды интегрируя его, мы получаем решение 92 — 4 = 0\). Поэтому у нас есть один корень
\[ \lambda = \frac{-b}{2a} = -1 \]
Тогда \(\xi = y — x\) и мы можем выбрать \(\eta = x\). Таким образом, решение
\[ u(\xi, \eta) = \eta \phi(\xi) + \psi(\xi) \]
или в исходных координатах
\[ u(x, y) = x \phi(y — x) + \psi(y — x) \]
, где \(\phi\) и \(\psi\) — произвольные функции.

Пример: \(u_{xx} — 4u_{xy} + 4u_{yy} = \cos (2x+y)\)
PDE является параболическим, и у нас есть один корень 92}{2} \cos (2x + y) + x \phi(x+2y) + \psi(x+2y) \]
, где \(\phi\) и \(\psi\) — произвольные функции.
Эллиптический кейс
Мы не будем использовать метод характеристик для решения эллиптических уравнений, потому что УЧП сокращается лишь незначительно, т.е. канонической формой является уравнение Пуассона.
Дифференциальные уравнения. Краевые задачи
Онлайн-заметки Пола
Дом / Дифференциальные уравнения / Краевые задачи и ряды Фурье / Краевые задачиПоказать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
 е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.Раздел 8-1: Краевые задачи
Перед тем, как мы начнем этот раздел, мы должны ясно дать понять, что мы собираемся только коснуться темы краевых задач. Материала по теме краевых задач достаточно, чтобы мы могли посвятить ей целый класс. Цель этого раздела — дать краткий (и мы имеем в виду очень краткий) взгляд на идею краевых задач и дать достаточно информации, чтобы позволить нам решить некоторые основные уравнения в частных производных в следующей главе.
Теперь, покончив с этим, первое, что нам нужно сделать, это определить, что именно мы подразумеваем под краевой задачей (сокращенно BVP). В задачах с начальным значением у нас было дифференциальное уравнение, и мы указывали значение решения и соответствующее количество производных в одной и той же точке (в совокупности называемых начальными условиями).
 Например, для дифференциального уравнения второго порядка начальные условия таковы:
Например, для дифференциального уравнения второго порядка начальные условия таковы:\[y\left( {{t_0}} \right) = {y_0}\hspace{0.25in}y’\left( {{t_0}} \right) = {y’_0}\]
В случае краевых задач у нас будет дифференциальное уравнение, и мы зададим функцию и/или производные в различных точках, которые мы назовем граничными значениями. Для дифференциальных уравнений второго порядка, которые будут рассматриваться исключительно здесь, любое из следующего может и будет использоваться в качестве граничных условий.
\[\begin{equation}y\left( {{x_0}} \right) = {y_0}\hspace{0.25in}y\left( {{x_1}} \right) = {y_1}\label{eq: уравнение1}\конец{уравнение}\] \[\begin{equation}y’\left( {{x_0}} \right) = {y_0}\hspace{0.25in}y’\left( {{x_1}} \right) = {y_1}\label{ уравнение:eq2}\конец{уравнение}\] \[\begin{equation}y’\left( {{x_0}} \right) = {y_0}\hspace{0.
 25in}y\left({{x_1}} \right) = {y_1}\label{eq :eq3}\end{уравнение}\]
\[\begin{equation}y\left( {{x_0}} \right) = {y_0}\hspace{0.25in}y’\left( {{x_1}} \right) = {y_1}\label{eq :eq4}\end{уравнение}\]
25in}y\left({{x_1}} \right) = {y_1}\label{eq :eq3}\end{уравнение}\]
\[\begin{equation}y\left( {{x_0}} \right) = {y_0}\hspace{0.25in}y’\left( {{x_1}} \right) = {y_1}\label{eq :eq4}\end{уравнение}\]Как упоминалось выше, мы будем рассматривать исключительно дифференциальные уравнения второго порядка. Мы также ограничимся линейными дифференциальными уравнениями. Итак, для целей нашего обсуждения здесь мы будем рассматривать почти исключительно дифференциальные уравнения в форме
\[\begin{equation}y» + p\left( x \right)y’ + q\left( x \right)y = g\left( x \right)\label{eq:eq5}\end{ уравнение}\]
вместе с одним из наборов граничных условий, указанных в \(\eqref{eq:eq1}\) – \(\eqref{eq:eq4}\). Время от времени мы будем рассматривать некоторые другие граничные условия, но всегда будет дифференциальное уравнение, которое можно записать в этой форме.
Как мы скоро увидим, многое из того, что мы знаем о проблемах с начальными значениями, здесь не работает.
 Мы, конечно, можем решить \(\eqref{eq:eq5}\) при условии, что коэффициенты постоянны, и для некоторых случаев, когда они не являются постоянными. Ничего из этого не изменится. Изменения (и, возможно, проблемы) возникают, когда мы переходим от начальных условий к граничным.
Мы, конечно, можем решить \(\eqref{eq:eq5}\) при условии, что коэффициенты постоянны, и для некоторых случаев, когда они не являются постоянными. Ничего из этого не изменится. Изменения (и, возможно, проблемы) возникают, когда мы переходим от начальных условий к граничным.Одним из первых изменений является определение, которое мы все время видели в предыдущих главах. В предыдущих главах мы говорили, что дифференциальное уравнение однородно, если \(g\left(x\right) = 0\) для всех \(x\). Здесь мы будем говорить, что краевая задача есть однородный , если в дополнение к \(g\left( x \right) = 0\) мы также имеем \({y_0} = 0\) и \({y_1} = 0\) (независимо от граничных условий мы использовать). Если какой-либо из них не равен нулю, мы будем называть BVP неоднородным .
Теперь важно помнить, что когда мы говорим однородный (или неоднородный), мы говорим что-то не только о самом дифференциальном уравнении, но также и о граничных условиях.
Самое большое изменение, которое мы здесь увидим, произойдет, когда мы перейдем к решению задачи с граничными значениями.
 При решении линейных начальных задач единственное решение будет гарантировано в очень мягких условиях. Мы рассмотрели эту идею только для IVP первого порядка, но эта идея распространяется и на IVP более высокого порядка. В этом разделе мы увидели, что все, что нам нужно, чтобы гарантировать уникальность решения, — это некоторые основные условия непрерывности. В случае с краевыми задачами у нас часто не будет решения или будет бесконечно много решений даже для очень хороших дифференциальных уравнений, которые дали бы единственное решение, если бы у нас были начальные условия вместо граничных.
При решении линейных начальных задач единственное решение будет гарантировано в очень мягких условиях. Мы рассмотрели эту идею только для IVP первого порядка, но эта идея распространяется и на IVP более высокого порядка. В этом разделе мы увидели, что все, что нам нужно, чтобы гарантировать уникальность решения, — это некоторые основные условия непрерывности. В случае с краевыми задачами у нас часто не будет решения или будет бесконечно много решений даже для очень хороших дифференциальных уравнений, которые дали бы единственное решение, если бы у нас были начальные условия вместо граничных.Прежде чем мы приступим к решению некоторых из них, давайте сначала ответим на вопрос, почему мы вообще говорим об этом. Как мы увидим в следующей главе, в процессе решения некоторых дифференциальных уравнений в частных производных мы столкнемся с краевыми задачами, которые также необходимо будет решить. Фактически, большая часть процесса решения будет связана с решением BVP. В этих случаях граничные условия будут представлять такие вещи, как температура на любом конце стержня или поток тепла в/из любого конца стержня.
 Или, может быть, они будут обозначать расположение концов вибрирующей струны. Значит, граничными условиями действительно будут условия на границе какого-то процесса.
Или, может быть, они будут обозначать расположение концов вибрирующей струны. Значит, граничными условиями действительно будут условия на границе какого-то процесса.Итак, разобравшись с базовыми вещами, давайте найдем несколько решений нескольких задач с граничными значениями. Обратите также внимание, что здесь действительно нет ничего нового. Мы знаем, как решить дифференциальное уравнение, и мы знаем, как найти константы, применяя условия. Единственное отличие состоит в том, что здесь мы будем применять граничные условия вместо начальных.
Пример 1. Решите следующую BVP. \[y» + 4y = 0\hspace{0.25in}y\left(0\right) = — 2\hspace{0.25in}y\left({\frac{\pi}{4}}\right) = 10\]
Показать решение
Итак, это простое дифференциальное уравнение, которое нужно решить, поэтому мы предоставим вам проверить, что общее решение этого уравнения таково:
\[y\left( x \right) = {c_1}\cos \left( {2x} \right) + {c_2}\sin \left( {2x} \right)\]
Теперь все, что нам нужно сделать, это применить граничные условия.

\[\begin{align*} — 2 & = y\left( 0 \right) = {c_1}\\ 10 & = y\left( {\frac{\pi} {4}} \right) = {c_2 }\конец{выравнивание*}\]
Тогда решение
\[y\left( x \right) = — 2\cos \left( {2x} \right) + 10\sin \left( {2x} \right)\]
Выше мы упомянули, что некоторые краевые задачи могут не иметь решений или иметь бесконечное число решений, нам лучше привести здесь пару таких примеров. Этот следующий набор примеров также покажет, насколько мало изменений в BVP требуется, чтобы перейти к этим другим возможностям.
Пример 2. Решите следующую BVP. \[y» + 4y = 0\hspace{0.25in}y\left(0\right) = — 2\hspace{0.25in}y\left({2\pi} \right) = — 2\]
Показать решение
Мы работаем с тем же дифференциальным уравнением, что и в первом примере, поэтому у нас все еще есть
.
 \[y\left( x \right) = {c_1}\cos \left( {2x} \right) + {c_2}\sin \left( {2x} \right)\]
\[y\left( x \right) = {c_1}\cos \left( {2x} \right) + {c_2}\sin \left( {2x} \right)\]После применения граничных условий получаем,
\[\begin{align*} — 2 & = y\left( 0 \right) = {c_1}\\ — 2 & = y\left( {2\pi } \right) = {c_1}\end{align *}\]
Итак, в этом случае, в отличие от предыдущего примера, оба граничных условия говорят нам, что мы должны иметь \({c_1} = — 2\), и ни одно из них ничего не говорит нам о \({c_2}\). Помните, однако, что все, что мы просим, это решение дифференциального уравнения, которое удовлетворяет двум данным граничным условиям, и следующая функция сделает это,
\[y\left( x \right) = — 2\cos \left( {2x} \right) + {c_2}\sin \left( {2x} \right)\]
Другими словами, независимо от значения \({c_2}\) мы получаем решение и, следовательно, в этом случае мы получаем бесконечно много решений краевой задачи.

Пример 3. Решите следующую BVP. \[y» + 4y = 0\hspace{0,25 дюйма}y\влево (0 \right) = — 2\hspace{0,25in}y\left({2\pi} \right) = 3\]
Показать решение
Опять же, у нас есть следующее общее решение,
\[y\left( x \right) = {c_1}\cos \left( {2x} \right) + {c_2}\sin \left( {2x} \right)\]
На этот раз граничные условия дают нам
\[\begin{align*} — 2 & = y\left( 0 \right) = {c_1}\\ 3 & = y\left( {2\pi } \right) = {c_1}\end{align* }\]
В этом случае у нас есть набор граничных условий, каждое из которых требует различных значений \({c_1}\) для выполнения. Однако это невозможно, поэтому в данном случае не имеет решения .
Итак, на примерах 2 и 3 мы видим, что лишь небольшое изменение граничных условий по отношению друг к другу и по отношению к примеру 1 может полностью изменить характер решения.
 Во всех трех этих примерах использовалось одно и то же дифференциальное уравнение, но разные наборы начальных условий приводили к отсутствию решений, одному решению или бесконечному количеству решений.
Во всех трех этих примерах использовалось одно и то же дифференциальное уравнение, но разные наборы начальных условий приводили к отсутствию решений, одному решению или бесконечному количеству решений.Обратите внимание, что такое поведение не всегда непредсказуемо. Если мы используем условия \(y\left( 0 \right)\) и \(y\left( {2\pi } \right)\), единственный способ, которым мы когда-либо получим решение краевой задачи, это если есть,
\[y\left( 0 \right) = a\hspace{0.25in}y\left( {2\pi } \right) = a\]
для любого значения \(a\). Также обратите внимание, что если у нас есть эти граничные условия, мы фактически получим бесконечно много решений.
Все примеры, которые мы работали до этого момента, включали одно и то же дифференциальное уравнение и один и тот же тип граничных условий, поэтому давайте поработаем еще с парой, чтобы убедиться, что у нас есть еще несколько примеров. Кроме того, обратите внимание, что с каждым из них мы можем немного изменить граничные условия, чтобы получить любое из возможных вариантов поведения решения (, т.
 е. ноль, одно или бесконечное множество решений).
е. ноль, одно или бесконечное множество решений).Пример 4. Решите следующую BVP. \[y» + 3y = 0\hspace{0.25in}y\left(0\right) = 7\hspace{0.25in}y\left({2\pi} \right) = 0\]
Показать решение
Общее решение этого дифференциального уравнения:
\[y\left( x \right) = {c_1}\cos \left({\sqrt 3 \,x} \right) + {c_2}\sin\left({\sqrt 3 \,x} \right) \]
Применение граничных условий дает,
\[\begin{align*}7 & = y\left( 0 \right) = {c_1}\\ 0 & = y\left( {2\pi } \right) = {c_1}\cos \left( { 2\sqrt 3 \,\pi } \right) + {c_2}\sin \left( {2\sqrt 3 \,\pi } \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}{c_2 } = — 7\cot \left( {2\sqrt 3 \,\pi } \right)\end{align*}\]
В этом случае мы получаем одно решение,
\[y\left( x \right) = 7\cos \left( {\sqrt 3 \,x} \right) — 7\cot \left({2\sqrt 3 \,\pi} \right)\sin \ влево ( {\ sqrt 3 \, x} \ вправо) \]
Пример 5.
 Решите следующую BVP.
\[y» + 25y = 0\hspace{0.25in}y’\left( 0 \right) = 6\hspace{0.25in}y’\left(\pi \right) = — 9\]
Решите следующую BVP.
\[y» + 25y = 0\hspace{0.25in}y’\left( 0 \right) = 6\hspace{0.25in}y’\left(\pi \right) = — 9\]Показать решение
Здесь общее решение
\[y\left( x \right) = {c_1}\cos \left( {5x} \right) + {c_2}\sin \left( {5x} \right)\]
и нам понадобится производная для применения граничных условий,
\[y’\left( x \right) = — 5{c_1}\sin \left( {5x} \right) + 5{c_2}\cos \left( {5x} \right)\]
Применение граничных условий дает,
\[\begin{align*}6 & = y’\left( 0 \right) = 5{c_2}\hspace{0.25in} \Rightarrow \hspace{0.25in}{c_2} = \frac{6}{5 }\\ — 9& = y’\left( \pi \right) = — 5{c_2}\hspace{0,25in} \Rightarrow \hspace{0,25in}{c_2} = \frac{9}{5}\end{align*} \]
Это невозможно, поэтому в данном случае нет решения .

Все рассмотренные до этого момента примеры были неоднородными, поскольку по крайней мере одно из граничных условий было ненулевым. Давайте поработаем с одним неоднородным примером, где дифференциальное уравнение также неоднородно, прежде чем мы поработаем с парой однородных примеров.
Пример 6. Решите следующую BVP. \[y» + 9y = \cos x\hspace{0.25in}y’\left( 0 \right) = 5\hspace{0.25in}y\left({\frac{\pi}{2}} \ справа) = — \frac{5}{3}\]
Показать решение
Дополнительное решение для этого дифференциального уравнения:
\[{y_c}\left( x \right) = {c_1}\cos \left( {3\,x} \right) + {c_2}\sin \left( {3\,x} \right)\]
Используя неопределенные коэффициенты или вариацию параметров, легко показать (мы оставим детали вам для проверки), что конкретное решение есть,
\[{Y_P}\left( x \right) = \frac{1}{8}\cos x\]
Общее решение и его производная (поскольку она нам понадобится для граничных условий):
\[\begin{align*}y\left( x \right) & = {c_1}\cos \left( {3\,x} \right) + {c_2}\sin \left( {3\,x} \right) + \frac{1}{8}\cos x\\ y’\left( x \right) & = — 3{c_1}\sin \left( {3\,x} \right) + 3{ c_2}\cos\left( {3\,x} \right) — \frac{1}{8}\sin x\end{align*}\]
Применение граничных условий дает,
\[\begin{align*}5 & = y’\left( 0 \right) = 3{c_2}\hspace{0.
 25in} \Rightarrow \hspace{0.25in}{c_2} = \frac{5}{3 } \\ — \ frac {5} {3} & = y \ left ( {\ frac {\ pi} {2}} \ right) = — {c_2} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма }{c_2} = \frac{5}{3}\end{align*}\]
25in} \Rightarrow \hspace{0.25in}{c_2} = \frac{5}{3 } \\ — \ frac {5} {3} & = y \ left ( {\ frac {\ pi} {2}} \ right) = — {c_2} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма }{c_2} = \frac{5}{3}\end{align*}\]Граничные условия тогда говорят нам, что мы должны иметь \({c_2} = \frac{5}{3}\), и они ничего не говорят нам о \({c_1}\), так что это может быть произвольно выбран. Тогда решение
\[y\left( x \right) = {c_1}\cos \left( {3\,x} \right) + \frac{5}{3}\sin \left( {3\,x} \right ) + \frac{1}{8}\cos x\]
и решений БВП будет бесконечно много.
Давайте теперь поработаем над парой однородных примеров, которые также будут полезны, когда мы перейдем к следующему разделу.
Пример 7. Решите следующую BVP. \[y» + 4y = 0\hspace{0,25 дюйма}y\влево (0 \right) = 0\hspace{0,25in}y\left({2\pi} \right) = 0\]
Показать решение
Здесь общее решение:
\[y\left( x \right) = {c_1}\cos \left( {2x} \right) + {c_2}\sin \left( {2x} \right)\]
Применение граничных условий дает,
\[\begin{align*}0 & = y\left( 0 \right) = {c_1}\\ 0 & = y\left( {2\pi } \right) = {c_1}\end{align*} \]
Таким образом, \({c_2}\) является произвольным, и решение
\[у\влево(х\вправо) = {c_2}\sin\влево({2x} \вправо)\]
и в этом случае мы получим бесконечно много решений.

Пример 8. Решите следующую BVP. \[y» + 3y = 0\hspace{0,25 дюйма}y\влево (0 \right) = 0\hspace{0,25in}y\left({2\pi} \right) = 0\]
Показать решение
Общее решение в этом случае:
\[y\left( x \right) = {c_1}\cos \left({\sqrt 3 \,x} \right) + {c_2}\sin\left({\sqrt 3 \,x} \right) \]
Применение граничных условий дает,
\[\begin{align*}0 & = y\left( 0 \right) = {c_1}\\ 0 & = y\left( {2\pi } \right) = {c_2}\sin \left( { 2\sqrt 3 \,\pi } \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}{c_2} = 0\end{align*}\]
В этом случае мы обнаружили, что обе константы равны нулю, поэтому решение:
\[у\влево( х \вправо) = 0\]
В предыдущем примере решением было \(y\left( x \right) = 0\).
 Однако обратите внимание, что это всегда будет решением любой однородной системы, заданной \(\eqref{eq:eq5}\), и любого из (однородных) граничных условий, заданных \(\eqref{eq:eq1}\) – \(\eqref{eq:eq4}\). Из-за этого мы обычно называем это решение тривиальное решение . Иногда, как в случае с последним примером, тривиальное решение является единственным решением, однако обычно мы предпочитаем, чтобы решения были нетривиальными. Это будет основной идеей в следующем разделе.
Однако обратите внимание, что это всегда будет решением любой однородной системы, заданной \(\eqref{eq:eq5}\), и любого из (однородных) граничных условий, заданных \(\eqref{eq:eq1}\) – \(\eqref{eq:eq4}\). Из-за этого мы обычно называем это решение тривиальное решение . Иногда, как в случае с последним примером, тривиальное решение является единственным решением, однако обычно мы предпочитаем, чтобы решения были нетривиальными. Это будет основной идеей в следующем разделе.Прежде чем мы покинем этот раздел, необходимо сделать одно важное замечание. В каждом из примеров, за одним исключением, дифференциальное уравнение, которое мы решали, имело вид
\[у» + \лямбда у = 0\]
Единственное исключение по-прежнему решало это дифференциальное уравнение, за исключением того, что оно не было однородным дифференциальным уравнением, и поэтому мы все еще каким-то образом решали это основное дифференциальное уравнение.

Итак, здесь, вероятно, может возникнуть несколько естественных вопросов. Все ли BVP включают это дифференциальное уравнение, и если нет, то почему мы потратили так много времени на решение этого уравнения, исключив все другие возможные дифференциальные уравнения?
Ответы на эти вопросы довольно просты. Во-первых, это дифференциальное уравнение определенно не единственное, используемое в краевых задачах. Тем не менее, он демонстрирует все то поведение, о котором мы хотели здесь поговорить, и имеет дополнительный бонус, заключающийся в том, что его очень легко решить. Таким образом, используя почти исключительно это дифференциальное уравнение, мы можем увидеть и обсудить важное поведение, которое нам нужно обсудить, и освобождает нас от множества потенциально запутанных деталей решения или запутанных решений. Время от времени мы будем рассматривать другие дифференциальные уравнения в оставшейся части этой главы, но по-прежнему будем работать почти исключительно с этим.
Есть еще одна важная причина обратить внимание на это дифференциальное уравнение.
 Когда мы перейдем к следующей главе и кратко рассмотрим решение дифференциальных уравнений в частных производных, мы увидим, что почти все примеры, с которыми мы будем работать, сводятся именно к этому дифференциальному уравнению. Кроме того, в этих задачах мы будем работать с некоторыми «настоящими» задачами, которые на самом деле решены местами, а не являются просто «придуманными» задачами для целей примера. По общему признанию, в них будут некоторые упрощения, но в некоторых случаях они приближаются к реальной проблеме.
Когда мы перейдем к следующей главе и кратко рассмотрим решение дифференциальных уравнений в частных производных, мы увидим, что почти все примеры, с которыми мы будем работать, сводятся именно к этому дифференциальному уравнению. Кроме того, в этих задачах мы будем работать с некоторыми «настоящими» задачами, которые на самом деле решены местами, а не являются просто «придуманными» задачами для целей примера. По общему признанию, в них будут некоторые упрощения, но в некоторых случаях они приближаются к реальной проблеме.Уравнения эллипсов | Колледж Алгебра
Результаты обучения
- Определение фокусов, вершин, осей и центра эллипса.
- Напишите уравнения эллипсов с центром в начале координат.
- Напишите уравнения эллипсов без центра в начале координат.
Коническое сечение, или коническое , представляет собой форму, полученную в результате пересечения прямого кругового конуса с плоскостью. Угол, под которым плоскость пересекает конус, определяет форму.

Конические сечения также могут быть описаны набором точек на координатной плоскости. Далее в этой главе мы увидим, что график любого квадратного уравнения с двумя переменными представляет собой коническое сечение. Знаки уравнений и коэффициенты переменных членов определяют форму. В этом разделе основное внимание уделяется четырем вариантам стандартной формы уравнения эллипса. Эллипс — это множество всех точек [латекс]\влево(х,у\вправо)[/латекс] на плоскости, сумма расстояний от которых до двух фиксированных точек является константой. Каждая фиксированная точка называется фокус (множественное число: фокусы ) эллипса.
Мы можем нарисовать эллипс, используя кусок картона, две кнопки, карандаш и нитку. Поместите кнопки в картон, чтобы сформировать фокусы эллипса. Отрежьте кусок веревки длиннее, чем расстояние между двумя кнопками (длина веревки представляет собой константу в определении). Прикрепите каждый конец веревки к картону и начертите кривую карандашом, натянутым на веревку.
 В результате получается эллипс.
В результате получается эллипс.Каждый эллипс имеет две оси симметрии. Более длинная ось называется большой осью , а более короткая ось называется малой осью . Каждая конечная точка большой оси является вершиной эллипса (множественное число: вершин ), а каждая конечная точка малой оси является ко-вершиной эллипса. Центр эллипса является серединой большой и малой осей. Оси перпендикулярны в центре. Фокусы всегда лежат на большой оси, и сумма расстояний от фокусов до любой точки эллипса (постоянная сумма) больше, чем расстояние между фокусами.
В этом разделе мы ограничиваем эллипсы теми, которые расположены вертикально или горизонтально в координатной плоскости. То есть оси будут лежать или быть параллельными осям x и y . Позже в этой главе мы увидим эллипсы, вращающиеся в координатной плоскости.
Для работы с горизонтальными и вертикальными эллипсами в координатной плоскости мы рассмотрим два случая: те, которые центрированы в начале координат, и те, которые центрированы в точке, отличной от начала координат.
 Сначала мы научимся выводить уравнения эллипсов, а потом научимся записывать уравнения эллипсов в стандартной форме. Позже мы будем использовать полученные знания для построения графиков.
Сначала мы научимся выводить уравнения эллипсов, а потом научимся записывать уравнения эллипсов в стандартной форме. Позже мы будем использовать полученные знания для построения графиков.Чтобы вывести уравнение эллипса с центром в начале координат, мы начнем с фокусов [латекс](-c,0)[/латекс] и [латекс](с,0)[/латекс]. Эллипс — это множество всех точек [латекс](х,у)[/латекс], для которых сумма расстояний от [латекс](х,у)[/латекс] до фокусов постоянна, как показано на рисунок ниже.
Если [латекс](а,0)[/латекс] является вершиной эллипса, расстояние от [латекс](-c,0)[/латекс] до [латекс](а,0)[/латекс ] представляет собой [латекс]а-(-с)=а+с[/латекс]. Расстояние от [латекс](с,0)[/латекс] до [латекс](а,0)[/латекс] равно [латекс]а-с[/латекс]. Сумма расстояний от фокусов до вершины равна
[латекс](а+с)+(а-с)=2а[/латекс]
Если [латекс](х,у)[/латекс] является точкой на эллипсе, то мы можем определить следующие переменные:
[латекс]\begin{align}d_1&=\text{расстояние от } (-c,0) \text{ до } (x,y) \\ d_2&= \text{расстояние от } (c,0 ) \text{ to } (x,y) \end{align}[/latex]
По определению эллипса [latex]d_1+d_2[/latex] является константой для любой точки [latex](x, y)[/latex] на эллипсе.
 Мы знаем, что сумма этих расстояний равна [latex]2a[/latex] для вершины [latex](a,0)[/latex]. Отсюда следует, что [latex]d_1+d_2=2a[/latex] для любой точки эллипса. Вывод стандартной формы уравнения эллипса основан на этом соотношении и формуле расстояния. Вывод выходит за рамки этого курса, но уравнение: 92}=1[/latex]
Мы знаем, что сумма этих расстояний равна [latex]2a[/latex] для вершины [latex](a,0)[/latex]. Отсюда следует, что [latex]d_1+d_2=2a[/latex] для любой точки эллипса. Вывод стандартной формы уравнения эллипса основан на этом соотношении и формуле расстояния. Вывод выходит за рамки этого курса, но уравнение: 92}=1[/latex]для эллипса с центром в начале координат, большая ось которого лежит на оси Y .
Написание уравнений эллипсов с центром в начале координат в стандартной форме
Стандартные формы уравнений рассказывают нам об основных характеристиках графиков. Найдите минутку, чтобы вспомнить некоторые стандартные формы уравнений, с которыми мы работали в прошлом: линейные, квадратичные, кубические, экспоненциальные, логарифмические и так далее. Научившись интерпретировать стандартные формы уравнений, мы наводим мосты между алгебраическими и геометрическими представлениями математических явлений.
Ключевыми характеристиками эллипса являются его центр, вершины, ко-вершины, фокусы, а также длины и положения большой и малой осей.
 Как и в случае с другими уравнениями, мы можем определить все эти функции, просто взглянув на стандартную форму уравнения. Существует четыре варианта стандартной формы эллипса. Эти вариации классифицируются сначала по расположению центра (начало или не начало), а затем по положению (горизонтальное или вертикальное). Каждый представлен вместе с описанием того, как части уравнения соотносятся с графиком. Интерпретация этих частей позволяет нам сформировать ментальную картину эллипса. 92[/латекс]. Когда нам даны координаты фокусов и вершин эллипса, мы можем использовать соотношение, чтобы найти уравнение эллипса в стандартной форме.
Как и в случае с другими уравнениями, мы можем определить все эти функции, просто взглянув на стандартную форму уравнения. Существует четыре варианта стандартной формы эллипса. Эти вариации классифицируются сначала по расположению центра (начало или не начало), а затем по положению (горизонтальное или вертикальное). Каждый представлен вместе с описанием того, как части уравнения соотносятся с графиком. Интерпретация этих частей позволяет нам сформировать ментальную картину эллипса. 92[/латекс]. Когда нам даны координаты фокусов и вершин эллипса, мы можем использовать соотношение, чтобы найти уравнение эллипса в стандартной форме.Рисунок: (а) горизонтальный эллипс с центром (0,0), (б) вертикальным эллипсом с центром (0,0)
Как: Учитывая вершины и фокусы, сосредоточенного на происхождении, написать его уравнение в стандартной форме.
- Определить, находится ли главная ось на 92[/latex] в стандартную форму уравнения, определенного на шаге 1.
Пример: запись уравнения эллипса с центром в начале координат в стандартной форме
Какое уравнение стандартной формы имеет эллипс с вершинами [латекс](\pm 8,0)[/латекс] и фокусами [латекс] (\pm 5,0)[/латекс]?
Показать Показать решение
попробуйте
Уравнение стандартной формы эллипса с вершинами [латекс]\влево(0,\pm 8\справа)[/латекс] и фокусами [латекс](0,\pm \sqrt{5 })[/латекс]?
Показать решение
Написание уравнений эллипсов, не центрированных в начале координат
Как и графики других уравнений, график эллипса можно перевести.
 Если эллипс переместить [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр эллипса будет [latex]\left(h,k\right)[/latex] . Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [латекс]x[/латекс] на [латекс]\влево(хч\вправо)[/латекс] и 9{2}[/латекс]. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти уравнение эллипса в стандартной форме, когда заданы вершины и фокусы.
Если эллипс переместить [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр эллипса будет [latex]\left(h,k\right)[/latex] . Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [латекс]x[/латекс] на [латекс]\влево(хч\вправо)[/латекс] и 9{2}[/латекс]. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти уравнение эллипса в стандартной форме, когда заданы вершины и фокусы.(a) Горизонтальный эллипс с центром [латекс]\левый(h,k\правый)[/латекс] (b) Вертикальный эллипс с центром [латекс]\левый(h,k\правый)[/латекс]
Как: Учитывая вершины и фокусы эллипса, не центрированные в начале координат, напишите его уравнение в стандартной форме.
- Определить, параллельна ли большая ось 9{2}[/latex] в стандартную форму уравнения, определенного на шаге 1.
Пример: Написание уравнения эллипса с центром в точке, отличной от начала координат
Уравнение стандартной формы эллипса с вершинами [латекс]\влево(-2,-8\вправо)[/латекс] и [латекс]\влево(-2,\текст{2}\вправо)[/латекс] и фокусы [латекс]\влево(-2,-7\вправо)[/латекс] и [латекс]\влево(- 2,\text{1}\right)?[/latex]
Показать решение
Попробуйте
Уравнение стандартной формы эллипса с вершинами [латекс]\влево(-3,3\вправо)[/латекс] и [латекс]\влево(5,3\вправо)[/ латекс] и фокусы [латекс]\влево(1 — 2\sqrt{3},3\вправо)[/латекс] и [латекс]\влево(1+2\sqrt{3},3\вправо)?[/ латекс]
Показать решение
Решение прикладных задач с использованием эллипсов
Многие реальные ситуации могут быть представлены эллипсами, включая орбиты планет, спутников, лун и комет, а также формы килей лодок, рулей и некоторых крыльев самолетов.
 Медицинское устройство под названием литотриптер использует эллиптические отражатели для разрушения камней в почках путем создания звуковых волн. Некоторые здания, называемые камерами шепота, спроектированы с эллиптическими куполами, так что человек, шепчущий в одном фокусе, может быть легко услышан кем-то, стоящим в другом фокусе. Это происходит из-за акустических свойств эллипса. Когда звуковая волна возникает в одном фокусе шепчущей камеры, звуковая волна будет отражаться от эллиптического купола и обратно в другой фокус. В комнате для шепота в Музее науки и промышленности в Чикаго два человека, стоящие в фокусах на расстоянии около 43 футов друг от друга, могут слышать шепот друг друга.
Медицинское устройство под названием литотриптер использует эллиптические отражатели для разрушения камней в почках путем создания звуковых волн. Некоторые здания, называемые камерами шепота, спроектированы с эллиптическими куполами, так что человек, шепчущий в одном фокусе, может быть легко услышан кем-то, стоящим в другом фокусе. Это происходит из-за акустических свойств эллипса. Когда звуковая волна возникает в одном фокусе шепчущей камеры, звуковая волна будет отражаться от эллиптического купола и обратно в другой фокус. В комнате для шепота в Музее науки и промышленности в Чикаго два человека, стоящие в фокусах на расстоянии около 43 футов друг от друга, могут слышать шепот друг друга.Пример: обнаружение фокусов комнаты для шепота
Скульптурный зал в здании Капитолия в Вашингтоне, округ Колумбия, представляет собой комнату для шепота. Его размеры составляют 46 футов в ширину и 96 футов в длину.
а. Какова стандартная форма уравнения эллипса, представляющего контур комнаты? Подсказка: предположим, что это горизонтальный эллипс, и пусть центр комнаты будет точкой [латекс]\влево(0,0\вправо)[/латекс].

б. Если два сенатора, стоящие в фокусах этой комнаты, слышат шепот друг друга, как далеко друг от друга находятся сенаторы? Округлите до ближайшего фута.
Показать решение
Попробуйте
Предположим, комната для шепота имеет длину 480 футов и ширину 320 футов.
а. Какова стандартная форма уравнения эллипса, представляющего комнату? Подсказка: предположим, что это горизонтальный эллипс, и пусть центр комнаты будет точкой [латекс]\влево(0,0\вправо)[/латекс].
б. Если два человека стоят в фокусах этой комнаты и слышат шепот друг друга, как далеко друг от друга находятся люди? Округлите до ближайшего фута.
Показать раствор
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Основные уравнения прямых и плоскостей
Основные уравнения прямых и плоскостейУравнение прямой
Важным предметом школьной алгебры является «уравнение прямой».
 Это означает уравнение относительно x и y, набор решений которого представляет собой линию в (x, y)
самолет.
Это означает уравнение относительно x и y, набор решений которого представляет собой линию в (x, y)
самолет.Самая популярная форма в алгебре — это форма «пересечение наклона»
у = тх + б.
Это фактически использует x как параметр и записывает y как функцию x: y = f(x) = мх+б. Когда x = 0, y = b и точка (0,b) является пересечением прямой с осью Y.
Думая о линии как о геометрическом объекте, а не о графике функции, имеет смысл относиться к x и y более беспристрастно. Общее уравнение для строка (нормальная форма)
топор + по = с,
с условием, что по крайней мере один из a или b отличен от нуля. Это может легко преобразовать в форму пересечения наклона, решив для y:
у = (-а/б) + с/б,
, за исключением особого случая b = 0, когда линия параллельна оси y.
Если коэффициенты в нормальной форме умножаются на ненулевую константу, множество решений точно такое же, поэтому, например, все эти уравнения имеют ту же строку, что и решение.

2x + 3 y = 4
4x + 6y = 8
-x — (3/2) y = -2
(1/2)x + (3/4)y = 1В общем, если k ненулевая константа, то это уравнения для одна и та же строка , так как они имеют одинаковые решения.
ax + by = c
(ka)x + (kb)y = kc.Популярный выбор для k в случае, когда c не равно нулю, это k = (1/с). Тогда уравнение становится
(а/с)х + (б/с)у = 1.
Другая полезная форма уравнения состоит в том, чтобы разделить на |(a,b)|, квадратный корень из 2 + b 2 . Этот выбор будет объяснен в разделе Normal Vector.
Упражнение . Если на прямой стоит O, покажите, что уравнение принимает вид ax + by = 0 или y = mx.
Упражнение: Найдите точки пересечения этой прямой с координатные оси.
Упражнение : Уравнение прямой, проходящей через (0,0) и точка (h,k)?
Нахождение уравнения прямой через 2 точки на плоскости
Для любых двух точек P и Q через эти точки проходит ровно одна прямая PQ.
 Если известны координаты точек P и Q, то коэффициенты a, b, c
уравнение для прямой можно найти, решив систему линейных уравнений.
Если известны координаты точек P и Q, то коэффициенты a, b, c
уравнение для прямой можно найти, решив систему линейных уравнений.Пример : Для P = (1, 2), Q = (-2, 5) найдите уравнение ax + by = c строки PQ.
Поскольку точка P находится на прямой, ее координаты удовлетворяют уравнению: a1 + b2 = c, или а + 2b = с.
Поскольку Q находится на прямой, его координаты удовлетворяют уравнению: a(-2) + b5 = c, или -2 а + 5b = с.Умножьте первое уравнение на 2 и прибавьте, чтобы исключить a из уравнения: 4b + 5b = 9b = 2c + c = 3c, поэтому b = (1/3)c. Затем подставляя в первый уравнение, a = c — 2b = c — (2/3)c = (1/3)c.
Это дает уравнение [(1/3)c]x + [(1/3)c}y = c . Почему нет с решено для? Помните, что существует бесконечное количество уравнений для линии, каждая из которых кратна другой. Мы можем вынести c (или положить c = 1 для того же результата) и получить (1/3)x + (1/3)y =1 как один из вариантов уравнение для прямой.
 Другим выбором может быть c = 3: x+y = 3 , что
очистил знаменатели.
Другим выбором может быть c = 3: x+y = 3 , что
очистил знаменатели.Этот метод всегда работает для любых различных P и Q. Конечно, существует формула также для а, б, в. Это можно найти в виде определители , или перекрестное произведение .
Упражнения : Найдите уравнения этих линий. Обратите внимание на особые случаи.
Линия через (3, 4) и (1, -2).
Линия через (3, 4) и (-6, -8).
Линия через (3, 4) и (3, 7).Соединение с параметрической формой линии
Для двух точек P и Q точки прямой PQ можно записать как F(t) = (1-t)P + tQ, поскольку t охватывает все действительные числа. Если и P, и Q удовлетворяют одному и тому же уравнение ax+by = c, то вычисление показывает, что это верно и для (1-t)P + tQ для любого выбора t.
Вот это вычисление. Пусть P = (p 1 , p 2 ), Q = (q 1 , q 2 ). Тогда, поскольку точки лежат на прямой, мы знаем, что оба
ap 1 + bp 2 = c
aq 1 + bq 2 = c.
Для точки F(t) нужно проверить a[(1-t)p 1 +tq 1 ] + b[(1-t)p 2 +tq 2 ] = с. Но левую часть можно переставить как (1-t)(ap 1 + bp 2 ) + t(aq 1 + bq 2 ), и это равно (1-t)c + tc = c. Итак равенство выполняется. Сравните это явное вычисление с вычислением, данным для плоскости, использующей скалярное произведение. Вычисления те же, но показывает больше деталей, а один скрывает координаты и показывает более концептуальный картина.
Уравнение плоскости
Плоскость в трехмерном пространстве имеет уравнение
топор+бы+ч=д,
, где хотя бы одно из чисел a, b, c должно быть ненулевым.
Что касается линии, если уравнение умножается на любую ненулевую константу k до получаем уравнение kax+kby+kcz=kd, плоскости решений совпадают.
Если с не равно нулю, часто полезно думать о плоскости как о графике функция z от x и y.
 Уравнение можно переставить так:
Уравнение можно переставить так:z = -(a/c)x + (-b/c) y + d/c
Еще один полезный вариант, когда d не равен нулю, — разделить на d так, чтобы константа срок = 1,
(a/d)x + (b/d)y + (c/d)z = 1.
Другой полезной формой уравнения является деление на |(a,b,c)|, квадрат корень a 2 + b 2 + c 2 . Этот выбор будет объяснено в разделе «Вектор нормали».
Упражнение: Где плоскость ax + by + cz = d пересекает координату топоры?
Упражнение: Что особенного в уравнении плоскости, проходящей через 0,
Нахождение уравнения плоскости через 3 точки в пробел
По заданным точкам P, Q, R в пространстве найдите уравнение плоскости через 3 точки.
Пример : P = (1, 1, 1), Q = (1, 2, 0), R = (-1, 2, 1). Ищем коэффициенты уравнения ax + by + cz = d, где P, Q и R удовлетворяют уравнениям, таким образом:
а + b + с = d
а + 2b + 0с = d
-а + 2b + с = dВычитание первого уравнения из второго и последующее сложение первого уравнения к третьему, мы исключаем a, чтобы получить
б — в = 0
4б + в = 2dСложение уравнений дает 5b = 2d или b = (2/5)d, затем решение для c = b = (2/5)d и тогда a = d — b — c = (1/5)d.

Таким образом, уравнение (с ненулевой константой, оставленной для выбора) имеет вид d(1/5)x + d(2/5)y + d(2/5)z = d, поэтому один выбор константы дает
х + 2у + 2г = 5
или другой вариант: (1/5)x + (2/5)y + (2/5)z = 1
Учитывая координаты P, Q, R, есть формула для коэффициентов плоскость, которая использует определители или перекрестное произведение .
Упражнение. Какое уравнение плоскости через точки I, J, K?
Упражнение: Какое уравнение плоскости через (1, 1, 1), (-1, 1, -1) и (1, -1, -1)?
Упражнение: Сравните этот метод нахождения уравнения плоскости с векторным произведением метод.
Соединение с параметрической формой плоскости
Для 3 точек P, Q, R все точки плоскости можно записать в параметрическом форма F(s,t) = (1 — s — t)P + sQ + tR, где s и t варьируются по всем действительным числам.
Вычисление, подобное приведенному выше для уравнения прямой, показывает, что если P, Q, R удовлетворяют одному и тому же уравнению ax + by + cz = d, тогда все точки F(s,t) также удовлетворяют тому же уравнению.

- Прямой метод с переходом в новый центр координат и поворотом вокруг нового центра координат (для линий) 92/=1/14

 При этом числа одновременно не равны нулю. Уравнение (1) называется
общим уравнением кривой
второго порядка. Если нет точек с действительными координатами, удовлетворяющих
уравнению , то говорят, что уравнение (1) определяет мнимую кривую
второго порядка. Уравнение может служить примером
уравнения второй степени, определяющего мнимую кривую, в данном случае
мнимую окружность.
При этом числа одновременно не равны нулю. Уравнение (1) называется
общим уравнением кривой
второго порядка. Если нет точек с действительными координатами, удовлетворяющих
уравнению , то говорят, что уравнение (1) определяет мнимую кривую
второго порядка. Уравнение может служить примером
уравнения второй степени, определяющего мнимую кривую, в данном случае
мнимую окружность.
 23
23 Тогда уравнение эллипса запишется в
виде
Тогда уравнение эллипса запишется в
виде Эти точки называются вершинами эллипса.
Эти точки называются вершинами эллипса.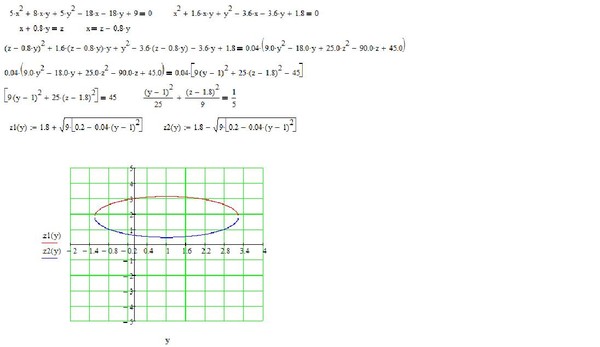 Уравнение этой окружности
Уравнение этой окружности
 Из этого следует, что
можно ввести обозначение и записать уравнение гиперболы в виде . Разделив на , получим уравнение гиперболы
Из этого следует, что
можно ввести обозначение и записать уравнение гиперболы в виде . Разделив на , получим уравнение гиперболы Следовательно, нет точек кривой, расположенных в полосе
. Кроме того, из явного уравнения можно видеть, что при
возрастании на полуинтервале ордината возрастает и стремится к
бесконечности.
Следовательно, нет точек кривой, расположенных в полосе
. Кроме того, из явного уравнения можно видеть, что при
возрастании на полуинтервале ордината возрастает и стремится к
бесконечности.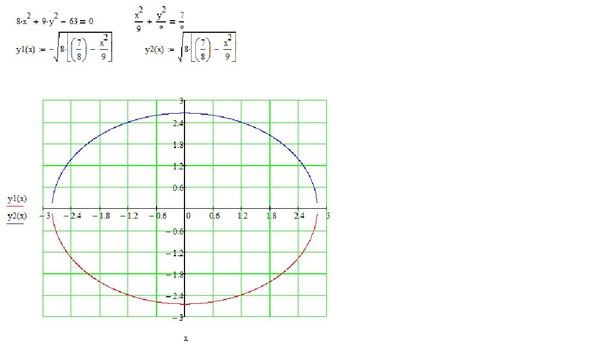 Вид кривой показан на рисунке 26.
Вид кривой показан на рисунке 26. 27). Если точка лежит на параболе, то справедливо
27). Если точка лежит на параболе, то справедливо
 Следовательно, вершины гиперболы , лежат на оси .
Следовательно, вершины гиперболы , лежат на оси . Строить кривую в
данном случае удобно, перенося начало координат в эту точку, то есть,
сделав замену .
Строить кривую в
данном случае удобно, перенося начало координат в эту точку, то есть,
сделав замену . Если в уравнении знак -, то
направление ветвей противоположно направлению оси, которой параллельна ось
симметрии параболы.
Если в уравнении знак -, то
направление ветвей противоположно направлению оси, которой параллельна ось
симметрии параболы.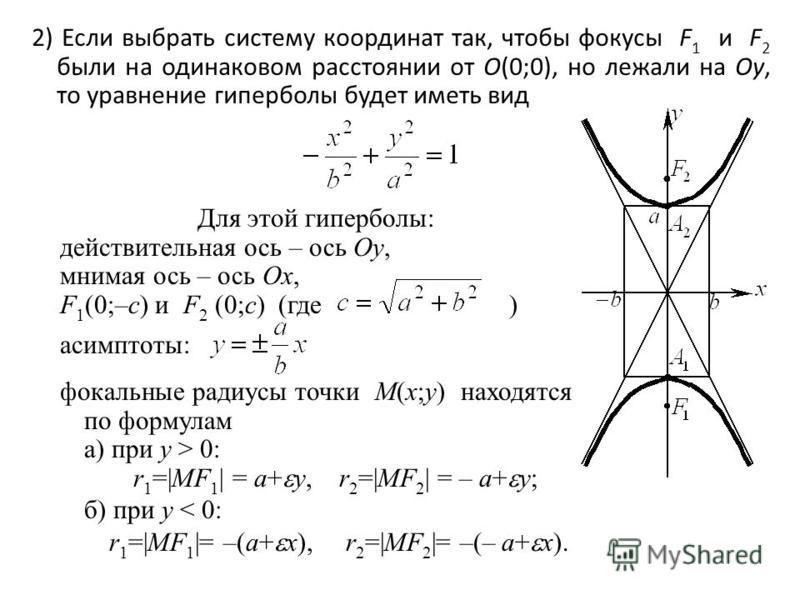 Поскольку из уравнения
следует, что , то
ветви параболы направлены вниз и фокус лежит на ниже вершины, то
есть его координаты .
Поскольку из уравнения
следует, что , то
ветви параболы направлены вниз и фокус лежит на ниже вершины, то
есть его координаты . com
com Общее уравнение второй степени
можно значительно упростить, заменив
другая система координат. Подходящий
вращение системы координат будет
исключить все смешанные термины в xy, xz
и ыз. Подходящий перевод устранит большинство или все термины первой степени в x, y и z.
Путем подходящего переноса и поворота системы координат общее уравнение второй степени
можно привести к одной из следующих канонических форм:
Общее уравнение второй степени
можно значительно упростить, заменив
другая система координат. Подходящий
вращение системы координат будет
исключить все смешанные термины в xy, xz
и ыз. Подходящий перевод устранит большинство или все термины первой степени в x, y и z.
Путем подходящего переноса и поворота системы координат общее уравнение второй степени
можно привести к одной из следующих канонических форм: Таким образом
если P (x, y, z) — точка на сфере 2), то P'(ax, by, cz) — соответствующая точка на эллипсоиде 3).
Таким образом
если P (x, y, z) — точка на сфере 2), то P'(ax, by, cz) — соответствующая точка на эллипсоиде 3).

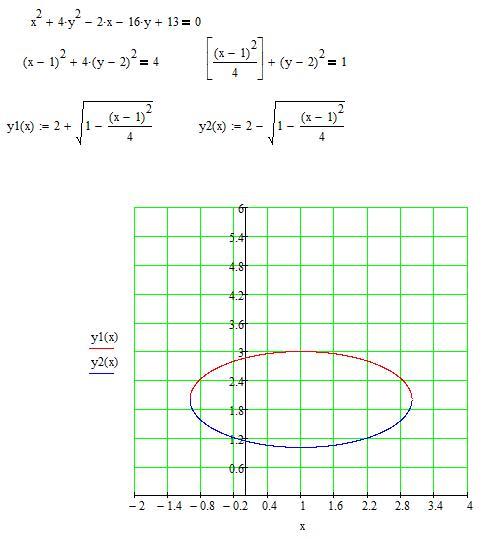 Умножение на матрицу вращения преобразует
координаты точки из одной системы в другую систему.
Умножение на матрицу вращения преобразует
координаты точки из одной системы в другую систему.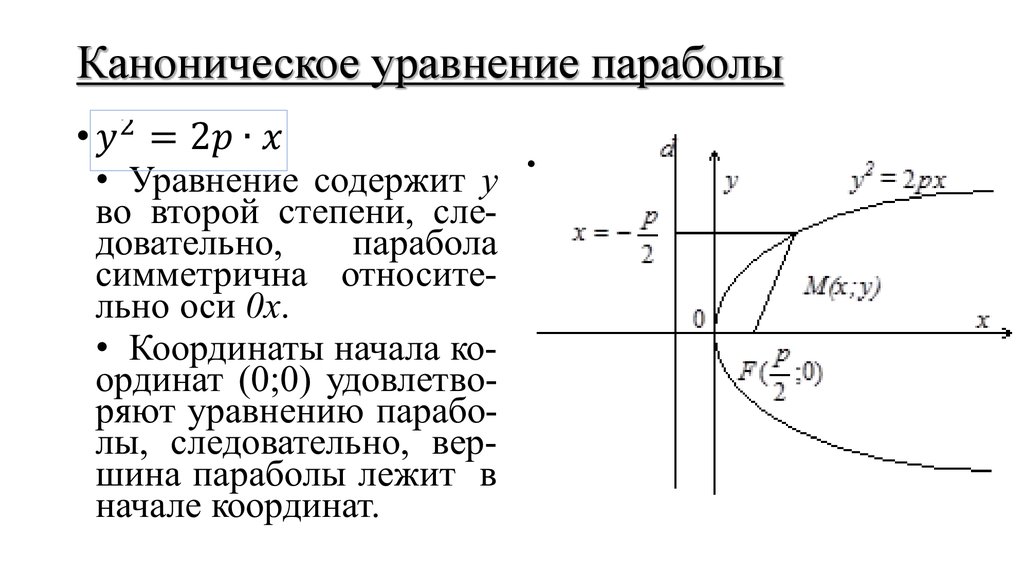 — направляющие косинусы
ось x c , λ 2 , µ 2 , ν 2 – направляющие косинусы оси y c , λ 3 , µ 3
— направляющие косинусы
ось x c , λ 2 , µ 2 , ν 2 – направляющие косинусы оси y c , λ 3 , µ 3 Общие поговорки. Альманах бедного Ричарда.
Общие поговорки. Альманах бедного Ричарда. Наказание за это настоящее. Ад реален.
Наказание за это настоящее. Ад реален.
 r.t. \(\eta\) и \(\xi\), чтобы получить решение 92 + б\лямбда + с = 0 \]
r.t. \(\eta\) и \(\xi\), чтобы получить решение 92 + б\лямбда + с = 0 \]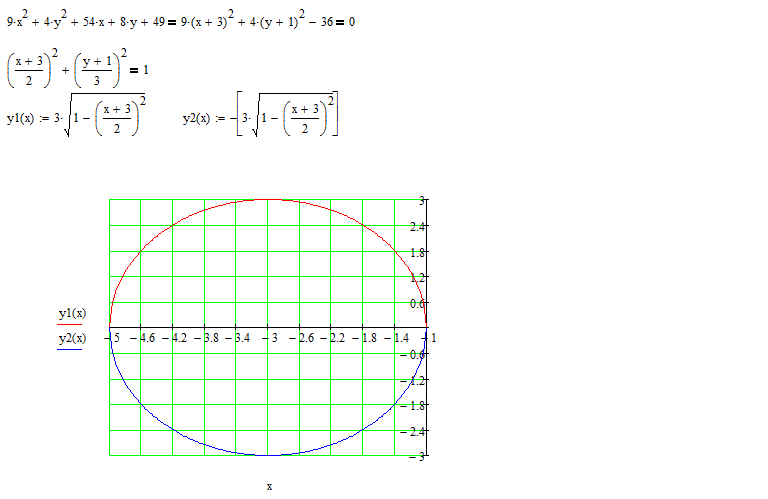
 е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Например, для дифференциального уравнения второго порядка начальные условия таковы:
Например, для дифференциального уравнения второго порядка начальные условия таковы: 25in}y\left({{x_1}} \right) = {y_1}\label{eq :eq3}\end{уравнение}\]
\[\begin{equation}y\left( {{x_0}} \right) = {y_0}\hspace{0.25in}y’\left( {{x_1}} \right) = {y_1}\label{eq :eq4}\end{уравнение}\]
25in}y\left({{x_1}} \right) = {y_1}\label{eq :eq3}\end{уравнение}\]
\[\begin{equation}y\left( {{x_0}} \right) = {y_0}\hspace{0.25in}y’\left( {{x_1}} \right) = {y_1}\label{eq :eq4}\end{уравнение}\]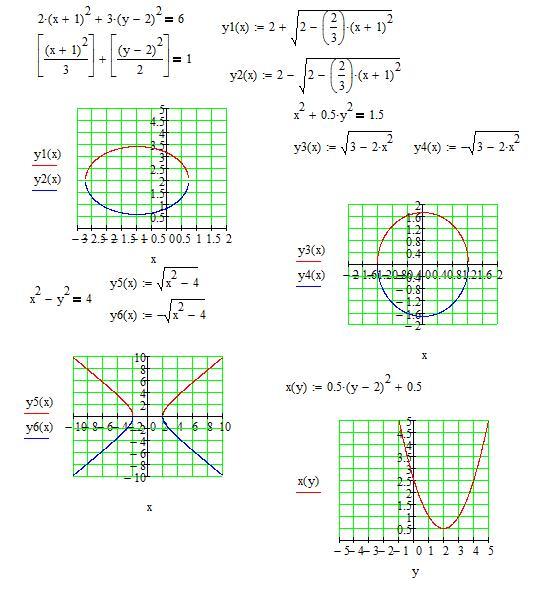 Мы, конечно, можем решить \(\eqref{eq:eq5}\) при условии, что коэффициенты постоянны, и для некоторых случаев, когда они не являются постоянными. Ничего из этого не изменится. Изменения (и, возможно, проблемы) возникают, когда мы переходим от начальных условий к граничным.
Мы, конечно, можем решить \(\eqref{eq:eq5}\) при условии, что коэффициенты постоянны, и для некоторых случаев, когда они не являются постоянными. Ничего из этого не изменится. Изменения (и, возможно, проблемы) возникают, когда мы переходим от начальных условий к граничным. При решении линейных начальных задач единственное решение будет гарантировано в очень мягких условиях. Мы рассмотрели эту идею только для IVP первого порядка, но эта идея распространяется и на IVP более высокого порядка. В этом разделе мы увидели, что все, что нам нужно, чтобы гарантировать уникальность решения, — это некоторые основные условия непрерывности. В случае с краевыми задачами у нас часто не будет решения или будет бесконечно много решений даже для очень хороших дифференциальных уравнений, которые дали бы единственное решение, если бы у нас были начальные условия вместо граничных.
При решении линейных начальных задач единственное решение будет гарантировано в очень мягких условиях. Мы рассмотрели эту идею только для IVP первого порядка, но эта идея распространяется и на IVP более высокого порядка. В этом разделе мы увидели, что все, что нам нужно, чтобы гарантировать уникальность решения, — это некоторые основные условия непрерывности. В случае с краевыми задачами у нас часто не будет решения или будет бесконечно много решений даже для очень хороших дифференциальных уравнений, которые дали бы единственное решение, если бы у нас были начальные условия вместо граничных. Или, может быть, они будут обозначать расположение концов вибрирующей струны. Значит, граничными условиями действительно будут условия на границе какого-то процесса.
Или, может быть, они будут обозначать расположение концов вибрирующей струны. Значит, граничными условиями действительно будут условия на границе какого-то процесса.
 \[y\left( x \right) = {c_1}\cos \left( {2x} \right) + {c_2}\sin \left( {2x} \right)\]
\[y\left( x \right) = {c_1}\cos \left( {2x} \right) + {c_2}\sin \left( {2x} \right)\]
 Во всех трех этих примерах использовалось одно и то же дифференциальное уравнение, но разные наборы начальных условий приводили к отсутствию решений, одному решению или бесконечному количеству решений.
Во всех трех этих примерах использовалось одно и то же дифференциальное уравнение, но разные наборы начальных условий приводили к отсутствию решений, одному решению или бесконечному количеству решений. е. ноль, одно или бесконечное множество решений).
е. ноль, одно или бесконечное множество решений).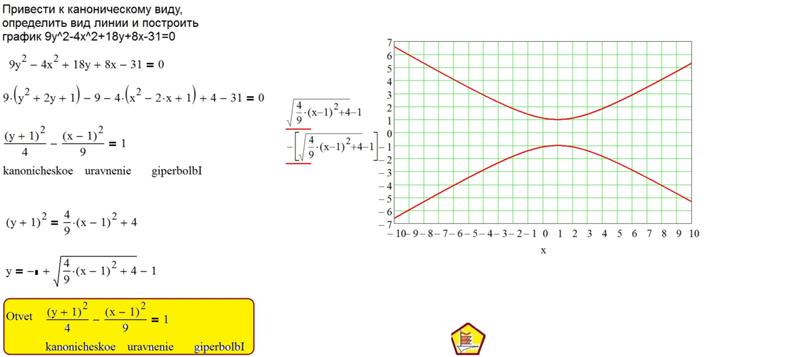 Решите следующую BVP.
\[y» + 25y = 0\hspace{0.25in}y’\left( 0 \right) = 6\hspace{0.25in}y’\left(\pi \right) = — 9\]
Решите следующую BVP.
\[y» + 25y = 0\hspace{0.25in}y’\left( 0 \right) = 6\hspace{0.25in}y’\left(\pi \right) = — 9\]
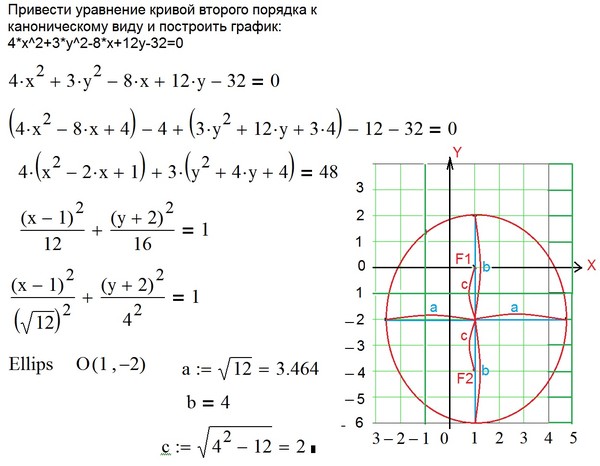 25in} \Rightarrow \hspace{0.25in}{c_2} = \frac{5}{3 } \\ — \ frac {5} {3} & = y \ left ( {\ frac {\ pi} {2}} \ right) = — {c_2} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма }{c_2} = \frac{5}{3}\end{align*}\]
25in} \Rightarrow \hspace{0.25in}{c_2} = \frac{5}{3 } \\ — \ frac {5} {3} & = y \ left ( {\ frac {\ pi} {2}} \ right) = — {c_2} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма }{c_2} = \frac{5}{3}\end{align*}\]
 Однако обратите внимание, что это всегда будет решением любой однородной системы, заданной \(\eqref{eq:eq5}\), и любого из (однородных) граничных условий, заданных \(\eqref{eq:eq1}\) – \(\eqref{eq:eq4}\). Из-за этого мы обычно называем это решение тривиальное решение . Иногда, как в случае с последним примером, тривиальное решение является единственным решением, однако обычно мы предпочитаем, чтобы решения были нетривиальными. Это будет основной идеей в следующем разделе.
Однако обратите внимание, что это всегда будет решением любой однородной системы, заданной \(\eqref{eq:eq5}\), и любого из (однородных) граничных условий, заданных \(\eqref{eq:eq1}\) – \(\eqref{eq:eq4}\). Из-за этого мы обычно называем это решение тривиальное решение . Иногда, как в случае с последним примером, тривиальное решение является единственным решением, однако обычно мы предпочитаем, чтобы решения были нетривиальными. Это будет основной идеей в следующем разделе.
 Когда мы перейдем к следующей главе и кратко рассмотрим решение дифференциальных уравнений в частных производных, мы увидим, что почти все примеры, с которыми мы будем работать, сводятся именно к этому дифференциальному уравнению. Кроме того, в этих задачах мы будем работать с некоторыми «настоящими» задачами, которые на самом деле решены местами, а не являются просто «придуманными» задачами для целей примера. По общему признанию, в них будут некоторые упрощения, но в некоторых случаях они приближаются к реальной проблеме.
Когда мы перейдем к следующей главе и кратко рассмотрим решение дифференциальных уравнений в частных производных, мы увидим, что почти все примеры, с которыми мы будем работать, сводятся именно к этому дифференциальному уравнению. Кроме того, в этих задачах мы будем работать с некоторыми «настоящими» задачами, которые на самом деле решены местами, а не являются просто «придуманными» задачами для целей примера. По общему признанию, в них будут некоторые упрощения, но в некоторых случаях они приближаются к реальной проблеме.
 В результате получается эллипс.
В результате получается эллипс. Сначала мы научимся выводить уравнения эллипсов, а потом научимся записывать уравнения эллипсов в стандартной форме. Позже мы будем использовать полученные знания для построения графиков.
Сначала мы научимся выводить уравнения эллипсов, а потом научимся записывать уравнения эллипсов в стандартной форме. Позже мы будем использовать полученные знания для построения графиков. Мы знаем, что сумма этих расстояний равна [latex]2a[/latex] для вершины [latex](a,0)[/latex]. Отсюда следует, что [latex]d_1+d_2=2a[/latex] для любой точки эллипса. Вывод стандартной формы уравнения эллипса основан на этом соотношении и формуле расстояния. Вывод выходит за рамки этого курса, но уравнение: 92}=1[/latex]
Мы знаем, что сумма этих расстояний равна [latex]2a[/latex] для вершины [latex](a,0)[/latex]. Отсюда следует, что [latex]d_1+d_2=2a[/latex] для любой точки эллипса. Вывод стандартной формы уравнения эллипса основан на этом соотношении и формуле расстояния. Вывод выходит за рамки этого курса, но уравнение: 92}=1[/latex] Как и в случае с другими уравнениями, мы можем определить все эти функции, просто взглянув на стандартную форму уравнения. Существует четыре варианта стандартной формы эллипса. Эти вариации классифицируются сначала по расположению центра (начало или не начало), а затем по положению (горизонтальное или вертикальное). Каждый представлен вместе с описанием того, как части уравнения соотносятся с графиком. Интерпретация этих частей позволяет нам сформировать ментальную картину эллипса. 92[/латекс]. Когда нам даны координаты фокусов и вершин эллипса, мы можем использовать соотношение, чтобы найти уравнение эллипса в стандартной форме.
Как и в случае с другими уравнениями, мы можем определить все эти функции, просто взглянув на стандартную форму уравнения. Существует четыре варианта стандартной формы эллипса. Эти вариации классифицируются сначала по расположению центра (начало или не начало), а затем по положению (горизонтальное или вертикальное). Каждый представлен вместе с описанием того, как части уравнения соотносятся с графиком. Интерпретация этих частей позволяет нам сформировать ментальную картину эллипса. 92[/латекс]. Когда нам даны координаты фокусов и вершин эллипса, мы можем использовать соотношение, чтобы найти уравнение эллипса в стандартной форме. Если эллипс переместить [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр эллипса будет [latex]\left(h,k\right)[/latex] . Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [латекс]x[/латекс] на [латекс]\влево(хч\вправо)[/латекс] и 9{2}[/латекс]. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти уравнение эллипса в стандартной форме, когда заданы вершины и фокусы.
Если эллипс переместить [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, центр эллипса будет [latex]\left(h,k\right)[/latex] . Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [латекс]x[/латекс] на [латекс]\влево(хч\вправо)[/латекс] и 9{2}[/латекс]. Мы можем использовать это соотношение вместе с формулами средней точки и расстояния, чтобы найти уравнение эллипса в стандартной форме, когда заданы вершины и фокусы. Медицинское устройство под названием литотриптер использует эллиптические отражатели для разрушения камней в почках путем создания звуковых волн. Некоторые здания, называемые камерами шепота, спроектированы с эллиптическими куполами, так что человек, шепчущий в одном фокусе, может быть легко услышан кем-то, стоящим в другом фокусе. Это происходит из-за акустических свойств эллипса. Когда звуковая волна возникает в одном фокусе шепчущей камеры, звуковая волна будет отражаться от эллиптического купола и обратно в другой фокус. В комнате для шепота в Музее науки и промышленности в Чикаго два человека, стоящие в фокусах на расстоянии около 43 футов друг от друга, могут слышать шепот друг друга.
Медицинское устройство под названием литотриптер использует эллиптические отражатели для разрушения камней в почках путем создания звуковых волн. Некоторые здания, называемые камерами шепота, спроектированы с эллиптическими куполами, так что человек, шепчущий в одном фокусе, может быть легко услышан кем-то, стоящим в другом фокусе. Это происходит из-за акустических свойств эллипса. Когда звуковая волна возникает в одном фокусе шепчущей камеры, звуковая волна будет отражаться от эллиптического купола и обратно в другой фокус. В комнате для шепота в Музее науки и промышленности в Чикаго два человека, стоящие в фокусах на расстоянии около 43 футов друг от друга, могут слышать шепот друг друга.