§ Признак делимости на 2, 4 и 8
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность.
Площадь круга - Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Чтобы выполнить большой и важный труд, необходимы две вещи: ясный план и ограниченное время.
на главную
Введите тему
Русский язык Поддержать сайт
Признаки делимости
на 2, 4 и 8
Признаки делимости
на 3, 6 и 9
Признаки делимости
на 5, 25 и 10
Признак делимости на 11
Чтобы понять делится ли одно число на другое не обязательно проводить сложные вычисления или иметь при себе калькулятор.
Математики придумали специальные правила, который помогут вам узнать делятся ли числа нацело друг на друга. Эти правила называются признаками делимости.
Признак делимости на 2
Запомните!
Число делится на 2, если его последняя цифра делится на 2 или является нулём.
Примеры:
- 52 делится на 2.
Последняя цифра 2 делится на 2 нацело 2 : 2 = 1.
- 300 делится на 2. Последняя цифра 0.
- 11 не делится на 2. Последняя цифра 1 не делится на 2.
Признак делимости на 4
Запомните!
Число делится на 4, если две его последние цифры нули или образуют число, делящееся на 4.
Примеры:
- 548 делится на 4. Две последние цифры 48 делятся на 4 нацело (48 : 4 = 12).
- 600 делится на 4. Две последние цифры нули.
- 755 не делится на 4. Две последние цифры 55 не делятся на 4.
Признак делимости на 8
Запомните!
Число делится на 8, если три последние его цифры нули или образуют число, делящееся на 8.
Примеры:
- 1128 делится на 8. Три последние цифры 128 делятся на 8 нацело (128 : 8 = 16).
- 7000 делится на 8. Три последние цифры нули.
- 6755 не делится на 4. Три последние цифры
755 не делятся на 4.
Признаки делимости
на 2, 4 и 8
Признаки делимости
на 3, 6 и 9
Признаки делимости
на 5, 25 и 10
Признак делимости на 11
Признаки делимости (Лунгу Алена)
Признаки делимости на 10, на 5 и на 2Всякое натуральное число, запись которого оканчивается цифрой 0,делится без остатка на 10. Чтобы получить частное, достаточно отбросить эту цифру 0.
Например, 280 делится без остатка на 10, так как 280:10=28.
При делении же числа 283 на 10 получаем неполное частное 28 и остаток 3 (т.е. последнюю цифру записи этого числа). Поэтому если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.
Число 10=2*5. Поэтому число 10 делится без остатка на 2, и на 5.
Отсюда и любое число, запись которого оканчивается цифрой 0, делится без остатка и на 5, и на 2.
Например, 60=6*10=6*(2*5)=(6*2)*5=12*5, значит, 60:5=12.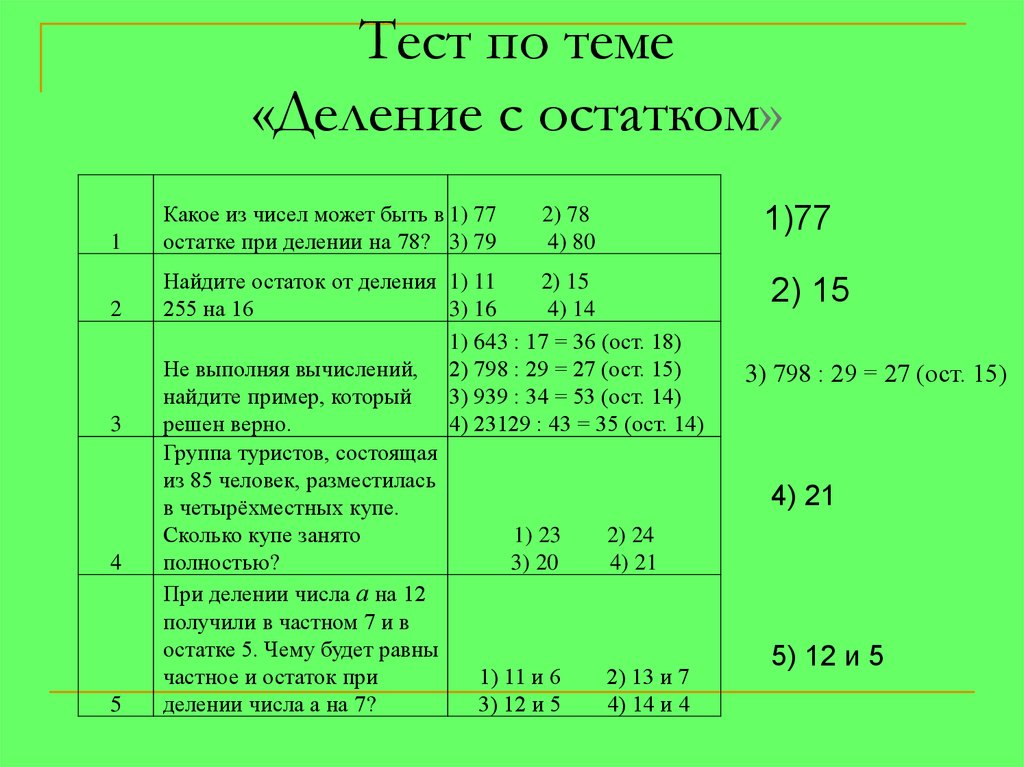
А из того что 60=6*(2*5)=(6*5)*2=30*2, получаем, что 60:2=30.
Каждое число можно представить в виде суммы полных десятков и единиц, например: 246=240+6, 1435=1340+5. Так как полные десятки делятся на 5, то и все число делится на 5 лишь в том случае, когда на 5 делится число единиц. Это возможно только тогда, когда в разряде единиц стоит цифра 0 или 5.
Например,числа 870 и 875 делятся без остатка на 5, а числа 872 и 873 на 5 без остатка не делятся.
Числа, делящиеся без остатка на 2, называются чётными, а числа, которые при делении на 2 дают остаток 1, называются нечётными. Из однзначных чисел числа 0, 2, 4, 6 и 8 чётны, а числа 1, 3, 5, 7 и 9 нечётны. Поэтому и цифры 0, 2, 4, 6, 8 называют чётными, а цифры 1, 3, 5, 7, 9 — нечётными. Все полные десятки делятся на 2 без остатка (т.
е. они четны). Значит, любое натуральное число чётно лишь в том случае, когда в рязряде единиц стоит чётная цифра, и нечётно, когда в разряде единиц стоит нечётная цифра.
Например, числа 2, 60, 84, 96, 308 чётные, а числа 3, 51, 85, 97, 509 нечётные.
Признаки делимости на 9 и на 3Узнаем,не выполняя деления, можно ли 846 яиц разложить в 9 корзин поровну.
В числе 846 содержится 8 сотен, 4 десятка и 6 единиц. Если раскладывать поровну в 9 корзин одну сотню яиц, то в каждую корзину можно положить 11 яиц, а одно яйцо останется. От восьми сотен останется 8 яиц.
Если раскладывать поровну в 9 корзин один десяток яиц, то в каждую корзину надо положить одно яйцо и одно яйцо останется. От четырёх десятков останется 4 яйца.
Не разложенными в корзины останутся 8 яиц от сотен, 4 яйца от десятков и еще 6 яиц: 8+4+6=18. Число 18 является суммой цифр числа 846.
Так как 18 яиц можно разложить поровнц в 9 корзин ( по 2 яйца в каждую), то и все 846 яиц можно разложить поровну в 9 корзин. Это значит, что число 846 делится без остатка на 9.
Пример 1. Число 75 455 делится на 9, так как сумма его цифр: 7+6+4+5+5=27 — делится на 9.
Пример 2. Число 51 634 не делится на 9, так как сумма его цифр: 5+1+6+3+4=19 — не делится на 9.
Так же обосновывается признак делимости на 3.
2, 4, 8 и 5, 10
Пример: 456 791 824
Это число четыреста пятьдесят шесть тысяч семьсот девяносто один восемьсот двадцать четыре. Мы можем сказать, делится ли 2 на это число без остатка, просто взглянув на последнюю цифру.
456 791 824 — последняя цифра 4. Это означает, что число ЧЕТНОЕ и на него без остатка делится 2. 456 791 824 делится на 2.
Пример: 34 807
Проверьте последнюю цифру этого номера.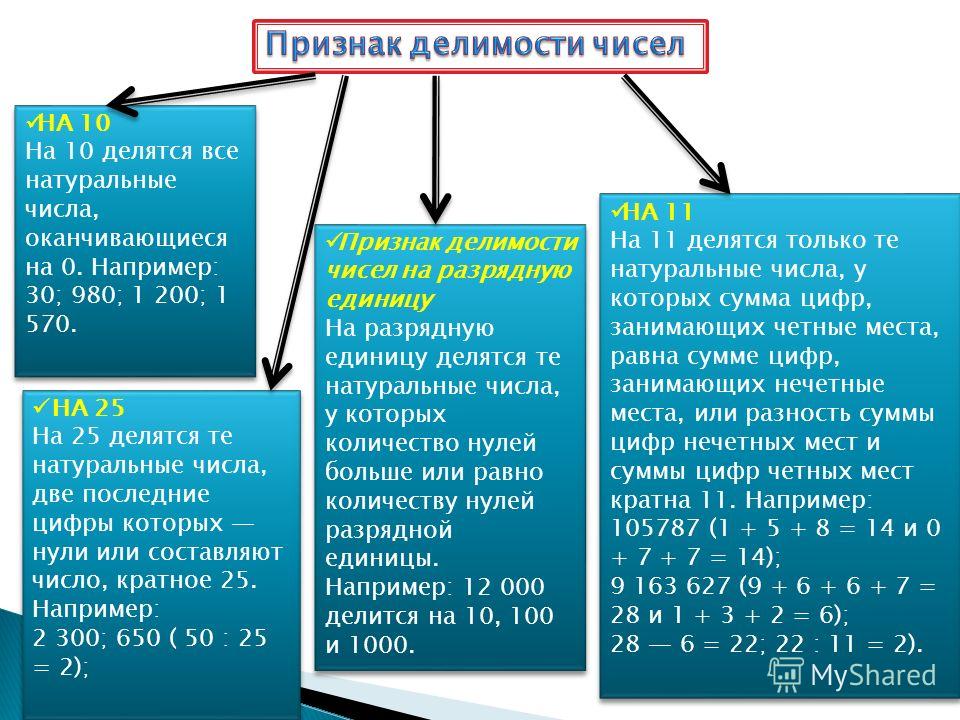
34 807 — последняя цифра 7. Это означает, что число НЕЧЕТНОЕ и 2 не делится на него без остатка. Будет остаток. Значит, 34 807 не делится на 2.
Правило для 4 : Если две последние цифры целого числа делятся на 4, то и все число делится на 4.
Пример: 456 791 824
Для этого правила посмотрим на две последние цифры: 456,791824. 4 делится без остатка на 24? Да. Это означает, что 4 тоже делится поровну на 456 791 824 и остатка не будет.
Пример: 723 810
Снова взглянем на две последние цифры: 723 810. 4 делится без остатка на 10? Нет. Это означает, что 4 не делится на 7223 810 без остатка и будет остаток.
Правило для 8 : Если последние три цифры целого числа делятся на 8, то и все число делится на 8.
Пример: 456 791 824
Для этого правила мы рассмотрим последние три цифры числа: 456 791 824. 8 делится без остатка на 824? ДА, 8 входит в число 824 103 раза, и ничего не остается.
Значит, это число делится на 8.
Пример: 923 780
Снова сосредоточимся на трех последних цифрах числа: 923 780. 8 делится поровну на 780? НЕТ, 8 входит в число 780 97 раз с остатком 4. Значит, это число не делится на 8.
Правила для 2, 4 и 8 должны выглядеть одинаково. Это потому, что эти числа связаны. Think about the powers of 2.
2 1 = 2
2 2 = 4
2 3 =
Используемая экспонента или степень двойки также является количеством цифр, которые мы должны использовать при выполнении теста.
Правило для 5 : Число, которое делится на 5, должно заканчиваться на 5 или 0.
Пример: 34 780
Для этого правила мы просто смотрим на последнюю цифру: 34 780. Последняя цифра — 0, поэтому это число делится на 5.
Пример: 13 569
Снова обратим внимание на последнюю цифру: 13 569.
Последняя цифра — 9, поэтому это число не делится на 5.
Правило для 10 : Числа, которые делятся на 10, должны быть четными и делиться на 5, потому что простые делители 10 — это 5 и 2. По сути, это означает, что для того, чтобы число делилось на 10, последняя цифра должна быть 0,9.0007
Пример: 23 890
Взгляните на последнюю цифру: 23 890. Последняя цифра — 0. Значит, это число четное и делится на 5. Это означает, что оно также делится на 10.
Пример: 85 395
Взгляните на последнюю цифру: 85 395. Последняя цифра — 5. Значит, это число нечетное и делится на 5. Поскольку число нечетное, оно не делится на 10. Чтобы делиться на 10, оно должно оканчиваться на 0.
Давайте соберем все воедино. Взгляните на этот пример.
1 782 645 988
Это число заканчивается на 8….
Оно делится на 2, но не делится ни на 5, ни на 10.
Это число оканчивается на 88….
делится на 4, потому что 4 идет в 88 поровну.
Это число заканчивается на 988….
Оно не делится на 8, потому что 8 не входит в число 988 равномерно.
45 981 400
Этот номер заканчивается на 0….
Оно делится на 2, 5 и 10.
Это число заканчивается на 00….
Оно делится на 4. (Вы можете подумать: «Эй, 4 не делится на 00 без остатка» , но он показывает, что 4 должно быть кратно 100. 4 равномерно входит в 100, поэтому оно также будет равномерно кратно 100.)
Это число заканчивается на 400….
Оно делится на 8, потому что 8 войдет в 400, 50 раз без остатка.
Чем полезны правила делимости?
Правила делимости помогают нам находить множители чисел. Вместо того, чтобы на самом деле выполнять длинное деление, мы можем использовать правило, чтобы определить, является ли число делителем, прежде чем делить и получать ответ.
Как узнать, делится ли число на 4?
В этом посте мы собираемся изучить критерии делимости числа 4 и понять, как они работают.
Критерии делимости числа 4 — это правила, позволяющие узнать, можно ли разделить число на 4. Их легко выучить, и их объяснения легко понять.
Если число можно выразить, умножив другое число на 4, оно делится на 4.
Вам необходимо знать пару свойств умножения: ассоциативное и распределительное. Если вы не понимаете их четко, вы можете просмотреть их в этом посте.
Признаки деления одно- и двузначных чисел на 4
Сначала мы узнаем, как определить, удовлетворяет ли одно- или двузначное число признаку делимости на 4. Легко: это когда делим и видим, что остаток равен нулю.
Например: 24 делится на 4?
Да, потому что при делении 24 на 4 в частном получается 6, а в остатке 0.
24 = 6 x 4
Критерии деления трех- и четырехзначных чисел на 4 Чтобы числовое число делилось на 4, оно должно удовлетворять одному из двух условий:
- Последние две цифры равны нулю .
- Последние две цифры делятся на 4.
Например: 500 и 339 делятся на 4?
500 делится на четыре, потому что его последние две цифры равны нулю.
339 не делится на четыре, потому что 39 (две его последние цифры) не делится на четыре.
Применение известных нам правил, чтобы увидеть, выполняются они или нет, помогает нам определить, делится ли число на четыре. Но мы не знаем аргументации, давайте продолжим и попробуем понять.
Объяснение критериев деления числа на 4
Каким образом два простых правила могут сказать нам, соответствует ли число критериям делимости на 4? Откуда берутся эти правила?
Причина очень проста, и мы собираемся объяснить ее в три шага.
- Число 100.
Начнем с наименьшего возможного числа, две последние цифры которого равны нулю, 100. Если мы разделим 100 на 4, в частном получится 25, а в остатке 0. 100 делится на 4 .
100 = 25 x 4
Все числа, в которых две последние цифры равны нулю, можно выразить, умножив другое число на 100. Мы выберем одно, например, 4300.
4300 = 43 x 100
Поскольку мы знаем, что 100 делится на четыре, мы также можем сказать, что 4300 делится. Вот математическое объяснение:
4300 = 43 х 100 = 43 х (25 х 4) = (43 х 25) х 4 = 1075 х 4
Мы можем использовать ту же операцию для любого числа, которое имеет эти характеристики. Таким образом, мы обнаруживаем первое правило: любое число, две последние цифры которого равны нулю, делится на 4.
- Другие номера.
Для всех остальных чисел, тех, которые больше ста и у которых нет нуля в последних двух цифрах, мы можем применить процесс, аналогичный упомянутому ранее. Они могут быть выражены как сумма числа с нулем в последних двух цифрах плюс еще одно число. Возьмем случайное число, например, 6548.
6548 = 6500 + 48
Поскольку мы знаем, что 6500 делится на 4, мы не должны забывать проверить, делится ли 48.
Ну да, последние две цифры делятся на 4.
48 = 12 х 4
Таким образом, мы можем выразить это следующим образом:
6548 = 6500 + 48 = (65 х 100) + 48 =
= (65 х 25 х 4) + (12 х 4) = (1625 х 4) + (12 х 4) =
= (1625 + 12) х 4 = 1637 х 4
Вот как мы понимаем второе правило: любое число делится на 4, если его последние две цифры делятся на 4. делится на четыре. Мы изучили необходимые критерии для деления числа на 4, но понимание этого помогает понять, почему критерии существуют, и если однажды мы забудем какой-либо из них… Я уверен, что мы вспомним, откуда они взялись!
Чтобы по-настоящему понять критерии деления на 4, которые мы узнали, возможно, вы хотели бы освежить в памяти, как делить на трехзначное число.
Если вы хотите узнать больше об основных материалах по математике, зарегистрируйтесь в Smartick и попробуйте его бесплатно.
Подробнее:
- Автор
- Последние сообщения
Smartick
Команда создания контента.