MFA4
%PDF-1.5 % 1 0 obj >/OCGs[10 0 R 11 0 R 12 0 R 13 0 R]>>/Pages 3 0 R/Type/Catalog>> endobj 2 0 obj >stream application/pdf
did:8131562f-a02e-4b5a-a359-7d8c54758a7duuid:5D20892493BFDB11914A8590D31508C8proof:pdfuuid:fd1603a4-a34b-db4b-86b6-99033162b00fxmp.did:f240d579-7443-4b56-9253-97c502551584uuid:5D20892493BFDB11914A8590D31508C8proof:pdf
3FalseConquerorSans-Bold.otf
00
endstream
endobj
3 0 obj
>
endobj
15 0 obj
>/Resources>/Font>/ProcSet[/PDF/Text]/Properties>>>/Thumb 22 0 R/TrimBox[0.
eR.$#&1du0>ʜZ3)yB/
:IJ6?X-$JWD’笣eQ&}ךp땯Эk&}wПризнаки делимости чисел | Образовательная социальная сеть
МБОУ «Средняя общеобразовательная школа №18»
ЭМР Саратовской области
Исследовательский проект
на тему:
«Признаки делимости чисел».
Автор работы: ученики 6 а класса
Руководитель: Пастухова Наталья Алексеевна,
учитель математики
Г. Энгельс 2014 г.
Автор проекта
Учащиеся 6а класса
Предмет исследования
Признаки делимости чисел.
Краткая аннотация проекта
Данный проект предназначен для обобщения, расширения и систематизации знаний по теме «Признаки делимости» в курсе математики 6 класса, учебник Н.Я. Виленкина. Время проведения проекта 1 – 4 четверть.
Основополагающий вопрос проекта
Как узнать, не выполняя деления, делится ли число на 4, 25, 11?
Задачи проекта
1. Изучить историю математики о делимости чисел.
2. Узнать признаки делимости на натуральные чисел от 2 до 25.
3. Изучить свойства делимости чисел.
4. Исследовать применение признаков делимости при решении цифровых головоломок и практических задач.
Гипотеза: признаки делимости способствуют эффективному и рациональному решению задач.
Введение.
Мы заинтересовался историей делимости чисел.
Кто из древних учёных занимался делимостью чисел? Кто такой Эратосфен? Что такое решето Эратосфена? Что собой представляет таблица простых чисел? Есть ли последнее простое число?
На уроках математики мы изучали основные признаки делимости чисел на 2,3,5, 9 и на 10. Но оказывается, признаков делимости гораздо больше. Есть признаки делимости на 4, 8,11,13,7 и другие числа. Неоценимо значение признаков делимости для развития умений устного счета, а также при решении цифровых головоломок и некоторых практических задач.
Старинная восточная притча:
Давным-давно жил-был старик, который, умирая, оставил своим трем сыновьям 19 верблюдов. Он завещал старшему сыну половину, среднему – четвертую часть, а младшему – пятую.
Не сумев найти решения самостоятельно (ведь задача в «целых верблюдах» решения не имеет), братья обратились к мудрецу.
— О, мудрец!- сказал старший брат. — Отец оставил нам 19 верблюдов и велел разделить между собой: старшему – половину, среднему – четверть, младшему – пятую часть. Но 19 не делится ни на 2, ни на 4, ни на 5. Можешь ли ты, о, достопочтенный, помочь нашему горю, ибо мы хотим выполнить волю отца?
— Нет ничего проще, — ответил им мудрец. – Возьмите моего верблюда и идите домой.
Братья дома легко разделили 20 верблюдов пополам, на 4 и на 5. Старший брат получил 10, средний – 5, а младший – 4 верблюда. При этом один верблюд остался (10+5+4=19). Раздосадованные, братья вернулись к мудрецу и пожаловались:
— О, мудрец, опять мы не выполнили волю отца! Вот этот верблюд – лишний.
— Это не лишний, — сказал мудрец,- это мой верблюд. Верните его и идите домой.
1. Из истории математики о делимости чисел
Делимость – это способность одного числа делиться на другое без остатка.
Признаки делимости были широко известны в эпоху Возрождения, поскольку, пользуясь ими, можно было приводить дроби с большими числителями и знаменателями к несократимому виду.
ЭРАТОСФЕН (около 275–194 до н.э.), один из самых разносторонних ученых античности. Эратосфен занимался самыми различными вопросами — ему принадлежат интересные исследования в области математики, астрономии и других наук. Трактаты Эратосфена были посвящены решению геометрических и арифметических задач.
Самым знаменитым математическим открытием Эратосфена стало так называемое «решето», с помощью которого находятся простые числа.
Делитель – это число, которое делит данное число без остатка. Все целые числа (кроме 0 и 1) имеют минимум два делителя: 1 и самого себя. Числа, не имеющие других делителей, называются простыми числами. Числа, имеющие другие делители, называются составными (или сложными) числами. Простых чисел – бесконечное множество.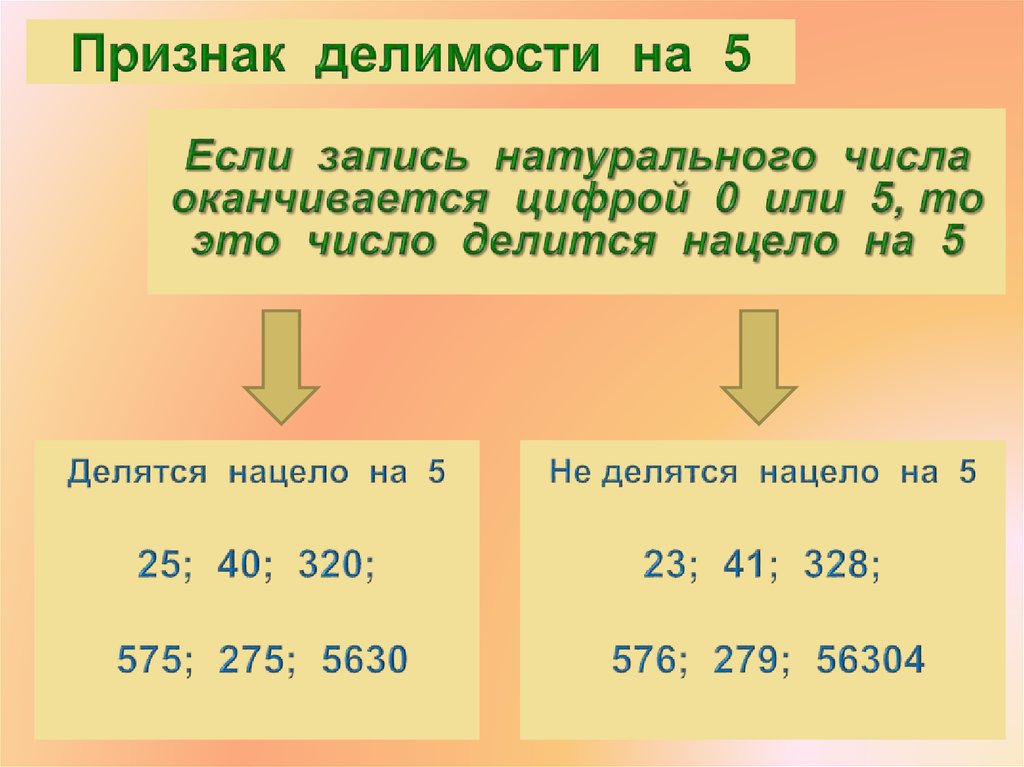
Наименьшим простым числом является 2, это единственное чётное простое число. Все остальные простые числа следует искать среди нечётных чисел, но, разумеется, далеко не всякое нечётное число является простым. Так, например, нечётные числа 3, 5, 7, 11, 13 простые, а такие нечётные числа как 9, 15, 21 — составные, 9 имеет 3 делителя, число 15 – 4 делителя и т.д. Любое составное число можно разлагать на сомножители до тех пор, пока оно не распадётся на одни только простые числа. Простые числа являются как бы первичными элементами, из которых составляются все числа.
В математике Эратосфена интересовал как раз вопрос о том, как найти все простые числа среди натуральных чисел от 1 до N. Эратосфен считал 1 простым числом. Математики считают 1 числом особого вида, которое не относится ни к простым, ни к составным числам. Эратосфен придумал для этого следующий способ. Сначала вычеркивают все числа, делящиеся на 2 (исключая само число 2). Потом берут первое из оставшихся чисел (а именно 3).
Ясно, что это число — простое. Вычеркивают все идущие после него числа, делящиеся на 3. Первым оставшимся числом будет 5. Вычеркивают все идущие после него числа, делящиеся на 5, и т.д. Числа, которые уцелеют после всех вычеркиваний, и являются простыми. Так как во времена Эратосфена писали на восковых табличках и не вычеркивали, а «выкалывали» цифры, то табличка после описанного процесса напоминала решето. Поэтому метод Эратосфена для нахождения простых чисел получил название «решето Эратосфена».
Большой вклад в изучение признаков делимости чисел внес Б. Паскаль.
БЛЕЗ ПАСКАЛЬ (Blaise Pascal) (1623–1662), французский религиозный мыслитель, математик и физик, один из величайших умов 17 столетия. Юный Блез очень рано проявил выдающиеся математические способности, научившись считать раньше, чем читать. Свой первый математический трактат «Опыт теории конических сечений» он написал в 24 года. Примерно в это же время он сконструировал механическую суммирующую машину, прообраз арифмометра.
Работы Паскаля в области точных наук, или ранний период его творчества относится к 1640-1650 году. За эти 10 лет разносторонний ученый сделал очень много: он нашел алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, сформулировал способ вычисления биноминальных коэффициентов, изложил ряд основных положений элементарной теории вероятности, впервые точно определил и применил для доказательства метод математической индукции.
Признак делимости Паскаля.
Натуральное число а разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа а на соответствующие остатки, получаемые при делении разрядных единиц на число b, делится на это число. Например: число 2814 делится на 7, так как 2*6 + 8*2 + 1*3 + 4 = 35 делится на 7. (Здесь 6-остаток отделения 1000 на 7, 2- остаток от деления 100 на 7 и 3- остаток от деления 10 на 7).
2. Признаки делимости
Признак делимости на 2.
Число делится на 2 в том и, только в том случае, если его последняя цифра чётная.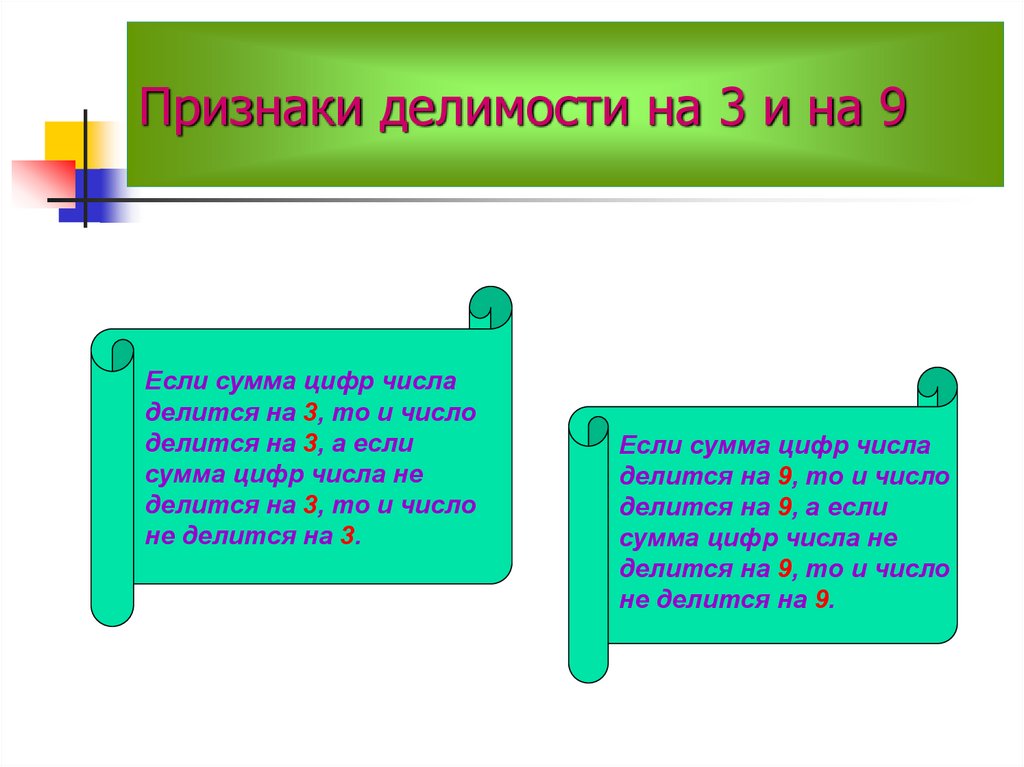
Пример: 124, 200, 152, 68, 406.
Признак делимости на 3.
Число делится на 2 в том и, только в том случае, если сумма его цифр делится на 3.
Пример: 144 на 3, т.к. 1+4+4 =9 делится на 3.
Признак делимости на 4.
Число делится на 4 в том и только в том случае, если две его последние цифры образуют двузначное число, делящееся на 4.
Пример: 724 делится на 4, т.к. 24 делится на 4.
Признак делимости на 5.
Число делится на 5 в том и только в том случае, если оно оканчивается на 0 или на 5.
Пример: 720, 655 делятся на 5.
Признак делимости на 6.
Число делится на 6 в том и только в том случае, если оно чётное и делится на 3.
Пример: 720 делится и на 2 и на 3.
Признак делимости на 7.
Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из числа десятков делится на 7.
Пример: 259 делится на 7, т. к. 25 — (2 * 9) = 7 делится на 7.
Признак делимости на 8.
Число делится на 8 в том и только в том случае, если его последние три цифры образуют число, делящееся на 8.
Пример: 6136 делится на 8, т.к. 136 делится на 8.
Признак делимости на 9.
Число делится на 9 в том и только в том случае, если сумма его цифр делится на 9.
Пример: 6102 делится на 9, т.к. 6+1+0+2 = 9 делится на 9.
Признак делимости на 10.
Число делится на 10 в том и только в том случае, если оно оканчивается на 0.
Пример: 720 делится на 10.
Признак делимости на 11.
Число делится на 11 тогда и только тогда, если модуль разности суммы цифр, стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, делится на 11
Пример: 100397 делится на 11, т.к. .
1+0+9=10; 0+3+7=10; =0 (нумерация идет слева направо).
Можно проверить делимость числа на 11 другим способом:
испытуемое число разбивают справа налево на группы по две цифры в каждой и складывают эти группы. Если получаемая сумма кратна 11, то испытуемое число кратно 11.
Пример:15235 делится на 11, т.к. разбивая на группы и складывая их: 1+52+35=88 делится на 11.
Признак делимости на 12.
Число делится на 12 в том и только в том случае, если оно делится одновременно и на 3, и на 4.
Пример: 720 делится на 12, т.к. число делится и на 3, и на 4.
Признак делимости на 13.
Число делится на 13 тогда:
— когда сумма числа десятков с учетверенным числом единиц делится на 13.
Пример: 845 делится на 13, так как на 13 делятся 84+ 5*4 = 104 и 10+4*4=26.
— когда разность числа десятков с девятикратным числом единиц делится на 13.
Пример: 845 делится на 13, так как на 13 делятся 84-9*5=39.
Признак делимости на 14.
Число делится на 14 в том и только в том случае, если оно делится одновременно и на 2, и на 7.
Пример: 420 делится на 14, т.к. число делится и на 2, и на 7.
Признак делимости на 15.
Число делится на 15 в том и только в том случае, если оно делится одновременно и на 3, и на 5.
Пример: 420 делится на 15, т.к. число делится и на 2, и на 5.
Признак делимости на 17.
Число делится на 17 тогда:
— когда модуль разности числа десятков и пятикратного числа единиц делится на 17.
Пример: 221 делится на 17, так как делится на 17.
— когда модуль суммы числа десятков и двенадцатикратного числа единиц делится на 17.
Пример: 221 делится на 17, так как делится на 17.
Признак делимости на 18.
Число делится на 18 в том и только в том случае, если оно делится одновременно и на 2, и на 9.
Пример: 432 делится на 18, т.к. число делится и на 2, и на 9.
Признак делимости на 19.
Число делится на 19 тогда и только тогда, когда число десятков, сложенное с удвоенным числом единиц, делится на 19.
Пример: 646 делится на 19, так как на 19 делятся и
Признак делимости на 20.
Число делится на 20 тогда и только тогда, когда число, образованное двумя последними цифрами, делится на 20.
Другая формулировка: число делится на 20 тогда и только тогда, когда последняя цифра числа — 0, а предпоследняя — чётная.
Пример: 640 делится на 20, т.к. 40 делится на 20.
Признак делимости на 21.
Число делится на 21 в том и только в том случае, если оно делится одновременно и на 3, и на 7.
Пример: 231 делится на 21, т.к. число делится и на 3, и на 7.
Признак делимости на 22.
Число делится на 22 в том и только в том случае, если оно делится одновременно и на 2, и на 11.
Пример: 352 делится на 22, т.к. число делится и на 2, и на 11.
Признак делимости на 23.
Признак 1: число делится на 23 тогда и только тогда, когда число сотен, сложенное с утроенным числом, образованным двумя последними цифрами, делится на 23.
Пример: 28842 делится на 23, так как на 23 делятся и
Признак 2: число делится на 23 тогда и только тогда, когда число десятков, сложенное с семикратным числом единиц, делится на 23.
Пример: 391 делится на 23, так как делится на 23.
Признак 3: число делится на 23 тогда и только тогда, когда число сотен, сложенное с семикратным числом десятков и утроенным числом единиц, делится на 23.
Пример: 391 делится на 23, так как делится на 23.
Признак делимости на 24.
Число делится на 24 в том и только в том случае, если оно делится одновременно и на 3, и на 8.
Пример: 8136 делится на 24, т.к. число делится и на 3, и на 8.
Признак делимости на 25.
Число делится на 25 тогда и только тогда, когда две его последние цифры составляют число, которое делится на 25.
Пример: 175делится на 25, т.к. 75 делится на 25.
3. Свойства делимости чисел.
При решении задач на делимость часто бывают полезными свойства, связанные с последовательным расположением натуральных чисел
- Одно из п последовательных натуральных чисел делится на п;
Пример: 3; 4; 5; 6; 7 – 5 последовательных натуральных чисел, 5 делится на 5.
- Одно из двух последовательных четных чисел делится на 4;
Пример: 10; 12 — 2 последовательных четных числа, 12 делится на 4.
- Произведение трех последовательных натуральных чисел делится на 6;
Пример: 5*6*7=210 210 делится на 6, т.
к. 210 делится на 2 и на 3.
- Произведение двух последовательных четных чисел делится на 8.
Пример: 4*6=24 24 делится на 8.
- Свойство 1. Если каждое слагаемое суммы делится на одно и то же число, то и сумма делится на это число.
Пример: 66 + 121= 187 делится на 11, т.к. 66 и 121 делятся на 11.
- Свойство 2. Если уменьшаемое и вычитаемое делятся на одно и то же число, то и разность делится на это число.
Пример: 1125 – 75 =1050 делится на 25, т.к. 1125 и 75 делятся на 25
- Свойства 3. Если в произведении нескольких натуральных чисел хотя бы один из сомножителей делится на какое-то число, то и все произведение делится на это число.
Пример: 21*5*9 = 945делится на 7, т.к. 21 делится на 7.
- Свойство 4. Если некоторое целое число делится на другое, а это другое – на третье, то и первое число делится на третье.
Пример: 171 делится на 57, а 57 делится на 19, значит 171 делится на 19.
4. Применение признаков делимости при решении цифровых головоломок и практических задач.
Задача № 1.
Туристическое агентство «Дуремар» предложило Карабасу три путевки «в страну Дураков» — две взрослые и одну детскую за 3543 золотые монеты. Известно, что детская путевка на 500 золотых монет дешевле. Каким образом Карабас смог понять, что его обманывают?
Решение.
3543+500= 4043, но 4043 не делится на 3.
Задача № 2
Семеро друзей. У одного гражданина было 7 друзей.
Первый посещал его каждый вечер, второй — каждый второй вечер, третий — каждый третий вечер, четвертый – каждый четвертый вечер и так до седьмого друга, который являлся каждый седьмой вечер.
Часто ли случалось, что все семеро друзей встречались у хозяина в один и тот же вечер?
Решение.
Решается с использованием признаков делимости на 2, на 3, на 4, на 5, на 6, на 7. НОД (2, 3, 4, 5, 6, 7) = 420
Ответ: 1 раз в 420 дней.
Задача № 3
Напишите какое-нибудь девятизначное число, в котором нет повторяющихся цифр (все цифры разные) и которое делится без остатка на 11.
Напишите наибольшее из таких чисел. Напишите наименьшее из таких чисел.
Решение.
Используем признак делимости на 11.
Ответ: 987652413; 102347586
Задача № 4
Ваня задумал простое трехзначное число, все цифры которого различны. На какую цифру оно может заканчиваться, если его последняя цифра равна сумме первых двух. Приведите примеры таких чисел.
Решение
Только на 7.
Ответ 167, 257, 347, 527.
Задача № 5
Найдите наибольшее четырехзначное число, все цифры которого различны и которое делится на 2, 5, 9, 11.
Ответ: 8910.
Задача № 6.
Катя утверждает, что она придумала признак делимости на 81: «Если сумма цифр числа делится на 81, то и само это число делится на 81.» Верно ли Катино утверждение? Если да, то докажите его. Если нет, приведите пример опровергающий пример Кати.
Ответ: опровергающий пример 9999999918.
Задача № 7.
Произведение цифр трехзначного числа равно 135. Какова сумма цифр этого числа?
Решение.
Число 135 делится на 5, 3, 9, значит число состоит из этих цифр, сумма этих цифр равна 17.
Ответ: 17.
Задача №8
Петин счет в банке содержит 500 долларов. Банк разрешает совершать операции только двух видов: снимать 300 долларов или добавлять 198 долларов. Какую максимальную сумму Петя может снять со счета, если других денег у него нет?
Решение
Поскольку 300 и 198 делятся на 6, Петя сможет снять лишь сумму, кратную 6 долларам. Максимальное число, кратное 6 и не превосходящее 500, — это 498.
Докажем, что снять 498 долларов возможно. Произведем следующие операции: 500-300=200, 200+198=398, 398-300=98, 98+198=296, 296+198=494. Сумма, лежащая в банке, уменьшилась на 6 долларов.
Проделав аналогичную процедуру 16 раз, Петя снимет 96 долларов, у него останется на счету 404 доллара. Затем он может снять 300, положить 198 и снова снять 300, в результате он снимет 2доллара, и у него останется 498 долларов.
Заключение
В результате выполнения данной работы у нас расширились знания по математике.
Мы узнали, что кроме известных мне признаков на 2, 3, 5, 9 и 10 существуют еще признаки делимости на 4, 6, 7, 8, 11, 12, 13, 14, 15, 19 и 25. Поняли, что в некоторых случаях без признаков делимости просто невозможно обойтись.
Познакомившись с признаками делимости чисел, мы считаем, что полученные знания сможем использовать в своей учебной деятельности, самостоятельно применить тот или иной признак к определенной задаче, применить изученные признаки в реальной ситуации.
Считаем, что применение признаков делимости чисел в изучении математики является эффективным. Знание их значительно ускоряет решение многих заданий интеллектуальных конкурсов, математического конкурса -игры «Кенгуру». В современном мире тоже используют признаки делимости! Например, в банковском деле, при денежных расчетах в магазине.
Библиографический список
1. И. Я. Депман, «История арифметики», Москва, 1965, «Просвещение»
2. Г. И. Глейзер, «История математики в школе 7 – 8 классы», Москва, 1982, «Просвещение»
3.
«1001 вопрос и ответ. Большая книга знаний», Москва, 2004, «Мир книги»
4. Энциклопедический словарь юного математика / Сост.А.П.Савин.-М.: Педагогика, 1989
5. Я.И. Перельман, «Живая математика», Москва, 1978, «Наука»
6. Б.А. Кордемский, «Математическая смекалка», Москва, 1994, «Юнисам»
7. http://www.doronchenko.ru/2009/01/13/vse_pro_chislo_13.html
8. http://ru.wikipedia.org/wiki/3
9. htpp: // www.krugosvet.ru/articles/07/1000723/1000723a1.htm
Видео-вопрос: Определение делимости чисел путем нахождения их частного и остатка
Стенограмма видео
Заполните пропуски в следующей таблице.
В таблице четыре заголовка. Деление, частное, остаток и делимость. В верхней строке таблицы вычисление деления равно 220, деленному на 64. Нам говорят, что ответом на это вычисление являются три остатка 28. В числе 220 три 64. И у нас есть остаток 28. остаток, 220 не делится на 64. Мы можем проверить этот ответ, сначала умножив 64 на три, используя стандартное умножение столбца.
Три умножить на четыре равно 12. Ставим двойку в столбец единиц и переносим единицу. Три умножить на шесть равно 18. Прибавляя тот, который мы несли, получаем 19. Следовательно, 64, умноженное на три, равно 192.
Чтобы вычислить остаток, нам нужно вычесть 192 из 220. Ноль минус два даст нам отрицательное число. Поэтому нам нужно пойти по соседству и одолжить один из столбца десятков. 10 минус два равно восьми. Нам снова нужно заимствовать, на этот раз из столбца сотен. Это оставляет нам 11 минус девять в столбце десятков. Это равно двум. А один минус один равно нулю. Следовательно, наш остаток равен 28. 220 разделить на 64 равно трем остаткам 28,9.0005
Мы можем заполнить пробелы, вычислив деление 195 на 28. Мы могли бы сделать это, используя метод автобусной остановки. Однако, поскольку 28 не превращается в 19, нам все равно придется делить 195 на 28. Поэтому проще начать с записи чисел в таблице умножения на 28. Один, умноженный на 28, равен 28. Два, умноженный на 28, равен 56.
Быстрый способ сделать это — добавить 28 к нашему предыдущему ответу. 28 плюс 20 равно 48. И добавление восьми к этому дает нам 56. Мы можем вычислить три, умноженные на 28, прибавив 28 к 56. Это дает нам 84, поскольку 56 плюс 20 равно 76. И добавление восьми к этому дает нам 84
Мы можем повторить этот метод, чтобы вычислить четыре, пять, шесть и семь, умноженные на 28. Мы можем остановиться на этом этапе, так как 196, ответ на семь, умноженный на 28, больше 195. Это означает, что наше частное будет быть шесть. В числе 195 шесть 28-х. Чтобы вычислить остаток, нам нужно вычесть 168 из 195. Опять же, наш первый шаг — взять единицу из столбца десятков. 15 минус восемь равно семи. Восемь минус шесть равно двум. Наконец, один минус один равно нулю. Это означает, что остаток равен 27. Поскольку остаток есть, мы можем сказать, что 195 точно не делится на 28. Вычисление 195, деленное на 28, равно шести остаткам 27.
Здесь важно отметить, что остаток никогда не может быть больше числа, на которое мы делим.
В этом случае остаток должен быть меньше 28. Максимально возможный остаток в этом случае равен 27, так как 196 разделить на 28 будет равно семи. Если мы разделим любое из чисел в таблице умножения на 28 на 28, остатка не будет. И число будет кратным.
Правило делимости на 13 — Методы, примеры
Правило делимости на 13 гласит, что число делится на 13, когда цифра, занимающая единицу, умножается на 4, а произведение прибавляется к остальной части числа. либо дает 0, либо кратно 13. Другими словами, сумма, полученная после сложения произведения умножения цифры единиц на 4 и остатка числа слева от нее, должна быть 0 или делиться на 13.
| 1 | Что такое правило делимости числа 13? |
| 2. | Правило делимости на 13 для больших чисел |
| 3. | Правило делимости на 13 и 14 |
| 4. | Тест на делимость 13 и 17 |
5. | Часто задаваемые вопросы о правиле делимости 13 |
Что такое правило делимости числа 13?
Правило делимости 13 на помогает нам определить, делится ли число на 13 без остатка. Делимость — это термин, используемый для проверки того, полностью ли число делится на другое число с 0 в остатке. Правила делимости в математике помогают нам легко узнать, делится ли число на другое число, не выполняя операции деления. Наиболее часто используемые правила делимости от 2 до 13.
Правило делимости на 13 с примерами
Существует 4 правила делимости, чтобы проверить, делится ли число на 13 или нет. Изучим эти 4 правила подробно на примерах.
Делимость на 13 Правило 1:
Сгруппируйте заданное число в наборы по 3, начиная справа, или в порядке единиц. Из самой правой группы из 3 цифр поочередно применить операции вычитания и сложения и найти результат. Если результат равен 0 или его можно полностью разделить на 13, не оставляя остатка, то число делится на 13.
Например, в числе 1 139 502, применяя попеременно операции вычитания и сложения из крайней правой группы из 3 цифр, мы получаем 502 — 139 + 1 = 364. 364/13 дает 28 в частном и 0 в остатке. Следовательно, 1139502 делится на 13.
Делимость на 13 Правило 2:
Умножьте цифру разряда единиц на 4 и прибавьте произведение с остатком числа слева от цифры разряда единиц. Если полученное число равно 0 или кратно 13, то число делится на 13.
Например, в числе 416 разряд единиц равен 6. Умножив разряд единиц на 4, мы получим (4 × 6), что равно 24. Прибавив 24 к остальным цифрам слева, мы получаем 41 + 24 = 65. Поскольку 65 кратно 13, 416 делится на 13.
Делимость на 13 Правило 3:
Возьмите две последние цифры числа и вычтите их из произведения 4 и остальной номер. Если полученное число равно 0 или кратно 13, то можно сказать, что число делится на 13. Например: В числе 520 последние две цифры равны 20. Произведение 4 на остаток числа (5 ) равно 5 × 4, что равно 20.
Вычитая их, мы получаем 20-20, что равно 0. Следовательно, 520 делится на 13. Этот метод деления на 13 можно легко применить и он очень эффективен для трехзначных чисел. .
Делимость на 13 Правило 4:
Умножьте цифру в разряде единиц на 9 и найдите разницу между полученным произведением и остальным числом слева от него. Если число равно 0 или кратно 13, то можно сказать, что данное число делится на 13.
Например, в числе 793, умножая последнюю цифру (3) на 9, получаем 3×9, что равно 27. Вычитая это из остального числа, равного 79, мы получаем 79 — 27, что равно 52. Поскольку 52 кратно 13, мы можем сказать, что 793 делится на 13.
Правило делимости на 13 для больших чисел
Делимость числа на 13 проста, если числа двузначные или если мы знакомы с первыми несколькими числами, кратными 13. Но что мы делаем, когда нам дают большее число и просят проверить его на делимость на 13? Как обсуждалось в разделе выше, существует 4 правила, чтобы определить, делится ли число на 13 или нет.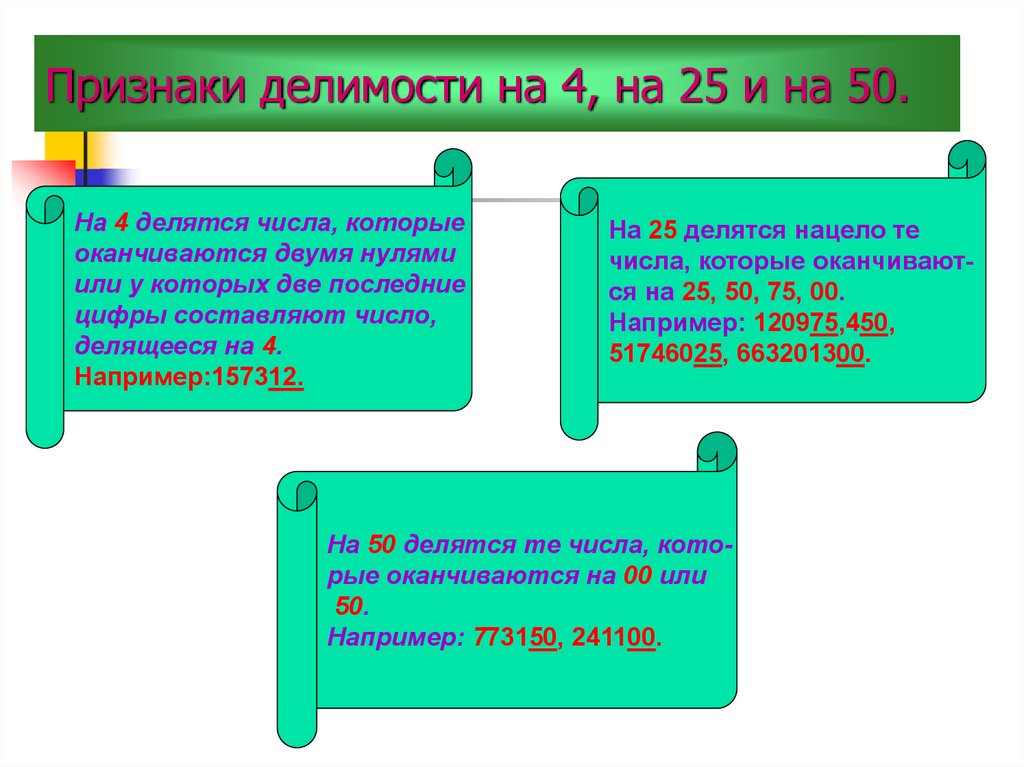
Теперь возьмем пятизначное число и применим одно из правил для проверки его делимости на 13.
Правило делимости на 13 и 14
Правила делимости 13 и 14 различны. По правилу делимости на 13 число считается делящимся на 13, если произведение 4 и последней цифры числа прибавляется к остальной части числа, что дает 0 или число, кратное 13. Правило делимости Закона о 14 гласит, что для того, чтобы число делилось на 14, оно должно делиться на 2 и 7. Возьмем пример и найдем, делится ли число на 13 и 14.
| Делимость на 13 для 156 | Делимость на 14 для 156 |
|---|---|
| Умножьте последнюю цифру на 4. 4 × 6 = 24. Прибавьте ее к остальным цифрам, что равно 15. Следовательно, 15 + 24 = 39. | Делится ли 156 на 2? Да, так как 156/2 = 0. Делится ли 156 на 7? Чтобы проверить это, умножьте последнюю цифру на 2. Получится (6 × 2 = 12). Вычтите его из оставшейся части числа (15). 15 -12 = 3, |
| Является ли число 39 кратным 13? Да. Следовательно, 156 делится на 13. | Является ли 3 кратным 7? Нет, следовательно, 156 не делится на 14. |
Тест на делимость 13 и 17
Поскольку 13 и 17 — два разных числа, их правила делимости также различны. Мы знаем, что есть четыре способа узнать, делится ли число на 13. Чтобы проверить, делится ли число на 17, мы умножаем цифру разряда единиц на 5 и находим разницу между произведением и остальной частью числа. количество. Если разность кратна 17 или 0, то данное число делится на 17. Проверим правила делимости 13 и 17 на числе 187.
| Делимость на 13 для 187 | Делимость на 17 для 187 |
|---|---|
Умножьте последнюю цифру на 4. 4 × 7 = 28. Прибавьте ее к остальной части числа, то есть 18. Следовательно, 18 + 28 = 46. | Умножьте последнюю цифру на 5,5 × 7 = 35. Найдите разницу между произведением и остальной частью числа, равной 18. Следовательно, 35 -18 = 17, |
| Является ли 46 кратным 13? Нет, следовательно, 187 не делится на 13. | Является ли 17 кратным 17? Да, следовательно, 187 делится на 17. |
☛ Похожие темы
- Правило делимости 3
- Правило делимости числа 4
- Правило делимости числа 5
- Правило делимости 6
- Правило делимости числа 7
- Правило делимости числа 8
- Правило делимости на 9
- Правило делимости 11
Часто задаваемые вопросы о правиле делимости на 13
Что такое правило делимости числа 13?
Правило делимости 13 — это набор правил для проверки, можно ли полностью разделить число на 13, не оставляя остатка. Есть 4 способа, которыми это можно сделать.
Они следующие.
- Правило 1: Сгруппируйте данное число в наборы по 3, начиная справа. Из самой правой группы из 3 цифр поочередно применить операции вычитания и сложения и найти результат. Если результат равен 0 или его можно полностью разделить на 13, не оставляя остатка, то число делится на 13.
- Правило 2: Умножьте цифру единиц на 4 и прибавьте произведение к оставшейся части числа слева от цифры разряда единиц. Если полученное число равно 0 или кратно 13, то число делится на 13.
- Правило 3: Возьмите две последние цифры числа и вычтите их из произведения 4 и остального числа. Если полученное число равно 0 или кратно 13, то можно сказать, что число делится на 13.
- Правило 4: Умножьте число в разряде единиц на 9 и найдите разницу между полученным произведением и остальным числом слева от него. Если число равно 0 или кратно 13, то можно сказать, что данное число делится на 13.
Что такое правило делимости чисел 13 и 17?
Правила делимости чисел 13 и 17 следующие:
- Чтобы число делилось на 13, мы умножаем цифру, стоящую в разряде единиц, на 4 и прибавляем произведение к оставшейся части числа слева от него. Если сумма кратна 13, то можно сказать, что данное число делится на 13.
- Чтобы число делилось на 17, мы умножаем цифру разряда единиц на 5 и вычитаем произведение с остатком числа слева от него. Если полученная разность равна 0 или кратна 17, то данное число делится на 17,
Используя правило делимости на 13, проверьте, делится ли 2197 на 13.
Давайте воспользуемся следующим правилом, чтобы проверить, делится ли число 2197 на 13. Умножьте разряд единицы числа на 4 и прибавьте произведение к остальная часть числа слева от него. Если сумма кратна 13, то мы можем сказать, что данное число делится на 13. Последняя цифра при умножении на 4 дает 4 × 7 = 28. Добавьте 28 к остальной части числа, что равно 219.
, 219 + 28 = 247. Мы не знаем, кратно ли 247 13 или нет. Итак, мы повторяем процесс снова. Умножив последнюю цифру 7 на 4, мы получим 4 × 7 = 28. Теперь прибавьте 28 к оставшейся части числа, равному 24, 24 + 28 = 52. 52 — четвертое число, кратное 13. Следовательно, 2197 делится на 13.
Как узнать, делится ли большое число на 13?
Чтобы узнать, делится ли большое число на 13, воспользуемся одним из правил. Есть четыре правила, чтобы определить, делится ли число на 13. Давайте применим первое правило, которое гласит, что «Сгруппируйте данное число в наборы по 3, начиная справа или с разряда единиц. Из самой правой группы из 3 цифр поочередно примените операции вычитания и сложения и найдите результат. Если результат равен 0 или может быть разделить на 13 полностью, не оставляя остатка, то число делится на 13». Например, в числе 2 232 516, попеременно применяя сложение и операции вычитания из крайней правой группы из 3 цифр, мы получаем 516 — 232 + 2 = 286.