Проекции онлайн: Онлайн калькулятор. Проекция вектора на вектор

Вычислить проекции вектора на оси координат. Калькулятор онлайн.Вычисление проекции вектора на вектор

Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:

Пр a b = |b|cos(a,b) или

Где a b — скалярное произведение векторов , |a| — модуль вектора a .

Инструкция . Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b . При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .

Заданы :
две координаты вектора
три координаты вектора
a: ; ;
b: ; ;

Классификация проекций вектора

Виды проекций по определению проекция вектора

Виды проекций по системе координат

Свойства проекции вектора

1. Геометрическая проекция вектора есть вектор (имеет направление).
2. Алгебраическая проекция вектора есть число.

Теоремы о проекциях вектора

Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.

Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:

Пр a b = |b|cos(a,b)

Виды проекций вектора

1. проекция на ось OX.
2. проекция на ось OY.
3. проекция на вектор.

Проекция на ось OX	Проекция на ось OY	Проекция на вектор
Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак.	Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак.	Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак.
Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.	Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак.	Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак.
Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB.	Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB.	Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB.
Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор).	Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор).	Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор).

1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).

Пример 1 . Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .

Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.

Пример 2 . Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.

Действительно, длина вектора равна 2, а направление противоположно направлению оси.

Проектирование различных линий и поверхностей на плоскость позволяет построить наглядное изображение предметов в виде чертежа. Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.

Рис. 3.22. Векторная проекция вектора на плоскость.

Рис. 3.23. Векторная проекция вектора на ось.

В векторной алгебре часто приходится проектировать вектор на ОСЬ, то есть на прямую, имеющую определенную ориентацию. Такое проектирование выполняется легко, если вектор и ось L лежат в одной плоскости (рис. 3.23). Однако задача усложняется, когда это условие не выполнено. Построим проекцию вектора на ось, когда вектор и ось не лежат в одной плоскости (рис. 3.24).

Рис. 3.24. Проектирование вектора на ось
в общем случае.

Через концы вектора проводим плоскости, перпендикулярные прямой L. В пересечении с этой прямой данные плоскости определяют две точки А1 и B1 — вектор , который будем называть векторной проекцией данного вектора. Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.

Наряду с векторной проекцией, существует и СКАЛЯРНАЯ ПРОЕКЦИЯ, которая равна модулю векторной проекции, если векторная проекция совпадает с ориентацией оси L, и равна величине, ей противоположной, если векторная проекция и ось L имеют противоположную ориентацию. Скалярную проекцию будем обозначать:

Векторная и скалярная проекции не всегда терминологически разделяются строго на практике. Обычно пользуются термином «проекция вектора», подразумевая под этим скалярную проекцию вектора. При решении же необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» — в соответствии с установленным смыслом.

Докажем теорему, позволяющую вычислять скалярную проекцию заданного вектора.

ТЕОРЕМА 5. Проекция вектора на ось L равна произведению его модуля на косинус угла между вектором и осью, то есть

(3.5)

Рис. 3.25. Нахождение векторной и скалярной
Проекций вектора на ось L
( и ось L одинаково ориентированы).

ДОКАЗАТЕЛЬСТВО . Выполним предварительно построения, позволяющие найти угол G Между вектором и осью L. Для этого построим прямую MN, параллельную оси L и проходящую через точку О — начало вектора (рис. 3.25). Угол и будет искомым углом. Проведем через точки А и О две плоскости, перпендикулярные оси L. Получим:

Так как ось L и прямая MN параллельны.

Выделим два случая взаимного расположения вектора и оси L.

1. Пусть векторная проекция и ось L одинаково ориентированны (рис. 3.25). Тогда соответствующая скалярная проекция .

2. Пусть и L ориентированы в разные стороны (рис. 3.26).

Рис. 3.26. Нахождение векторной и скалярной проекций вектора на ось L ( и ось L ориентированы в противоположные стороны).

Таким образом, в обоих случаях справедливо утверждение теоремы.

ТЕОРЕМА 6. Если начало вектора приведено к некоторой точке оси L, и эта ось расположена в плоскости s, вектор образует с векторной проекцией на плоскость s угол , а с векторной проекцией на ось L — угол , кроме того сами векторные проекции образуют между собой угол , то

а на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.

Предварительные сведения

Основное понятие – непосредственно понятие вектора.

Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем еще несколько понятий, связанных с понятием вектора.

Определение 3

Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).

Определение 4

Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:

1. Эти векторы коллинеарны.
2. Если они будут направлены в одну сторону (рис. 3).

Обозначение: $\overline{a}\overline{b}$

Определение 5

Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:

1. Эти векторы коллинеарны.
2. Если они направлены в разные стороны (рис. 4).

Обозначение: $\overline{a}↓\overline{d}$

Определение 6

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Перейдем к определению равенства двух векторов

Определение 7

Два вектора будем называть равными, если они удовлетворяют двух условиям:

1. Они сонаправлены;
2. Их длины равны (рис. 5).

Геометрическая проекция

Как мы уже сказали ранее, результатом геометрической проекции будет вектор.

Определение 8

Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A»$ — начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B»$ — конец искомого вектора. Вектор $\overline{A»B»}$ и будет искомым вектором.

Рассмотрим задачу:

Пример 1

Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.

Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A»$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B»$ (рис. 7).

Пусть в пространстве даны два вектора и . Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается .

Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице).

Под углом между вектором и осью l понимают угол между векторами и .

Итак, пусть l – некоторая ось и – вектор.

Обозначим через A 1 и B 1 проекции на ось l соответственно точек A и B . Предположим, что A 1 имеет координату x 1 , а B 1 – координату x 2 на оси l .

Тогда проекцией вектора на ось l называется разность x 1 – x 2 между координатами проекций конца и начала вектора на эту ось.

Проекцию вектора на ось l будем обозначать .

Ясно, что если угол между вектором и осью l острый, то x 2 > x 1 , и проекция x 2 – x 1 > 0; если этот угол тупой, то x 2 x 1 и проекция x 2 – x 1 l , то x 2 = x 1 и x 2 – x 1 =0.

Таким образом, проекция вектора на ось l – это длина отрезка A 1 B 1 , взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.

Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.

Рассмотрим некоторые основные свойства проекций .

ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ

Рассмотрим несколько векторов .

Линейной комбинацией данных векторов называется любой вектор вида , где — некоторые числа. Числа называются коэффициентами линейной комбинации. Говорят также, что в этом случае линейно выражается через данные векторы , т.е. получается из них с помощью линейных действий.

Например, если даны три вектора то в качестве их линейной комбинации можно рассматривать векторы:

Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.

Векторы называются линейно зависимыми , если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.

В противном случае, т.е. когда соотношение выполняется только при , эти векторы называются линейно независимыми .

Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Доказательство :

Аналогично можно доказать следующую теорему.

Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Доказательство .

БАЗИС

Базисом называется совокупность отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать .

В предыдущем пункте мы видели, что два неколлинеарных вектора на плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой плоскости.

Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.

Справедливо следующее утверждение.

Теорема. Пусть в пространстве задан базис . Тогда любой вектор можно представить в виде линейной комбинации , где x , y , z – некоторые числа. Такое разложение единственно.

Доказательство .

Таким образом, базис позволяет однозначно сопоставить каждому вектору тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой тройке чисел x, y, z при помощи базиса можно сопоставить вектор, если составить линейную комбинацию .

Если базис и , то числа x, y, z называются координатами вектора в данном базисе. Координаты вектора обозначают .

ДЕКАРТОВА СИСТЕМА КООРДИНАТ

Пусть в пространстве задана точка O и три некомпланарных вектора .

Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т.е. совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.

Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.

Рассмотрим в выбранной системе координат произвольную точку M . Введём понятие координаты точки M . Вектор , соединяющий начало координат с точкой M . называется радиус-вектором точки M .

Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: .

Координаты радиус-вектора точки M . называются координатами точки M . в рассматриваемой системе координат. M(x,y,z) . Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой.

Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату.

Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат.

Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной.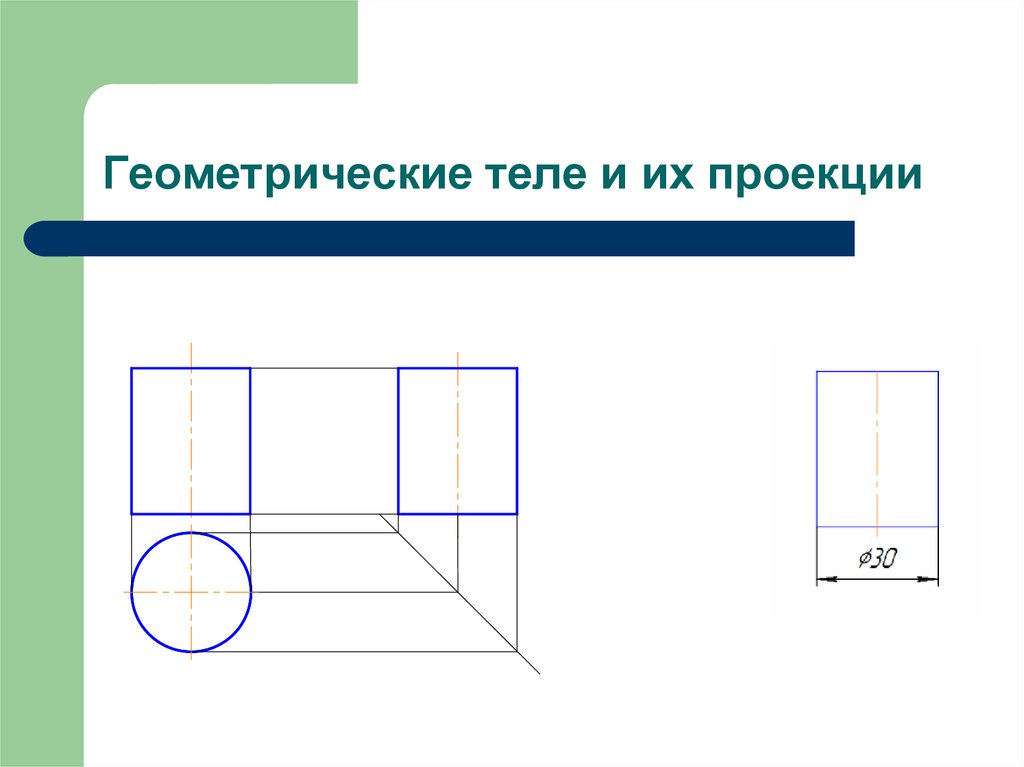

Несложно показать, что .

Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.

Введение…………………………………………………………………………3

1. Значение вектора и скаляра………………………………………….4

2. Определение проекции, оси и координатой точки…………………5

3. Проекция вектора на ось………………………………………………6

4. Основная формула векторной алгебры……………………………..8

5. Вычисление модуля вектора по его проекциям……………………9

Заключение………………………………………………………………………11

Литература………………………………………………………………………12

Введение:

Физика неразрывно связана с математикой. Математика дает физике средства и приемы общего и точного выражения зависимости между физическими величинами, которые открываются в результате эксперимента или теоретических исследований.Ведь основной метод исследований в физике – экспериментальный. Это значит – вычисления ученый выявляет с помощью измерений. Обозначает связь между различными физическими величинами. Затем, все переводится на язык математики. Формируется математическая модель. Физика — есть наука, изучающая простейшие и вместе с тем наиболее общие закономерности. Задача физики состоит в том, чтобы создать в нашем сознании такую картину физического мира, которая наиболее полно отражает свойства его и обеспечивает такие соотношения между элементами модели, какие существуют между элементами.

Итак, физика создает модель окружающего нас мира и изучает ее свойства. Но любая модель является ограниченной. При создании моделей того или иного явления принимаются во внимание только существенные для данного круга явлений свойства и связи. В этом и заключается искусство ученого — из всего многообразия выбрать главное.

Физические модели являются математическими, но не математика является их основой. Количественные соотношения между физическими величинами выясняются в результате измерений, наблюдений и экспериментальных исследований и лишь выражаются на языке математики.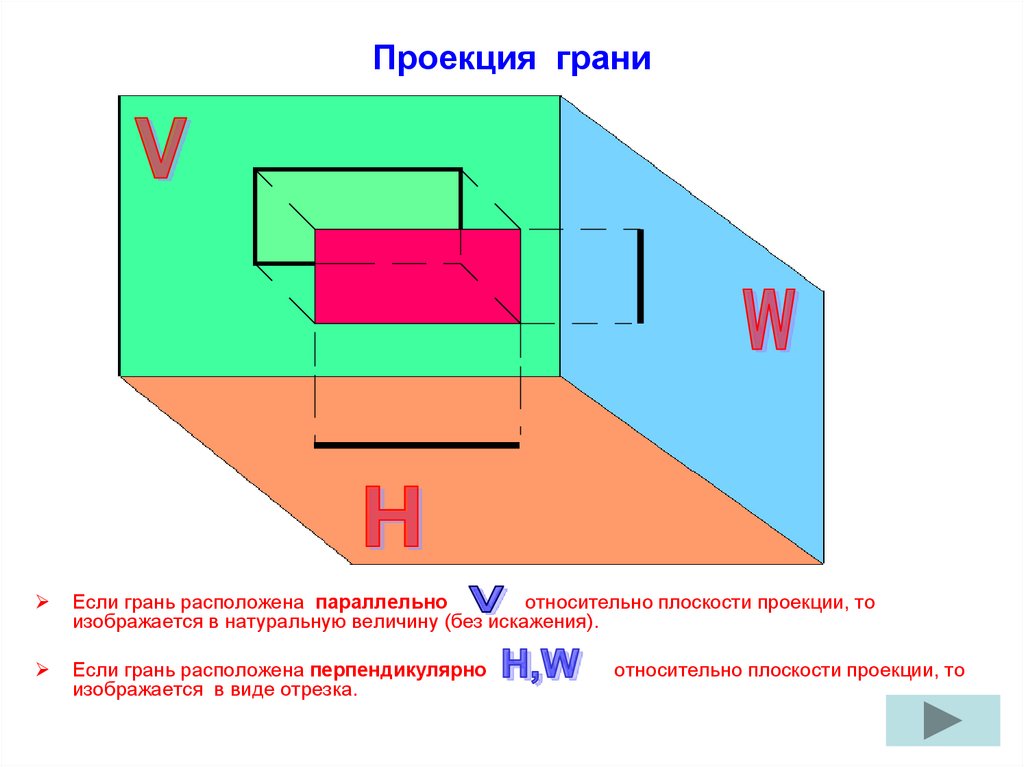 Однако другого языка для построения физических теорий не существует.

1. Значение вектора и скаляра.

В физике и математике вектор — это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они «скалярами» .

Они записываются либо буквами обычного шрифта, либо цифрами (а, б, t, G, 5, −7….). Скалярные величины могут быть положительными и отрицательными. В то же время некоторые объекты изучения могут обладать такими свойствами, для полного описания которых знание только числовой меры оказывается недостаточным, необходимо ещё охарактеризовать эти свойства направлением в пространстве. Такие свойства характеризуются векторными величинами (векторами). Векторы, в отличие от скаляров, обозначаются буквами жирного шрифта: a, b, g, F, С ….
Нередко вектор обозначают буквой обычного (нежирного) шрифта, но со стрелкой над ней:

Кроме того, часто вектор обозначают парой букв (обычно заглавных), причём первая буква обозначает начало вектора, а вторая — его конец.

Модуль вектора, то есть длину направленного прямолинейного отрезка, обозначают теми же буквами, как и сам вектор, но в обычном (не жирном) написании и без стрелки над ними, либо точно также как и вектор (то есть жирным шрифтом или обычным, но со стрелкой), но тогда обозначение вектора заключается в вертикальные черточки.
Вектор – сложный объект, который одновременно характеризуется и величиной и направлением.

Не бывает также положительных и отрицательных векторов. А вот равными между собой векторы быть могут. Это когда, например, aиb имеют одинаковые модули и направлены в одну сторону. В этом случае справедлива запись a = b. Надо также иметь в виду, что перед символом вектора может стоять знак минус, например, — с, однако, этот знак символически указывает на то, что вектор -с имеет такой же модуль, как и вектор с, но направлен в противоположную сторону.

Вектор -с называют противоположным (или обратным) вектору с.
В физике же каждый вектор наполнен конкретным содержанием и при сравнении однотипных векторов (например, сил) могут иметь существенное значение и точки их приложения.

2.Определение проекции, оси и координатой точки.

Ось – это прямая, которой придается какое–то направление.
Ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, которая называется началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до других интересующих нас точек.

Проекцией точки на ось называется основание перпендикуляра, опущенного из этой точки на данную ось. То есть, проекцией точки на ось является точка.

Координатой точки на данной оси называется число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении.

3.Проекция вектора на ось.

Проекцией вектора на ось называется вектор, который получается в результате перемножения скалярной проекции вектора на эту ось и единичного вектора этой оси. Например, если а x – скалярная проекция вектора а на ось X, то а x ·i — его векторная проекция на эту ось.

Обозначим векторную проекцию также, как и сам вектор, но с индексом той оси на которую вектор проектируется. Так, векторную проекцию вектора а на ось Х обозначим а x (жирная буква, обозначающая вектор и нижний индекс названия оси) или

(нежирная буква, обозначающая вектор, но со стрелкой наверху (!) и нижний индекс названия оси).

Скалярной проекцией вектора на ось называется число , абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Обычно вместо выражения скалярная проекция говорят просто – проекция . Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектора, то его проекция обозначается а x . При проектировании этого же вектора на другую ось, если ось Y , его проекция будет обозначаться а y .

Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть

а x = х к − x н.

Проекция вектора на ось — это число. Причем, проекция может быть положительной, если величина х к больше величины х н,

отрицательной, если величина х к меньше величины х н

и равной нулю, если х к равно х н.

Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.

Из рисунка видно, что а x = а Cos α

То есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора . Если угол острый, то
Cos α > 0 и а x > 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.

Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу — отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против.

Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.

4. Основная формула векторной алгебры.

Спроектируемвектор а на оси Х и Y прямоугольной системы координат. Найдем векторные проекции вектора а на эти оси:

а x = а x ·i, а y = а y ·j.

Но в соответствии справилом сложения векторов

а = а x + а y .

а = а x ·i + а y ·j.

Таким образом, мы выразили вектор через его проекции и орты прямоугольной системы координат (или через его векторные проекции).

Векторные проекции а x и а y называютсясоставляющими или компонентами вектора а. Операция, которую мы выполнили, называется разложением вектора по осямпрямоугольной системы координат.

Если вектор задан в пространстве, то

а = а x ·i + а y ·j + а z ·k.

Эта формула называется основной формулой векторной алгебры. Конечно, ее можно записать и так.

Проекция точки на плоскость онлайн

Полином Чебышева с свободным членом Создать вектор(диофант) по матрице Египетские дроби. Часть вторая Египетские (аликвотные) дроби По сегменту определить радиус окружности Круг и площадь, отсекаемая перпендикулярами Деление треугольника на равные площади параллельными Определение основных параметров целого числа Свойства обратных тригонометрических функций Разделить шар на равные объемы параллельными плоскостями Взаимосвязь между организмами с различными типами обмена веществ Аутотрофные и миксотрофные организмы Рассечение круга прямыми на равные площади Период нечетной дроби онлайн. Первые полторы тысяч разложений. Представить дробь, как сумму её множителей Решение системы из двух однородных диофантовых уравнений Расчет основных параметров четырехполюсника Цепочка остатков от деления в кольце целого числа Система счисления на базе ряда Фибоначчи онлайн Уравнение пятой степени. Частное решение. Рассчитать площадь треугольника по трем сторонам онлайн Общее решение линейного диофантового неоднородного уравнения Частное решение диофантового уравнения с несколькими неизвестными Онлайн разложение дробно рациональной функции Корни характеристического уравнения

Коэффициенты плоскости Координаты точки разделенные хотя бы одним пробелом Координаты проекции точки В данном материале  мы рассмотрим решение задачи нахождения координат  проекции точки на какую либо плоскость  в пространстве.     Теории практически не будет и думаю для тех кто интересуется могут понять это все из ниже разобранного примера   Найти проекцию точки M(1,-3,2) на плоскость 2x+5y-3z-19=0   Проекция точки М на данную поверхность — есть точка пересечения с данной плоскостью прямой, проходящей через точку М перпендикулярно к данной плоскости. Уравнение прямой, проходящей через точку M(1,-3,2) перпедикулярно к плоскости 2x+5y-3z-19=0 имеет вид   или в виде системы   Добавив сюда исходное уравнение плоскости получим полноценную систему линейных уравнений которая легко решается     В данном примере проекция точки имеет координаты (3,2,-1)   Удачных расчетов!!   Проекция точки на прямую >> Поиск по сайту

Русский и английский алфавит в одну строку Часовая и минутная стрелка онлайн. Угол между ними. Массовая доля химического вещества онлайн Декoдировать текст \u0xxx онлайн Универсальный калькулятор комплексных чисел онлайн Перемешать буквы в тексте онлайн Частотный анализ текста онлайн Поворот точек на произвольный угол онлайн Обратный и дополнительный код числа онлайн Площадь многоугольника по координатам онлайн Остаток числа в степени по модулю Расчет пропорций и соотношений Как перевести градусы в минуты и секунды Расчет процентов онлайн Поиск объекта по географическим координатам Растворимость металлов в различных жидкостях DameWare Mini Control. Настройка. Время восхода и захода Солнца и Луны для местности Калькулятор географических координат Расчет значения функции Эйлера Перевод числа в код Грея и обратно Теория графов. Матрица смежности онлайн Произвольный треугольник по заданным параметрам НОД двух многочленов. Greatest Common Factor (GCF) Географические координаты любых городов мира Площадь пересечения окружностей на плоскости Онлайн определение эквивалентного сопротивления Непрерывные, цепные дроби онлайн Сообщество животных. Кто как называется? Проекция точки на плоскость онлайн Калькулятор онлайн расчета количества рабочих дней Из показательной в алгебраическую. Подробно Расчет заряда и разряда конденсатора через сопротивление Система комплексных линейных уравнений Расчет понижающего конденсатора Построить ненаправленный граф по матрице Месторождения золота и его спутники Определение формулы касательной к окружности Дата выхода на работу из отпуска, декрета онлайн Каноническое уравнение гиперболы по двум точкам Онлайн расчеты Подписаться письмом

Мастер проекций

Формат угловых единиц

44° 30′ 15» з. д. –44,754305°

 Вывод

Значение вокруг центрального меридиана

Географические координаты: WGS84ETRS89NAD83

Линейные единицы: метр междунар. Нога

 Предварительный просмотр карты 

Показать географическую протяженность

Показать исходную точку проекции

Об этом инструменте

Мастер проекций — это веб-приложение, которое помогает картографам выбирать подходящую проекцию для своей карты. В зависимости от экстента и свойства искажения карты приложение возвращает список предлагаемых картографических проекций с дополнительными параметрами проекций, если это необходимо. Рядом с каждой проекцией есть ссылки PROJ и WKT, которые открывают всплывающее окно со строкой PROJ или общеизвестного текста, доступной для копирования в буфер обмена. Обе строки используются во многих картографических и ГИС-приложениях. Мастер проекций отображает предварительный просмотр карты в правой части списка с предлагаемой проекцией. Предварительный просмотр показывает, как будут выглядеть спроецированные данные с использованием D3.

Этот инструмент основан на руководстве по выбору Джона П. Снайдера и дополнении к этому руководству для карт мира и полушария, написанном Группой картографии и геовизуализации Университета штата Орегон. Projection Wizard v2.0 также учитывает результаты исследования, опубликованного Šavrič и др. . в 2015 г. Все публикации, относящиеся к Projection Wizard , перечислены внизу этой страницы.

Когда вы публикуете научную статью, в которой используется Projection Wizard или обсуждаете его функциональные возможности, просьба ссылаться на следующую статью: Шаврич Б., Дженни Б. и Дженни Х. (2016). Мастер проекций — онлайн-инструмент выбора картографической проекции. Картографический журнал, 53–2, с. 177–185. Дой: 10.1080/00087041.2015.1131938.

Как использовать этот инструмент?

Использование Мастер проецирования очень просто и требует всего два шага:

1 В списке переключателей выберите свойство искажения карты.

2 Выберите географический экстент, используя поля ввода в левой части карты или изменив прямоугольник на карте.

Якоря в углах прямоугольника позволяют изменять его размер. Прямоугольник также можно перетаскивать по карте. Любое изменение прямоугольника отражается в полях ввода и наоборот. Изменения свойств прямоугольника или искажения интерактивно обновляют список предлагаемых картографических проекций и предварительный просмотр карты под веб-картой.

a Кнопка Выбрать текущую видимую область регулирует размер прямоугольника в соответствии с текущим видом карты, выбирая примерно 80% видимой карты.

b Кнопка Выбрать весь мир устанавливает размер прямоугольника в полный экстент.

c Кнопка Показать весь мир полностью уменьшает масштаб.

d Кнопка Настроить открывает диалоговое окно Параметры мастера проекции , которое позволяет пользователю изменять инструмент.

Настройка этого инструмента

Диалоговое окно «Параметры мастера проекции» позволяет изменить инструмент в соответствии с вашими потребностями. Параметры влияют на параметры проекции, элементы в строках PROJ и WKT и предварительный просмотр карты. Вы можете:

A переключаться между десятичными градусами и форматами DMS для угловых единиц,

B округлять значение центрального меридиана до ближайшего градуса,

C выбирать систему географических координат для выходных строк,

D выберите между метрами и международными футами для линейных единиц в строках и

E отобразите выбранный экстент и/или начальную точку (точки) проекции в предварительном просмотре карты.

Критерии выбора, полученные на основе географического охвата

Протяженность географического района:
Карта мира — показывает не менее двух третей полного экстента
Карта, показывающая полушарие — показывает от одной шестой до двух третей полного размера
Карта, показывающая континент или меньшие области – показывает менее одной шестой полной протяженности

Преобладающая протяженность и ориентация области, показанной на карте:
Протяженность с востока на запад, в результате чего получается ландшафтно-ориентированная карта – отношение между центральным меридианом и самыми длинными параллельными длинами меньше 0,8
Протяженность с севера на юг, в результате чего получается портретно-ориентированная карта – отношение между центральным меридианом и самыми длинными параллельными длинами более 1,25
Равный экстент, в результате чего получается карта квадратной формы – другие значения отношения

Широта картируемой области карты квадратной формы:
Центр на полюсе – центральная широта более 75º северной широты или 75º южной широты
Центр вдоль экватора – центральная широта между 15º северной широты и 15º южной широты
Центр вдали от полюса или экватора – все остальные значения центральной широты

Широта закартированной области ландшафтно-ориентированной карты:
Центр на полюсе – центральная широта больше 70º северной или 70º южной широты, или географическая область в конической проекции в противном случае обнажит отверстие на полюсе.
Центр вдоль экватора – центральная широта находится между 15º северной широты и 15º южной широты, или географическая область находится в пределах 23,43665º северной широты и 23,43665º южной широты для карт, изображающих полушарие.
Центр вдали от полюса или экватора – все остальные значения центральной широты

Дополнительные примечания и советы

Для карт мира:

• Конформные проекции бесполезны для карт мира, потому что они искажают формы континентов таким образом, что читатели карт не привыкли видеть.
• Прямоугольные проекции обычно не рекомендуются для большинства карт мира. Однако есть некоторые редкие явления, основанные на долготе, которые лучше всего представлены на карте с прямыми меридианами, например, на карте, показывающей часовые пояса мира.
• Мелкомасштабные карты мира обычно изображают мир на непрерывном пространстве без перерывов. Когда картографы наносят на карту только явления суши или только явления океана, возможен выбор прерывистой проекции. Прерывание может быть применено к большинству равновеликих и скомпрометированных проекций карты мира. В зависимости от назначения карты (т. е. показывает ли она сушу или океан) расположение пересечений и центральных меридианов корректируется.

Для карт, изображающих полушарие:

• Конформные проекции бесполезны для карт полушария, поскольку они сильно искажают форму и площадь вдоль границы проецируемого полушария. Сохранение углов редко требуется для карт полушарий.

Для карт, показывающих континент или меньшие области:

• Компромиссные проекции бесполезны для карт, показывающих континент или меньшую область.
• Чтобы уменьшить общее искажение площади для конформных проекций, можно также применить масштабный коэффициент k . Применяются различные значения для k и сравниваются шаблоны искажения области вдоль центра и на границе карты.
• Чтобы уменьшить общее искажение для равновеликих проекций (не для азимутальных проекций), можно также сжать карту в направлении север-юг (с коэффициентом s ) и расширить карту в направлении восток-запад ( с коэффициентом 1/ с ). Коэффициент s можно определить методом проб и ошибок, сравнивая образцы искажений вдоль центра и на границе карты.
• В некоторых редких случаях полезно сохранить масштаб вдоль больших кругов на региональных и крупномасштабных картах. Читатели карт могут делать точные измерения вдоль этих линий с сохранением масштаба. Важно помнить, что ни одна проекция не может правильно отображать все расстояния и что эти «равноудаленные» проекции правильно сохраняют только некоторые расстояния.
• При составлении карты определенной страны или штата картограф также может использовать официальную проекцию штата. Часто эта проекция не только минимизирует искажения картографируемой области, но и может упростить работу картографа. Большинство базовых данных штата доступны вместе с официальным прогнозом. Большинство стран используют конформную проекцию для своих официальных крупномасштабных карт, которая предпочтительнее для геодезии, навигации и военного использования. Официальные прогнозы по интересующим областям можно искать в Реестре геодезических параметров EPSG.

Журнал обновлений

Мастер проекций 2.0 (июнь 2020 г.)

• Границы географической области определяются на основе уравнений сферической поверхности.
• Преобладающая протяженность вычисляется как отношение между центральным меридианом и самыми длинными параллельными длинами на сфере.
• Обновлены критерии широты отображаемой области ландшафтно-ориентированной карты.
• Проекция для показа тропиков 9Добавлена ​​категория 0025 для карт полушария, когда географическая область находится в пределах 23,43665º северной широты и 23,43665º южной широты.
• Дополнительные предложения были добавлены в список подходящих картографических проекций для конформного свойства в очень больших масштабах карты.
• Проекция Кассини добавлена ​​в список подходящих картографических проекций для эквидистантного свойства и портретно-ориентированных карт.
• Проекция Plate Carrée была заменена эквидистантной цилиндрической для ландшафтно-ориентированной карты и географической области вдоль экватора.
• В список равновеликих картографических проекций мира добавлена ​​равновеликая проекция Земли.
• Проекции, которые чрезмерно выпирают наружу и прерывают проекции, удалены из мировых списков.
• Список равноудаленных проекций мира теперь отображается в виде выпадающего меню. Для каждой проекции в меню рядом с параметрами были добавлены ползунки (и переключатели), так что теперь пользователь может настраивать произвольные точки.
• Обновления карты предварительного просмотра были добавлены, когда пользователь наводит курсор на имя проекции в мировых списках.
• Карта предварительного просмотра теперь обрезается точно по географической области, выбранной пользователем.
• Параметры проекции для мировой проекции теперь округляются до целых градусов, до половины градуса и до десятых долей градуса в зависимости от размера выбранной географической области.
• Параметры проекции для карт, отображающих полушарие и тропики, теперь округляются до двух знаков после запятой.
Строковые значения
• PROJ были округлены максимум до семи знаков после запятой, а к строке были добавлены данные об датуме или эллипсоиде и линейные единицы измерения.
Для каждой предлагаемой проекции предусмотрено
• строки WKT.
• Добавлена ​​кнопка Настроить , которая открывает диалоговое окно Параметры мастера проекции . Теперь пользователи могут переключаться между десятичными градусами и форматами DMS для угловых единиц, округлять значение центрального меридиана до ближайшего градуса, указывать тип географических координат для своих выходных строк, выбирать между метрами и международными футами для линейных единиц, а также отображать географическую протяженность и точки начала проекции в предварительном просмотре карты.
• Во время перетаскивания отдельных вершин или всего прямоугольника были добавлены непрерывные обновления выходных данных, карты предварительного просмотра и входных данных экстента.
• Пользовательский интерфейс, всплывающие окна, карты предварительного просмотра, сторонние библиотеки и содержимое справки были обновлены.

Это обновление было подготовлено в сотрудничестве с @jwasilgeo и @jgravois.

Мастер проекций 1.2 (май 2017 г.)

• Код PROJ исправлен для азимутальной проекции Ламберта.
• Содержание справки обновлено.

Мастер проецирования 1.1.1 (февраль 2016 г.)

• Содержание справки обновлено.
• Добавлен список публикаций и связанных статей о Projection Wizard.

Мастер проекций 1.1 (декабрь 2015 г.)

• Проекция Паттерсона добавлена ​​в список скомпрометированных картографических проекций.
• Содержание справки обновлено.

Мастер проекций 1.0 (октябрь 2014 г.)

• Предварительный просмотр карты добавлен в список соответствующих проекций карты.
• Критерии выбора для карты полушария обновлены на одну шестую полного географического экстента.
• Обновлены критерии широты отображаемой области ландшафтно-ориентированной карты. Карта имеет центр на полюсе, когда центральная широта превышает 70º северной широты или 70º южной широты, или более 67,5º северной широты или 67,5º южной широты для отображения между одной шестой и одной восьмой полной географической протяженности.

Инструмент выбора картографической проекции (июнь 2013 г.)

• Исходное веб-приложение

Публикации и сопутствующие статьи

Дженни Б., Шаврич Б., Арнольд Н. Д., Марстон Б. Э. и Преппернау К. А. (2017). Руководство по выбору картографических проекций для карт мира и полушария. В: М. Лапейн и Э. Л. Усери (редакторы), Выбор картографической проекции, Конспекты лекций по геоинформации и картографии (стр. 213–228). Берлин, Гейдельберг, Нью-Йорк: Springer. Дои: 10.1007/978-3-319-51835-0_9

Шаврич Б., Дженни Б. и Дженни Х. (2016). Мастер проекций — онлайн-инструмент выбора картографической проекции. Картографический журнал, 53–2, с. 177–185. Doi: 10.1080/00087041.2015.1131938

Шаврич, Б.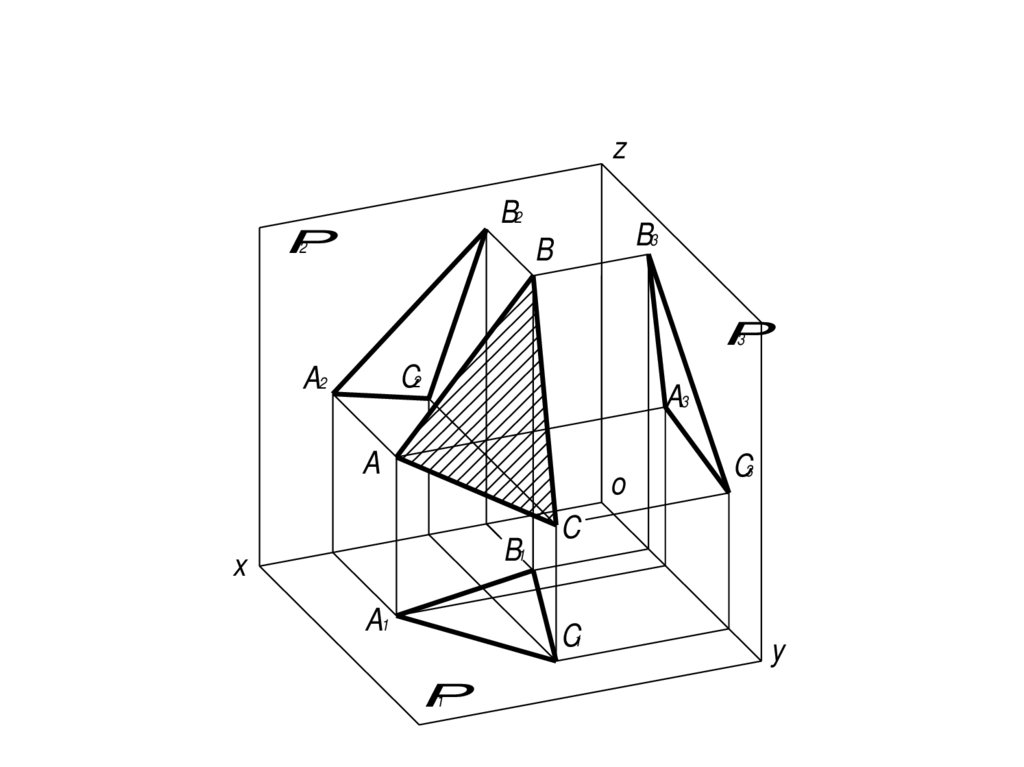 (2016). Мастер проекций: бесплатное веб-приложение для выбора картографической проекции. Информационный бюллетень ISPRS SC, 9–4. п. 5. Доступно в Интернете: http://www.isprs-sc.org/material/isprs_sc_vol9_no4.pdf

Шаврич Б., Дженни Б., Уайт Д. и Стребе Д. Р. (2015). Пользовательские настройки проекций карты мира. Картография и географическая информатика, 42–5, с. 398–409. Doi: 10.1080/15230406.2015.1014425

Шаврич Б., Дженни Б. и Дженни Х. (2014). Инструмент выбора проекции карты. Презентация на 34-м ежегодном собрании NACIS 2014, Питтсбург, Пенсильвания, 8–11 октября.

Снайдер, Дж. П. (1987). Картографические проекции – рабочее руководство. Professional Paper 1395. Вашингтон, округ Колумбия: Геологическая служба США. Doi: 10.3133/pp1395

Опубликовано GIS Lounge и Maps Mania.

Шаблон финансовых прогнозов | Выберите из 70+ подготовленных CPA финансовых шаблонов Excel на ProjectionHub

Выбор шаблона финансового прогноза

Команда ProjectionHub разработала более 80 шаблонов финансовых прогнозов, чтобы дать вам преимущество при создании собственного проекта финансового моделирования.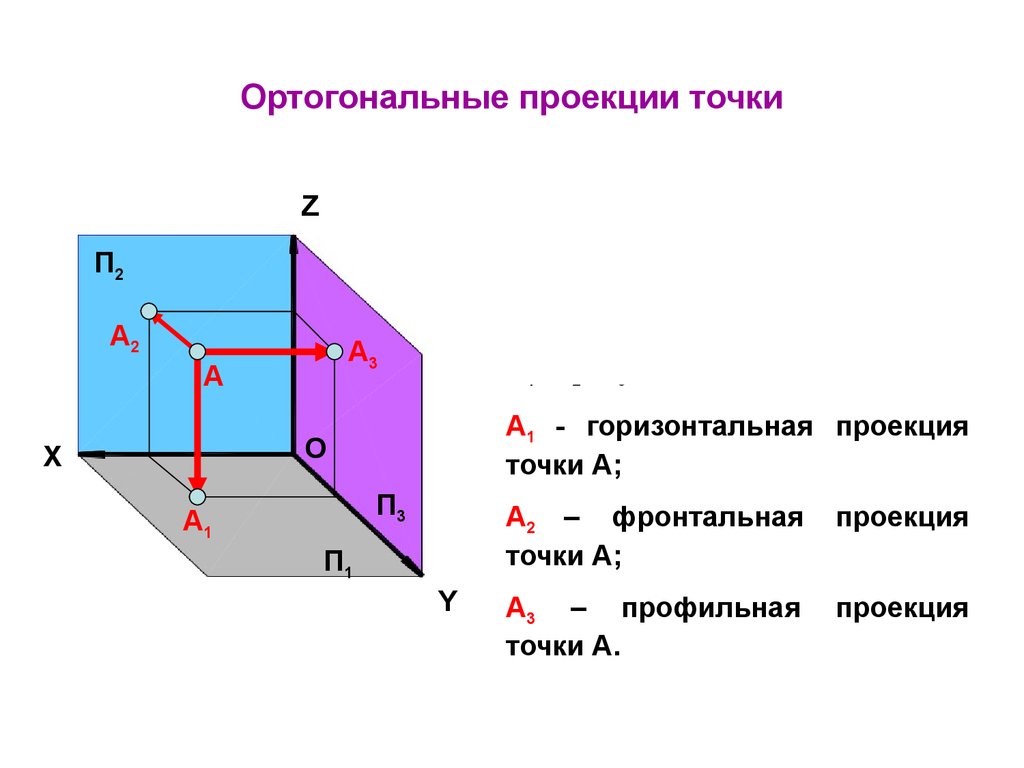

Шаблоны бизнес-прогнозов основаны на Excel, и каждый из них содержит отчет о прибылях и убытках за 5 лет, балансовый отчет и прогноз движения денежных средств, а также ряд графиков и таблиц для визуализации ваших прогнозов.

Если вы купите шаблон, наша команда готова ответить на любые ваши вопросы. Ознакомьтесь с нашей библиотекой шаблонов ниже. Нужна помощь в выборе шаблона? Получите рекомендацию от нашей команды!

Вы консультант или советник, который часто работает над прогнозами для ваших клиентов? Оформите подписку на ProjectionHub+, чтобы получить всеохватывающий, экономящий время центр решений.

Сколько лет финансовых прогнозов я могу создать с помощью шаблона ProjectionHub?

Все наши шаблоны финансовых прогнозов представляют собой финансовые модели на 5 лет. Если вам нужен только финансовый прогноз на 3 года, вы можете просто скрыть последние два года модели. Шаблоны предоставят вам годовые и ежемесячные прогнозы на срок до 60 месяцев.

Как составить прогноз прибылей и убытков?

Чтобы создать прогноз прибылей и убытков, вам потребуется спрогнозировать как доходы, так и расходы.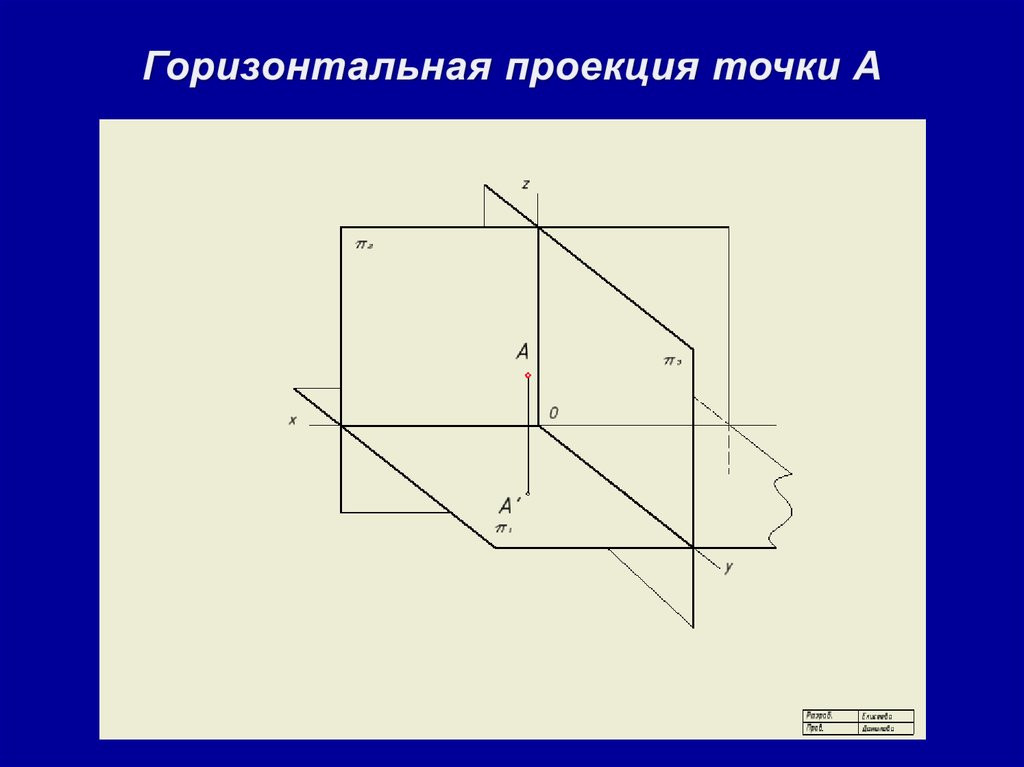 Если вы делаете прогноз для существующего бизнеса с историческими финансовыми данными, самый простой способ сделать прогноз — использовать ваши исторические данные в качестве основы для прогнозирования. Это подход, который мы используем в нашем существующем шаблоне бизнес-прогноза.

Если вы хотите создать прогноз прибылей и убытков для стартапа, вам потребуется разработать набор предположений и построить свои прогнозы с нуля. Вам потребуются предположения как о доходах, так и о расходах, чтобы получить предварительный отчет о прибылях и убытках. Вы можете увидеть пример из одного из наших шаблонов ниже.

Пример Проформа прибыли и убытков

Как спрогнозировать движение денежных средств для бизнеса?

Чтобы спрогнозировать денежный поток для бизнеса, вам необходимо создать прогнозируемые доходы и расходы, но вам также необходимо знать другие элементы, влияющие на денежный поток, такие как погашение кредита, амортизационные отчисления и новые полученные кредиты или инвестиции. Прогноз денежных потоков становится немного сложнее, чем простой прогноз прибылей и убытков. Все электронные таблицы бизнес-прогнозов премиум-класса ProjectionHub содержат прогноз денежных потоков на срок до 5 лет. Ниже приведен пример прогноза движения денежных средств на 5 лет из нашего шаблона для грузовиков с едой.

‍

Пример 5 Прогноз движения денежных средств на год

Как спрогнозировать баланс?

Чтобы спрогнозировать баланс, вам необходимо сначала создать прогноз отчета о прибылях и убытках и прогноз движения денежных средств. Кроме того, вам нужно будет знать все текущие активы и обязательства компании и уметь прогнозировать будущие активы и обязательства.

Прогнозирование баланса является наиболее сложным из трех финансовых отчетов. Нередко в прогнозе баланса есть ошибка, из-за которой он не балансируется, что может быть невероятно неприятно. Мы рекомендуем использовать шаблон прогноза баланса при попытке спрогнозировать баланс из-за сложности процесса.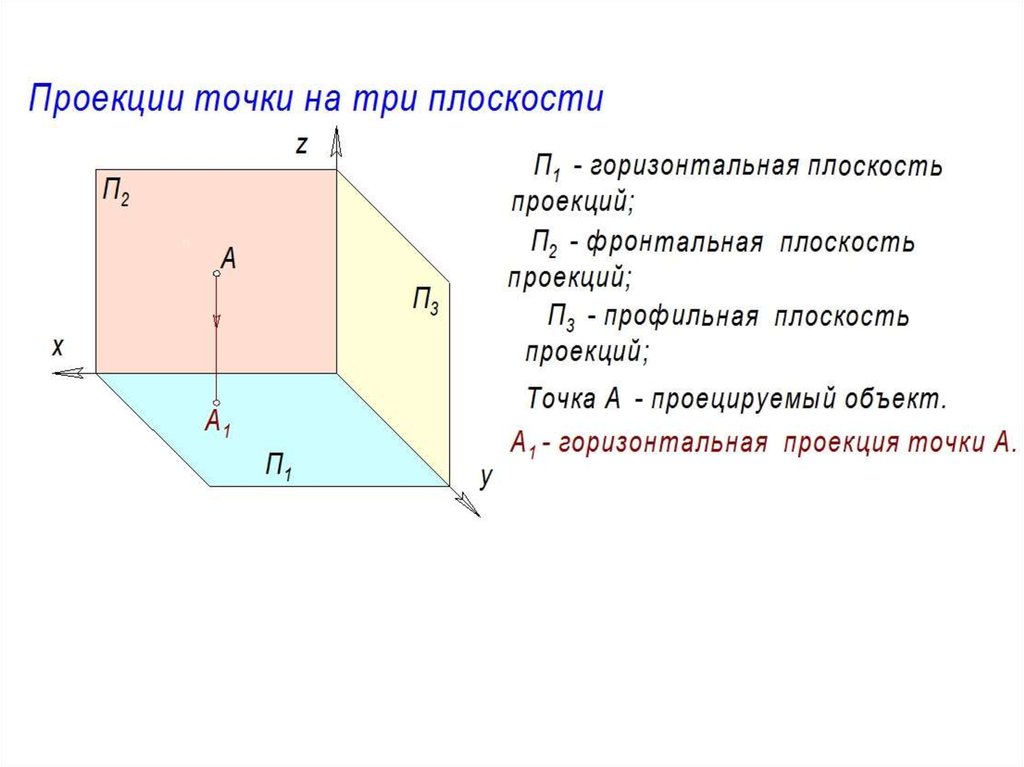 Все финансовые модели ProjectionHub также включают прогноз баланса на 5 лет.

Чтобы узнать больше о прогнозах баланса, вы можете прочитать — Полное руководство по прогнозам баланса.

Будут ли шаблоны проекций ProjectionHub работать с Excel и Google Sheets?

Да. Все наши шаблоны бизнес-проекций совместимы как с Excel, так и с Google Sheets.

Как спрогнозировать доход стартапа?

Прогнозирование дохода для стартапа должно представлять собой процесс создания ряда предположений, которые в конечном итоге приведут вас к прогнозируемому значению дохода. Все наши шаблоны предварительных форм будут включать вкладку входного дохода с набором предположений, которые вы должны заполнить. Есть два подхода к составлению прогнозов продаж, которые нам нравятся:

1. Подход к прогнозированию продаж на основе емкости
2. Подход к прогнозированию продаж на основе клиентской воронки

Я подробно описываю и привожу примеры каждого подхода к прогнозированию продаж в разделе «Два подхода к составлению прогнозов продаж для стартапов».

No related posts.