Проекция вектора на вектор онлайн калькулятор: Онлайн калькулятор. Проекция вектора на вектор

Содержание

вектор проекции вектора на вектор

Вы искали вектор проекции вектора на вектор? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить проекцию вектора а на ось вектора b, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вектор проекции вектора на вектор».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вектор проекции вектора на вектор,вычислить проекцию вектора а на ось вектора b,вычислить проекцию вектора на вектор,для заданных векторов вычислить проекцию вектора на вектор,как вычислить проекцию вектора на вектор,как найти проекцию,как найти проекцию вектора,как найти проекцию вектора на вектор,как найти проекцию вектора на вектор по координатам,как найти проекцию одного вектора на другой,как определить проекции векторов,как определить проекцию вектора,координаты проекции вектора на плоскость онлайн,координаты проекции вектора на плоскость примеры,найти проекцию вектора,найти проекцию вектора на вектор,найти проекцию вектора на вектор онлайн,найти проекцию вектора на вектор онлайн калькулятор,найти проекцию вектора на направление вектора,найти проекцию вектора онлайн,нахождение проекции вектора на вектор,онлайн калькулятор проекция вектора на вектор,онлайн найти проекцию вектора,определение проекции вектора,определение проекция вектора,определите проекции векторов,определите проекцию вектора,определить проекции векторов,проекции вектора,проекции вектора определение,проекции векторов,проекции формула,проекция вектор на вектор онлайн,проекция вектора,проекция вектора а на вектор б,проекция вектора а на вектор б формула,проекция вектора б на вектор а,проекция вектора на вектор,проекция вектора на вектор онлайн,проекция вектора на вектор онлайн калькулятор,проекция вектора на вектор формула,проекция вектора на другой вектор,проекция вектора на направление,проекция вектора на направление вектора,проекция вектора на направление другого вектора,проекция вектора определение,проекция вектора равна,проекция вектора формула,проекция векторов,проекция на направление вектора,проекция одного вектора на другой,проекция формула,формула проекции,формула проекции вектора,формула проекции вектора на вектор,формула проекция,формула проекция вектора,формула проекция вектора на вектор,чему равна проекция вектора на.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вектор проекции вектора на вектор. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить проекцию вектора на вектор).

Решить задачу вектор проекции вектора на вектор вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Проекция точки на плоскость онлайн

С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Для нахождения проекции точки M₀ на плоскость α, необходимо:

построить прямую L, проходящую через точку M₀ и ортогональной плоскости α.
найти пересечение данной плоскости α с прямой L(Рис.1).

Общее уравнение плоскости имеет вид:

где n

(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис.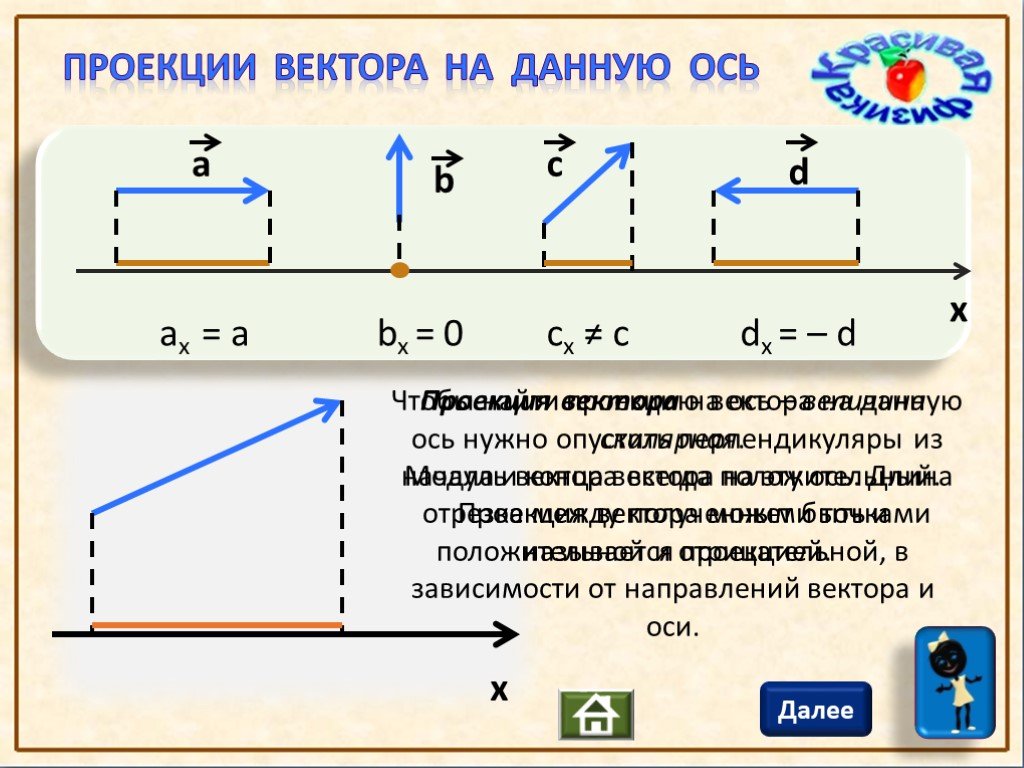 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональной плоскости (1) имеет следующий вид:

Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее

Выразим переменные x, y, z через рараметр t.

Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.

A(At+x₀)+B(Bt+y₀)+C(At+z₀)+D=0,

A²t+Ax₀+B²t+By₀+C²t+Cz₀+D=0,

Подставляя значение параметра t в выражения (4), находим проекцию M₁ точки M₀ на плоскость (1).

Пример 1.Найти проекцию M₁ точки M₀(4, -3, 2) на плоскость

Решение.

Нормальный вектор плоскости имеет вид:

n=(5, 1, −8),

т.е. A=5, B=1, C=−8.

Координаты точки M₀: x₀=4, y₀=−3, z₀=2.

Подставляя координаты точки M₀ и нормального вектора плоскости в (5), получим:

Из выражений (7) находим:

Ответ:

Проекцией точки M₀(4, -3, 2) на плоскость (6) является точка:

Калькулятор векторной проекции — Калькулятор векторной проекции онлайн

Векторы — это величины, имеющие как величину, так и направление. Векторы помогают одновременно представлять разные величины в одном выражении. Векторная проекция одного вектора на другой получается путем умножения данного вектора на косеканс угла между двумя векторами.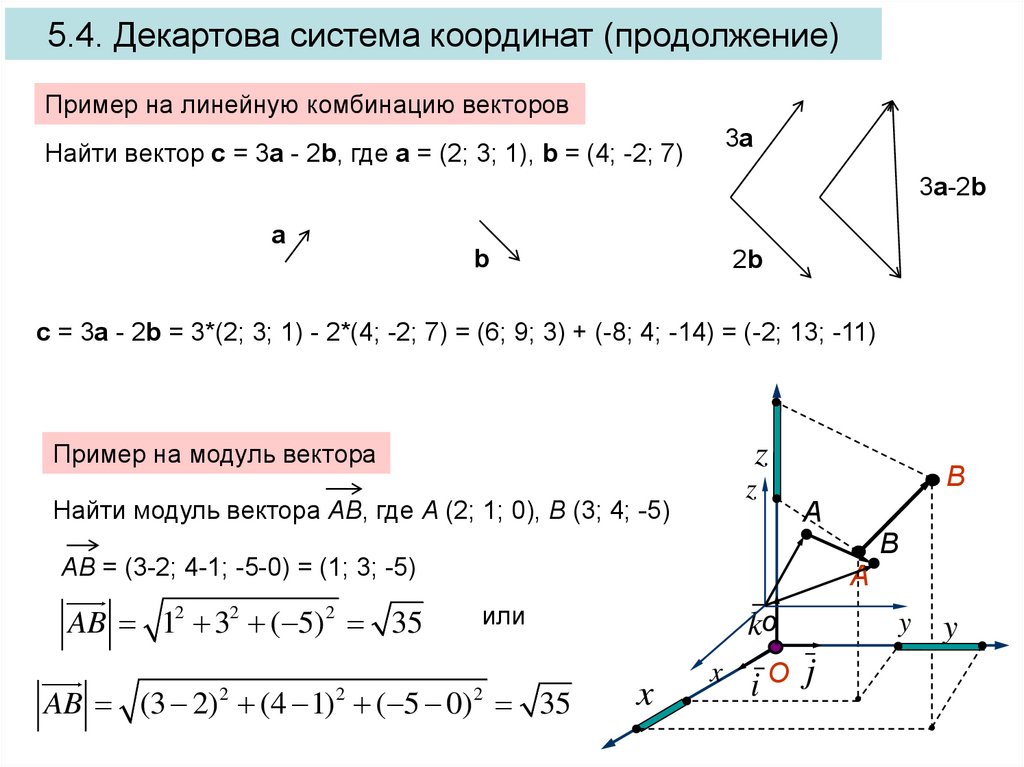

Что такое калькулятор векторной проекции?

Калькулятор векторной проекции — это онлайн-инструмент, который помогает рассчитать векторную проекцию для заданных двух векторов. Онлайн-калькулятор векторной проекции поможет вам рассчитать векторную проекцию для заданных двух векторов за несколько секунд.

Калькулятор векторной проекции

ПРИМЕЧАНИЕ. Вводите значения не более двух цифр.

Как пользоваться калькулятором векторной проекции?

Чтобы использовать калькулятор, выполните следующие действия:

Шаг 1: Введите коэффициенты двух векторов в указанные поля ввода.
Шаг 2: Нажмите кнопку «Вычислить» , чтобы вычислить проекцию вектора для заданных двух векторов.

Давайте рассмотрим пример, чтобы кратко понять.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Решенный пример на калькуляторе векторной проекции

Пример:

Найдите векторную проекцию для заданных двух векторов a = 4i + 2j — 5k и b = 3i — 2j + k и проверьте ее, используя онлайн-калькулятор векторной проекции. 92} × \overrightarrow{B}\)

\(= \frac{3}{14} × (3i — 2j + k)\)

= (9i — 6j + 3k) / 14

Следовательно, проекция вектора для заданных двух векторов равна (9i — 6j + 3k) / 14 или (9/14, -6/14, 3/14)

Точно так же вы можете использовать калькулятор векторной проекции, чтобы найти проекцию вектора для заданных двух векторы:

a = 4i + 2j — 5k и b = -1i + 4j — 3k
а = -2i — 5k и b = -7i + j + k

☛ Статьи по теме:

Векторы
Проекционный вектор

☛ Математические калькуляторы:

Как найти скалярную и векторную проекции одного вектора на другой — Криста Кинг Математика

Что такое скалярная и векторная проекции?

Скалярные проекции

Скалярная проекция одного вектора на другой (также называемая компонентой одного вектора вдоль другого) равна

???\text{comp}_a{b}=\frac{a\cdot{b}}{|a|}???

где ???a\cdot{b}??? скалярное произведение векторов ???a??? и ???б???, и ???|а|??? длина ???a??? (также называется величиной ???a???).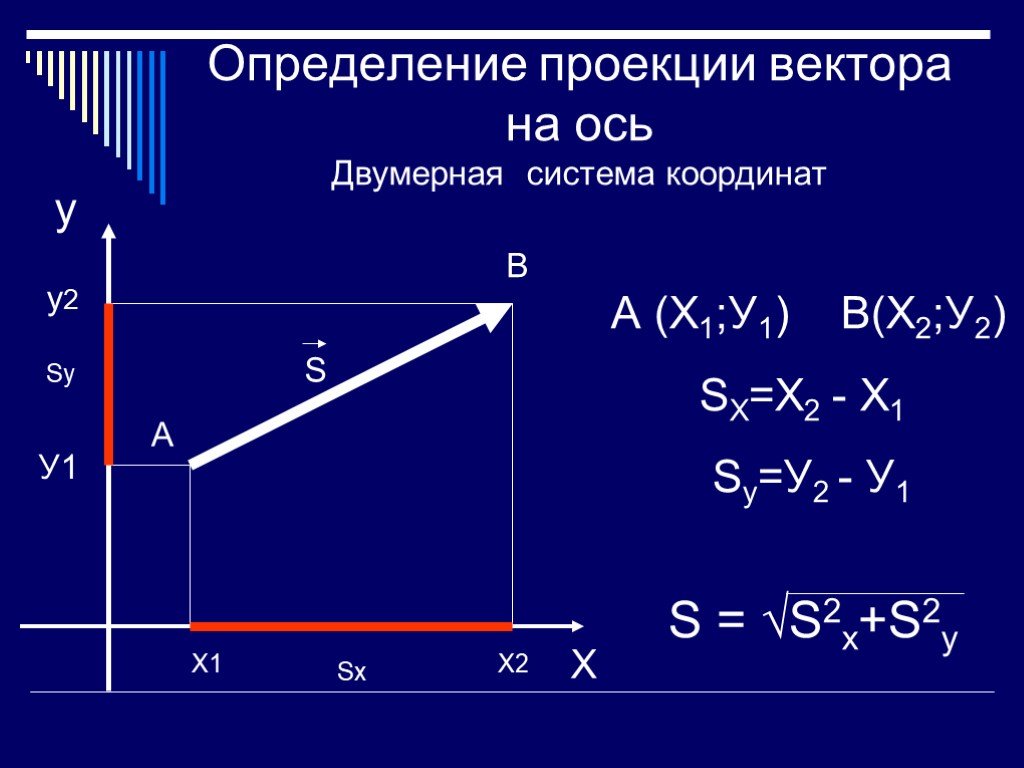

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Векторные проекции

Векторная проекция одного вектора на другой подобна тени, которую один вектор отбрасывает на другой вектор. Например, проекция зеленого на оранжевый будет синей:

???\text{proj}_a{b}=\left(\frac{a\cdot{b}}{|a|}\right)\frac{a}{|a|}???

где ???a\cdot{b}??? скалярное произведение векторов ???a??? и ???б???, и ???|а|??? длина ???a??? (также называется величиной ???a???).

Как найти скалярную и векторную проекции одного вектора на другой

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

Пошаговый пример, как найти скалярные проекции и векторные проекции

Пример

Найти скалярные и векторные проекции ???b??? на ???а???.

???a=i+2j-3k???

???b=6i+j???

Поскольку мы используем значение скалярной проекции в формуле векторной проекции, начнем с нахождения скалярной проекции. Нам понадобится скалярное произведение ???a??? и ???б??? и величина ???а???.

Приведем данные векторные уравнения к виду

???a=\langle1,2,-3\rangle???

???b=\langle6,1,0\rangle???

Возьмем скалярное произведение.

???a\cdot{b}=(1)(6)+(2)(1)+(-3)(0)???

???a\cdot{b}=6+2+0???

???a\cdot{b}=8???

Поскольку мы используем значение скалярной проекции в формуле для векторной проекции, начнем с нахождения скалярной проекции.

???|a|=\sqrt{1+4+9}???

???|a|=\sqrt{14}???

Подключим ???a\cdot b??? и ???|а|??? в формулу скалярной проекции.

???\text{comp}_a{b}=\frac{8}{\sqrt{14}}???

Поскольку у нас есть скалярная проекция, у нас уже есть все необходимое для нахождения векторной проекции.