Прогрессия арифметическая геометрическая: Арифметическая и геометрическая прогрессии — урок. Основной государственный экзамен (9 класс), Математика.

Арифметические,геометрические прогрессии — Математика

Если каждому натуральному числу n (n = 1, 2,…) поставлено в соответствие число xn, то говорят, что задана числовая последовательность x1, x2,…, xn…, обозначаемая {xn}. Числаx1, x2,…, xn… называются членами последовательности, а член с номером n – ее n-м членом. Арифметическая прогрессия Числовую последовательность {an}, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называют арифметической прогрессией. Число d называется разностью арифметической прогрессии: an+1 = an + d. Число Sn называется суммой n первых членов арифметической прогрессии. Свойства арифметической прогрессии: Геометрическая прогрессия Числовую последовательность {bn}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q ≠ 0, называют геометрической прогрессией. Число q называется называется знаменателем прогрессии: bn+1 = bnq. Число Sn называется суммой n первых членов геометрической прогрессии, Pn — произведением n первых членов геометрической прогрессии. Свойства геометрической прогрессии: Сумма первых трех членов возрастающей арифметической прогрессии равна 21. Если от первых двух членов этой прогрессии отнять по 1, а к третьему члену прибавить 2, то полученные три члена составят геометрическую прогрессию. Найти сумму восьми первых членов геометрической прогрессии. ____________________________________________________________________________ Обозначим через ai — члены арифметической прогрессии c разностью d, через bi — геометрической, с знаменателем q. Согласно формуле суммы арифметической прогрессии имеем S3 = (2a1 + 2d) · 3 / 2 = 21 или a1 + d = 7. По условию a1 — 1, a1 + d — 1, a1 + 2d + 2 — три последовательных члена геометрической прогрессии. Используем свойство геометрической прогрессии: (a1 + d — 1)2 = (a1 + 2d + 2)(a1 — 1). После замены переменной a1 = 7 — d и открытия скобок получаем квадратное уравнение d2 + 3d — 18 = 0, т.е. d1 = 3, d2 = -6. Условию удовлетворяет лишь d1 = 3 (т.к. арифметическая прогрессия возрастающая). В этом случае a1 = 4. Находим b1 = a1 — 1 = 3. b2 = a1 + d — 1 = 6, откуда q = 2. Наконец, согласно формуле суммы членов геометрической прогрессии получаем: S8 = [b1(q8 — 1)] / (q — 1) = 765. Ответ: S8 = 765.   Сумма трех чисел, которые составляют арифметическую прогрессию, равна 2, а сумма квадратов этих же чисел равна 14/9. Найти эти числа. ____________________________________________________________________________ Используя тот факт, что числа составляют арифметическую прогрессию, запишем их какa, a + d, a + 2d. Согласно условию их сумма равна 2, т.е. 3a + 3d = 2, a = 2/3 — d. Согласно второму условию a2 + (a + d)2 + (a + 2d)2 = 14/9. После раскрытия скобок получаем 27a2 + 45d2 + 54ad = 14. Делаем замену переменной a = 2/3 — d, раскрываем скобки и получаем: d2 = 1/9. d = ±1/3. Теперь легко найти числа, составляющие арифметическую прогрессию. При любом из значений d = ±1/3 числа будут равны 1/3, 2/3, 1. Ответ: 1/3, 2/3, 1.   Найти четыре числа, составляющие геометрическую прогрессию, в которой третий член больше первого на 9, а второй больше четвертого на 18. ____________________________________________________________________________ Используя тот факт, что числа составляют геометрическую прогрессию, запишем их какb, bq, bq2, bq3. По условию: 1) bq2 = b + 9. 2) bq = bq3 + 18. Домножаем первое уравнение на q и складываем со вторым: 9q + 18 = 0. Откуда q = -2. Из первого уравнения находим b. b = 3. Теперь легко найдем все числа: 3, -6, 12, -24. Ответ: 3, -6, 12, -24.   Найти сумму всех трехзначных чисел, которые делятся на 7. ___________________________________________________ Сначала найдем минимальное и максимальное трехзначные числа, которые делятся на 7. Это числа 105 и 994 соотвественно. Запишем a1 = 105, am = 994. Найдем m, т.е. количество трехзначных чисел, которые делятся на 7. Используем свойство прогрессии и получаем: 994 = 105 + 7(m — 1). Откуда m = 128. А теперь воспользуемся формулой суммы m членов арифметической прогрессии S128 = (105 + 994) · 128 / 2 = 70336. Ответ: 70336.

Арифметическая и геометрическая прогрессии | Формулы, сумма первых членов

1. Арифметическая прогрессия
2. Геометрическая прогрессия

 

Арифметическая прогрессия

Арифметической прогрессией называется числовая последовательность a₁,a₂,…a_n,…, у которой для любого n≥1 верно равенство: a_n+1=a_n+d, где  – определённое для данной прогрессии число (разность прогрессии). По определению d=a_n+1—a_n, где nϵN, n≥1.

Если d>0, то последовательность является возрастающей, если d, то убывающей.

Чтобы задать арифметическую прогрессию, необходимо знать её первый член a₁ и разность d.     

Пример арифметической прогрессии: 1, 3, 5, 7, …

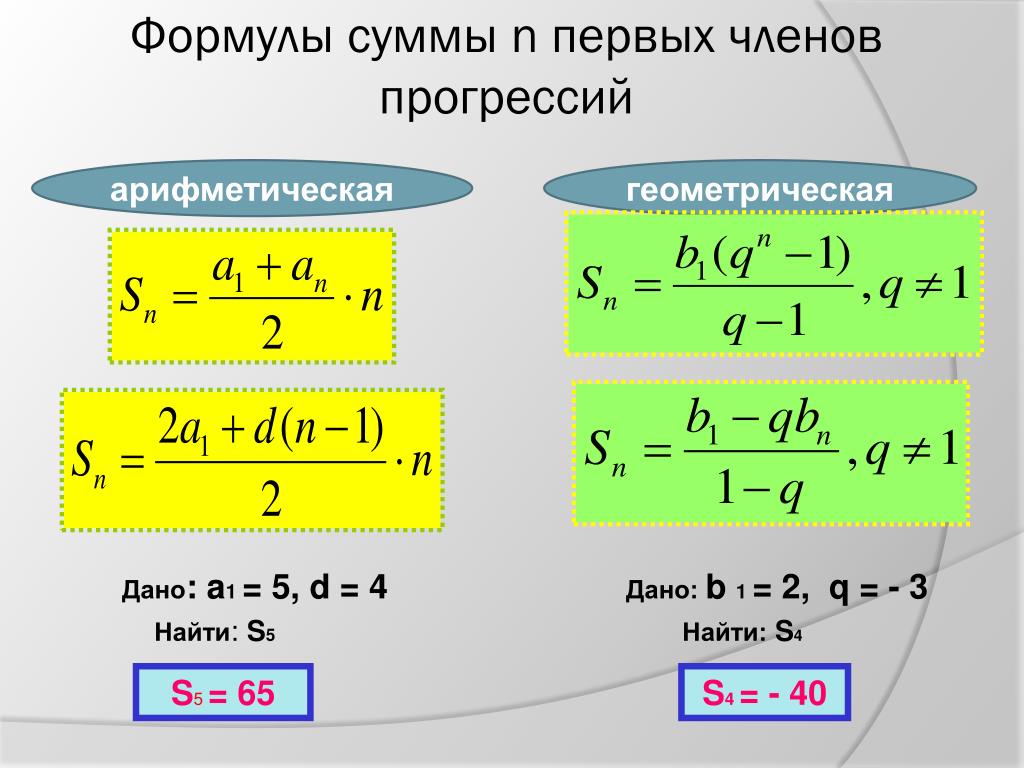
Формула n-го члена арифметической прогрессии:	Сумма n первых членов	Свойство арифметической прогрессии	Признак арифметической прогрессии
an=a1+d(n-1)	Sn=(a1+an)*n/2 Sn=(2a1+d(n-1))*n/2	если m+n=p+k, то am+an=ap+ak	для любого n≥2: an=(an-1+an+1)/2

Рассмотрим на примере нашей прогрессии  a₁=1, a₂=3, a₃=5, a₄=7,…

 

Геометрическая прогрессия

Геометрической прогрессией со знаменателем q≠0 называется числовая последовательность b₁,b₂,…b_n, у которой для любого n≥1  верно равенство: b_n+1=b_n*q. По определению q=b_n+1/b_n, где nϵN, n≥1.     

Пример геометрической прогрессии: 1, 2, 4, 8, …

Формула n-го члена геометрической прогрессии	Сумма n первых членов  прогрессии	Свойство  прогрессии	Признак прогрессии
bn=b1*qn-1	Sn=b1(1-qn)/(1-q)  (q ≠1) Sn=n*b1 (q=1)	Если m+n=p+k, то bm*bn=bp*bk	для любого n≥2: bn2=bn-1*bn+1

Рассмотрим на примере нашей прогрессии b₁=1, b₂=2, b₃=4, b₄=8,…

Геометрическая прогрессия со знаменателем |q| называется бесконечно убывающей прогрессией. Сумма всех членов бесконечно убывающей геометрической прогрессии с первым членом b₁ и знаменателем q равна S=b₁/(1-q).

Хотите, чтобы все темы были такими же понятными, записывайтесь на наши курсы:

Что такое арифметическая и геометрическая прогрессия

В математике последовательность — это список объектов (или событий), упорядоченных последовательно, так что каждый член идет до или после каждого другого члена. Ряд – это сумма последовательности членов. То есть ряд — это список чисел с операциями сложения между ними. Этот учебник научит вас арифметике и геометрической прогрессии, части последовательности и ряда.

Последовательность и ряды являются важными разделами математики. Несколько тем подпадают под последовательность и серию. В этом уроке вы подробно узнаете об арифметике и геометрической прогрессии.

Что такое арифметическая прогрессия (А.

П.)?

Последовательность называется арифметической прогрессией, если разница между элементом и предыдущим элементом всегда одинакова.

an+1 – an = константа (d) для всех натуральных чисел, где an+1 – член после

.

Постоянная разность, обычно обозначаемая буквой d, называется общей разностью.

Иллюстрация 1:

1, 5, 9, 13, … — А.П., первый член которой равен 1, а общая разность равна 5 — 1 = 4. 

Шаги арифметической прогрессии

Шаг 1: Получите

Шаг 2: Замените n на n+1 в an, чтобы получить an+1

Шаг 3: Вычислите an+1 — an

Шаг 4: Если an+1 — an не зависит от n, данная последовательность является арифметической прогрессией. В противном случае это не арифметическая прогрессия.

Следующий пример иллюстрирует процедуру:

Пример. Покажите, что последовательность , определяемая выражением an = 4n + 5, является А.П. Кроме того, найдите ее общее отличие.

Решение: имеем an = 4n + 5

.

Заменив n на (n+1), получим

ап+1 = 4(п+1) + 5 = 4п + 9

Теперь, an+1 — an = (4n + 9) — (4n + 5) = 4

Ясно, что an+1 — an не зависит от n и равен 4. Значит, данная последовательность является А.П. с общей разностью 4.

Общий член арифметической прогрессии

Пусть «a» будет первым членом, а «d» будет общей разностью A.P. Тогда его n-й член определяется как:

ан  = а + (n-1)d

где,

а = первый член

d = общая разница

Пример 1. Покажите, что последовательность 8,12, 16, 20, … является А.П. Найдите 16-й член и общий член.

Решение: Имеем (12 — 8) = (16 — 12) = (20 — 16)  = 4. Следовательно, данная последовательность является А.П. с общей разностью 4.

Первый член (а) = 8

16-й член = а16 = а + (16 — 1)d = а +15d

а16 = 8 + 15*4 = 68

Общий термин = n-й термин = an = a + (n-1)d

ан = 8 + (n-1)*4 = 4n + 4

Пример 2: Какой член последовательности 72, 70, 68, 66, …. 40?

Решение: Ясно, что данная последовательность является АП с первым членом = 72 и

.

общая разность = — 2.

Пусть n-й член равен 40. Тогда

72 + (n-1)(-2) = 40

⇒ 72 — 2n + 2 = 40

.

⇒ n = 17

Сумма n членов арифметической прогрессии

Сумма (Sn) n членов АП с первым членом «а» и общей разностью «d» равна 

Sn = n/2 [2a + (n-1)d]

Пример: Найдите сумму 20 слагаемых А.П. 1, 4, 7, 10, ….

Решение: пусть a будет первым членом, а d будет общей разностью заданных AP. 

Тогда а = 1, d = 3.

Нужно найти сумму 20 членов данного А.П. Подставляя a = 1, d = 3, n = 20 в Sn = n/2 [2a + (n-1)d], получаем

S20 = 20/2 [2×1 + (20 — 1)x3] = 10 x 59 = 590

Геометрическая прогрессия

Последовательность ненулевых чисел называется геометрической прогрессией (сокращенно Г.П.). Если отношение члена и предшествующего ему члена всегда является постоянной величиной.

Постоянное отношение называется обыкновенным отношением Г.П.

Общий термин геометрической прогрессии

Энный срок Г.П. с первым членом a и обыкновенным отношением r равно

ан = арн-1

Пример: найти 9-й член и общий член прогрессии 2, 6, 18, 54, …..

Решение: Данная прогрессия явно является G.P. с первым членом a = 2 и знаменателем = 3,

9-й член = a9 = ar(9 — 1) = 2*(3)8 = 13112

Сумма n слагаемых G.P.

Сумма n членов Г.П. с первым членом «а» и обыкновенным отношением «r» равно

Sn = a[(rn-1)/(r-1)], если r ≠ 1

Пример: Найдите сумму 7 членов G.P. 3, 6, 12, ….

Решение: Здесь a = 3, r = 2

S7 = а[(r7-1)/(r-1)] = 3[(27-1)/(2-1)] = 3(128 — 1) = 381

Мечтаете о карьере в области аналитики данных? Ознакомьтесь с курсом Аналитика данных и получите сертификат уже сегодня.

Вывод

На этом вы подошли к концу этого учебника по арифметике и геометрической прогрессии. Вы научились вычислять n-й член любого ряда, а также сумму n членов любого заданного ряда.

Арифметические и геометрические прогрессии — это основы статистики, необходимые для работы в Data Analytics. Изучите все основные концепции и усовершенствуйте свои навыки в нашей партнерской программе сертификации специалистов по анализу данных Университета Пердью. В сотрудничестве с IBM вы изучаете учебную программу с тщательно подобранными навыками, которые помогут вам быстро стать профессионалом в области анализа данных мирового класса.

У вас есть вопросы, связанные с арифметическими и геометрическими прогрессиями? Пожалуйста, оставьте их в разделе комментариев к этому уроку. Наши специалисты свяжутся с вами в кратчайшие сроки!

6.2: Арифметические и геометрические последовательности

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

40929

• Ричард В. Беверидж
• Общественный колледж Клэтсопа

Двумя распространенными типами математических последовательностей являются арифметические последовательности и геометрические последовательности. Арифметическая последовательность имеет постоянную разницу между каждой последовательной парой членов. Это похоже на линейные функции, которые имеют вид \(y=m x+b .\) Геометрическая последовательность имеет постоянное отношение между каждой парой последовательных членов. Это создаст эффект постоянного множителя.

Примеры

Арифметическая последовательность:
\(\{5,11,17,23,29,35, \dots\}\)
Обратите внимание, что здесь постоянная разность равна 6. Если мы хотим написать общий термин для этой последовательности, существует несколько подходов. Один из подходов состоит в том, чтобы взять постоянную разность в качестве коэффициента для члена \(n\): \(a_{n}=6 n+?\). Тогда нам просто нужно заполнить вопросительный знак значением, которое соответствует последовательности.

Мы могли бы сказать для последовательности:
\(\{5,11,17,23,29,35, \dots\}\)
\(a_{n}=6 n-1\)
Существует также формула, которую вы можете запомнить, согласно которой любая арифметическая последовательность с постоянной разностью \(d\) выражается как:
\(a_{n} =a_{1}+(n-1) d\)
Обратите внимание, что если мы подставим значения из нашего примера, мы получим тот же ответ, что и раньше:
\(a_{n}=a_{1}+(n -1) d\)
\(a_{1}=5, d=6\)
Итак, \(a_{1}+(n-1) d=5+(n-1) * 6=5+ 6 n-6=6 n-1\)
или \(a_{n}=6 n-1\)
Если члены арифметической последовательности становятся меньше, то постоянная разность является отрицательным числом.
\(\{24,19,14,9,4,-1,-6, \dots\}\)
\(a_{n}=-5 n+29\)

Геометрическая последовательность
In геометрическая последовательность всегда имеет постоянный множитель. Если множитель больше, чем \(1,\), то условия будут увеличиваться. Если множитель меньше \(1,\), то члены будут становиться меньше.

{n}\) 9{n-1}\) и т. д.

Упражнения 6.2
Определите, является ли каждая последовательность арифметической, геометрической или ни той, ни другой.
Если это арифметика, определить постоянную разницу.
Если оно геометрическое, определите постоянный коэффициент.
1) \(\quad\{18,22,26,30,34, \dots\}\)
2) \(\quad\{9,19,199,1999, \dots\}\)
3) \ (\quad\{8,12,18,27, \dots\}\)
4) \(\quad\{15,7,-1,-9,-17, \dots\}\)
5) \(\ четырехъядерный \ левый \ {\ гидроразрыва {1} {2}, \ гидроразрыва {2} {3}, \ гидроразрыва {3} {4}, \ гидроразрыва {4} {5}, \ гидроразрыва {5} 6}, \точки\справа\}\)
6) \(\quad\{100,-50,25,-12.5, \dots\}\)
7) \(\quad\{-8,12,32,52, \dots\}\)
8) \(\quad\{1,4,9,16,25, \dots\}\)

9) \(\quad\{11,101,1001,10001, \ldots\}\)
10) \( \quad\{12,15,18,21,24, \dots\}\)
11) \(\quad\{80,20,5,1.25, \dots\}\)
12) \(\quad \{5,15,45,135,405, \dots\}\)
13) \(\quad\{1,3,6,10,15, \dots\}\)
\(\begin{array}{ll} \text { 14) } & \{2,4,6,8,10, \dots\}\end{массив}\)
15) \(\quad\{-1,-2,-4,-8 ,-16, \dots\}\)
16) \(\quad\{1,1,2,3,5,8,13,21, \dots\}\)

---

Эта страница под названием 6.