Произведение векторов скалярное векторное смешанное произведение: §4. Скалярное, векторное и смешанное произведения векторов

свойства примеры и решения, геометрический смысл смешанного произведения векторов

Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.

Термин

Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.

Определение 1

Смешанным произведением a→, b→ и d→ является та величина, которая равняется скалярному произведению a→×b→ и d→ , где a→×b→ — умножение a→ и b→ . Операцию умножения a→, b→ и d→ зачастую обозначают a→·b→·d→ . Можно преобразовать формулу так:a→·b→·d→=(a→×b→,d→) .

Умножение в системе координат

Мы можем умножить вектора, если они указаны на координатной плоскости.

Возьмем i→, j→, k→

Произведение векторов в данном конкретном случае будет иметь следующий вид:a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→

Определение 2

Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.

Из этого следует:

a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→

Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.

a→×b→=( ayazbybz·i→-axazbxbz·j→+axaybxby·k→, dx·i→+dy·j→+dz·k→)==ayazbybz·dx-axazbxbz·dy+axaybxby·dz=axayazbxbybzdxdydz

Таким образом, можно сделать вывод, что:

a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz

Определение 3

Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz .

Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.

1. (λ·a→)·b→·d→=a→·(λ·b→)·d→=a→·b→·(λ·d→)=λ·a→·b→·d→    λ∈R ;
2. a→·b→·d→=d→·a→·b→=b→·d→·a→;   a→·d→·b→=b→·a→·d→=d→·b→·a→ ;
3. (a(1)→+a(2)→)·b→·d→=a(1)→·b→·d→+a(2)→·b→·d→a→·(b(1)→+b(2)→)·d→=a→·b(1)→·d→+a→·b(2)→·d→a→·b→·(d(1)→+d(2)→)=a→·b→·d(2)→+a→·b→·d(2)→

Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль.

Результатом умножения также будет нуль в том случае, если два или больше множителей равны.

Действительно, если a→=b→ , то, следуя определению векторного произведения [a→×b→]=a→·b→·sin 0 =0 , следовательно, смешанное произведение равно нулю, так как ([a→×b→], d→)=(0→, d→)=0 .

Если же a→=b→ или b→=d→ , то угол между векторами [a→×b→] и d→ равен π2 . По определению скалярного произведения векторов ([a→×b→], d→)=[a→×b→]·d→·cosπ2=0 .

Свойства операции умножения чаще всего требуются во время решения задач.
Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.

Пример 1

Докажите равенство ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→) , где λ — некоторое действительное число.

Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:

([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→)
Мы разобрали, что (([a→×b→], b→)=0. Из этого следует, что
([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→)==([a→×b→], d→)+([a→×b→], λ·a→)+0=([a→×b→], d→)+([a→×b→], λ·a→)

Согласно первому свойству ([a⇀×b⇀], λ·a→)=λ·([a⇀×b⇀],a→) , а ([a⇀×b⇀], a→)=0 . Таким образом, ([a⇀×b⇀], λ·a→) . Поэтому,
([a⇀×b⇀], d→+λ·a→+b→)=([a⇀×b⇀], d→)+([a⇀×b⇀], λ·a→)==([a⇀×b⇀], d→)+0=([a⇀×b⇀], d→)

Равенство доказано. , d→)≤≤a→·b→·1·d→·1=a→·b→·d→

Неравенство доказано.

Разбор типовых задач

Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz . 

Пример 3

В прямоугольной системе координат представлены 3 вектора с такими координатами: a→=(1, -2, 3),  b→(-2, 2, 1),  d→=(3,-2, 5) . Необходимо определить, чему равно произведение указанных векторов a→·b→·d→ .

Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz=1-23-2213-25==1·2·5+(-1)·1·3+3·(-2)·(-2)-3·2·3-(-1)·(-2)·5-1·1·(-2)=-7

Пример 4

Необходимо найти произведение векторовi→+j→, i→+j→-k→, i→+j→+2·k→ , где i→,j→, k→ — орты прямоугольной декартовой системы координат.

Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i→+j→=(1, 1, 0)i→+j→-k→=(1, 1, -1)i→+j→+2·k→=(1, 1, 2)

Используем формулу, которая использовалась выше
i→+j→×(i→+j→-k→, (i→+j→+2·k→)=11011-1112=0i→+j→×(i→+j→-k→, (i→+j→+2·k→)=0

Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. )=c→·npc→d→ , где npc→d→ — числовая проекция вектора d→ на направление вектора c→=[a→×b→] .

Абсолютная величина npc→d→ равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a→, b→ и d→ в качестве сторон. Исходя из этого, следует уточнить, что c→=[a→×b→] перпендикулярен a→ и вектору и вектору согласно определению умножения векторов. Величина c→=a→xb→ равняется площади параллелепипеда, построенного на векторах a→ и b→ .

Делаем вывод, что модуль произведения a→·b→·d→=c→·npc→d→ равен результату умножения площади основания на высоту фигуры, которая построена на векторах a→, b→ и d→ .

Определение 4

Абсолютная величина векторного произведения является объемом параллелепипеда: Vпараллелепипида=a→·b→·d→ .

Данная формула и является геометрическим смыслом.

Определение 5

Объем тетраэдра, который построен на a→,b→ и d→ , равняется 1/6 объема параллелепипеда Получаем, Vтэтраэда=16·Vпараллелепипида=16·a→·b→·d→ .

Для того, чтобы закрепить знания, разберем несколько типичных примеров

Пример 6

Необходимо найти объем параллелепипеда, в качестве сторон которого используются AB→=(3, 6, 3), AC→=(1, 3, -2), AA1→=(2, 2, 2) , заданные в прямоугольной системе координат. Объем параллелепипеда можно найти, используя формулу об абсолютной величине. Из этого следует:AB→·AC→·AA1→=36313-2222=3·3·2+6·(-2)·2+3·1·2-3·3·2-6·1·2-3·(-2)·2=-18

Тогда, Vпараллелепипеда=-18=18 .

Vпараллелепипида=18

Пример 7

В системе координат заданы точки A(0, 1,  0), B(3, -1, 5),  C(1, 0, 3), D(-2, 3, 1) . Следует определить объем тетраэдра, который расположен на этих точках.

Воспользуемся формулой Vтэтраэдра=16·AB→·AC→·AD→ . Мы можем определить координаты векторов по координатам точек: AB→=(3-0, -1-1, 5-0)=(3, -2, 5)AC→=(1-0, 0-1, 3-0) =(1,-1, 3)AD→=(-2-0, 3-1, 1-0)=(-2, 2, 1)

Дальше определяем смешанное произведение AB→·AC→·AD→ по координатам векторов: AB→·AC→·AD→=3-251-13-221=3·(-1)·1+(-2)·3·(-2)+5·1·2-5·(-1)·(-2)-(-2)·1·1-3·3·2=-7 Объем Vтэтраэдра=16·-7=76 .

Vтэтраэдра=76 .

НОУ ИНТУИТ | Лекция | Скалярное произведение векторов. Свойства. Векторное произведение векторов. Свойства. Смешанное произведение векторов. Свойства

< Лекция 10 || Лекция 7: 123

Аннотация: В лекции рассматриваются линейные операции над векторами, и дается практическое использование этих операций при решении различных задач

Ключевые слова: операции, вектор, длина, модуль, компланарность, коллинеарность, Произведение, базисными векторами, ПО, Главная диагональ, произведение вектора, равенство, векторное произведение, антисимметричность, координаты, разность, направляющие косинусы, аргумент, площадь

Умножение

Различают несколько видов операции умножения.

1. Умножение вектора на скалярную величину

. При умножении вектора на скаляр получают новый вектор , длина (модуль) которого изменяется в раз, а направление совпадает с направлением исходного вектора , если , или противоположно исходному вектору, если .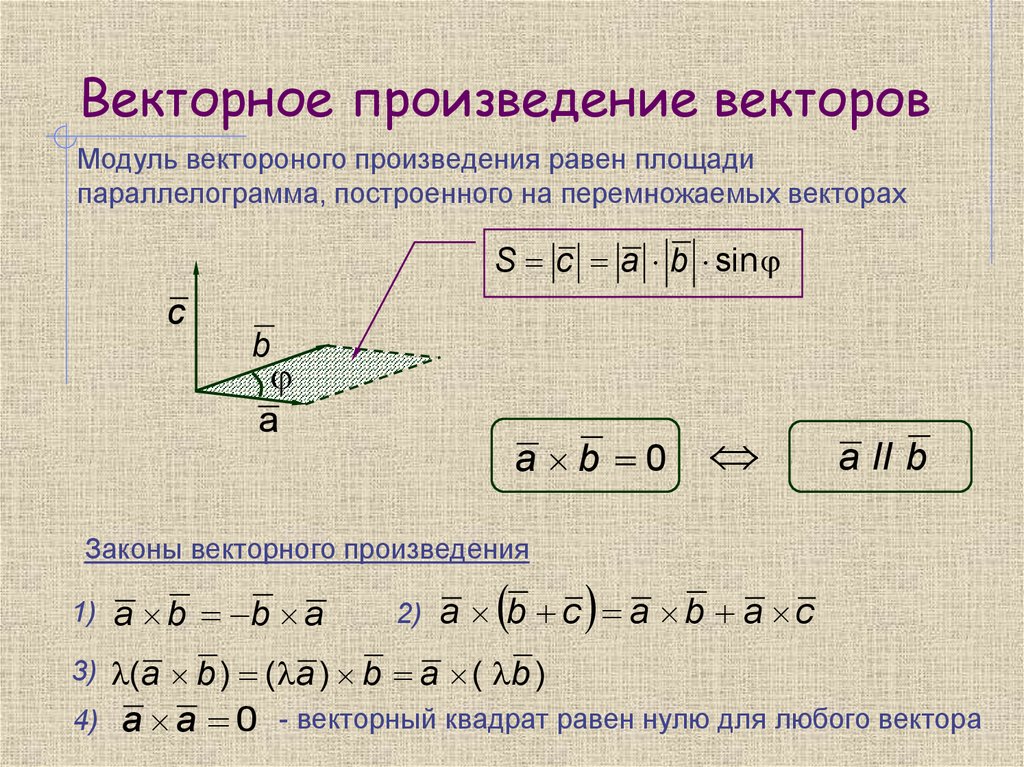 В координатной форме, если a = (a_x;a_y;a_z), то b = a= . Следовательно, операция умножения вектора на скаляр не влияет на компланарность (коллинеарность) векторов. Поэтому если несколько векторов до умножения на скаляр были компланарны (коллинеарны), то после умножения компланарность (коллинеарность) между ними сохранится.

Заметим, что любой вектор может быть представлен как произведение единичного, коллинеарного ему вектора на модуль рассматриваемого вектора, т.е. ^{1Модуль вектора можно обозначать |\overrightarrow{b}| или просто b.}

Из последнего равенства следует, что . Операция умножения вектора на скаляр обладает свойствами коммутативности и ассоциативности: , а также свойством дистрибутивности: .

2. Скалярное произведение векторов.

Определение 14. Скалярным произведением двух векторов и называется число S, равное . Эта операция обозначается или

В частности, скалярный квадрат вектора равен квадрату его длины, т.е.

Если один из перемножаемых векторов единичный, то:

В этом случае результат представляет собой проекцию вектора на направление единичного вектора . Следовательно, любой вектор можно представить как , где a

x,a_y,a_z — проекции вектора соответственно на оси 0х, 0у и 0z.

Если вектор представлен через проекции на базисные векторы, то говорят о разложении вектора по ортогональному базису. Из рис. 6.1 видно, что в этом случае вектор является главной диагональю прямоугольного параллелепипеда, ребра которого параллельны осям координат и равны длинам проекций вектора на эти оси. Из этого же рисунка следует, что модуль вектора численно будет равен .

Рис. 6.1.

Из определения скалярного произведения следует, что любой вектор, независимо от типа, можно представить в виде:

где , и есть скалярное произведение вектора с ортами осей координат. Тогда из последнего равенства имеем

где , и — углы, которые составляет вектор соответственно с осями 0х, 0у и 0z.

Можно заметить, что скалярное произведение коммутативно и дистрибутивно, т.е. и . Можно убедиться самостоятельно в том, что всегда выполняется равенство

Замечание 1. Если скалярное произведение двух векторов равно нулю, то эти векторы ортогональны. Действительно, если ни один из векторов не нулевой, то, по определению скалярного произведения, последнее может быть равно нулю только тогда, когда

intuit.ru/2010/edi»>Замечание 2. , где — единичные векторы (орты) осей координат ^{2При этом оси координат могут быть взаимноперпендикулярны (ортогональны), хотя это и не обязательно. Данное замечание выполняется и для произвольной системы координат (косоугольной, криволинейной).}

Замечание 3. .

Замечание 4. Скалярное произведение векторов в координатной форме

Замечание 5. Используя формулу скалярного произведения векторов и , можно найти выражение косинуса угла между этими векторами через их проекции на орты:

Если , то это значит, что угол между векторами больше 90 , т.е. тупой, а если , то угол острый.

Замечание 6. Механический смысл скалярного произведения векторов. Скалярное произведение силы F на вектор перемещения S равно работе А этой силы при перемещении материальной точки по вектору S: A = FS.

Дальше >>

< Лекция 10 || Лекция 7: 123

math — Скалярное тройное произведение и детерминант

спросил 13 лет, 11 месяцев назад

Изменено 13 лет, 11 месяцев назад

Просмотрено 2к раз

Я заметил кое-что сегодня, когда пытался решить проблему. Скалярное тройное произведение такое же, как определитель или матрица три на три с тремя векторами в качестве строк:

A = [ A , B , C ]

DET (A) = ( A x B ) * C

I наткнулся на это в Realling Rendering ,

I наткнулся на это в Realling Rendering ,

I. и я действительно не могу понять, почему это так, и если это даже полезно. Кажется, это как-то связано с кратким методом вычисления перекрестного произведения с использованием детерминанта, в котором вы записываете единичные векторы вдоль верхней части матрицы, но я всегда думал, что это скорее мнемоника, а не на самом деле здравая математика.

Есть ли здесь настоящие отношения или это просто какое-то счастливое стечение обстоятельств?

С точностью до знака определитель матрицы размера n на n равен объему параллелепипеда, натянутого на его n n-мерных векторов строк (или столбцов) (или объему единичного куба линейно преобразуется этой матрицей). Произведение (axb).c в трех измерениях делает то же самое; axb задает вектор, перпендикулярный a и b и имеющий длину, равную площади параллелограмма, натянутого на a и b; (axb).c дает высоту c над этим параллелограммом, умноженную на его площадь. Так что нет, это не случайно.

Совершенно не случайно; это довольно стандартный результат. Обратите внимание, что векторные произведения a X b сами часто записываются в детерминантной форме, где верхняя строка представляет собой единичные векторы i j k , следующая строка представляет собой a1 a2 a3, а нижняя строка представляет собой b1 b2 b3.

 |i j k|
|а1 а2 а3|
|б1 б2 б3|
 

Теперь, взяв скалярное произведение этого с другим вектором с, вы получите то же самое, как если бы вы только что написали с в верхней строке.

 |i j k| |с1 с2 с3| |с1 с2 с3| |а1 а2 а3|
|а1 а2 а3| . (c1,c2,c3) = |a1 a2 a3| = -|а1 а2 а3| = |b1 b2 b3|
|б1 б2 б3| |б1 б2 б3| |б1 б2 б3| |с1 с2 с3|
 

Редактировать: Также на странице википедии для скалярного тройного произведения говорится, что это эквивалентно определителю матрицы с использованием векторов в виде строк или столбцов. КЭД

4

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Скалярное тройное произведение

: примеры и свойства

К настоящему времени вы, вероятно, столкнулись с большим количеством векторного материала и задались вопросом, как теоретические принципы, такие как умножение точек, соотносятся с реальной жизнью. Вот тут-то и появляется скалярный тройной продукт . Этот продукт обеспечивает простой способ нахождения объемов некоторых сложных форм с помощью комбинации ранее рассмотренных теоретических принципов.

Эта статья покажет, как мы можем взять векторы и применить их к физическому контексту.

Скалярное тройное произведение Значение

Скалярное тройное произведение — это принцип, который мы используем для нахождения объема параллелепипеда — шестигранной фигуры, каждая сторона которой представляет собой параллелограмм или тетраэдр.

Скалярное тройное произведение на самом деле включает в себя две ранее замеченные векторные операции — точечное и перекрестное умножение.

В результате перекрестного умножения двух векторов будет получена векторная величина, но последующее точечное умножение для нахождения скалярного произведения приведет к уменьшению векторов до скалярного значения.

Вот как мы можем вычислить объем фигур, названных выше, из трех векторов — мы получаем одно число в конце процесса.

Вы можете вспомнить определение векторной величины следующим образом.

Векторная величина представлена ​​в терминах \(x,y,z\) и, как таковая, имеет три компонента. Векторы также имеют определенную величину и направление .

Определение скалярной величины следующее.

Скалярная величина — это сингулярное значение, которое имеет только величину. У него нет направления.

Скалярное тройное произведение векторов

Мы знаем, что векторы могут использоваться для описания движения и обычно имеют форму движения в направлениях \(x,\, y,\, z\). В векторной форме они становятся \(\vec{i},\, \vec{j},\, \vec{k}\) соответственно, и с помощью этих обозначений мы можем выполнять множество операций над векторами.

Чтобы найти скалярное тройное произведение трех векторов, вы должны быть знакомы с принципом скалярного произведения и перекрестного произведения и с тем, как они работают. Если вы этого не сделаете, вы можете проверить наши статьи о скалярных произведениях и векторных произведениях соответственно для освежения знаний.

Скалярное тройное произведение находит скалярное произведение вектора на векторное произведение двух векторов. Это более сложная методология, чем скалярное произведение двух, но она полезна при нахождении объемов определенных форм.

Сначала находим векторное произведение первых двух векторов. Это приведет к одному вектору, который будет использоваться в скалярном произведении с третьим вектором. И это приведет к скалярному значению.

Скалярная формула тройного произведения

Рассмотрим три вектора \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\), где \[\vec{a}=a_1\vec{i }+a_2\vec{j}+a_3\vec{k},\]\[\vec{b}=b_1\vec{i}+b_2\vec{j}+b_3\vec{k},\] и \[\vec{c}=c_1\vec{i}+c_2\vec{j}+c_3\vec{k}.\] Чтобы найти скалярное тройное произведение этих векторов, мы должны найти векторное произведение двух из них и найдите скалярное произведение этого результата с третьим вектором. В математической записи это выглядит как \[\vec{a}\cdot (\vec{b}\times\vec{c}).\]Это абсолютное значение этой формулы дает нам объем параллелепипеда.

Для объема тетраэдра можно применить следующую формулу: \(\frac{1}{6}\left[|\vec{a}\cdot (\vec{b}\times\vec{c}) |\right]\), когда векторы описывают три некомпланарные стороны фигуры.

Из векторного произведения мы знаем, что перекрестное произведение \(\vec{b}\times \vec{c}\) задается как \[\vec{b}\times \vec{c}=(b_2c_3 -b_3c_2)\vec{i}-(b_1c_3-b_3c_1)\vec{j}+(b_1c_2-b_2c_1)\vec{k}.\]Если мы затем рассмотрим скалярное произведение результата векторного произведения и вектора \ (\vec{a}\) получаем формулу скалярного тройного произведения,\[\vec{a}\cdot (\vec{b}\times\vec{c})=a_1(b_2c_3-b_3c_2)+a_2 (b_3c_1-b_1c_3)+a_3(b_1c_2-b_2c_1).\]

Свойства скалярного тройного произведения

Как было сказано ранее, скалярное тройное произведение используется для нахождения объема параллелепипеда, но что это на самом деле означает?

Если мы рассматриваем векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) как три непараллельные стороны параллелепипеда, мы можем провести скалярная формула тройного произведения, чтобы получить результат для объема формы.

Когда мы пытаемся найти объем фигур, порядок применения этих векторов не имеет значения, пока процесс цикличен. Это означает: \[\vec{a}\cdot (\vec{b}\times\vec{c})=\vec{b}\cdot (\vec{c}\times\vec{a})=\ vec{c}\cdot (\vec{a}\times\vec{b}).\]

Давайте рассмотрим пример.

Показать, что \(\vec{a}\cdot (\vec{b}\times\vec{c})=\vec{b}\cdot (\vec{c}\times\vec{a})\ ), используя приведенные ниже векторы,

\[\vec{a}=5\vec{i}+2\vec{j}+6\vec{k},\]\[\vec{b}=-2\ vec{i}+17\vec{j}+1\vec{k},\] и \[\vec{c}=8\vec{i}-5\vec{j}+13\vec{k} .\]

Решение

Используя нашу общую формулу для \(\vec{a}\cdot (\vec{b}\times\vec{c})\),

\[\begin{align} \vec{a}\cdot (\vec{b}\times\vec{c})&=a_1(b_2c_3-b_3c_2)+a_2(b_3c_1-b_1c_3)+a_3(b_1c_2-b_2c_1)\\&=5[( 17\cdot13)-(1\cdot-5)]+2[(1\cdot8)-(-2\cdot13)]\\ & \qquad +6[(-2\cdot-5)-(17\cdot8 )]\\&=5(226)+2(34)+6(-126)\\&=1130+68-756\\&=442.\end{align}\]

Затем мы можем снова использовать общую формулу для \(\vec{b}\cdot (\vec{c}\times\vec{a})\), где мы сдвигаем буквы — там, где были \(a’s\ ) теперь будут \(b’s\), \(b’s\) будут заменены на \(c’s\) и \(c’s\) заменены на \(a’s\).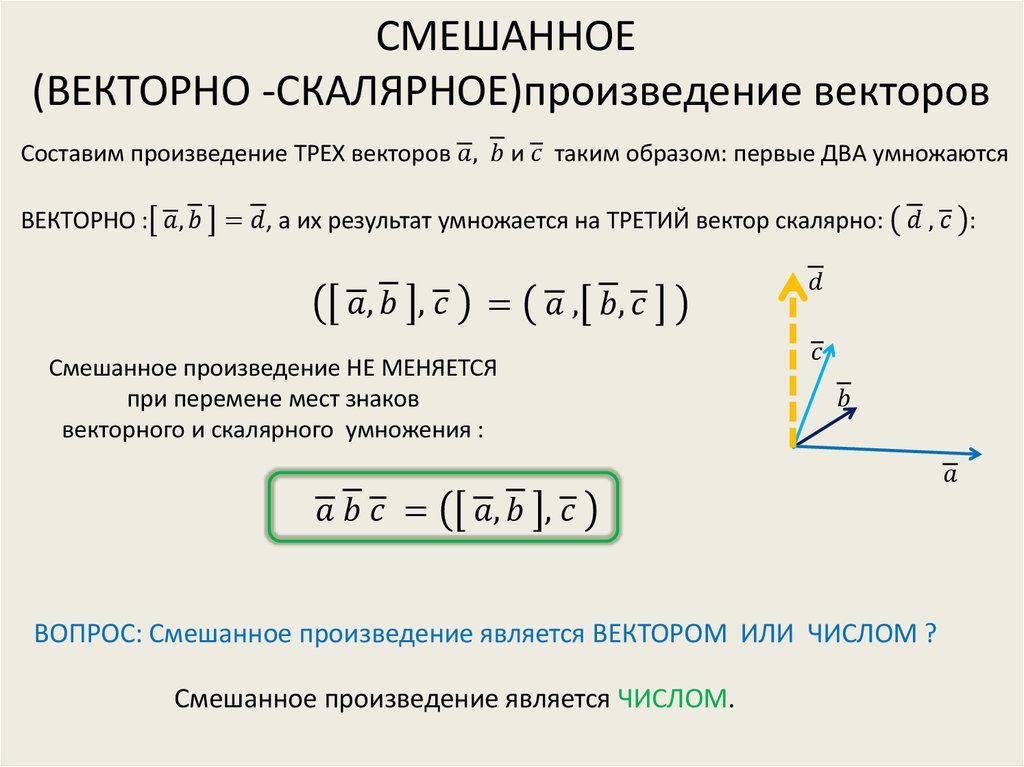 Это будет иметь вид \[\begin{align}\vec{b}\cdot (\vec{c}\times\vec{a})&=b_1(c_2a_3-c_3a_2)+b_2(c_3a_1-c_1a_3)+ b_3(c_1a_2-c_2a_1)\\&=-2[(-5\cdot6)-(13\cdot2)]+17[(13\cdot5)-(8\cdot6)]\\& \qquad+1[( 8\cdot2)-(-5\cdot5)]\\&=-2(-56)+17(17)+1(41)\\&=112+289+41\\&=442.\end{align}\]

Как видите, числа в процессе меняются, но поскольку процесс цикличен, конечный результат один и тот же.

Таким образом, \[\vec{a}\cdot (\vec{b}\times\vec{c})=\vec{b}\cdot (\vec{c}\times\vec{a}). \]

Существует еще одно свойство скалярного тройного произведения, которое еще не обсуждалось. Давайте объединим наши три вектора в матрицу \(3\times 3\),\[\begin{bmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\ \c_1&c_2&c_3\end{bmatrix}\]

Если вы расширите приведенную выше матрицу, вы должны получить скалярное тройное произведение. Посмотрим как!

\[\begin{align} \begin{bmatrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{bmatrix} &=a_1(b_2c_3-b_3c_2)+a_2(b_3c_1-b_1c_3)+a_3(b_1c_2-b_2) &=\vec{a}\cdot (\vec{b}\times\vec{c}) \end{align}\]

Скалярное тройное произведение совпадает с определителем этой матрицы. Чтобы узнать, почему это так, см. нашу статью о детерминантах матрицы.

Ключевым выводом здесь является то, что миноры и расширение определителя матрицы \(3\x 3\) отражают формулу скалярного тройного произведения, так что это может быть более простым способом запомнить процесс для вас.

Рассмотрим пример нахождения скалярного тройного произведения путем расширения определителя.

Найдите объем параллелепипеда, образованного смежными ребрами, заданными векторами \[\vec{a}=3\vec{i}-1\vec{j}-2\vec{k},\]\[ \vec{b}=\vec{i}+3\vec{j}-2\vec{k},\] и \[\vec{c}=6\vec{i}-2\vec{j} +\vec{k}.\] 93\).

Обратите внимание, что даже если вы получите отрицательный определитель, вам нужно взять модуль скалярного тройного произведения, чтобы получить объем.

Кроме того, есть много других свойств скалярных тройных произведений, которые выходят за рамки дополнительной математики.

1. Скалярное тройное произведение не изменится, если мы поменяем местами операции, не меняя положения векторов. \[\vec{a}\cdot (\vec{b}\times\vec{c})=(\vec{a}\times \vec{b})\cdot\vec{c}.\]
2. Скалярное тройное произведение инвертируется, если поменять местами любые два из трех заданных векторов. \[\vec{a}\cdot (\vec{b}\times\vec{c})=-\vec{a}\cdot (\vec{c}\times\vec{b}).\]
3. Скалярное тройное произведение равно нулю, если любой из трех заданных векторов компланарен, и наоборот.

Пример скалярного тройного произведения

Давайте начнем с примера, где нам нужно найти объем параллелепипеда.

Найдите объем параллелепипеда с тремя непараллельными сторонами, описанными векторами \[\vec{a}=2\vec{i}+1\vec{j}-1\vec{k},\] \[\vec{b}=-5\vec{i}+14\vec{j}-7\vec{k},\] и \[\vec{c}=16\vec{i}-3\ vec{j}+12\vec{k}.\] 93.\end{align}\]

Давайте теперь рассмотрим пример, где нам нужно найти объем тетраэдра.

Найдите объем тетраэдра с тремя некомпланарными сторонами, описанными векторами \[\vec{a}=-4\vec{i}+12\vec{j}+2\vec{k},\ ]\[\vec{b}=3\vec{i}+1\vec{j}-1\vec{k},\] и \[\vec{c}=4\vec{i}+3\ vec{j}+2\vec{k}.