Глава 3. Производная функции одной переменной
УДК 517.1
Составители: О.Я. Шевалдина
Научный редактор: канд. физ.-мат. наук В.И. Максимов
Задачи экономики в курсе математического анализа: Методические указания по курсу «Математика», «Математический анализ» для студентов экономических / О.Я. Шевалдина. Екатеринбург: ГОУ ВПО «УГТУ – УПИ», 2008. 34 с.
Методические указания содержат кратко изложенный теоретический материал, типовые задачи, рекомендации к их решению по теме «Исследование функций с помощью производных. Приложение производной в экономической теории» курса «Математика». Приводятся простейшие приложения математики в экономике (предельный анализ, эластичность функций, максимизация прибыли, оптимизация налогообложения предприятий и др.). Предлагаются задачи для самостоятельной работы студентов (в том числе, с экономическим содержанием). Наряду с традиционными упражнениями приводятся тестовые задания открытой и закрытой формы. Теоретические сведения, а также набор предлагаемых задач можно использовать в процессе аудиторной и самостоятельной работы студентов, при проведении контрольных работ, собеседований и экзаменов. Методические указания предназначаются для студентов всех специальностей факультета экономики и управления.
Подготовлено кафедрой «Анализ систем и принятия решений»
ГОУ ВПО «Уральский государственный
технический университет – УПИ» , 2008
3.1. Производная функции в точке
Пусть функция определена на множестве и– предельная точка множества Х. Напомним: для любой точки приращениеопределяется формулой.Приращением функции в точкеназывается функция аргумента:
.
Определение.
Если существует конечный предел,
то значение этого предела называют производной функции в точке, обозначают или.
Используются и другие символические обозначения производной:
, ,.
Лагранж1Ньютон2Лейбниц3
Таким образом, по определению
, (3.1)
где .
Пример 3.1. Найдем производную функции в любой точкеобласти определения:
.
Следовательно, функция имеет в каждой точкепроизводную.
Экономисты используют для обозначения производной также символ (т. е.) и терминмаржинальное значение функции в точке .
X Физический смысл производной
Производная – скорость изменения функции в точке . В частности, если– время, – координата точки, движущейся по прямой в момент , то
Геометрический смысл производной. Связь с существованием касательной
Пусть график функции ;,– две точки графика функции(рис. 3.1).
Угол между секущей АВ и осью Ох обозначим .
Г
Определение. Если существует , то прямаяс угловым коэффициентом, проходящая через точку, называетсякасательной к графику функции в точке.
Теорема 3.1. График функции имеет в точкекасательную тогда и только тогда, когда функцияимеет в точкепроизводную.
Доказательство.
Необходимость. Пусть . Так как функциянепрерывна, то. Но. Поэтому, то есть функцияимеет в точкеконечную производную.
Достаточность. Если существует , то есть, то. Так как функции,непрерывные, то, то есть существует касательная к графику функции в точке.
Замечание. Так как , то приполучаем.Таким образом, – это тангенс угла наклона касательной к графику функциив точке.
Уравнения касательной и нормали
Найдем уравнение касательной. Будем искать его в виде . Так как, то, откуда. Поскольку угловой коэффициент касательной, то ее уравнение имеет вид
.
Определение. Нормальной прямой (или нормалью) к графику функции в точке называется прямая, проходящая через точкуперпендикулярно касательной в этой точке.
Угловой коэффициент нормали связан с угловым коэффициентом касательной формулой
.
Уравнение нормали к графику функции в точке
.
Бесконечные производные
Если функция непрерывна в точке иравенили, то говорят, что функцияимеет в точке
Пример 3.2. Рассмотрим функцию ,. Имеем
–вертикальная касательная к графику функции (рис. 3.2).
Пример 3.3. Рассмотрим функцию ,. Имеем:. Следовательно, прямая– вертикальная касательная к графику функции (рис. 3.3).
Односторонние производные
Пусть определена на множествеи– предельная точка.
Если существует конечный предел , то его называютлевой производной функции в точке и обозначают.
Аналогично . Число(если оно существует), называетсяправой производной функции в точке.
Теорема 3.2. Пусть – предельная точка. Функцияимеет производную в точкетогда и только тогда, когда,, причем
.
Пример 3. 4. . .
Имеем: ,.
Так как , функцияне имеет производной в нуле.
Пример 3.5. Пусть . Выясним, существует ли производная этой функции в точке.
Имеем: .
Итак, функция в точкеимеет производную.
Пример 3.6.
, то есть непрерывна в точке. Однако
не существует. Действительно, если , а если. Следовательно, предел по Гейне не существует.
studfiles.net
Производная функции одной переменной. Правила дифференцирования. Производная сложной функции
Определение производной
Рассмотрим функцию 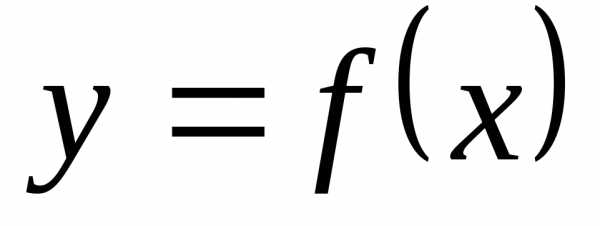
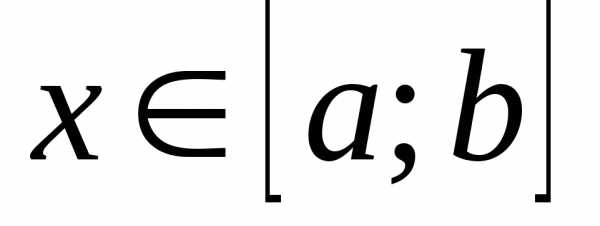 (рис.
31). Возьмем произвольную точку
(рис.
31). Возьмем произвольную точку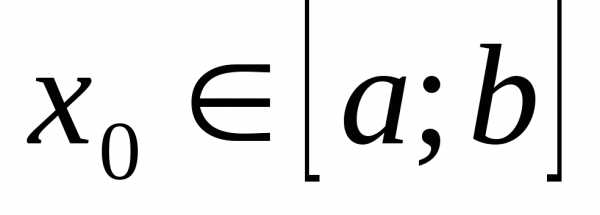 .
Для любого
.
Для любого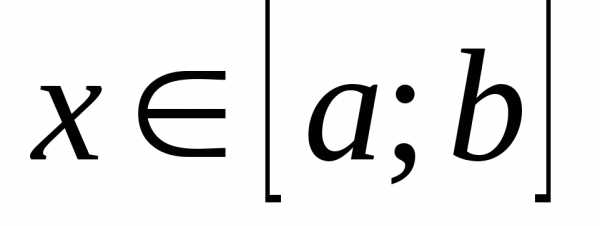 разностьх – х0называется
приращением аргументах в точке х0и обозначается
разностьх – х0называется
приращением аргументах в точке х0и обозначается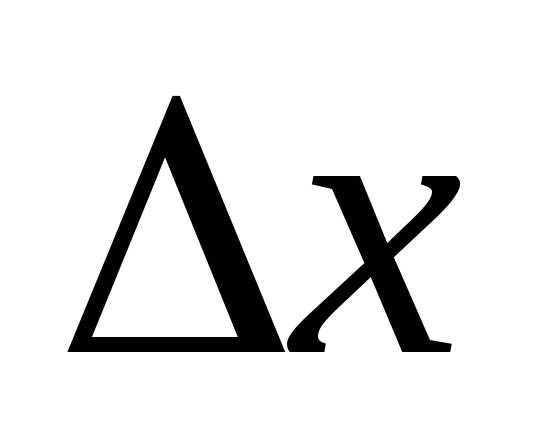 .
Таким образом,
.
Таким образом,Разность называется приращением функции в точкех0.
Производной функции 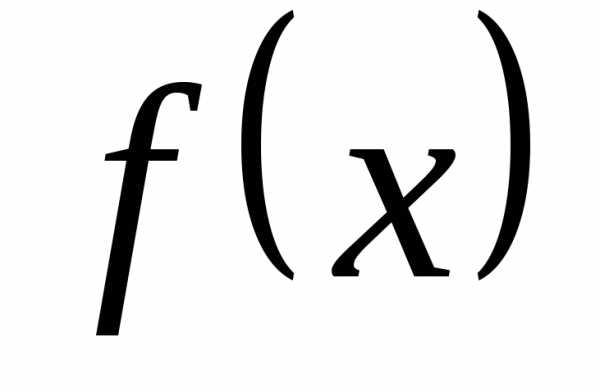 в точке х0называется предел
отношения приращения функции
в точке х0называется предел
отношения приращения функции к приращению аргумента
к приращению аргумента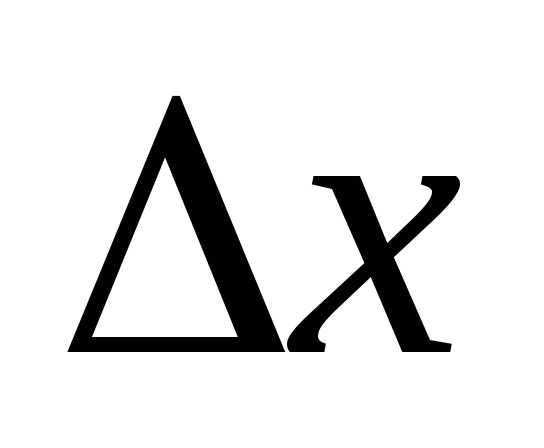
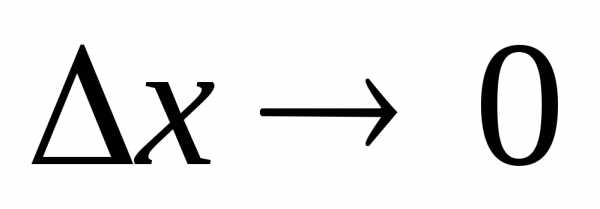 ,
если этот предел существует и обозначается
,
если этот предел существует и обозначается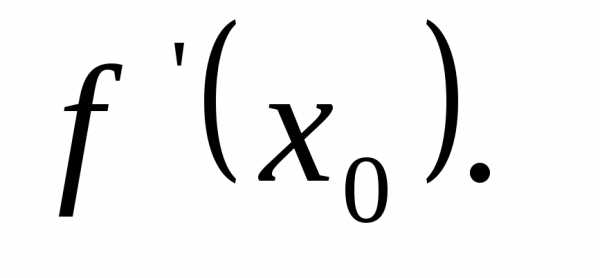
Пример.Вычислим по определению производную функции в заданной точке:
Решение. Согласно определению производной, имеем:
;
Ответ. 1) –3; 2) 4а + b;
3) 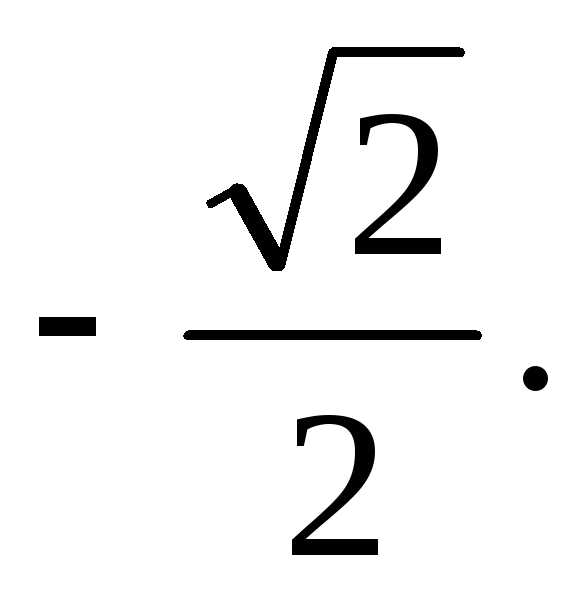
Задание. Вычислить по определению производную функции в заданной точке:
Решение.
__________________________________________________________________________________________________________________________________________________________Ответ: 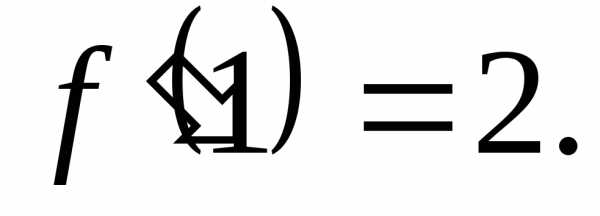
Функция, имеющая производную в точке х0,называется дифференцируемой
в этой точке. Если же функция дифференцируема
в каждой точке некоторого интервала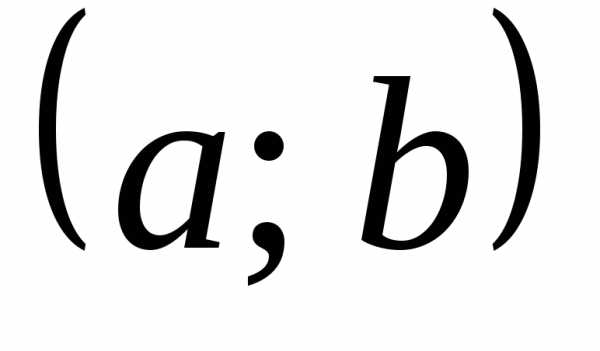 ,
то она дифференцируема на этом интервале.
Необходимое условие существования
производной вытекает из следующей
теоремы.
,
то она дифференцируема на этом интервале.
Необходимое условие существования
производной вытекает из следующей
теоремы.
Теорема. Если функция 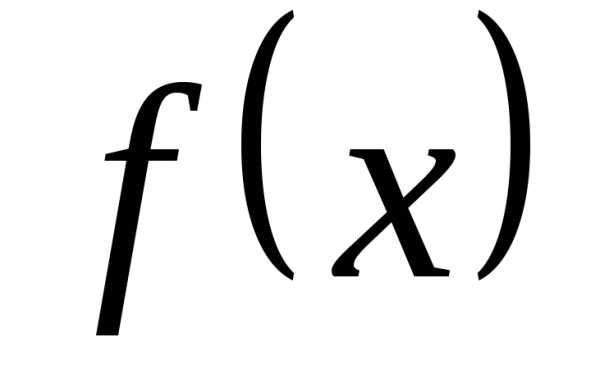 дифференцируема в точке х0, то она
непрерывна в этой точке.
дифференцируема в точке х0, то она
непрерывна в этой точке.
Однако непрерывность функции в точке не является достаточным условием дифференцируемости функции в точке.
Пример.Функция 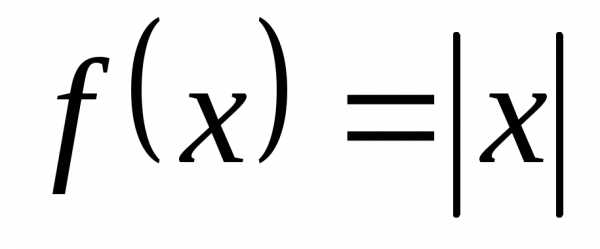 непрерывна в точкех
непрерывна в точкех
Геометрический смысл производной
Касательной к кривой Lв точкеМ0 Î Lназывается прямаяМ0Т, занимающая предельное положение секущейМ0М (МÎ L)приМ ® М0(если такое положение существует).
Геометрический смысл производной:
производная функции 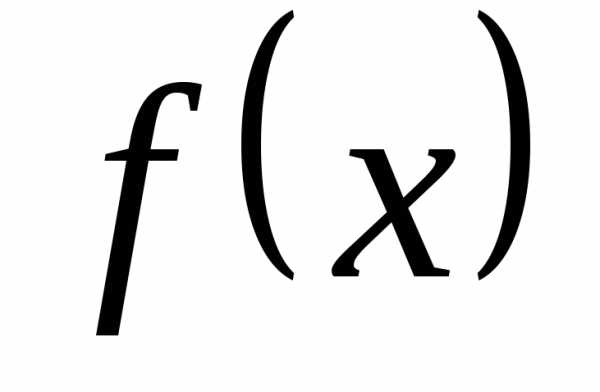 в точкех0 равна угловому
коэффициенту касательной, проведенной
к графику данной функции в его точке с
абсциссой х0:
.
в точкех0 равна угловому
коэффициенту касательной, проведенной
к графику данной функции в его точке с
абсциссой х0:
.
Уравнение касательной к кривой Lв точке (х0;f (х0)), записанное как уравнение прямой, проходящей через точку (х0;f (х0
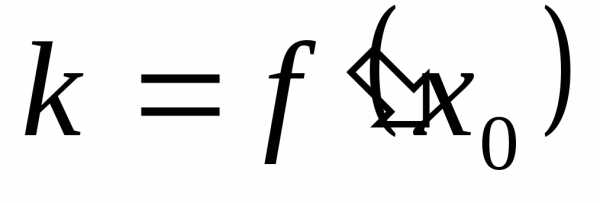 имеет вид:
имеет вид:или
.
Уравнение нормали к кривой (прямой, проходящей через точку кривой L с абсциссой х0 перпендикулярно касательной) составляется аналогичным образом с учетом того, что ее угловой коэффициент равен:
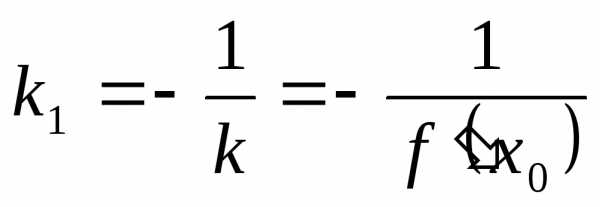 ,
,
то естьили.
Пример.Составим уравнения касательной и нормали к данной кривой в данной точке:
Решение.
Согласно определению производной, имеем:
Тогда уравнение касательной примет вид: или
Уравнение нормали запишем в виде:
Согласно определению производной, имеем:
Т
огда уравнение касательной примет
вид: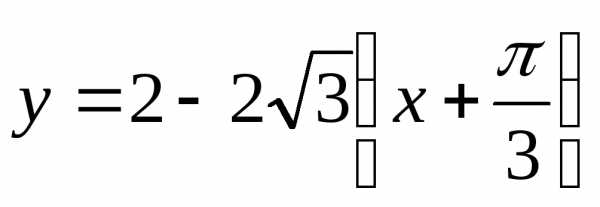 .
.
Уравнение нормали запишем в виде:
Механический смысл производной
Положим, что материальная точка движется
прямолинейно по закону 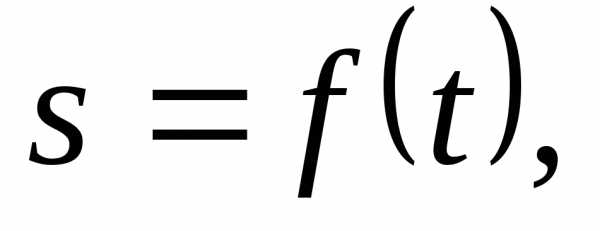 тогда ее средняя скорость за промежуток
временивычисляется по формуле:
тогда ее средняя скорость за промежуток
временивычисляется по формуле:
Как известно, мгновенной скоростью в
момент времени t0 называется предел (если он существует),
которому стремится средняя скорость
за промежуток временипри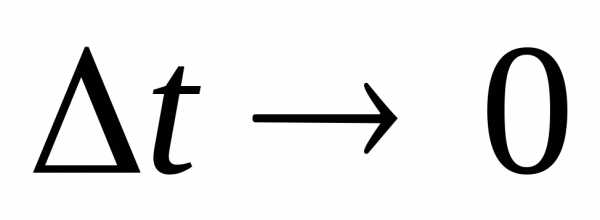 ,
т.е.
,
т.е.
Таким образом, мгновенная скорость движения материальной точки в любой момент времени tесть производная от путиsпо времениt.
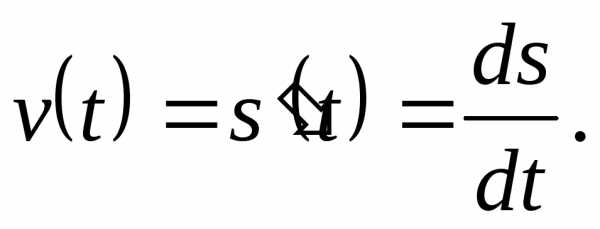
В этом состоит физический смысл производной.
Пример.Найдем скорость движения материальной точки в момент времениt = 4, если закон движения задан формулой:
Решение. Найдем по определению: , тогда
studfiles.net
1.17. Свойства функций непрерывных на отрезке.
Функция  называетсянепрерывной
на отрезке
называетсянепрерывной
на отрезке  если она непрерывна в каждой точке
интервала
если она непрерывна в каждой точке
интервала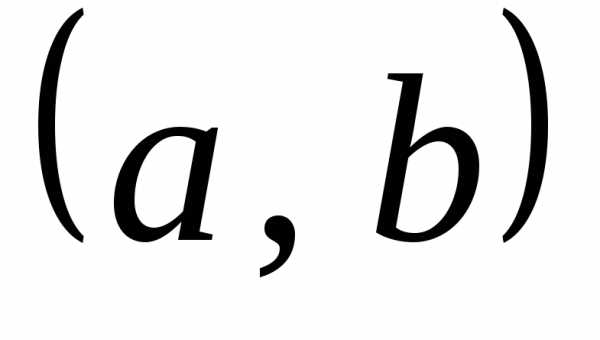 ,
а на концах отрезка выполняются равенства
,
а на концах отрезка выполняются равенства
.
Всевозможные
функции непрерывные на отрезке 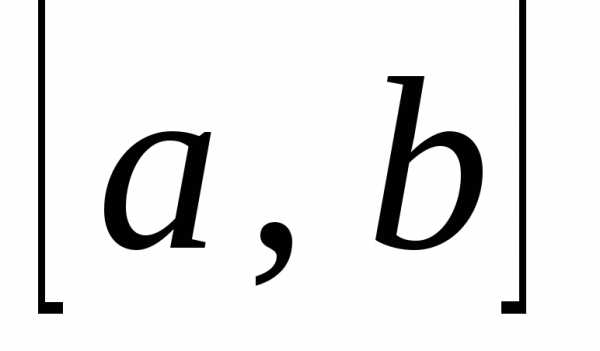 образуют множество, которое называют
– класс функций
образуют множество, которое называют
– класс функций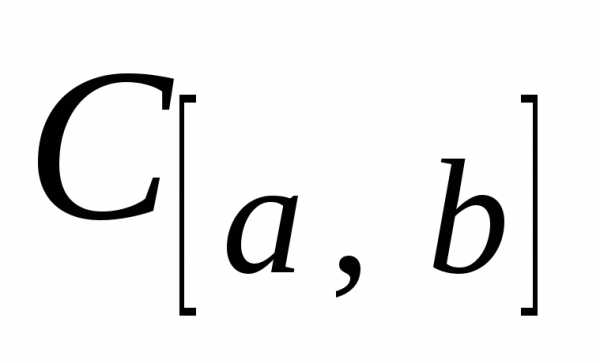 .
Функция
.
Функция является элементом этого множества
является элементом этого множества
.
Теорема 1. (Об ограниченности непрерывной на отрезке функции).
Если , то она ограничена на этом отрезке.
Теорема 2. (О наибольшем и наименьшем значении непрерывной на отрезке функции).
Если , то существуют такие точки, что
.
Теорема 3. Если
,
причем,
то, каково бы ни было число,
найдется хотя бы одна такая точка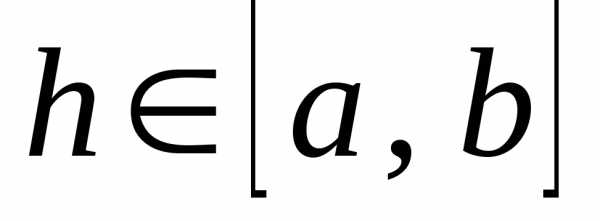 ,
в которой буде выполняться соотношение
,
в которой буде выполняться соотношение
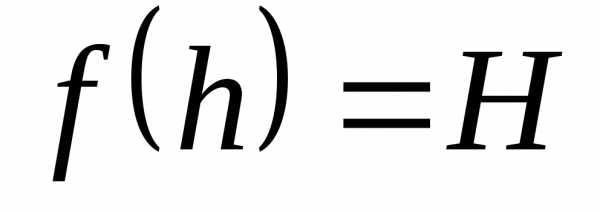 .
.
и ,то для любого значенияС, заключенного между А и В, существует такая точка х0[a, b], что (х0) = С.
Все три теоремы принимаются без доказательства.
2. Дифференциальное исчисление
2.1. Производная и дифференциал числовой функции одной переменной.
Рассмотрим функцию
одной переменной 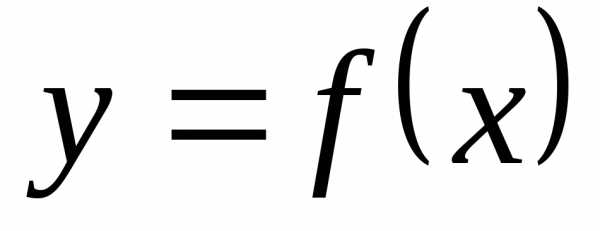 .
Выберем в области определения произвольную
точку
.
Выберем в области определения произвольную
точку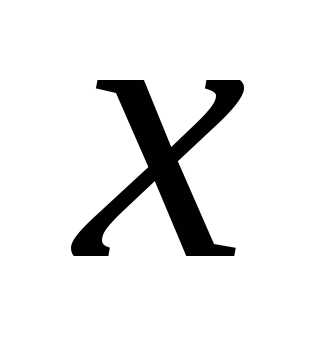 и зафиксируем ее. Дадим этой точке
приращение
и зафиксируем ее. Дадим этой точке
приращение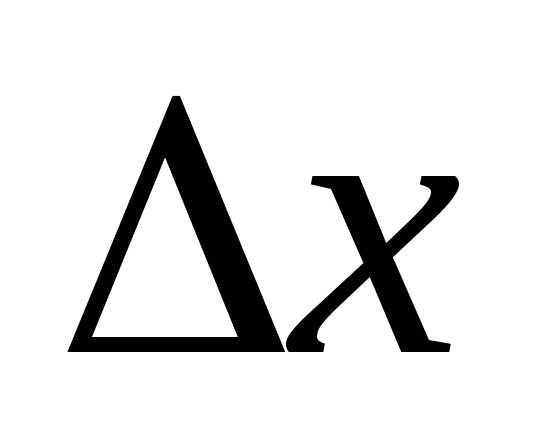 и образуем новую точку –
и образуем новую точку –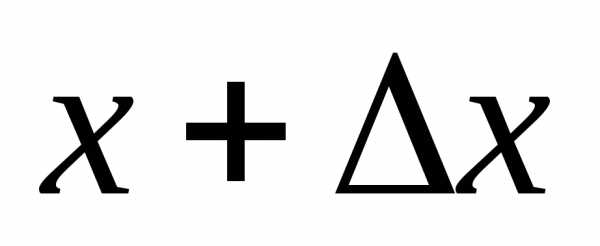 .
Вычислим приращение функции
.
Вычислим приращение функции
(2.1.1)
Составим отношение
приращений функции к приращению аргумента 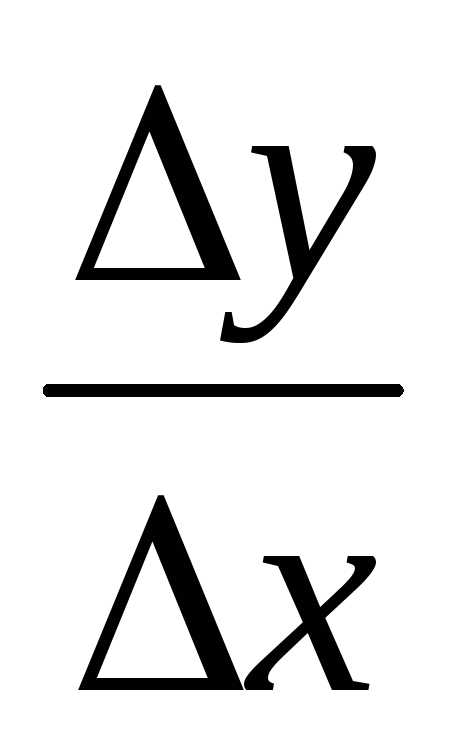 .
Если существует предел этого отношения
при
.
Если существует предел этого отношения
при ,
то этот предел называетсяпроизводной числовой функции одной переменной и
обозначается
,
то этот предел называетсяпроизводной числовой функции одной переменной и
обозначается
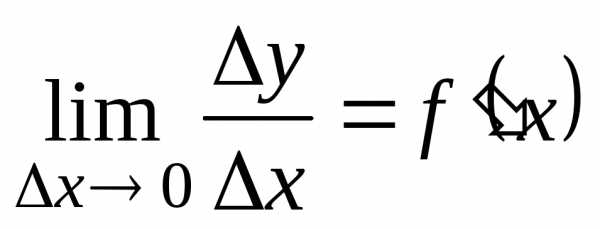 (2.1.2)
(2.1.2)
Применим к соотношению (2.1.2) теорему о связи величины, имеющей конечный предел с бесконечно малой величиной (Теорема 1, раздел 1.8)
(2.1.3)
Умножим равенство
(2.1.3) на 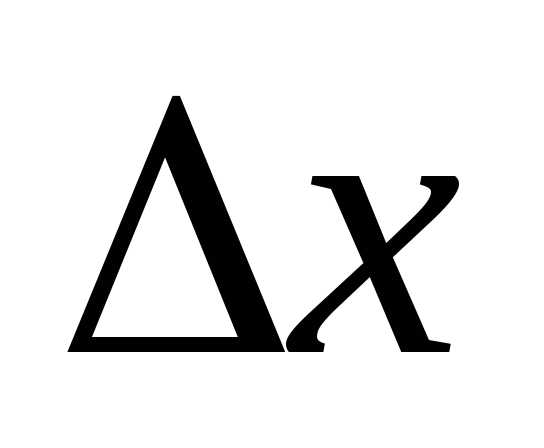
. (2.1.4)
В правой части
формулы (2.1.4) два слагаемых. Первое
является линейным относительно 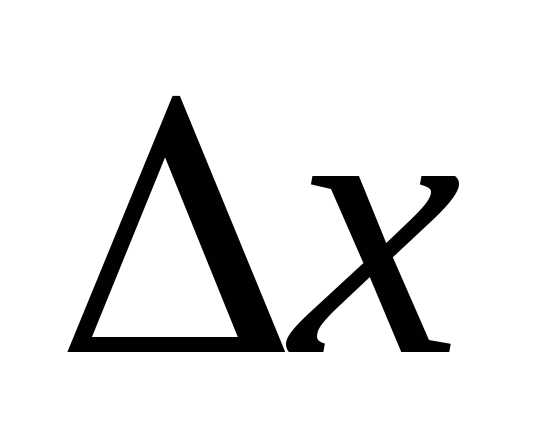 и более крупным – это главная часть
БМВ. Второе – нелинейно и является БМВ
более высокого порядка малости, чем
первое. Формулу (2.1.4) можно переписать
в виде
и более крупным – это главная часть
БМВ. Второе – нелинейно и является БМВ
более высокого порядка малости, чем
первое. Формулу (2.1.4) можно переписать
в виде
(2.1.5)
Главная и линейная часть формулы (2.1.5) обозначается
, (2.1.6)
и называется дифференциалом числовой функции одной переменной.
Применим формулу
(2.1.6) для функции 
.
Таким образом, для независимой переменной получаем
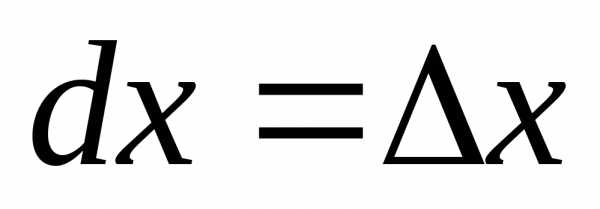 .
.
Формула (2.1.6) принимает симметричный вид
, (2.1.7)
и мы получаем еще одно широко используемое обозначение производной
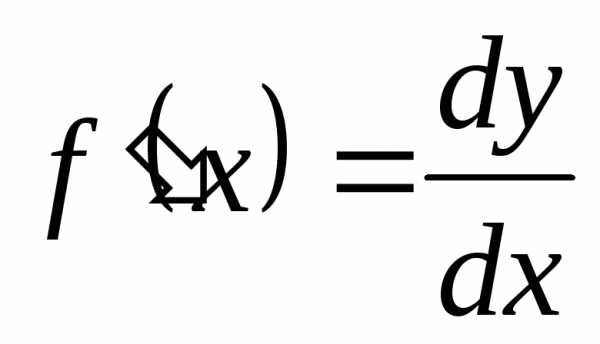 . (2.1.8)
. (2.1.8)
Иногда используют формулу
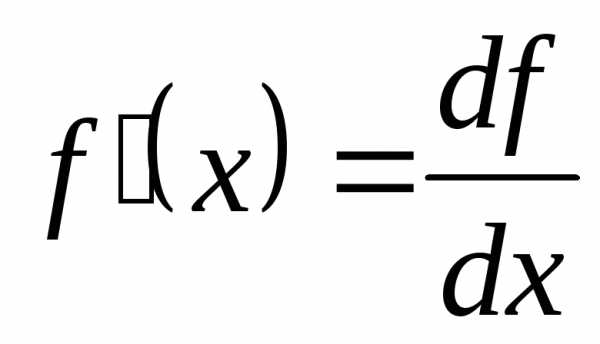 .
.
Сформулируем без доказательства две теоремы о дифференцируемости числовых функций одной переменной.
Теорема 1. Для дифференцируемости числовой функции одной переменной необходимо и достаточно, чтобы для этой функции существовала конечная производная.
Теорема 2. Всякая дифференцируемая в некоторой точке числовая функция одной переменной непрерывна в этой точке.
2.2. Геометрический смысл производной и дифференциала числовой функции одной переменной.
Выясним, что означает производная и дифференциал функции одной переменной с точки зрения геометрии.
Из прямоугольных
треугольников  и
и находим
находим
.
Здесь  – угол
наклона секущей линии. Если
то
– угол
наклона секущей линии. Если
то и секущая линия будет стремиться занять
положение касательной линии
и секущая линия будет стремиться занять
положение касательной линии .
Тогда,
.
Тогда,
. (2.2.1)
Таким образом, геометрический смысл производной функции одной переменой состоит в том, что она равна тангенсу угла наклона касательной линии к графику функции в заданной точке.
Из прямоугольного
треугольника  находим
находим
. (2.2.2)
Таким образом, геометрический смысл дифференциала функции одной переменной состоит в том, что он равен приращению ординаты касательной линии к графику функции в заданной точке.
Из курса физики
известен физический смысл производной
функции. Если 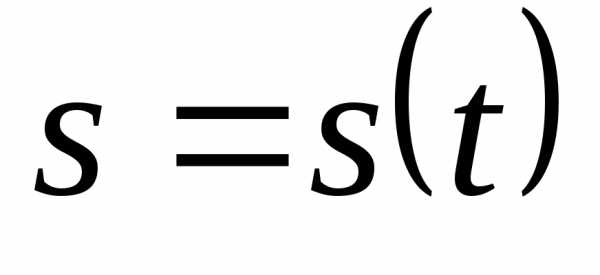 есть функция пути по времени, то
производная этой функцииесть скорость движения рассматриваемого
объекта.
есть функция пути по времени, то
производная этой функцииесть скорость движения рассматриваемого
объекта.
studfiles.net
ответы на вопросы 1-7
1)Производная функции одной переменной и ее геометрический смысл.
Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Итак, по определению
Производная функции есть некоторая функция , произведенная изданной функции.
Производная в точке равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна . В этом заключается геометрический смысл производной.
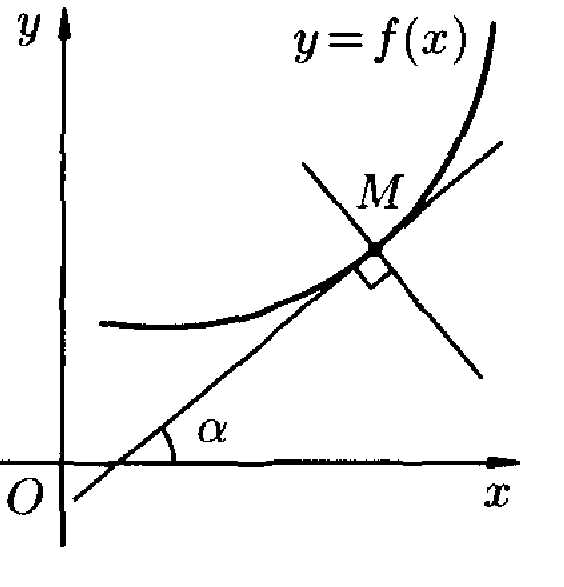
Если точка касания М имеет координаты , угловой коэффициент касательной есть . Пользуясь уравнением прямой, проходящей через заданную точку в заданном направлении можно записать уравнение касательной .
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой. Уравнение нормали имеет вид .
2)Дифференцируемость функции одной переменной, схема вычисления производной. Производная сложной функции.
Функция , имеющая производную в каждой точке интервала ,называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
Вычисление производной функции производится по следующей схеме :
1)Находим приращение функции на отрезке , ;
2)Делим приращение функции на приращение аргумента : ;
3)Находим предел , устремляя к нулю.
.
Производная сложной функции.
Если функция имеет производную в точке , а функция имеет производную в соответствующей точке , то сложная функция имеет производную в точке , которая находится по формуле .
3)Основные правила дифференцирования функции одной переменной.
Пусть функции — две дифференцируемые в некотором интервале функции.
1)Производная суммы (разности) двух функций равна сумме(разности) производных этих функций:
2)Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:
3)Производная частного двух функций ,если равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя:
.
4)Производная функции, заданной параметрически.
Пусть зависимость между аргументом и функцией задана параметрически в виде двух уравнений ,где — вспомогательная переменная ,называется параметром.
Найдем производную ,считая , что функции имеют производные и что функция имеет обратную . По правилу дифференцирования обратной функции .
Функцию , определяемую параметрическими уравнениями, можно рассматривать как сложную функцию , где .
По правилу дифференцирования сложной функции имеем: .
Из всего этого получаем
5)Производная функции, заданной неявно.
Под неявным заданием функции понимают задание функции в виде уравнения ,не разрешенного относительно .
Если неявная функция задана уравнением , то для нахождения производной от по нет необходимости разрешать уравнение относительно : достаточно продифференцировать это уравнение по ,рассматривая при этом как функцию , и полученное затем уравнение разрешить относительно .
6)Логарифмическое дифференцирование.
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать. А затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.
1)Логарифмируем обе части равенства с помощью натурального логарифма.
2)Используем свойства логарифма .
3)Дифференцируем обе части равенства по , с учетом что -сложная функция.
4)Выражаем ;
5).
7)Теоремы Ролля и Лагранжа. Геометрическая интерпретация этих теорем.
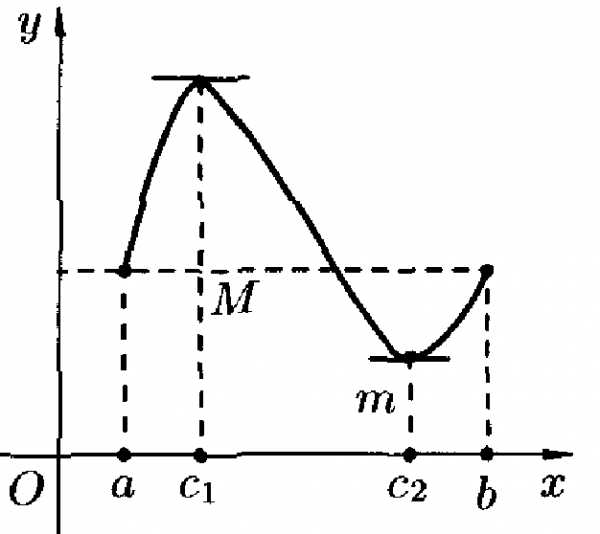
Теорема Ролля: Если функция непрерывна на отрезке , дифференцируема на интервале и на концах отрезка принимает одинаковые значения , то найдется хотя бы одна точка , в которой производная обращается в нуль, т.е. .
Геометрически теорема Ролля означает, что на графике функции найдется точка, в которой касательная к графику параллельна оси .
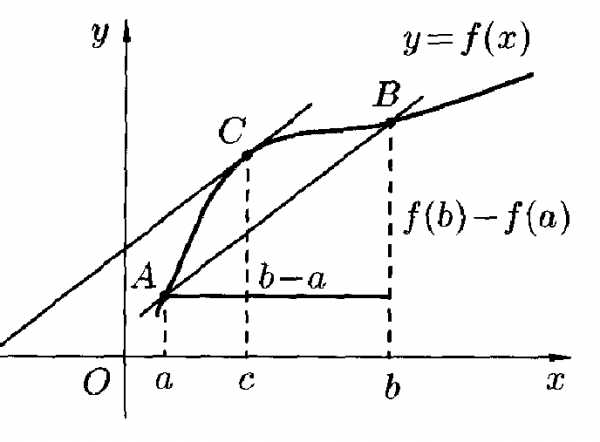
Теорема Лагранжа : Если функция непрерывна на отрезке , дифференцируема на интервале , то найдется хотя бы одна точка такая, что выполняется равенство
.
Геометрический смысл теоремы Лагранжа таков: на графике функции найдется точка , в которой касательная к графику функции параллельна секущей .
studfiles.net
Дифференциальное исчисление функций одной переменной
§1. Производная
Пусть функция f определена в V(x0).
Придадим точке х0 произвольное приращение 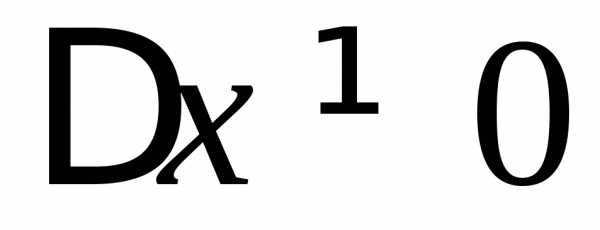 так, чтобыx0+
так, чтобыx0+ x
x V(x0).
Тогда функция f(x)
получит приращение
V(x0).
Тогда функция f(x)
получит приращение
.
Рассмотрим
—
функцию, определённую в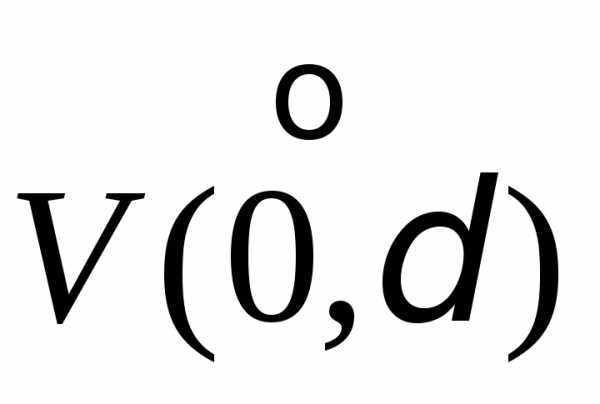 .
.
Определение 1. Производной функции f в точке х0называется предел при отношения приращения функции к вызвавшему его приращению аргумента, если этот предел существует.
Обозначается 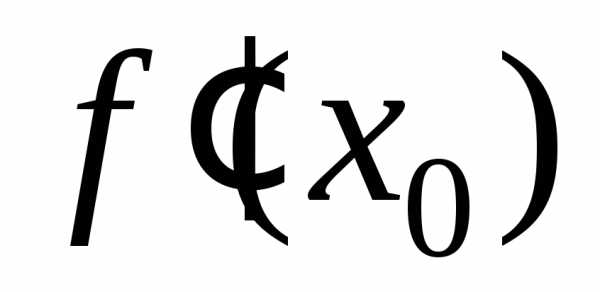 ,
,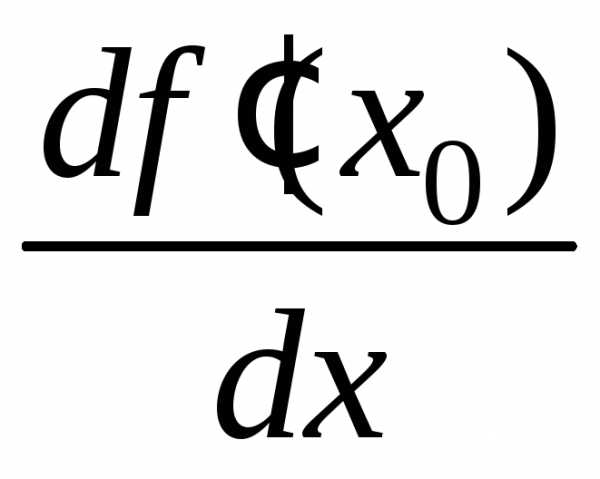 ,
,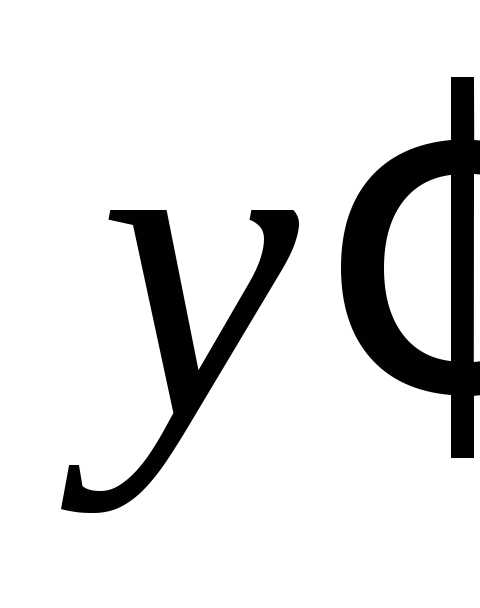 ,
,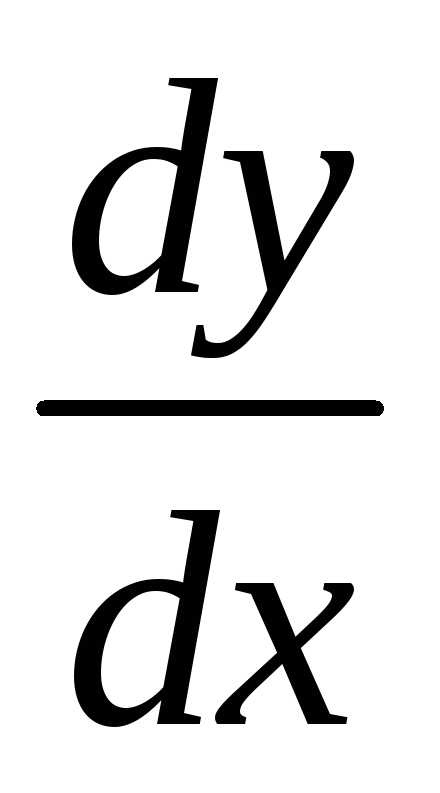 ,
,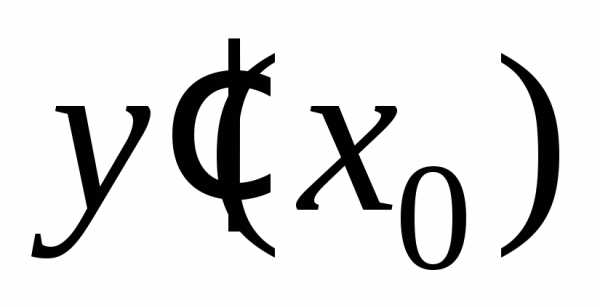 .
.
Таким образом, по определению 1 . (1)
Обозначения 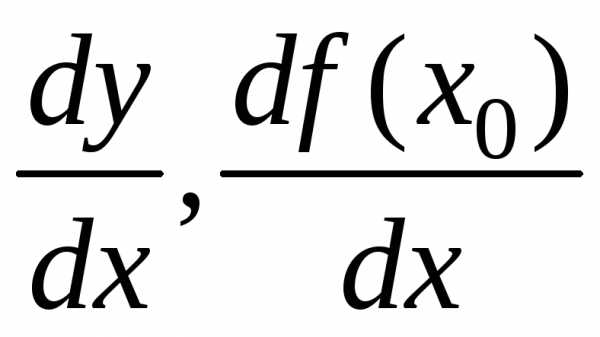 ввёл Лейбниц (1646-1716), а
ввёл Лейбниц (1646-1716), а ,
,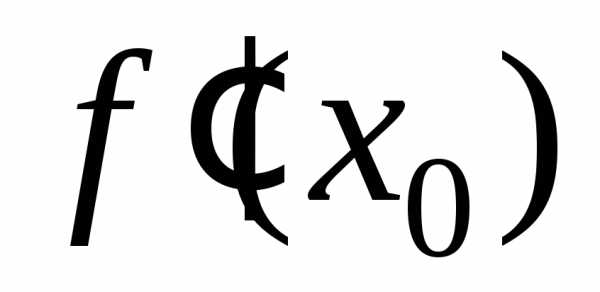 -Лагранж
(1736-1813).
-Лагранж
(1736-1813).
Производная функции в точке – число.
Пусть
,,х V(x0).
Тогда (1) равносильно
V(x0).
Тогда (1) равносильно
. (2)
Если 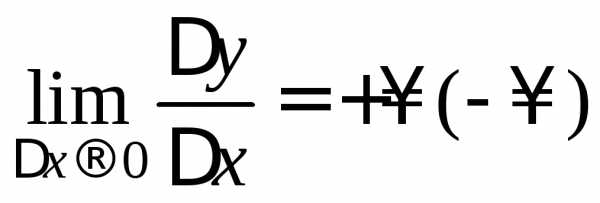 ,
то говорят, что в точкех0 существует бесконечная производная,
равная
,
то говорят, что в точкех0 существует бесконечная производная,
равная 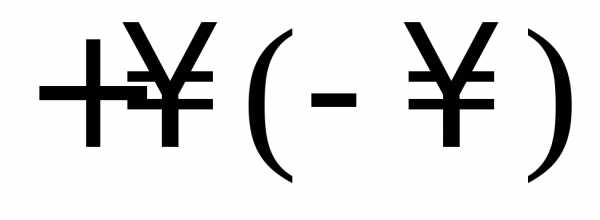 .
Обозначается().
.
Обозначается().
Определение 2. Правой (левой) производной функции в точке х0 называют правый (левый) предел отношения 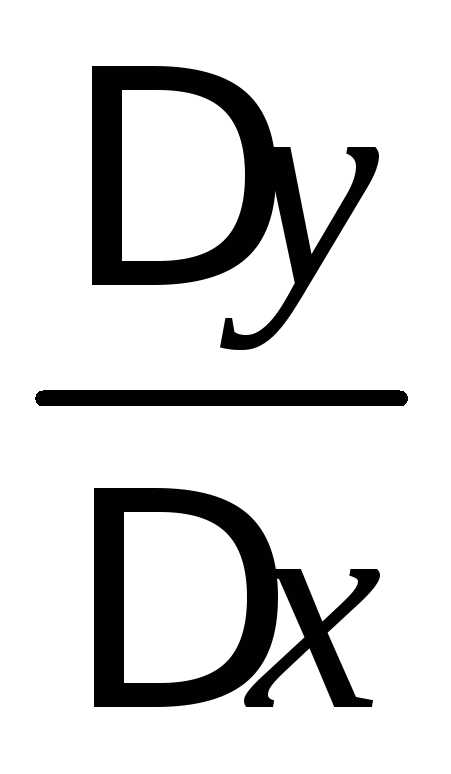 при,
если этот предел существует.
при,
если этот предел существует.
, .
Правая и левая производные называются односторонними производными в точке х0.
Справедливо
следующее утверждение:
функция f имеет в точке х0 производную тогда и только тогда, когда 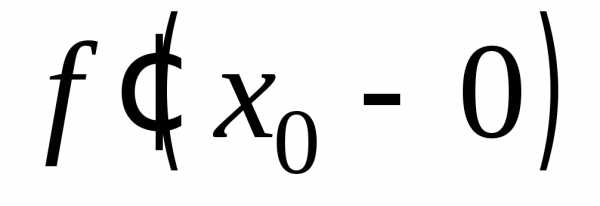 и
и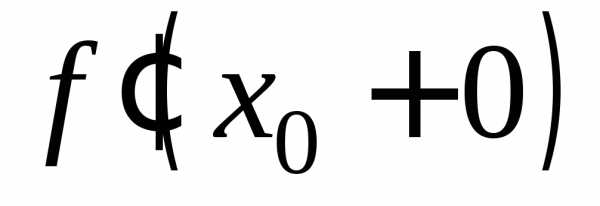 существуют и равны. Тогда.
существуют и равны. Тогда.
Пусть f имеет производную 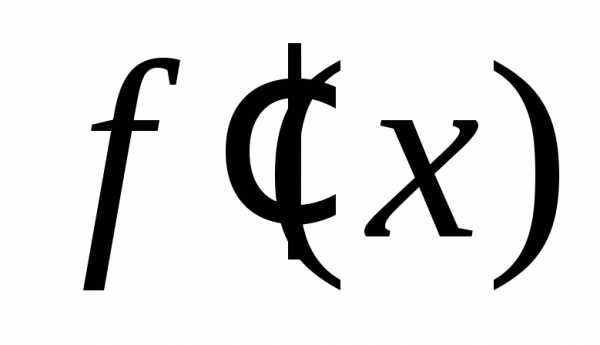 в каждой точке
в каждой точке .
Поставим в соответствие точкех производную функции в этой точке:
,
.
Поставим в соответствие точкех производную функции в этой точке:
, .
Это соответствие определяет функцию
.
Это соответствие определяет функцию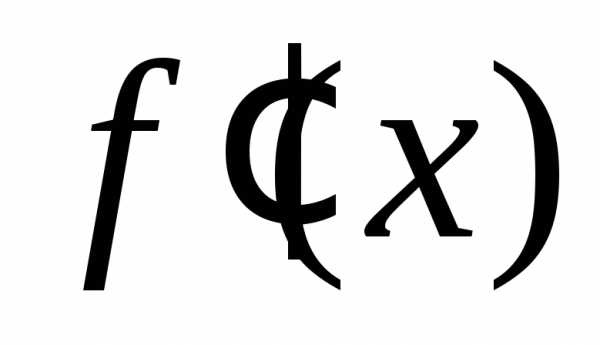 аргументах,
определённую на
аргументах,
определённую на  .
Она называетсяпроизводной
функцией от
функции f.
.
Она называетсяпроизводной
функцией от
функции f.
Значение 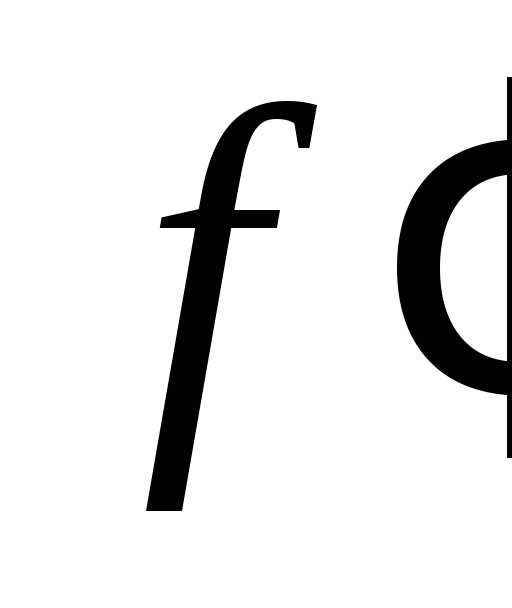 в
точкех является производной функции в точке х (может быть
числом,
в
точкех является производной функции в точке х (может быть
числом,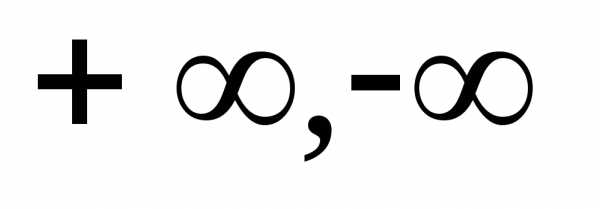 ).
).
Примеры.
1) y=f(x)=c  ..
..
Выберем 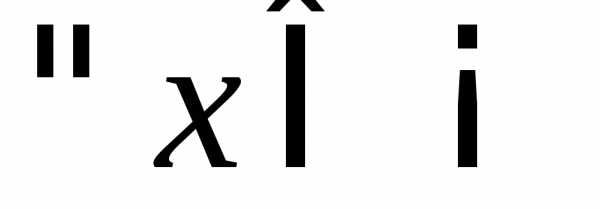 ,
придадим значениюх приращение
,
придадим значениюх приращение  .
Тогда
.
Тогда
.
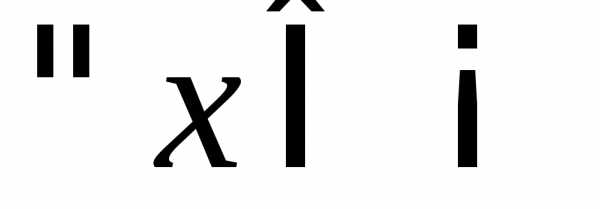 .
.
Производная
постоянной функции тождественно равна
нулю:  .
.
2) y=f(x)=x,  .
.
Выберем 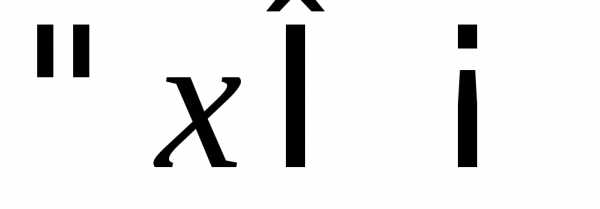 ,
придадим значениюх приращение
,
придадим значениюх приращение  .
Тогда
.
Тогда
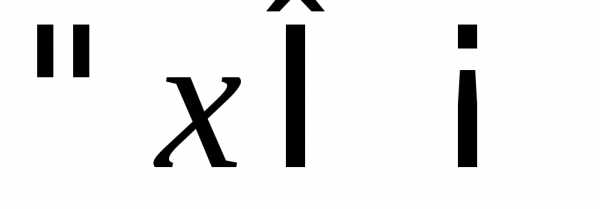 .
.
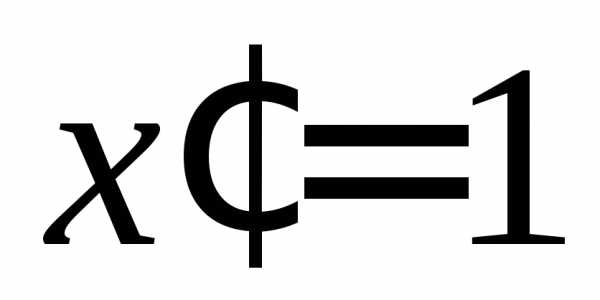 .
.
3) y=f(x)=|x|  .
.
Пусть х<0, .
Пусть х>0, .
Пусть х=0, ,
.
Т.к.
,то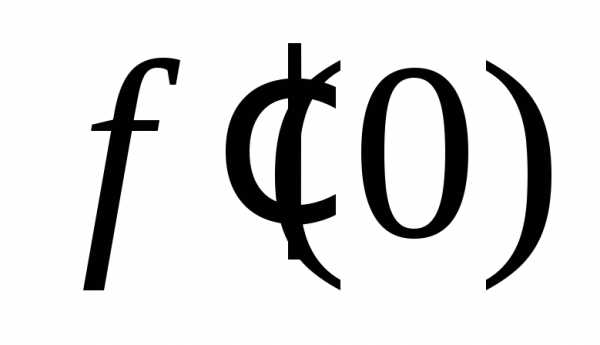 не существует.
не существует.
§2. Дифференцируемость и дифференциал функции
1. Дифференцируемость функции
Пусть y=f(x)
определена в некоторой окрестности
точки х0V(х0).
Возьмём 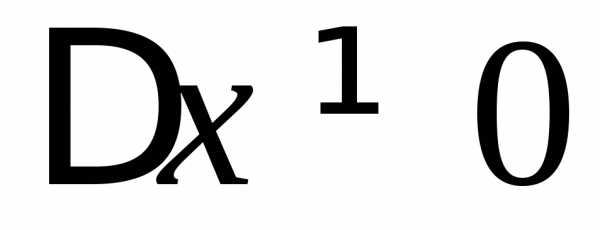 :,.
:,.
Определение 1. Функция f(x)
называется дифференцируемой
в точке х0,
если её приращение 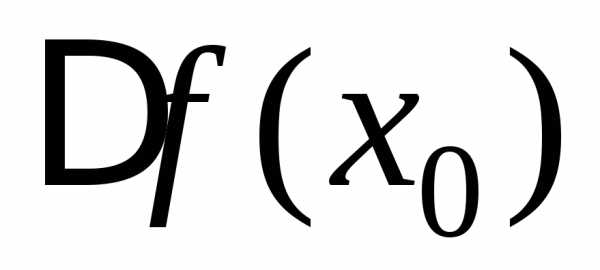 в этой точке, соответствующее приращению
аргумента
в этой точке, соответствующее приращению
аргумента ,
может быть представлено в виде
,
может быть представлено в виде
, (1)
где  —
некоторое число, не зависящее от
—
некоторое число, не зависящее от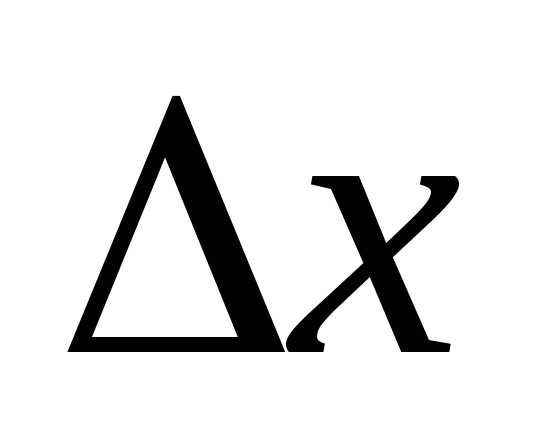 ,
,
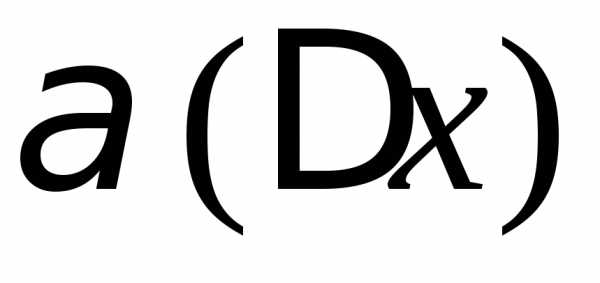 —
функция от
—
функция от  ,
бесконечно малая при,
т.е..
,
бесконечно малая при,
т.е..
Замечание 1. В (1) мы предполагали, что 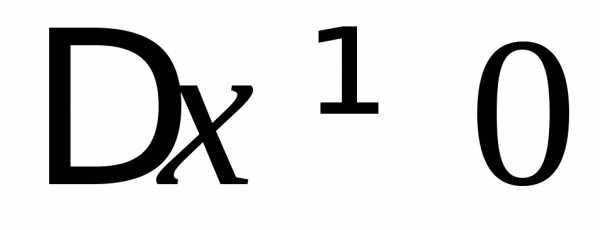 .
Значит, в точке
.
Значит, в точке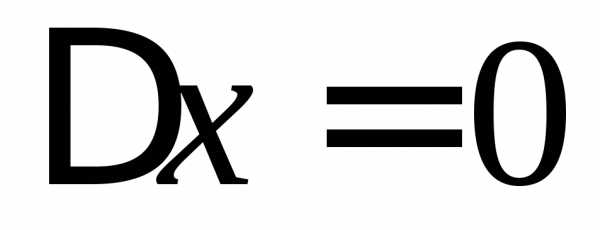 функция
функция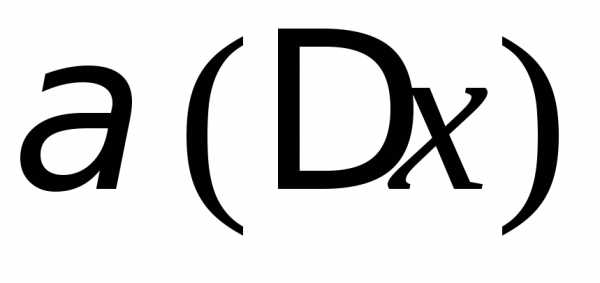 ,
вообще говоря, не определена. Будем
считать, что.
В таком случае
,
вообще говоря, не определена. Будем
считать, что.
В таком случае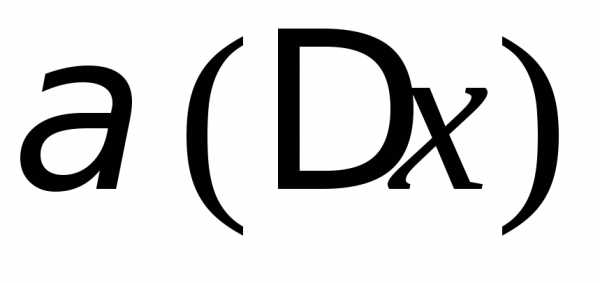 непрерывна в точке
непрерывна в точке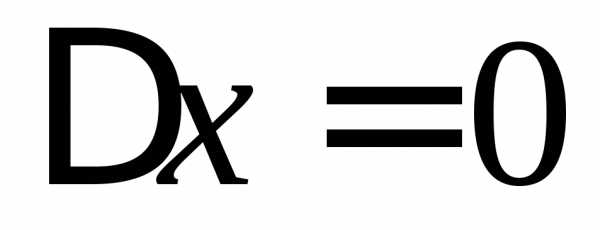 ,
и равенство (1) справедливо и при
,
и равенство (1) справедливо и при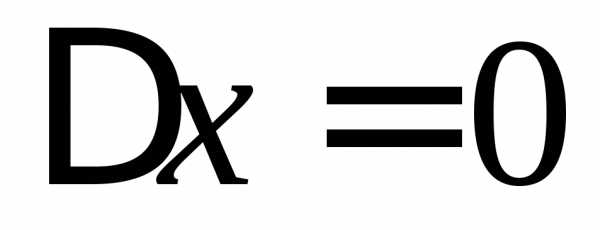 .
.
Замечание 2. Так как при , то. Тогда (1) можно записать в виде:
. (2)
Пример. Доказать, что функция дифференцируема в точкех=1.
Придадим х=1
приращение 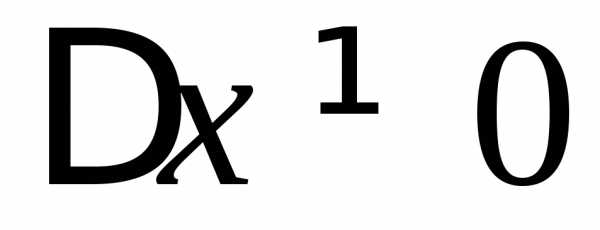 ,
получим.
Тогда
,
получим.
Тогда
.
Здесь А=-1, . Значит,f(x) дифференцируема в точке х=1.
Теорема
1 (необходимое
и достаточное условие дифференцируемости).
Для того, чтобы функция f(x)
была дифференцируема в точке х0 необходимо и достаточно, чтобы она
в этой точке имела производную 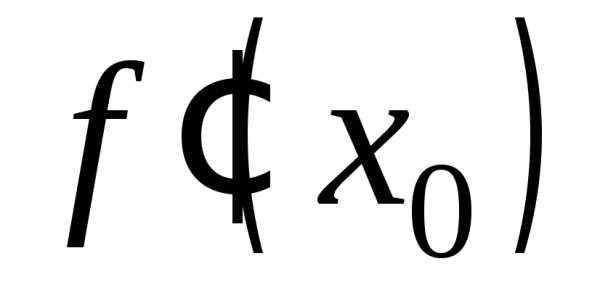 ,
при этом.
,
при этом.
Доказательство.
 1) Необходимость.
1) Необходимость.
Пусть f(x)
дифференцируема в точке х0, т. е.
,
где.
Пусть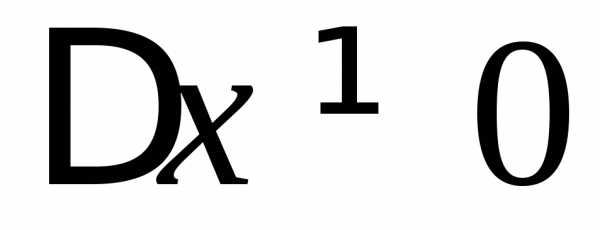 .
Тогда
.
Тогда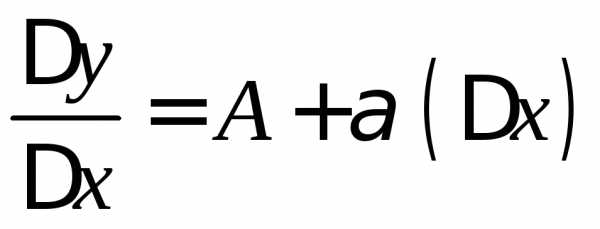 .
.
Так как существует 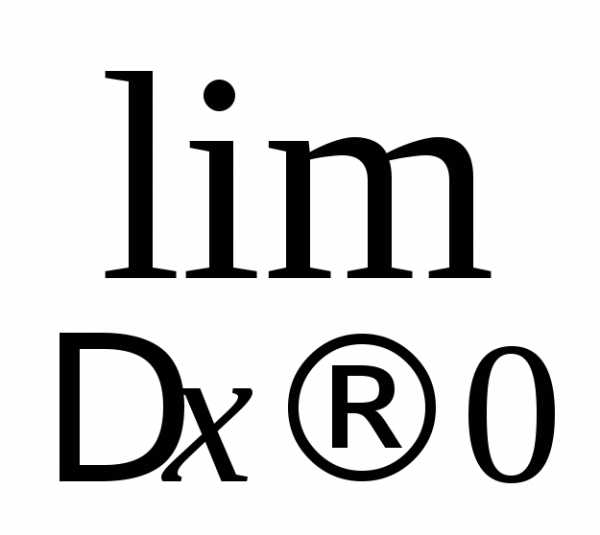 правой части:,
то существует и
правой части:,
то существует и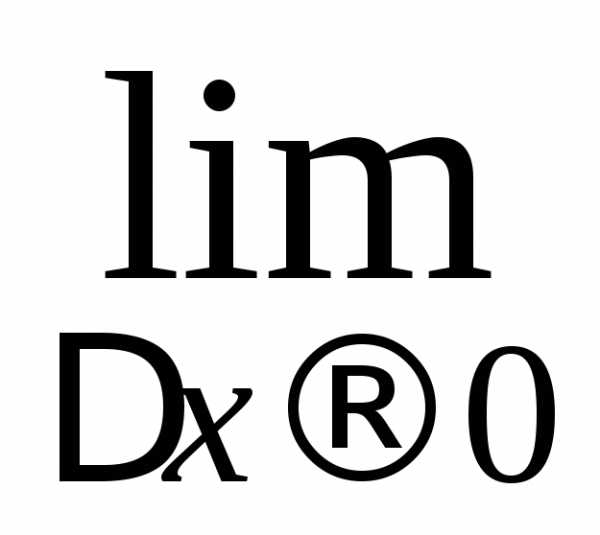 левой части:
левой части: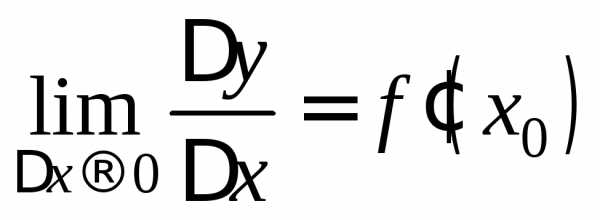 ,
и эти пределы равны:.
,
и эти пределы равны:.
2) Достаточность.
Пусть существует 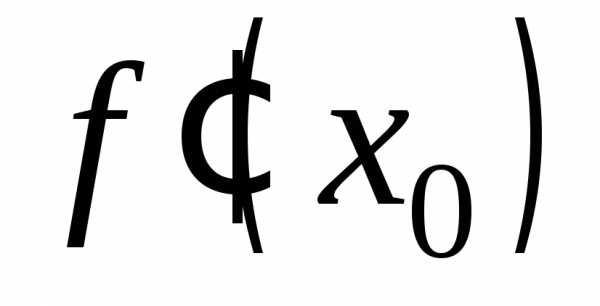 ,
то есть существует.
Тогда по необходимому и достаточному
условию существования предела функции
в точке,
где
,
то есть существует.
Тогда по необходимому и достаточному
условию существования предела функции
в точке,
где 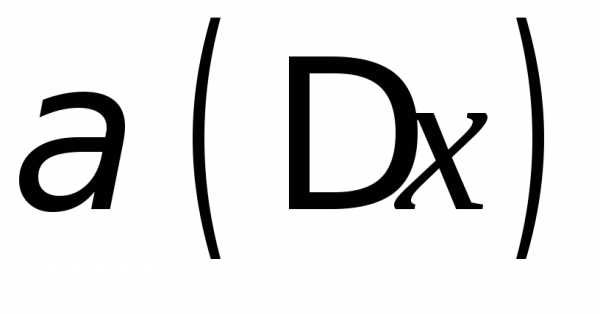 — бесконечно малая при.
Следовательно, по определению (1)f(x)
дифференцируема в точке х0.
— бесконечно малая при.
Следовательно, по определению (1)f(x)
дифференцируема в точке х0.
Из этой теоремы следует определение 2, эквивалентное определению 1.
Определение 2. Функция f(x) называется дифференцируемой в точке х0, если она в этой точке имеет конечную производную.
Операция нахождения производной функции f(x) в точке или на множестве называется дифференцированием функции f(x).
Теорема 2 (непрерывность дифференцируемой функции). Если функция f(x) дифференцируема в точке х0, то она непрерывна в этой точке.
Доказательство.
 Так как f(x)
дифференцируема в точке х0,
то
Так как f(x)
дифференцируема в точке х0,
то
.
Значит,
по определению функция непрерывна в
точке х0.
Следствие. Если функция f(x)имеет в точке х0 производную, то она непрерывна в этой точке.
Замечание. Предположение, обратное т. 2, неверно. Функция, непрерывная в точке х0, может не быть не дифференцируемой в этой точке.
Пример. y=f(x)=|x| — непрерывна в точке х0=0, но не дифференцируема в ней.
studfiles.net
Тема 4.7. Дифференциальное исчисление функции одной переменной. Производная и дифференциал.
Рассмотрим функцию y=f(x), непрерывную в некоторой окрестности точки x. Из этого следует, что в этой точке бесконечно малому приращению аргумента x соответствует бесконечно малое приращение функцииf.
О. Производной функции y=f(x) по аргументу х называется конечный предел отношения приращения функции f =f(x+x) – f(x). к приращению аргумента x , при стремлении x к 0:
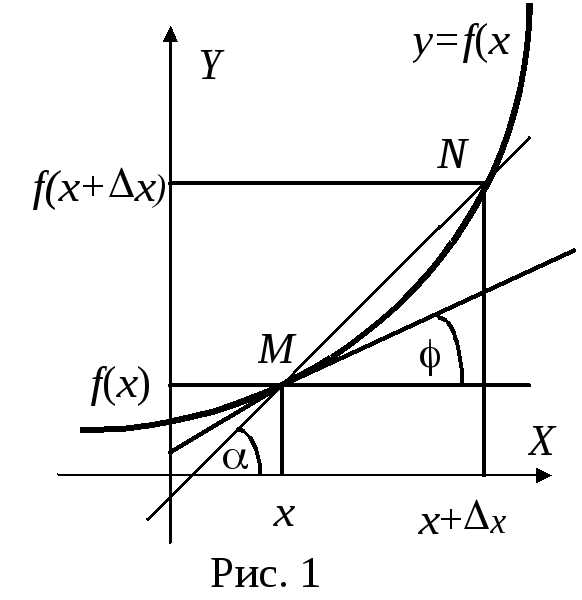
Пусть x стремится к нулю. При этом точка N будет двигаться вдоль кривой y = f(x), приближаясь к точке M, а секущая MN будет приближаться к касательной к графику функции, при этом её угол наклона будет стремиться к углу наклона касательной к кривой в точке x. Таким образом, геометрический смысл производной заключается в том, что производная функции f(x) в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.
Физический смысл производной: производная есть скорость изменения функции в точке х.
Нахождение производной функции y = f(x) называется дифференцированием.
Производная функции f(x) не существует в тех точках, в которых функция не является непрерывной. В то же время функция может быть непрерывной в точке x0, но не иметь в этой точке производной.
Так функция y = x не имеет производной в точке x = 0, хотя является непрерывной в этой точке.
Таблица производных основных элементарных функций.
Таблица производных.
1. (xn)’=nxn-1 2. (ax)’=axlna 3. (ex)’=ex
4.
(logax)’=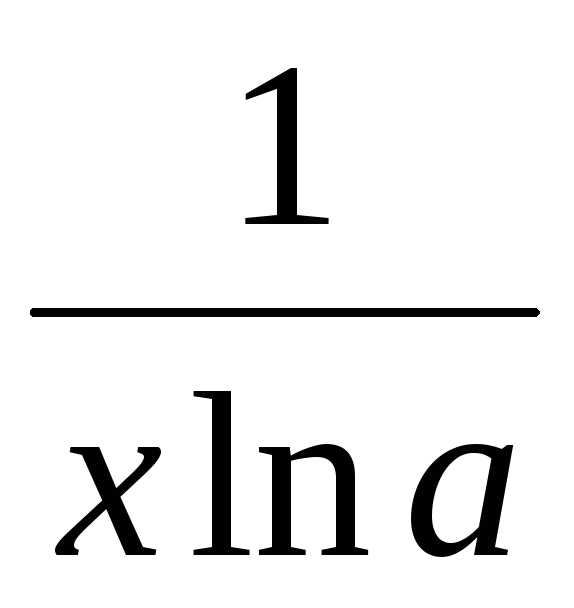 5.
(lnx)’=
5.
(lnx)’= 6.
(sinx)’=cosx
6.
(sinx)’=cosx
7.
(cosx)’=-sinx 8. (tgx)’=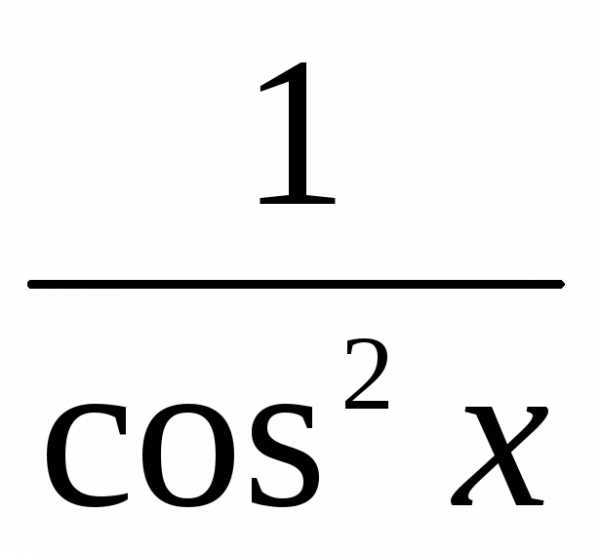 9.(ctgx)’=-
9.(ctgx)’=-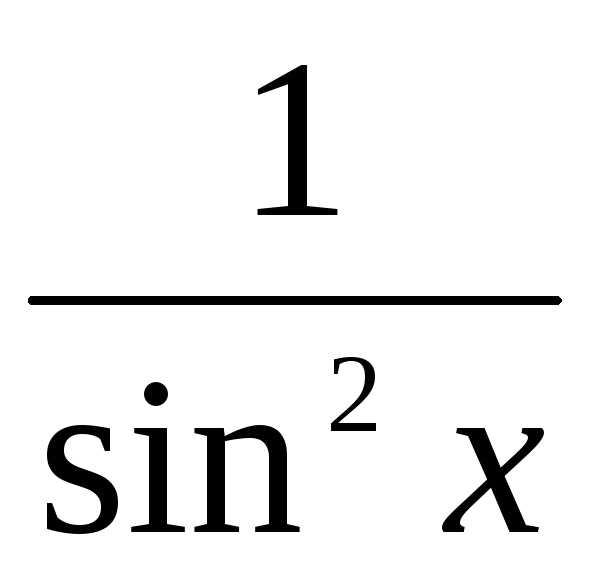
10.
(arcsinx)’=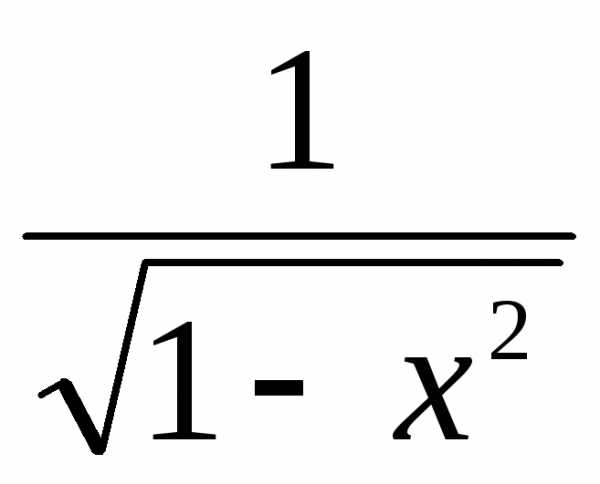 11.
(arccosx)’=-
11.
(arccosx)’=-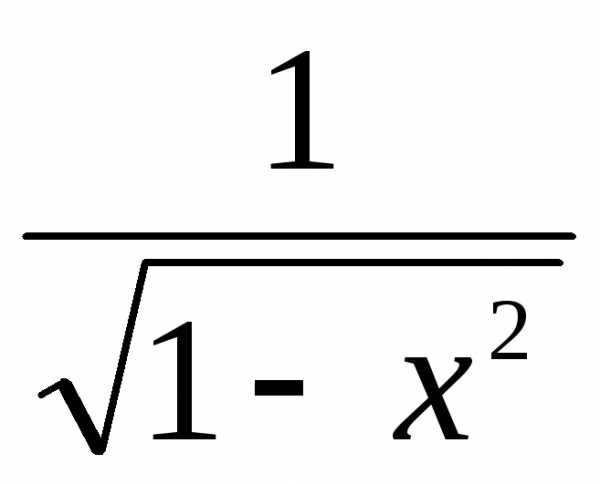
12.
(arctgx)’=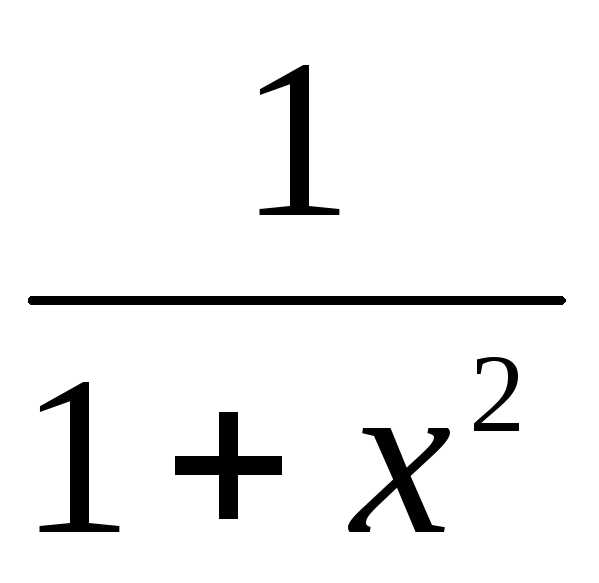 13.
(arcctgx)’=-
13.
(arcctgx)’=-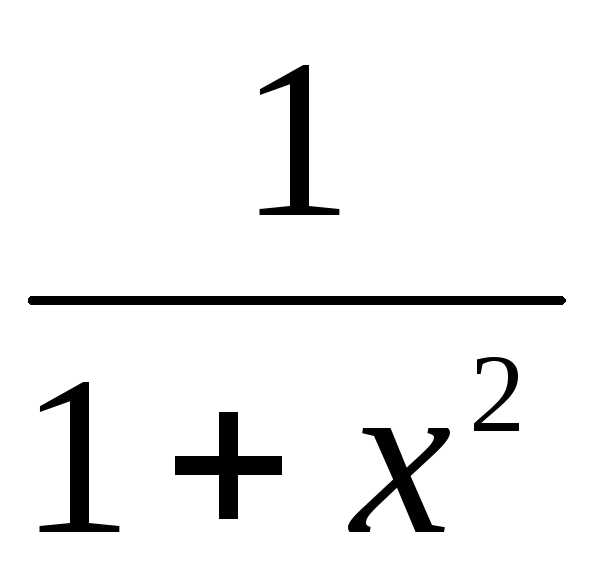 14.(х)
‘=1
14.(х)
‘=1
Свойства операции дифференцирования.
1. (с)’=0, c-const 2. (f(x)+g(x)-r(x))’=f ‘(x)+g ‘(x)-r ‘(x)
3. (f(x)g(x))’=f ‘(x)g(x)+g ‘(x)f(x), 4. (cf(x))’=c(f ‘(x))
5. .
Пример. Найти производную функции y=x3.
Воспользуемся первой формулой в таблице, где n=3, и получим
y=3x3-1=3x2.
Пример. Найти производную функции y=
y=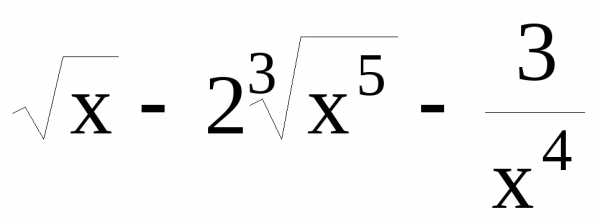
Для того чтобы воспользоваться формулой преобразуем функцию к табличному виду:
. Тогда ;;
Пример. Найти производную функции y=sinx+ex.
Применим правила дифференцирования к сумме двух табличных функций:
у =(sinx)+(ex)=cosx+ex.
Пример.y=5x-x5
y=5xlnx-5x4
Пример. Найти производную функции y=lnxtgx.
По правилу дифференцирования произведения функции получим:
у
=(
lnx)tgx+
lnx(tgx)= 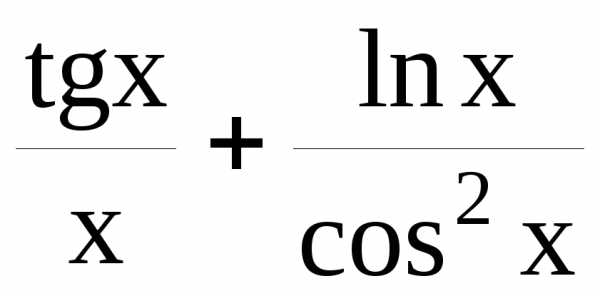
Пример. Найти производную функции y=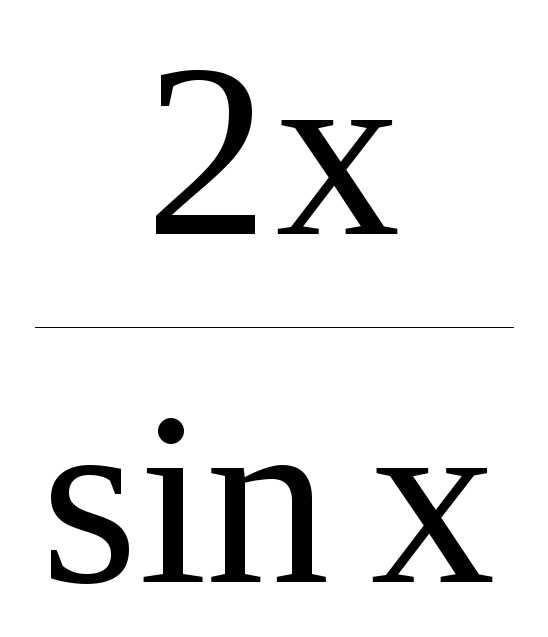 .
.
Теорема о производной сложной функции.
Пусть функция g(x) имеет производную в точке x, а функция f(z) имеет производную в точке z = g(x). Тогда сложная функция F(x) = f(g(x)) имеет в точке x производную F (x) = f (z) g (x).
Приведем примеры вычисления производной сложной функции.
Пример. Найти производную функции y=(3x5+2)6.
Воспользуемся правилом дифференцирования сложной функции. Обозначим 3x5+2=t, тогда у=t6. Получаем
у =(t6)t(3x5+2)x=6t5(35x4+0)=6(3x5+2)515x4=90x4(3x5+2)5.
Пример. Найти производную функции y=sin5x.
Рассуждая аналогично предыдущему примеру, обозначим sinx=t. Тогда получим степенную функцию y=t4. Берем производную сначала от степени функции, затем от основной функции:
у =5t4(sinx)= 5t4cosx=5sin4xcosx.
В дальнейшем для упрощения решения примеров, особые обозначения промежуточных результатов будем опускать.
Пример. Найти производную функции y=cosx4.
у =-sinx44x3=-4x3 sinx4.
Пример. Найти производную функции y=arcsin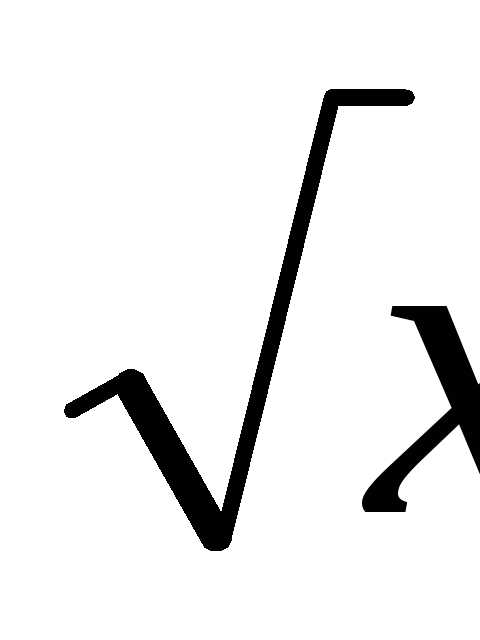 .
.
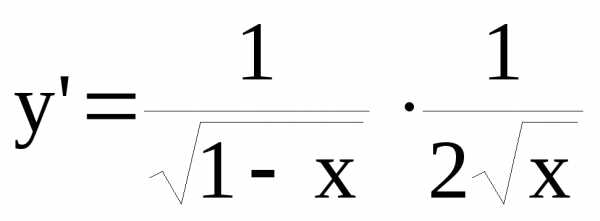
Нужно
обратить внимание на то, что в производной
функции y=arcsinx
в качестве аргумента используется 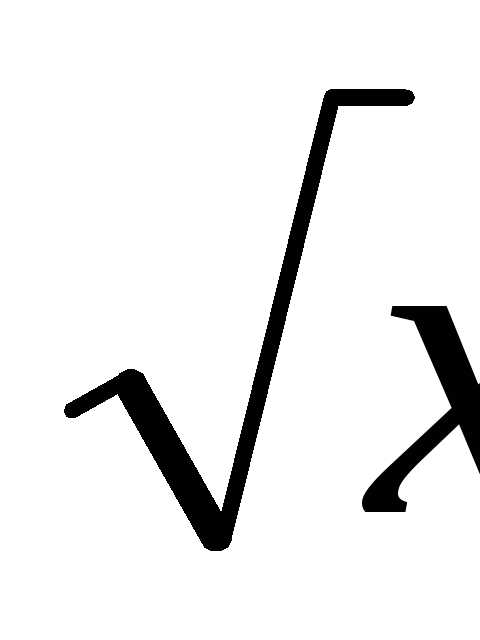 .
Поэтому производная имеет выше указанный
вид. Типичной ошибкой студентов является
следующий вид решения:
.
Поэтому производная имеет выше указанный
вид. Типичной ошибкой студентов является
следующий вид решения:
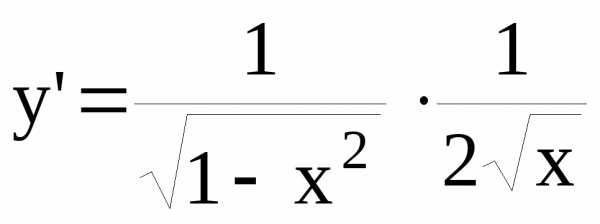
Пример. Найти производную функции y=ln3tg(e—x).
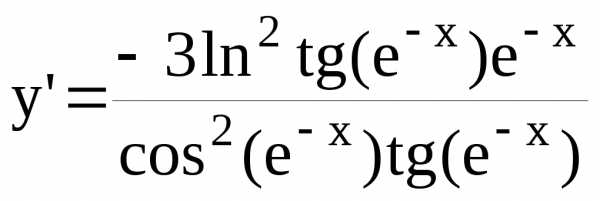
studfiles.net
Производная функции одной переменной
(определение, геометрический смысл)
Рассмотрим функцию , определенную в точке x и в некоторой окрестности этой точки.
Определение 1. Производной функции в точке x называется предел отношения приращения функции в точке x к приращению аргумента при условии стремления приращения аргумента к нулю, если такой предел существует:
(1)
Для обозначения производной используют символы:
Определение 2. Односторонние пределы называются соответственно левой производной и правой производной функции в точке x (если эти пределы существуют). Их обозначают . Для существования производной функции в точке x необходимо, чтобы ее правая и левая производные в этой точке существовали и были равны:
Примеры с решениями
Пример 1. Найти для функции пользуясь определением производной.
Решение. Пусть – приращение аргумента. Найдем соответствующие ему приращение функции в точке x = 2:
Воспользуемся определением производной:
Ответ:
Пример 2. Найти для функции в точке х = 0.
Решение. Пусть – приращение аргумента. Найдем соответствующее ему приращение функции в точке x = 0:
Воспользуемся определением:
Ответ: .
Заметим, что функция не имеет производной в точке x=0, так как
С геометрической точки зрения значение производной функции в точке x0 представляет собой угловой коэффициент касательной, проведенной к графику функции в точке M0 (x0; f(x0)), т.е. , где – угол наклона касательной к оси Оx.
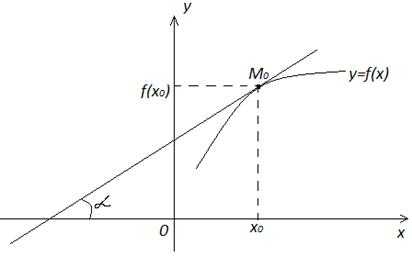
Уравнение касательной, проведенной к графику функции в точке с абсциссой x0 , имеет вид:
. (2)
Уравнение нормали к графику той же функции в точке с абсциссой x0:
(3)
если .
Если в точке x0 функция имеет бесконечную производную, т.е. или или , то касательная к графику этой функции в точке с абсциссой x0 перпендикулярна оси
Уравнение касательной в этих случаях имеет вид: x = x0, а уравнение нормали – . Если же , то уравнение нормали: x = x0.
Углом между кривыми и называется угол между касательными, проведёнными к этим кривым в точке их пересечения
(4)
если .
Если же , то касательные перпендикулярны и .
Пример 3.Составить уравнения касательной и нормали к графику функции в точке с абсциссой x0 = 2.
Решение. Воспользуемся уравнениями касательной (2) и нормали (3).
В эти уравнения надо поставить x0 = 2; и найденное в примере 1 значение . Получим уравнение касательной: и уравнение нормали:
Ответ: – уравнение касательной;
– уравнение нормали.
Пример 4. Пользуясь определением, найти значение производной функции в точках
Решение. Выведем формулу производной функции в любой точке , пользуясь определением. Зададим аргументу приращение и найдем соответствующее ему приращение функции:
Итак, . Вычислим значения производной в указанных точках:
Ответ:
Если при прямолинейном движении точки задан закон движения то скорость движения v в момент времени t0 есть производная по времени: , а ускорение а в момент времени t0 определяется производной скорости движения по времени:
Примеры для самостоятельного решения
3.1. Вычислить приращение функции в точке , соответствующее приращению аргумента .
3.2. Вычислить приращение функции в точке , соответствующее приращению аргумента
3.3. Найти приращение функции в точке для любого приращения аргумента
3.4. Найти приращение функции в точке x = 2 для любого приращения аргумента
3.5. Пользуясь определением производной, вычислить для функции .
3.6. Пользуясь определением производной, вычислить для функции .
3.7. Пользуясь определением производной, вывести формулу производной функции в любой точке, и найти значения этой производной в точках:
3.8. Пользуясь определением производной, вывести формулу производной функции в любой точке, и найти значения этой
производной в точках:
3.9. Найти угловой коэффициент касательной к графику функции в точке M(2;2), составить уравнения касательной и нормали к этой кривой в точке M, сделать чертеж.
3.10. Составить уравнения касательной и нормали к графику функции в точке с абсциссой x0 = 2 . Сделать чертеж.
3.11. На графике функции найти точку, касательная к которой параллельна биссектрисе первого координатного угла. Составить уравнение этой касательной. Сделать чертеж.
3.12. На графике функции найти точку, касательная к которой перпендикулярна прямой . Составить уравнение этой касательной. Сделать чертеж.
3.13. Составить уравнения касательных к графику функции , приходящих через точку A(2;2). Сделать чертеж.
3.14. Закон движения точки: где S – расстояние в метрах, t – время в секундах. Найти скорость этой точки в момент времени t = 4.
Ответы
3.1. ; 3.2. ;3.3. ; 3.4. ;
3.5. – 4; 3.6. – 4; 3.7.
3.8.
3.9. – уравнение касательной; – уравнение нормали; 3.10. – уравнение касательной; – уравнение нормали; 3.11. – точка касания; – уравнение касательной; 3.12. – точка касания; – уравнение касательной; 3.13. ;3.14. .
infopedia.su
