Тема урока: «Производная тригонометрических функций
| Предмет: | Математика |
|---|---|
| Категория материала: | Конспекты |
| Автор: | Борамбаева Гульмира Ернаровна это Вы? |
Урок по алгебре и началам анализа для учащихся 10 класса. По теме «Производная тригонометрических функций» Целью урока является обеспечить усвоение правил дифференцирования и техники вычисления производных в разнообразных ситуаций. В начале урока повторяют простейшие вычисления производных., затем решают по образцу.
учащиеся работают по вариантам по таблице, затем проверяют друг друга Закрепление проводится в виде игры, учащиеся по очереди выходят к доске и выполняют задания.Результат решения соответствует определенной букве.
Алгебра 10 класс.
Тема урока: «Производная тригонометрической функции»
Цели:
1. Образовательные.
обеспечить усвоение правил дифференцирования и техники вычисления производных в разнообразных ситуациях.организовать вычисление производных тригонометрических функций по образцу и в измененной ситуации с целью формирования целостной системы дифференцирования 2. Развивающие.создать условия для быстрой актуализации и практическому применению ранее полученных знанийобеспечить развитие у учащихся сравнивать познавательные объектыобеспечить условия для развития у учащихся умений анализировать.3. Воспитательные.содействовать развитию у учащихся чувства ответственности за личную и коллективную деятельностьсодействовать учащимся в осознании ценности совместной деятельности.
Оборудование урока: доска, мел, таблица с формулами, карточки с заданиями.
Ход урокаI. Организационный момент.
Учитель: «На прошлых уроках мы познакомились с правилами вычисления производных, научились находить производные сложных функций. Назовите функции, производные которых вы уже умеете вычислять».
Выслушиваются ответы учеников.
Учитель: «Сегодня мы проверим ваши умения самостоятельно применять полученные знания для вычисления производных функций».II. Презентация (историческая справка-это д/з, которое выполняет один из учеников)1) Математика развивалась стремительно, но без понятия производной многие исследования не имели смысла.В 1679 году Пьер Ферма находил экстремумы функции, касательные, наибольшие и наименьшие значения функций. Но в своих записях он использовал сложнейшую символику Виета, и поэтому эти исследования не привели к созданию теории интегральных и дифференциальных исчислений.
Функция
Производная
f(x) = sin(2x + 1) – 3cos(1 – x)
f’(x) = 2cos(2x + 1) – 3sin(1 – x)
f(x) = 4sinx + x²
f’(x) = 4cosx + 2x
f(x) = 3sinx7
f’(x) = 21xcosx
f(x) = tgx + ctgx
f’(x) =
f(x) = 3sinx
f’(x) =3cosx
f(x) = cos6x
f’(x) = – 6sinx
f(x) = 4tg7x
f’(x) =28cos²x
f(x) = cos(x + 2)
f’(x) = –sin(x + 2)
f(x) = cosx³
f’(x) = –3x²sinx³
f(x) = –2ctg10x
f’(x) =20/sin²10x
III.
Актуализация опорных знаний учащихся Фронтальный опрос по ранее изученным формулам вычисления производных.Чему равна производная:
от числаот переменной «х»от выражения kx + bот суммы функцийот произведения двух функцийот частногостепенной функциисложной функциитригонометрических функцийУчащиеся выходят к доске по одному и записывают формулы в столбик.
Затем идет проверка с помощью таблицы.
C´ = 0, X´ = 1, (kx + b) ´= k
(U + V)´ = U´ +V´; (U · V)´ = U´V +UV´
; (СU)’ = СU’
(sin x)´= cos x; (cos x) ´= sin x; (tg x) ´= ; (сtg x) ´= —
IV. Устная работа
1) Проверить верно ли найдена производная
()’= {1/2};
()’= {};
( )’=.
2) Найти производные функций:
G(x) = sinx + 4×6,
F(x) = –17tgx + 1,
F(x) = cos(4x – 11),
Y = tgxctgx
3) Задайте формулой функцию f(x):
f ´(x) = 2x
f ´(x) = 3×2 – sinx
f ´(x) = 5 – cosx
(f(x) = x2 + C),
(f(x) = x3 + cosx + C),
(f(x) = 5x – sinx + C).
4) Производные каких функций записаны на доске?
(действие обратное дифференцированию будем изучать в 11 классе.)
V. Коллективная работа по учебнику
№ 42.12 Найти значение производной функции в данной точке
г) у = ctg²x – 1, у'(π/4)-?
Решение.
у'(х)= -2ctgx/sin²x, у'(π/4)= -4
№42.17 При каких значениях аргумента скорости изменения функций равны?
а) f(x)=cos2x, g(x)=sinx
Решение.
f ‘ (x)= – 2sin2x, g’ (x)= cosx. — 2sin2x = cosx, cosx(4sinx + 1)=0, x=π/2+πn x=(-1)arcsin+ πn
№42.21 Определите абсциссы точек, в которых в которых угловой коэффициент касательной равен 0
а) f(x)=tg³x
Решение.
f ‘ (x)=3tg²x/cos²x, f ‘ (x)=0, sinx=0, x=πn
VI. Контроль и самопроверка знаний и способов действий.
У каждого из учеников на столе находится тестовое задание (по вариантам). Решают в тетради, на полях записывают правильные ответы.
Самоконтроль. Ответы на доске.
Тест.
Вариант 1
Вариант 2
Y= sin2x
1.
sin 2x
2. 2sin x
3. –sin 2x
Y= cos2x
1.- sin 2x
2. sin 2x
3. 2sin x
Y = 3cos 2 x
4. 6sin 4x
5.-3sin 2x
6. -6sin 2x
Y= 3sin 2x
1.3cos 2x
2. 6cos 2x
3. -6cos 4x
Y= 4tg 3x
7.4/cos23x
8. 4/cos2х
9. 12/cos23x
Y= 3ctg2x
1. -3/sin22x
2. 6/sin22x
3.- 6/sin22x
Вычислить Y´(π) Y= sin 2x – 3cos 3x
1. 2cos 2x – 3sin 3x
2. 2cos 2x + 9sin 3x
3. -2cos 2x + 3sin 3x
Вычислить Y´(π/2) Y= cos 2x – sin 3x
1. -2sin 2x – 3cos 3x
2. 2cos 2x – 3sin 3x
3. –sin 2x – cos 3x
Вариант 3
Вариант 4
y=sinx
1. 5 xcosx
2. 5 cosx
3. 5 x sinx
y=cos(3x+π/6)
1.- 21sin(3x+π/6)cos(3x+π/6)
2. -7sin(3x+π/6)
3. 7cos (3x+π/6)
y=1/cosx
4.2/cosx
5. 1/sinx
6. 2sinx/cosx
y=1/sinx
1. 1/cosx
2. -2cos/ xsin³x
3.-2/sinx
y=1/ tg3x
7.
3cos²3x
8. 3/tg²3x
9. -3/sin²3x
y=2/ctg2x
1. -2sin²2x
2. 2/ctg2x
3.4/cos²2x
y=, у'(0)-?
1. 1 /(2)
2. cosx/(2)
3. cosx(1+sinx)
y'(0)=1/2
y=, у'(π/2)-?
1. -1 /(1+sinx)
2. cosx /(1+sinx)²
3. sinx /(1+sinx)²
у'(π/2) =-1/2
В-1,3. Ответ:1692(номер нашей школы) В-2,4. Ответ:1231
VII. Закрепление и применение знаний и способов действий учащихся.Проводится в виде игры. Задания написаны на доске. Учащиеся выходят по очереди. Результат решения соответствует какой-либо букве. Буквы лежат на отдельном столе. Ученик находит полученную букву, на обратной стороне которой написан её порядковый номер в фразе. Фраза записывается на доске. Учитель называет оценку каждому вышедшему к доске.Ключ к расшифровке высказывания.
Буква
№ окошка
cos²π– 4×2 + 7
– 8x
1/tgπ/4 + 3×2
1/x + 5
1,12,16
x6 – 4sinx
6×5 – 4cosx
20×4 — cosx
80×3 + sinx
2,7,9,13,17
2sin4x+16
8cos4x
4,6,30,35
sin²x + 13
sin2x
cos² 2x
sin4x
3,10,34
2×6 + (sinx)/2
12×5 + ½(cosx)
— 5х
7×5 – 20×3
x²sin2x
2xsin2x + 2x²cos2x
11,19,12,24,27
— ctg3x
+ 3/(sin²3x)
sinx+ tg6x
5xcosx+
29,36
x+ 3sinx/3
1 + cosx
20,23,28,33
2×3 – x2 + x
6×2 – 2x + 1
x/cosx
sin6xcos3x+cos6xsin3x
9cos9x
Величие человека — в его способности мыслить.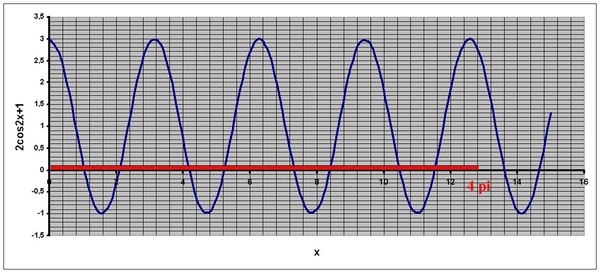
ʹ (x)=
Решите уравнения:№229
№238. Вычислите значение производной f(x) в точке
№239. Напишите уравнение касательной к графику функции
а).
№240. Вычислите производные функции.
4. Тестовые задания
1 вариант.
Найдите производную функции b) -4cosx c) 4cosx d) -4sinxНайдите производную функции 2sinx b) -2sinx c) 2cosx d) -2cosxНайдите производную функции a)-4sin(4x-1) b) cos(4x-1) c) –cos(4x-1) d) -4cos(4x-1) Найдите производную функции и вычислите a)-3 b) -1 c) 3 d) 16
5. Найдите производную функции
a) — b) c) d)
6. Найдите производную функции
a) cosx+cos2x b) cosx+0.5cos2x c) 2cosx d) 1.5cosx
7. Найдите производную функции
a) b) cos2x c) d) 2cosx
8. Найдите производную функции
a) 4sin2x b) 1 c) 0 d)
9. Найдите производную функции
a) b) c) d)
II-вариант.
Найдите производную функции 10sinx b) 10cosx c) -10sinx d)-10cosxНайдите производную функции 5sinx b) -5cosx c) 5cosx d) -5sinxНайдите производную функции cos(9x-2) b) –cos(9x-2) c) -9sin(x-2) d) -9cos(9x-2)Найдите производную функции и вычислите -8 b) 24 c) -24 d) 8Найдите производную функции b) c) d) Найдите производную функции b) c) d)
7.
Новые вопросы
Ответы
Y=x в степени n умножить на cos(2x), x пренадлежит R, n пренадлежит R
Похожие вопросы
Найти площадь прямоугольного треугольника, у которого стороны, образующие прямой угол, равны 4 см и 5 см…
Запиши в виде выражения и найдите его значениесумма чисел 7 и (-20) увеличьте на 18…
К пристани причалили 2 теплохода на каждом из которых было по 750 человек и 3 теплохода на каждом из которых было по 630 человек сколько всего человек привезли теплоходы…
Діаметр земної кулі 12 640 км. Знайдіть довжину екватора (число π округліть до десятих).
…
Решите пж срочно умоляю
надо 5,7,8…
Раскройте скобки в выражениях только 1) 2) 3)…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
2(х).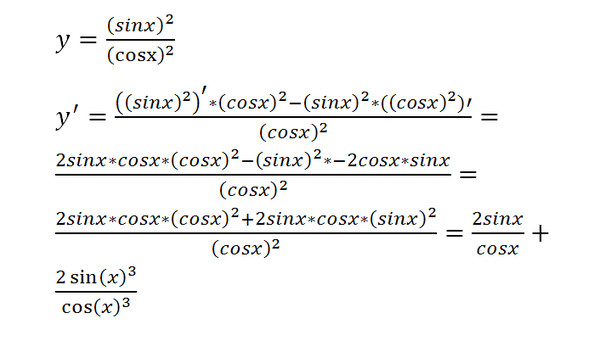
Цепное правило полезно для нахождения производной функции, которую можно было бы дифференцировать, если бы она была по x, но она представлена в виде другого выражения, которое также можно было бы дифференцировать, если бы оно стояло само по себе.
В этом случае:
- Мы знаем, как дифференцировать cos(x) (ответ -sin(x))
- Мы знаем, как дифференцировать 2x (ответ 2)
Это означает цепное правило позволит нам дифференцировать выражение cos(2x).
Использование цепного правила для нахождения производной от cos(2x)
Чтобы выполнить дифференцирование cos(2x), цепное правило говорит, что мы должны дифференцировать выражение, как если бы оно было только через x, пока мы затем умножаем это результат производной от того, что на самом деле выражает выражение (в данном случае производная от 2x).
Давайте вызовем функцию в аргументе cos, g(x), что означает, что функция имеет форму cos(x), за исключением того, что она не имеет x в качестве угла, вместо этого она имеет другую функцию от x (2x ) как угол
Если:
g(x) = 2x
Отсюда следует, что:
cos(2x) = cos(g(x))
Итак, если функция f(x) = cos(x) и функция g(x) = 2x, то функция cos(2x) может быть записана как составная функция.
f(x) = cos(x)
f(g(x)) = cos(g(x)) (но g(x) = 2x))
f(g(x)) = cos( 2x)
Определим эту составную функцию как F(x):
F(x) = f(g(x)) = cos(2x)
Мы можем найти производную от cos(2x) (F'( x)) с использованием цепного правила.
Цепное правило:
Для двух дифференцируемых функций f(x) и g(x)
Если F(x) = f(g(x))
6 Тогда производная F(x) есть F'(x) = f'(g(x)).g'(x)
Теперь мы можем просто подставить f(x) и g(x) в цепное правило. Но прежде чем мы это сделаем, кратко повторим производную функции cos.
Производная cos(x) по x равна -sin(x)
Производная cos(z) по z равна -sin(z)
Аналогичным образом, производная cos(2x) относительно 2x равна -sin(2x).
Мы будем использовать этот факт как часть цепного правила, чтобы найти производную от cos(2x) относительно x .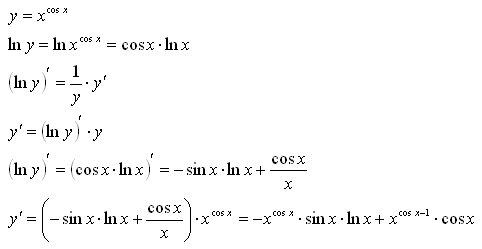
Как найти производную от cos(2x) с помощью цепного правила: Определение правила Используя цепное правило, производная от cos(2x) равна -2sin(2x) , просто примечание к синтаксису и обозначение: cos(2x) иногда записывается в приведенных ниже формах (с производной в соответствии с приведенным выше расчетом). Просто имейте в виду, что не все приведенные ниже формы математически правильны. 3 производная функции, вы просто дифференцируете первую производную. Исходя из вышеизложенного, мы нашли, что первая производная cos(2x) = -2sin(2x). Таким образом, чтобы найти вторую производную от cos(2x), нам просто нужно дифференцировать -2sin(2x) . Мы можем использовать цепное правило, чтобы найти производную от -2sin(2x), и это даст нам результат -4cos( 2x) ► Вторая производная от cos(2x) равна -4cos(2x) = f'(g(x))(2) g(x) = 2x ⇒ g'(x) = 2 = (-sin(2x)).(2) f(g(x)) = cos(2x) ⇒ f'(g(x)) = -sin( 2x) = -2sin(2x) cos2x ► Derivative of cos2x = -2sin(2x) cos 2 x ► Derivative of cos 2 x = -2sin(2x) cos 2x ► Derivative of cos 2x = -2sin(2x) cos (2x) ► Производная от cos (2x) = -2sin(2x) Вторая производная от cos(2x)
Опубликовано DerivativeIt
Просмотреть все сообщения DerivativeIt
Вопрос Видео: Нахождение третьей производной тригонометрических функций
Стенограмма видео
Определите, что третья производная функции 𝑦 равна шестикратному отрицательному косинусу двух 𝑥.
Нам дано 𝑦, которое является тригонометрической функцией в 𝑥. И нас просят найти третью производную от 𝑦. Это будет третья производная от 𝑦 по 𝑥. Итак, начнем с нахождения первой производной от 𝑦 по 𝑥. Это производная минус шесть от двух 𝑥 по отношению к 𝑥.
И для этого мы можем вспомнить один из наших стандартных результатов тригонометрических производных. Для любой действительной константы 𝑎 производная отрицательного косинуса 𝑎𝑥 по отношению к 𝑥 равна 𝑎, умноженной на грех 𝑎𝑥. И мы видим, что наша производная не совсем в таком виде. Мы возьмем постоянный множитель шесть вне нашей производной.
Итак, это дает нам следующее выражение, и мы можем видеть, что оно точно в этой форме с нашим значением 𝑎, равным двум. Таким образом, установив наше значение 𝑎 равным двум, мы можем дифференцировать отрицательные значения cos двух 𝑥 по отношению к 𝑥, чтобы получить удвоенный грех двух 𝑥. Тогда мы можем упростить наш коэффициент в этом выражении. Шесть раз два равно 12. Итак, мы показали, что d𝑦 на d𝑥 равно 12 sin of two 𝑥. Но помните, нам нужно найти выражение для третьей производной от 𝑦 по 𝑥. Нам нужно снова различать это. Мы дифференцируем, чтобы найти d два 𝑦 по d𝑥 в квадрате, равно производной 12 sin двух 𝑥 по отношению к 𝑥. И еще раз упростим это выражение.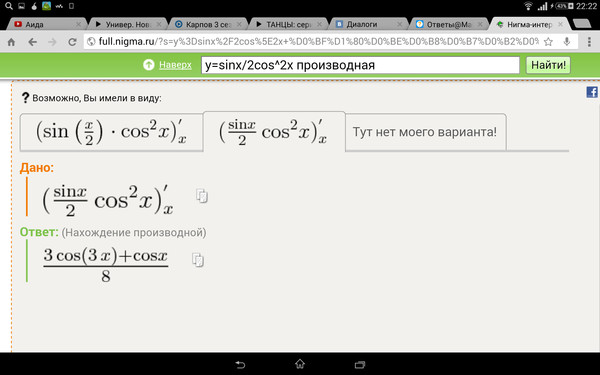
Мы возьмем постоянный множитель 12 вне нашей производной.
Таким образом, чтобы найти выражение для d два 𝑦 в квадрате d𝑥, нам нужно дифференцировать грех двух 𝑥 относительно 𝑥. И снова мы можем сделать это, используя стандартный результат тригонометрической производной. Для любой реальной константы 𝑎 производная от греха 𝑎𝑥 по 𝑥 равна 𝑎, умноженной на косинус 𝑎𝑥. Мы снова видим, что значение нашей константы 𝑎 равно двум. Таким образом, используя 𝑎 равно двум, мы получаем d два 𝑦 на d𝑥 в квадрате равно 12, умноженным на два, потому что два 𝑥. И мы можем упростить наш коэффициент. 12 умножить на два равно 24. Итак, мы показали, что вторая производная от 𝑦 по отношению к 𝑥 равна 24-кратному косинусу двух 𝑥.
Чтобы найти нашу третью производную от 𝑦 по 𝑥, нам просто нужно продифференцировать это по 𝑥 еще раз. Итак, нам нужно продифференцировать 24 cos от двух 𝑥 по отношению к 𝑥. И мы можем сделать это, используя результат тригонометрической производной. Для любой действительной константы 𝑎 производная от косинуса 𝑎𝑥 по 𝑥 равна отрицательному 𝑎, умноженному на грех 𝑎𝑥.