Производная функции заданной параметрически: Производная параметрически заданной функции

21.2. Функция, заданная параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.

Найдем производную у’_х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у’_х=y’_t•t’_x. С учетом равенства (21.2) получаем

Полученная формула позволяет находить производную у’_х от функции заданной параметрически, не находя непосредственной зависимости у от х.

<< Пример 21.2

Пусть  

Найти у’_х.

Решение: Имеем   x’_t=3t²,   y’_t=2t.   Следовательно,   у’_х=2t/t

2,   т. е. 

В этом можно убедиться, найдя непосредственно зависимость у от х.

Действительно,    Тогда    Отсюда  т. е.

22. Логарифмическое дифференцирование

В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать. А затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.

<< Пример 22.1

Найти производную функции 

Решение: Пользуясь формулой (22.1), получаем:

Отметим, что запоминать формулу (22.1) необязательно, легче запомнить суть логарифмического дифференцирования.

Существуют функции, производные которых находят лишь логарифмическим дифференцированием. К их числу относится так называемая степенно-показательная функция у=u^v, где u=u(x) и ν=ν(х) — заданные дифференцируемые функции от х. Найдем производную этой функции:

Сформулируем правило запоминания формулы (22.1): производная степенно-показательной функции равна сумме производной показательной функции, при условии u=const, и производной степенной функции, при условии ν=const.

§23. Производные высших порядков

Додати до моєї бази знань

Математика

23. Производные высших порядков

23.1. Производные высших порядков явно заданной функции

Производная у’=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.

Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у»

Итак, у»=(у’)’.

Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'» (или ƒ'»(х)). Итак, у'»=(y»)’

Производной n-го порядка (или n-й производной) называется производная от производной  (n-1) порядка:

y⁽ⁿ⁾=(y^(n-1))¢ .

Производные порядка выше первого называются производными высших порядков.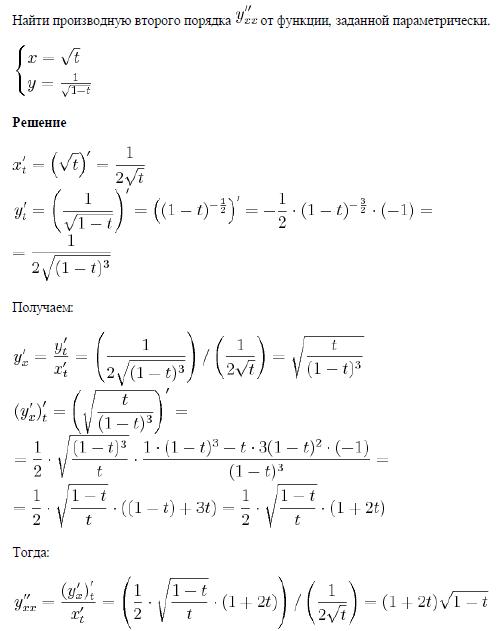

Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (у^ν или у⁽⁵⁾— производная пятого порядка).

<< Пример 23.1

Найти производную 13-го порядка функции у=sinx.

Решение:

23.2. Механический смысл производной второго порядка

Пусть материальная точка М движется прямолинейно по закону S=f(t). Как уже известно, производная S¢ _t равна скорости точки в данный момент времени: S’_t=V.

Покажем, что вторая производная от пути по времени есть величина, ускорения прямолинейного движения точки, т. е. S»=α.

Пусть в момент времени t скорость точки равна V, а в момент t+∆t — скорость равна V+∆V, т. е. за промежуток времени ∆t скорость изменилась на величину ∆V.

Отношение ∆V/∆t выражает среднее ускорение движения точки за время ∆t. Предел этого отношения при ∆t→0 называется ускорением точки М в данный момент t и обозначается буквой α:

Но V=S’_t. Поэтому α=(S’_t)’, т. е. α=S’_t‘

Производная параметрически заданной функции. Функции, заданные параметрически

До сих пор рассматривались уравнения линий на плоскости, связывающие непосредственно текущие координаты точек этих линий. Однако часто применяется другой способ задания линии, в котором текущие координаты рассматриваются как функции третьей переменной величины.

Пусть даны две функции переменной

рассматриваемые для одних и тех же значений t. Тогда любому из этих значений t соответствует определенное значение и определенное значение у, а следовательно, и определенная точка . Когда переменная t пробегает все значения из области определения функций (73), точка описывает некоторую линию С в плоскости Уравнения (73) называются параметрическими уравнениями этой линии, а переменная — параметром.

Предположим, что функция имеет обратную функцию Подставив эту функцию во второе из уравнений (73), получим уравнение

выражающее у как функцию

Условимся говорить, что эта функция задана параметрически уравнениями (73). Переход от этих уравнений к уравнению (74) называется исключением параметра. При рассмотрении функций, заданных параметрически, исключение параметра не только не обязательно, но и не всегда практически возможно.

Во многих случаях гораздо удобнее, задаваясь различными значениями параметра вычислять затем по формулам (73) соответствующие значения аргумента и функции у.

Рассмотрим примеры.

Пример 1. Пусть — произвольная точка окружности с центром в начале координат и радиусом R. Декартовы координаты х и у этой точки выражаются через ее полярный радиус и полярный угол, который мы здесь обозначим через t, следующим образом (см. гл. I, § 3, п. 3):

Уравнения (75) называются параметрическими уравнениями окружности. Параметром в них является полярный угол , который меняется в пределах от 0 до .

Если уравнения (75) почленно возвести в квадрат и сложить, то в силу тождества параметр исключится и получится уравнение окружности в декартовой системе координат определяющее две элементарные функции:

Каждая из этих функций задается параметрически уравнениями (75), но области изменения параметра для этих функций различны. Для первой из них ; графиком этой функции служит верхняя полуокружность. Для второй функции графиком ее является нижняя полуокружность.

Пример 2. Рассмотрим одновременно эллипс

и окружность с центром в начале координат и радиусом а (рис. 138).

Каждой точке М эллипса сопоставим точку N окружности, имеющую ту же абсциссу, что и точка М, и расположенную с ней по одну сторону от оси Ох. Положение точки N, а следовательно, и точки М, вполне определяется полярным углом t точки При этом для их общей абсциссы получим следующее выражение: х = a. Ординату у точки М найдем из уравнения эллипса:

Знак выбран потому, что ордината у точки М и ордината точки N должны иметь одинаковые знаки.

Таким образом, для эллипса получены следующие параметрические уравнения:

Здесь параметр t изменяется от 0 до .

Пример 3. Рассмотрим окружность с центром в точке а) и радиусом а, которая, очевидно, касается оси абсцисс в начале координат (рис. 139). Предположим, это эта окружность катится без скольжения по оси абсцисс. Тогда точка М окружности, совпадавшая в начальный момент с началом координат, описывает линию, которая называется циклоидой.

Выведем параметрические уравнения циклоиды, приняв за параметр t угол МСВ поворота окружности при перемещении ее фиксированной точки из положения О в положение М. Тогда для координат и у точки М мы получим следующие выражения:

Вследствие того что окружность катится по оси без скольжения, длина отрезка ОВ равна длине дуги ВМ. Так как длина дуги ВМ равна произведению радиуса а на центральный угол t, то . Поэтому . Но Следовательно,

Эти уравнения и являются параметрическими уравнениями циклоиды. При изменении параметра t от 0 до окружность совершит один полный оборот. Точка М при этом опишет одну арку циклоиды.

Исключение параметра t приводит здесь к громоздким выражениям и практически нецелесообразно.

Параметрическое задание линий особенно часто используется в механике, причем роль параметра играет время.

Пример 4.

Определим траекторию снаряда, выпущенного из орудия с начальной скоростью под углом а к горизонту. Сопротивлением воздуха и размерами снаряда, считая его материальной точкой, пренебрегаем.

Выберем систему координат. За начало координат примем точку вылета снаряда из дула. Ось Ох направим горизонтально, а ось Оу — вертикально, расположив их в одной плоскости с дулом орудия. Если бы не было силы земного тяготения, то снаряд двигался бы по прямой, составляющей угол а с осью Ох и к моменту времени t прошел бы путь Координаты снаряда в момент времени t были бы соответственно равны: . Вследствие земного тяготения снаряд должен к этому моменту вертикально опуститься на величину Поэтому в действительности в момент времени t координаты снаряда определяются по формулам:

В этих уравнениях — постоянные величины. При изменении t будут изменяться также координаты у точки траектории снаряда. Уравнения являются параметрическими уравнениями траектории снаряда, в которых параметром является время

Выразив из первого уравнения и подставив его во

второе уравнение, получим уравнение траектории снаряда в виде Это — уравнение параболы.

Формула производной функции, заданной параметрическим способом. Доказательство и примеры применения этой формулы. Примеры вычисления производных первого, второго и третьего порядка.

Пусть функция задана параметрическим способом:
(1)
где некоторая переменная, называемая параметром. И пусть функции и имеют производные при некотором значении переменной . Причем и функция имеет обратную функцию в некоторой окрестности точки . Тогда функция (1) имеет в точке производную , которая, в параметрическом виде, определяется по формулам:
(2)

Здесь и — производные функций и по переменной (параметру) . Их часто записывают в следующем виде:

;
.

Тогда систему (2) можно записать так:

Доказательство

По условию, функция имеет обратную функцию. Обозначим ее как
.
Тогда исходную функцию можно представить как сложную функцию:
.
Найдем ее производную, применяя правила дифференцирования сложной и обратной функций:
.

Правило доказано.

Доказательство вторым способом

Найдем производную вторым способом, исходя из определения производной функции в точке :
.
Введем обозначение:
.
Тогда и предыдущая формула принимает вид:
.

Воспользуемся тем, что функция имеет обратную функцию , в окрестности точки .
Введем обозначения:
; ;
; .
Разделим числитель и знаменатель дроби на :
.
При , . Тогда
.

Правило доказано.

Производные высших порядков

Чтобы найти производные высших порядков, надо выполнять дифференцирование несколько раз. Допустим, нам надо найти производную второго порядка от функции, заданной параметрическим способом, следующего вида:
(1)

По формуле (2) находим первую производную, которая также определяется параметрическим способом:
(2)

Обозначим первую производную, посредством переменной :
.
Тогда, чтобы найти вторую производную от функции по переменной , нужно найти первую производную от функции по переменной . Зависимость переменной от переменной также задана параметрическим способом:
(3)
Сравнивая (3) с формулами (1) и (2), находим:

Теперь выразим результат через функции и . Для этого подставим и применим формулу производной дроби :
.
Тогда
.

Отсюда получаем вторую производную функции по переменной :

Она также задана в параметрическом виде. Заметим, что первую строку также можно записать следующим образом:
.

Продолжая процесс, можно получить производные функции от переменной третьего и более высоких порядков.

Заметим, что можно не вводить обозначение для производной . Можно записать так:
;
.

Пример 1

Найдите производную от функции, заданной параметрическим способом:

Решение

Находим производные и по .
Из таблицы производных находим:
;
.
Применяем :

.
Здесь .

.
Здесь .

Искомая производная:
.

Ответ

Пример 2

Найдите производную от функции, выраженной через параметр :

Решение

Раскроим скобки, применяя формулы для степенных функций и корней :
.

Находим производную :

.

Находим производную . Для этого введем переменную и применим формулу производной сложной функции .

.

Находим искомую производную:
.

Ответ

Пример 3

Найдите производные второго и третьего порядков от функции, заданной параметрическим способом в примере 1:

Решение

В примере 1 мы нашли производную первого порядка:

Введем обозначение . Тогда функция является производной по . Она задана параметрическим способом:

Чтобы найти вторую производную по , нам надо найти первую производную по .

Дифференцируем по .
.
Производную по мы нашли в примере 1:
.
Производная второго порядка по равна производной первого порядка по :
.

Итак, мы нашли производную второго порядка по в параметрическом виде:

Теперь находим производную третьего порядка. Введем обозначение . Тогда нам нужно найти производную первого порядка от функции , которая задана параметрическим способом:

Находим производную по . Для этого перепишем в эквивалентном виде:
.
Из

.

Производная третьего порядка по равна производной первого порядка по :
.

Замечание

Можно не вводить переменные и , которые являются производными и , соответственно. Тогда можно записать так:
;
;
;
;
;
;
;
;
.

Ответ

В параметрическом представлении, производная второго порядка имеет следующий вид:

Производная третьего порядка:

Рассмотрим задание линии на плоскости, при котором переменные x, y являются функциями третьей переменной t (называемой параметром):

Для каждого значения t из некоторого интервала соответствуют определенные значения x и y, а , следовательно, определенная точка M (x, y) плоскости. Когда t пробегает все значения из заданного интервала, то точка M (x, y ) описывает некоторую линию L . Уравнения (2.2) называются параметрическими уравнениями линии L .

Если функция x = φ(t) имеет обратную t = Ф(x), то подставляя это выражение в уравнение y = g(t), получим y = g(Ф(x)), которое задает y как функцию от x . В этом случае говорят, что уравнения (2.2) задают функцию y параметрически.

Пример 1. Пусть M (x, y) – произвольная точка окружности радиуса R и с центром в начале координат. Пусть t – угол между осью Ox и радиусом OM (см. рис. 2.3). Тогда x, y выражаются через t:

Уравнения (2.3) являются параметрическими уравнениями окружности. Исключим из уравнений (2.3) параметр t. Для этого каждое из уравнений возведем в квадрат и сложим, получим: x 2 + y 2 = R 2 (cos 2 t + sin 2 t) или x 2 + y 2 = R 2 – уравнение окружности в декартовой системе координат. Оно определяет две функции: Каждая из этих функций задается параметрическими уравнениями (2.3), но для первой функции , а для второй .

Пример 2 . Параметрические уравнения

задают эллипс с полуосями a, b (рис. 2.4). Исключая из уравнений параметр t , получим каноническое уравнение эллипса:

Пример 3 . Циклоидой называется линия, описанная точкой, лежащей на окружности, если эта окружность катится без скольжения по прямой (рис. 2.5). Введем параметрические уравнения циклоиды. Пусть радиус катящейся окружности равен a , точка M , описывающая циклоиду, в начале движения совпадала с началом координат.

Определим координаты x , y точки M после того, как окружность повернулась на угол t
(рис. 2.5), t = ÐMCB . Длина дуги MB равна длине отрезка OB, так как окружность катится без скольжения, поэтому

OB = at, AB = MD = asint, CD = acost, x = OB – AB = at – asint = a(t – sint),

y = AM = CB – CD = a – acost = a(1 – cost).

Итак, получены параметрические уравнения циклоиды:

При изменении параметра t от 0 до 2π окружность поворачивается на один оборот, при этом точка M описывает одну арку циклоиды. Уравнения (2.5) задают y как функцию от x . Хотя функция x = a(t – sint) имеет обратную функцию, но она не выражается через элементарные функции, поэтому функция y = f(x) не выражается через элементарные функции.

Рассмотрим дифференцирование функции, заданной параметрически уравнениями (2.2). Функция x = φ(t) на некотором интервале изменения t имеет обратную функцию t = Ф(x) , тогда y = g(Ф(x)) . Пусть x = φ(t) , y = g(t) имеют производные, причем x»t≠0 . По правилу дифференцирования сложной функции y»x=y»t×t»x. На основании правила дифференцирования обратной функции , поэтому:

Полученная формула (2.6) позволяет находить производную для функции, заданной параметрически.

Пример 4. Пусть функция y , зависящая от x , задана параметрически:

Решение . .
Пример 5. Найти угловой коэффициент k касательной к циклоиде в точке M 0 , соответствующей значению параметра .
Решение. Из уравнений циклоиды: y» t = asint, x» t = a(1 – cost), поэтому

Угловой коэффициент касательной в точке M 0 равен значению при t 0 = π/4:

ДИФФЕРЕНЦИАЛ ФУНКЦИИ

Пусть функция в точке x 0 имеет производную. По определению:
поэтому по свойствам предела (разд. 1.8) , где a – бесконечно малая при Δx → 0 . Отсюда

Δy = f «(x0)Δx + α×Δx. (2.7)

При Δx → 0 второе слагаемое в равенстве (2.7) является бесконечно малой высшего порядка, по сравнению с , поэтому Δy и f » (x 0)×Δx – эквивалентные, бесконечно малые (при f «(x 0) ≠ 0).

Таким образом, приращение функции Δy состоит из двух слагаемых, из которых первое f «(x 0)×Δx является главной частью приращения Δy, линейной относительно Δx (при f «(x 0)≠ 0).

Дифференциалом функции f(x) в точке x 0 называется главная часть приращения функции и обозначается: dy или df (x 0) . Следовательно,

df (x0) =f «(x0)×Δx. (2.8)

Пример 1. Найти дифференциал функции dy и приращение функции Δy для функции y = x 2 при:
1) произвольных x и Δx ; 2) x 0 = 20, Δx = 0,1.

Решение

1) Δy = (x + Δx) 2 – x 2 = x 2 + 2xΔx + (Δx) 2 – x 2 = 2xΔx + (Δx) 2 , dy = 2xΔx.

2) Если x 0 = 20, Δx = 0,1, то Δy = 40×0,1 + (0,1) 2 = 4,01; dy = 40×0,1= 4.

Запишем равенство (2.7) в виде:

Δy = dy + a×Δx. (2.9)

Приращение Δy отличается от дифференциала dy на бесконечно малую высшего порядка, по сравнению с Δx, поэтому в приближенных вычислениях пользуются приближенным равенством Δy ≈ dy, если Δx достаточно мало.

Учитывая, что Δy = f(x 0 + Δx) – f(x 0), получаем приближенную формулу:

f(x 0 + Δx) ≈ f(x 0) + dy. (2.10)

Пример 2 . Вычислить приближенно .

Решение. Рассмотрим:

Используя формулу (2.10), получим:

Значит, ≈ 2,025.

Рассмотрим геометрический смысл дифференциала df(x 0) (рис. 2.6).

Проведем к графику функции y = f(x) касательную в точке M 0 (x0, f(x 0)), пусть φ – угол между касательной KM0 и осью Ox, тогда f»(x 0) = tgφ. Из ΔM0NP:
PN = tgφ×Δx = f «(x 0)×Δx = df(x 0). Но PN является приращением ординаты касательной при изменении x от x 0 до x 0 + Δx.

Следовательно, дифференциал функции f(x) в точке x 0 равен приращению ординаты касательной.

Найдем дифференциал функции
y = x. Так как (x)» = 1, то dx = 1×Δx = Δx. Будем считать, что дифференциал независимой переменной x равен ее приращению, т.е. dx = Δx.

Если x – произвольное число, то из равенства (2.8) получаем df(x) = f «(x)dx, откуда .
Таким образом, производная для функции y = f(x) равна отношению ее дифференциала к дифференциалу аргумента.

Рассмотрим свойства дифференциала функции.

Если u(x), v(x) – дифференцируемые функции, то справедливы следующие формулы:

Для доказательства этих формул используются формулы производных для суммы, произведения и частного функции. Докажем, например, формулу (2.12):

d(u×v) = (u×v)»Δx = (u×v» + u»×v)Δx = u×v»Δx + u»Δx×v = u×dv + v×du.

Рассмотрим дифференциал сложной функции: y = f(x), x = φ(t), т.е. y = f(φ(t)).

Тогда dy = y» t dt, но y» t = y» x ×x» t , поэтому dy =y» x x» t dt. Учитывая,

что x» t = dx, получаем dy = y» x dx =f «(x)dx.

Таким образом, дифференциал сложной функции y = f(x), где x =φ(t), имеет вид dy = f «(x)dx, такой же, как в том случае, когда x является независимой переменной. Это свойство называется инвариантностью формы дифференциал а.

Функцию можно задать несколькими способами. Это зависит от правила, которое используется при ее задании. Явный вид задания функции имеет вид y = f (x) . Бывают случаи, когда ее описание невозможно или неудобно. Если есть множество пар (х; у) ,которые необходимо вычислять для параметра t по промежутку (а; b) . Для решения системы x = 3 · cos t y = 3 · sin t с 0 ≤ t

Определение параметрической функции

Отсюда имеем, что x = φ (t) , y = ψ (t) определены на при значении t ∈ (a ; b) и имеют обратную функцию t = Θ (x) для x = φ (t) , тогда идет речь о задании параметрического уравнения функции вида y = ψ (Θ (x)) .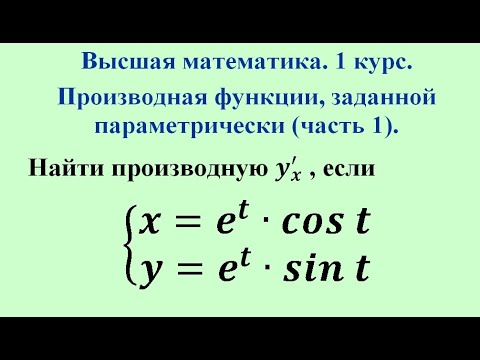

Бывают случаи, когда для исследования функции требуется заниматься поиском производной по х. Рассмотрим формулу производной параметрически заданной функции вида y x » = ψ » (t) φ » (t) , поговорим о производной 2 и n -ого порядка.

Вывод формулы производной параметрически заданной функции

Имеем, что x = φ (t) , y = ψ (t) , определенные и дифферецируемые при значении t ∈ a ; b , где x t » = φ » (t) ≠ 0 и x = φ (t) , тогда существует обратная функция вида t = Θ (x) .

Для начала следует переходить от параметрического задания к явному. Для этого нужно получить сложную функцию вида y = ψ (t) = ψ (Θ (x)) , где имеется аргумент x .

Исходя из правила нахождения производной сложной функции, получаем, что y » x = ψ Θ (x) = ψ » Θ x · Θ » x .

Отсюда видно, что t = Θ (x) и x = φ (t) являются обратными функциями из формулы обратной функции Θ » (x) = 1 φ » (t) , тогда y » x = ψ » Θ (x) · Θ » (x) = ψ » (t) φ » (t) .

Перейдем к рассмотрению решения нескольких примеров с использованием таблицы производных по правилу дифференцирования.

Пример 1

Найти производную для функции x = t 2 + 1 y = t .

Решение

По условию имеем, что φ (t) = t 2 + 1 , ψ (t) = t , отсюда получаем, что φ » (t) = t 2 + 1 » , ψ » (t) = t » = 1 . Необходимо использовать выведенную формулу и записать ответ в виде:

y » x = ψ » (t) φ » (t) = 1 2 t

Ответ: y x » = 1 2 t x = t 2 + 1 .

При работе с производной функции ч параметром t указывается выражение аргумента x через этот же параметр t , чтобы не потерять связь между значениями производной и параметрически заданной функции с аргументом, которому и соответствуют эти значения.

Чтобы определить производную второго порядка параметрически заданной функции, нужно использовать формулу производной первого порядка на полученной функции, тогда получаем, что

y «» x = ψ » (t) φ » (t) » φ » (t) = ψ «» (t) · φ » (t) — ψ » (t) · φ «» (t) φ » (t) 2 φ » (t) = ψ «» (t) · φ » (t) — ψ » (t) · φ «» (t) φ » (t) 3 .

Пример 2

Найти производные 2 и 2 порядка заданной функции x = cos (2 t) y = t 2 .

Решение

По условию получаем, что φ (t) = cos (2 t) , ψ (t) = t 2 .

Тогда после преобразования

φ » (t) = cos (2 t) » = — sin (2 t) · 2 t » = — 2 sin (2 t) ψ (t) = t 2 » = 2 t

Отсюда следует, что y x » = ψ » (t) φ » (t) = 2 t — 2 sin 2 t = — t sin (2 t) .

Получим, что вид производной 1 порядка x = cos (2 t) y x » = — t sin (2 t) .

Для решения нужно применить формулу производной второго порядка. Получаем выражение вида

y x «» = — t sin (2 t) φ » t = — t » · sin (2 t) — t · (sin (2 t)) » sin 2 (2 t) — 2 sin (2 t) = = 1 · sin (2 t) — t · cos (2 t) · (2 t) » 2 sin 3 (2 t) = sin (2 t) — 2 t cos (2 t) 2 sin 3 (2 t)

Тогда задание производной 2 порядка с помощью параметрической функции

x = cos (2 t) y x «» = sin (2 t) — 2 t cos (2 t) 2 sin 3 (2 t)

Аналогичное решение возможно решить другим методом. Тогда

φ » t = (cos (2 t)) » = — sin (2 t) · 2 t » = — 2 sin (2 t) ⇒ φ «» t = — 2 sin (2 t) » = — 2 · sin (2 t) » = — 2 cos (2 t) · (2 t) » = — 4 cos (2 t) ψ » (t) = (t 2) » = 2 t ⇒ ψ «» (t) = (2 t) » = 2

Отсюда получаем, что

y «» x = ψ «» (t) · φ » (t) — ψ » (t) · φ «» (t) φ » (t) 3 = 2 · — 2 sin (2 t) — 2 t · (- 4 cos (2 t)) — 2 sin 2 t 3 = = sin (2 t) — 2 t · cos (2 t) 2 s i n 3 (2 t)

Ответ: y «» x = sin (2 t) — 2 t · cos (2 t) 2 s i n 3 (2 t)

Аналогичным образом производится нахождение производных высших порядков с параметрически заданными функциями.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Сметанный крем с желатином для торта – рецепт

Окунь морской красный рецепты приготовления

Как найти вторую производную параметрической кривой — Криста Кинг Математика

Формула для второй производной параметрической кривой

Чтобы найти вторую производную параметрической кривой, нам нужно найти ее первую производную ???dy/dx???, используя формулу

???\frac{ dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}???

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. 92??? вторая производная параметрической кривой, ???dy/dx??? его первая производная и ???dx/dt??? является первой производной уравнения для ???x???. ???д/дт??? это обозначение, которое говорит нам взять производную от ???dy/dx??? относительно ???t???.

Как вычислить вторую производную параметрической кривой

Пройти курс

93}???

Получить доступ к полному курсу Calculus 2

Learn mathКриста Кинг 12 июля 2021 г. математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление II, исчисление 2, исчисление II, вычисление 2, полярные и параметрические, параметрические кривые, производная параметрической кривой, параметрические производные, параметрические вторые производные, вторая производная параметрической кривой

0 лайков

Производная функций в параметрических формах

Производные функций выражают скорость изменения функций. Мы умеем вычислять производные стандартных функций. Цепное правило, правило произведения и правило деления используются для вычисления производных сложных функций, которые состоят из композиции двух или более функций. Эти функции имеют две переменные, которые связаны друг с другом неявным или явным образом. Иногда мы встречаем функции, в которых переменные не связаны друг с другом явно или неявно, а связаны друг с другом через третью переменную. Давайте посмотрим, как подробно вычислить производные для таких функций.

Как найти производные функций в параметрических формах?

Допустим, у нас есть две переменные x и y, обычно такие переменные связаны друг с другом неявным или явным образом. Но в некоторых случаях эти переменные связаны друг с другом через третью переменную. Эта форма называется параметрической формой уравнения, а переменная называется параметром.

x = f(t) и y = g(t) здесь, t — параметр.

Производная таких функций определяется цепным правилом,

=

везде, где

Таким образом, =(asand)

Примеры задач

Вопрос 1: Найдите , если x = acos( ) , y = 1 03 asin( 9 0 3 ).

Решение:

x = ACOS (θ) и Y = ASIN (θ)

Теперь давайте найдем

⇒ Вопрос

.

.

⇒

40004.

9.

40004. 2: Найдите , если x = acos ² ( ), y = asin ² ( ).

Solution:

x = acos ² () , y = asin ² ()

Now, let’s find out

⇒

⇒

⇒

Вопрос 3: Найдите , если x = at ² + 2t, y = t при t = 0.

Решение:

x = в ² + 2t, y = t = t = t = t = t = t = t = t = t = t = t = t = t = t = t

Теперь давайте узнаем

⇒

⇒

⇒

Вопрос 4: Найдите , если x = ³ + 2T ^{2 9031, если x = 3 + 2T 2 2 2 , если x = 3 + 2t 2 , если x = 3 + 2t 2 . 2 at t = 1.}

Solution:

x = at ³ + 2t ² , y = t ²

Now, let’s find out

⇒

⇒

Вопрос 5: Найти , если x = 4t, y = при t = 1.

Решение:

x = 4t, y =

. Узнайте

⇒

⇒

AT T = 1

Вопрос 6: Найдите , если x = 4E ^T , y = cos (t) в T = 1.

Решение:

х = 4e ^T , y = cos (t)

Теперь давайте узнаем

⇒

AT = 1

⇒

ВОПРОС 7: Найти , ,

ВОПРОС 7: Найти , ,

ВОПРОС 7: , a

. = e ^t + sin(t), y = t ² , at = 0,

Решение:

Теперь узнаем

⇒

При t = 0

⇒

Вопрос 8: Найдите , , если x = tsin(t), y = cos(t), при t = .