Производная, таблица производных, примеры на производную
Главная » Математика
Математика
Автор Ольга Андрющенко На чтение 2 мин Просмотров 687 Опубликовано
Название производной происходит от слова «произведенная», то есть образованная от другой величины. Производная функции характеризует темп изменения функции.
Процесс определения производной какой-либо функции называется дифференцированием. Если говорить совсем просто, то для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию.
Содержание
- Определение производной
- ФОРМУЛЫ НАХОЖДЕНИЯ ПРОИЗВОДНЫХ ОСНОВНЫХ ФУНКЦИЙ
- ЧИСЛО, СТЕПЕННАЯ ФУНКЦИЯ, ФУНКЦИЯ С КОЭФФИЦИЕНТОМ
- ПРОИЗВОДНАЯ ОТ ПОКАЗАТЕЛЬНО-СТЕПЕННОЙ И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ
- ПРОИЗВОДНАЯ ОТ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
- ПРОИЗВОДНАЯ ОТ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Определение производной
Производная измеряет крутизну графика функции в определенной точке графика. Таким образом, производная — это наклон. Это означает, что это отношение изменения значения функции к изменению независимой переменной.
Таким образом, производная — это наклон. Это означает, что это отношение изменения значения функции к изменению независимой переменной.
Если независимой переменной оказывается «время», мы часто думаем об этом соотношении как о скорости изменения.
Если мы увеличим масштаб графика функции в некоторой точке так, чтобы функция выглядела почти как прямая линия, производная в этой точке — это наклон линии. Это то же самое, что сказать, что производная — это наклон касательной к графику функции в данной точке.
Наклон секущей линии (линия, соединяющая две точки на графике) приближается к производной, когда интервал между точками уменьшается до нуля.
Производная также является функцией: она меняется от места к месту. Например, скорость автомобиля может меняться от момента к моменту, когда водитель ускоряется или замедляется.
Последнее замечание очень важное и интересное: оно говорит нам о том, что когда мы закончили определять производную какой-то конкретной функции везде, мы получаем другую функцию! Тогда мы могли бы поговорить о его производной! Конечно, мы делаем это очень часто, не осознавая этого! Всякий раз, когда мы говорим об ускорении, мы говорим о производной, то есть о скорости изменения скорости. Вторые производные (и третьи производные и т. д.)
Вторые производные (и третьи производные и т. д.)
Мы использовали много слов, чтобы попытаться описать производную. Математики стараются избегать большого количества слов, стремясь к точности и лаконичности. Давайте посмотрим, что они могут сделать вместо этого.
ФОРМУЛЫ НАХОЖДЕНИЯ ПРОИЗВОДНЫХ ОСНОВНЫХ ФУНКЦИЙ
Некоторые функции уже имеют известную производную. Кстати, производная функции тоже функция.
ЧИСЛО, СТЕПЕННАЯ ФУНКЦИЯ, ФУНКЦИЯ С КОЭФФИЦИЕНТОМ
В таблице приведены формулы для определения производной степенной функции и функции, заданной числом.
ПРОИЗВОДНАЯ ОТ ПОКАЗАТЕЛЬНО-СТЕПЕННОЙ И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ
ПРОИЗВОДНАЯ ОТ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
ПРОИЗВОДНАЯ ОТ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Производная формула: простое для понимания руководство
В этой статье
Что такое производная формула?
Что такое производная?
Элементы производной
Основные формулы производных
Решение производных пошагово
Типы деривативов
Что такое производная формула?
Производные формулы — это уравнения, которые дают быстрые решения общих задач производных. Мы называем их правилами, такими как правило мощности и правило цепочки, и это лишь некоторые из них.
Мы называем их правилами, такими как правило мощности и правило цепочки, и это лишь некоторые из них.
Подробнее об этом позже.
Эти формулы взяты из предельного определения производной и упрощают процесс дифференцирования. Вот почему мы также можем называть их формулами дифференцирования.
Что такое производная?
Производная функции в точке xxx равна наклону касательной в xxx.
Это значение наклона представляет мгновенную скорость изменения в этой точке. Дифференцирование – это процесс нахождения производной функции.
Например, на приведенном ниже графике функция f(x)=ln(x)f(x) = \ln{(x)}f(x)=ln(x) выделена синим цветом. Красная линия — это f(x)=x−1f(x) = x-1f(x)=x−1, которая является касательной к fff в точке x=1x = 1x=1. Касательная линия к точке функции — это линия, которая едва касается функции в этой точке. Наклон этой касательной f(x)=x−1f(x) = x-1f(x)=x−1 равен 111, что означает, что производная f(x)=ln(x)f(x ) = \ln{(x)}f(x)=ln(x) равно 111 при x=1x = 1x=1.
Мы формально определяем производные, используя ограничения: Delta{x} \to 0} \frac{{f\left( {x + \Delta{x} } \right) — f\left( x\right)}}{\Delta{x} }=Lf'( x)=Δx→0limΔxf(x+Δx)−f(x)=L
Приведенное выше уравнение представляет собой предел средней скорости изменения fff на интервале [x,x+Δx][x, x +\Delta{x}][x,x+Δx] как Δx\Delta{x}Δx приближается к 0. Мы также знаем среднюю скорость изменения функции как наклон секущей.
В этих обозначениях Δx\Delta{x}Δx представляет небольшое изменение xxx. Если этот предел существует, то LLL является производной.
Элементы производной
Обозначение f’(a)f’(a)f’(a) представляет производную функции fff в некоторой точке aaa. Вы можете услышать, как это обозначение читается вслух как «производная от fff, оцениваемая как aaa», или как «fff, простое число как aaa».
Выражения f’(x)f’(x)f’(x) и dydx\frac{dy}{dx}dxdy представляют общую производную функцию fff. Последняя запись называется записью Лейбница. Подставляя любую точку aaa в результирующую функцию f’(x)f’(x)f’(x), мы можем определить наклон касательной к fff в любой точке кривой. 9{n-1}dxd(xn)=nxn−1
Подставляя любую точку aaa в результирующую функцию f’(x)f’(x)f’(x), мы можем определить наклон касательной к fff в любой точке кривой. 9{n-1}dxd(xn)=nxn−1
Специальный случай степенного правила
В этом случае nnn=1
ddx(x)=1\frac d{dx}(x)=1dxd (x)=1
Постоянное множественное правило
ddx(c⋅f(x))=c⋅f′(x)\frac d{dx}(c\cdot f(x))=c\cdot f ‘(x)dxd(c⋅f(x))=c⋅f'(x)
Цепное правило
ddxf(g(x))=f'(g(x))g'(x)\ frac{d}{dx}f(g(x)) = f'(g(x))g'(x)dxdf(g(x))=f'(g(x))g'(x )
Правило продукта
ddx[f(x)⋅g(x)]=f'(x)⋅g(x)+f(x)⋅g'(x)\frac{d}{dx}[ f(x) \cdot g(x)] = f'(x) \cdot g(x) + f(x)\cdot g'(x)dxd[f(x)⋅g(x)]=f ‘(х)⋅г(х)+f(х)⋅г'(х) 9xdxd(ex)=ex
По словам доктора Тима Шартье, два производных правила, которые меняют правила игры, — это правило продукта и правило частного:
Он также объясняет другие формулы дифференцирования для поиска с примерами:
youtube.com/embed/-R5wh_BIGm4″ title=»YouTube video player» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Решение производных шаг за шагом
Теперь мы обсудим, как найти производные. Мы можем решить производную двумя способами:
Используя формальное предельное определение производной
Использование основных формул производных
Вот шаги для нахождения производных с использованием определения предела:
Шаг 1
Подставьте свою функцию в определение предела формулы производной:
f'(x)=limΔx→0f(x+Δx)−f(x)Δx=Lf'(x) = \mathop{\lim}\limits_{\Delta{x} \to 0} \ frac{{f\left( {x + \Delta{x} } \right) — f\left( x\right)}}{\Delta{x} }=Lf'(x)=Δx→0limΔxf( х+∆x)−f(x)=L 92}{\Delta{x}}=Δx→0limΔx6xΔx+3Δx2
=limΔx→06x+3Δx= \mathop {\lim }\limits_{\Delta{x} \to 0}6x + 3 \Delta{x}=Δx→0lim6x+3Δx
Шаг 3.
 Оцените
ОценитеТеперь проверьте предел, когда Δx\Delta{x}Δx приближается к 0. Многочлены всегда непрерывны. Чтобы оценить этот предел, мы можем подставить Δx=0\Delta{x} = 0Δx=0 непосредственно в функцию, с которой мы остались.
f'(x)=limΔx→06x+3Δxf'(x)= \mathop {\lim }\limits_{\Delta{x} \to 0}6x + 3\Delta{x}f'(x )=Δx→0lim6x+3Δx
92f(x)=3×2 равно f’(x)=6xf’(x) = 6xf’(x)=6x. Это общая формула производной для любой точки на кривой fff.Чтобы найти производную в одной точке, мы можем подставить x=ax = ax=a в f’(x)=6xf’(x) = 6xf’(x)=6x.
Например, мы можем сказать, что:
f'(1)=6(1)=6f'(1) = 6(1) = 6f'(1)=6(1)=6, что представляет собой наклон касательной в точке x= 1х = 1х=1.
f'(5)=6(5)=30f'(5) = 6(5) = 30f'(5)=6(5)=30, что представляет собой наклон касательной при x=5x = 5x= 5.
f'(-60)=6(-60)=-360f'(-60) = 6(-60) = -360f'(-60)=6(-60)=-360, что представляет собой наклон касательная в точке x=-60x = -60x=-60.
 xf(x)=4×4+ex. 9x=16×3+ex
xf(x)=4×4+ex. 9x=16×3+exПрактический пример 3
Для более сложного примера найдем производную f(x)=sin(4x)cos(2x)f(x) = \sin{(4x)}\cos{(2x)}f(x )=sin(4x)cos(2x).
Во-первых, нам понадобится правило произведения. Это говорит о том, что производная произведения функций равна сумме первой функции, умноженной на производную от второй, и второй функции, умноженной на производную от первой.
f'(x)=sin(4x)⋅ddxcos(2x)+cos(2x)⋅ddxsin(4x)f'(x) = \sin{(4x)} \cdot \frac{d }{dx}\cos{(2x)} + \cos{(2x)} \cdot \frac{d}{dx}\sin{(4x)}f'(x)=sin(4x)⋅dxdcos (2x)+cos(2x)⋅dxdsin(4x)
Наряду с правилами производных синуса и косинуса нам также понадобится цепное правило, так как у нас есть композиция функций, использующая функции синуса и косинуса.
Цепное правило гласит, что производная композиции функций равна производной внешней функции, умноженной на производную внутренней функции.
Это означает, что производная sin(4x)\sin{(4x)}sin(4x) равна 4cos(4x)4\cos{(4x)}4cos(4x), а производная cos( 2x)\cos{(2x)}cos(2x) равно −2sin(2x)-2\sin{(2x)}−2sin(2x).

f'(x)=sin(4x)⋅ddxcos(2x)+cos(2x)⋅ddxsin(4x)f'(x) = \sin{(4x)} \cdot \frac{d }{dx}\cos{(2x)} + \cos{(2x)} \cdot \frac{d}{dx}\sin{(4x)}f'(x)=sin(4x)⋅dxdcos (2x)+cos(2x)⋅dxdsin(4x)
=sin(4x)⋅−2sin(2x)+cos(2x)⋅4cos(4x)= \sin{(4x)} \cdot -2\sin{(2x)} + \cos{(2x)} \cdot 4\cos{(4x)}=sin(4x)⋅−2sin(2x)+cos(2x)⋅4cos(4x)
= −2sin(4x)sin(2x)+4cos(2x)cos(4x)= -2\sin{(4x)}\sin{(2x)} + 4\cos{(2x) }\cos{(4x)}=−2sin(4x)sin(2x)+4cos(2x)cos(4x)
=4cos(2x)cos(4x)−2sin(4x)sin(2x )= 4\cos{(2x)}\cos{(4x)} — 2\sin{(4x)}\sin{(2x)}=4cos(2x)cos(4x)−2sin(4x)sin(2x )
Виды производных финансовых инструментов
Первая и вторая производные дают разную информацию о поведении функции.
Мы используем знак первой производной, чтобы определить, является ли функция возрастающей, убывающей или постоянной на интервале III:
Если f’(x)>0f’(x) > 0f’(x)>0 для каждого xxx на III, то fff увеличивается на III.
Если f'(x) для каждого x на I, то f убывает на I.

Если f’(x)=0f’(x) = 0f’(x)=0 для каждого xxx на III, то fff постоянна на III.
Мы находим вторые производные, просто взяв производную от первой производной. Вторые производные сообщают нам форму функции. Эта характеристика называется вогнутостью.
По знаку второй производной определяем интервалы вогнутости:
Если f’’(x)>0f’’(x) > 0f’’(x)>0 для каждого xxx на III, то fff вогнуто вверх на III.
Если f’’(x) для каждого x на I, то f вогнута вниз на III.
Если f’’(x)=0f’’(x) = 0f’’(x)=0 для каждого xxx на III, то fff не имеет вогнутости.
Доктор Ханна Фрай обсуждает тесты первой и второй производной:
Курс Outlier по исчислению производных поможет вам больше попрактиковаться в дифференцировании и других навыках вычисления производных.
 Вот почему:
Вот почему:Outlier предлагает доступные занятия в колледже за небольшую часть стоимости — на 80% дешевле, чем в традиционном колледже.
Заработайте 3 кредита колледжа за каждый пройденный курс. Курс аккредитован Университетом Питтсбурга, который входит в число 60 лучших школ.
Курсы исчисления являются интерактивными и преподаются всемирно известными профессорами математики, в том числе Тимом Шартье из колледжа Дэвидсона, Ханной Фрай из Университетского колледжа Лондона и Джоном Уршелем из Массачусетского технологического института.
Ресурсы курса включают наборы вопросов, викторины и цифровой учебник, основанный на активном обучении. У вас также будет доступ к бесплатным репетиторам и учебной группе.
Перевести кредиты легко.
Если вы выполните работу и не пройдете, вы получите полный возврат средств.
Окна экзамена гибкие, а лекции можно просматривать по запросу в любом месте.

Outlier (от соучредителя MasterClass) собрал лучших в мире преподавателей, дизайнеров игр и кинематографистов, чтобы создать онлайн-колледж будущего.
Ознакомьтесь с этими родственными курсами:
Исчисление I
Изучите курс
Исчисление I
Математика изменений.
Изучить курс
Введение в статистику
Изучить курс
Введение в статистику
Как данные описывают наш мир.
Изучить курс
Введение в микроэкономику
Изучить курс
Введение в микроэкономику
Почему маленькие решения имеют большое влияние.
Изучите курс
nth Производная: определение и примеры формул
Производная — это наклон касательной в точке. Здесь производные в точках A и B равны нулю. n-я производная относится к любой производной функции более высокого порядка.

Когда вы берете производную функции один раз, вы получаете первую производную. Дифференцируя новую функцию в другой раз, вы получите вторую производную. Точно так же третье, четвертое или пятое применение правил дифференцирования дает нам третью производную, четвертую производную и пятую производную соответственно. n -я производная — это формула для всех последовательных производных функции.
Примеры: Нахождение n-й производной
Посмотрите видео с тремя примерами:
n-я производная
Посмотрите это видео на YouTube.
Видео не видно? Нажмите здесь, чтобы посмотреть его на YouTube.
Нахождение n-й производной означает взять несколько производных (1-ю, 2-ю, 3-ю…) и найти закономерность. Если он существует, то у вас есть формула для n-й производной. Чтобы найти n-ю производную, найдите первые несколько производных, чтобы идентифицировать закономерность. Примените обычные правила дифференцирования к функции, затем найдите каждую последующую производную, чтобы получить

Пример 1 : Найдите n-ю производную f(x) = x n
Поскольку эта функция имеет показатели степени, используйте степенное правило, чтобы найти несколько первых производных. Как только вы вычислите первые 3-4 производные функции, вы должны получить представление об общей закономерности.
Первые три производные этой функции:
- f′(x) = nx n – 1
- f′′(x) = n(n – 1)x n – 2
- f′′′(x) = n(n – 1) (n – 2)x п – 3
Возникает закономерность: Каждая последующая производная добавляет еще один слой n минус (n -), что можно записать как:
n(n-1) (n-2)…(n – n + 1)
Формулу для n-й производной можно записать так:
f(n) = n(n – 1) (n – 2)…(n – n + 1)x n – n
Модель последовательное умножение называется факториалом и записывается как n!.
Пример 2 : Найти n-ю производную от f(x) = 1/x
Найдите первые три производные функции и затем решите:
- f′(x) = -1/x 2
- f′′(x) = 1 ∙ 2/x 3
- f′′′(x) = 1 ∙ 2 ∙ 3/x 4
Возникающая закономерность включает добавление дополнительного последовательного числа к числителю и еще одного показателя степени к знаменателю.


 xf(x)=4×4+ex. 9x=16×3+ex
xf(x)=4×4+ex. 9x=16×3+ex
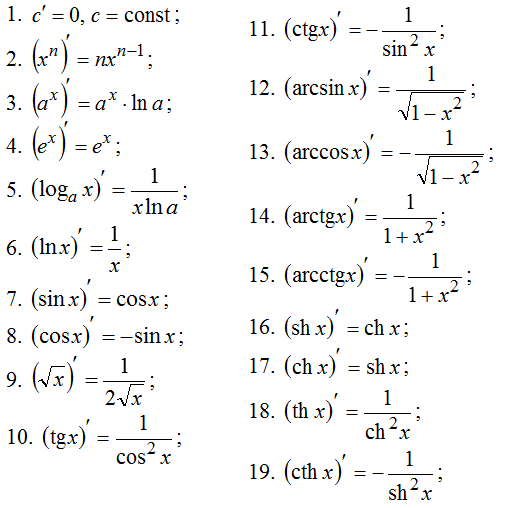
 Вот почему:
Вот почему: