Вероятность и пропорция: в чем разница?
В статистике студенты часто путают два термина: вероятность и пропорция .
Вот разница:
- Вероятность представляет шансы того, что какое-то событие произойдет. Это теоретически .
- Пропорция обобщает, как часто какое-то событие действительно происходило. Это эмпирический .
Мы часто используем вероятность, когда говорим о вероятности того, что какое-то событие произойдет в будущем.
Напротив, мы часто используем пропорцию, когда описываем, как часто какое-либо событие действительно происходило в прошлом.
Следующие примеры иллюстрируют различия между вероятностями и пропорциями в разных сценариях.
Пример 1: Вероятность и пропорция при подбрасывании монетыЕсли мы подбросим правильную монету, вероятность того, что она упадет орлом, составит 0,5 или 50% .
Однако если мы подбросим правильную монету 20 раз, то сможем подсчитать, сколько раз она выпадала орлом. Например, возможно, он приземлился орлом в 60% подбрасываний.
Вероятность выпадения орла является теоретической, но процентное соотношение случаев, когда монета выпадало орлом, является эмпирическим — мы могли бы подсчитать эту пропорцию.
Пример 2: Вероятность и пропорция в бросках кубиковЕсли мы бросим шестигранный кубик, вероятность того, что на нем выпадет число «4», составляет 1/6 или около 16,67% .
Однако, если мы бросим кубик 10 раз, то сможем подсчитать долю случаев, когда он выпал на 4. Например, возможно, он выпал на 4 в 20% бросков.
Вероятность выпадения «4» является теоретической, но доля случаев, когда кубик выпадал на «4», является эмпирической — мы могли бы подсчитать пропорцию.
Пример 3: Вероятность и пропорция в спиннерахЕсли мы вращаем спиннер, разделенный на четыре равные части — красную, синюю, зеленую и фиолетовую, — вероятность того, что он приземлится на фиолетовый цвет при любом заданном вращении, составляет 25% .
Однако, если мы повернем спиннер 100 раз, то сможем подсчитать, сколько раз он приземлялся на фиолетовый цвет. Например, возможно, он приземлился на фиолетовый во время 15% вращений.
Вероятность того, что спиннер приземлится на фиолетовый цвет, является теоретической, но доля случаев, когда он приземлялся на фиолетовый цвет, является эмпирической — мы могли бы посчитать эту пропорцию.
Пример 4: Вероятность против доли в колодах картВ стандартной колоде из 52 карт 4 дамы. Таким образом, вероятность выбора королевы при любом случайном розыгрыше составляет 4/52 = 7,69% .
Однако, если мы возьмем случайное взятие (и заменим вытянутую карту) 50 раз, мы сможем подсчитать долю случаев, когда мы вытягиваем даму. Например, возможно, мы рисуем даму в 10% розыгрышей.
Вероятность выбора ферзя является теоретической, но доля случаев, когда мы на самом деле выбираем королеву, является эмпирической — мы могли бы посчитать пропорцию.
Вероятность и вероятность: в чем разница?
Закон полной вероятности: определение и примеры
Основы учебного академического рисунка. Пропорции и их значение в рисовании — Ghenadie Sontu Fine Art
Соблюдение пропорций и их значение столь велико и значимо, что без них практически невозможно обойтись не только в изобразительном искусстве и архитектуре, но и в науке, технике, медицине и многих других сферах жизнедеятельности человека. Вот почему такое пристальное внимание уделяют изучению столь важного и необходимого предмета, как пропорция.
Изучение и постижение законов гармонии способно направить творческую деятельность архитекторов и художников на созидание новых, созвучных объективным законам восприятия и гармонии природы, произведений. Знание и изучение этих законов формирует мировоззрение и профессиональное отношение к творчеству и жизни. Об этом красноречиво свидетельствует утверждение: «Красота предмета образуется пропорциями, становясь строгой соразмерностью и гармоничностью».
К сожалению, нередко приходится слышать и видеть, как рисовальщики, даже имея за плечами немалый опыт, пренебрежительно относятся к пропорциям, сосредотачиваясь всецело на передаче характера и формы предмета. Между тем, из-за нарушенных пропорциональных величин изображение предмета, особенно живой формы, такой, как голова или фигура человека, приобретает уродливый вид, не говоря уже о недостаточной убедительности. Это относится не только к студентам, но и ко всем, кто недооценивает значение пропорции в учебном академическом рисунке. Пропорция в рисунке при создании реалистического изображения занимает главное положение наряду с такими понятиями, как композиция, объемная форма, конструкция и анатомия.
Хорошие пропорции в рисунке предполагают наличие полного сходства с изображаемым предметом. Иначе говоря, чем точнее определены пропорции предмета на рисунке, тем большего сходства с натурой достигает его изображение.
Следует помнить, что все тела, а также и их части должны сравниваться или соизмеряться друг с другом по признаку пропорциональных отношений.
Чтобы правильно определять соотношения частей предмета, рисующий должен, помимо знаний, обладать чувством пропорции/Чувство пропорции подразумевает наличие хорошего глазомера, а глазомер, как правило, развивается в процессе длительных упражнений в рисовании с натуры. Тренируя глазомер, необходимо развивать аналитическое мышление. Полагаясь только на глазомер, можно вновь повторить свои ошибки. Подобный подход недопустим при рисовании более сложных предметных форм, особенно таких, как голова человека. Немало примеров, когда студенты, полагаясь на глазомер, становятся заложниками натуры, срисовывая подряд все, что видит глаз. Такое рисование следует исключить из своей практики, так как это не грамотное рисование, а всего лишь слепое поверхностное копирование. Великий педагог П.П.Чистяков писал: «… Прежде всего расположи фигуру на бумаге, а затем приступай к ее построению. Построить — это значит взять правильные пропорции и поставить фигуру».
Для большей убедительности приведем множество примеров, касающихся возможности соблюдения пропорции не только в изобразительном искусстве и архитектуре, но и в области науки: в физике, химии, математике, технике и т.
д. К примеру, когда в строительной технологии нарушаются пропорции составов строительных материалов и размеров элементов конструкций, это может привести к разрушению сооружений. Архитектор, нарушая пропорции сооружения, тем самым разрушает принципы пропорциональной соразмерности его элементов. Если живописец нарушает пропорции в технологии грунтовки холста, это может привести к разрушению и холста и красочного слоя. В химии точные весовые пропорции реагентов обусловливают возможность получения необходимого вещества. Когда мы посещаем заповедники человеческой культуры и встречаемся с произведениями зодчества, музыкой или картинами художников, нас охватывает особое чувство необъяснимого волнения и восторга от увиденного и услышанного. И наоборот, когда эстетические качества сооружения или картины оставляют желать лучшего, мы испытываем чувство сожаления или равнодушия.
Сопоставляя выдающиеся памятники искусства и архитектуры, созданные в определенные исторические периоды культурами различных народов, и изучая их композиционную структуру, мы приходим к убеждению, что принципы пропорциональной соразмерности элементов являются непременным условием формирования облика объекта.
Пренебрежение пропорцией приводит к безграмотному, несостоятельному рисунку. Нетрудно представить, что если изображенный предмет непропорционален в своих отношениях, то он становится менее убедительным. Это очевидно в изображении головы человека, где лицевая часть доминирует в своих объемных размерах по отношению к черепной (мозговой) части, или когда голова человека по отношению к остальной фигуре слишком мала или велика и т.п. При изображении предметов нередко пренебрегают различиями в их размерах, пытаясь акцентировать внимание лишь на их конфигурации и форме, искажая тем самым пропорции и гармонию целого.
По мнению древних греков, гармония есть связь различных частей в единое целое. Для того чтобы получить это единое целое, необходимо связать части между собой таким образом, чтобы они представляли собой законченное единство.
Выдающиеся памятники древнего искусства и архитектуры обязаны своими соразмерностями и пропорциями человеку. Об этом свидетельствует фундаментальный тезис античной философии: «Человек — мера вещей».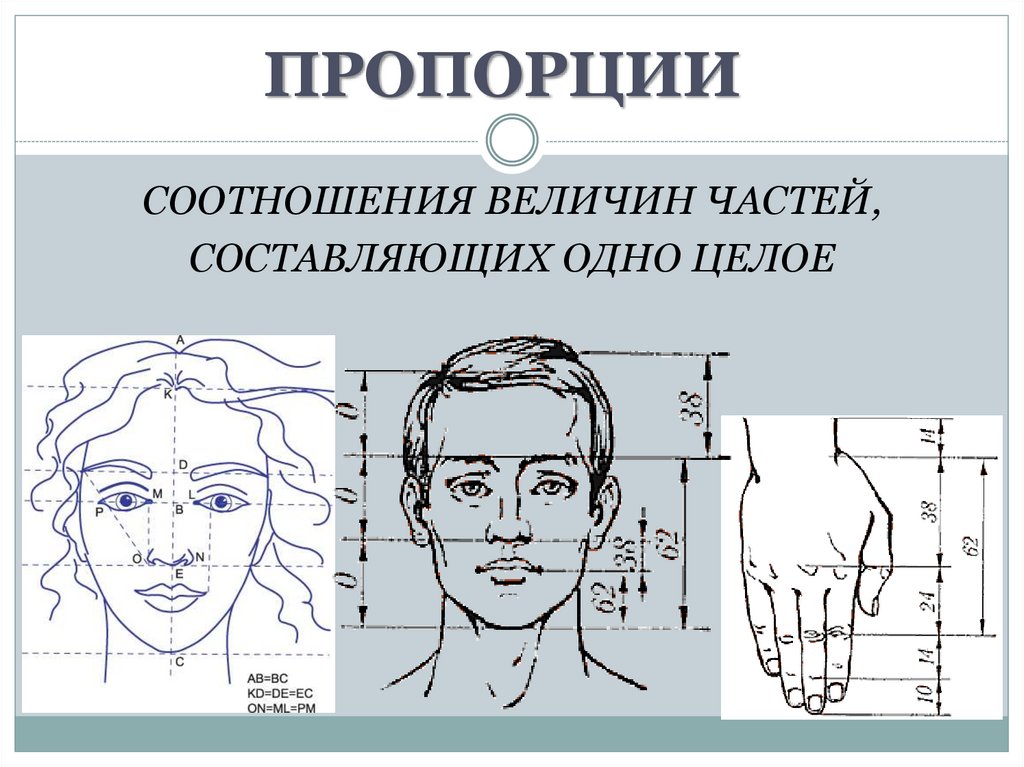
Именно человек является эталоном или модулем пропорционального строя архитектурных объектов древнего мира.
Пропорция человеческого тела имеет решающее значение при определении создаваемых вещей, оказывает влияние на формируемое им предметное окружение. Сообразно пропорциям человеческого тела зодчие устанавливали соразмерность и пропорцию храмов, сооружений и построек.
Пропорция есть соответствие между членами всего произведения и его целым по отношению к части, принятой за исходную, на чем и основана всякая соразмерность. Без соразмерности и пропорции не может быть правильной композиции, если в ней не будет членения, сопоставимого с телом хорошо сложенного человека.
Так, например, основной мерой в Древней Руси являлась давно известная, так называемая тьмутараканская сажень — 142 см (рис. 20). Она соответствовала двойному шагу человека. При пропорциональном сложении тела эта мера соотносится как 1 и . Новгородская мерная трость, в которой сопряжены парные меры Древней Руси, заключает в себе пропорцию храмов конца XII века, промеренных ею.
Новгородская мерная трость, как и меры античного Рима и классической Греции, принадлежит двойному квадрату — канону строителей египетских пирамид. Этими мерами соизмеряли архитектурные сооружения в Древней Руси, привнося в архитектуру свойство взаимопроникновения, т.е. гармонию. Вот почему человек является камертоном гармонического строя архитектуры и искусства, что нам и следует рассмотреть более детально. Но прежде рассмотрим пропорции простых и сложных предметов.
Как учить пропорции в 7-8 классе по математике
You are here: Главная → Статьи → Обучение соотношениям и пропорциямЧасто ученики учатся решать пропорции, запоминая шаги, но затем забывают их в мгновение ока после окончания школы. Они могут смутно помнить что-то о перекрестном умножении, но не более того. Как мы, педагоги, можем помочь им научиться и запомнить, как решать пропорции?
Соотношения и пропорции — это НЕ какие-то математические выдумки
На самом деле это не так.
Мы используем их постоянно, осознаем мы это или нет. Вы когда-нибудь говорили о скорости 55 миль в час? Или посчитайте, сколько времени нужно, чтобы добраться куда-нибудь с такой-то скоростью? Вы видели цены за единицу, такие как 1,22 доллара за фунт, 4 доллара за фут или 2,50 доллара за галлон. Вы когда-нибудь подсчитывали, сколько что-то стоит с учетом цены за единицу или какова ваша ежемесячная оплата, если с учетом почасовой ставки? Вы использовали соотношения (или коэффициенты) и пропорции.
Что такое пропорции?
Следующие две задачи связаны с пропорцией:
- Если 2 галлона бензина стоят 5,40 доллара, сколько будут стоить 5 галлонов?
- Если автомобиль проедет определенное расстояние за 3 часа, какое расстояние он сможет проехать за 7 часов?
Общая идея этих задач состоит в том, что у нас есть две величины, которые обе изменяются с одинаковой скоростью . Например, в верхней задаче у нас есть (1) бензин, измеряемый в галлонах, и (2) деньги, измеряемые в долларах.
Мы знаем оба количества (как в долларах, так и в галлонах) для одна ситуация (2 галлона стоят $5,40), мы знаем ОДНО количество для другой ситуации ( либо долларов , либо галлонов), и запрашивается недостающее количество (в данном случае стоимость 5 галлонов).
Вы можете сделать таблицу для систематизации информации. Ниже длинная строка —— означает «соответствует», а не вычитание.
Пример 1:
2 галлона —— 5,40 доллара 5 галлонов —— х долларов
Пример 2:
110 миль —— 3 часа х миль —— 4 часа
В обоих примерах две величины изменяются с одинаковой скоростью. Обе ситуации включают четыре числа, три из которых заданы, а одно неизвестно. Как мы можем решить эти типы проблем?
Множество способов решения пропорции
На самом деле есть несколько способов найти ответ на пропорцию — все они включают пропорциональное мышление .
- Если два галлона стоят 5,40 доллара и меня спрашивают, сколько стоят 5 галлонов, поскольку количество галлонов увеличилось в 2,5 раза, я могу просто умножить доллары на 2,5.
- Если два галлона стоят 5,40 доллара, я сначала подсчитываю, сколько стоит 1 галлон, а затем умножаю это на пять, чтобы получить стоимость 5 галлонов. Теперь 1 галлон будет стоить 5,40 долл. США : 2 = 2,70 долл. США, а затем 2,70 долл. США × 5 = 13,50 долл. США.
- Я могу составить пропорцию и решить ее перекрестным умножением:
5,40
2 галлона= x
5 галлоновПосле умножения на косинусу я получаю:
5,40 · 5 = 2 х
х = 5,40 · 5
2= 13,50 долл. США
- Я пишу пропорцию, как указано выше, но вместо перекрестного умножения я просто умножаю обе части уравнения на 5.
- Я пишу пропорцию так: (и это все еще работает, потому что вы можете записать два соотношения для пропорции несколькими разными способами)
5,40
х= 2 галлона
5 галлонов
Я хочу сказать, что для решения таких задач, как выше, вам не нужно помнить, как написать пропорцию или как ее решить — вы ВСЕГДА можете решить их, просто используя здравый смысл и калькулятор.
И ученики тоже должны это понимать. Заставьте их понять основную идею так хорошо, чтобы они могли решать проблемы с пропорциями, не используя уравнение, если это необходимо. Тем не менее, я считаю, что вы также должны научить перекрестному умножению, поскольку это очень необходимая «уловка» или сокращение при решении уравнений.
Одна из основных идей, которая всегда работает при решении пропорций, заключается в том, чтобы сначала найти удельную норму, а затем умножить ее, чтобы получить требуемое. Например: если автомобиль проедет 110 миль за 3 часа, какое расстояние он проедет за четыре часа? Сначала вычислите удельную скорость (какое расстояние проезжает машина за 1 час), а затем умножьте ее на 4.
Как учить пропорции
Чтобы познакомить учащихся с пропорциями, дайте им для заполнения таблицы эквивалентных ставок , например, приведенную ниже. Это поможет им научиться пропорциональные рассуждения .
| Miles | 45 | |||||||||||
| Hours | 1 | 2 | 3 | 4 | 5 |
| Dollars | 3. 30 | |||||||||||
| Pounds | 1 | 2 | 3 | 4 | 5 |
Работайте с этими таблицами (сначала используя простые числа), пока учащиеся не привыкнут к ним. Вы можете связать некоторые из них с реальными жизненными ситуациями. Например, вы можете взять ситуацию из задачи на пропорции слов в учебной программе по математике и составить из нее эквивалентную таблицу оценок.
По мере продвижения дайте учащимся таблицы с эквивалентными ставками для заполнения там, где «данные» находятся посередине:
| Dollars | 45 | |||||||||||
| Hours | 1 | 2 | 3 | 4 | 5 |
| Dollars | 42 | |||||||||||
| Hours | 1 | 2 | 3 | 4 | 5 | 9 | 0077 |
| Dollars | 15. 50 | |||||||||||
| Meters | 0.10 | 0.20 | 0.30 | 0.40 | 0,50 |
Конечно, студенты должны заметить, что легко заполнить таблицу, если вы сначала выясните, а затем найдите по общему уровню.
Следующий шаг: проблемы с пропорциями и мышление
После изучения таблиц эквивалентных ставок учащиеся готовы решать текстовые задачи. Сначала выберите простые, и дайте им подумать! Они вполне могут найти ответ самостоятельно, составив таблицу или рассчитав удельную ставку. Итак… на самом деле вам не нужно писать настоящую пропорцию, чтобы решить проблему с пропорциональным словом.
Однако я не хочу записывать уравнения или перекрестное умножение; студенты, изучающие алгебру и курсы предварительной алгебры, все еще должны научиться решать пропорции с перекрестным умножением.
Просто научиться пользоваться здравым смыслом еще важнее.
Определения
Вы заметили, что я не дал определения терминам соотношение и пропорция? Ну, я не хотел путать. Иногда вам не нужно заранее учить точные определения, но вы можете начать с обучения решению текстовых задач — даже задач из реальной жизни.
ОТНОШЕНИЕ — это две «вещи» (числа или количества) по сравнению друг с другом. Например, «3 доллара за галлон» — это соотношение, а «40 миль в час» — другое. Вот еще: 15 девочек против 14 мальчиков, 569слов за 2 минуты, 23 зеленых шара против 41 синего шара. В вашем учебнике по математике может быть сказано, что это сравнение двух чисел или величин.
Родственный термин, СТАВКА, определяется как соотношение, в котором две величины имеют разные единицы измерения. Некоторые люди различают и говорят, что две величины в отношении должны иметь одну и ту же единицу; некоторые люди не различают и позволяют также называть «3 доллара за галлон» соотношением.
ПРОПОРЦИЯ — это уравнение, в котором два отношения равны. Например, «3 доллара за галлон» равно «6 долларов за два галлона». Или, 2 учителя на 20 учеников равняются 3 учителям на 30 учеников. Или
| 3 литра 48 квадратных метров | = | 10 литров 160 квадратных метров |
Конечно, чтобы это была задача , вам нужно сделать одно из этих четырех чисел неизвестным (не заданным).
См. также
Бесплатные рабочие листы пропорций
Бесплатные рабочие листы для простых задач на пропорции.
Меню уроков математики
Пропорции в подобных треугольниках — тригонометрия
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
Помощь по тригонометрии » Треугольники » Подобные треугольники » Пропорции в подобных треугольниках
Какие из следующих сдвигов неверны?
Возможные ответы:
Правильный ответ:
Объяснение:
Фактическая смена для равна .
Сообщить об ошибке
Стороны прямоугольного треугольника равны , и . Аналогичный прямоугольный треугольник имеет стороны , и . Что ?
Возможные ответы:
Недостаточно информации для определения.
Правильный ответ:
Пояснение:
Подобные треугольники по определению имеют пропорциональные стороны. В этом случае мы можем разделить соответствующие части, чтобы найти масштабный коэффициент.
Соответствующие части: две самые маленькие стороны, средние стороны и самые большие стороны.
Таким образом:
– коэффициент масштабирования.
Затем мы используем это, чтобы найти недостающую сторону.
Следовательно, .
Сообщить об ошибке
Соответствующие стороны двух треугольников имеют меры и .
Если другая сторона маленького треугольника равна , чему равна сторона большего треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы можем найти масштабный коэффициент, разделив 18 на 6.
Мы получаем, что масштабный коэффициент равен 3.
Умножая другую сторону на 3, мы получаем новую сторону, 21.
Сообщить об ошибке
Какой набор следующих размеров треугольника НЕ имеет тех же пропорций, что и треугольник 3-4-5?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы определить, имеют ли размеры треугольника одинаковые пропорции, отношения размеров также должны быть такими же, как у треугольника 3-4-5.
Следующие коэффициенты масштабирования, умноженные на треугольник 3-4-5, дают аналогичные пропорции.
Единственные размеры, которые нельзя получить путем умножения определенного масштабного коэффициента на 3-4-5, это:
Сообщить об ошибке Эти треугольники
подобны. Используйте это, чтобы найти x:
Возможные ответы:
Правильный ответ:
Пояснение:
Изначально нам даны гипотенуза и один катет большого треугольника, но оба катета маленького треугольника. Чтобы составить пропорцию, нам нужно знать обе стороны большого треугольника, и мы можем найти недостающую, используя теорему Пифагора:
, где a и b — катеты, а c — гипотенуза.
вычесть 64 из обеих сторон
извлечь квадратный корень из обеих сторон пропорция для решения x:
разделить обе стороны на 8
Сообщить об ошибке
Эти два треугольника подобны.