Проверь какие из данных углов являются прямыми обозначь эти углы буквами: Проверь, какие из данных углов на чертеже являются прямыми. Обозначь эти углы буквами и запиши их обозначения

ГДЗ по математике 4 класс учебник Моро, Бантова 2 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бантова М. А.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

❤️️Ответ к странице 109. Математика 4 класс учебник 2 часть. Авторы: М.И. Моро, М.А. Бантова.

Решебник — страница 109Готовое домашнее задание

Номер 2.

Рассмотри чертёж. Назови диагонали квадрата и точку их пересечения. Что можно сказать о свойствах диагоналей квадрата, зная, что квадрат тоже прямоугольник? У диагоналей квадрата есть ещё одно свойство. При пересечении диагоналей квадрата получаются четыре прямых угла. Проверь это свойство по чертежу.

Ответ:

КМ и LN – диагонали квадрата, Е – точка их пересечения. Диагонали квадрата точкой пересечения делятся пополам.

Номер 3.

Используя свойства диагоналей квадрата, начерти в тетради квадрат, длина диагонали которого 5 см.

Ответ:

Номер 4.

Построить 4 прямых угла с общей вершиной можно и на нелинованной бумаге.
1) Отложи на прямой отрезок АВ. Радиусом, равным больше половины длины отрезка, проведи 2 окружности с центрами в точках А и В (чертёж 1). Обозначь точки пересечения окружностей буквами С и D. Проведи прямую через точки С и D. Точку пересечения прямых обозначь буквой О. Проверь, что все 4 угла с вершиной в точке О прямые. Вместо окружностей можно проводить дуги (части окружностей) любого радиуса, который всегда должен быть больше половины длины отрезка АВ.
2) Построй 4 прямых угла с общей вершиной в точке О, следуя плану пункта 1, но вместе окружностей проводи дуги (чертёж 2). Любую точку отрезка CD соедини отрезками с точками А и В. Убедись, что полученный треугольник – равнобедренный. Начерти так же ещё 2 равнобедренных треугольника; 1 равносторонний.

Ответ:

1) 1. Отложи на прямой отрезок АВ = 3 см. 2. Радиусом больше, чем половина отрезка (в нашем случае больше 1,5 см, например, 2 см) проведи 2 окружности с центрами в точках А и В. 3. Точки пересечения обозначь буквами C и D. 4. Проведи через полученные точки прямую, а точку пересечения этой прямой и прямой АВ обозначь буквой D. 5) Проверь, что все 4 угла с вершиной в точке О.
2) Треугольник будет равнобедренным, так как его стороны AK и BK являются радиусами равных окружностей, а значит, эти стороны равны. Чтобы получить равносторонний треугольник, радиус окружностей должен быть равен отрезку AB. Затем нужно соединить точку пересечения окружностей с точками A и B.

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127

Занимательная геометрия — презентация онлайн

НАЧАЛЬНАЯ ШКОЛА
Окружающий нас мир — это мир ГЕОМЕТРИИ,
которая является частью великой МАТЕМАТИКИ.
С давних времён людям необходимо было
размечать земельные участки под поля, дороги,
строения. Так родилась геометрия, что в переводе
с греческого языка означает ЗЕМЛЕМЕРИЕ.
Без знания геометрии невозможно построить дома,
дачи, создать машины, мебель, одежду, игрушки и
многое другое.
Давайте совершим увлекательное путешествие в
страну геометрию.
Перед тобой точка.
.
Её можно поставить на бумаге карандашом, ручкой,
фломастером.
А теперь и вы поставьте на листе бумаги одну красную
и две синие точки.
Любую линию можно провести, не отрывая карандаша
от бумаги.
Что мы возьмём с собой в путешествие
На рисунке внизу Учёный Ластик показывает,
как провести такую прямую линию.
Возьми линейку, прижми её рукой к бумаге и
проведи карандашом вдоль линейки. Вот
видишь, и у тебя получилась прямая линия.
ЗАДАНИЕ
1. Проведи три
прямых линии.
Одну – красную,
вторую – зелёную,
третью – синюю.
2. Поставь точку и
проведи через неё
несколько прямых
линий.
Значит, через одну точку можно провести сколько угодно прямых
.
О
Точка О — это точка пересечения этих прямых.
Линии бывают разные – прямые, ломаные, кривые
кривая
прямые
ломаная
Пятачок очень торопится на день рождения ослика Иа.
У него воздушный шарик на нитке. Посмотри, как
расположена нитка — точно сверху вниз. Нитка
представляет пример ВЕРТИКАЛЬНОЙ линии.
Оглянись вокруг и с помощью веревочки и груза
попробуй определить, какие предметы в классе
расположены вертикально.
Начерти в тетради несколько разноцветных
вертикальных прямых линий.
Кроме вертикальных линий, существуют
линии, которые называются ГОРИЗОНТАЛЬНЫМИ.
Они получили свое название от слова горизонт.
Проведи сам несколько
горизонтальных линий. Найди и
перечисли в каких предметах
встречаются горизонтальные линии
Как расположены в здании колонны,
ступени.
Мы узнали, что через одну точку можно провести
много прямых линий.
.
А сколько прямых линий можно провести
через 2 точки?
.
Только одну
.
Попробуй и ты, поставь 2 точки и проведи прямую. Сможешь ли ты
провести через эти точки ещё прямые?
Прямая линия не имеет
ни начала, ни конца. Но
посмотри, что делают с
прямой три поросёнка.
Они вырезают из неё
кусок.
Этот кусок прямой называется ОТРЕЗКОМ.
В геометрии прямые разрезаются на отрезки точками.
Если на прямой поставить две точки, это означает,
что из прямой вырезали отрезок.
Прямую можно разрезать или разделить на бесконечное число
отрезков. Поставь на прямой четыре точки. Сосчитай, сколько
отрезков получилось.
Перед вами 3 отрезка, которые обозначены дугами
3 отрезок
2 отрезок
1 отрезок
Начерти 2 отрезка . Первый отрезок [АВ] = 5 см
Второй отрезок [CD]= 3 см
А
5 см
В
С
3 см
D
Одной точкой прямую линию можно разрезать на два
ЛУЧА. Посмотри, как это сделала Резиночка.
1 луч
А
Луч всегда имеет начало (точку), но
не имеет конца, а значит, он не имеет
и длины.
2 луч
Если мы из одной точки
плоскости проведём в
разные стороны 2 луча,
то они образуют УГОЛ
Посмотри, получилась горка, которая в геометрии
называется УГЛОМ.
Точка, над которой стоит Волк, называется ВЕРШИНОЙ угла,
а лучи, которые выходят из вершины, называются его
СТОРОНАМИ.
Углы бывают разные
Учёный Ластик и Резиночка рассказывают и показывают,
как сравнить разные углы.
Надо сложить углы так,
чтобы вершины их совпали и
одна сторона первого угла прошла
по стороне второго угла.
Ты видишь, что вторая сторона
угла находится внутри первого
угла. Значит, угол, который держит
Резиночка, меньше.
Если стороны углов совпадут, значит, углы одинаковые.
Обрати внимание, какой домик построил себе Буратино. Все
окошки в нём имеют одинаковые углы, и называются эти углы
ПРЯМЫМИ.
Вот ещё два прямых
угла в руках у
Резиночки.
«Как же нам определить прямой
угол?» — спрашивает
Динозаврик.
На этот вопрос ему отвечает
ученый Ластик. Если угол
треугольника совпадёт
с
нарисованным углом,
то он прямой.
Учёный Ластик показывает,
как с помощью треугольника
начертить прямой угол.
Угол, который меньше прямого угла, называется ОСТРЫМ.
Карлсон проверяет, какой угол
он начертил. А ты знаешь?
Угол, который больше прямого, называется ТУПЫМ
Сколько прямых углов в
домике?..
А
острых
углов?.. А тупых углов?..
Сосчитай и запиши.
ПОСМОТРИ И СОСЧИТАЙ:
Сколько углов у Мальвины?.. А сколько их у Пьеро?.. А у Буратино?..
.
вершина
звено
.
вершина
вершина
звено
звено
вершина
Давайте соединим точки прямыми линиями
То, что мы начертили, называется ЛОМАНОЙ линией.
Сколько ломаных линий
ты видишь на рисунке?..
Из скольких отрезков состоит
самая длинная ломаная линия.
А как ты думаешь, что получится, если соединить три
отрезка в замкнутую ломаную линию? Давай спросим у
Учёного Ластика. А Резиночке поможем её дорисовать.
Если соединить три отрезка, как сделал это ученый
Ластик, получится ТРЕУГОЛЬНИК или замкнутая линия
Треугольник – геометрическая фигура. Он имеет три
угла и три стороны.
Загадка : Он призван геометрии служить
В нем 2 прямых ( тупых ) угла не могут жить!
Как ты думаешь, почему
на рисунке у Пятачка
получился треугольник, а у
Винни-Пуха нет?
Пятачок рассказал, из каких трёх отрезков можно
построить треугольник.
Надо выбрать самый большой отрезок и приложить к
нему два других. Если эти два отрезка по длине больше
самого большого отрезка, то из них можно построить
треугольник.
КАКИЕ УГЛЫ
МОЖЕТ ИМЕТЬ
ТРЕУГОЛЬНИК
Весёлые поросята и
Резиночка приготовили
тебе задание.
Проверь себя.
Постарайся правильно
найти и запиши номера
треугольников:
прямоугольный
равнобедренный
тупоугольный
остроугольный
равносторонний .
Длину отрезка можно измерить не только циркулем-измерителем,
но и ЛИНЕЙКОЙ. Видишь, как это делает весёлая компания: Сова,
Винни-Пух и Пятачок?
А теперь посмотри внимательно на линейку и запомни!
Расстояние между двумя соседними чёрточками с
цифрами на линейке называется САНТИМЕТРОМ. Чтобы
измерить длину отрезка, нужно приложить к нему линейку
и сосчитать, сколько сантиметров от одного конца отрезка
до другого..
Посмотри на линейку ещё раз. Пятачок поможет тебе с
помощью увеличительного стекла увидеть между двумя
чёрточками с цифрами чёрточку поменьше, она делит каждый
сантиметр пополам.
Начерти несколько отрезков разной длины, каждый
отрезок обозначь другим цветом.
Для измерения больших величин используют другие
единицы, или меры длины. Например, ДЕЦИМЕТР — это
мера длины, состоящая из 10 сантиметров.
см
см
см см см
см
см см см
см
МЕТР — это мера длины, состоящая из 10 дециметров
или 100 сантиметров.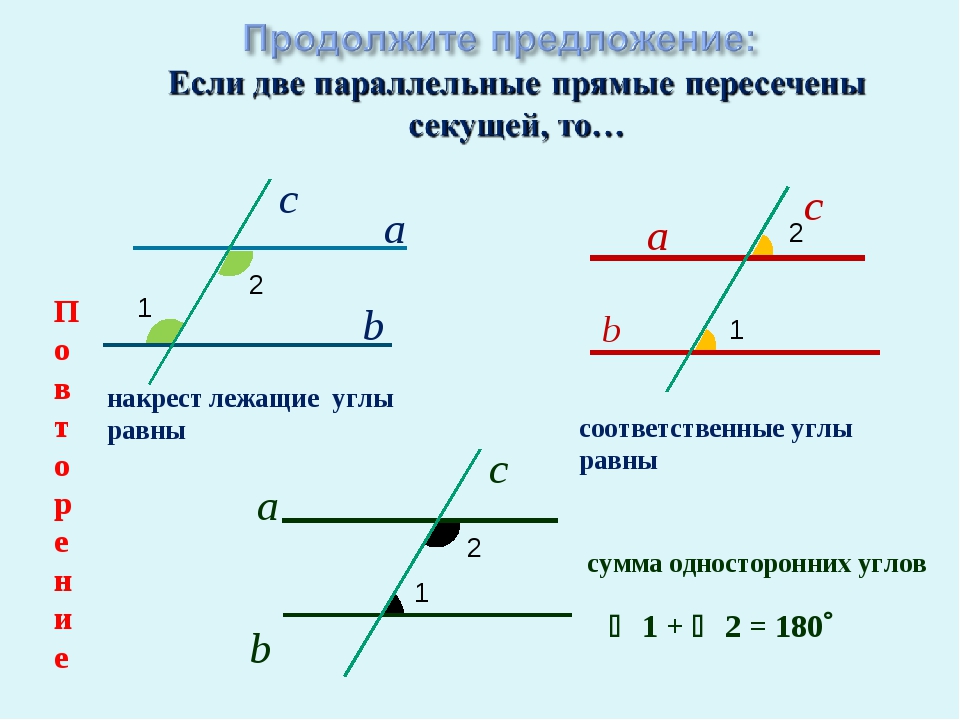
10 10 10
10
10 10
1 метр
10 10 10 10
На рисунке изображены приборы, с помощью которых измеряют
длину.
метр
СКЛАДНОЙ МЕТР
ИЗМЕРИТЕЛЬ
САНТИМЕТР
Пятачок и Винни-Пух предлагают продолжить изучение линейки. Теперь они
находят самые короткие чёрточки — их больше всего. Эти короткие чёрточки
делят половину сантиметра на пять частей. Каждая такая часть называется
МИЛЛИМЕТРОМ. 1 сантиметр состоит из 10 миллиметров.
1МИЛЛИМЕТР
1
Для измерения большого расстояния используют большую меру длины, и
называется она КИЛОМЕТРОМ. В 1 километре 1000 метров.
1000 метров = 1 километру
приходится изображать очень
большие расстояния. Как же
можно на небольшом листке
поместить несколько
километров?
Например, если 1 сантиметр
будет обозначать 100
километров, то на одной карте
можно провести линию,
изображающую расстояние от
Санкт-Петербурга до Москвы.
А если 1 сантиметр будет обозначать 1 метр то на листе бумаги
можно изобразить лишь автомобиль, который едет из Москвы в
Санкт-Петербург.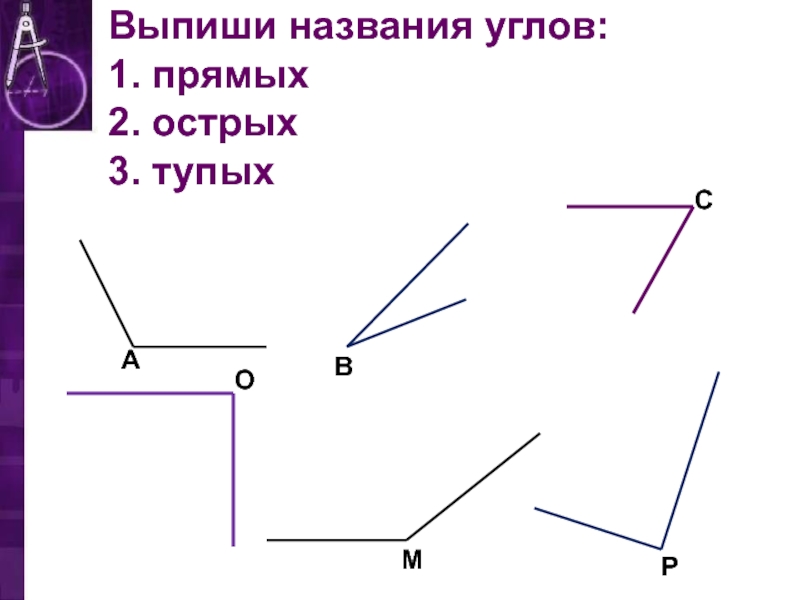
Посмотри: что начертил на листе Учёный Ластик? .
Как, по-твоему, можно назвать эту геометрическую фигуру?
Сколько у неё сторон? А сколько углов?
Геометрическая фигура, которую нарисовал Ластик,
называется ЧЕТЫРЁХУГОЛЬНИКОМ.
Точки в углах четырехугольника называются вершинами
четырехугольника, а отрезки соединяющиеся эти точки –
сторонами четырёхугольника.
Можно ли назвать прямоугольником
геометрическую фигуру, которую начертил
Винни — Пух?
НЕТ
ПРЯМОУГОЛЬНИКОМ называется четырехугольник, у
которого все углы прямые, а противоположные стороны
равны. ПРОТИВОПОЛОЖНЫМИ называются стороны,
которые лежат напротив друг друга.
Прямоугольник, у которого все четыре стороны
одинаковые, называется КВАДРАТОМ. Помоги
Сове начертить квадрат.
Четырёхугольник, у которого все стороны равны,
называется РОМБОМ.
Чтобы начертить ромб на листе в клетку, необходимо:
1. Поставить точку.
2.Отступить от этой
точки равное
количество клеток
вправо и влево и
поставить две
точки.
3. Отступить от
этой точки равное
количество клеток
вверх и вниз и
опять поставить
две точки.
4. Соединить все точки между собой прямыми линиями.
На самом деле мы начертили квадрат.
А теперь начертим ромб. Будем действовать так же ,
но изменим расстояние между точками в 3 пункте.
.
1. Поставить точку.
2.Отступить от этой точки равное
количество клеток вправо и влево и
поставить две точки.
3. Отступить от этой точки
равное количество клеток
вверх и вниз и опять поставить
две точки.
4. Соединить все точки
между собой прямыми
линиями.
Мы начертили ромб
.
. .
.
Попробуй вспомнить, как называются эти
геометрические фигуры
НАЧАЛЬНАЯ
ШКОЛА

41. ЗАНИМАТЕЛЬНАЯ ГЕОМЕТРИЯ

В новом путешествии в страну геометрии тебе
предстоит познакомиться с новыми, более сложными
геометрическими понятиями.
Посмотри на рисунок. Рядом с Незнайкой находятся разные
предметы, но все они имеют сходство между собой и
представляют одну и ту же геометрическую фигуру.
Эта
фигура
называется
КРУГОМ.
Круг можно
нарисовать легко и
быстро, если
обвести
карандашом какойлибо круглый
предмет. Попробуй
нарисовать круг
этим способом.
Ты уже знаком с циркулем-измерителем для измерения
отрезков. Для того чтобы начертить круг, удобнее всего
воспользоваться циркулем, у которого на одном конце
игла, а на другом — грифель-карандаш.
Чтобы начертить круг таким
циркулем, надо поставить
ножку с иглой на бумагу, а
ножкой с грифелем очертить
круг.
Посмотри,
как
это
сделал
Учёный
Ластик.
Закрась
круг
зеленым
карандашом.
Всё, что закрашено зелёным
цветом, называют КРУГОМ!
А черная линия карандаша
циркуля, называется
ОКРУЖНОСТЬЮ этого круга
ОКРУЖНОСТЬ
Круг
Круг
Начерти сам несколько окружностей
Точка, в которую Сова
ставит ножку циркуля с иглой,
называется
ЦЕНТРОМ
ОКРУЖНОСТИ.
Центр окружности
является также и
ЦЕНТРОМ КРУГА.
Сова поставила точку на окружности и соединила
центр окружности с точкой на окружности.
Отрезок, который
начертила Сова,
называется
РАДИУСОМ
ОКРУЖНОСТИ.
Радиус окружности
является и
РАДИУСОМ КРУГА.
Обозначь красным карандашом точки пересечения
прямой линии с окружностью. Проведи по отрезку,
который у тебя получился, красным карандашом. Этот
отрезок называется ДИАМЕТРОМ ОКРУЖНОСТИ или
ДИАМЕТРОМ КРУГА. У разных окружностей и кругов
диаметры разные по длине.
Проведи цветными карандашами по диаметру первой
окружности и диаметру второй окружности.
Одна точка может быть центром нескольких окружностей.
Посмотри, Буратино начертил две окружности.
.
Возьми циркуль и
начерти из одной
точки три окружности
ВОПРОС : Центр принадлежит окружности?
Центр принадлежит кругу?
НЕТ
ДА
Посмотри на рисунок и вместе с Пятачком и ВинниПухом определи, сколько точек пересечения с
окружностью имеют прямые:
1
Точки пересечения
Точка касания
Помоги Буратино разрезать
пирог на четыре части.
Каждый кусок пирога, вырезанный из центра круга и его
окружности, представляет собой СЕКТОР. На рисунке изображено
четыре сектора.
Начерти круг и раздели его на шесть равных
частей . Каждую часть ( сектор ) раскрась своим
цветом.
3
4
Подумай вместе с Пятачком, какие
геометрические фигуры находятся
внутри круга. Запиши их названия.
Если геометрическая
фигура лежит внутри круга
и касается его окружности
всеми вершинами, то
окружность называется
ОПИСАННОЙ.
Какие геометрические
фигуры описаны
окружностями?
А если, наоборот, окружность внутри какойлибо геометрической фигуры касается всех его
сторон, то окружность — ВПИСАННАЯ.
На каком из рисунков окружность можно назвать
вписанной?
В первой части ты познакомился с таким понятием, как ломаная
линия. Если соединить начало и конец ломаной линии, то
получится МНОГОУГОЛЬНИК или замкнутая линия
Почтальон Печкин начертил четыре многоугольника.
Название многоугольника зависит от того, сколько углов
он имеет. Например, многоугольник, в котором пять
углов, называется пятиугольником, шесть углов —
шестиугольником. Многоугольники, у которых все
стороны и углы равны, называются ПРАВИЛЬНЫМИ.
Назови, какие многоугольники начертил кот Леопольд.
Буратино с Мальвиной
окружностями.
Посмотри: в третьей
окружности правильный
восьмиугольник — у него
больше всего углов. С
увеличением количества
углов правильный
многоугольник всё больше
напоминает форму круга.
описали
разные
многоугольники
На рисунке изображён треугольник. Начерти такой же у себя в
тетради. Раскрась его стороны цветными карандашами: первую —
красным, вторую — синим, третью — зелёным.
Измерь линейкой длину сторон и запиши результаты в тетрадь:
Попробуй сложить длины всех сторон.
Полученная сумма длин трёх сторон называется
ПЕРИМЕТРОМ ТРЕУГОЛЬНИКА.
Сумма длин всех сторон многоугольника будет называться
ПЕРИМЕТРОМ МНОГОУГОЛЬНИКА.
Начертим прямоугольник , длина — 5см, ширина — 3 см . Найди
длину всех его сторон?
Сначала начертим прямоугольник
Обозначим длину буквой «а»
Ширину буквой «в»
а
в
в
а
Чтобы найти длину всех сторон нам
надо сложить их поочерёдно.
а + в + а + в = (подставляем величины)
5 + 3 + 5 + 3 = 16 (см )
Ответ: 16 сантиметров длина всех сторон
Сумма всех сторон геометрической фигуры называется – ПЕРИМЕТР
и обозначается буквой Р
Мы знаем, что противоположные стороны прямоугольника равны. Длина и
ширина повторяются 2 раза. Значит это можно представить так ( а + в) х 2
А теперь ещё раз вычислим периметр прямоугольника –
Р=(а+в)х2
Р = ( 5 + 3 ) х 2 = 16 (см)
Используй это свойство при решении следующих задач!
Задача
Длина садового участка 10 метров, ширина участка 5 метров
Какой длины нужно поставить забор по периметру участка?
Как мы оформляем задачу в тетради.
Задача
Дано:
а = 10 м
в=5м
Р=?
Р=а+в+а+в=(а+в)х2
Р = ( 10 + 5 ) х 2 = 30 (м)
Ответ : 30 метров длина забора
На рисунке изображены три разные геометрические фигуры. Как ты
думаешь, какая из фигур самая большая, а какая самая маленькая
Для того чтобы сравнить две или несколько геометрических фигур,
необходимо измерить их площадь. Как это сделать? Сначала нужно
сосчитать, какое количество мер площади находится внутри каждой из
этих фигур. А что такое мера площади? Ты уже знаешь, что меры
длины — это сантиметр, метр, дециметр, километр. Мерами же
площади являются квадратный сантиметр, квадратный метр,
квадратный дециметр и квадратный километр.
КВАДРАТНЫМ САНТИМЕТРОМ называется квадрат
со стороной 1 сантиметр.
1 КВАДРАТНЫЙ
САНТИМЕТР
1 см
1 см
Каждая клеточка в тетради по математике
имеет длину полсантиметра.
Чтобы начертить 1 квадратный сантиметр в
тетради, нужно обвести четыре клеточки.
Посмотри, как это сделала Резиночка.
Возьми линейку и начерти квадраты, сторона которого
равна 1 сантиметру, 3 см, 5 см.
Посмотри на рисунок. На листках около Мальвины и Пьеро
обведено по четыре клеточки. Расположены они по-разному, но и те
и другие имеют площадь 1 квадратный сантиметр. Значит можно
сказать, что площадь любых четырех клеточек в тетради по
математике равна 1 квадратному сантиметру.
На рисунке изображена геометрическая фигура,
разбитая на квадраты площадью 1 квадратный
сантиметр.
Попробуй определить площадь этой геометрической
фигуры. Для этого нужно сосчитать, из скольких
квадратов площадью 1 квадратный сантиметр состоит
геометрическая фигура.
Определи подобным способом площади прямоугольников:
Сова с Пятачком расскажут тебе, что нужно сделать,
чтобы определить площадь прямоугольника с помощью
линейки.
1. Необходимо измерить линейкой длину сторон
прямоугольника. На рисунке длина сторон равна 4 и 3
3
сантиметрам.
2
1
0
0
1
2
3
4
2. А теперь попробуй перемножить длины сторон
прямоугольника:
2
4 х 3 = 12( см )
3. Площадь прямоугольника получилась 12 квадратных
сантиметров.
1 метр
Подумай, для чего нужно определять площадь различных фигур?
Например, для того, чтобы знать, сколько необходимо купить обоев
для оклеивания стен. А ещё для чего, как ты думаешь? При
определении большой площади неудобно пользоваться такими
маленькими мерами, как квадратный сантиметр. Единица измерения,
которую используют при определении больших площадей, называется
квадратным метром.
1 квадратный метр
1 метр
КВАДРАТНЫЙ МЕТР — это квадрат, сторона которого равна 1 метру.
Вычисли площади всех прямоугольников
4см
5см
3см
3см
5см
5см
2см
6см
3см
Площадь геометрических
фигур обозначается
буквой S . Теперь
попробуем вывести
формулу площади фигуры.
Нам надо перемножить
3см
4см
длину на ширину. Мы с
2см
вами уже знаем, что
длина обозначается
буквой « а », а ширина
буквой «в» Теперь мы
запишем вычисление
с помощью букв. S = а х в
Нам осталось подставить
вместо букв их значения
S = 4 х 3 =12(см 2) — площадь первого четырёхугольника. Вычисли все остальные
пощади четырехугольников по формуле S = а х в
«Как определить площадь
сложной геометрической фигуры?»
— спрашивает у Пятачка Винни-Пух.
Пятачок объясняет:
1) надо разделить геометрическую
фигуру на прямоугольники;
первый
второй
третий
четвертый
пятый
2) определить площадь каждого прямоугольника,
а затем результаты вписать в квадратики;
+
+
+
+
=
2
( см )
3) сложить площади всех прямоугольников и результат записать.
А теперь сами начертите сложную геометрическую фигуру и определите
ёе площадь.
Посмотри, на рисунке прямоугольный треугольник.
Как можно определить его
площадь? Попробуй вписать в
него квадрат. Закрась полученный
квадрат красным карандашом. А
затем вместе с Винни-Пухом
попытайся совместить
незакрашенные части так,
чтобы получился квадрат,
Видишь, получилось два квадрата,
вычисли их площади, и ты узнаешь, чему равна площадь треугольника.
3 см
3 см
Дано
а = 3см
S=?
Задача
2
S1= а х а = 3 х 3 = 9(см )
Площадь 1 квадрата
2 квадрат = 1 квадрату
Значит их площади
равны. Теперь находим
площадь треугольника.
2
S1 + S 2 = 9+ 9 =18(см )
Ответ: Площадь треугольника равна
18 квадратным сантиметрам.
Для
того
чтобы
определить
площадь
прямоугольного
треугольника, нужно перемножить длины сторон, которые
образуют прямой угол, и разделить полученный результат
пополам.
2
1) 4х5=20(см )
2
2). 20:2 =10 (см )
Начерти свой прямоугольный треугольник
Определи площадь своего треугольника.
Его площадь равна . . . квадратным сантиметрам
Посмотри на рисунок. На нём изображены пары одинаковых
фигур. Такие фигуры называются СИММЕТРИЧНЫМИ.
Как же получить симметричную фигуру?
Для этого надо поднести
зеркало к геометрической
фигуре, и в зеркале ты
увидишь её симметричное
отражение. Линия, по
которой зеркало
соприкасается с бумагой,
называется
ОСЬЮ СИММЕТРИИ.
Примеры
симметричных фигур
Посмотри на рисунок. Приложи зеркало к линии,
проходящей через равнобедренный треугольник.
Что ты увидел?
Правильно, ты видишь точно такой же треугольник.
Линия, проведенная таким образом, называется
ОСЬЮ СИММЕТРИИ ФИГУРЫ.
Равносторонний
треугольник имеет три
оси симметрии.
Проведи по ним
разными
карандашами.
Квадрат имеет четыре оси симметрии.
Проведи оси симметрии прямоугольника
8 см
3 см
Все геометрические фигуры, с которыми
знакомились до сих пор, называются ПЛОСКИМИ.
Плоские они потому, что их можно вырезать из бумаги и
положить на стол.
Но в геометрии существуют ещё и объёмные фигуры.
Каждая такая фигура называется ГЕОМЕТРИЧЕСКИМ
ТЕЛОМ.
С некоторыми из них мы познакомимся.
Рассмотри вместе с Резиночкой знакомый тебе предмет.
Этот предмет имеет форму куба. КУБ — это геометрическое тело.
.
.
.
.
.
.
.
.
.
Куб имеет восемь вершин. Буратино показывает, где
находится одна из вершин куба.
Куб можно составить из шести квадратов, как показано
на чертеже. Эти квадраты называются ГРАНЯМИ куба.
Попробуй вырезать такую фигуру из бумаги и сложить из
неё куб. Линии, по которым соединяются грани куба,
называются РЁБРАМИ куба.
Посчитай,
сколько рёбер у куба
.
Если взять листок бумаги
и сложить его так, как
показывает Резиночка,
а сбоку присоединить два
круга, получится
геометрическое тело,
которое называется
ЦИЛИНДРОМ.
Какие предметы на
рисунке напоминают
тебе форму цилиндра?
Такое геометрическое
тело называется ШАРОМ.
Это тело легко
передвигается по
плоскости.
Посмотри на рисунок и найди предметы, которые
напоминают тебе форму шара. Назови их.
Разгадай геометрический кроссворд
1
3
2
7
5
4
8
6
По горизонтали.
2. Что остаётся на листе бумаги, если
прикоснуться к нему отточенным
карандашом?
4. Как называется расстояние между
концами чего-либо?
5. Как называется прямоугольник, у
Которого все стороны равны?
6.Какая мера длины состоит из 10
дециметров или 100 сантиметров?
По вертикали.
1. Какая линия не имеет ни начала, ни конца?
3. Что можно вычислить, если перемножить
длину двух сторон прямоугольника?
5. Какое геометрическое тело имеет 8 вершин?
7. Какая мера длины состоит из 10
сантиметров?
8. Как называется четырёхугольник, у
которого все стороны равны?
Я учусь математике. Пропись раскраска.
Изд-ва «Флер», «Свет» 1995 г. Составитель Левик О.Н
Художник Лукьянскова С.Э.

Что такое углы? Определение, свойства, типы, части, примеры

Угол образуется, когда две прямые или лучи пересекаются в общей конечной точке. Общая точка касания называется вершиной угла. Слово «угол» происходит от латинского слова «angulus», означает «угол».

Символ ∠ обозначает угол. Углы измеряются в градусах (°) с помощью транспортира.

Внутренние углы: Внутренние углы — это углы, образованные внутри или внутри формы.

Внешние углы: Внешние углы — это углы, образованные вне формы, между любой стороной фигуры и продолженной смежной стороной. Здесь ∠ACD — внешний угол.

Дополнительные углы: Углы, сумма которых составляет 90° (прямой угол), называются дополнительными углами.

Дополнительные углы: Углы, сумма которых составляет 180° (прямой угол), называются дополнительными углами.

Существует множество повседневных примеров использования угла, таких как вешалки для одежды, наконечники стрел, ножницы, частично открытые двери, пирамиды, край стола, край линейки и т. д.

Сумма всех трех внутренних углов треугольника равна 180°. Следовательно, 90° + 30° + x = 180°.

1 Сумма всех углов вокруг точки равна 360° 180° 270° 900 02 90° Правильный ответ: 360° Сумма всех углов вокруг точка равна 360°. 2 Углы, сумма которых не превышает 90°, называются вертикальными углами дополнительными углами углы отражения дополнительные углы Правильный ответ: дополнительные углы Углы, сумма которых равна 90°, называются дополнительными углами. 3 Углы, противоположные друг другу при пересечении двух прямых, называются вертикальными углами дополнительными углами отражающими углами дополнительными углами ответ: вертикальные углы Когда две прямые линии пересекаются друг с другом, углы, противолежащие друг другу, называются вертикальными углами.

Укажите типы углов в зависимости от направления цикла?

         Углы ​​бывают двух типов в зависимости от направления цикла:

• Положительные углы: Положительные углы измеряются против или против часовой стрелки от базовой линии. Положительные углы записываются со знаком плюс или без него перед углами. Он рисуется из плоскости (+x, +y).
  
• Отрицательные углы: Отрицательные углы измеряются по часовой стрелке от базовой линии. Он рисуется из начала координат в плоскости (+x, -y).

Всегда ли сумма углов на прямой составляет 180°?

• Углы, имеющие общую вершину и одну сторону прямой, в сумме дают 180°.
• Углы с общей вершиной, занимающей пространство вокруг точки, в сумме дают 360°.

Какие бывают типы углов, основанные на измерении?

Типы углов, основанные на измерении:

• Прямой угол
• Угол прямой
• Угол рефлекса
• Тупой угол
• Острый угол
• Полный уголок

Какое применение углов в математике?

Инженеры и архитекторы используют углы для строительства, измерения, проектирования и т. д. Архитекторы и инженеры используют их для проектирования дорог, зданий и спортивных сооружений.

Углы и пары углов

Углы, которые они образуют, не менее важны, чем лучи и отрезки. Без них не было бы ни одной из известных вам геометрических фигур (за исключением разве что круга).

Углы

Два луча с одинаковыми концами образуют угол. Эта конечная точка называется вершиной , а лучи называются сторонами угла. В геометрии угол измеряется в градусах от 0° до 180°. Число градусов указывает величину угла. На рисунке 1 лучи АВ и АС образуют угол. A — это вершина. и являются сторонами угла.

Рисунок 1  ∠BAC.

Символ ∠ используется для обозначения угла. Символ m ∠ иногда используется для обозначения меры угла.

Угол может называться по-разному (рис. 2).

Рисунок 2  Различные названия одного и того же угла.

• По букве вершины — следовательно, угол на рисунке можно обозначить ∠ A .

• По цифре (или строчной букве) внутри — поэтому угол на рисунке можно обозначить как ∠1 или ∠ х .

• По буквам трех точек, которые его образуют, поэтому угол на рисунке можно обозначить ∠ BAC или ∠ CAB . Буква центра всегда является буквой вершины.

Пример 1: На рисунке 3(a) используйте три буквы для переименования ∠3; (b) используйте один номер для переименования ∠ KMJ .

 

Рисунок 3  Различные названия одного и того же угла

(a) ∠3 совпадает с ∠ IMJ или ∠ ОМИ;

(б) ∠ KMJ совпадает с ∠ 4 .

Постулат 9 (постулат транспортира): Предположим, что O является точкой на . Рассмотрим все лучи с конечной точкой O , лежащие по одну сторону от . Каждому лучу может быть сопоставлено ровно одно вещественное число от 0° до 180°, как показано на рис. 4. Положительная разность между двумя числами, представляющими два разных луча, является мерой угла, сторонами которого являются два луча.

Рисунок 4  Использование постулата транспортира

Пример 2: Используйте рисунок 5, чтобы найти следующее: (a) м ∠ SON , (b) м ∠ ROT и (c) м ∠ 90 145 МЧС .

Рисунок 5  Использование постулата о транспортире.

• (а)

м ∠ SON = 40° −0°

м ∠ SON = 40°

• (б)

м ∠ ROT = 160° −70°

м ∠ ROT = 90°

• (с)

м ∠ МОЭ = 180° −105°

м ∠ МОЭ = 75°

Постулат 10 (постулат сложения углов): Если лежит между и , то м ∠ AOB + м ∠ BOC = м ∠ AOC (рис. 6).

Рисунок 6  Сложение углов.

Пример 3: На рисунке 7, если м ∠1 = 32° и м ∠2 = 45°, найдите м ∠ NEC .

Рисунок 7  Сложение углов.

Потому что между и , по Постулат 10 ,

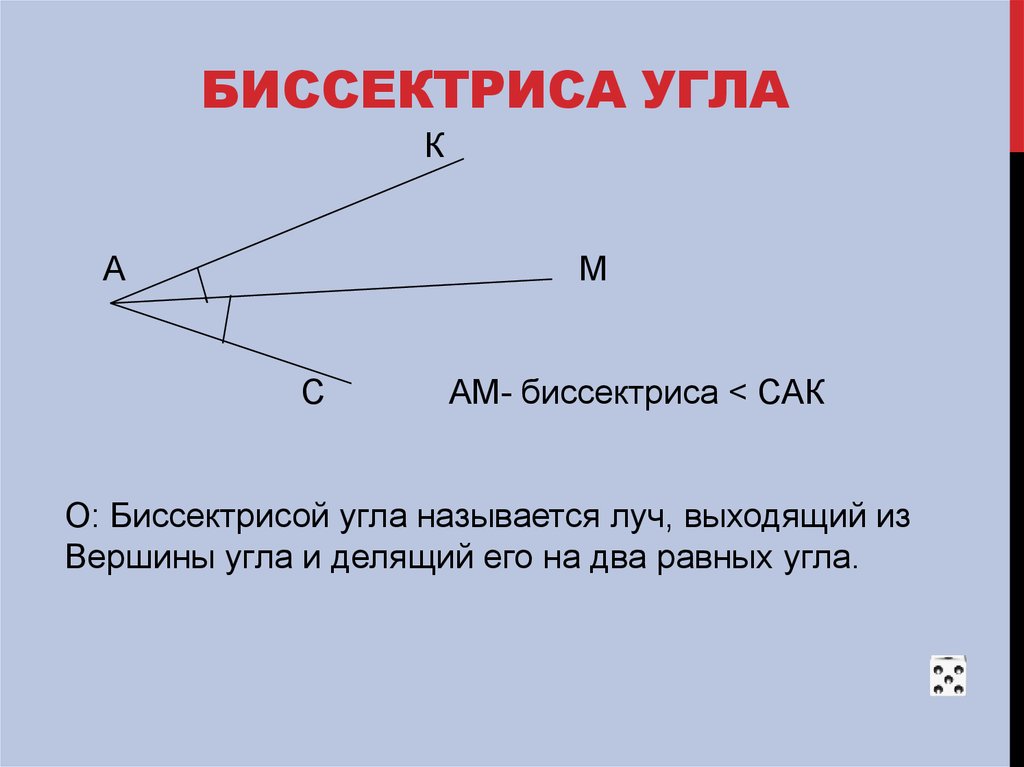
Биссектриса угла

Биссектриса угла — это луч, который делит угол на два равных угла. На рисунке 8 это биссектриса ∠ XOZ , потому что = м ∠ XOY = м ∠ YOZ .

Рисунок 8  Биссектриса угла

Теорема 5: Угол, который не является прямым, имеет ровно одну биссектрису.

Некоторым углам даются специальные названия, основанные на их размерах.

Прямой угол

А прямой угол имеет меру 90°. Символ внутри угла указывает на то, что угол образован прямым. На рисунке 9 ∠ ABC — прямой угол.

Рисунок 9  Прямой угол.

Теорема 6: Все прямые углы равны.

Острый угол

Острый угол — это любой угол, градусная мера которого меньше 90°. На Рисунке 10 ∠ b означает остроту.

Рисунок 10  Острый угол.

Тупой угол

Тупой угол — это угол, градусная мера которого больше 90°, но меньше 180°. На рисунке 11 ∠4 тупой.

Рисунок 11  Тупой угол.

Угол прямой

В некоторых текстах по геометрии угол с мерой 180° называется прямым углом . На рисунке 12 ∠ BAC представляет собой прямой угол.

Рисунок 12  Прямой угол

Пример 4: Используйте рисунок 13, чтобы определить каждый названный угол как острый, прямой, тупой или прямой: (a) ∠ BFD , (b) ∠ AFE , (c) ∠ BFC , (d) ∠ ДФА .