исследование линейных систем уравнений
Вы искали исследование линейных систем уравнений? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и исследование матрицы на совместимость, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «исследование линейных систем уравнений».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как исследование линейных систем уравнений,исследование матрицы на совместимость,исследование на совместимость матрицы,исследование на совместность системы линейных уравнений,исследование систем линейных уравнений,исследование системы линейных уравнений на совместность,исследование системы на совместность онлайн,исследовать на совместность систему линейных уравнений онлайн,исследовать на совместность систему на совместность онлайн,исследовать на совместность систему уравнений,исследовать систему линейных уравнений,исследовать систему линейных уравнений на совместность,исследовать систему линейных уравнений на совместность онлайн,исследовать систему на совместность и определенность не решая ее,исследовать систему на совместность и решить ее если она совместна,исследовать систему на совместность онлайн,исследовать систему уравнений на совместимость и определенность не решая ее,исследовать систему уравнений на совместность,как исследовать систему линейных уравнений на совместность,как определить совместность системы линейных уравнений,как проверить на совместность систему,как проверить систему на совместность,как проверить совместность системы линейных уравнений,как проверить совместность системы уравнений,матрицы исследование на совместимость,проверить на совместность систему,проверить систему на совместность,проверить совместность системы уравнений,проверка на совместность системы,совместность системы линейных уравнений как проверить.
Где можно решить любую задачу по математике, а так же исследование линейных систем уравнений Онлайн?
Решить задачу исследование линейных систем уравнений вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Системы линейных алгебраических уравнений | Высшая математика
Вернуться к списку тем
Решить систему уравнений \(\left\{ \begin{aligned}& x_1+x_2-2x_3=4;\\& -5x_1-4x_2+x_3=-11;\\& 2x_1-x_2-3x_3=7. \end{aligned} \right.\) тремя способами: по формулам Крамера, методом Гаусса-Жордана, средствами матричного исчисления. Сделать проверку правильности вычисления обратной матрицы.
\end{aligned} \right.\) тремя способами: по формулам Крамера, методом Гаусса-Жордана, средствами матричного исчисления. Сделать проверку правильности вычисления обратной матрицы.
Открыть решение
Доказать совместность системы линейных уравнений \(\left\{ \begin{aligned}& x_1-2x_2+3x_3=6;\\& 2x_1+3x_2-4x_3=20;\\& 3x_1-2x_2-5x_3=6.\end{aligned} \right.\) и решить её: а) средствами матричного исчисления; б) методом Гаусса; в) по формулам Крамера.
Открыть решение
Исследуйте квадратную систему линейных уравнений \(\left\{\begin{aligned}& x_1-\lambda x_2=3;\\& 2x_1+4x_2=\lambda.\end{aligned} \right.\) при различных значениях вещественного параметра \(\lambda\). Решите, если это возможно, данную систему методом Крамера при \(\lambda=\frac{1}{2}\).
Открыть решение
Проверить систему \(\left\{ \begin{aligned}& 2x_1-x_2+x_3-x_4=2;\\& x_1+x_2+2x_3=1;\\& x_1-x_2+3x_4=1; \\& 3x_1+3x_3-x_4=3. \end{aligned} \right.\) на совместность. В случае, если система совместна, построить решение.
\end{aligned} \right.\) на совместность. В случае, если система совместна, построить решение.
Открыть решение
Доказать совместность системы \(\left\{ \begin{aligned}& -x_1-9x_2-4x_3=-8;\\& 2x_1+7x_2+3x_3+x_4=6;\\& 3x_1+5x_2+2x_3+2x_4=4.\end{aligned} \right.\) и решить её тремя способами: по формулам Крамера, методом Гаусса и средствами матричного исчисления.
Открыть решение
Дана система \(\left\{ \begin{aligned}& 2x_1+3x_2+x_3+2x_4-x_5=3;\\& -x_1+x_2+2x_3+2x_4-3x_5=3;\\& x_1+4x_2+3x_3+4x_4-4x_5=6.\end{aligned} \right.\). С помощью теоремы Кронекера-Капелли установить совместность системы.
Открыть решение
Исследовать СЛАУ \(\left\{ \begin{aligned}& x_1+2x_2-x_3+x_4=1;\\& 3x_1-x_2+2x_3-x_4=-1;\\& 2x_1+3x_2-2x_3+x_4=-3.\end{aligned} \right.\) на совместность и в случае совместности решить её методом Гаусса. Указать число базисных решений и найти одно из них.
Открыть решение
Используя метод Жордана-Гаусса, исследовать совместность системы уравнений \(\left\{ \begin{aligned}& x_1+2x_2+x_3+5x_4+7x_5=8;\\& 2x_1+2x_2+2x_3+6x_4+12x_5=12;\\& x_1+3x_2+3x_3+5x_4+12x_5=16.
Открыть решение
Исследовать на совместность и несовместность систему \(\left\{ \begin{aligned}& x_1+x_2+x_3=1;\\& x_1+(1+\lambda)x_2+x_3=1;\\& x_1+x_2+(1+\lambda)x_3=1.\end{aligned} \right.\) и найти общее решение в зависимости от значения параметра \(\lambda\).
Открыть решение
Используя теорему Кронекера-Капелли, исследовать на совместность систему линейных уравнений: \(\left\{ \begin{aligned}& 2x_1-x_2+3x_3+5x_4=4;\\& x_1+2x_2+6x_3+3x_4=-2;\\& x_1-8x_2-12x_3+x_4=14; \\& 4x_1+3x_2+15x_3+11x_4=0.\end{aligned} \right.\)
Открыть решение
Исследовать однородную СЛАУ \(\left\{ \begin{aligned}& x_1+2x_2+x_3+4x_4+x_5=0;\\& 2x_1+x_2+3x_3+x_4-5x_5=0;\\& x_1+3x_2-x_3+6x_4-x_5=0.\end{aligned} \right.\) на существование нетривиального решения. В случае существования найти общее решение и выделить из него фундаментальную систему решений.
В случае существования найти общее решение и выделить из него фундаментальную систему решений.
Открыть решение
Найти фундаментальную систему решений заданной СЛАУ: \(\left\{ \begin{aligned}& 2x_1+2x_3+2x_4+x_5=0;\\& 6x_1+2x_2+4x_3+5x_4+x_5=0;\\& 6x_1+4x_2+2x_3+4x_4-x_5=0\\& 8x_1+8x_2+4x_4-4x_5=0.\end{aligned} \right.\)
Открыть решение
Методом Жордана-Гаусса исследовать совместность системы уравнений: \(\left\{ \begin{aligned}& 2x_1+3x_2+7x_3+2x_4+x_5=13;\\& 4x_1+2x_2+10x_3+12x_4+14x_5=14;\\& 5x_1+3x_2+13x_3+14x_4+16x_5=20.\end{aligned} \right.\)
Открыть решениеИсследовать на совместность и найти общее решение системы: \(\left\{ \begin{aligned}& 3x_1-5x_2+2x_3+4x_4=2;\\& 7x_1-4x_2+x_3+3x_4=5;\\& 5x_1+7x_2-4x_3-6x_4=3.\end{aligned} \right.\)
Открыть решение
Исследовать на совместность и найти общее решение системы: \(\left\{ \begin{aligned}& 9x_1-3x_2+5x_3+6x_4=4;\\& 6x_1-2x_2+3x_3+4x_4=5;\\& 3x_1-x_2+3x_3+14x_4=-8. \end{aligned} \right.\)
\end{aligned} \right.\)
Открыть решение
Система уравнений в питоне символьно
Задавать вопрос
спросил
Изменено 1 год, 8 месяцев назад
Просмотрено 87 раз
Я хочу решить эту систему символически, но это не сработало. где я сделал ошибку? и как я могу это решить?
импортировать numpy как np
из символов импорта sympy, матрица
Y, C, I0, G0, a, b = символы ('Y, C, I_0, G_0, a, b')
npA = np.массив (([1, -1], [-b, 1]))
npd = np.массив ((I0 + G0, а))
х = np.linalg.solve (npA, npd)
Икс
Я получаю эту ошибку
------------------------------------------------------ -------------------------------------------------- TypeError Traceback (последний последний вызов)в <модуле> 5 npA = np. массив(([1, -1], [-b, 1])) 6 npd = np.массив((I0 + G0, а)) ----> 7 x = np.linalg.solve(npA, npd) 8 х <__array_function__internals> в решении (*args, **kwargs) ~\anaconda3\lib\site-packages\numpy\linalg\linalg.py в решении (a, b) 392 подпись = 'DD-> D', если isComplexType(t), иначе 'dd->d' 393 extobj = get_linalg_error_extobj(_raise_linalgerror_singular) --> 394 r = gufunc(a, b, подпись=подпись, extobj=extobj) 395 396 возвратная обертка (r.astype (result_t, copy = False)) TypeError: для ufuncsolve1 не найден цикл, соответствующий указанной сигнатуре и кастингу.
- python
- system
- символы
- решение уравнений
Вы пытаетесь решить такое уравнение: Ax = b. Я не думаю, что вы можете так смешивать команды из разных библиотек, есть некоторая совместимость, но вы должны проверить документацию
Здесь возможность
из символов импорта sympy, уравнение, решить
a_x, a_y, b_x, b_y = символы ('a_x, a_y, b_x, b_y')
eq_x = Eq(a_x - a_y, b_x)
eq_y = Eq(-b_x * a_x + a_y, b_y)
результат = решить ([eq_x, eq_y], (b_x, b_y))
печать (результат [b_x])
печать (результат [b_y])
Выход
а_х - а_у -а_х**2 + а_х*а_у + а_у
2
Если вам нужна более общая настройка (и более похожая на математический подход), то это может быть полезно
из символов импорта sympy, Matrix,solve_linear_system
# a: параметр матрицы
# b: член неоднородности
a, x_1, x_2, b_1, b_2 = символы ('b, x_1, x_2, b_1, b_2')
А = Матрица ([[1, -1], [-а, 1]])
х = Матрица ([[x_1, x_2]]). T
б = Матрица ([[b_1, b_2]]).T
A_augmented = A.row_join(b)
результат = Solve_linear_system (A_augmented, * x)
печать (результат)
T
б = Матрица ([[b_1, b_2]]).T
A_augmented = A.row_join(b)
результат = Solve_linear_system (A_augmented, * x)
печать (результат)
Выход
{x_1: (-b_1 - b_2)/(b - 1), x_2: (-b*b_1 - b_2)/(b - 1)}
Примечание
solve_linear_system принять расширенную матрицу в качестве входных данных [A|b], и вы должны либо расширить неизвестные векторы (как указано выше), либо явно передать все ее координаты 0
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Символьные решения одновременных УЧП первого порядка в одном неизвестном « Журнал Mathematica
dx. doi.org/doi:10.3888/tmj.20-2
doi.org/doi:10.3888/tmj.20-2
Мы предлагаем и реализуем алгоритм решения переопределенной системы дифференциальных уравнений в частных производных в одном неизвестном. Наш подход основан на методе Бура-Майера для определения условий совместимости с помощью скобок Якоби-Майера. Мы рекурсивно решаем совместимые системы, имитируя то, что можно было бы сделать с ручкой и бумагой: решить одно уравнение, подставить его решение в остальные уравнения и повторять процесс, пока не будут исчерпаны уравнения системы. Метод, который мы используем для оценки непротиворечивости базовой системы, отличается от традиционного использования дифференциальных базисов Грёбнера, но кажется более эффективным и простым в реализации.
Введение
Поиск решений многих задач приводит к переопределенным системам дифференциальных уравнений в частных производных (УЧП). Эти задачи включают вычисление дискретных симметрий дифференциальных уравнений [1], вычисление дифференциальных инвариантов [2] и определение обобщенных операторов Казимира конечномерной алгебры Ли [3]. В этой статье мы сосредоточимся исключительно на интеграции одновременных систем скалярных УЧП первого порядка; то есть наши системы имеют как минимум два уравнения, одну зависимую переменную (неизвестную функцию) и несколько независимых переменных. Нашей конечной целью является автоматизация поиска общих символьных решений этих систем. Принятый нами подход использует метод Бура-Майера [4] для нахождения условий совместимости (т. е. препятствий для интегрируемости) базовой системы УЧП и итеративного добавления этих условий совместимости к системе до тех пор, пока не будет найдена непротиворечивая или несогласованная система. Это отличается от традиционного подхода, который использует дифференциальные базисы Грёбнера [5] для обнаружения условий совместимости. Когда это применимо, он имеет то преимущество, что его легко реализовать и он эффективен. Недавно, используя технику дифференциальной геометрии, Кругликов и Лычагин [6] распространили метод Бура–Майера на системы УЧП от нескольких зависимых и независимых переменных смешанных порядков (т.
В этой статье мы сосредоточимся исключительно на интеграции одновременных систем скалярных УЧП первого порядка; то есть наши системы имеют как минимум два уравнения, одну зависимую переменную (неизвестную функцию) и несколько независимых переменных. Нашей конечной целью является автоматизация поиска общих символьных решений этих систем. Принятый нами подход использует метод Бура-Майера [4] для нахождения условий совместимости (т. е. препятствий для интегрируемости) базовой системы УЧП и итеративного добавления этих условий совместимости к системе до тех пор, пока не будет найдена непротиворечивая или несогласованная система. Это отличается от традиционного подхода, который использует дифференциальные базисы Грёбнера [5] для обнаружения условий совместимости. Когда это применимо, он имеет то преимущество, что его легко реализовать и он эффективен. Недавно, используя технику дифференциальной геометрии, Кругликов и Лычагин [6] распространили метод Бура–Майера на системы УЧП от нескольких зависимых и независимых переменных смешанных порядков (т. е. порядки отдельных уравнений в системе могут быть разными). В нашем подходе для ситуации, когда процесс завершения приводит к непротиворечивой системе, мы решаем последнюю, имитируя то, что можно было бы сделать с ручкой и бумагой: решить одно уравнение, подставить его в следующее уравнение и продолжать процесс до тех пор, пока уравнения системы исчерпаны.
е. порядки отдельных уравнений в системе могут быть разными). В нашем подходе для ситуации, когда процесс завершения приводит к непротиворечивой системе, мы решаем последнюю, имитируя то, что можно было бы сделать с ручкой и бумагой: решить одно уравнение, подставить его в следующее уравнение и продолжать процесс до тех пор, пока уравнения системы исчерпаны.
Чтобы зафиксировать идеи, рассмотрим систему УЧП
| (1) |
где to – независимые переменные, – частная производная неизвестной функции по , а ранг матрицы Якоби – . В дальнейшем мы будем говорить, что свойство выполняется локально, если оно истинно на открытом шаре своей области действия. Система уравнений (1) интегрируема (т. е. допускает локально гладкое решение), если получаемые из нее выражения локально удовлетворяют условиям
| (2) |
Чтобы убедиться в этом, рассмотрим решение системы уравнений (1). Затем локально, . Таким образом, последняя дифференциальная форма локально точна. Так, в частности, он локально закрыт. Следовательно, его внешний дифференциал равен нулю; то есть , или, что то же самое, после некоторых вычислений , откуда следует (2). Обратно, если система уравнений (2) локально выполняется, то дифференциальная форма локально замкнута и по лемме Пуанкаре также локально точна. Следовательно, для некоторой локально гладкой функции . Поэтому локально определяется как , где – произвольная постоянная.
Затем локально, . Таким образом, последняя дифференциальная форма локально точна. Так, в частности, он локально закрыт. Следовательно, его внешний дифференциал равен нулю; то есть , или, что то же самое, после некоторых вычислений , откуда следует (2). Обратно, если система уравнений (2) локально выполняется, то дифференциальная форма локально замкнута и по лемме Пуанкаре также локально точна. Следовательно, для некоторой локально гладкой функции . Поэтому локально определяется как , где – произвольная постоянная.
Бур и Майер (см., например, [4]) показали, что (1) при условии на матрицу Якоби относительно интегрируема тогда и только тогда, когда
всякий раз, когда выполняется (1). Отныне сокращайте фразу «всякий раз, когда (1) выполняется» до .
Для заданной системы уравнений (1), удовлетворяющей указанному условию невырожденности, возникают четыре случая.
Первый случай, когда и все скобки Якоби–Майера равны нулю, когда выполняется (1). В этом случае мы можем решить (1) для to . Затем решение системы получается путем интегрирования точной дифференциальной формы.
В этом случае мы можем решить (1) для to . Затем решение системы получается путем интегрирования точной дифференциальной формы.
Второй случай, когда существуют различные индексы и такие, что . Тогда (1) несовместно и решений нет.
В третьем случае , и все скобки Якоби–Майера равны нулю в (1). Мы должны дополнить (1) дополнительными уравнениями, пока не дойдем до первого или второго случая. Эти уравнения получаются путем решения системы линейных УЧП первого порядка , где и . Например, дополнительное уравнение , где – произвольная константа, получается путем решения системы линейных УЧП первого порядка , где . Решение пополненной системы зависит от произвольных констант. Общее решение исходной системы уравнений (1) получим, выразив одну из произвольных констант через остальные, затем исключив оставшуюся константу между полученными уравнениями и их частными производными первого порядка по произвольным константы.
В четвертом и последнем случае некоторые скобки равны нулю в (1), а другие скобки имеют вид , где зависят хотя бы от некоторых . В этом случае мы должны добавить уравнения к уравнениям в (1) и действовать, как в третьем случае.
В этом случае мы должны добавить уравнения к уравнениям в (1) и действовать, как в третьем случае.
Только что описанная процедура является сутью подхода Бура–Майера к решению (1). Необходимо решить переопределенные системы линейных скалярных УЧП и убедиться, что уравнения, добавляемые к исходной системе, совместимы с ними, а уравнения результирующих систем линейно независимы. В нашей реализации подхода Бура–Майера мы дополняем исходную систему уравнений (1), добавляя к ней соответствующие ограничения совместимости, заданные скобками Якоби–Майера, до тех пор, пока не получим либо совместимую, либо несовместимую систему. Начиная с ограничений совместимости, мы итеративно решаем совместимую систему, полученную с помощью встроенной функции . Оставшаяся часть этой статьи посвящена реализации и тестированию этого подхода.
Реализация и тесты
Здесь мы сосредоточимся на кодировании алгоритма, описанного во введении. В частности, мы начинаем с итеративного решения системы согласованных УЧП первого порядка с одной зависимой переменной. Затем реализуем тест на непротиворечивость системы УЧП первого порядка по одному неизвестному. Наконец, мы связываем последние две программы таким образом, чтобы одна функция использовалась для вычисления общего решения входной системы, когда оно существует, или для указания на его противоречивость.
Затем реализуем тест на непротиворечивость системы УЧП первого порядка по одному неизвестному. Наконец, мы связываем последние две программы таким образом, чтобы одна функция использовалась для вычисления общего решения входной системы, когда оно существует, или для указания на его противоречивость.
Итеративное решение согласованной системы УЧП первого порядка в одном неизвестном
Наша программа для итеративного решения совместимой системы скалярных УЧП первого порядка состоит из основной функции и трех вспомогательных функций, , и .
— рекурсивная функция, принимающая на вход решаемую систему, зависимую переменную, список независимых переменных, контейнер для списка последовательных решений, список уравнений, которые не удалось решить, используемую строку в качестве корня для формирования имен промежуточных зависимых переменных и переменной, которая используется для подсчета и именования промежуточных зависимых переменных. Результатом является список правил и список нерешенных уравнений.
Функция имитирует то, что можно было бы сделать вручную при решении системы УЧП первого порядка с одним неизвестным: решить уравнение, подставить его решение в оставшиеся уравнения и продолжать до тех пор, пока это возможно. На каждом этапе количество независимых переменных уменьшается на одну и необходимо переименовывать переменные перед продолжением. Кроме того, зависимые переменные являются каррированными функциями, которые необходимо отменить, чтобы обеспечить правильное применение цепного правила во время подстановки в оставшиеся PDE. Это, пожалуй, самая сложная часть нашей реализации.
Функция берет выходные данные и преобразует их в решение решаемой системы. Вспомогательная функция преобразует выражение, зависящее от нескольких переменных, в чистую функцию этих переменных. Наконец, функция составляет и решает совместимую систему скалярных УЧП. Его входные данные такие же, как и у , а его выходные данные отформатированы как у .
Тест на совместимость и завершение
В этом подразделе реализуется тест на совместимость, обеспечиваемый методом Бура-Майера, как описано во введении, с использованием . Входными данными являются базовая система УЧП, зависимая переменная и список независимых переменных; выводит пару: первый элемент указывает, совместима ли система, а второй элемент дает завершенную систему.
Входными данными являются базовая система УЧП, зависимая переменная и список независимых переменных; выводит пару: первый элемент указывает, совместима ли система, а второй элемент дает завершенную систему.
Функция вычисляет попарные скобки Якоби–Майера системы УЧП согласно уравнению (3) и заменяет в этих скобках некоторые частные производные первого порядка неизвестной функции, полученные из базовой системы УЧП. Функция проверяет, содержит ли выражение производную от неизвестной функции.
Собираем все вместе
Здесь мы используем определенные до сих пор функции для решения переопределенной системы УЧП первого порядка с одним неизвестным. Функция принимает в качестве аргументов решаемую систему , ее зависимые и независимые переменные и . Функция проверяет, дает ли данное правило решение системы УЧП первого порядка с одним неизвестным.
Тесты
Этот подраздел в основном касается примеров, взятых из различных указанных источников. Для удобства предупреждения подавляются встроенной функцией. Используются неопределенные глобальные переменные (, , и т. д.), поэтому убедитесь, что нет конфликтов с вашим собственным сеансом.
Для удобства предупреждения подавляются встроенной функцией. Используются неопределенные глобальные переменные (, , и т. д.), поэтому убедитесь, что нет конфликтов с вашим собственным сеансом.
Представленные здесь примеры возникают при поиске дифференциальных инвариантов гиперболических УЧП [2].
За исключением примера 9, дается для всех систем, поэтому здесь он показан только один раз.
Рассматриваемые здесь две системы PDE находятся в Mansion [4].
Вторая запись показывает, что есть два нерешенных УЧП. Несложно разделить эти УЧП относительно и получить новые УЧП, которые легко решаются с помощью встроенной функции . Разделение может быть выполнено автоматически с помощью следующей однострочной строки.
Несложно разделить эти УЧП относительно и получить новые УЧП, которые легко решаются с помощью встроенной функции . Разделение может быть выполнено автоматически с помощью следующей однострочной строки.
Последний пример принадлежит Булю [ 8].
Заключение
В данной статье представлен и реализован алгоритм, основанный на методе Бура–Майера, для решения переопределенной системы УЧП с одним неизвестным. Эффективность нашего подхода мы продемонстрировали на рассмотрении 13 примеров.
Благодарности
Выражаю благодарность за частичную финансовую поддержку Центра передового опыта в области математических и статистических наук DST-NRF Школы информатики и прикладной математики Университета Витватерсранда, Йоханнесбург, Южная Африка. Я благодарю профессора Ф. М. Магомеда за выделение необходимых средств и его команду за гостеприимство во время моего визита прошлым летом. Эта статья посвящается моей дочери Катлего в день ее шестнадцатилетия.
Я благодарю профессора Ф. М. Магомеда за выделение необходимых средств и его команду за гостеприимство во время моего визита прошлым летом. Эта статья посвящается моей дочери Катлего в день ее шестнадцатилетия.
Каталожные номера
| [1] | PE Hydon, «Как построить дискретные симметрии дифференциальных уравнений в частных производных», European Journal of Applied Mathematics , 11 (5), 2000, стр. 515–527. |
| [2] | И. К. Джонпиллай, Ф. М. Магомед и К. Вафо Сох, «Основы совместных инвариантов для () линейных гиперболических уравнений», Journal of Nonlinear Mathematical Physics , 9 (Приложение 2), 2002 , стр. 49–59. doi:10.2991/jnmp.2002.9.s2.5. |
| [3] | Дж. К. Ндогмо и П. Винтерниц, «Обобщенные операторы Казимира разрешимых алгебр Ли с абелевыми нильрадикалами», Journal of Physics A: Mathematical and General , 27 (8), 1994 , стр.  2787–2800. iopscience.iop.org/article/10.1088/0305-4470/27/8/016/meta. 2787–2800. iopscience.iop.org/article/10.1088/0305-4470/27/8/016/meta. |
| [4] | P. Mansion, Théorie des équations aux dérivées partielles du premier ordre , Paris: Gauthier-Villars, 1875. |
| [5] | Б. Бухбергер и Ф. Винклер, Основы Грёбнера и приложения , Кембридж: Издательство Кембриджского университета, 1998. |
| [6] | Б. Кругликов и В. Лычагин, «Совместимость, мультискобки и интегрируемость систем УЧП», Acta Applicandæ Mathematicæ , 109 (1), 2010, стр. 151–196. doi:10.1007/s10440-009-9446-0. |
| [7] | Н. Салтыков, «Классические методы интеграции уравнений с производными частями дю премьер-министра в несоответствующей функции», Мемориал математических наук , 50 , 1931 стр. 1–72. www.numdam.org/item?id=MSM_ 1931__ 50__ 1_ 0. |
| [8] | Г. Буль, «Об одновременных дифференциальных уравнениях первого порядка, в которых число переменных превышает число уравнений более чем на единицу», Philosophical Transactions of the Royal Society of London , 152 (5) , 1862, стр. |

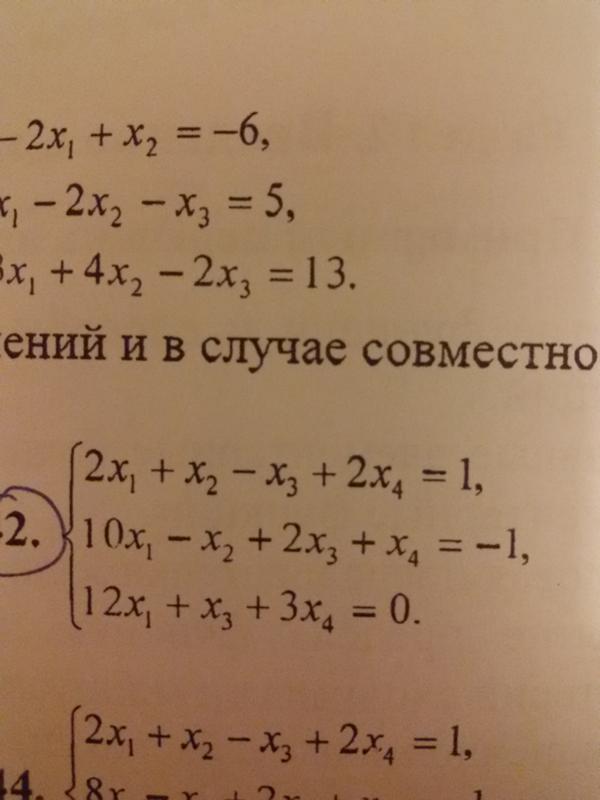 массив(([1, -1], [-b, 1]))
6 npd = np.массив((I0 + G0, а))
----> 7 x = np.linalg.solve(npA, npd)
8 х
<__array_function__internals> в решении (*args, **kwargs)
~\anaconda3\lib\site-packages\numpy\linalg\linalg.py в решении (a, b)
392 подпись = 'DD-> D', если isComplexType(t), иначе 'dd->d'
393 extobj = get_linalg_error_extobj(_raise_linalgerror_singular)
--> 394 r = gufunc(a, b, подпись=подпись, extobj=extobj)
395
396 возвратная обертка (r.astype (result_t, copy = False))
TypeError: для ufuncsolve1 не найден цикл, соответствующий указанной сигнатуре и кастингу.
массив(([1, -1], [-b, 1]))
6 npd = np.массив((I0 + G0, а))
----> 7 x = np.linalg.solve(npA, npd)
8 х
<__array_function__internals> в решении (*args, **kwargs)
~\anaconda3\lib\site-packages\numpy\linalg\linalg.py в решении (a, b)
392 подпись = 'DD-> D', если isComplexType(t), иначе 'dd->d'
393 extobj = get_linalg_error_extobj(_raise_linalgerror_singular)
--> 394 r = gufunc(a, b, подпись=подпись, extobj=extobj)
395
396 возвратная обертка (r.astype (result_t, copy = False))
TypeError: для ufuncsolve1 не найден цикл, соответствующий указанной сигнатуре и кастингу.
 T
б = Матрица ([[b_1, b_2]]).T
A_augmented = A.row_join(b)
результат = Solve_linear_system (A_augmented, * x)
печать (результат)
T
б = Матрица ([[b_1, b_2]]).T
A_augmented = A.row_join(b)
результат = Solve_linear_system (A_augmented, * x)
печать (результат)