Проверка статистических гипотез — Questionstar
5.2 Индуктивная статистика
5.2.1 Проверка статистических гипотез
Проверка статистических гипотез
Проверка статистических гипотез – это пятиступенчатая процедура, которая на основании данных выборки и при помощи теории вероятностей позволяет сделать вывод об обоснованности гипотезы.
Другими словами, этот способ проверить, действительны ли результаты, полученные на выборке, и для генеральной совокупности.
Люди «ошибочно уверенны» в своих знаниях и недооценивают вероятность того, что их убеждения могут оказаться ложными. Им свойственно искать искать такую дополнительную информацию, которая лишь подтверждает их собственные убеждения.
Макс Базерман
Пошаговый алгоритм:
1.Формулировка основной и альтернативной гипотезы
2.Выбор уровня значимости
3.Определение подходящего статистического критерия
4.Формулировка правила принятия решения
5.
Принятие решения на основании данных выборки
Пол и частота пользования интернетом:
| Пол | |||
| Пользование интернетом | Мужской | Женский | Сумма по строке |
| редко | 5 | 10 | 15 |
| часто | 10 | 5 | 15 |
| Сумма по столбцу | 15 | 15 | n=30 |
Вопрос:
Можем ли мы на основании этой выборки утверждать, что во всем населении среди мужчин больше активных интернет пользователей, чем среди женщин?
Шаг 1: Формулировка основной и альтернативной гипотезы
Нулевая гипотеза (H0) – это утверждение статус-кво, что никакой разницы или никакого эффекта на самом деле нет.
Альтернативная гипотеза (H1) утверждает, что некоторая разница (или эффект) все таки должна быть.
H0: в отношении частоты пользования интернетом разницы между мужчинами и женщинами нет.
H1: мужчины и женщины пользуются интернетом с разной частотой.
Шаг 2: Выбор уровня значимости
Значимость (α) – вероятность того, что верная нулевая гипотеза будет отвергнута.
β – вероятность того, что ложная нулевая гипотеза будет принята.
| Нулевая гипотеза (H0) верна | Нулевая гипотеза (H0) ложна | |
| Нулевая гипотеза отвергнута | ложноположительное (ошибка первого рода) | H0 верно принята |
| Нулевая гипотеза | H0 верно отвергнута | ложноотрицательное (ошибка второго рода) |
Аналогия: суд над маньяком
H0: заключенный не виновен
Аналогия: шорох в кустах – это лев?
H0: льва в кустах нет
Уровни значимости, принятые в маркетинговых исследованиях:
α – уровень значимости
0,01 (1%)
0,05 (5%)
(1-α) – уровень доверия (доверительная вероятность)
0,99 (99%)
0,95 (95%)
Шаг 3: Определение статистического критерия
Критерий χ2 (хи-квадрат) используется для проверки статистической значимости взаимосвязей между переменными, наблюдаемых в перекрестных таблицах.
H0: взаимосвязи между переменными нет
Тест χ2 проверяет равенство частотных распределений.
Какие распределения/частоты мы должны проверить?
fо – ожидаемые частоты (расчётные значения), которые бы стояли в ячейках, в случае когда связи между переменными нет.
fн – реально наблюдаемые частоты, т.е. значения, которые стоят в составленной нами таблице
Расчёт χ2 следует производить только на основе абсолютных значений частот. Если исходные данные представлены в процентах, то их необходимо пересчитать а абсолютные частоты.
В нашем примере:
Шаг 4: Формулировка правила принятия решения
Kн – наблюдаемое (расчётное) значение статистического критерия.
Kкрит– критическое значение статистического критерия для заданного уровня значимости.
Если вероятность Kн меньше уровня значимости (α), то H0 надо отклонить.
или
Если Kн>Kкрит , то H0 надо отклонить.
Таблица критических значений χ2 для различных α
df=(r-1)(c-1)
df – количество степеней свободы
r – количество строк
c – количество столбцов
df=(2-1)(2-1)=1
H0 не может быть отклонена
Шаг 5: Принятие решения
Нашлись ли доказательства? Что из этого следует?
— H0 отсутствия различий не может быть отклонена
— Различия не являются статистически значимыми на уровне 0,05
— Полученные на выборке результаты не могут быть обобщены на генеральную совокупность
Пол и частота пользования интернетом
| Пол | |||
| Пользование интернетом | Мужской | Женский | Сумма по строке |
| редко | 5 | 10 | 15 |
| часто | 10 | 5 | 15 |
| Сумма по столбцу | 15 | 15 | n=30 |
Вопрос:
Можем ли мы на основании этой выборки утверждать, что во всем населении среди мужчин больше активных интернет пользователей, чем среди женщин?
Ответ:
Данная выборка не дает оснований для таких утверждений.
Если выборка была произведена должным образом, то мы можем с 95% доверительной вероятностью констатировать, что взаимосвязи между полом и частотой пользования интернетом нет. В противном случае – мы не знаем ответа.
Проверка гипотез
Общий обзор
Определение нулевой и альтернативной гипотезы, уровня статистической значимости
Получение статистики критерия, определение критической области
Получение значения р (достигнутого уровня значимости)
Применение значения р
Проверка гипотез против доверительных интервалов
Общий обзор
Часто делают выборку, чтобы определить аргументы против гипотезы относительно популяции (генеральной совокупности). Этот процесс известен как проверка гипотез (проверка статистических гипотез или проверка значимости), он представляет количественную меру аргументов против определенной гипотезы.
Установлено 5 стадий при проверке гипотез:
- Определение нулевой () и альтернативной гипотезы () при исследовании. Определение уровня значимости критерия.
- Отбор необходимых данных из выборки.
- Вычисление значения статистики критерия, отвечающей .
- Вычисление критической области, проверка статистики критерия на предмет попадания в критическую область.
- Интерпретация достигнутого уровня значимости р и результатов.
Определение нулевой и альтернативной гипотез, уровня статистической значимости
При проверке значимости гипотезу следует формулировать независимо от используемых при ее проверке данных (до проведения проверки). В таком случае можно получить действительно продуктивный результат.
Всегда проверяют нулевую гипотезу (), которая отвергает эффект (например, разница средних равняется нулю) в популяции.
Например, при сравнении показателей курения у мужчин и женщин в популяции нулевая гипотеза означала бы, что показатели курения одинаковые у женщин и мужчин в популяции.
Затем определяют альтернативную гипотезу (), которая принимается, если нулевая гипотеза неверна. Альтернативная гипотеза больше относится к той теории, которую собираются исследовать. Итак, на этом примере альтернативная гипотеза заключается в утверждении, что показатели курения различны у женщин и мужчин в популяции.
Разницу в показателях курения не уточнили, т.е. не установили, имеют ли в популяции мужчины более высокие или более низкие показатели, чем женщины. Такой подход известен как
В некоторых случаях можно использовать односторонний критерий для гипотезы , в котором направление эффекта задано.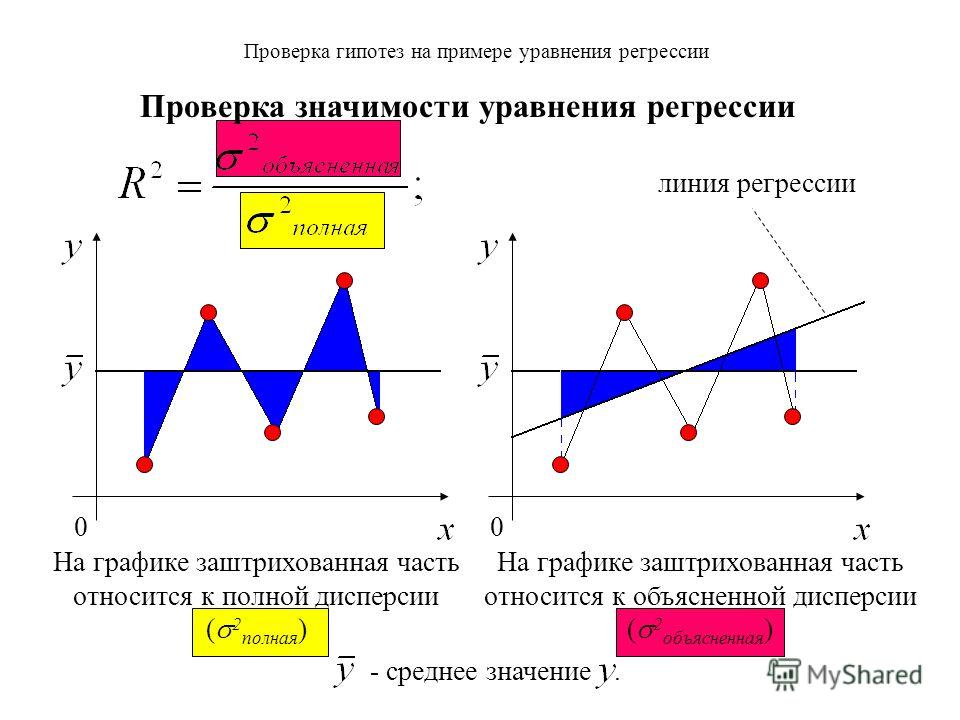
Его можно применить, например, если рассматривать заболевание, от которого умерли все пациенты, не получившие лечения; новый препарат не мог бы ухудшить положение дел.
Уровень значимости. Важным этапом проверки статистических гипотез является определение уровня статистической значимости , т.е. максимально допускаемой исследователем вероятности ошибочного отклонения нулевой гипотезы.
Получение статистики критерия, определение критической области
После того как данные будут собраны, значения из выборки подставляют в формулу для вычисления статистики критерия (примеры различных статистик критериев см. ниже). Эта величина количественно отражает аргументы в наборе данных против нулевой гипотезы.
Критическая область. Для принятия решения об отклонении или не отклонении нулевой гипотезы необходимо также определить критическую область проверки гипотезы.
Выделяют 3 вида критических областей:
- двусторонняя:
Рис.1 Двусторонняя критическая область
1 Двусторонняя критическая область- левосторонняя:
Рис. 2 Левосторонняя критическая область
- правосторонняя:
Рис. 3 Правосторонняя критическая область
— заданный исследователем уровень значимости.
Если наблюдаемое значение критерия (K) принадлежит критической области (Kкр, заштрихованная область на рис.1-3), гипотезу отвергают, если не принадлежит — не отвергают.
Для краткости можно записать и так:
| K | > Kкр — отклоняем H0
| K | < Kкр — не отклоняем H0
Все статистики критерия подчиняются известным теоретическим распределениям вероятности. Получение значения
р (достигнутого уровня значимости)
Значение статистики критерия, полученное из выборки, связывают с уже известным распределением, которому она подчиняется, чтобы получить значение р
Большинство компьютерных пакетов обеспечивают автоматическое вычисление двустороннего значения р.
Значение р — это вероятность получения нашего вычисленного значения критерия или его еще большего значения, если нулевая гипотеза верна.
Иными словами, p — это вероятность отвергнуть нулевую гипотезу при условии, что она верна.
Нулевая гипотеза всегда относится к популяции, представляющей больший интерес, нежели выборка. В рамках проверки гипотезы мы либо отвергаем нулевую гипотезу и принимаем альтернативу, либо не отвергаем нулевую гипотезу. Подробнее об ошибках при проверке гипотез
Применение значения
р Следует решить, сколько аргументов позволят отвергнуть нулевую гипотезу в пользу альтернативной.
-
Традиционно полагают, если р < 0,05, (=0,05) то аргументов достаточно, чтобы отвергнуть нулевую гипотезу, хотя есть небольшой шанс против этого. Тогда можно отвергнуть нулевую гипотезу и сказать, что результаты значимы на 5% уровне.
-
Напротив, если р > 0,05, то аргументов недостаточно, чтобы отвергнуть нулевую гипотезу. Не отвергая нулевую гипотезу, можно заявить, что результаты не значимы на 5% уровне. Данное заключение не означает, что нулевая гипотеза истинна, просто недостаточно аргументов (возможно, маленький объем выборки), чтобы ее отвергнуть.
Уровень значимости (т.е. выбранная «граница отсечки») 5% задается произвольно. На уровне 5% можно отвергнуть нулевую гипотезу, когда она верна. Если это может привести к серьезным последствиям, необходимо потребовать более веских аргументов, прежде чем отвергнуть нулевую гипотезу, например, выбрать значение = 0,01 (или 0,001).
Определение результата только как значимого на определенном уровне граничного значения (например 0, 05) может ввести в заблуждение. Например, если р = 0,04, то нулевую гипотезу отвергаем, но если р = 0,06, то ее не отвергли бы. Действительно ли они различны? Мы рекомендуем всегда указывать точное значение р, обычно получаемое путем компьютерного анализа.
Проверка гипотез против доверительных интервалов
Доверительные интервалы и проверка гипотез тесно связаны. Первоначальная цель проверки гипотезы состоит в том, чтобы принять решение и предоставить точное значение р.
Доверительный интервал (ДИ) количественно определяет изучаемый эффект (например, разницу в средних) и дает возможность оценить значение результатов. ДИ предоставляют интервал вероятных значений для истинного эффекта, поэтому его также можно использовать для принятия решения даже без точных значений р.
Например, если бы гипотетическое значение для данного эффекта (например, значение, равное нулю) находилось вне 95% ДИ, можно было бы счесть гипотетическое значение неправдоподобным и отвергнуть . В этом случае станет известно, что р < 0,05, но не станет известно его точное значение
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Альфа-уровень (уровень значимости): что это такое?
Уровень значимости или альфа-уровень — это вероятность принятия неправильного решения, когда нулевая гипотеза верна.
Альфа-уровни (иногда называемые просто «уровнями значимости») используются при проверке гипотез. Обычно эти тесты выполняются с альфа-уровнем 0,05 (5%), но обычно используются другие уровни: 0,01 и 0,10.
Посмотрите видео для обзора:
Что такое альфа-уровень?
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Содержание (нажмите, чтобы перейти в этот раздел) :
- Ошибки типа I и II
- Как рассчитать альфа-уровень для одно- и двусторонних тестов?
- Почему обычно используется альфа-уровень 0,05?
1. Альфа-уровни/уровни значимости: ошибки типа I и типа II
При проверке гипотез возможны две ошибки: ошибки типа I и типа II.
Ошибка типа I : Поддержка альтернативной гипотезы, когда верна нулевая гипотеза.
Ошибка типа II : Альтернативная гипотеза не подтверждается, когда альтернативная гипотеза верна.
В качестве примера с залом суда предположим, что нулевая гипотеза состоит в том, что человек невиновен, а альтернативная гипотеза состоит в том, что он виновен. если вы осуждаете невиновного человека (ошибка первого рода), вы поддерживаете альтернативную гипотезу (о том, что он виновен). Ошибка второго рода — отпустить виновного на свободу.
Альфа-уровень — это вероятность ошибки первого рода, или вы отвергаете нулевую гипотезу, если она верна. Родственный термин, бета, является противоположным; вероятность отклонения альтернативной гипотезы, если она верна.
На этом графике крайний правый край показывает область отклонения.
2. Как рассчитать альфа-уровень для одно- и двусторонних тестов?
Посмотрите обзорное видео:
Как рассчитать альфа-уровень
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Нужна помощь с конкретным вопросом домашнего задания? Посетите нашу страницу обучения!
Альфа-уровни могут контролироваться вами и связаны с уровнями достоверности .
Чтобы получить α, вычтите уровень достоверности из 1. Например, если вы хотите быть на 95 % уверены в правильности своего анализа, уровень альфы будет равен 1 – 0,95 = 5 %, при условии, что у вас есть односторонний тест. Для двусторонних тестов разделите альфа-уровень на 2. В этом примере двусторонняя альфа будет равна 0,05/2 = 2,5 процента. См.: Односторонний тест или два? для разницы между односторонним тестом и двусторонним тестом.
3. Почему обычно используется альфа-уровень 0,05?
Учитывая, что альфа-уровень — это вероятность совершения ошибки типа I, кажется логичным сделать эту область как можно меньше. Например, если мы установим альфа-уровень на 10%, то есть большая вероятность того, что мы можем неправильно отвергнуть нулевую гипотезу, в то время как альфа-уровень 1% сделает область крошечной. Так почему бы не использовать крошечную площадь вместо стандартных 5%?
Чем меньше альфа-уровень, тем меньше область, в которой вы отвергли бы нулевую гипотезу.
Поэтому, если у вас крошечная область, больше шансов, что вы НЕ отклоните нулевое значение, когда на самом деле вы должны. Это ошибка второго рода.
Другими словами, чем больше вы пытаетесь избежать ошибки Типа I, тем больше вероятность того, что ошибка Типа II может закрасться. Ученые обнаружили, что уровень альфа 5% является хорошим балансом между этими двумя проблемами.
Ссылки
Гоник, Л. (1993). Мультяшный путеводитель по статистике. HarperPerennial.
Эверитт, Б.С.; Скрондал, А. (2010), Кембриджский статистический словарь, издательство Кембриджского университета.
Изображение предоставлено Техасским университетом.
НАЗВАТЬ ЭТО КАК:
Стефани Глен . «Альфа-уровень (уровень значимости): что это такое?» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/what-is-an-alpha-level/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Z-Score: определение, формула и расчет
Содержание (общее) :
- Что такое Z-Score?
- Формулы оценки Z.
- Как рассчитать Z-показатель.
- Подробнее о показателях Z и стандартных отклонениях.
- Как это используется в реальной жизни?
Содержание (технология) :
- Как найти Z-показатель на TI-89.
- Как найти Z-значение в Excel.
- Как найти критическое значение z на TI-83.
- Оценка Z в SPSS (новое окно)
Посмотрите видео, чтобы узнать, что такое z-оценка.
Что такое Z-показатель?
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Проще говоря, z-показатель (также называемый стандартным показателем ) дает вам представление о том, насколько далека точка данных от среднего значения.
Но с технической точки зрения это мера того, на сколько стандартных отклонений ниже или выше генеральной совокупности означает необработанный результат.
Z-значение может быть помещено на кривую нормального распределения . Z-показатели варьируются от -3 стандартных отклонений (которые находятся в крайнем левом углу кривой нормального распределения) до +3 стандартных отклонений (которые находятся в крайнем правом углу кривой нормального распределения). Чтобы использовать z-оценку, вам необходимо знать среднее значение μ, а также стандартное отклонение σ населения.
Z-показатели позволяют сравнить результаты с «нормальной» популяцией. Результаты тестов или опросов имеют тысячи возможных результатов и единиц измерения; эти результаты часто могут показаться бессмысленными. Например, знание того, что чей-то вес составляет 150 фунтов, может быть хорошей информацией, но если вы хотите сравнить его со «средним» весом человека, просмотр обширной таблицы данных может быть ошеломляющим (особенно если некоторые веса записаны в килограммах).
. Z-оценка может сказать вам , где вес этого человека составляет по сравнению со средним весом населения в .
Вернуться к началу
Формула Z-оценки: одна выборка
Базовая формула z-оценки для выборки:
z = (x – μ) / σ оценка теста 190. Тест имеет среднее значение (μ) 150 и стандартное отклонение (σ) 25. Предполагая нормальное распределение, ваша оценка z будет:
- z = (x – μ) / σ
- = (190 – 150) / 25 = 1,6.
Показатель z показывает, сколько стандартных отклонений от среднего составляет ваш показатель. В этом примере ваша оценка составляет 1,6 стандартных отклонения выше среднего значения .
Вы также можете увидеть формулу оценки z, показанную слева. Это точно такая же формула , что и z = x – μ / σ, за исключением того, что x̄ (выборочное среднее) используется вместо μ (среднее значение генеральной совокупности) и s (выборочное стандартное отклонение) используется вместо σ (выборочное среднее значение).
стандартное отклонение населения). Тем не менее, шаги для его решения точно такие же.
Формула Z-оценки: стандартная ошибка среднего
Если у вас есть нескольких выборок и вы хотите описать стандартное отклонение этих выборочных средних (стандартная ошибка), вы должны использовать эту формулу z-оценки:
z = ( x – μ) / (σ / √n)
Этот показатель z покажет вам, сколько стандартных ошибок существует между средним значением выборки и средним значением генеральной совокупности.
Пример задачи: Обычно средний рост женщин составляет 65 дюймов со стандартным отклонением 3,5 дюйма. Какова вероятность найти случайную выборку из 50 женщин со средним ростом 70 дюймов, если предположить, что рост распределен нормально?
- z = (x – μ) / (σ / √n)
- = (70 – 65) / (3,5/√50) = 5 / 0,495 = 10,1
Суть здесь в том, что мы имеем дело с выборочным распределением средних, поэтому мы знаем, что должны включить в формулу стандартную ошибку.
Мы также знаем, что 99% значений находятся в пределах 3 стандартных отклонений от среднего в нормальном распределении вероятностей (см. правило 68 95 99,7). Следовательно, вероятность того, что любая выборка женщин будет иметь средний рост 70 дюймов, составляет менее 1%.
Не знаете, когда использовать σ, а когда σ √n? См.: Sigma / sqrt (n) — для чего используется?
Вернуться к началу
Вы можете легко рассчитать z-значение на калькуляторе TI-83 или в Excel. Однако, если у вас нет ни того, ни другого, вы можете рассчитать его вручную.
Как рассчитать z-показатель в статистике
Посмотрите это видео на YouTube.
Пример вопроса: Вы сдаете SAT и набираете 1100 баллов. Средний балл SAT равен 1026, а стандартное отклонение равно 209.. Насколько хорошо вы набрали баллы на тесте по сравнению со средним тестируемым?
Шаг 1: Запишите значение X в уравнение z-показателя . В этом примере вопрос значением X является ваш балл SAT, 1100.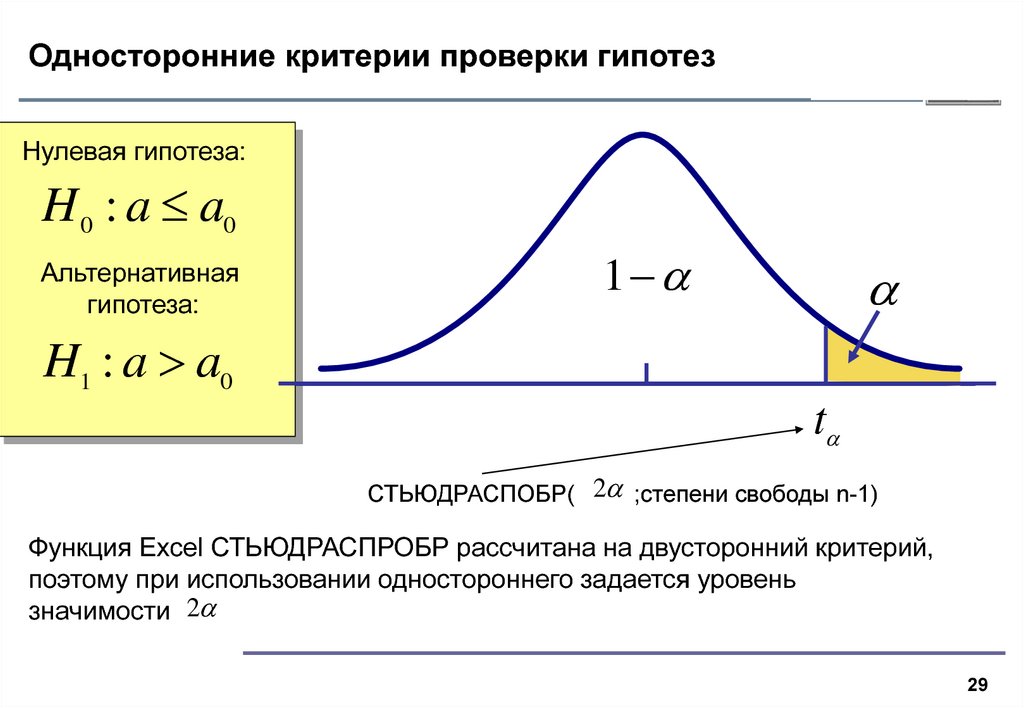
Шаг 2: Поместите среднее значение μ в уравнение z-балла .
Шаг 3: Запишите стандартное отклонение σ в уравнение z-показателя .
Шаг 4: Найдите ответ с помощью калькулятора :
(1100 – 1026) / 209= 0,354. Это означает, что ваша оценка была на 0,354 std dev выше среднего.
Шаг 5: ( Необязательный ) Найдите свое z-значение в z-таблице, чтобы узнать, какой процент тестируемых набрал меньше вас баллов. Z-показатель 0,354 равен 0,1368 + 0,5000* = 0,6368 или 63,68%.
*Зачем добавлять 0,500 к результату? Показанная z-таблица имеет баллы СПРАВА от среднего значения. Следовательно, мы должны добавить 0,500 для всей области, НАЛЕВО от среднего значения. Дополнительные примеры того, когда нужно добавить (или вычесть) 0,500, см. в нескольких примерах: Площадь под кривой нормального распределения.
Нравится объяснение? Прочтите «Руководство по статистике практического мошенничества», в котором есть еще сотни пошаговых объяснений, таких как это!
Вернуться к началу
Технически, z-значение — это число стандартных отклонений от среднего значения эталонной совокупности (население, чьи известные значения были записаны, как на этих диаграммах, которые CDC составляет с учетом веса людей).
Например:
- Z-показатель, равный 1, соответствует 1 стандартному отклонению выше среднего.
- Оценка 2 соответствует 2 стандартным отклонениям выше среднего.
- Оценка -1,8 соответствует стандартному отклонению -1,8 ниже среднего значения.
Z-оценка показывает, где находится оценка на кривой нормального распределения. Z-оценка ноль говорит о том, что значения точно средние , а оценка +3 говорит о том, что значение намного выше среднего.
Вернуться к началу
Вы можете использовать z-таблицу и график нормального распределения, чтобы получить визуальное представление о том, как z-значение 2,0 означает «выше среднего». Допустим, у вас есть вес человека (240 фунтов), и вы знаете, что его z-показатель равен 2,0. Вы знаете, что 2,0 выше среднего (из-за высокого положения на кривой нормального распределения), но вы хотите знать насколько выше среднего этот вес?
Показатель z в центре кривой равен нулю.
Z-показатели справа от среднего являются положительными , а z-показатели слева от среднего отрицательными . Если вы посмотрите на результат в z-таблице, вы сможете сказать, какой процент 90 101 90 102 населения выше или ниже вашего балла. В таблице ниже показан выделенный z-показатель 2,0, показывающий 0,9772 (что преобразуется в 97,72%). Если вы посмотрите на тот же показатель (2,0) кривой нормального распределения выше, вы увидите, что он соответствует 97,72%.
Это говорит о том, что 97,72 % оценок населения находятся ниже этого конкретного показателя, а 100 % – 97,72 % = 2,28 % оценок лежат выше этого показателя. Всего 2,28% населения имеют вес выше, чем у этого человека… Вероятно, это хороший признак того, что им нужно сесть на диету!
Технологии
Редактор статистики/списка TI-89 Titanium содержит простое меню, в котором вы можете найти Z-оценку за считанные секунды. В этом разделе показано, как найти z-оценку для критического значения в левом хвосте.
Кривая нормального распределения симметрична, поэтому это также будет площадь в правом хвосте.
Не уверены, является ли ваш тест левосторонним или правосторонним? См. «Тест с левым или правым хвостом», чтобы помочь вам принять решение.
Обратите внимание, что у вас должен быть установлен Редактор статистики/списка, чтобы иметь возможность сделать распределение частот TI-89, используя эти инструкции.
Z-оценка TI 89: Шаги
Пример задачи : Найдите z-оценку для α = 0,012 для левостороннего теста на стандартной кривой нормального распределения.
Шаг 1: Нажмите Apps, перейдите к Stats/List Editor и нажмите ENTER.
Если вы не видите Редактор статистики/списков, вы можете скачать его здесь. Это официальное приложение TI, и вам нужно будет перенести его на свой калькулятор с помощью кабеля, который изначально поставлялся с вашим TI-89.
Шаг 2: Нажмите F5 2 1, чтобы перейти к экрану Inverse Normal .
Шаг 3: Введите 0,012 в поле Area .
Шаг 4: Введите 0 для среднего значения µ и 1 для стандартного отклонения σ.
Шаг 5: Нажмите ENTER.
Шаг 6: Прочтите результат: калькулятор должен указать « Обратное = -2,25713 ». Это ваш показатель z.
Совет : Если вам дано среднее значение и стандартное отклонение, введите их вместо 0 и 1 на шаге 4.
Вот как можно найти показатель z на TI 89!
Z-оценка в Excel: обзор
Z-оценку в Excel можно быстро рассчитать с помощью базовой формулы . Формула для расчета z-показателя:
z = (x-μ) / σ,
, где μ — среднее значение генеральной совокупности, а σ — стандартное отклонение генеральной совокупности.
Примечание : если стандартное отклонение генеральной совокупности неизвестно или размер выборки меньше 6, следует использовать t-показатель вместо z-показателя.
Z-оценка в Excel: шаги
Посмотрите видео или прочитайте шаги ниже:
Как рассчитать z-оценку в Excel (все версии)
Посмотрите это видео на YouTube.
Пример вопроса: Вы сдали GRE и набрали 650 баллов за словесную часть теста. Рассчитайте z-оценку в Excel, чтобы определить, насколько хороша ваша оценка по сравнению с общей популяцией участников теста. Среднее значение совокупности (μ) равно 469, а стандартное отклонение совокупности (σ) равно 119.
Шаг 1: Введите среднее значение совокупности в пустую ячейку. В этом примере введите «469» в ячейку A2. Необязательно: введите слово «среднее» в качестве заголовка столбца в ячейке A1, чтобы вы помнили, что означает значение в ячейке A2.
Шаг 2: Введите стандартное отклонение генеральной совокупности в пустую ячейку . В этом примере введите «119» в ячейку B2. Необязательно: введите слова «стандартное отклонение» в качестве заголовка столбца в ячейке B1, чтобы вы помнили, что означает значение в ячейке B2.
Шаг 3: Введите значение X (в этом примере задачи X — это ваш балл GRE) в пустую ячейку. В этом примере введите «650» в ячейку C2. Необязательно: введите слова «X» в качестве заголовка столбца в ячейке B1, чтобы вы помнили, что означает значение в ячейке B2.
Шаг 4: Введите следующую формулу в пустую ячейку:
=(C2-A2)/B2
Шаг 5: Нажмите «Ввод». Z-оценка появится в ячейке D2: z-оценка 1,521008 в этом примере задачи указывает на то, что ваша оценка GRE была 1,521008.
Вот и все! Вы нашли z-значение в Excel.
Совет: Однажды введя формулу, вы можете использовать ее снова и снова. Просто введите новое среднее значение, стандартное отклонение и значение X в соответствующие поля.
Ссылки
Base, C. (2018). Понимание базовой статистики. Cengage Learning.
ЦКЗ. Антропометрические справочные данные для детей и взрослых: США, 2007–2010 гг.
Салкинд, Н.