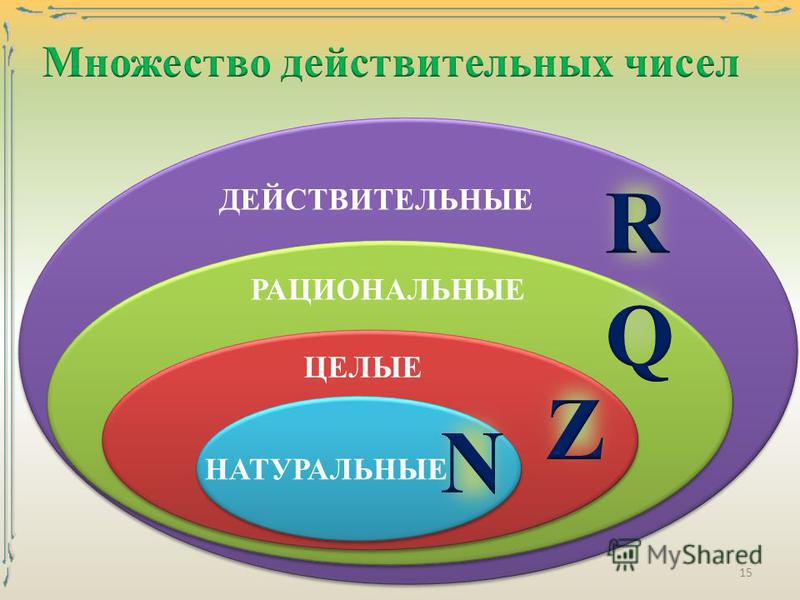
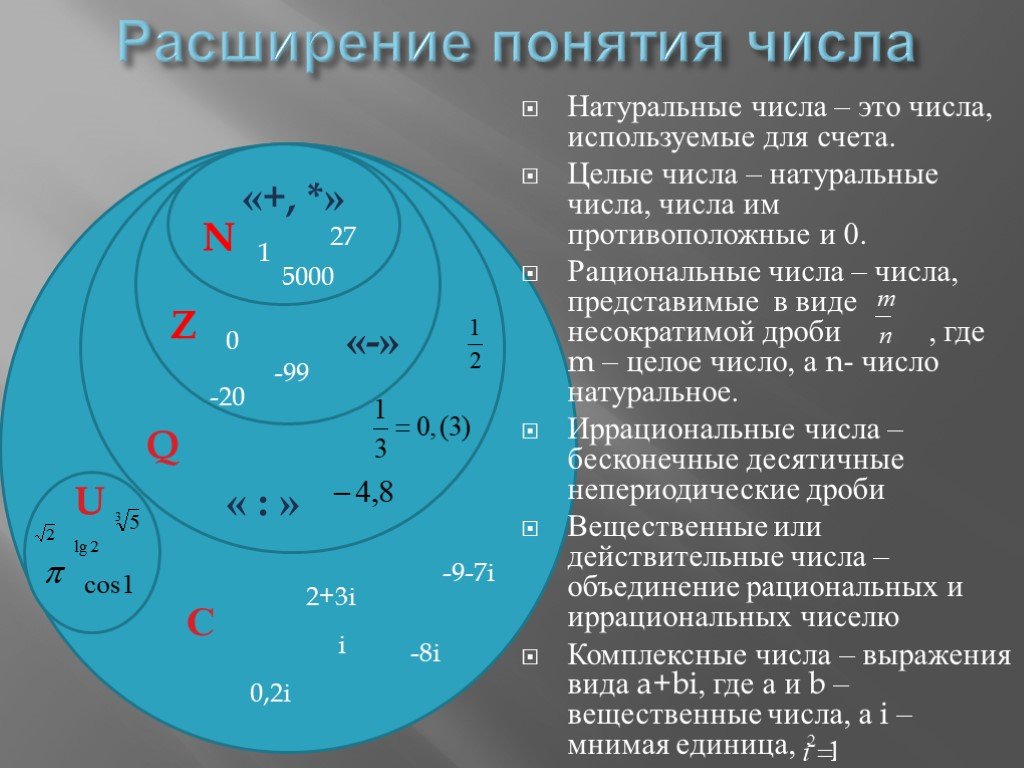
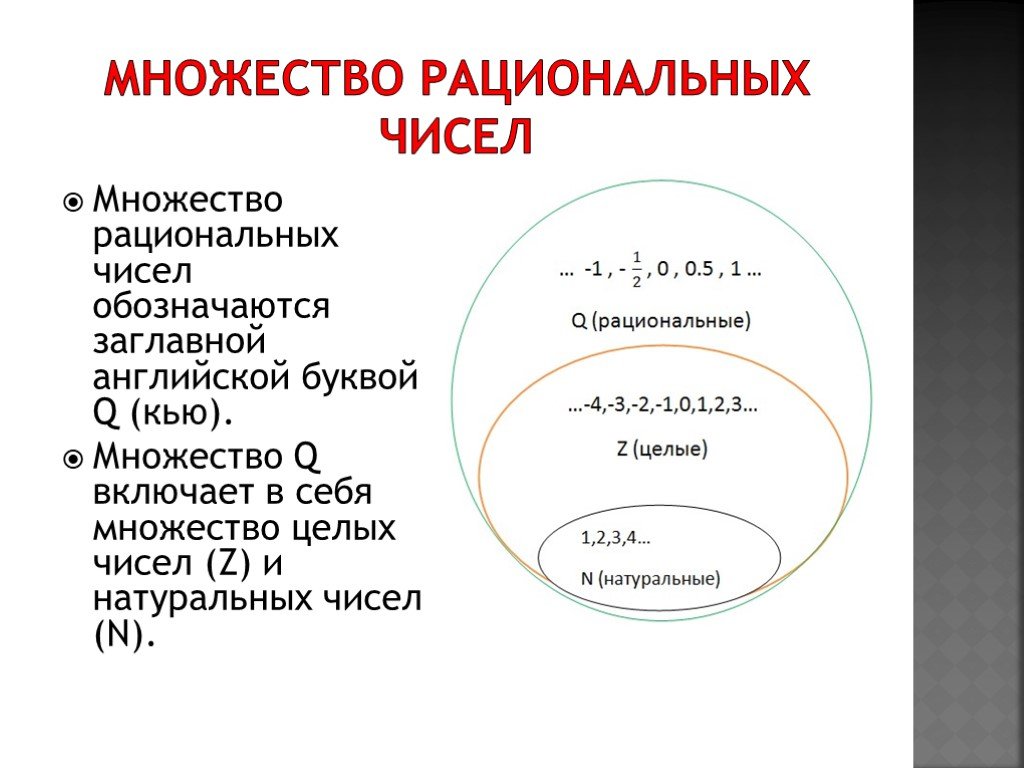
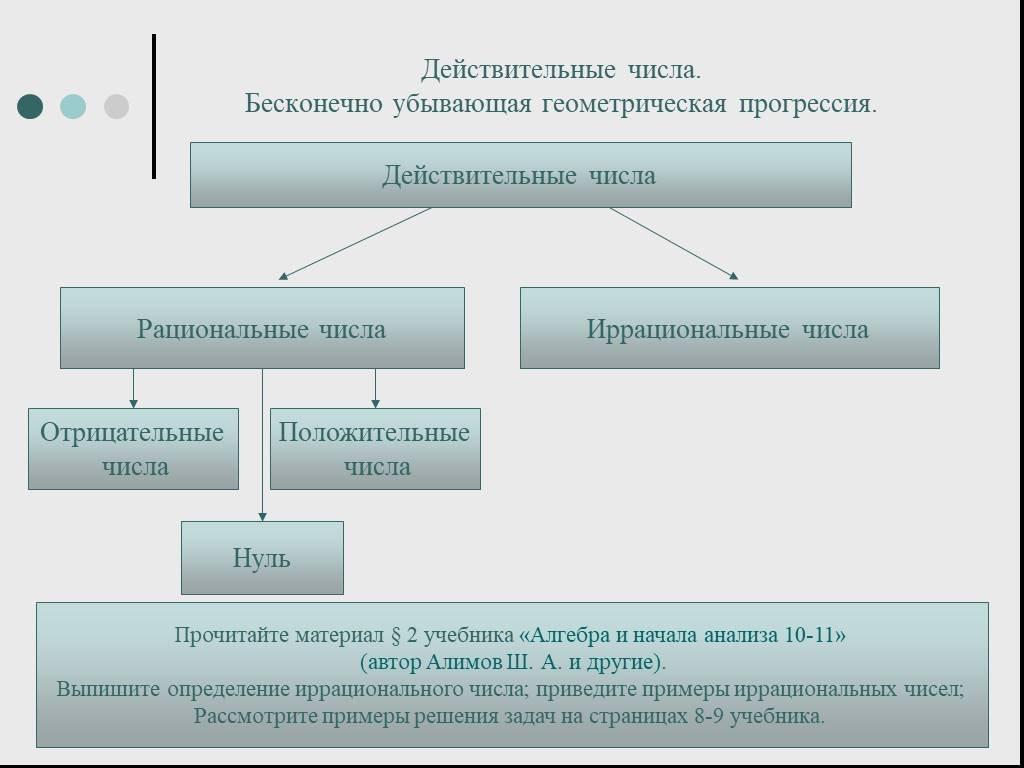
Рациональные числа. Иррациональные числа. Действительные числа
Introduction
These Website Standard Terms and Conditions written on this webpage shall manage your use of this website. These Terms will be applied fully and affect to your use of this Website. By using this Website, you agreed to accept all terms and conditions written in here. You must not use this Website if you disagree with any of these Website Standard Terms and Conditions.
Minors or people below 18 years old are not allowed to use this Website.
Intellectual Property Rights
Other than the content you own, under these Terms, Buckle LLC and/or its licensors own all the intellectual property rights and materials contained in this Website.
You are granted limited license only for purposes of viewing the material contained on this Website.
Restrictions
You are specifically restricted from all of the following
- publishing any Website material in any other media;
- selling, sublicensing and/or otherwise commercializing any Website material;
- publicly performing and/or showing any Website material;
- using this Website in any way that is or may be damaging to this Website;
- using this Website in any way that impacts user access to this Website;
- using this Website contrary to applicable laws and regulations, or in any way may cause harm to the Website, or to any person or business entity;
- engaging in any data mining, data harvesting, data extracting or any other similar activity in relation to this Website;
- using this Website to engage in any advertising or marketing.
Certain areas of this Website are restricted from being access by you and Buckle LLC may further restrict access by you to any areas of this Website, at any time, in absolute discretion. Any user ID and password you may have for this Website are confidential and you must maintain confidentiality as well.
Your Content
In these Website Standard Terms and Conditions, “Your Content” shall mean any audio, video text, images or other material you choose to display on this Website. By displaying Your Content, you grant Buckle LLC a non-exclusive, worldwide irrevocable, sub licensable license to use, reproduce, adapt, publish, translate and distribute it in any and all media.
Your Content must be your own and must not be invading any third-party’s rights. Buckle LLC reserves the right to remove any of Your Content from this Website at any time without notice.
No warranties
This Website is provided “as is,” with all faults, and Buckle LLC express no representations or warranties, of any kind related to this Website or the materials contained on this Website.
Also, nothing contained on this Website shall be interpreted as advising you.
Limitation of liability
In no event shall Buckle LLC, nor any of its officers, directors and employees, shall be held liable for anything arising out of or in any way connected with your use of this website whether such liability is under contract. Buckle LLC, including its officers, directors and employees shall not be held liable for any indirect, consequential or special liability arising out of or in any way related to your use of this Website.
Indemnification
You hereby indemnify to the fullest extent Buckle LLC from and against any and/or all liabilities, costs, demands, causes of action, damages and expenses arising in any way related to your breach of any of the provisions of these Terms.
Severability
If any provision of these Terms is found to be invalid under any applicable law, such provisions shall be deleted without affecting the remaining provisions herein.
Variation of Terms
Buckle LLC is permitted to revise these Terms at any time as it sees fit, and by using this Website you are expected to review these Terms on a regular basis.
Assignment
The Buckle LLC is allowed to assign, transfer, and subcontract its rights and/or obligations under these Terms without any notification. However, you are not allowed to assign, transfer, or subcontract any of your rights and/or obligations under these Terms.
Entire Agreement
These Terms constitute the entire agreement between Buckle LLC and you in relation to your use of this Website, and supersede all prior agreements and understandings.
Governing Law & Jurisdiction
These Terms will be governed by and interpreted in accordance with the laws of the State of New York, and you submit to the non-exclusive jurisdiction of the state and federal courts located in New York for the resolution of any disputes.
1.1.1 Целые числа
Видеоурок: Натуральные, целые, рациональные, иррациональные и действительные числа
Лекция: Целые числа
Целые и натуральные числа
К целым числам можно отнести все числа натурального ряда, им противоположные, а также ноль.
То есть это все не дробные положительные, отрицательные числа, а так же ноль — иными словами, все не дробные числа на числовой прямой. Используя термин «натуральные числа» мы понимаем, что это не отрицательные и не дробные числа.
У Вас может возникнуть вопрос, чему же равно максимальное или минимальное целое число — таковых не существует, поскольку числовой ряд бесконечный.
Среди всего множества чисел, целые числа обозначаются буквой Z, а натуральные — N.
Все натуральные числа используются для счета.
Например, на дереве висит 5 яблок, стол сервирован на 8 персон. Мы же не можем сказать, что на столе 7,5 тарелок, или у цветка -3 листка. Числа, противоположные натуральным, — это не дробные и отрицательные числа.
Арифметические действия
Существует несколько математических операций, которые можно производить с целыми числами. Хотелось пояснить каждую из них.
1. Сложение / Вычитание
При необходимости сложить два числа, имеющие одинаковые знаки, следует сложить их модули и поставить общий знак. Например,
|+4| + |+6| = |+10|,
|-8| + |-3| = |-11|.
Если необходимо сложить целые числа, которые имеют противоположные знаки, следует от числа с большим модулем вычесть второе число. Перед суммой поставить знак большего модуля. Например,
|-10| + |+3| = |-7|,
|+5| + |-2| = |+3|.
2. Умножение / Деление
Если следует получить произведение (частное) двух чисел, следует перемножить их модули.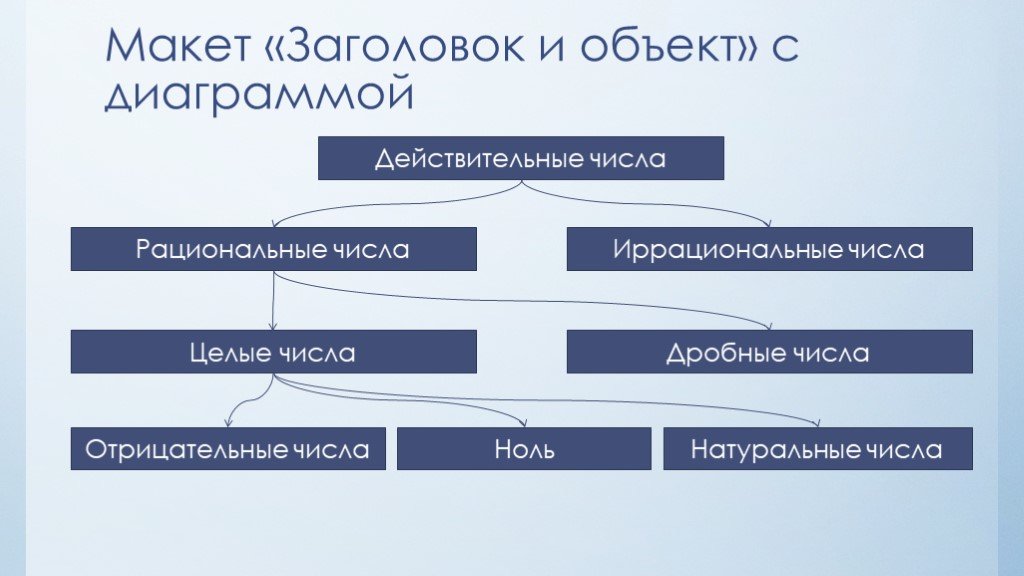
Перед произведением (частным) ставится знак «+» в том случае, если перемножались (делились) числа с одинаковыми знаками. Если умножение (деление) происходило между числами с разными знаками, то ставят знак «-«.
Например,
|-5| * |-6| = |+30|,
|+3| * |+7| = |+21|,
|-4| * |+3| = |-12|.
Основные правила, используемые при делении, умножении, сложении и вычитании целых чисел
.Рассмотрим арифметические действия, которые производятся над тремя целыми числами а, б, с.
Вечевые порядки. Принятие христианства- Вконтакте
- Сайт
РЕШЕНО: Какие числа в следующем наборе являются натуральными числами, целыми числами, целыми числами, рациональными числами, иррациональными числами, действительными числами? {67, (4)/(13),-5,9,11 (2)/(3), √(2), 0,-3, π}.
Проблема
Определить, является ли каждое утверждение истинным или ложным…
Вопрос
Пошаговый ответ
Видео Ответ
Решено проверенным специалистом
Проблема решена!
Попробуйте Numerade бесплатно в течение 7 дней
Расшифровка
давайте определим категории, в которые вписываются все эти различные числа. будет натуральным числом. Следовательно, как натуральное число, оно будет целым числом, а также целым числом.
Теперь целые числа просто по определению являются рациональными числами, а все рациональные числа на самом деле являются числами. Число 67 соответствует категориям натуральных, целых, рациональных и риелей. Далее у нас 4/13. Сейчас. Это число не является ах, целым числом, то есть его можно записать как дробь и онли как дробь или десятичную дробь. Следовательно, это не натуральное, целое или целое. Однако он по-прежнему записывается как отношение двух целых чисел, то есть как дробь. Итак, это рациональное число, а значит, и действительное. Только две категории в этой следующей отрицательной 5,9. Опять же, это не может быть натуральным числом, потому что оно десятичное и к тому же отрицательное, поэтому оно не может быть натуральным или целым. И это не целое число, потому что есть десятичная точка. Тем не менее, его также можно записать в виде дроби, что делает его рациональным, и он не умножается на I. Значение — риель. Далее 11 и 2/3. Это снова дробь, так что она не натуральная, целая или целое число, тем не менее, она все еще рациональна, и это все еще риель.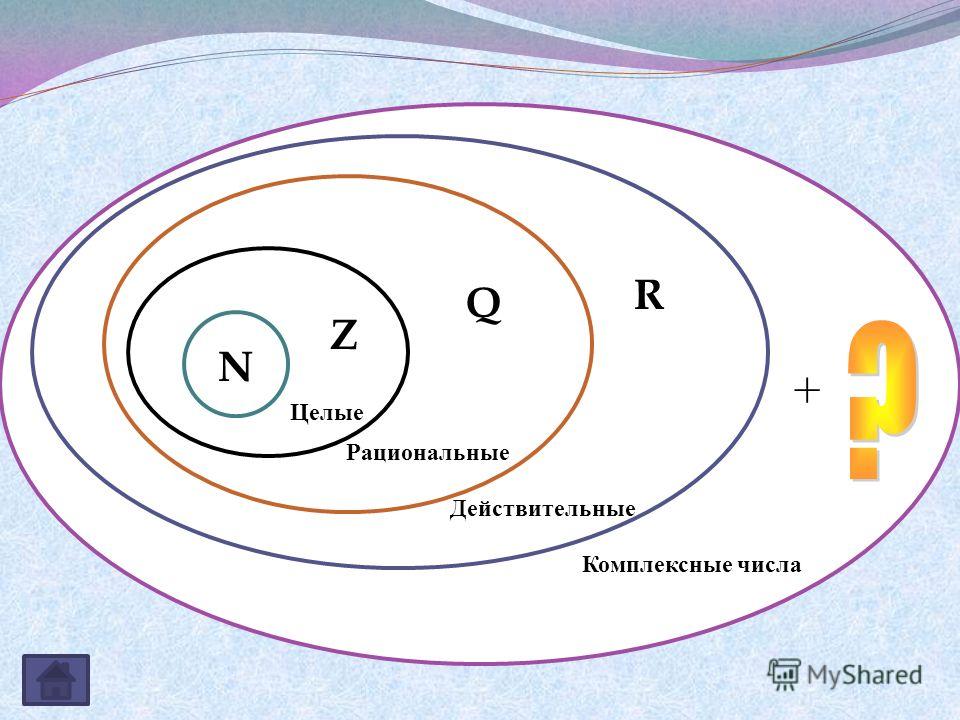
Все в порядке. Далее у нас есть квадратный корень из двух. Это немного другое, потому что, если бы он попытался записать это в виде дроби, вы бы обнаружили, что это невозможно. Его можно записать только в виде квадратного корня из двух. Таким образом, это не рационально, и это на самом деле, Onley риель до следующего, мы имеем ноль. Это довольно важная цифра. Ну, оно не больше нуля, так что это не натуральное число. Однако это не дробь, т.е. На самом деле это и дырка, и целое число. А так как это дыра в целом числе, то это также рациональное число, а также любовник Ариэль. Далее у нас есть отрицательная тройка, теперь отрицательная тройка. Сначала это выглядит как целое число, но оно меньше нуля. Следовательно, оно не натуральное, целое или дырочное, но все же является целым числом, поскольку оно не записывается как дробь. Хорошо, теперь мы также знаем, что поскольку это целое число, оно должно быть рациональным. И поскольку это рациональное целое число, не умноженное на I, это Израиль и, наконец, еще одно очень важное число.
Пи. Дело в том, что пирог — это децибел. Следовательно, это не может быть целое, натуральное число или целое число. Впрочем, пирог тоже не дробь. Невозможно написать круг как одно число над другим. Следовательно, это не рационально. На самом деле, онлей риель, поэтому мы не классифицировали все эти разные числа.
Действительное число 1,21 рационально или иррационально?
Множество рациональных и иррациональных чисел называется действительными числами. Они могут быть как положительными, так и отрицательными и обозначаются знаком «R». Этот набор включает в себя все натуральные числа, десятичные дроби и дроби. Этот модуль включает в себя все натуральные числа, десятичные дроби и дроби. В системе счисления действительные числа представляют собой комбинацию рациональных и иррациональных чисел. В общем случае над этими числами можно производить все арифметические операции, а также их можно представить на числовой прямой. Любое число, которое можно представить в виде дроби p/q, называется рациональным числом.
В этой дроби значение числителя записывается как «p», а значение знаменателя представлено как «q», где «q» не равно нулю. Натуральные числа, целые числа, десятичные или целые числа — все они являются частью рациональных чисел.
Примеры: 1/2, -2/3, 0,5 и 0,333 — рациональные числа.
Иррациональные числа — это действительные числа, которые не могут быть представлены в виде дроби p/q, где «p» и «q» — целые числа, а знаменатель «q» больше нуля (q≠0).
Примеры: (пи) — иррациональное число π = 3,14159265… Десятичное число в этом случае никогда не заканчивается ни в какой точке. Поэтому такие числа, как √2, √-7 и т. д., являются иррациональными числами.
Действительное число 1,21 рационально или иррационально?
Решение:
Любое число, которое можно представить в виде дроби p/q, называется рациональным числом. когда число упрощается, оно дает результат в виде десятичных знаков, который либо завершается, либо повторяется после десятичного числа.
Итак, данное здесь число действительное число 1.21 является рациональным числом , так как оно оканчивается после десятичного числа.
Примеры вопросов
Вопрос 1. Определите, является ли -55 рациональным числом.
Решение:
Любое число, которое можно представить в виде дроби p/q, называется рациональным числом. когда число упрощается, оно дает результат в виде десятичных знаков, который либо завершается, либо повторяется после десятичного числа.
Таким образом, здесь данное число -55 является рациональным числом, так как оно заканчивается после запятой.
Вопрос 2: Является ли число 23,25 рациональным или иррациональным?
Решение:
Любое число, которое можно представить в виде дроби p/q, называется рациональным числом. когда число упрощается, оно дает результат в виде десятичных знаков, который либо завершается, либо повторяется после десятичного числа.
Таким образом, данное здесь число 23,25 является рациональным числом, так как оно заканчивается после запятой.
Вопрос 3: Определите, является ли 2/51 рациональным или иррациональным числом.
Решение:
Любое число, которое можно представить в виде дроби p/q, называется рациональным числом. когда число упрощается, оно дает результат в виде десятичных знаков, который либо завершается, либо повторяется после десятичного числа.
Итак, здесь данное число 2/51 представлено в виде дроби, а рациональное число может быть выражено в виде дроби. Следовательно,
2/51 является рациональным числом.
Вопрос 4: Является ли 7,656545 рациональным числом?
Решение:
Любое число, которое можно представить в виде дроби p/q, называется рациональным числом. когда число упрощается, оно дает результат в виде десятичных знаков, который либо завершается, либо повторяется после десятичного числа.
Иррациональные числа — это действительные числа, которые не могут быть представлены в виде дроби p/q, где «p» и «q» — целые числа, а знаменатель «q» больше нуля (q≠0). Итак, здесь данное число 7,656545 является рациональным числом, так как оно заканчивается после запятой в конечной точке.
Вопрос 5: Является ли 0,23224554… рациональным числом?
Решение:
Любое число, которое можно представить в виде дроби p/q, называется рациональным числом. когда число упрощается, оно дает результат в виде десятичных знаков, который либо завершается, либо повторяется после десятичного числа.
Иррациональные числа — это действительные числа, которые не могут быть представлены в виде дроби p/q, где «p» и «q» — целые числа, а знаменатель «q» больше нуля (q≠0). Итак, здесь дано число 0.23224554…. не является рациональным числом, это иррациональное число, поскольку оно не заканчивается или не повторяется после десятичного числа.
