Решение задач по электротехнике (ТОЭ)
- Главная
- Заказать
- Примеры решений
- Теория электротехники
- Оплата и гарантии
- Цены
- Контакты
- Сотрудничество
! Вы всегда можете найти недорогие готовые решения по теме Расчет цепей синусоидального тока, просто перейдя по этой ссылке
В электрической цепи однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1) полное сопротивление электрической цепи и его характер;
2) действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;
4) построить векторную диаграмму токов и топографическую диаграмму напряжений для всей цепи.
Дано
E = 130 В;
f = 50 Гц;
R1 = 9 Ом;
L1 = 15,9 мГн;
C2
L2 = 9,4 мГн;
R3 = 8 Ом;
C3 = 500 мкФ;
Схема 1.
 (-6))=6,37 Ом;
(-6))=6,37 Ом;Общее сопротивление цепи:
Характер входного сопротивления активно-индуктивный, на это указывает наличие действительной части и положительная мнимая часть сопротивления.
Комплекс действующего значения входного напряжения:
E=E•(cosφ+jsinφ)=130•(cos0o+jsin0o)=130+0j В;
Действующие комплексные токи в цепи:
I1=E/Zвх =130/(10,632+0,669j)=12,179-0,767j=12,203•e(-4oj) А;
I2=I1•((R3-jXC3))/(R3+j(XL2-XC2-XC3))=(12,179-0,767j)•(8-6,37j)/(8+j•(2,95-10,01-6,37))=
=7,631+2,346j=7,983•e(17oj) А;
I3=I1-I2=12,179-0,767j-7,631-2,346j=4,548-3,113j=5,511•e(-35oj) А;
Падения напряжения на элементах:
UL1=I1•jXL1=(12,179-0,767j)•4,99j=3,83+60,77j В;
UR1=I1•R1=(12,179-0,767j)•9=109,61-6,90j В;
UL2=I2•jXL2=(7,631+2,346j)•2,95j=-6,92+22,51j В;
UC2=I2•(-jXC2)=(7,631+2,346j)•(-10,01j)=23,48-76,39j В;
UR3=I3•R3=(4,548-3,113j)•8=36,38-24,90j В;
UC3=I4•(-jXC3)=(4,548-3,113j)•(-6,37j)=-19,83-28,97j=35,11•e(-124oj) В;
Показания вольтметра (измеряющего действующее значение напряжения):
UV=UC3=35,11 В;
Показания ваттметра (измеряющего активную мощность):
Pw=Re(E•I1*)=Re(130•(12,179+0,767j))=1583,3 Вт;
I* — сопряженный ток.
Рисунок 3. Топографическая диаграмма напряжений
Рисунок 4. Векторная диаграмма токов
! Вы всегда можете найти недорогие готовые решения по теме Расчет цепей синусоидального тока, просто перейдя по этой ссылке
Электротехника — ТОЭ, ОТЦ — решение задач
2. Расчет цепи синусоидального тока со смешанным соединением элементов
2.1 Содержание домашнего задания
В домашнем задании предусматривается расчет электрической цепи со смешанным соединением элементов, состоящей из двух параллельных ветвей, в каждой из которых последовательно включено не менее двух элементов.
В домашнем задании необходимо:
По исходной схеме (рис. 2.1) нарисовать электрическую схему согласно заданному варианту (табл. 1). Элементы, сопротивления которых равны нулю, исключаются из схемы.

Рис. 2.1. Исходная принципиальная электрическая схема
Методом проводимостей рассчитать токи в параллельных ветвях и неразветвленной части цепи.
Вычислить активную, реактивную и полную мощности параллельных ветвей и всей цепи.
Построить векторную диаграмму токов и напряжений.
Изменяя одно из реактивных сопротивлений параллельной ветви, добиться, чтобы схема работала в режиме резонанса токов. Если в заданной цепи резонанс токов невозможен, ввести в одну из параллельных ветвей дополнительное реактивное сопротивление (индуктивность или емкость).
Построить векторную диаграмму токов и напряжений при работе цепи в резонансе токов.
При расчетах считать напряжение, приложенное к цепи, равным U=100 (В), сопротивления элементов заданы в табл.
 1.
1.
2.2 Пример расчета электрической цепи со смешанным соединением элементов
Рассмотрим порядок расчета электрической цепи соответствующей варианту 72.
Задано:
R1=0, R2=20 Ом,
XL1.1=10 Ом, XC2.1=0,
XC1=40 Ом, XL2=20 Ом,
XL1.2=0 Ом, XC2.2=0 Ом..
Данному варианту соответствует электрическая схема рис. 2.2
Рис. 2.2. Электрическая схема цепи, согласно варианту 72
Расчет производится в следующем порядке:
Определяем полное сопротивление первой ветви:
Ом.
Определяем полное сопротивление второй ветви:
Ом.
Примечание: расчет вести до четырех значащих цифр.
Определяем активную проводимость первой ветви:
.
Определяем реактивную проводимость первой ветви:
Сим.
Определяем полную проводимость первой ветви:
Сим.
Определяем активную составляющую первого тока:
.
Определяем реактивную составляющую первого тока:
А.
Определяем полный ток первой ветви:
А.
Определяем активную проводимость второй ветви:
Сим.
Определяем реактивную проводимость второй ветви:
Сим.
Определяем полную проводимость второй ветви:
Сим.
Определяем активную составляющую тока второй ветви:
А.
Определяем реактивную составляющую тока второй ветви:
А.
Определяем полный ток второй ветви:
А.
Определяем активную проводимость всей цепи:
Сим.
Определяем реактивную проводимость всей цепи:
Сим.
Определяем полную проводимость всей цепи:
Сим.
А.
19. Определяем реактивную составляющую тока в неразветвленной части цепи:
А.
20. Определяем полный ток в неразветвленной части цепи:
А.
21. Определяем коэффициент мощности первой ветви:
.
22. Определяем коэффициент мощности второй ветви:
.
23. Определяем коэффициент мощности всей цепи:
.
24. Определяем полную мощность первой ветви:
ВА.
25. Определяем активную мощность первой ветви:
.
26.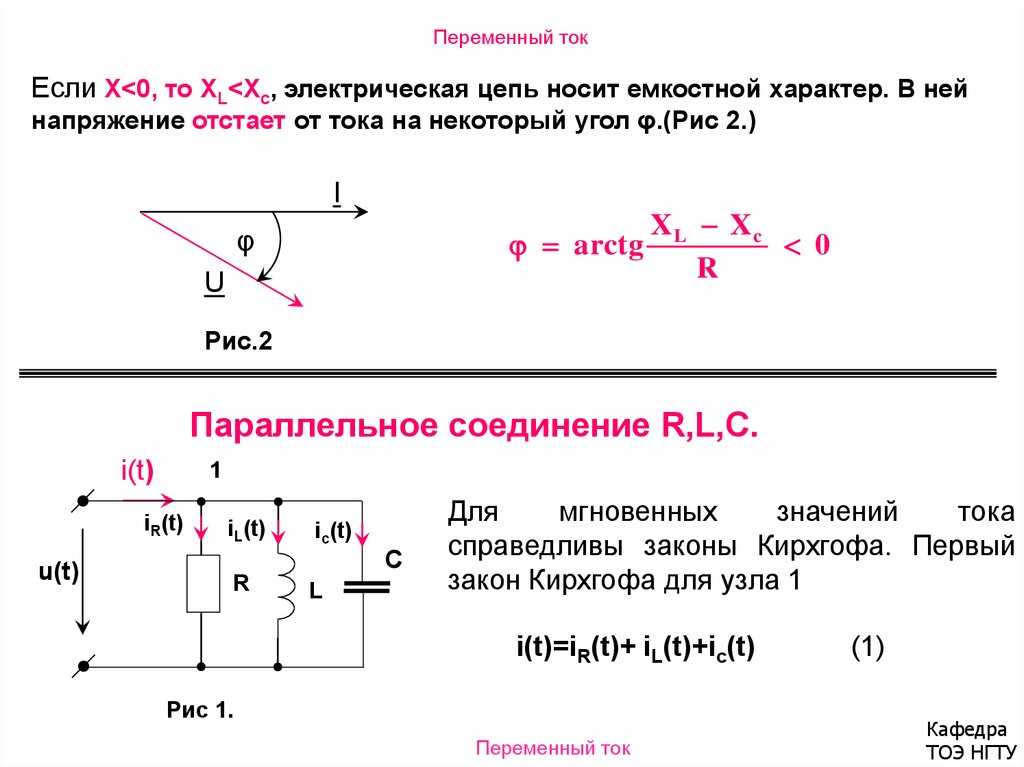 Определяем
реактивную мощность первой ветви:
Определяем
реактивную мощность первой ветви:
ВАр.
27. Определяем полную мощность второй ветви:
ВА.
28. Определяем активную мощность второй ветви:
Вт.
29. Определяем реактивную мощность второй ветви:
ВАр.
30. Определяем полную мощность всей цепи:
ВА.
31. Определяем активную мощность всей цепи:
Вт.
32. Определяем реактивную мощность всей цепи:
ВАр.
33. Векторная диаграмма токов строится на основании первого закона Кирхгофа для цепей синусоидального тока:
.
Векторная диаграмма токов строится в следующем порядке:
33.1. За базовую ось принимаем вектор напряжения U
 Строим этот вектор горизонтально
в масштабе mU.
Строим этот вектор горизонтально
в масштабе mU.33.2. По активной и реактивной составляющей первого тока строится вектор тока I1. Но так как активная составляющая первого тока I1a=0, то полный ток I1 будет равен реактивной составляющей I1р, которая имеет емкостный характер и опережает вектор напряжения U на угол 90° (X=XL1.1 – XC1<0). Этот вектор строим перпендикулярно к вектору напряжения U против часовой стрелки (φ1=-90°) в масштабе m1.
33.3. Аналогично
строим вектор тока второй ветви. Активная
составляющая тока I2a совпадает
по фазе с вектором напряжения U,
реактивная составляющая тока второй
ветви I2р носит
индуктивный характер (X2=XL2>0)
и отстает от вектора напряжения U на
угол 90°. Этот вектор строим перпендикулярно
к вектору напряжения по часовой стрелке.
Вектор полного тока второй ветви будет
равен диагонали параллелограмма
построенного на векторах I2a и I2р.
Этот вектор строим перпендикулярно
к вектору напряжения по часовой стрелке.
Вектор полного тока второй ветви будет
равен диагонали параллелограмма
построенного на векторах I2a и I2р.
34. Векторная диаграмма напряжений для первой ветви строится на основании второго закона Кирхгофа:
.
Рис 2.3. Векторная диаграмма токов и напряжений
Векторная диаграмма напряжений строится в следующем порядке:
34.1. Строится вектор падения напряжения на индуктивном сопротивлении XL1.1, модуль которого равен:
В.
На индуктивности напряжение опережает ток на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I1 против часовой стрелки.
34.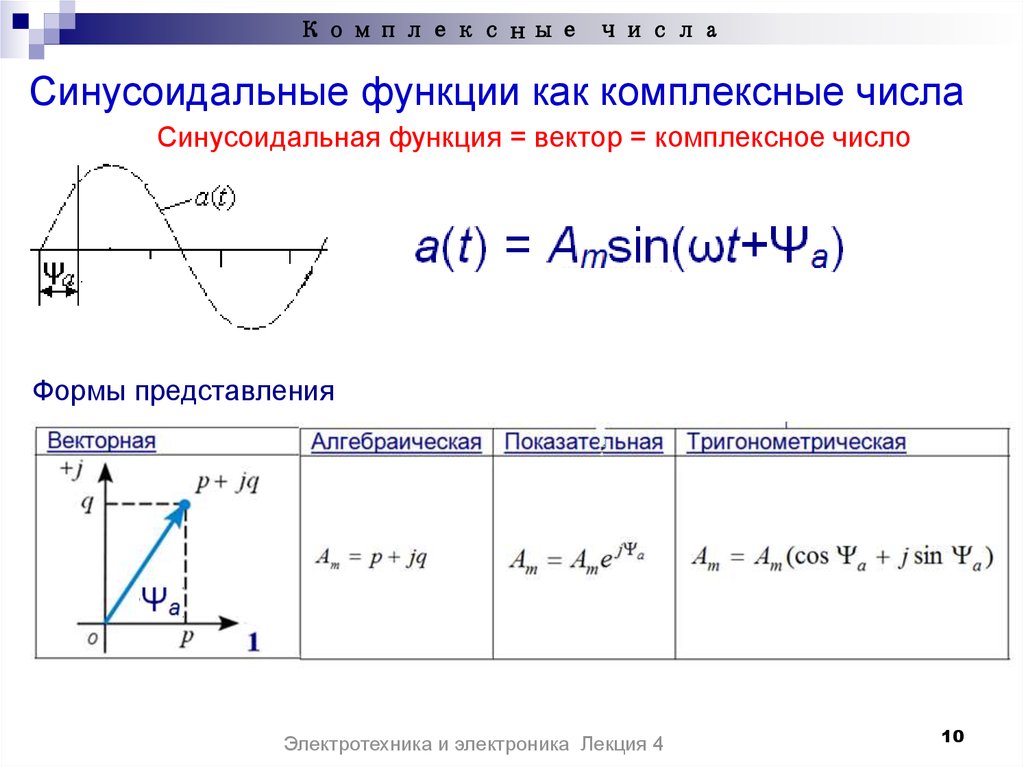 2. Из
конца вектора UL1.1 строится вектор падения напряжения на
емкостном сопротивлении XC1 , модуль которого равен:
2. Из
конца вектора UL1.1 строится вектор падения напряжения на
емкостном сопротивлении XC1 , модуль которого равен:
В.
На емкости напряжение отстает от тока на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I1 по часовой стрелке. Если вычисления и построения сделаны верно, то конец вектора UC1 будет совпадать с концом вектора U.
35. Векторная диаграмма напряжений для второй ветви строится на основании второго закона Кирхгофа:
.
Векторная диаграмма напряжений для второй ветви строится в следующем порядке:
35.1. Строится вектор падения напряжения на активном сопротивлении R2, модуль которого равен
В.
На
активном сопротивлении напряжение и
ток совпадают по фазе, поэтому этот
вектор строим совпадающим по направлению
с вектором тока I2.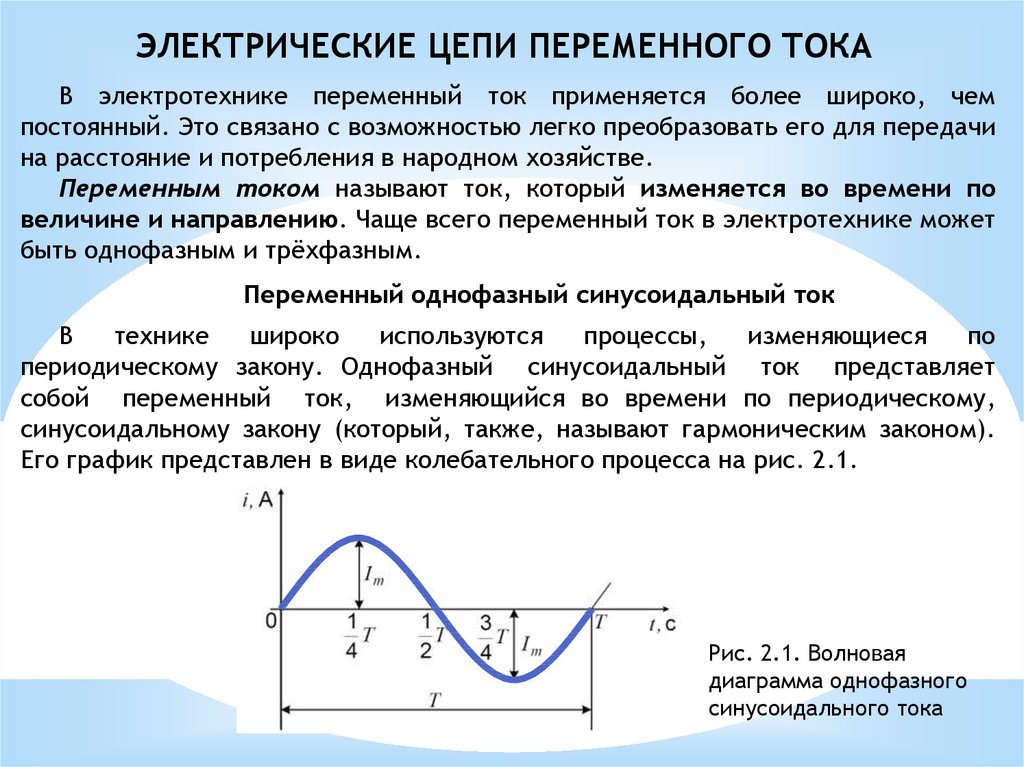
35.2. Из конца вектора UR2 строится вектор падения напряжения на индуктивном сопротивлении XL2, модуль которого равен:
В.
Напряжение на индуктивности опережает ток на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I2 против часовой стрелки.
Если вычисления и построения сделаны верно, конец вектора напряжения UL2 будет совпадать с концом вектора U.
Рекомендуемый масштаб:
mu=1B/мм,
mI=0,05А/мм.
36. Для обеспечения резонанса токов в электрической схеме с двумя параллельными ветвями должны выполняться следующие условия:
параллельные ветви должны иметь разный характер проводимостей (одна индуктивный, другая емкостный).

реактивные проводимости параллельных ветвей должны быть равны по модулю, т.е.
.
В данном варианте первое условие выполняется, т.к. первая ветвь носит емкостный, а вторая – активно-индуктивный характер.
Для достижения резонанса токов, т.к. необходимо в первую ветвь включить дополнительно емкость, величину сопротивления которого можно вычислить следующим образом:
,
,
Ом.
37. После включения дополнительной емкости в первую ветвь изменится ток в этой ветви и падения напряжения на индуктивности и емкости.
Сим,
А,
А,
В,
В,
Векторная диаграмма, построенная аналогично п.п. 33-35, представлена на рис. 2.4.
Рекомендуемый масштаб:
mu=1B/мм,
mI=0,05А/мм.
Цепи переменного тока — мощность в зависимости от напряжения и тока
В цепи переменного тока — переменный ток генерируется источником синусоидального напряжения
Напряжение
Токи в цепях с чисто резистивными, емкостными или индуктивными нагрузками.
Мгновенное напряжение в синусоидальной цепи переменного тока может быть выражено в виде во временной области как0003 , где U (T) = напряжение в цепи во время T (V) U MAX = максимальное напряжение при амплитуде . T = Время (S) ω = 2 π F = угловая частота синусоидальной волны (RAD/S) F = частота (Гц, 1/с) F = частота (Гц, 1/с) F = частота (Гц, 1/с) θ = фазовый сдвиг синусоидальной волны (рад) The momentary voltage can alternatively be expressed in the frequency-domain (or phasor) form as U = U(jω) = U max e jθ (1a) где U(jω) = U = комплексное напряжение (В) Вектор представляет собой комплексное число, выраженное в полярной форме, состоящее из величины, равной пиковой амплитуде синусоидального сигнала, и фазового угла равен фазовому сдвигу синусоидального сигнала относительно косинусоидального сигнала. Обратите внимание, что конкретная угловая частота — ω — не используется явно в векторном выражении. Мгновенный ток может быть выражен во временной области как i(t) = ток в момент времени t (А) I max = максимальный ток при амплитуде синусоидальная волна (А) Токи в цепях с чистыми резистивными, емкостными или индуктивными нагрузками указаны на рисунке выше. Ток в «реальной» цепи с резистивной, индуктивной и емкостной нагрузкой указан на рисунке ниже. Мгновенный ток в цепи переменного тока можно альтернативно выразить в частотной области (или векторной форме) как I = I(jω) = I MAX E Jθ (2A) , где I = I (Jω) = Комплекс. Системы переменного тока являются фиксированными — например, 60 Гц в Северной Америке и 50 Гц в большей части остального мира. Угловая частота для Северной Америки ω = 2 π 60 = 377 RAD/S Угловая частота для большей части остального мира составляет ω = 2 π 50 = 314 RAD/S Напряжение на резистивную нагрузку в системе переменного тока может быть выражено как U = R I (4) , где R = сопротивление (OHM) Для нагрузки сопротивления в цепи переменного тока. в фазе с током. Напряжение на индуктивную нагрузку в системе переменного тока может быть выражена как U = J ω L I (5) , где L = индуст (Henry) (Henry) (Henry). Для индуктивной нагрузки ток в цепи переменного тока равен π/2 (90 o ) фаза после напряжение (или напряжение до тока). Напряжение на индуктивную нагрузку в системе переменного тока может быть выражено как U = 1 / (J ω C) I (6) , где CI. = емкость (фарад) Для емкостной нагрузки ток в цепи переменного тока опережает напряжение на π/2 (90 o ) фаза . В реальной электрической цепи присутствует смесь резистивных, емкостных и индуктивных нагрузок со сдвигом фаз напряжение/ток в пределах — π/2 <= φ <= π/2 , как показано на рисунке ниже. Ток в «реальной» цепи с резистивной, индуктивной и емкостной нагрузкой . φ — фазовый угол между током и напряжением. где0003 U z = падение напряжения на нагрузке (вольт, В) I z = ток через нагрузку (ампер, А) Z = полное сопротивление нагрузки, Ом, мс ) Полное сопротивление в цепи переменного тока можно рассматривать как комплексное сопротивление. Результирующее полное сопротивление для последовательных импедансов может быть выражено как z = z 1 + z 2 (7b) Полученный импеданс для импедансов в параллеле может быть выражено как 1 / Z = 1 / Z 1 + + 1 / Z = 1 / Z 1 . 1 / Z 2 (7C) Допуск — это перевернутый импеданс Y = 1 / Z (8) , где

Ток
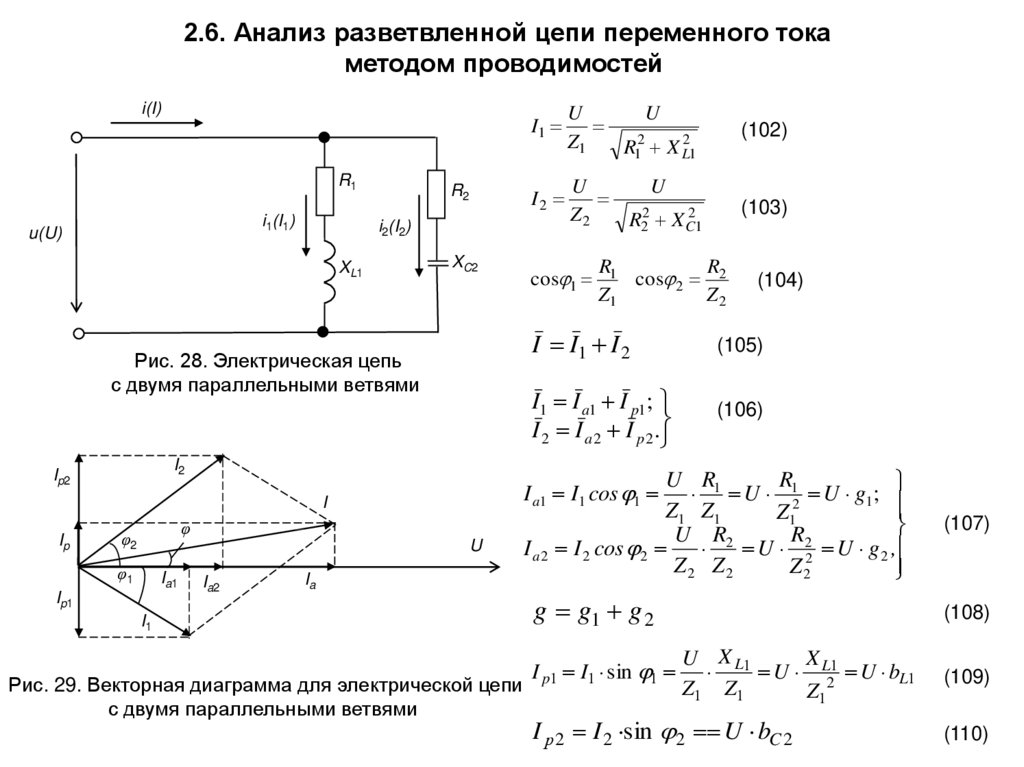
Устойчивая нагрузка
Индуктивная нагрузка
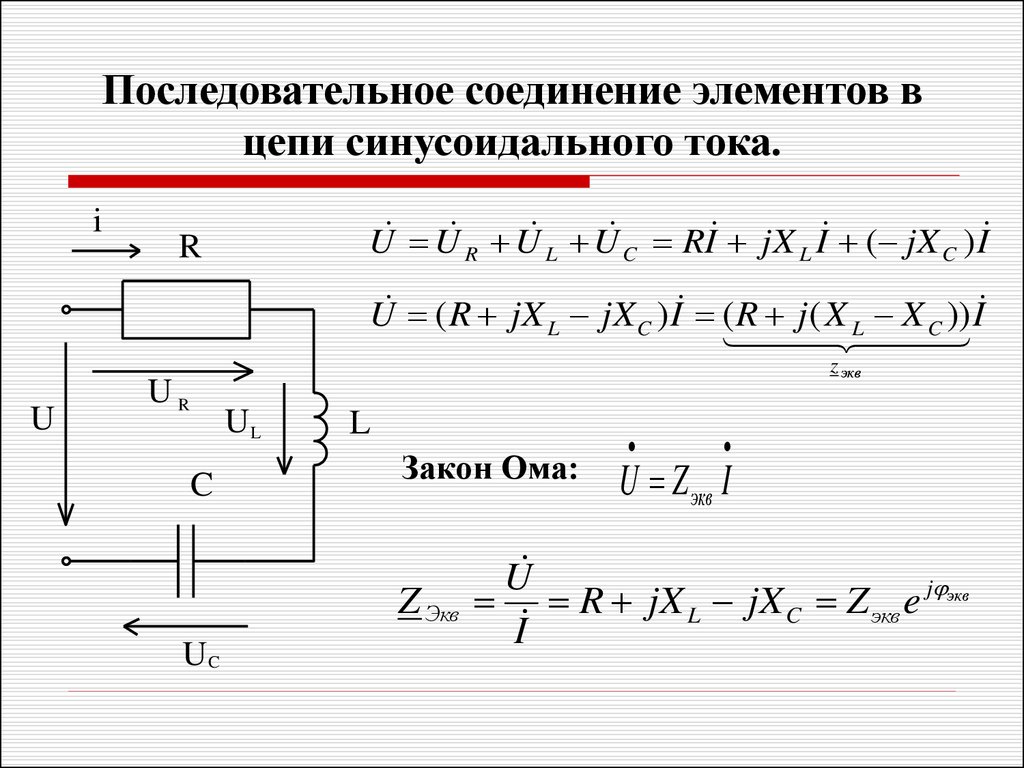
емкостная нагрузка
 Импеданс действует как частотно-зависимый резистор, где сопротивление является функцией частоты синусоидального возбуждения.
Импеданс действует как частотно-зависимый резистор, где сопротивление является функцией частоты синусоидального возбуждения. Полные сопротивления в серии
Импедансы в параллельном
Доход
0019 Y = проводимость (1/Ом)
Среднеквадратичное значение или эффективное напряжение
Среднеквадратичное значение — это эффективное значение синусоидального напряжения или тока.
ОБР — среднее квадрат корня — или эффективное напряжение может быть выражено как
U ОБРАТА = U EFF
= U MAX / (2) 1/2
/ (2) 1/2 9002 9 № 9 = № 1/2 9 № 1/2 / (2). 0,707 U max (9)
0,707 U max (9) , где
U среднеквадратичные среды = U EFF
= среднеквадратичное напряжение (V)
U MAX 9002 = максимальный уровень.
среднеквадратичный средний средний квадрат — или эффективный ток может быть выражен как
I среднеквадратичных средств = I EFF
= I MAX / (2) 1/2 9 / (2) 1/2
= 0.707 I max (10)
where
I rms = I eff
= RMS current (A)
I max = максимальный ток (амплитуда) источника синусоидального напряжения (А)
Вольтметры и амперметры переменного тока показывают среднеквадратичное значение напряжения или тока, или 0,707-кратное максимальное пиковое значение. Максимальные пиковые значения в 1,41 раза превышают значения вольтметра.
Максимальные пиковые значения в 1,41 раза превышают значения вольтметра.
Пример
- для системы 230 В . U max = 169 В
Трехфазное напряжение переменного тока — фаза-фаза и фаза-нейтраль
В трехфазной системе переменного тока напряжение может подаваться между линиями и нейтралью (потенциал фазы), или между линиями (линейный потенциал). Результирующие напряжения для двух распространенных систем – европейской 400/230 В и североамериканской 208/120 В для одного периода указаны на рисунках ниже.
400V/230V AC
print 400/230V Three Phase Diagram
- L1, L2 and L3 are the three phases line to to neutral potentials — phase potentials
- L1 to L2, L1 to L3 и L2 до L3 — трехфазные межфазные потенциалы — линейные потенциалы
- L2, L2 и L3 — результирующий потенциал трех фаз в симметричной цепи — результирующий потенциал = 0
Модуль линейных потенциалов равен 3 1/2 (1,73) модуль фазового потенциала.
U RMS, строка = 1,73 U ОБЗА, Фаза (11)
208V/120 В AC
Печать 208/120 В Три фазового диаграммы
Power
Active -OR or True -True -True -True или True мощность, совершающая фактическую работу в цепи, можно рассчитать как
P = U ОБЗОР I ОБЗОР COS φ (12)
, где
P = активная реальная мощность (W)
φ = фазовый угол между током и напряжением (Rad, Degrees)
Cos φ также называется коэффициентом мощности.
Реактивная мощность в цепи может быть рассчитана как0022
Калькулятор коэффициента мощности
Создано Bogna Szyk
Отзыв от Adena Benn формула
Этот калькулятор коэффициента мощности удобен для анализа переменного тока (AC), протекающего в электрических цепях. Вы, наверное, уже знаете, что можно моделировать постоянный ток (DC) с помощью закона Ома. См. наш калькулятор закона Ома для получения дополнительной информации. В случае с переменным током эта задача не так проста, так как такие цепи содержат как активную, так и реактивную мощность, учитываемую в нашем трехфазном калькуляторе.
Вы, наверное, уже знаете, что можно моделировать постоянный ток (DC) с помощью закона Ома. См. наш калькулятор закона Ома для получения дополнительной информации. В случае с переменным током эта задача не так проста, так как такие цепи содержат как активную, так и реактивную мощность, учитываемую в нашем трехфазном калькуляторе.
Этот калькулятор поможет вам узнать значения различных типов мощности в цепи и предоставит вам формулу коэффициента мощности, которая выражает соотношение между реальной и полной мощностью.
Действительная, реактивная и полная мощность
Если вы хотите понять коэффициент мощности, вам в первую очередь необходимо более глубокое понимание его компонентов: активной, реактивной и полной мощности.
Активная мощность (также называемая истинной или активной мощностью), обозначается цифрой P , совершает реальную работу в электрической цепи и рассеивается в резисторах. Посетите наш калькулятор рассеиваемой мощности, чтобы узнать больше.
 Это единственная форма мощности, которая появляется в цепи постоянного тока. В цепи переменного тока нет фиксированных значений тока и напряжения — они изменяются синусоидально. Если между этими двумя значениями нет фазового сдвига , то вся передаваемая мощность активна. Измеряем мощность в ватт .
Это единственная форма мощности, которая появляется в цепи постоянного тока. В цепи переменного тока нет фиксированных значений тока и напряжения — они изменяются синусоидально. Если между этими двумя значениями нет фазового сдвига , то вся передаваемая мощность активна. Измеряем мощность в ватт .Реактивная мощность , обозначаемый как Q , передается, когда ток и напряжение сдвинуты по фазе на 90 градусов. В таком случае чистая энергия, передаваемая в цепи переменного тока, равна нулю, и мы не теряем реальной мощности. Реактивная мощность никогда не появляется в цепях постоянного тока. В цепях переменного тока это связано с реактивным сопротивлением катушек индуктивности и конденсаторов. Мы измеряем его в вольт-амперах-реактивных (вар).
Полная мощность , обозначаемая S , представляет собой комбинацию активной и реактивной мощностей.
 Это произведение среднеквадратичных значений напряжения и тока в цепи без учета влияния фазового угла. Это также векторная сумма P и Q. Мы измеряем полную мощность в Вольт-Ампер (ВА).
Это произведение среднеквадратичных значений напряжения и тока в цепи без учета влияния фазового угла. Это также векторная сумма P и Q. Мы измеряем полную мощность в Вольт-Ампер (ВА).
Вас интересуют другие мощные калькуляторы? Наш калькулятор среднеквадратичного напряжения может быть именно тем, что вы ищете.
Треугольник мощностей
Полную мощность находим векторным сложением активной и реактивной мощностей. Вы можете использовать графический метод, чтобы представить эти три значения в форме треугольника, называемого треугольником мощности .
Каждая сторона треугольника представляет одну из трех форм мощности, передаваемой в цепи переменного тока. Катеты прямоугольного треугольника представляют действительную и реактивную мощности, а гипотенуза — полную мощность.
Одним из следствий использования треугольника мощности является то, что вы можете легко установить математическое соотношение между тремя значениями с помощью теоремы Пифагора:
S² = P² + Q²
а полная мощность, обозначенная как φ , представляет собой импеданс цепи фазовый угол .
Формула коэффициента мощности
Коэффициент мощности — это отношение реальной и полной мощности в цепи. Если реактивной мощности нет, то коэффициент мощности равен 1. Если, наоборот, активная мощность равна нулю, то полная мощность также равна 0,9.0003
Формула коэффициента мощности:
коэффициент мощности = P/S
Например, коэффициент мощности 0,87 означает, что 87% тока, подаваемого в цепь, выполняет реальную работу. Остальную мощность, а именно 13%, приходится отдавать на компенсацию реактивной мощности. Знание того, как рассчитать коэффициент мощности, может быть полезным, например, при расчетах, касающихся генераторов, описанных в нашем Калькуляторе мощности генератора.
Как рассчитать коэффициент мощности?
Вы также можете рассчитать коэффициент мощности с помощью треугольника мощности. Используя принципы тригонометрии, вы можете записать это как
P / S = cos φ
Поскольку коэффициент мощности равен отношению между реальной и полной мощностью,
коэффициент мощности = cos φ
Это означает, что вы можете быстро рассчитать остальные значения, определяющие цепь переменного тока, зная только одно из трех значений — действительную, реактивную или полную мощность, а также либо коэффициент мощности, либо фазовый угол. Конечно, вы можете использовать этот калькулятор коэффициента мощности вместо того, чтобы вычислять числа вручную! 🙂
Конечно, вы можете использовать этот калькулятор коэффициента мощности вместо того, чтобы вычислять числа вручную! 🙂
Сопротивление, реактивное сопротивление и импеданс
Тремя основными компонентами цепи переменного тока являются резисторы, конденсаторы и катушки индуктивности. Вы можете использовать этот калькулятор коэффициента мощности не только для описания мощности, которая передается через каждый из этих компонентов, но и для установления того, что происходит, когда через них проходит электрический ток, а именно, каким сопротивлением, реактивным сопротивлением и импедансом обладают такие элементы.
Сопротивление , обозначается R , выраженный в омах (Ом), является мерой того, насколько проводник (в первую очередь резистор) уменьшает протекающий через него электрический ток I . Это значение напрямую связано с реальной мощностью, протекающей в цепи переменного тока. Мы можем записать это соотношение
P = I²R.
Реактивное сопротивление , обозначаемое как X и также измеряемое в омах (Ом), представляет собой инерцию, противодействующую движению электронов в компоненте цепи. Он в основном присутствует в конденсаторах и катушках индуктивности. Если вы пропускаете переменный ток через компонент с высоким реактивным сопротивлением, падение напряжения составит 90 градусов не совпадают по фазе с током. Реактивное сопротивление связано с реактивной мощностью уравнением
Q = I²X.Полное сопротивление , обозначаемое Z и измеряемое в омах (Ом), является эквивалентом переменного сопротивления в цепях постоянного тока. Он присутствует во всех компонентах всех электрических цепей. Его можно рассчитать векторным сложением сопротивления (см. ниже) и реактивного сопротивления или по формуле
S = I²Z.
Соотношение между сопротивлением, реактивным сопротивлением и импедансом аналогично треугольнику мощности:
Z² = R² + X²
Идеальные резисторы имеют ненулевое сопротивление, но нулевое реактивное сопротивление, в то время как идеальные катушки индуктивности или конденсаторы имеют нулевое сопротивление, но ненулевое реактивное сопротивление.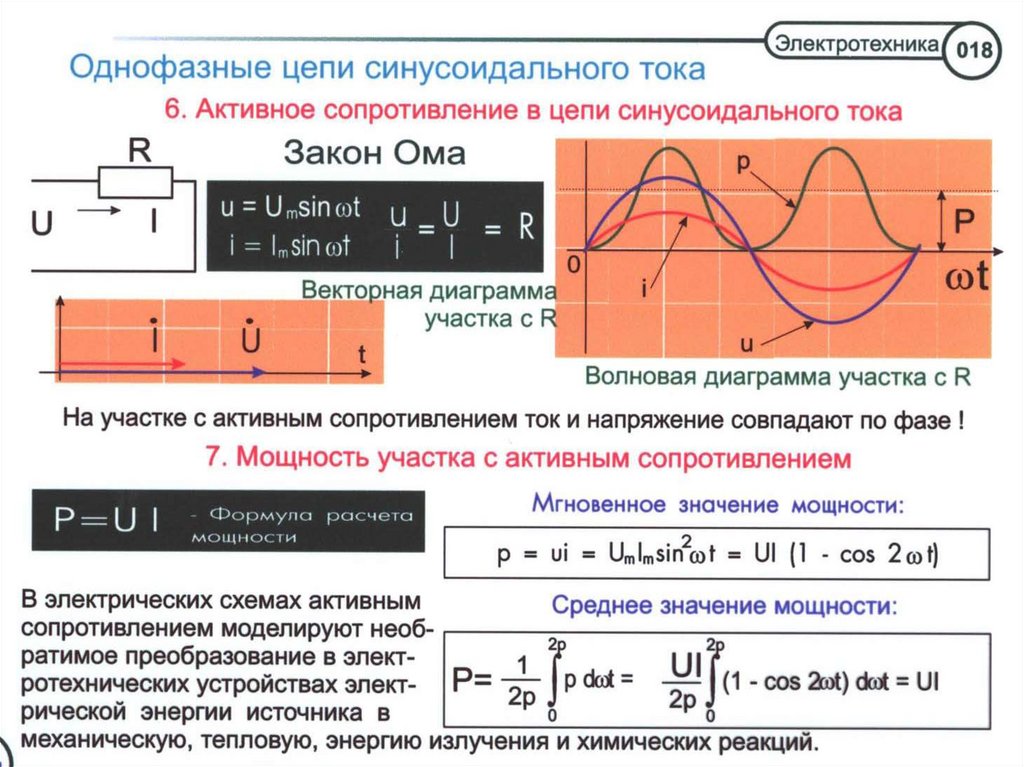 Все компоненты электрической цепи обладают некоторым полным сопротивлением.
Все компоненты электрической цепи обладают некоторым полным сопротивлением.
Часто задаваемые вопросы
Что такое коэффициент мощности в цепи переменного тока?
Коэффициент мощности переменного тока определяется как отношение активной мощности P к полной мощности S , поскольку это отношение равно cos ϕ. Как правило, вы можете выразить это как десятичное значение, например, 0,85, или как процент: 85%.
Что такое треугольник коэффициента мощности?
Треугольник мощности графически представляет три части, составляющие мощность цепи переменного тока:
- Полная мощность (ВА) измеряется в вольт-амперах.
- Реальная мощность (Вт) , которая выполняет работу, измеряемую в ваттах.
- Реактивная мощность (ВАр) измеряется в реактивных вольт-амперах.
ϕ угол между реальной и кажущейся мощностью в градусах. Чем больше фазовый угол, тем больше реактивная мощность.
Чем больше фазовый угол, тем больше реактивная мощность.
Что такое единица измерения коэффициента мощности?
Коэффициент мощности не имеет единиц измерения. Он безразмерный. Вы можете рассчитать коэффициент мощности как отношение активной мощности к полной мощности, поэтому он не имеет единиц измерения. Коэффициент мощности измеряет, сколько эффективной мощности используется.
Каково значение коэффициента мощности?
В цепях переменного тока коэффициент мощности может принимать значения от 0 до 1,0. Когда коэффициент мощности равен 1,0 (единица) или 100 %, фазовый угол между током и напряжением будет равен 0°, поскольку cos⁻¹(1.0) = 0° . Когда коэффициент мощности равен нулю (0), фазовый угол равен 90° по формуле cos⁻¹(0) = 90° . Чем выше коэффициент мощности, тем эффективнее будет система.
Что означает коэффициент мощности 0,75?
Коэффициент мощности 0,75 означает, что только 75% мощности, подаваемой на ваше устройство, используется эффективно, а 25% тратится впустую. Потери энергии равны реактивной мощности. Для запуска оборудования всегда требуется некоторая мощность, даже если оно не выполняет никакой реальной работы. По этой причине коэффициент мощности обычно равен 9.0009 менее 1,0 (100%).
Потери энергии равны реактивной мощности. Для запуска оборудования всегда требуется некоторая мощность, даже если оно не выполняет никакой реальной работы. По этой причине коэффициент мощности обычно равен 9.0009 менее 1,0 (100%).
Как рассчитать поправку на коэффициент мощности?
Если вам нужно скорректировать плохой коэффициент мощности цепи, следуйте этим инструкциям:
- Измерьте фактическую мощность P с помощью ваттметра.
- Рассчитайте полную мощность S путем умножения напряжения нагрузки В на ток нагрузки I
S = I × V. - Найдите коэффициент мощности по формуле
коэффициент мощности = P/S, - Найдите угол
cos⁻¹(коэффициент мощности)и нарисуйте треугольник степени. - Рассчитайте реактивной мощности Q по теореме Пифагора:
Q = √(S² - P²).

 1.
1.
 Это единственная форма мощности, которая появляется в цепи постоянного тока. В цепи переменного тока нет фиксированных значений тока и напряжения — они изменяются синусоидально. Если между этими двумя значениями нет фазового сдвига , то вся передаваемая мощность активна. Измеряем мощность в ватт .
Это единственная форма мощности, которая появляется в цепи постоянного тока. В цепи переменного тока нет фиксированных значений тока и напряжения — они изменяются синусоидально. Если между этими двумя значениями нет фазового сдвига , то вся передаваемая мощность активна. Измеряем мощность в ватт . Это произведение среднеквадратичных значений напряжения и тока в цепи без учета влияния фазового угла. Это также векторная сумма P и Q. Мы измеряем полную мощность в Вольт-Ампер (ВА).
Это произведение среднеквадратичных значений напряжения и тока в цепи без учета влияния фазового угла. Это также векторная сумма P и Q. Мы измеряем полную мощность в Вольт-Ампер (ВА).