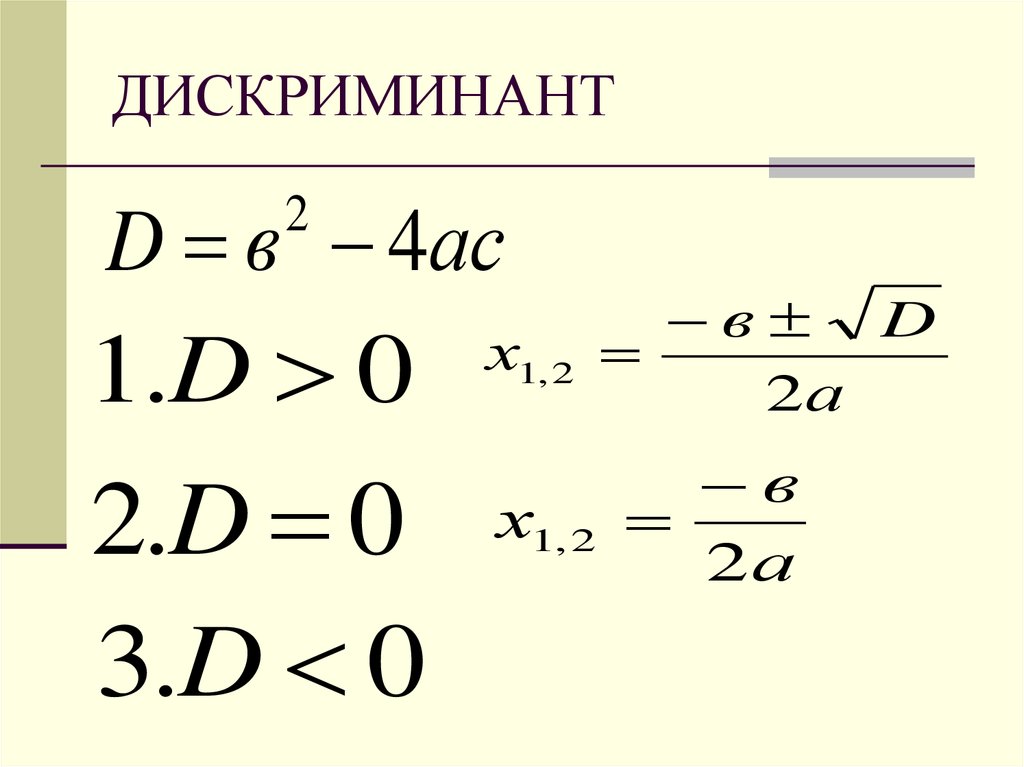Онлайн калькулятор: Дискриминант
УчебаМатематикаАлгебра
Вычисление дискриминанта квадратного многочлена и многочленов более высоких степеней.
В алгебре дискриминантом многочлена называется функция от многочлена, описывающая некоторые свойства корней, без их вычисления.1
Из школьного курса хорошо известна формула дискриминанта квадратного многочлена . Дискриминант равен . Формула используется для вычисления корней квадратного уравнения.
Однако зная дискриминант можно предсказать некоторые свойства корней, не вычисляя их. В случае квадратичного полинома дискриминант равен нулю тольк в том случае, если имеется один двойной корень. Если дискриминант положителен — то имеются два различных вещественных корня, а если отрицательный — то два комплексно сопряженных.
Следующий калькулятор вычисляет дискриминант квадратичного полинома, а ниже него можно почитать немного теории.
Дискриминант квадратного многочлена
Квадратный многочлен
Дискриминант
Корни многочлена
Дискриминант
Дискриминант многочлена степени n: может быть определен через результант или через корни.
Через корни полинома, дискриминант выражается следующим образом:
Через результант дискриминант можно выразить так:
где Res — результант многочлена A и его первой производной A’. Если коротко, то результант это определитель Матрицы Сильвестра составленной из A и A’.
В случае квадратного многочлена A производная A’ будет равна . Еси записать матрицу Сильвестра для этих двух многочленов и посчитать детерминант, то мы придем к уже известному:.
Дискриминант полиномов более высоких степеней
Используя второе определение, можно вывести формулы для дискриминанта полиномов более высоких степеней (если перейти по ссылке ниже можно получить формулы для полиномов степеней 3 и 4 и других).
Последовательность OEIS A007878 содержит 5 членов суммы для вычисления дискриминанта полинома 3-й степени, 16 членов для 4-й, 59 членов для 5-й, и наконец 3815311 членов для полиномов 12-й степени.
Следующий калькулятор вычисляет дискриминант многочлена любой степени:
Дискриминант
Коэффициенты многочлена
Введите коэффициенты многочлена, через пробел начиная от более высокой степени к меньшей
Точность вычисления
Округленно
Дискриминант
Входной многочлен
Производная
Википедия: Дискриминант ↩
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Решение неоднородной системы линейных алгебраических уравнений матричным методом
- • Метод Крамера с подробным решением
- • Умножение многочленов
- • Решение квадратного уравнения
- • Решение системы линейных алгебраических уравнений методом Гаусса
- • Раздел: Алгебра ( 46 калькуляторов )
Алгебра дискриминант линейная алгебра Математика Многочлены
PLANETCALC, Дискриминант
Timur2020-11-03 14:19:37
Калькулятор Дискриминантной Формулы — Mathcracker.
 Com
ComИнструкции: Используйте этот калькулятор для нахождения дискриминанта квадратного уравнения, показывая все шаги. Пожалуйста, введите правильное квадратное уравнение в поле формы ниже.
Дискриминантная формула
Этот калькулятор будет использовать формулу дискриминанта, показывая все шаги для квадратного уравнения, которое вы предоставите.
Вам нужно предоставить действительное квадратное уравнение, например, 2x²+x-1=0, которое уже упрощено, или вы можете предоставить что-то, что является действительным квадратичным выражением, но требует дальнейшего упрощения, например, 2x²+3x-1 = 3/4x — 4/5.
После ввода правильного квадратного уравнения достаточно нажать кнопку «Вычислить», и все шаги вычисления будут предоставлены вам.
Упрощенное квадратное уравнение в форме ax² + bx + c = 0 будет использоваться для вычисления дискриминанта, который сразу укажет на характер корней: Два вещественных корня, один вещественный корень или два комплексных корня.
Дискриминантная формула
Как найти дискриминант квадратного уравнения ? Как только вы получили квадратное уравнение в форме ax² + bx + c = 0, вы можете напрямую применить формулу дискриминанта:
\[\displaystyle \Delta = b^2 — 4ac\]
Дискриминантное значение
После того, как вы применили приведенную выше формулу и получили значение \(\Delta\) для дискриминанта, каково его значение?
- Шаг 1: Если \(\Delta > 0\): то квадратное уравнение имеет два различных действительных корня
- Шаг 2: Если \(\Delta = 0\): то квадратное уравнение имеет только один действительный корень
- Шаг 3: Если \(\Delta
Что означает
два сопряженных комплексных корня
? Графически это просто парабола, которая не пересекает ось x.
С другой стороны, два разных вещественных корня графически означают, что парабола пересекает ось x в двух точках. Дискриминант, равный нулю, означает, что парабола является касательной к оси x.
Зачем заботиться о дискриминанте?
Дискриминант предоставляет вам простую форму для оценки типов корней квадратного уравнения без фактического решения уравнения.
Естественно, мы видим, что дискриминант буквально появляется в
квадратичная формула
поэтому он явно связан с процессом вычисления
квадратичные корни
. 2 — 3x — 10 = 0\) имеет два различных действительных корня.
2 — 3x — 10 = 0\) имеет два различных действительных корня.
Больше квадратичных калькуляторов
Разбирательство с
квадратичные функции
и уравнений очень часто встречается в алгебре.
Вычисление корней квадратных уравнений
тесно связана с
вычисление дискриминанта
и
нахождение вершины
.
С геометрической точки зрения, дискриминант указывает на тип расположения параболы, которая представляет квадратичную функцию, и оси x.
2+4*х+3=0;х`), калькулятор возвращает результат -20.Вычисление дискриминанта полинома позволяет определить число корней квадратного уравнения:
- Когда вычисление дискриминанта дает отрицательное число, уравнение не имеет корня
- , когда дискриминант равен нулю, уравнение имеет корень, двойной корень
- , когда вычисление дискриминанта является положительным числом, уравнение имеет два различных корня. 92+x+1;x`), который возвращает -3.
Расчет онлайн с дискриминантом (расчет дискриминанта онлайн)
См. также
Список связанных калькуляторов:
- Степень многочлена : степень.
 Функция степени вычисляет в режиме онлайн степень многочлена.
Функция степени вычисляет в режиме онлайн степень многочлена. - Расчет дискриминанта онлайн: дискриминант. Калькулятор, который позволяет вычислить дискриминант квадратного уравнения онлайн.
- Калькулятор частного и остатка: евклидово_деление. Калькулятор позволяет найти в режиме онлайн частное и остаток при евклидовом делении двух многочленов или двух целых чисел.
- Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
- Калькулятор решения для x: уравнение_решателя. Решатель уравнений позволяет решать уравнения с неизвестным с шагами расчета: линейное уравнение, квадратное уравнение, логарифмическое уравнение, дифференциальное уравнение.
- Оценка многочлена: оценка. Функция оценки позволяет рассчитать оценку полинома онлайн.
Прочие ресурсы
- Упражнение по уравнениям
- Бесплатные математические игры с уравнениями
- Научитесь решать уравнения
Поиск корней квадратного уравнения с использованием дискриминанта
Все ресурсы предварительного исчисления
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
Precalculus Помощь » Графические функции » Решение квадратных уравнений » Найдите корни квадратного уравнения, используя дискриминант
Верно или неверно: для квадратичной функции вида ax 2 + bx + c = 0, если дискриминант b
2 — 4ac = 0, существует ровно один действительный корень.
Возможные ответы:
Верно
Неверно
Правильный ответ:
Верно
Объяснение:
Это правда. Дискриминант b 2 — 4ac — это часть квадратичной формулы, которая находится внутри функции квадратного корня. Когда вы подставляете константы a, b и c в b 2 — 4ac и оценить, могут произойти три случая:
b 2 — 4ac > 0
b 2 — 4ac = 0
b 2 901 00 — 4ac < 0
В первом случае наличие положительного числа под функцией квадратного корня даст результат, который является ответом положительного числа. Однако, поскольку квадратичная функция включает , этот сценарий дает два реальных результата.
В среднем случае (в нашем примере) . Возвращаясь к квадратной формуле , вы можете видеть, что когда все, что находится под квадратным корнем, равно просто 0, вы получаете только , поэтому у вас ровно один действительный корень.

В последнем случае, если b 2 — 4ac < 0, это означает, что перед квадратным корнем находится отрицательное число. Это означает, что у вас не будет реальных корней уравнения; однако у вас будет ровно два мнимых корня уравнения.
Сообщить об ошибке
Верно или неверно: для квадратичной функции вида ax 2 + bx + c = 0, если дискриминант b 2 — 4ac > 0, существует ровно 2 различных действительных корня уравнения .
Неверно
Верно
Правильный ответ:
Верно
Объяснение:
Это правда. Дискриминант b 2 — 4ac — это часть квадратичной формулы, которая находится внутри функции квадратного корня. Когда вы подставляете константы a, b и c в b 2 — 4ac и оцениваете, могут произойти три случая:
b 2 — 4ac > 0
b 2 — 4ac = 0
b 2 — 4ac < 0
В первом случае (случай нашего примера) наличие положительного числа под функцией квадратного корня даст результат, который является положительным числовым ответом.
 Однако, поскольку квадратичная функция включает , этот сценарий дает два реальных результата.
Однако, поскольку квадратичная функция включает , этот сценарий дает два реальных результата.В среднем корпусе . Возвращаясь к квадратной формуле , вы можете видеть, что когда все, что находится под квадратным корнем, равно просто 0, вы получаете только , поэтому у вас ровно один действительный корень.
В последнем случае, если b 2 — 4ac < 0, это означает, что перед квадратным корнем находится отрицательное число. Это означает, что у вас не будет реальных корней уравнения; однако у вас будет ровно два мнимых корня уравнения.
Сообщить об ошибке
Верно или неверно: для квадратичной функции вида ax 2 + bx + c = 0, если дискриминант b 2 — 4ac < 0, существует ровно два различных действительных корня.
Возможные ответы:
Верно
Ложно
Правильный ответ:
Ложно
Объяснение:
Это неверно.

b 2 — 4ac > 0
b 2 — 4ac = 0
90 002 б 2 — 4ac < 0В первом случае наличие положительного числа под функцией извлечения квадратного корня приведет к положительному числовому ответу. Однако, поскольку квадратичная функция включает , этот сценарий дает два реальных результата.
В среднем корпусе . Возвращаясь к квадратной формуле , вы можете видеть, что когда все, что находится под квадратным корнем, равно просто 0, вы получаете только , поэтому у вас ровно один действительный корень.
Для последнего случая (случай нашего примера), если b 2 — 4ac < 0, это означает, что у вас есть отрицательное число под квадратным корнем. Это означает, что у вас не будет реальных корней уравнения; однако у вас будет ровно два мнимых корня уравнения.

Сообщить об ошибке
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: реальный или воображаемый. Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Возможные ответы:
Дискриминант: 0
Один действительный корень:
Дискриминант: 441
Два действительных корня: или
Дискриминант: 281
Два мнимых корня:
Дискриминант: 281
Два мнимых корня корни:
Дискриминант: 441
Два действительных корня: или
Правильный ответ:
Дискриминант: 441
Два действительных корня: или
900 10 Объяснение:В приведенном выше уравнении a = 4, b = 19 и c = -5. Следовательно:
b 2 — 4ac = (19) 2 — 4(4)(-5) = 361 + 80 = 441.
Когда дискриминант больше 0, существует два различных действительных корня.
 Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два действительных корня.
Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два действительных корня.Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная функция:
Подставляя наши значения a, b и c, мы получаем:
Это упрощает до:
, что упрощает до
900 02, который дает нам два ответа:или
Эти значения x — два различных действительных корня данного уравнения.
Сообщить об ошибке
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: 4x 2 + 12x + 10 = 0,
Затем укажите, сколько у него корней, действительные они или мнимые. Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Возможные ответы:
Дискриминант: 304
Типы корней: Два различных действительных корня
Точные корни:
Дискриминант: -16
9000 2 типа корней: нет настоящих корней; 2 различных мнимых корняТочные корни:
Дискриминант: -16
Типы корней: действительных корней нет; 2 различных мнимых корня
Точные корни:
Дискриминант: 16
Типы корней: Два различных действительных корня
Точные корни: -1, -2
Дискриминант: 304 Корни: Два различных действительных корня
Точные корни:
Правильный ответ:
Дискриминант: -16
Типы корней: Нет действительных корней; 2 различных мнимых корня
Точные корни:
Объяснение:
В приведенном выше уравнении a = 4, b = 12 и c = 10.
 Следовательно:
Следовательно:б 2 — 4ас = (12) 2 — 4(4)(10) = 144 — 160 = -16.
Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два различных мнимых корня.
Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная функция:
Подставляя наши значения a, b и c, мы получаем:
Это упрощает до:
Другими словами, два разных воображаемых корня: и
Сообщите об Ошибка
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: -3x 2 + 6x — 3 = 0.
Затем укажите, сколько корней оно имеет и являются ли они действительными или мнимыми. . Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.

Возможные ответы:
Дискриминант: 0
Один действительный корень: x = -1
Дискриминант: 72
Два различных действительных корня:
Дискриминант : 0
Один действительный корень: x = 1
Дискриминант: -72
Два различных мнимых корня:
Дискриминант: 72
Два различных действительных корня:
Правильный ответ:
Дискриминант: 0
90 002 Один действительный корень: x = 1Объяснение:
В приведенном выше уравнении a = -3, b = 6 и c = -3. Следовательно:
b 2 — 4ac = (6) 2 — 4(-3)(-3) = 36 — 36 = 0.
Когда дискриминант больше 0, существуют два различных действительных корня. . Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня.
 В этом случае существует ровно один действительный корень.
В этом случае существует ровно один действительный корень.Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная формула:
Подставляя наши значения a, b и c, мы получаем:
Это упрощает до:
, что упрощает до
900 02, что дает нам один ответ: x = 1Это значение x — это единственный действительный корень данного уравнения.
Сообщить об ошибке
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: x 2 + 5x + 4 = 0.
Затем укажите, сколько корней оно имеет и являются ли они реальный или воображаемый. Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Возможные ответы:
Дискриминант: 41
Два мнимых корня:
Дискриминант: 9
Два действительных корня: x = 1 или x = 4
Дискриминант: 9
Два действительных корня: x = — 1 или x = -4
Дискриминант: 0
Один действительный корень:
Дискриминант: 41
Два мнимых корня:
Правильный ответ:
Диск riminant: 9
Два действительных корня: x = -1 или х = -4
Объяснение:
В приведенном выше уравнении a = 1, b = 5 и c = 4.
 Следовательно:
Следовательно:b 2 — 4ac = (5) 2 — 4(1)(4) = 25 — 16 = 9.
Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два действительных корня.
Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная функция:
Подставляя наши значения a, b и c, мы получаем:
Это упрощает до:
, что упрощает до
90 005
, что дает нам два ответа:
x = -1 или x = -4
Эти значения x являются двумя различными действительными корнями данного уравнения.
Сообщить об ошибке
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: -x 2 + 3x — 3 = 0.
Затем укажите, сколько у него корней и являются ли они действительными или мнимыми.
 Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.Возможные ответы:
Дискриминант: -8
Два мнимых корня:
Дискриминант: -21
Два мнимых корня:
Дискриминант: -21
Два мнимых корня:
Дискриминант: -8
Два мнимых корня: .
Дискриминант: 0
Один действительный корень:
Правильный ответ:
Дискриминант: -8
Два мнимых корня: .
Объяснение:
В приведенном выше уравнении a = -1, b = 3 и c = -3. Следовательно:
b 2 — 4ac = (3) 2 — 4(-1)(-3) = 9 — 12 = -3.
Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня.
 В этом случае у нас есть два различных мнимых корня.
В этом случае у нас есть два различных мнимых корня.Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная функция:
Подставив наши значения a, b и c, мы получим:
Это упрощает до:
Потому что это упрощает до . Другими словами, наши два различных мнимых корня равны и
Сообщить об ошибке
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: x 2 + 2x + 10 = 0,
Затем укажите, сколько у него корней и являются ли они реальными или мнимыми. Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Возможные ответы:
Дискриминант: 36
Два действительных корня: x = -5 или x = 7
Дискриминант: 36
Два действительных корня: x = 5 или x = -7 9 0005
Дискриминант: 0
Один действительный корень: x = -1
Дискриминант: -36
Два мнимых корня:
Дискриминант: -36
Два мнимых корня:
Правильный ответ:
Дискриминант: -36
Два мнимых корня:
Объяснение:
В приведенном выше уравнении a = 1, b = 2 и c = 10.
 Следовательно:
Следовательно:b 2 — 4ac = (2) 2 — 4(1)(10) = 4 — 40 = -36.
Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два различных мнимых корня.
Наконец, мы используем квадратичную функцию, чтобы найти эти точные корни. Квадратичная функция:
Подставляя наши значения a, b и c, мы получаем:
Это упрощает до:
Потому что , это упрощает до . Мы можем упростить это до . Другими словами, наши два различных воображаемых корня — это и .
Сообщить об ошибке
Используйте формулу b 2 — 4ac, чтобы найти дискриминант следующего уравнения: x 2 + 8x + 16 = 0.
Затем укажите, сколько у него корней и являются ли они действительными или мнимыми.
 Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.Возможные ответы:
Дискриминант: 72
Два различных действительных корня:
Дискриминант: 0
Один действительный корень: x = 4
Дискриминант ant: 0
Один действительный корень: x = -4
Дискриминант: 128
Два различных действительных корня:
Дискриминант: 0
Один действительный корень: x = 0
Правильный ответ:
Дискриминант: 0
Один действительный корень: x = -4
Объяснение:
В приведенном выше уравнении a = 1, b = 8 и c = 16. Следовательно:
b 2 — 4ac = (8) 2 — 4(1)(16) = 64 — 64 = 0.
Когда дискриминант больше 0, существуют два различных действительных корня. Когда дискриминант равен 0, существует ровно один действительный корень.

- Степень многочлена : степень.

 Функция степени вычисляет в режиме онлайн степень многочлена.
Функция степени вычисляет в режиме онлайн степень многочлена.

 Однако, поскольку квадратичная функция включает , этот сценарий дает два реальных результата.
Однако, поскольку квадратичная функция включает , этот сценарий дает два реальных результата.

 Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два действительных корня.
Когда дискриминант равен 0, существует ровно один действительный корень. Когда дискриминант меньше нуля, действительных корней нет, но есть ровно два различных мнимых корня. В этом случае у нас есть два действительных корня. Следовательно:
Следовательно:
 В этом случае существует ровно один действительный корень.
В этом случае существует ровно один действительный корень. Следовательно:
Следовательно: Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения. В этом случае у нас есть два различных мнимых корня.
В этом случае у нас есть два различных мнимых корня.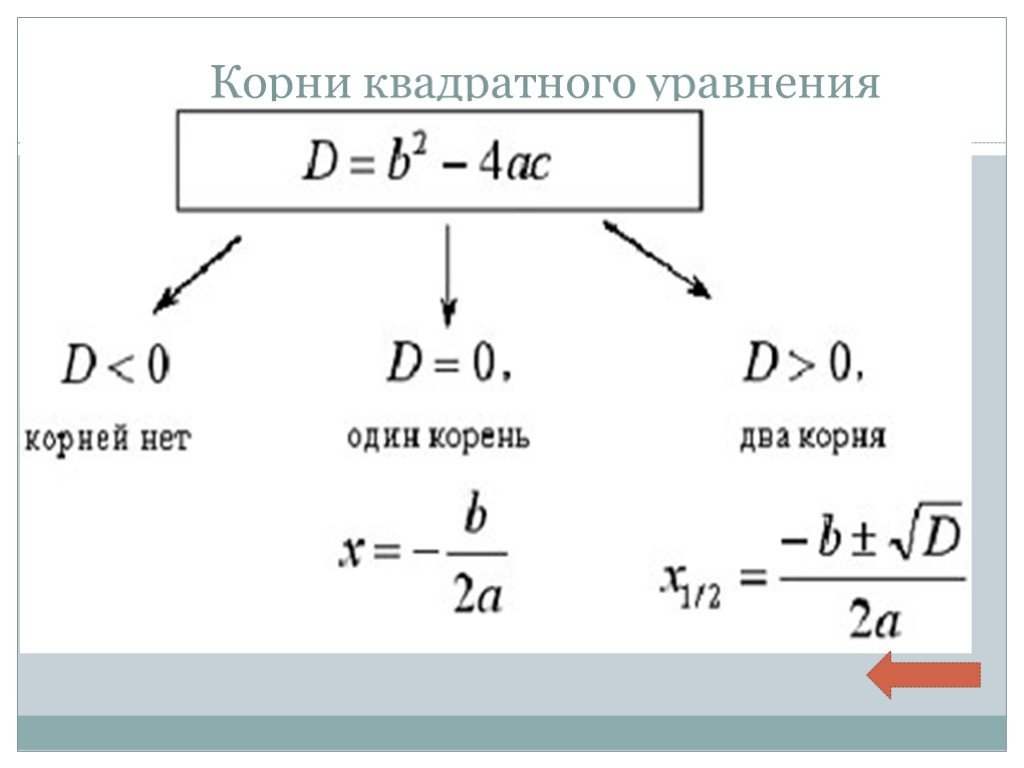 Следовательно:
Следовательно: Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.
Наконец, используйте квадратичную функцию, чтобы найти точные корни уравнения.